专题4.2 平面直角坐标系同步测试(浙教版)(原卷版)
八年级数学上册4.2平面直角坐标系同步练习(新版)浙教版【含解析】
第 1 页（共 9 页）
A. ������(5, 30∘ ) C. ������(4, 240∘ )
B. ������(2, 90∘ ) D. ������(3, 60∘ )
9. 如图，是雷达探测器测得的结果，图中显示在点 ������，������ ，������ ，������ ，������ ，������ 处有目标出现，目标的表 示方法为 (������, ������)，其中，������ 表示目标与探测器的距离；������ 表示以正东为始边，逆时针旋转后的角 度．例如，点 ������，������ 的位置表示为 ������(5, 30∘ )，������(4, 240∘ )．用这种方法表示点 ������ ，������ ，������ ，������ 的位 置，其中正确的是 ( )
A. (1,0)
B. (2,0)
C. (1, −2)
D. (1, −1) ) D. 6，8，9 )
5. 已知点 ������(0,0)，������(0,4)，������(3, ������ + 4)，������(3, ������)．记 ������(������) 为 ������������������������ 内部（不含边界）整点的个数， 其中整点是指横坐标和纵坐标都是整数的点，则 ������(������) 所有可能的值为 ( A. 6，7 B. 7，8 C. 6，7，8
15. 在体育课上，七年级（5）班 49 名同学在操场上练习队列，他们站成 7 × 7 方队，每横队 7 人， 每纵队 7 人，小敏是第 2 纵队的排头，位置记作 (1,2)，小娟是第 5 纵队的队尾，则小娟的位置 应记作 的视角 ∠������������������ = ． 度． 16. 如图，������ 岛在 ������ 岛的北偏东 50∘ 方向，������ 岛在 ������ 岛的北偏西 40∘ 方向，同从 ������ 岛看 ������，������ 两岛
初中数学浙教版八年级上册第四章《平面直角坐标系》练习题普通用卷
初中数学浙教版八年级上册第四章4.2平面直角坐标系练习题一、选择题1.在平面直角坐标系的第二象限内有一点P，点P到x轴的距离为2，到y轴的距离为3，则点P的坐标是()A. (−3,2)B. (3,−2)C. (2,−3)D. (−2,3)2.在平面直角坐标系中，若点P(m+3,m−1)在x轴上，则m的值是()A. −3B. 1C. 3D. −13.已知点A在第二象限，到x轴的距离是5，到y轴的距离是6，点A的坐标为()A. (−5,6)B. (−6,5)C. (5,−6)D. (6,−5)4.已知点P(3−m,m−1)在第四象限，则m的取值范围在数轴上表示正确的是()A. B.C. D.5.若点p(a,b)在第二象限，则点Q(−a,b)所在象限是()A. 第一象限B. 第二象限C. 第三象限D. 第四象限6.如图小手盖住的点的坐标可能是()A. (−3,−4)B. (2,−3)C. (−6,3)D. (−4,−6)7.若A(2x−4,6−2x)在第二象限，则x的取值范围是()A. x<2B. 2<x<3C. x>3D. x<38.若点P(x,y)满足xy<0，x<0，则P点在()A. 第二象限B. 第三象限C. 第四象限D. 第二、四象限9.在平面直角坐标系中，一个智能机器人接到如下指令：从原点O出发，按向右，向上，向右，向下的方向依次不断移动，每次移动1m.其行走路线如图所示，第1次移动到A1，第2次移动到A2，…，第n次移动到A n.则△OA6A2020的面积是()A. 505m2B. 504.5m2C. 505.5m2D. 1010m210.坐标平面上有一点A，且A点到x轴的距离为3，A点到y轴的距离恰为到x轴距离的3倍.若A点在第二象限，则A点的坐标为()．A. (−3,1)B. (−9,3)C. (−3,9)D. (−1,3)二、填空题11.一只跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到(0,1)，然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→⋯]，且每秒跳动一个单位，那么第36秒时跳蚤所在位置的坐标是______．12.若点P(2−a,2a+3)到两坐标轴的距离相等．则点P的坐标是______．13.在平面直角坐标系中，点M(a−3,a+4)，点N(5,9)，若MN//y轴，则a=．14.已知点P的坐标(2−a,3a+6)，且点P到两坐标轴的距离相等，则点P的坐标是______．三、解答题15.如图，在平面直角坐标系中，点A、B分别在x轴、y轴的正半轴上，且满足√OB−3+|OA−1|=0．(1)求点A、B的坐标；(2)若OC=√3，求点O到直线CB的距离；(3)在(2)的条件下，若点P从C点出发以一个单位每秒的速度沿直线CB从点C到B的方向运动，连接AP.设△ABP的面积为S，点P的运动时间为t秒，求S与t的函数关系式．16.已知平面直角坐标系中有一点M(2m−3,m+1)．(1)若点M到y轴的距离为2时，求点M的坐标；(2)点N(5,−1)且MN//x轴时，求点M的坐标．17.在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位．其行走路线如图．(1)填写下列各点的坐标：A4(______ ，______ )，A8(______ ，______ )，A12(______ ，______ )；(2)写出点A4n的坐标(n是正整数)；(3)写出点A100和A101的坐标，并指出蚂蚁从点A100到点A101的移动方向．18.如图，△ABC在直角坐标系内的位置如图，且C点坐标是(−2,1)(1)则点A的坐标________和点B的坐标________ ；(2)请在这个坐标系内画出△A1B1C1，使△A1B1C1与△ABC关于y轴对称；(3)请直接写出△A1B1C1的面积．答案和解析1.【答案】A【解析】解：由题意，得|y|=2，|x|=3．又∵在第二象限内有一点P，∴x=−3，y=2，∴点P的坐标为(−3,2)，故选：A．根据各象限内点的坐标特征，可得答案．本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限(+,+)；第二象限(−,+)；第三象限(−,−)；第四象限(+,−)．2.【答案】B【解析】解：∵点P(m+3,m−1)在x轴上，∴m−1=0，解得m=1．故选：B．根据x轴上点的纵坐标为0列方程求解即可．本题考查了点的坐标，熟记x轴上点的纵坐标为0是解题的关键．3.【答案】B【解析】解：A位于第二象限，到x轴的距离为5，到y轴的距离为6，则点A的坐标为(−6,5)，故选：B．根据第二象限内点到x轴的距离是点的纵坐标，点到y轴的距离是横坐标的相反数，可得答案．本题考查了点的坐标，第二象限内点到x轴的距离是点的纵坐标，点到y轴的距离是横坐标的相反数．4.【答案】B【解析】解：由点P(3−m,m−1)在第四象限，得{3−m>0m−1<0，解得m<1和m<3．故选：B．根据第四象限内点的横坐标大于零，纵坐标小于零，可得不等式组，根据解不等式组，可得答案．本题考查了点的坐标，利用第四象限内的点的横坐标大于零，纵坐标小于零得出不等式组是解题关键．5.【答案】A【解析】解：∵点p(a,b)在第二象限，∴a<0，b>0，∴−a>0，∴点Q(−a,b)在第一象限．故选：A．根据第二象限内点的坐标特征确定出a、b的正负情况，然后判断出点Q的坐标所在的象限即可．本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限(+,+)；第二象限(−,+)；第三象限(−,−)；第四象限(+,−)．6.【答案】B【解析】解：A、点(−3,−4)在第三象限，不在所示区域；B、点(2,−3)在第四象限，在所示区域；C、点(−6,3)在第二象限，不在所示区域；D、点(−4,−6)在第三象限，不在所示区域；故选：B．找到横坐标为正，纵坐标为负的点的选项即可．本题考查点的坐标的相关知识；用到的知识点为：第四象限的点的横坐标为正，纵坐标为负．7.【答案】A【解析】解：∵A(2x−4,6−2x)在第二象限，∴{2x−4<06−2x>0，解得：x<2，故选：A．由第二象限内点的横坐标为负数、纵坐标为正数列出不等式组，解之可得．本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．8.【答案】A【解析】【分析】本题考查了平面直角坐标系中点的坐标，根据实数的性质得到y>0，然后根据第二象限内点的坐标特征进行判断．【解答】解：∵xy<0，x<0，∴y>0，∴点P在第二象限．故选：A．9.【答案】A【解析】【分析】本题主要考查点的坐标的变化规律，三角形的面积的有关知识，根据图象可得移动4次图象完成一个循环，从而可得出OA6，OA2020，再利用三角形的面积公式计算可得．【解答】解：由题意知OA4n=2n，∴OA4=2m，∵2020÷4=505，∴OA2020=505×2=1010m，∴点A6到OA2020的距离为1m，×1×1010=505m2．则△OA6A2020的面积是12故选A．10.【答案】B【解析】【解答】本题考查了点的坐标，主要利用了点到x轴的距离等于纵坐标的长度，点到y轴的距离等于横坐标的长度，需熟练掌握并灵活运用，根据点到x轴的距离等于纵坐标的长度求出点A的纵坐标，再根据点到y轴的距离等于横坐标的长度求出横坐标，即可得解．【解答】解：∵A点到x轴的距离为3，A点在第二象限，∴点A的纵坐标为3，∵A点到y轴的距离恰为到x轴距离的3倍，A点在第二象限，∴点A的横坐标为−9，∴点A的坐标为(−9,3)．故选B．11.【答案】(6,0)【解析】解：跳蚤运动的速度是每秒运动一个单位长度，(0,0)→(0,1)→(1,1)→(1,0)用的秒数分别是1秒，2秒，3秒，到(2,0)用4秒，到(2,2)用6秒，到(0,2)用8秒，到(0,3)用9秒，到(3,3)用12秒，到(4,0)用16秒，…，可知当点离开x轴时的横坐标为时间的平方，当点离开y轴时的纵坐标为时间的平方，依此类推，到(6,0)用36秒．则第36秒时跳蚤所在位置的坐标是(6,0)．故答案为：(6,0)．根据题目中所给的质点运动的特点，从中找出规律，即可得出答案．本题主要考查点的坐标问题，解决本题的关键是读懂题意，能够正确确定点运动的规律，从而可以得到到达每个点所用的时间．12.【答案】(7,−7)或(73,7 3 )【解析】解：由P(2−a,2a+3)到两坐标轴的距离相等，得：2−a=2a+3或2−a=−2a−3，解得a=−5或a=−13，当a=−5时，2−a=7，即点的坐标为(7,−7)，当a=−13时，2−a=73，即点的坐标为(73,73)；故答案为：(7,−7)或(73,7 3 ).根据点到两坐标轴的距离相等，可得关于a的方程，根据解方程，可得答案．本题考查了点的坐标，利用点到两坐标轴的距离相等得出关于a的方程是解题关键．13.【答案】8【解析】【分析】本题主要平行于坐标轴的点的坐标特征，掌握直线平行于x轴时点的纵坐标相等，直线平行于y轴时点的横坐标相等是解题的关键．由MN//y轴知a−3=5，可得a的值．【解答】解：∵MN//y轴，∴a−3=5，解得a=8，故答案为8．14.【答案】(3,3)或(6,−6)【解析】【分析】因为这个点到两坐标轴的距离相等，即到坐标轴形成的角的两边距离相等，所以这个点一定在各象限的角平分线上．点P到两坐标轴的距离相等就是横纵坐标相等或互为相反数，就可以得到方程求出a的值，从而求出点的坐标．解：∵点P到两坐标轴的距离相等就是横纵坐标相等或互为相反数，∴分以下两种情考虑：①横纵坐标相等时，即当2−a=3a+6时，解得a=−1，∴点P的坐标是(3,3)；②横纵坐标互为相反数时，即当(2−a)+(3a+6)=0时，解得a=−4，∴点P的坐标是(6,−6)．故答案为或(3,3)或(6,−6)．15.【答案】解：(1)∵√OB−3+|OA−1|=0，∴OB−3=0，OA−1=0，∴OB=3，OA=1，∴A点的坐标为(1,0)，B点坐标为(0,3)；(2)在Rt△BOC中，BC=√(√3)2+32=2√3，设点O到直线CB的距离为x，1 2×2√3x=12×3√3，解得x=1.5，故点O到直线CB的距离为1.5；(3)设点O到直线CB的距离为y，1 2×2√3y=12×3×(√3+1)，解得y=3+√32，当0≤t<2√3时，BP=2√3−t，∴S=12(2√3−t)×3+√32=−3+√34t+3+√32；当t>2√3时，BP=t−2√3，∴S=12(t−2√3)×3+√32=3+√34t−3+√32．【解析】本题主要考查点的坐标的确定，点到直线的距离，三角形的面积，算术平方根的非负性，绝对值的非负性，注意分类讨论．(1)根据算术平方根的非负性，绝对值的非负性可求解OA，OB的值，进而求解A，B 的坐标；(2)利用勾股定理易求BC的长，设点O到直线CB的距离为x，根据△BOC的面积可求(3)设点O到直线CB的距离为y，易求y值，再分两种当0≤t<2√3时；当t>2√3时，利用三角形的面积公式可求解S与t的函数关系式．16.【答案】解：(1)∵点M(2m−3,m+1)，点M到y轴的距离为2，∴|2m−3|=2，解得m=2.5或m=0.5，当m=2.5时，点M的坐标为(2,3.5)，当m=0.5时，点M的坐标为(−2,1.5)；综上所述，点M的坐标为(2,3.5)或(−2,1.5)；(2)∵点M(2m−3,m+1)，点N(5,−1)且MN//x轴，∴m+1=−1，解得m=−2，故点M的坐标为(−7,−1)．【解析】本题考查点的坐标，解题的关键是明确题意，求出m的值．(1)根据“点M到y轴的距离为l”得|2m−3|=2，求出m的值，再分别求解可得；(2)由MN//x轴得m+1=−1，求得m的值即可．17.【答案】(1)2；0；4；0；6；0(2)(2n,0)(3)A100(50,0)，A101(50,1)，从点A100到点A101的移动方向与从点O到A1的方向一致，为从下向上【解析】解：(1)由图可知，A4，A8，A12都在x轴上，∵蚂蚁每次移动1个单位，∴OA4=2，OA8=4，OA12=6，∴A4(2,0)，A8(4,0)，A12(6,0)；故答案为：2，0；4，0；6，0；(2)根据(1)OA4n=4n÷2=2n，∴点A4n的坐标(2n,0)；(3)∵100÷4=25，∴100是4的倍数，∴A(50,0)，∵101÷4=25…1，∴A101与A100横坐标相同，∴A101(50,1)，∴从点A100到点A101的移动方向与从点O到A1的方向一致，为从下向上．(1)观察图形可知，A4，A8，A12都在x轴上，求出OA4、OA8、OA12的长度，然后写出坐标即可；(2)根据(1)中规律写出点A4n的坐标即可；(3)根据100是4的倍数，可知从点A100到点A101的移动方向与从点O到A1的方向一致．此题主要考查了点的变化规律，比较简单，仔细观察图形，确定出A4n都在x轴上是解题的关键．18.【答案】解：(1)(0,3)，(−4,4)；(2)如图所示：△A1B1C1就是所要求画的三角形；(3)S△A1B1C1=4×3−12×2×3−12×2×2−12×1×4=5．【解析】【分析】本题主要考查平面直角坐标系中点的坐标，轴对称变换以及三角形的面积，正确得出对应点位置是解题关键．(1)根据点A，点B在直角坐标系内的位置，即可得出A、B的坐标；(2)直接利用关于y轴对称点的性质得出对应点位置即可；(3)利用△A1B1C1 的面积=长方形面积减去三个直角三角形面积求解即可．【解答】解：(1)由图可得，A(0,3)，B(−4,4)，故答案为(0,3)，(−4,4)；(2)见答案；(3)见答案．。
专题4.2平面直角坐标系-2021-2022学年八年级数学上册尖子生同步培优题典(原卷版)【浙教版】
2021-2022学年八年级数学上册尖子生同步培优题典【浙教版】专题4.2平面直角坐标系姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分100分，试题共24题，选择10道、填空6道、解答8道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2021春•潼南区期末）在平面直角坐标系中，已知点P（﹣2，3），则点P在（）A．第一象限B．第二象限C．第三象限D．第四象限2．（2021春•陵城区期末）点M在第二象限，距离x轴5个单位长度，距离y轴3个单位长度，则M点的坐标为（）A．（5，﹣3）B．（﹣5，3）C．（3，﹣5）D．（﹣3，5）3．（2021•海曙区模拟）在平面直角坐标系中，点P（m，2m﹣2），则点P不可能在（）A．第一象限B．第二象限C．第三象限D．第四象限4．（2019秋•下城区期末）在平面直角坐标系中，位于第二象限的点（）A．横坐标小于纵坐标B．横坐标大于纵坐标C．横坐标和纵坐标的和小于0D．横坐标与纵坐标的积大于05．（2020•思明区校级模拟）已知直线L的解析式为x＝3，直线M的解析式为y＝﹣2，直线L、直线M画在坐标平面上的图形大致是（）A．B．C．D．6．（2020春•海淀区校级期末）已知直线AB∥x轴，A点的坐标为（1，2），并且线段AB＝3，则点B的坐标为（）A．（﹣2，2）B．（4，2）C．（1，5）或（1，﹣1）D．（﹣2，2）或（4，2）7．（2020秋•建平县期末）若xy＞0，则关于点P（x，y）的说法正确的是（）A．在一或二象限B．在一或四象限C．在二或四象限D．在一或三象限8．（2021春•聊城期末）如图，在平面直角坐标系中，放置半径为1的圆，圆心到两坐标轴的距离都等于半径，若该圆向x轴正方向滚动2017圈（滚动时在x轴上不滑动），此时该圆圆心的坐标为（）A．（2018，1）B．（4034π+1，1）C．（2017，1）D．（4034π，1）9．（2021春•孝义市期末）如图是某市部分平面示意图，为准确表示地理位置，可以建立平面直角坐标系用坐标表示地理位置，若汽车站的坐标是（3，4），图书馆的坐标是（﹣2，6），则火车站的坐标为（）A．（﹣3，3）B．（﹣3，﹣3）C．（﹣5，3）D．（﹣5，﹣3）10．（2021春•延长县期末）如图是利用平面直角坐标系画出的天安门附近的部分建筑分布图，若这个坐标系分别以正东、正北方向为x轴、y轴的正方向，表示弘义阁的点的坐标为（﹣1，﹣1），表示本仁殿的点的坐标为（2，﹣2），则表示乾清门的点的坐标是（）A．（﹣1，2）B．（2，﹣1）C．（2，0）D．（0，2）二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上11．（2021•紫金县模拟）已知点P（2m+4，m﹣1）在第一象限，到x轴的距离为2，则m＝．12．（2021春•椒江区期末）在平面直角坐标系中，点A（5，3），B（a，3），若0＜AB≤6，则a的取值范围为．13．（2021春•仙居县期末）在平面直角坐标系中，若点A（m﹣2，m+3）在第三象限，则m的取值范围是．14．（2021•惠阳区二模）已知平面直角坐标系中的点P（a﹣3，2）在第二象限，则a的取值范围是．15．（2021春•夏津县期末）已知点P的坐标（2﹣a，3a+6），且点P到两坐标轴的距离相等，则点P的坐标是．16．（2021•青田县模拟）如图，动点P从（0，3）出发沿所示方向运动，每当碰到长方形的边时反弹，反弹时反射角等于入射角，当点P第2021次碰到长方形的边时点P的坐标为．17．（2021春•大同期末）大同市御东五大场馆，各美其美，形成一道壮观的城市天际风景线，展现了古都大同恢弘现代气派．如图，利用平面直角坐标系画出各个场馆的示意图，其中文瀛湖的坐标是（2，﹣1），美术馆的坐标是（﹣2，1），则大剧院的坐标是．18．（2020•北仑区模拟）一只电子跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到（0，1），然后按图中箭头所示方向跳动，且每秒跳动一个单位，那么第2020秒时电子跳蚤所在位置的坐标是．三．解答题（共6小题）19．（2019秋•吴兴区期末）在平面直角坐标系中，已知点M（m﹣1，2m+3）（1）若点M在y轴上，求m的值．（2）若点M在第一、三象限的角平分线上，求m的值．20．（2019春•新宾县期中）已知点M（3|a|﹣9，4﹣2a）在y轴的负半轴上．（1）求M点的坐标；（2）求（2﹣a）2019+1的值．21．（2021春•怀化期末）如图，方格纸中每个小方格都是长为1个单位的正方形，若学校位置坐标为A（1，2），解答以下问题：（1）请在图中建立适当的直角坐标系，并写出图书馆（B）位置的坐标；（2）若体育馆位置坐标为C（﹣3，3），请在坐标系中标出体育馆的位置，并顺次连接学校、图书馆、体育馆，得到△ABC，求△ABC的面积．22．（2021春•大余县期末）在图中标明了李明同学家附近的一些地方，已知李明同学家位于（﹣2，﹣1）．（1）建立的平面直角坐标系，写出学校，邮局的坐标．（2）某星期日早晨，李明同学从家里出发，沿着（﹣1，﹣2）、（1，﹣2）、（2，﹣1）、（1，﹣1）、（1，3）、（﹣1，0）、（0，﹣1）的路线转了一下后回到家里，用线段顺次连接李明家和他在路上经过的地点，你能得到什么图形？23．（2021春•梁平区期末）如图，我们把杜甫（绝句）整齐排列放在平面直角坐标系中：（1）“两”、“岭”和“船”的坐标依次是：、和；（2）将第2行与第3行对调，再将第3列与第7列对调，“雪”由开始的坐标依次变换为：和；（3）“泊”开始的坐标是（2，1），使它的坐标变换到（5，3），应该哪两行对调，同时哪两列对调？24.（2020春•渌口区期末）点P是平面直角坐标系中的一点且不在坐标轴上，过点P向x轴、y轴作垂线段，若垂线段的长度的和为4，则点P叫做“垂距点”，例如：如图中的点(1,3)P是“垂距点”．（1）在点(2,2)A-，1(2B，5)2-，(1,5)C-中，“垂距点”是；（2）若3(2D m，5)2m是“垂距点”，求m的值．。
初中数学浙教版八年级上册第四章《平面直角坐标系》练习题普通用卷
初中数学浙教版八年级上册第四章4.2平面直角坐标系练习题一、选择题1.在平面直角坐标系的第二象限内有一点P，点P到x轴的距离为2，到y轴的距离为3，则点P的坐标是()A. (−3,2)B. (3,−2)C. (2,−3)D. (−2,3)2.在平面直角坐标系中，若点P(m+3,m−1)在x轴上，则m的值是()A. −3B. 1C. 3D. −13.已知点A在第二象限，到x轴的距离是5，到y轴的距离是6，点A的坐标为()A. (−5,6)B. (−6,5)C. (5,−6)D. (6,−5)4.已知点P(3−m,m−1)在第四象限，则m的取值范围在数轴上表示正确的是()A. B.C. D.5.若点p(a,b)在第二象限，则点Q(−a,b)所在象限是()A. 第一象限B. 第二象限C. 第三象限D. 第四象限6.如图小手盖住的点的坐标可能是()A. (−3,−4)B. (2,−3)C. (−6,3)D. (−4,−6)7.若A(2x−4,6−2x)在第二象限，则x的取值范围是()A. x<2B. 2<x<3C. x>3D. x<38.若点P(x,y)满足xy<0，x<0，则P点在()A. 第二象限B. 第三象限C. 第四象限D. 第二、四象限9.在平面直角坐标系中，一个智能机器人接到如下指令：从原点O出发，按向右，向上，向右，向下的方向依次不断移动，每次移动1m.其行走路线如图所示，第1次移动到A1，第2次移动到A2，…，第n次移动到A n.则△OA6A2020的面积是()A. 505m2B. 504.5m2C. 505.5m2D. 1010m210.坐标平面上有一点A，且A点到x轴的距离为3，A点到y轴的距离恰为到x轴距离的3倍.若A点在第二象限，则A点的坐标为()．A. (−3,1)B. (−9,3)C. (−3,9)D. (−1,3)二、填空题11.一只跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到(0,1)，然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→⋯]，且每秒跳动一个单位，那么第36秒时跳蚤所在位置的坐标是______．12.若点P(2−a,2a+3)到两坐标轴的距离相等．则点P的坐标是______．13.在平面直角坐标系中，点M(a−3,a+4)，点N(5,9)，若MN//y轴，则a=．14.已知点P的坐标(2−a,3a+6)，且点P到两坐标轴的距离相等，则点P的坐标是______．三、解答题15.如图，在平面直角坐标系中，点A、B分别在x轴、y轴的正半轴上，且满足√OB−3+|OA−1|=0．(1)求点A、B的坐标；(2)若OC=√3，求点O到直线CB的距离；(3)在(2)的条件下，若点P从C点出发以一个单位每秒的速度沿直线CB从点C到B的方向运动，连接AP.设△ABP的面积为S，点P的运动时间为t秒，求S与t的函数关系式．16.已知平面直角坐标系中有一点M(2m−3,m+1)．(1)若点M到y轴的距离为2时，求点M的坐标；(2)点N(5,−1)且MN//x轴时，求点M的坐标．17.在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位．其行走路线如图．(1)填写下列各点的坐标：A4(______ ，______ )，A8(______ ，______ )，A12(______ ，______ )；(2)写出点A4n的坐标(n是正整数)；(3)写出点A100和A101的坐标，并指出蚂蚁从点A100到点A101的移动方向．18.如图，△ABC在直角坐标系内的位置如图，且C点坐标是(−2,1)(1)则点A的坐标________和点B的坐标________ ；(2)请在这个坐标系内画出△A1B1C1，使△A1B1C1与△ABC关于y轴对称；(3)请直接写出△A1B1C1的面积．答案和解析1.【答案】A【解析】解：由题意，得|y|=2，|x|=3．又∵在第二象限内有一点P，∴x=−3，y=2，∴点P的坐标为(−3,2)，故选：A．根据各象限内点的坐标特征，可得答案．本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限(+,+)；第二象限(−,+)；第三象限(−,−)；第四象限(+,−)．2.【答案】B【解析】解：∵点P(m+3,m−1)在x轴上，∴m−1=0，解得m=1．故选：B．根据x轴上点的纵坐标为0列方程求解即可．本题考查了点的坐标，熟记x轴上点的纵坐标为0是解题的关键．3.【答案】B【解析】解：A位于第二象限，到x轴的距离为5，到y轴的距离为6，则点A的坐标为(−6,5)，故选：B．根据第二象限内点到x轴的距离是点的纵坐标，点到y轴的距离是横坐标的相反数，可得答案．本题考查了点的坐标，第二象限内点到x轴的距离是点的纵坐标，点到y轴的距离是横坐标的相反数．4.【答案】B【解析】解：由点P(3−m,m−1)在第四象限，得{3−m>0m−1<0，解得m<1和m<3．故选：B．根据第四象限内点的横坐标大于零，纵坐标小于零，可得不等式组，根据解不等式组，可得答案．本题考查了点的坐标，利用第四象限内的点的横坐标大于零，纵坐标小于零得出不等式组是解题关键．5.【答案】A【解析】解：∵点p(a,b)在第二象限，∴a<0，b>0，∴−a>0，∴点Q(−a,b)在第一象限．故选：A．根据第二象限内点的坐标特征确定出a、b的正负情况，然后判断出点Q的坐标所在的象限即可．本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限(+,+)；第二象限(−,+)；第三象限(−,−)；第四象限(+,−)．6.【答案】B【解析】解：A、点(−3,−4)在第三象限，不在所示区域；B、点(2,−3)在第四象限，在所示区域；C、点(−6,3)在第二象限，不在所示区域；D、点(−4,−6)在第三象限，不在所示区域；故选：B．找到横坐标为正，纵坐标为负的点的选项即可．本题考查点的坐标的相关知识；用到的知识点为：第四象限的点的横坐标为正，纵坐标为负．7.【答案】A【解析】解：∵A(2x−4,6−2x)在第二象限，∴{2x−4<06−2x>0，解得：x<2，故选：A．由第二象限内点的横坐标为负数、纵坐标为正数列出不等式组，解之可得．本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．8.【答案】A【解析】【分析】本题考查了平面直角坐标系中点的坐标，根据实数的性质得到y>0，然后根据第二象限内点的坐标特征进行判断．【解答】解：∵xy<0，x<0，∴y>0，∴点P在第二象限．故选：A．9.【答案】A【解析】【分析】本题主要考查点的坐标的变化规律，三角形的面积的有关知识，根据图象可得移动4次图象完成一个循环，从而可得出OA6，OA2020，再利用三角形的面积公式计算可得．【解答】解：由题意知OA4n=2n，∴OA4=2m，∵2020÷4=505，∴OA2020=505×2=1010m，∴点A6到OA2020的距离为1m，×1×1010=505m2．则△OA6A2020的面积是12故选A．10.【答案】B【解析】【解答】本题考查了点的坐标，主要利用了点到x轴的距离等于纵坐标的长度，点到y轴的距离等于横坐标的长度，需熟练掌握并灵活运用，根据点到x轴的距离等于纵坐标的长度求出点A的纵坐标，再根据点到y轴的距离等于横坐标的长度求出横坐标，即可得解．【解答】解：∵A点到x轴的距离为3，A点在第二象限，∴点A的纵坐标为3，∵A点到y轴的距离恰为到x轴距离的3倍，A点在第二象限，∴点A的横坐标为−9，∴点A的坐标为(−9,3)．故选B．11.【答案】(6,0)【解析】解：跳蚤运动的速度是每秒运动一个单位长度，(0,0)→(0,1)→(1,1)→(1,0)用的秒数分别是1秒，2秒，3秒，到(2,0)用4秒，到(2,2)用6秒，到(0,2)用8秒，到(0,3)用9秒，到(3,3)用12秒，到(4,0)用16秒，…，可知当点离开x轴时的横坐标为时间的平方，当点离开y轴时的纵坐标为时间的平方，依此类推，到(6,0)用36秒．则第36秒时跳蚤所在位置的坐标是(6,0)．故答案为：(6,0)．根据题目中所给的质点运动的特点，从中找出规律，即可得出答案．本题主要考查点的坐标问题，解决本题的关键是读懂题意，能够正确确定点运动的规律，从而可以得到到达每个点所用的时间．12.【答案】(7,−7)或(73,7 3 )【解析】解：由P(2−a,2a+3)到两坐标轴的距离相等，得：2−a=2a+3或2−a=−2a−3，解得a=−5或a=−13，当a=−5时，2−a=7，即点的坐标为(7,−7)，当a=−13时，2−a=73，即点的坐标为(73,73)；故答案为：(7,−7)或(73,7 3 ).根据点到两坐标轴的距离相等，可得关于a的方程，根据解方程，可得答案．本题考查了点的坐标，利用点到两坐标轴的距离相等得出关于a的方程是解题关键．13.【答案】8【解析】【分析】本题主要平行于坐标轴的点的坐标特征，掌握直线平行于x轴时点的纵坐标相等，直线平行于y轴时点的横坐标相等是解题的关键．由MN//y轴知a−3=5，可得a的值．【解答】解：∵MN//y轴，∴a−3=5，解得a=8，故答案为8．14.【答案】(3,3)或(6,−6)【解析】【分析】因为这个点到两坐标轴的距离相等，即到坐标轴形成的角的两边距离相等，所以这个点一定在各象限的角平分线上．点P到两坐标轴的距离相等就是横纵坐标相等或互为相反数，就可以得到方程求出a的值，从而求出点的坐标．解：∵点P到两坐标轴的距离相等就是横纵坐标相等或互为相反数，∴分以下两种情考虑：①横纵坐标相等时，即当2−a=3a+6时，解得a=−1，∴点P的坐标是(3,3)；②横纵坐标互为相反数时，即当(2−a)+(3a+6)=0时，解得a=−4，∴点P的坐标是(6,−6)．故答案为或(3,3)或(6,−6)．15.【答案】解：(1)∵√OB−3+|OA−1|=0，∴OB−3=0，OA−1=0，∴OB=3，OA=1，∴A点的坐标为(1,0)，B点坐标为(0,3)；(2)在Rt△BOC中，BC=√(√3)2+32=2√3，设点O到直线CB的距离为x，1 2×2√3x=12×3√3，解得x=1.5，故点O到直线CB的距离为1.5；(3)设点O到直线CB的距离为y，1 2×2√3y=12×3×(√3+1)，解得y=3+√32，当0≤t<2√3时，BP=2√3−t，∴S=12(2√3−t)×3+√32=−3+√34t+3+√32；当t>2√3时，BP=t−2√3，∴S=12(t−2√3)×3+√32=3+√34t−3+√32．【解析】本题主要考查点的坐标的确定，点到直线的距离，三角形的面积，算术平方根的非负性，绝对值的非负性，注意分类讨论．(1)根据算术平方根的非负性，绝对值的非负性可求解OA，OB的值，进而求解A，B 的坐标；(2)利用勾股定理易求BC的长，设点O到直线CB的距离为x，根据△BOC的面积可求(3)设点O到直线CB的距离为y，易求y值，再分两种当0≤t<2√3时；当t>2√3时，利用三角形的面积公式可求解S与t的函数关系式．16.【答案】解：(1)∵点M(2m−3,m+1)，点M到y轴的距离为2，∴|2m−3|=2，解得m=2.5或m=0.5，当m=2.5时，点M的坐标为(2,3.5)，当m=0.5时，点M的坐标为(−2,1.5)；综上所述，点M的坐标为(2,3.5)或(−2,1.5)；(2)∵点M(2m−3,m+1)，点N(5,−1)且MN//x轴，∴m+1=−1，解得m=−2，故点M的坐标为(−7,−1)．【解析】本题考查点的坐标，解题的关键是明确题意，求出m的值．(1)根据“点M到y轴的距离为l”得|2m−3|=2，求出m的值，再分别求解可得；(2)由MN//x轴得m+1=−1，求得m的值即可．17.【答案】(1)2；0；4；0；6；0(2)(2n,0)(3)A100(50,0)，A101(50,1)，从点A100到点A101的移动方向与从点O到A1的方向一致，为从下向上【解析】解：(1)由图可知，A4，A8，A12都在x轴上，∵蚂蚁每次移动1个单位，∴OA4=2，OA8=4，OA12=6，∴A4(2,0)，A8(4,0)，A12(6,0)；故答案为：2，0；4，0；6，0；(2)根据(1)OA4n=4n÷2=2n，∴点A4n的坐标(2n,0)；(3)∵100÷4=25，∴100是4的倍数，∴A(50,0)，∵101÷4=25…1，∴A101与A100横坐标相同，∴A101(50,1)，∴从点A100到点A101的移动方向与从点O到A1的方向一致，为从下向上．(1)观察图形可知，A4，A8，A12都在x轴上，求出OA4、OA8、OA12的长度，然后写出坐标即可；(2)根据(1)中规律写出点A4n的坐标即可；(3)根据100是4的倍数，可知从点A100到点A101的移动方向与从点O到A1的方向一致．此题主要考查了点的变化规律，比较简单，仔细观察图形，确定出A4n都在x轴上是解题的关键．18.【答案】解：(1)(0,3)，(−4,4)；(2)如图所示：△A1B1C1就是所要求画的三角形；(3)S△A1B1C1=4×3−12×2×3−12×2×2−12×1×4=5．【解析】【分析】本题主要考查平面直角坐标系中点的坐标，轴对称变换以及三角形的面积，正确得出对应点位置是解题关键．(1)根据点A，点B在直角坐标系内的位置，即可得出A、B的坐标；(2)直接利用关于y轴对称点的性质得出对应点位置即可；(3)利用△A1B1C1 的面积=长方形面积减去三个直角三角形面积求解即可．【解答】解：(1)由图可得，A(0,3)，B(−4,4)，故答案为(0,3)，(−4,4)；(2)见答案；(3)见答案．。
八年级数学上册 4.1 探索确定位置的方法、4.2平面直角坐标系专题训练 (新版)浙教版
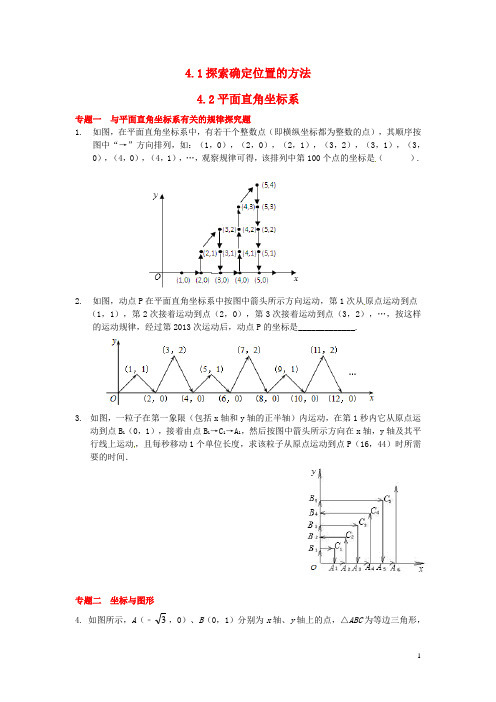
4.1探索确定位置的方法4.2平面直角坐标系专题一与平面直角坐标系有关的规律探究题1. 如图，在平面直角坐标系中，有若干个整数点（即横纵坐标都为整数的点），其顺序按图中“→”方向排列，如：（1，0），（2，0），（2，1），（3，2），（3，1），（3，0），（4，0），（4，1），…，观察规律可得，该排列中第100个点的坐标是（）.2. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2013次运动后，动点P的坐标是_____________.3.如图，一粒子在第一象限（包括x轴和y轴的正半轴）内运动，在第1秒内它从原点运动到点B1（0，1），接着由点B1→C1→A1，然后按图中箭头所示方向在x轴，y轴及其平行线上运动，且每秒移动1个单位长度，求该粒子从原点运动到点P（16，44）时所需要的时间．专题二坐标与图形4. 如图所示，A（﹣3，0）、B（0，1）分别为x轴、y轴上的点，△ABC为等边三角形，点P （3，a ）在第一象限内，且满足2S △ABP =S △ABC ，则a 的值为（ ）A 、47B 、2C 、3D 、25. 如图，△ABC 中，点A 的坐标为（0，1），点C 的坐标为（4，3），如果要使△ABD 与△ABC 全等，那么点D 的坐标是____________.6. 如图，在直角坐标系中，△ABC 满足，∠ACB ＝90°，AC ＝4，BC ＝2，点A 、C 分别在x 、y 轴上，当A 点从原点开始在x 轴正半轴上运动时，点C 随着在y 轴正半轴上运动．（1）当A 点在原点时，求原点O 到点B 的距离OB ；（2）当OA ＝OC 时，求原点O 到点B 的距离OB ；课时笔记【知识要点】1. 确定物体在平面上的位置两种常用的方法（1）行列法：用第几行、第几列来确定物体的位置,也就是用有序数对确定物体的位置. y xA O CB（2）方向、距离法：用方向和距离来确定物体的位置（或称方位）.2. 平面直角坐标系的概念在平面内画两条互相垂直，并且有公共原点O 的数轴，其中一条叫做x 轴（又叫横轴），通常画成水平，另一条叫做y 轴（又叫纵轴），画成与x 轴垂直.这样，我们就在平面内建立了平面直角坐标系，简称直角坐标系.坐标系所在的平面就叫做坐标平面，两坐标轴的公共原点O 叫做直角坐标系的原点.3. 坐标的概念对于平面内任意一点M ，作1MM x ⊥轴，2MM y ⊥轴，设垂足1M ，2M 在各自数轴上所表示的数分别为x ，y ，则x 叫做点M 的横坐标，y 叫做点M 的纵坐标，有序实数对（x ，y ）叫做点M 的坐标.4. 象限的概念与各象限内坐标特征（1）象限：x 轴和y 轴把坐标平面分成四个象限，如图，象限以数轴为界，x 轴，y 轴上的点不属于任何象限.（2）四个象限中点的坐标的符号特征如表.【温馨提示】1. 平面内确定物体的位置一般由两个数据确定，并且这两个数据有一定的顺序. 坐标为 （1，2）和（2，1）是不同的两对有序实数对，即它们表示不同的两点，因此不能错写顺序.2. 选取基础点的方法不同，得到的数据也会不同，但不会改变物体原有的位置.3. 在建立直角坐标系表示给定的点或图形的位置时，应选择适当的点作为原点，适当的直线作为坐标轴，适当的距离作为单位长度，这样有助于表示和解决有关问题.【方法技巧】 1. 用有序实数对来确定位置，关键在于确定两个垂直方向上的两个数据，并且这两个数据有顺序性.2. 用方向、距离法确定位置时，要先确定中心和东西、南北基础线，然后由一点的方位角和中心到这点的距离来确定这个点的位置.参考答案：1. D 【解析】 因为1+2+3+…+13=91，所以第91个点的坐标为（13，0）．因为在第14行点的走向为向上，故第100个点在此行上，横坐标就为14，纵坐标为从第92个点向上数8个点，即为8．故第100个点的坐标为（14，8）．故选D ．2. （2013，1） 【解析】 根据动点P 在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点 （3，2），∴第4次运动到点（4，0），第5次接着运动到点（5，1），…，∴横坐标为运动次数，经过第2013次运动后，动点P 的横坐标为2013，纵坐标为1，0，2，0，每4次一轮，∴经过第2013次运动后，动点P 的纵坐标为：2013÷4=503余1，故纵坐标为四个数中第三个，即为1，∴经过第2013次运动后，动点P 的坐标是（2013，2）.故答案为（2013，1）．3. 解：设粒子从原点到达A n 、B n 、C n 时所用的时间分别为a n 、b n 、c n ，则有：a 1=3，a 2=a 1+1，a 3=a 1+12=a 1+3×4，a 4=a 3+1，a 5=a 3+20=a 3+5×4，a 6=a 5+1，a 2n-1=a 2n-3+（2n-1）×4，a 2n =a 2n-1+1，∴a 2n-1=a 1+4[3+5+…+（2n-1）]=4n 2-1，a 2n =a 2n-1+1=4n 2，∴b 2n-1=a 2n-1-2（2n-1）=4n 2-4n+1，b 2n =a 2n +2×2n=4n 2+4n ，c 2n-1=b 2n-1+（2n-1）=4n 2-2n ，c 2n =a 2n +2n=4n 2+2n=（2n ）2+2n ，∴c n =n 2+n ，∴粒子到达（16，44）所需时间是到达点c 44时所用的时间，再加上44-16=28（s ），所以t=442+44+28=2008（s ）．4. C 【解析】 过P 点作PD ⊥x 轴，垂足为D ，由A （﹣，0）,B （0，1），得OA =3，OB =1．由勾股定理，得AB =22OB OA +=2．∴S △ABC =21×2×3=3． 又S △ABP =S △AOB +S 梯形BODP ﹣S △ADP =21×3×1+21×（1+a ）×3﹣21×（3+3）×a =2333a -+． 由2S △ABP =S △ABC ，得3+3-3a =3．∴a=3．故选C．5、（4，﹣1）或（﹣1，3）或（﹣1，﹣1）【解析】△ABD与△ABC有一条公共边AB，当点D在AB的下边时，点D有两种情况①坐标是（4，﹣1）；②坐标为（﹣1，3）．当点D在AB的上边时，坐标为（﹣1，﹣1）；故点D的坐标是（4，﹣1）或（﹣1，3）或（﹣1，﹣1）．AC CB．6、解：当A点在原点时，AC在y轴上，BC⊥y轴，所以OB=AB=2225（2）当OA=OC时，△OAC是等腰直角三角形，AC=4，OA=OC=22．过点B作BE⊥OA于E，过点C作CD⊥OC，且CD与BE交于点D，BC=2，CD=BD=2．BE OE．BE=BD+DE=BD+OC=32，OB=2225。
最新2019-2020年度浙教版八年级数学上册《平面直角坐标系》同步练习题1及答案-精品试题
浙教版八年级上第四章4.2《平面直角坐标系》同步练习一、选择题1、点P（m，n）是第四象限的点，且│m│=3，│n│=5，则点P的坐标是（）A．（3，5）B．（3，-5）C．（-3，-5）D．（-3，5）2、平行于x轴的一条直线上的点的纵坐标一定都（）A．相等B．等于0 C．大于0 D．小于03、若点P(a，a－2)在第三象限，则a的取值范围是( )A．－2＜a＜0 B．0＜a＜2 C．a＞2 D．a＜04、若a为整数，且点（3a-9，2a-10）在第四象限，则a的值是（）A．4 B．5 C．6 D．75、点M(2，－1)向上平移2个单位得到的点的坐标是( )A．(2，0) B．(2，1) C．(2，2) D．(2，－3)<0，x-y<0，那么点O（x，y）在（）6．如果xyA．第一象限B．第二象限C．第三象限D．第四象限7．(4分)如图，在平面直角坐标系中，点P(－1，2)向右平移3个单位后的坐标是( )A．(2，2) B．(－4，2)C．(－1，5) D．(－1，－1)8．点(－4，b)沿y轴正方向平移2个单位得到点(a＋1，3)，则a，b的值分别为( )A．a＝－3，b＝3 B．a＝－5，b＝3C．a＝－3，b＝1 D．a＝－5，b＝1二、填空题9、点A（3，-4）•到x•轴的距离是_____，•到y•轴的距离是_____，•到原点的距离是_______．10、若点A（2a，1-a）在第四象限，则a的取值范围为_______．11、点A在y轴上距离原点4个单位长度，则点A的坐标为________．12、若点A（m，-n）在第二象限，则点B（-m，│n│）在第__ __象限．13、如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→”方向排列，如(1，0)，(2，0)，(2，1)，(1，1)，(1，2)，(2，2)……根据这个规律，第2 012个点的横坐标为_ ___．14．在平面直角坐标系中，一青蛙从点A(－1，0)处向右跳2个单位，再向上跳2个单位到点A′处，则点A′的坐标为．15．将点P(－2，1)先向左平移1个单位，再向上平移2个单位得到点P′，则点P′的坐标为．16．在平面直角坐标系中，已知点A(－4，0)，B(0，2)，现将线段AB向右平移，使点A与坐标原点O重合，则点B平移后的坐标是．学_科_网]三、解答题17．若a 为实数，且点P （2a+2，3a-15）在第四象限，求代数式+│a-2006│的值．18．已知点A （5，y-1），B （x+3，-2）分别在第一象限和第三象限的角平分线上，求x+y 的值．19．如图:（1）写出△ABC 的三个顶点的坐标；（2）判断D （2，-2），E （0，1），F （1，-1）中哪些点在△ABC 内，哪些点在△ABC 外部；（3）求△ABC 的面积．20．一次数学游戏中，老师让甲，乙，丙三个人对已知点A （m ，n ）各提出一个限制条件：甲说m-n=0，乙说点A 在第一象限，丙说│m │=2，最后丁立刻就说出了A 点坐标，•你知道丁说的正确坐标是什么吗？244a a ++21．(10分)如图，已知点A(－4，－1)，B(－5，－4)，C(－1，－3)，△ABC经过平移得到的△A′B′C′，△ABC中任意一点P(x1，y1)平移后的对应点为P′(x1＋6，y1＋4)．(1)请在图中作出△A′B′C′；(2)写出点A′，B′，C′的坐标．答案：1、A2、B3、A4、D5、B6、B；7、A；8、B；9、a>1 10、4，11，5 12、（0，4）或（0，-4）13、一14、（1，2）。
八年级数学上册 4.2 平面直角坐标系同步练习 (新版)浙教版
6.2 平面直角坐标系基础训练:1.填空题:(1)平面直角坐标系中点A（a， 0）必在(2)点A(1- ,2)在第象限(3)若点(a ,2)在第二象限,且在两坐标轴的夹角平分线上,则a=2.选择题:(1) 已知点(0 ，0),(0 ，-2),(-3 ，0),(0 ，4),(-3 ，1)其中在X轴上的点的个数是( )(A) 0 (B) 1 (C) 2 (D) 3(2)如果a-b＜0,且ab＜0,那么点(a，b)在( )(A)第一象限, (B)第二象限(C)第三象限, (D)第四象限.(3)横坐标为负,纵坐标为零的点在( )(A)第一象限 (B)第二象限 (C)X轴的负半轴 (D)Y轴的负半轴3.在平面直角坐标系中画出点A(0，-2)，B(1 ，2) ，C(-1， 2)，D(-3， 0)然后用线段把各点顺次连结起来.4.已知直角三角形ABC的顶点A(2 ，0)，B(2 ，3)。
A是直角顶点,斜边长为5，求顶点C的坐标.12 6.2 平面直角坐标系②基础训练:1.填空题:(1)已知点A （m ，n ）在第四象限，那么点B （n ，m ）在第 象限 (2)若点P(3a-9,1-a)是第三象限的整数点(横、纵坐标都是整数)，那么a= (3)已知点P （x 2-3，1）在一、三象限夹角平分线上，则x= 。
2.选择题:(1)如图，正三角形的边长为4，则点C 的坐标是（ ）(A)（4，-2） (B)（4，2）(C)（32，-2） (D)（-2，32）(2)如果xy ＜0，那么点P （x ，y ）在（ ） (A) 第二象限 (B) 第四象限(C) 第四象限或第二象限 (D) 第一象限或第三象限(3)在x 轴上，且到原点的距离为2的点的坐标是（ ）(A) （2，0） (B) （-2，0） (C) （2，0）或（-2，0） (D) （0，2）3. 直角坐标系中，正三角形的一个顶点的坐标是（0，3），另两个顶点B 、C 都在x 轴上，求B ，C 的坐标。
浙教版数学八年级上册4.2《平面直角坐标系》同步习题3
1 / 34.2 平面直角坐标系（2）一. 选择题1．坐标平面内下列各点中，在x 轴上的点是（ ）A 、（0，3）B 、)0,3(-C 、)2,1(-D 、)3,2(--2．如果y x <0，),(y x Q 那么在（ ）象限 A 、 第四 B 、 第二 C 、 第一、三 D 、 第二、四3．已知03)2(2=++-b a ，则),(b a P --的坐标为（ ）A 、 )3,2(B 、 )3,2(-C 、 )3,2(-D 、 )3,2(--4．若点),(n m P 在第三象限，则点),(n m Q --在（ ）Ａ、第一象限 Ｂ、第二象限 Ｃ、第三象限 Ｄ、第四象限5. 如图：正方形ABCD 中点A 和点C 的坐标分别为)3,2(-和)2,3(-，则点B 和点D 的坐标分别为（ ） A 、)2,2(和)3,3( B 、)2,2(--和)3,3( C 、 )2,2(--和)3,3(-- D 、 )2,2(和)3,3(-- 6．已知平面直角坐标系内点),(y x 的纵、横坐标满足y （ ）A 、 x 轴上方（含x 轴）B 、 x 轴下方（含x 轴）C 、 y 轴的右方（含y 轴）D 、 y 轴的左方（含y 轴）二. 填空7．有了平面直角坐标系，平面内的点就可以用一个 来表示了。
点)4,3(-的横坐标是 ，纵坐标是 。
8．若)4,2(表示教室里第2列第4排的位置，则)2,4(表示教室里第 列第 排的位置。
9．设点P 在坐标平面内的坐标为),(y x P ，则当P 在第一象限时x 0， y 0， 当点P 在第四象限时，x 0，y 0.10．到x 轴距离为2，到y 轴距离为3的坐标为_____11．按照下列条件确定点),(y x P 位置：2 / 3⑴ 若x=0, y≥0，则点P 在 ____ ⑵ 若xy=0，则点P____ ⑶ 若022=+y x ，则点P 在____ ⑷ 若3-=x ，则点P 在_____ ⑸ 若y x = ，则P 在_________12．温度的变化是人们经常谈论的话题。
精品解析：浙教版八年级数学上册基础训练：4.2 平面直角坐标系(二)(原卷版)
浙教版八年级数学上册基础训练平面直角坐标系（二）1. 在平面直角坐标系中，正方形ABCD的顶点A，B，C的坐标分别为(－1，1)，(－1，－1)，(1，－1)，则顶点D的坐标为______．2. 如图，若小明家A的位置表示为(1，1)，学校B的位置表示为(3，3)，则工厂C的位置表示为_________．3. 在平面直角坐标系中，对于平面内任一点(a，b)，若规定以下三种变换：①△(a，b)＝(－a，b)；②○(a，b)＝(－a，－b)；③□(a，b)＝(a，－b)．按照以上变换，例如：△(○(1，2))＝(1，－2)，则○(□(3，4))＝_______．4. 如图，若“士”所在位置坐标为(－1，－2)，“相”所在位置的坐标为(2，－2)，则“将”所在位置的坐标为_________．5. 在平面直角坐标系中，A，B，C三点的位置如图所示，若点A，B，C的横坐标之和为a，纵坐标之和为b，求a－b的值．6. 如图，在平面直角坐标系中，以点O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M，N为圆心，大于MN长为半径画弧，两弧在第二象限交于点P.若点P的坐标为(2a，b＋1)，求a与b的数量关系．7. 已知点P在第二象限，有序数对(m，n)中的整数m，n满足m－n＝－6，则符合条件的点P 共有()A. 5个B. 6个C. 7个D. 无数个8. 如图，长方形ABCD的面积为8，点C的坐标为(0，1)，点D的坐标为(0，3)，则点A的坐标为________，点B的坐标为_________．9. 如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向每次移动1个单位，依次得到点P1(0，1)，P2(1，1)，P3(1，0)，P4(1，－1)，P5(2，－1)，P6(2，0)，…，则点P60的坐标是_________．10. 如图，在平面直角坐标系中，点A(0，1)，B(2，0)，C(4，3)．(1)求△ABC的面积．(2)设点P在坐标轴上，且△ABP与△ABC的面积相等，求点P的坐标．11. 如图，在平面直角坐标系中，每个最小方格的边长均为1个单位，P1，P2，P3，…均在格点上，其顺序按图中“→”方向排列，如：点P1(0，0)，P2(0，1)，P3(1，1)，P4(1，－1)，P(－1，－1)，P6(－1，2)，….根据这个规律，求点P2021的坐标．512. 如图，在平面直角坐标系中，O为坐标原点，在长方形OABC中，点A(10，0)，C(0，4)，D为OA的中点，P为BC边上一点．若△POD为等腰三角形，求所有满足条件的点P的坐标．。
精品解析：浙教版八年级数学上册基础训练：4.2 平面直角坐标系(一)(原卷版)
平面直角坐标系(一)1. 如图，在平面直角坐标系中，已知正方形网格的格点A的坐标为(－3，5)，则它到x轴的距离是_____，到y轴的距离是_ __，到原点的距离是_____．格点B，C的坐标分别为B_____，C_____．若点D(－3，－4)，则它到x轴的距离为_____，到y轴的距离为____，到原点的距离为__．2. 在平面直角坐标系中，点P(－2，－3)所在的象限是( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 已知点P(0，m)在y轴的负半轴上，则点M(－m，－m＋1)在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限4. 已知点P(3－m，m)在第二象限，则m的取值范围是( )A. m>0B. m<0C. m>3D. 0<m<35. 若y轴上的点M到x轴的距离为，则点M的坐标为( )A. ，0)B. (0，－C. (0,D. (0，或(0，－6. 如图，在第二象限内的点是( )A. P1，P2，P3B. P1，P2C. P1，P3D. P17. 若点P(2－a，3a＋6)到两坐标轴的距离相等，则点P的坐标为( )A. (3，3)B. (3，－3)C. (6，－6)D. (3，3)或(6，－6)8. 如图，在平面直角坐标系中，已知点B，C在x轴上，AB⊥x轴于点B，DA⊥AB.若AD＝5，点A的坐标为(－2，7)，则点D的坐标为( )A. (－2，2)B. (－2，12)C. (3，7)D. (－7，7)9. 已知点A(5，4)，B(5，8)，则线段AB的位置特征和AB的长度分别是( )A. 与x轴相交，AB＝4B. 与y轴相交，AB＝3C. 与x轴平行，AB＝3D. 与y轴平行，AB＝410. 在如图所示的平面直角坐标系中，写出点A，B，C，D，E，F的坐标．11. (1)已知点P(a－1，3a＋6)在y轴上，求点P的坐标．(2)已知点A(－3，m)，B(n，4)，若AB∥x轴，求m的值，并确定n的取值范围．12. 在平面直角坐标系中，点A的坐标是(3a－5，a＋1)．(1)若点A在y轴上，求a的值及点A的坐标．(2)若点A到x轴的距离与到y轴的距离相等，求a的值及点A的坐标．13. 在平面直角坐标系中，若点A(a，－b)在第一象限，则点B(a，b)在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限14. 已知点P(x－2，x＋3)在第一象限，则x的取值范围是_____．15. 已知点M(|x|，x+1)在第一、三象限的角平分线上，则x＝_______．16. 在平面直角坐标系中，我们把横、纵坐标都是整数的点叫做整点，且规定：正方形的内部不包含边界上的点．观察如图所示的中心在原点、一边平行于x轴的正方形：边长为1的正方形内部有1个整点，边长为2的正方形内部有1个整点，边长为3的正方形内部有9个整点……则边长为8的正方形内部的整点个数为_______．17. 如图，已知点A的坐标为(－3，－4)，点B的坐标为(5，0)．(1)求证：OA＝OB.(2)求△AOB的面积．(3)求原点O到AB的距离．18. 在平面直角坐标系xOy中，对于点P(x，y)，我们把P1(y－1，－x－1)叫做点P的友好点，已知点A1的友好点为A2，点A2的友好点为A3，点A3的友好点为A4……这样依次得到点An(n为正整数)．(1)若点A1的坐标为(2，1)，则点A3的坐标为，点A2021的坐标为．(2)若点A2021的坐标为(－3，2)，设点A1(x，y)，求x＋y的值．(3)设点A1的坐标为(a，b)，若点A1，A2，A3，…，An均在y轴的左侧，求a，b的取值范围．19. 如图，已知点A(－1，0)和点B(1，2)，在坐标轴上确定点P，使得△ABP为直角三角形，则满足这样条件的点P共有( )A. 2个B. 4个C. 6个D. 7个。
浙教版八年级数学上册同步练习：4.2 平面直角坐标系(1
4.2 平面直角坐标系（1）（巩固练习）姓名 班级第一部分1、如图，请写出多边形ABCDEF 各顶点的坐标.2、如图，将△ABC 置于直角坐标系中，如果A 点的坐标为(－2，3)，请写出B 点和C 点的坐标.ABCOxy3、如图，这是某市部分简图，请以火车站为坐标原点建立平面直角坐标系，并分别写出各地的坐标.体育场文化宫医院火车站宾馆市场超市4、如图，如果“士”所在位置的坐标为(－1，－2)，“相”所在位置的坐标为(2，－2)，那么“炮”所在位置的坐标为 .yxO -1-111ABCDEF11Oyx5、在如图所示的直角坐标系内，描出下列各组点，并分别依次用线段连接起来. (1)（－5，0）、（0，－2）、（3，0）、（0，0）、（0，4）、（－2，0）； (2)（－4，1）、（－4，3）、（1，6）、（1，4）.6、如图，⊙O 的半径为5，圆心与坐标原点重合. 在直角坐标系中，把横坐标、纵坐标都是整数的点称为格点.(1) 写出⊙O 上所有格点的坐标： .(2) 直线l 为经过⊙O 上任意两个格点的直线.求直线l 同时经过第一、二、四的概率.第二部分1. 已知点A (－2，3)，则点A 在………………………………………………（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 2.如图，小手盖住的点的坐标可能为………………（ ）A. (5，2)B. (－6，3)C. (－4，－6)D. (3，－4)yxO -1-111O xy(第2题图)3.如图，小明从点O 出发，先向西走40米，再向南走30米到达点M ，如果点M 的位置用(－40，－30)表示，那么(10，20)表示的位置是（ ）A. 点AB. 点BC. 点CD. 点D 4. 写出一个位于第一象限的点的坐标 .5. 点A 在x 轴上，位于原点左侧，距离坐标原点7个单位长度，则此点的坐标为 .6. 若点M 的坐标是(a ，b )，且a >0，b <0，则点M 在第 象限.7. 已知点P 在第二象限，它的横坐标与纵坐标的和为1，点P 的坐标是____________（写出符合条件的一个点即可）.8. 若点A 在y 轴的正半轴上，且到原点的距离为4个单位，则点A 的坐标是 . 9. 如图中标明了李明同学家附近的一些地方.(1) 根据图中所建立的平面直角坐标系，写出李明家，学校，邮局的坐标； (2) 若图中1个单位长度表示1km ，则学校与公园相距多远?10. 如果点A 的坐标为(a 2+1，－1－b 2)，那么点A 在第几象限?为什么?-22324o -2图5-11-131邮局游乐场学校水果店汽车站公园商店李明家yx(第3题图)参考答案第一部分11Oyx【分析】关键是正确确定各点在直角坐标系中的位置. 【解】如右图所示：6、如图，⊙O 的半径为5，圆心与坐标原点重合. 在直角坐标系中，把横坐标、纵坐标都是整数的点称为格点.(1) 写出⊙O 上所有格点的坐标： .(2) 直线l 为经过⊙O 上任意两个格点的直线.求直线l 同时经过第一、二、四的概率.【分析】(1)观察图形，根据各格点的位置确定坐标. (2)分别求出经过⊙O 上任意两个格点的直线l 的条数，和经过⊙O 上第一、二、四象限格点的直线的条数，进而求得概率.【解】(1) (1，2)，(1，－2)，(－1，2)，(－1，－2)，(2，1)，(2，－1)，(－2，1)，(－2，－1).(2) 经过⊙O 上8个格点中任意两个格点的直线l 共有7+6+…+2+1=28条. 经过⊙O 上第一、二、四象限格点的直线共有4条. ∴直线l 同时经过第一、二、四的概率为P =71284 . 第二部分1. 已知点A (－2，3)，则点A 在………………………………………………（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 答案：B2.如图，小手盖住的点的坐标可能为………………（ ）y xO -1-111yxO -1-111O xy(第2题图)A. (5，2)B. (－6，3)C. (－4，－6)D. (3，－4) 解析：注意各象限点的坐标的符号特征. 答案：D3.如图，小明从点O 出发，先向西走40米，再向南走30米到达点M ，如果点M 的位置用(－40，－30)表示，那么(10，20)表示的位置是（ ）A. 点AB. 点BC. 点CD. 点D答案：B4. 写出一个位于第一象限的点的坐标 .答案：形如（a ，b ）且a >0，b >0.5. 点A 在x 轴上，位于原点左侧，距离坐标原点7个单位长度，则此点的坐标为 .解析：注意x 轴上点的纵坐标为0. 答案：（－7，0）6. 若点M 的坐标是(a ，b )，且a >0，b <0，则点M 在第 象限.解析：横坐标为正数，纵坐标为负数的点在第四象限. 答案：四7. 已知点P 在第二象限，它的横坐标与纵坐标的和为1，点P 的坐标是____________（写出符合条件的一个点即可）.解析：注意第二象限点的坐标的符号特征，即横坐标为负，纵坐标为正. 答案：形如（a ，1－ a ）且a <0.8. 若点A 在y 轴的正半轴上，且到原点的距离为4个单位，则点A 的坐标是 .解析：注意y 轴上点的横坐标为0. 答案：（0，4）9. 如图中标明了李明同学家附近的一些地方.(1) 根据图中所建立的平面直角坐标系，写出李明家，学校，邮局的坐标；(2) 若图中1个单位长度表示1km ，则学校与公园相距多远?解：(1) 李明家（－2，－1），学校（1，3），邮局（0，－1）；-22324o -2图5-11-131邮局游乐场学校水果店汽车站公园商店李明家yx(第3题图)(2) 由于学校的坐标为（1，3），公园的坐标为（1，－2），过这两个点的直线与x轴垂直，故它们之间的距离是3－(－2)=5km.10. 如果点A的坐标为(a2+1，－1－b2)，那么点A在第几象限?为什么?分析：要确定A点在哪一象限，关键是判断横坐标与纵坐标的符号.解：∵a2≥0，－b2≤0，∴a2+1>0，－1－b2<0，即横坐标为正数，纵坐标为负数，∴点A在第四象限.。
4.2平面直角坐标系(一)同步练习含试卷分析详解浙教版八年级数学上
4.2 平面直角坐标系（一）一、选择题1、平行于x轴的一条直线上的点的纵坐标一定都（）A．相等 B．等于0 C．大于0 D．小于02、点P（m，n）是第四象限的点，且│m│=3，│n│=5，则点P的坐标是（）A．（3，5） B．（3，-5） C．（-3，-5） D．（-3，5）3、若a为整数，且点（3a-9，2a-10）在第四象限，则a的值是（）A．4 B．5 C．6 D．74、若点P(a，a－2)在第三象限，则a的取值范围是( )A．－2＜a＜0 B．0＜a＜2C．a＞2 D．a＜05、如果xy<0，x-y<0，那么点O（x，y）在（）二、填空题6、若点A（2a，1-a）在第四象限，则a的取值范围为_______．7、点A（3，-4）•到x•轴的距离是_____，•到y•轴的距离是_____，•到原点的距离是_______．8、点A在y轴上距离原点4个单位长度，则点A的坐标为________．9、若点A（m，-n）在第二象限，则点B（-m，│n│）在第__ __象限．10、如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→”方向排列，如(1，0)，(2，0)，(2，1)，(1，1)，(1，2)，(2，2)……根据这个规律，第2 012个点的横坐标为_ ___．三、解答题11．若a为实数，且点P（2a+2，3a-15）在第四象限，求代数式+│a-2006│的值．12．已知点A （5，y-1），B （x+3，-2）分别在第一象限和第三象限的角平分线上，求x+y 的值．13．如图:（1）写出△ABC 的三个顶点的坐标；（2）判断D （2，-2），E （0，1），F （1，-1）中哪些点在△ABC 内，哪些点在△ABC 外部；（3）求△ABC 的面积．14．一次数学游戏中，老师让甲，乙，丙三个人对已知点A （m ，n ）各提出一个限制条件：甲说m-n=0，乙说点A 在第一象限，丙说│m │=2，最后丁立刻就说出了A 点坐标，•你知道丁说的正确坐标是什么吗？15．已知点A （3x-1，2x ）到x 轴，y 轴的距离相等，求x 的值．4.2（1）1、A2、B3、A4、D5、B6、a>17、4，3，58、（0，4）或（0，-4）9、一 10、45 12．113．（1）A（2，0），B（-3，0），C（1，-3）（2）D，E在△ABC外部，F在△ABC内部（3）15 214．A（2，2）15．x=1或x=15.。
专题4.3平面直角坐标系中点的坐标规律专项训练(30道)(举一反三)(浙教版)(原卷版)
专题4.3 平面直角坐标系中点的坐标规律专项训练（30道）【浙教版】考卷信息：本套训练卷共30题，题型针对性较高，覆盖面广，选题有深度，涵盖了平面直角坐标系中的规律问题所有类型！一．选择题（共18小题）1．（2022春•宽城县期末）如图，在平面直角坐标系xOy中，正方形ABCD的顶点A（1，﹣1），D（3，﹣1），规定把正方形ABCD“先沿y轴翻折，再向下平移1个单位”为一次变换，这样连续经过2022次变换后，点C的坐标为（）A．（﹣3，﹣2023）B．（3，﹣2024）C．（3，﹣2025）D．（﹣3，﹣2026）2．（2022春•西平县期末）在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点，如图，由里向外数第2个正方形开始，分别是由第1个正方形各顶点的横坐标和纵坐标都乘2，3，…得到的，你观察图形，猜想由里向外第2021个正方形四条边上的整点个数共有（）A．2021个B．4042个C．6063个D．8084个3．（2022春•厦门期末）如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），按这样的运动规律，经过第2019次运动后，动点P的坐标是（）A．（2022，0）B．（2022，1）C．（2022，2）D．（2022，0）4．（2022春•上思县期中）如图，已知A1（1，0），A2（1，﹣1），A3（﹣1，﹣1），A4（﹣1，1），A5（2，1），则点A2020的坐标是（）A．（506，505）B．（﹣506，507）C．（﹣506，506）D．（﹣505，505）5．（2022春•柳南区校级期中）如图，在平面直角坐标系中，一动点从原点O出发，按向上，向右，向下，向右的方向不断地移动，每移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0），那么A2020坐标为（）A．（2022，1）B．（2022，0）C．（1010，1）D．（1010，0）6．（2022春•永川区期末）如图，在平面直角坐标系中，有若干个整数点，其顺序按图中方向排列，如（1，0），（2，0），（2，1），（3，2），（3，1），（3，0），……，根据这个规律探索可得，第120个点的坐标为（）A．（16，0）B．（15，14）C．（15，0）D．（14，13）7．（2022春•黄梅县期中）如下图所示，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次运动到点（2，0），第3次运动到点（3，﹣1），…，按照这样的运动规律，点P第2021次运动到点（）A．（2022，1）B．（2022，0）C．（2022，﹣1）D．（2022，0）8．（2022春•青川县期末）如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（3，1），（3，0），（3，﹣1）…根据这个规律探索可得，第100个点的坐标为（）A．（14，0）B．（14，﹣1）C．（14，1）D．（14，2）9．（2022•苏州一模）如图，动点P从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P第2015次碰到矩形的边时，点P的坐标为（）A．（3，0）B．（7，4）C．（8，1）D．（1，4）10．（2022春•绥中县期末）如图，在平面直角坐标系中，每个最小方格的边长均为1个单位长度，P1，P2，P3，…均在格点上，其顺序按图中“→”方向排列，如：P1（0，0），P2（0，1），P3（1，1），P4（1，﹣1），P5（﹣1，﹣1），P6（﹣1，2）…根据这个规律，点P2021的坐标为（）A．（﹣505，﹣505）B．（﹣505，506）C．（506，506）D．（505，﹣505）11．（2022春•海城市期中）如图，将边长为1的正方形OAPB沿x轴正方向连续翻转8次，点P依次落在点P、P2、P3、P4、…P x的位置，则点P9的横坐标是（）A．5B．6C．7D．912．（2022秋•石柱县校级月考）如图，在一张无穷大的格纸上，格点的位置可用数对（m，n）表示，如点A的位置为（3，3），点B的位置为（6，2）．点M从（0，0）开始移动，规律为：第1次向右移动1个单位到（1，0），第2次向上移动2个单位到（1，2），第3次向右移动3个单位到（4，2），…，第n 次移动n 个单位（n 为奇数时向右，n 为偶数时向上），那么点M 第27次移动到的位置为（ ）A ．（182，169）B ．（169，182）C ．（196，182）D ．（196，210）13．（2022•重庆模拟）如图，在平面直角坐标系上有个点P （1，0），点P 第一次向上跳动1个单位至P 1（1，1），紧接着第二次向左跳动2个单位至点P 2（﹣1，1），第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，…，依此规律跳动下去，点P 第100次跳动至点P 100的坐标是（ ）A ．（﹣24，49）B ．（﹣25，50）C ．（26，50）D ．（26，51）二．填空题（共10小题）14．（2022•烟台模拟）我们把1，1，2，3，5，8，13，…这组数称为斐波那契数列，为了进一步研究，依次以这列数为半径作90°圆弧P 1P 2̂，P 2P 3̂，P 3P 4̂，…得到斐波那契螺旋线，然后顺次连接P 1P 2，P 2P 3，P 3P 4，…得到螺旋折线（如图），已知点P 1（0，1），P 2（﹣1，0），P 3（0，﹣1），则该折线上的点P 8的坐标为 ．15．（2022春•长汀县期末）在平面直角坐标系中，对于点P（x，y），我们把点P'（y﹣1，﹣x﹣1）叫做点P的友好点，已知点A1的友好点为点A2，点A2的友好点为点A3，点A3的友好点为点A4，……以此类推，当点A1的坐标为（2，1）时，点A2022的坐标为．16．（2022春•海淀区校级期中）在平面直角坐标系中，点P从原点O出发，速度为每秒1个单位长度，且点P只能向上或向右运动，请回答下列问题：（1）将表格填写完整：点P出发时间可得到整数点的坐标可得到整数点的个数1秒（0，1）（1，0）22秒（1，1）（2，0）（0，2）343秒（0，3）（1，2）（2，1）（3，0）（2）当点P从点O出发10秒，可得到的整数点的个数是．（3）当点P从点O出发秒时，可得到整数点（28，7）．17．（2022•东城区二模）在平面直角坐标系中，小明玩走棋的游戏，其走法是：棋子从原点出发，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位，…，依此类推，第n步的走法是：当n能被3整除时，则向上走1个单位；当n被3除，余数为1时，则向右走1个单位；当n被3除，余数为2时，则向右走2个单位，当走完第8步时，棋子所处位置的坐标是；当走完第2016步时，棋子所处位置的坐标是．18．（2022春•上杭县期末）如图，点A（0，1），点A1（2，0），点A2（3，2），点A3（5，1），…，按照这样的规律下去，点A2021的坐标为（）A．（6062，2020）B．（3032，1010）C．（3030，1011）D．（6063，2021）二．填空题（共9小题）19．（2022•潍坊期中）如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是（﹣2，3），则经过第2021次变换后点A的对应点的坐标为．20．（2022•曲靖）如图：图象①②③均是以P0为圆心，1个单位长度为半径的扇形，将图形①②③分别沿东北，正南，西北方向同时平移，每次移动一个单位长度，第一次移动后图形①②③的圆心依次为P1P2P3，第二次移动后图形①②③的圆心依次为P4P5P6…，依此规律，P0P2018＝个单位长度．21．（2022•朝阳区一模）在平面直角坐标系xOy中，动点P从原点O出发，每次向上平移1个单位长度或向右平移2个单位长度，在上一次平移的基础上进行下一次平移．例如第1次平移后可能到达的点是（0，1）、（2，0），第2次平移后可能到达的点是（0，2）、（2，1）、（4，0），第3次平移后可能到达的点是（0，3）、（2，2）、（4，1）、（6，0），依此类推…．我们记第1次平移后可能到达的所有点的横、纵坐标之和为l1，l1＝3；第2次平移后可能到达的所有点的横、纵坐标之和为l2，l2＝9；第3次平移后可能到达的所有点的横、纵坐标之和为l3，l3＝18；按照这样的规律，l4＝；l n＝（用含n的式子表示，n是正整数）．22．（2022•锦州）如图，在平面直角坐标系上有点A（1，0），点A第一次跳动至点A1（﹣1，1），第四次向右跳动5个单位至点A4（3，2），…，依此规律跳动下去，点A第100次跳动至点A100的坐标是．23．（2022春•黄石校级月考）如图在直角坐标系中第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换△OA2B2，第三次将△OA2B2变换成△OA3B3，已知：A（1，3），A1（﹣2，﹣3），A2（4，3），A3（﹣8，﹣3），B（2，0），B1（﹣4，0），B2（8，0），B3（﹣16，0）．（1）观察每次变化前后的三角形有何变化，找出其中的规律，按此变化规律将△OA3B3变换成△OA4B4则点A4的坐标为，点B4的坐标为．（2）若按第（1）题中找到的规律将△OAB进行了n次变换，得到的△OA n B n推测点A n坐标为，点Bn坐标为．24．（2022春•龙港区期末）如图，两种大小不等的正方形间隔排列在平面直角坐标系中，已知小正方形的边长为1且A1的坐标为（2，2），A2的坐标为（5，2）．（1）A3的坐标为；（2）A n的坐标为．（用含n的代数式表示）25．（2022春•新余期末）如图，在平面直角坐标系中，一电子蚂蚁按照设定程序从原点O出发，按图中箭头所示的方向运动，第1次从原点运动到点（1，2），第2次接着运动到点（2，0），第3次接着运动到点（2，﹣2），第4次接着运动到点（4，﹣2），第5次接着运动到点（4，0），第6次接着运动到点（5，2）．…按这样的运动规律，经过2021次运动后，电子蚂蚁运动到的位置的坐标是．26．（2022•广水市期末）如图，把正方形铁片OABC置于平面直角坐标系中，顶点A的坐标为（3，0），点P（1，2）在正方形铁片上．将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°，第一次旋转至图①位置，第二次旋转至图②位置，…，则正方形铁片连续旋转2021次后，点P的坐标为．27．（2022•东城区校级模拟）如图，在平面直角坐标系xOy中，B1（0，1），B2（0，3），B3（0，6），B4（0，10），…，以B1B2为对角线作第一个正方形A1B1C1B2，以B2B3为对角线作第二个正方形A2B2C2B3，以B3B4为对角线作第三个正方形A3B3C3B4，…，如果所作正方形的对角线B n B n+1都在y轴上，且B n B n+1的长度依次增加1个单位长度，顶点A n都在第一象限内（n≥1，且n为整数），那么A1的纵坐标为；用n的代数式表示A n的纵坐标：．三．解答题（共3小题）28．（2022春•西城区校级期中）在直角坐标系中，我们把横，纵坐标都为整数的点叫敝整点，该坐标轴的单位长度为1cm，整点P从原点O出发，速度为1cm/s，且整点p作向上或向右运动（如图1所示）．运动时间（s）与整点（个）的关系如下表：整点P运动的时间（秒）可以得到整点P的坐标可以得到整点P的个数1（0，1）（1，0）22（0，2）（1，1）（2，0）33（0，3）（1，2）（2，1）（3，0）4………根据上表的运动规律回答下列问题：（1）当整点p从点O出发4s时，可以得到的整点的个数为个；（2）当整点p从点O出发8s时，在直角坐标系中描出可以得到的所有整点，并顺次连接这些整点；（3）当整点P从点O出发时，可以得到整点（16，4）的位置．29．（2022春•海门市期末）在平面直角坐标系xOy中，点A（x1，y1），B（x2，y2），若x2﹣x1＝y2﹣y1≠0，则称点A与点B互为“对角点”，例如：点A（﹣1，3），点B（2，6），因为2﹣（﹣1）＝6﹣3≠0，所以点A与点B互为“对角点”．（1）若点A的坐标是（4，﹣2），则在点B1（2，0），B2（﹣1，﹣7），B3（0，﹣6）中，点A的“对角点”为点；（2）若点A的坐标是（﹣2，4）的“对角点”B在坐标轴上，求点B的坐标；（3）若点A的坐标是（3，﹣1）与点B（m，n）互为“对角点”，且点B在第四象限，求m，n的取值范围．30．（2022秋•庐阳区校级期中）如图，在平面直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换成△OA2B2，第三次将△OA2B2变换成△OA3B3．（1）观察每次变换前后的三角形的变化规律，若将△OA3B3变换成△OA4B4，则A4的坐标是，B4的坐标是．（2）若按第（1）题找到的规律将△OAB进行n次变换，得到△OA n B n，比较每次变换中三角形顶点坐标有何变化，找出规律，推测A n的坐标是，B n的坐标是．（3）若按第（1）题找到的规律将△OAB进行n次变换，得到△OA n B n，则△OA n B n的面积S为。
4.2.2用坐标系确定点的位置 同步练习卷2024-2025学年浙教版数学八年级上册
浙教版八年级上册《4.2.2 用坐标系确定点的位置》同步练习卷一、选择题1．在平面直角坐标系中，已知点A的坐标为（1，1）．如果把y轴往左移3个单位，那么点A的坐标变为（）A．（1，4）B．（1，-2）C．（4，1）D．（-2，1）2．如图，AD∥BC，∠A=90°，点D的坐标为（3，5），AD=5，则点B的坐标为（）A．（2，0）B．（-2，0）C．（-5，0）D．（0，-2）3．如图，将边长为4的正方形ABCD放在平面直角坐标系中，AB平行于x轴．若点A的坐标为（-1，1），则点C的坐标为（）A．（3，4）B．（4，5）C．（3，5）D．（5，5）4．如图，等边△OAB边长为2，顶点O在平面直角坐标系的原点，点A在x轴正半轴上，则点B的坐标为（）A．（1，1）B．（√3，1）C．（1，√3）D．（√3，√3）5．如图，正方形ABCD的顶点A，D的坐标分别是（2，0），（0，1），则顶点B的坐标是（）A．（-3，2）B．（3，-2）C．（3，2）D．（2，3）6．一个长方形的长为8，宽为4，分别以两组对边中点的连线为坐标轴建立平面直角坐标系，下面哪个点不在长方形上（）A．（4，-2）B．（-2，4）C．（4，2）D．（0，-2）二、填空题7．在平面直角坐标系xOy中，若点A的坐标为（-3，3），点B的坐标为（2，0），则△ABO的面积为______ ．8．如图，在平面直角坐标系中，点A的坐标为（-2，0），点B在y轴正半轴上，以点B为圆心，BA长为半径作弧，交x轴正半轴于点C，则点C的坐标为 ______ ．9．如图，矩形ABCD中，A（-4，1），B（0，1），C（0，3），则D点坐标是______ ．10．如图，将正方形OABC放在平面直角坐标系中，O是原点，A的坐标为（1，2），则点C的坐标为 ______ ．三、解答题11．如图，长方形ABCD的长BC=600，宽AB=400，请选择合适的比例尺，并建立适当的平面直角坐标系，使点B的坐标为（-2，-1），点D的坐标为（4，3），并写出其余顶点的坐标．12．如图，在平面直角坐标系中，四边形ABCD的各个顶点坐标分别是A（0，0），B（2，5），C（9，8），D（12，0），在图中画出四边形ABCD，并求出它的面积．13．温州一位老人制作的仿真郑和宝船尺寸如图，已知在某一直角坐标系中点A坐标为（9，0），请你直接在图中画出该坐标系，并写出其余5点的坐标．14．从前，有一个农夫找了一处秘密的地点将自己的财宝藏起来，他运用平面直角坐标系的知识确定了一棵古树的坐标是（2，5），附近一所教堂的坐标是（-3，5），而在（3，-1）处是一口废弃多年早已被人们遗忘了的枯井，于是这个农夫秘密地将财宝藏到了井底，并将井口填平，且制作了如图所示的一张藏宝图，图中点A表示教堂的位置，点B表示古树的位置．他临死前将藏宝图交给了儿子，请你帮助他的儿子找回财宝．。
浙教版初中数学八年级上册《4.2 平面直角坐标系》同步练习卷
浙教新版八年级上学期《4.2 平面直角坐标系》同步练习卷一．填空题（共49小题）1．在平面直角坐标系中，点（3，﹣5）在第象限．2．已知a＜b＜0，则点A（a﹣b，b）在第象限．3．点A（﹣2，1）在第象限．4．点P（3，2）在第象限．5．请写出一个在第二象限的点的坐标．6．已知a是整数，点A（2a+1，2+a）在第二象限，则a＝．7．已知点P在第二象限，它的横坐标与纵坐标的和为1，点P的坐标是（写出一个符合条件的一个点即可）．8．若点M（1+a，2b﹣1）在第二象限，则点N（a﹣1，1﹣2b）在第象限．9．已知第二象限内的点P到x轴，y轴的距离分别是2和3，则点P的坐标是．10．点（2，﹣3）在第象限．11．点P在第二象限内，并且到x轴的距离为2，到y轴的距离为3，则点P的坐标为．12．如果点M（a+b，ab）在第二象限，那么点N（a，b）在第象限．13．如果a＞0，b＜0，那么点P（a，b）在第象限．14．若，则点P（x，y）在象限．15．直角坐标系中，第四象限内的点M到横轴的距离为28，到纵轴的距离为6，则M点的坐标是．16．在直角坐标系中，点B（1，﹣2）在第二象限，说法是：的．17．在直角坐标系中，点A（3，2）在第一象限．．18．直角坐标系中，点（﹣2，3）在第一象限．．（判断对错）19．如图，等边三角形ABC的边长为1，顶点B与原点O重合，点C在x轴的正半轴上，过点B作BA1⊥AC于点A1，过点A1作A1B1∥OA，交OC于点B1；过点B1作B1A2⊥AC于点A2，过点A2作A2B2∥OA，交OC于点B2；……，按此规律进行下去，点A2020的坐标是．20．如图，正方形AOBO2的顶点A的坐标为A（0，2），O1为正方形AOBO2的中心；以正方形AOBO2的对角线AB为边，在AB的右侧作正方形ABO3A1，O2为正方形ABO3A1的中心；再以正方形ABO3A1的对角线A1B为边，在A1B 的右侧作正方形A1BB1O4，O3为正方形A1BB1O4的中心；再以正方形A1BB1O4的对角线A1B1为边，在A1B1的右侧作正方形A1B1O5A2，O4为正方形A1B1O5A2的中心：…；按照此规律继续下去，则点O2018的坐标为．21．在平面直角坐标系中，点A（，1）在射线OM上，点B（，3）在射线ON上，以AB为直角边作Rt△ABA1，以BA1为直角边作第二个Rt△BA1B1，以A1B1为直角边作第三个Rt△A1B1A2，…，依此规律，得到Rt△B2017A2018B2018，则点B2018的纵坐标为．22．如图，在平面直角坐标系中，等腰直角三角形OAA1的直角边OA在x轴上，点A1在第一象限，且OA＝1，以点A1为直角顶点，OA1为一直角边作等腰直角三角形OA1A2，再以点A2为直角顶点，OA2为直角边作等腰直角三角形OA2A3…依此规律，则点A2018的坐标是．23．如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，﹣1），P5（2，﹣1），P6（2，0），…，则点P2017的坐标是．24．如图，Rt△OA0A1在平面直角坐标系内，∠OA0A1＝90°，∠A0OA1＝30°，以OA1为直角边向外作Rt△OA1A2，使∠OA1A2＝90°，∠A1OA2＝30°，以OA2为直角边向外作Rt△OA2A3，使∠OA2A3＝90°，∠A2OA3＝30°，按此方法进行下去，得到Rt△OA3A4，Rt△OA4A5，…，Rt△OA2016A2017，若点A0（1，0），则点A2017的横坐标为．25．在平面直角坐标系中，点P（x，y）经过某种变换后得到点P'（﹣y+1，x+2），我们把点P'（﹣y+1，x+2）叫做点P（x，y）的终结点．已知点P1的终结点为P2，点P2的终结点为P3，点P3的终结点为P4，这样依次得到P1、P2、P3、P4、…P n、…，若点P1的坐标为（2，0），则点P2017的坐标为．26．如图，在平面直角坐标系中，等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上，且OA1＝A1A2＝1，以OA2为直角边作第二个等腰直角三角形OA2A3，以OA3为直角边作第三个等腰直角三角形OA3A4，…，依此规律，得到等腰直角三角形OA2017A2018，则点A2017的坐标为．27．如图，四条直线l1：y1＝x，l2：y2＝x，l3：y3＝﹣x，l4：y4＝﹣x，OA1＝1，过点A1作A1A2⊥x轴，交l1于点A2，再过点A2作A2A3⊥l1交l2于点A3，再过点A3作A3A4⊥l2交y轴于点A4…，则点A2017坐标为．28．把多块大小不同的30°直角三角板如图所示，摆放在平面直角坐标系中，第一块三角板AOB的一条直角边与y轴重合且点A的坐标为（0，1），∠ABO ＝30°；第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1；第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2；第四块三角板的斜边B2B3与第三块三角板的斜边B1B2垂直且交y轴于点B3；…按此规律继续下去，则点B2017的坐标为．29．如图，在平面直角坐标系中，直线l：y＝x+2交x轴于点A，交y轴于点A1，点A2，A3，…在直线l上，点B1，B2，B3，…在x轴的正半轴上，若△A1OB1，△A2B1B2，△A3B2B3，…，依次均为等腰直角三角形，直角顶点都在x轴上，则第n个等腰直角三角形A n B n﹣1B n顶点B n的横坐标为．30．如图，在平面直角坐标系中，△A1A2A3，△A3A4A5，△A5A6A7，△A7A8A9，…，都是等边三角形，且点A1，A3，A5，A7，A9的坐标分别为A1（3，0），A3（1，0），A5（4，0），A7（0，0），A9（5，0），依据图形所反映的规律，则A100的坐标为．31．如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，﹣1），P5（2，﹣1），P6（2，0），…，则点P60的坐标是．32．如图，在平面直角坐标系中，每个最小方格的边长均为1个单位长，P1，P2，P3，…，均在格点上，其顺序按图中“→”方向排列，如：P1（0，0），P2（0，1），P3（1，1），P4（1，﹣1），P5（﹣1，﹣1），P6（﹣1，2）…根据这个规律，点P2016的坐标为．33．如图，正方形A1A2A3A4，A5A6A7A8，A9A10A11A12，…，（每个正方形从第三象限的顶点开始，按顺时针方向顺序，依次记为A1，A2，A3，A4；A5，A6，A7，A8；A9，A10，A11，A12；…）的中心均在坐标原点O，各边均与x轴或y轴平行，若它们的边长依次是2，4，6…，则顶点A20的坐标为．34．如图，在平面直角坐标系中，点A（0，）、B（﹣1，0），过点A作AB 的垂线交x轴于点A1，过点A1作AA1的垂线交y轴于点A2，过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去，直至得到点A2015为止，则点A2015坐标为．35．如图，在平面直角坐标系中，A、B两点分别在x轴和y轴上，OA＝1，OB ＝，连接AB，过AB中点C1分别作x轴和y轴的垂线，垂足分别是点A1、B1，连接A1B1，再过A1B1中点C2作x轴和y轴的垂线，照此规律依次作下去，则点∁n的坐标为．36．如图，在在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB ＝90°，直角边AO在x轴上，且AO＝1．将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1，且A1O＝2AO，再将Rt△A1OB1绕原点O 顺时针旋转90°得到等腰三角形A2OB2，且A2O＝2A1O…，依此规律，得到等腰直角三角形A2014OB2014，则点A2014的坐标为．37．如图，在平面直角坐标系中，已知点A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2），把一根长为2014个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在A处，并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上，则细线的另一端所在位置的点的坐标是．38．在平面直角坐标系xOy中，对于点P（x，y），我们把点P′（﹣y+1，x+1）叫做点P伴随点．已知点A1的伴随点为A2，点A2的伴随点为A3，点A3的伴随点为A4，…，这样依次得到点A1，A2，A3，…，A n，…．若点A1的坐标为（3，1），则点A3的坐标为，点A2014的坐标为；若点A1的坐标为（a，b），对于任意的正整数n，点A n均在x轴上方，则a，b应满足的条件为．39．如图，在平面直角坐标系xOy中，已知点M0的坐标为（1，0），将线段OM0绕原点O逆时针方向旋转45°，再将其延长到M1，使得M1M0⊥OM0，得到线段OM1；又将线段OM1绕原点O逆时针方向旋转45°，再将其延长到M2，使得M2M1⊥OM1，得到线段OM2；如此下去，得到线段OM3，OM4，OM5，…根据以上规律，请直接写出OM2014的长度为．40．如图，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时反射角等于入射角，当小球第1次碰到矩形的边时的点为P1，第2次碰到矩形的边时的点为P2，…，第n次碰到矩形的边时的点为P n，则点P3的坐标是；点P2014的坐标是．41．在平面直角坐标系中，点A1（1，0），A2（2，3），A3（3，2），A4（4，5）…用你发现的规律，确定点A2013的坐标为．42．如图是某同学在课外设计的一款软件，蓝精灵从O点第一跳落到A1（1，0），第二跳落到A2（1，2），第三跳落到A3（4，2），第四跳落到A4（4，6），第五跳落到A5．到达A2n后，要向方向跳个单位落到A2n+1．43．如图，在平面直角坐标系中，点A、B、C的坐标分别是（﹣1，﹣1）、（0，2）、（2，0），点P在y轴上，且坐标为（0，﹣2）．点P关于点A的对称点为P1，点P1关于点B的对称点为P2，点P2关于点C的对称点为P3，点P3关于点A的对称点为P4，点P4关于点B的对称点为P5，点P5关于点C的对称点为P6，点P6关于点A的对称点为P7…，按此规律进行下去，则点P2013的坐标、是．44．如图，所有正三角形的一边平行于x轴，一顶点在y轴上．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1、A2、A3、A4…表示，其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位，则顶点A3的坐标是，A92的坐标是．45．如图，在直角坐标系中，已知点A（﹣3，0）、B（0，4），对△OAB连续作旋转变换，依次得到△1、△2、△3、△4…，则△2013的直角顶点的坐标为．46．如图，在平面直角坐标系中，一动点从原点O出发，按向上，向右，向下，向右的方向不断地移动，每次移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0），…那么点A4n+1（n为自然数）的坐标为（用n表示）．47．将正方形ABCD的各边按如图所示延长，从射线AB开始，分别在各射线上标记点A1、A2、A3、…，按此规律，点A2012在射线上．48．如图，在平面直角坐标系中，线段OA1＝1，OA1与x轴的夹角为30°，线段A1A2＝1，A2A1⊥OA1，垂足为A1；线段A2A3＝1，A3A2⊥A1A2，垂足为A2；线段A3A4＝1，A4A3⊥A2A3，垂足为A3；…按此规律，点A2012的坐标为．49．如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2011次运动后，动点P的坐标是．浙教新版八年级上学期《4.2 平面直角坐标系》同步练习卷参考答案与试题解析一．填空题（共49小题）1．在平面直角坐标系中，点（3，﹣5）在第四象限．【分析】应先判断出所求的点的横纵坐标的符号，进而判断其所在的象限．【解答】解：∵点P（3，﹣5）的横坐标是正数，纵坐标是负数，∴点P在平面直角坐标系的第四象限．故答案填：四．【点评】解决本题的关键是掌握好四个象限的点的坐标的特征：第一象限正正，第二象限负正，第三象限负负，第四象限正负．2．已知a＜b＜0，则点A（a﹣b，b）在第三象限．【分析】先根据a＜b＜0判断出a﹣b＜0，再根据点在坐标系中各象限的坐标特点解答．【解答】解：∵a＜b＜0，∴a﹣b＜0，∴点A（a﹣b，b）的横坐标小于0，纵坐标小于0，符合点在第三象限的条件，故答案填：三．【点评】本题主要考查了点在第三象限内坐标的符号特征，比较简单．3．点A（﹣2，1）在第二象限．【分析】根据点在第二象限的坐标特点解答即可．【解答】解：∵点A的横坐标﹣2＜0，纵坐标1＞0，∴点A在第二象限内．故答案填：二．【点评】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．4．点P（3，2）在第一象限．【分析】根据各象限内点的坐标的符号规律判断．【解答】解：因为P点坐标符号为（+，+），所以在第一象限．故填：一．【点评】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点，另本题数值较小，也可画出坐标系，确定点的位置．5．请写出一个在第二象限的点的坐标（﹣4，2）．【分析】只需让横坐标为负数，纵坐标为正数即可．【解答】解：令横坐标为负数，纵坐标为正数，如（﹣1，3），（﹣3，5）等，答案不唯一．【点评】用到的知识点为：第二象限点的坐标的符号为（﹣，+）．6．已知a是整数，点A（2a+1，2+a）在第二象限，则a＝﹣1．【分析】第二象限的点的坐标，横坐标小于0，纵坐标大于0，因而就得到关于a的不等式组，求出a的范围，又由于a是整数，就可以求出a的值．【解答】解：根据题意得：，解得：﹣2＜a＜，又∵a是整数，∴a＝﹣1．故填：﹣1．【点评】本题主要考查了坐标平面内各象限点的坐标的符号，常与不等式、方程结合起来求一些字母的取值范围，此类题往往转化成解不等式或不等式组的问题．这是一个常见的题目类型．7．已知点P在第二象限，它的横坐标与纵坐标的和为1，点P的坐标是（写出一个符合条件的一个点即可）P（﹣0.5，1.5）（答案不唯一）．【分析】由点P在第二象限，可知点P的横坐标小于0，纵坐标大于0，又横坐标与纵坐标的和为1，则P（﹣2，3）或（﹣3，4）等．【解答】解：∵点P在第二象限，∴点P的横坐标小于0，纵坐标大于0，∵横坐标与纵坐标的和为1，∴P（﹣2，3）或（﹣3，4），P（﹣0.5，1.5）（答案不唯一）故答案为：P（﹣0.5，1.5）（答案不唯一）．【点评】本题是一个开放性的题目，考查了平面直角坐标系中各个象限内点的符号．8．若点M（1+a，2b﹣1）在第二象限，则点N（a﹣1，1﹣2b）在第三象限．【分析】先根据已知点的坐标得到所求点的符号，进而判断所在象限即可．【解答】解：∵点M（1+a，2b﹣1）在第二象限，∴1+a＜0，2b﹣1＞0，∴a﹣1＜0，1﹣2b＜0，∴点N（a﹣1，1﹣2b）在第三象限．故答案填：三．【点评】解决本题的关键是掌握好四个象限的点的坐标的特征：第一象限正正，第二象限负正，第三象限负负，第四象限正负．9．已知第二象限内的点P到x轴，y轴的距离分别是2和3，则点P的坐标是（﹣3，2）．【分析】先根据题意确定P点坐标的符号，再根据其坐标到x轴，y轴的距离分别是2和3求出符合条件的坐标即可．【解答】解：∵第二象限点的特点是（﹣，+），点P到x轴的距离是2，∴|y|＝2，y＝2；又∵点P到y轴的距离是3，∴|y|＝3，y＝﹣3．∴点P的坐标是（﹣3，2）．故填（﹣3，2）．【点评】解答此题用到的知识点为：点到y轴的距离是横坐标的绝对值，点到x 轴的距离是纵坐标的绝对值．需根据象限内的符号再进行进一步的确定．10．点（2，﹣3）在第四象限．【分析】根据第四象限内点的坐标特点解答即可．【解答】解：∵点（2，﹣3）横坐标为正，纵坐标为负，∴应在第四象限．故填：四．【点评】解答此题的关键是熟记平面直角坐标系中各个象限内点的符号．四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．11．点P在第二象限内，并且到x轴的距离为2，到y轴的距离为3，则点P的坐标为（﹣3，2）．【分析】应先判断出点P的横纵坐标的符号，进而根据到坐标轴的距离判断其具体坐标．【解答】解：∵点P在第二象限内，∴点的横坐标小于0，纵坐标大于0，∵点到x轴的距离为2，到y轴的距离为3，∴点的横坐标是﹣3，纵坐标是2．则点P的坐标为（﹣3，2）．故答案填（﹣3，2）．【点评】本题主要考查了平面直角坐标系中第二象限的点的坐标的符号特点及点的坐标的几何意义：点到x轴的距离为点的纵坐标的绝对值，到y轴的距离为点的横坐标的绝对值．12．如果点M（a+b，ab）在第二象限，那么点N（a，b）在第三象限．【分析】先根据点M（a+b，ab）在第二象限确定出a+b＜0，ab＞0，再进一步确定a，b的符号即可求出答案．【解答】解：∵点M（a+b，ab）在第二象限，∴a+b＜0，ab＞0；∵ab＞0可知ab同号，又∵a+b＜0可知a，b同是负数．∴a＜0 b＜0，即点N在第三象限．故答案填：三．【点评】本题主要考查了点在各象限内坐标的符号及不等式的解法，比较简单．13．如果a＞0，b＜0，那么点P（a，b）在第四象限．【分析】根据a＞0，b＜0和第四象限内的坐标符号特点可确定p在第四象限．【解答】解：∵a＞0，b＜0，∴点P（a，b）在第四象限．故填：四．【点评】主要考查了平面直角坐标系中各个象限的点的坐标的符号特点．四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．14．若，则点P（x，y）在二、四象限．【分析】因为，所以x，y异号，分情况讨论即可得出点P（x，y）所在象限．【解答】解：∵，∴x，y异号，当x＞0时，y＜0，点P（x，y）在四象限．当x＜0时，y＞0，点P（x，y）在二象限．故点P（x，y）在第二象限或第四象限．【点评】本题考查象限点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键．15．直角坐标系中，第四象限内的点M到横轴的距离为28，到纵轴的距离为6，则M点的坐标是（6，﹣28）．【分析】先根据M在第四象限内判断出点M横纵坐标的符号，再根据距离的意义即可求出点M的坐标．【解答】解：∵点M在第四象限内，∴点的横坐标大于0，纵坐标小于0，又∵P到x轴的距离是28，即纵坐标是﹣28，到y轴的距离是6，横坐标是6，故点P的坐标为（6，﹣28）．故填（6，﹣28）．【点评】解答此题的关键是熟记平面直角坐标系中各个象限内点的坐标符号及点的坐标的几何意义．16．在直角坐标系中，点B（1，﹣2）在第二象限，说法是：错误的．【分析】点的横坐标是正数，纵坐标是负数，符合第四象限的条件．【解答】解：因为1＞0，﹣2＜0，所以点B（1，﹣2）在第四象限．所以原说法是错误的，故填：错误．【点评】本题主要考查点在象限的条件，每个象限内的点的坐标符号各有特点，该知识点是中考的常考点．17．在直角坐标系中，点A（3，2）在第一象限．正确．【分析】先判断出所求的点的横纵坐标的符号，进而判断其所在的象限．【解答】解：因为点A（3，2）的横坐标是正数，纵坐标也是正数，所以点A在平面直角坐标系的第一象限．故答案为正确．【点评】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．18．直角坐标系中，点（﹣2，3）在第一象限．错．（判断对错）【分析】根据点（﹣2，3）的横坐标与纵坐标的符号判断其所在的象限即可．【解答】解：∵﹣2＜0，3＞0，∴点（﹣2，3）在第二象限，∴点（﹣2，3）在第一象限错误．故答案为B．【点评】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．19．如图，等边三角形ABC的边长为1，顶点B与原点O重合，点C在x轴的正半轴上，过点B作BA1⊥AC于点A1，过点A1作A1B1∥OA，交OC于点B1；过点B1作B1A2⊥AC于点A2，过点A2作A2B2∥OA，交OC于点B2；……，按此规律进行下去，点A2020的坐标是（，）．【分析】根据△ABC是等边三角形，得到AB＝AC＝BC＝1，∠ABC＝∠A＝∠ACB＝60°，解直角三角形得到A（，），C（1，0），根据等腰三角形的性质得到AA1＝A1C，根据中点坐标公式得到A1（，），推出△A1B1C是等边三角形，得到A2是A1C的中点，求得A2（，），推出A n（，），即可得到结论．【解答】解：∵△ABC是等边三角形，∴AB＝AC＝BC＝1，∠ABC＝∠A＝∠ACB＝60°，∴A（，），C（1，0），∵BA1⊥AC，∴AA1＝A1C，∴A1（，），∵A1B1∥OA，∴∠A1B1C＝∠ABC＝60°，∴△A1B1C是等边三角形，∴A2是A1C的中点，∴A2（，），同理A3（，），…∴A n（，），A2020的坐标是（，）．故答案为：（，）．【点评】本题考查了点的坐标，等边三角形的性质，关键是能根据求出的数据得出规律，题目比较好，但是有一定的难度．20．如图，正方形AOBO2的顶点A的坐标为A（0，2），O1为正方形AOBO2的中心；以正方形AOBO2的对角线AB为边，在AB的右侧作正方形ABO3A1，O2为正方形ABO3A1的中心；再以正方形ABO3A1的对角线A1B为边，在A1B 的右侧作正方形A1BB1O4，O3为正方形A1BB1O4的中心；再以正方形A1BB1O4的对角线A1B1为边，在A1B1的右侧作正方形A1B1O5A2，O4为正方形A1B1O5A2的中心：…；按照此规律继续下去，则点O2018的坐标为（21010﹣2，21009）．【分析】由题意Q1（1，1），O2（2，2），O3（，4，2），O4（，6，4），O5（10，4），O6（14，8）…观察可知，下标为偶数的点的纵坐标为2，下标为偶数的点在直线y＝x+1上，点O2018的纵坐标为21009，可得21009＝x+1，同侧x＝21010﹣2，可得点O2018的坐标为（21010﹣2，21009）．【解答】解：由题意Q1（1，1），O2（2，2），O3（，4，2），O4（，6，4），O5（10，4），O6（14，8）…观察可知，下标为偶数的点的纵坐标为2，下标为偶数的点在直线y＝x+1上，∵点O2018的纵坐标为21009，∴21009＝x+1，∴x＝21010﹣2，∴点O2018的坐标为（21010﹣2，21009）．故答案为（21010﹣2，21009）．【点评】本题考查规律型：点的坐标，一次函数的应用，解题的关键是学会探究规律的方法，灵活运用所学知识解决问题，属于中考常考题型．21．在平面直角坐标系中，点A（，1）在射线OM上，点B（，3）在射线ON上，以AB为直角边作Rt△ABA1，以BA1为直角边作第二个Rt△BA1B1，以A1B1为直角边作第三个Rt△A1B1A2，…，依此规律，得到Rt△B2017A2018B2018，则点B2018的纵坐标为32019．【分析】根据题意，分别找到AB、A1B1、A2B2……及BA1、B1A2、B2A3……线段长度递增规律即可【解答】解：由已知可知点A、A1、A2、A3……A2018各点在正比例函数y＝的图象上点B、B1、B2、B3……B2018各点在正比例函数y＝的图象上两个函数相减得到横坐标不变的情况下两个函数图象上点的纵坐标的差为：①由已知，Rt△A1B1A2，…，到Rt△B2017A2018B2018都有一个锐角为30°∴当A（B）点横坐标为时，由①AB＝2，则BA1＝2，则点A1横坐标为，B1点纵坐标为9＝32当A1（B1）点横坐标为3时，由①A1B1＝6，则B1A2＝6，则点A2横坐标为，B2点纵坐标为27＝33当A2（B2）点横坐标为9时，由①A2B2＝18，则B2A3＝18，则点A3横坐标为，B3点纵坐标为81＝34依稀类推点B2018的纵坐标为32019故答案为：32019【点评】本题是平面直角坐标系规律探究题，考查了含有特殊角的直角三角形各边数量关系，解答时注意数形结合．22．如图，在平面直角坐标系中，等腰直角三角形OAA1的直角边OA在x轴上，点A1在第一象限，且OA＝1，以点A1为直角顶点，OA1为一直角边作等腰直角三角形OA1A2，再以点A2为直角顶点，OA2为直角边作等腰直角三角形OA2A3…依此规律，则点A2018的坐标是（0，21009）．【分析】本题点A坐标变化规律要分别从旋转次数与点A所在象限或坐标轴、点A到原点的距离与旋转次数的对应关系．【解答】解：由已知，点A每次旋转转动45°，则转动一周需转动8次，每次转动点A到原点的距离变为转动前的倍∵2018＝252×8+2∴点A2018的在y轴正半轴上，OA2018＝＝21009故答案为：（0，21009）【点评】本题是平面直角坐标系下的规律探究题，除了研究动点变化的相关数据规律，还应该注意象限符号．23．如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，﹣1），P5（2，﹣1），P6（2，0），…，则点P2017的坐标是（672，1）．【分析】先根据P6（2，0），P12（4，0），即可得到P6n（2n，0），P6n+1（2n，1），再根据P6（2×336，0），可得P2016（672，0），进而得到P2017（672，1）．×336【解答】解：由图可得，P6（2，0），P12（4，0），…，P6n（2n，0），P6n+1（2n，1），2016÷6＝336，（2×336，0），即P2016（672，0），∴P6×336∴P2017（672，1），故答案为：（672，1）．【点评】本题主要考查了点的坐标变化规律，解决问题的关键是根据图形的变化规律得到P6n（2n，0）．24．如图，Rt△OA0A1在平面直角坐标系内，∠OA0A1＝90°，∠A0OA1＝30°，以OA1为直角边向外作Rt△OA1A2，使∠OA1A2＝90°，∠A1OA2＝30°，以OA2为直角边向外作Rt△OA2A3，使∠OA2A3＝90°，∠A2OA3＝30°，按此方法进行下去，得到Rt△OA3A4，Rt△OA4A5，…，Rt△OA2016A2017，若点A0（1，0），则点A2017的横坐标为（）2016．【分析】由含30°角的直角三角形的性质和勾股定理求出OA1、OA2，得出规律，即可得出结果．【解答】解：∵∠OA0A1＝90°，OA1＝，∠A2OA1＝30°，同理：OA2＝（）2，…，OA n＝（）n，∴OA2017的长度为（）2017；∵2017×30°÷360＝168…1，∴OA2017与OA1重合，∴点A2017的横坐标为（）2017×＝（）2016＝（）2016故答案为：（）2016．【点评】本题考查了勾股定理、含30°角的直角三角形的性质；熟练掌握勾股定理，通过计算得出规律是解决问题的关键．25．在平面直角坐标系中，点P（x，y）经过某种变换后得到点P'（﹣y+1，x+2），我们把点P'（﹣y+1，x+2）叫做点P（x，y）的终结点．已知点P1的终结点为P2，点P2的终结点为P3，点P3的终结点为P4，这样依次得到P1、P2、P3、P4、…P n、…，若点P1的坐标为（2，0），则点P2017的坐标为（2，0）．【分析】求得点P2、P3、P4、P5的值，即可发现其中规律，即可解题．【解答】解：P1坐标为（2，0），则P2坐标为（1，4），P3坐标为（﹣3，3），P4坐标为（﹣2，﹣1），P5坐标为（2，0），∴P n的坐标为（2，0），（1，4），（﹣3，3），（﹣2，﹣1）循环，∵2017＝2016+1＝4×504+1，∴P2017坐标与P1点重合，故答案为（2，0）．【点评】本题考查了学生发现点的规律的能力，本题中找到P n坐标得规律是解题的关键．26．如图，在平面直角坐标系中，等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上，且OA1＝A1A2＝1，以OA2为直角边作第二个等腰直角三角形OA2A3，以OA3为直角边作第三个等腰直角三角形OA3A4，…，依此规律，得到等腰直角三角形OA2017A2018，则点A2017的坐标为（0，（）2016）或（0，21008）．【分析】根据等腰直角三角形的性质得到OA1＝1，OA2＝，OA3＝（）2，…，OA2017＝（）2016，再利用A1、A2、A3、…，每8个一循环，再回到y轴的正半轴的特点可得到点A2017在y轴的正半轴上，即可确定点A2017的坐标．【解答】解：∵等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上，且OA1＝A1A2＝1，以OA2为直角边作第二个等腰直角三角形OA2A3，以OA3为直角边作第三个等腰直角三角形OA3A4，…，∴OA1＝1，OA2＝，OA3＝（）2，…，OA2017＝（）2016，∵A1、A2、A3、…，每8个一循环，再回到y轴的正半轴，2017÷8＝252…1，∴点A2017在y轴正半轴上，∵OA2017＝（）2016，∴点A2017的坐标为（0，（）2016）即（0，21008）．故答案为（0，（）2016）或（0，21008）．【点评】本题考查了规律型：点的坐标，等腰直角三角形的性质：等腰直角三角形的两底角都等于45°；斜边等于直角边的倍．也考查了直角坐标系中各象限内点的坐标特征．27．如图，四条直线l1：y1＝x，l2：y2＝x，l3：y3＝﹣x，l4：y4＝﹣x，OA1＝1，过点A1作A1A2⊥x轴，交l1于点A2，再过点A2作A2A3⊥l1交l2于点A3，再过点A3作A3A4⊥l2交y轴于点A4…，则点A2017坐标为（（）2016，0）．【分析】先利用各直线的解析式得到x轴、l1、l2、y轴、l3、l4依次相交为30的角，各点的位置是每12个一循环，由于2017＝168×12+1，则可判定点A2017在x轴的正半轴上，再规律得到OA2016＝（）2015，然后表示出点A2017坐标．【解答】解：∵y1＝x，l2：y2＝x，l3：y3＝﹣x，l4：y4＝﹣x，∴x轴、l1、l2、y轴、l3、l4依次相交为30的角，∵2017＝168×12+1，∴点A2017在x轴的正半轴上，∵OA2＝＝，OA3＝（）2，OA4＝（）3，…OA2017＝（）2016，∴点A2017坐标为（（）2016，0）．故答案为（（）2016，0）．【点评】本题考查了规律型：点的坐标：解答此题的关键是利用三角函数确定各点到原点的距离和点的位置的循环规律．28．把多块大小不同的30°直角三角板如图所示，摆放在平面直角坐标系中，第一块三角板AOB的一条直角边与y轴重合且点A的坐标为（0，1），∠ABO ＝30°；第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1；第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2；第四块三角板的斜边B2B3与第三块三角板的斜边B1B2垂直且交y轴于点B3；…按此规律继续下去，则点B2017的坐标为（0，﹣31009）．【分析】根据题意和图象可以发现题目中的变化规律，从而可以求得点B2017的坐标．【解答】解：由题意可得，OB＝OA•tan60°＝1×＝，OB1＝OB•tan60°＝＝（）2＝3，OB2＝OB1•tan60°＝（）3，…∵2017÷4＝504…1，∴点B2017的坐标为（0，﹣）即（0，﹣31009），故答案为：（0，﹣31009）．【点评】本题考查规律型：点的坐标，解答本题的关键是明确题意，找出题目中坐标的变化规律，求出相应的点的坐标．29．如图，在平面直角坐标系中，直线l：y＝x+2交x轴于点A，交y轴于点A1，点A2，A3，…在直线l上，点B1，B2，B3，…在x轴的正半轴上，若△A1OB1，△A2B1B2，△A3B2B3，…，依次均为等腰直角三角形，直角顶点都在x轴上，则第n个等腰直角三角形A n B n﹣1B n顶点B n的横坐标为2n+1﹣2．【分析】先求出B1、B2、B3…的坐标，探究规律后，即可根据规律解决问题．【解答】解：由题意得OA＝OA1＝2，∴OB1＝OA1＝2，B1B2＝B1A2＝4，B2A3＝B2B3＝8，∴B1（2，0），B2（6，0），B3（14，0）…，2＝22﹣2，6＝23﹣2，14＝24﹣2，…∴B n的横坐标为2n+1﹣2．故答案为2n+1﹣2．【点评】本题考查规律型：点的坐标、等腰直角三角形的性质等知识，解题的关键是从特殊到一般，探究规律，利用规律解决问题，属于中考常考题型．30．如图，在平面直角坐标系中，△A1A2A3，△A3A4A5，△A5A6A7，△A7A8A9，…，都是等边三角形，且点A1，A3，A5，A7，A9的坐标分别为A1（3，0），A3（1，0），A5（4，0），A7（0，0），A9（5，0），依据图形所反映的规律，则A100的坐标为（，﹣）．【分析】根据等边三角形的性质可得出A2（2，），A4（，﹣），A6（2，2），A8（，﹣），…，根据点的变化找出变化规律“A4n+2（2，n+），A4n+4（，﹣）（n为自然数）”，依此规律即可得出点A100的坐标．【解答】解：观察，发现规律：A2（2，），A4（，﹣），A6（2，2），A8（，﹣），…，∴A4n+2（2，n+），A4n+4（，﹣）（n为自然数），∵100＝4×24+4，∴A100的坐标为（，﹣）．故答案为：（，﹣）．【点评】本题考查了等边三角形的性质以及规律型中点的坐标，解题的关键是找出点坐标变化的规律“A4n+2（2，n+），A4n+4（，﹣）（n为自然数）”．本题属于中档题，难度不大，解决该题型题目时，根据等边三角形的性质找出第三个顶点的坐标，根据坐标的变化找出变化规律是关键．31．如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，﹣1），P5（2，﹣1），P6（2，0），…，则点P60的坐标是（20，0）．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4.2平面直角坐标系同步测试
一.选择题
1．（2018秋•吉州区期末）点A（3，3﹣π）所在的象限是（）
A．第一象限B．第二象限C．第三象限D．第四象限
2．（2019春•桥东区校级月考）若点A（﹣1，m）在第二象限，则m的值可以是（）A．﹣2 B．﹣1 C．0 D．1
3．（2019春•桥东区校级月考）如图所示，点B的坐标为（）
A．（1，2）B．（2，﹣1）C．（2，1）D．（1，﹣2）
4．（2019春•裕华区校级期中）在平面直角坐标系中，点P（4，﹣3）到x轴的距离（）A．4 B．3 C．5 D．﹣3
5．（2019春•潮阳区校级期末）已知点P位于x轴上方，距离x轴4个单位长度，位于y轴右侧，距y轴3个单位长度，则点P坐标是（）
A．（﹣3，4）B．（﹣4，3）C．（3，4）D．（4，3）
6．（2019春•普陀区期末）如果点A（a，b）在第二象限，那么a、b的符号是（）A．0＞a，0＞b B．0＜a，0＞b C．0＞a，0＜b D．0＜a，0＜b
7．（2019春•孝义市期中）在平面直角坐标系内，点P（x，x+5）的位置一定不在（）A．第一象限B．第二象限C．第三象限D．第四象限
8．（2019春•九龙坡区校级期中）若点P（2m﹣4，2m+4）在y轴上，那么m的值为（）A．2 B．﹣2 C．±2 D．0
9．（2019春•孝义市期中）规定以下两种变换：①f（a，b）＝（﹣a，b），如f（1，2）＝（﹣1，2）；②g （a，b）＝（﹣a，﹣b），如：g（1，2）＝（﹣1，﹣2）．按照以上变换有f[g（2，3）]＝f（﹣2，﹣3）
＝（2，﹣3）．则g[f（3，4）]（）
A．（3，4）B．（3，﹣4）C．（﹣3，4）D．（﹣3，﹣4）
10．（2019春•曾都区校级期中）在平面直角坐标系中，一只电子狗从原点O出发，按向上→向右→向下→向右的方向依次不断移动，每次移动1个单位长度，其行走路线如图所示，则A2019的坐标为（）
A．（1009，1）B．（1009，0）C．（2018，1）D．（2018，0）
二.填空题
11．（2019春•桥西区期末）点P（2，4）到y轴的距离是
12．（2019秋•资阳区校级月考）若点P（2x﹣1，3x+2）是x轴上的点，则x＝；若点P（2x﹣1，3x+2）是y轴上的点，则x＝．
13．（2019春•海珠区期末）若第二象限内的点P（x，y）满足|x|＝4、y2＝9，则点P的坐标是．14．（2019春•微山县期中）已知点P的坐标为（2m+1，m﹣4）并且满足点P到两坐标轴的距离相等，则点P的坐标是．
15．（2019春•尚志市期末）在平面直角坐标系中，点P（2n﹣1，3+3n）在坐标轴上，则n的值是．
三.解答题
16．如图，写出坐标系中各点的坐标．
17．（2019春•德城区期末）已知点P（2m+4，m﹣1），请分别根据下列条件，求出点P的坐标．（1）点P在x轴上；
（2）点P的纵坐标比横坐标大3；
（3）点P在过点A（2，﹣4）且与y轴平行的直线上．
18．（2018秋•高邮市期末）在平面直角坐标系xOy中，有一点P（a，b），实数a，b，m满足以下两个等式：2a﹣6m+4＝0，b+2m﹣8＝0．
（1）当a＝1时，点P到x轴的距离为；
（2）若点P在第一三象限的角平分线上，求点P的坐标；
（3）当a＜b时，则m的取值范围是．
19．（2019春•颍泉区校级期中）在平面直角坐标系xOy中，对于点P（x，y），若点Q的坐标为（ax+y，x+ay），其中a为常数，则称点Q是点P的“a级关联点”例如，点P（1，4）的“3级美联点”为Q（3×1+4，1+3×4），即Q（7，13）．
（1）已知点A（﹣2，6）的“级关联点”是点A1，求点A1的坐标．
（2）已知点M（m﹣1，2m）的“﹣3级关联点”M′位于y轴上．求点M′的坐标．
20．（2018秋•平度市期中）如图，在平面直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变换成△OA2B2，第三次将OA2B2变换成△OA3B3；已知变换过程中各点坐标分别为A（1，3），A1（2，3），A2（4，3），A3（8，3），B（2，0），B1（4，0），B2（8，0），B3（16，0）．
（1）观察每次变换前后的三角形有何变化，找出规律，按此规律再将△OA3B3变换成△OA4B4，则A4的坐标为，B4的坐标为．
（2）按以上规律将△OAB进行n次变换得到△OA n B n，则A n的坐标为，B n的坐标为；
（3）△OA n B n的面积为．。