材料力学基本第十二章 简单的超静定系统
合集下载
单位力法与超静定
[ M ( x ) M ( x )]2 U0 U 1 f A dx l 2 EI M 2 ( x) M 2 ( x) M ( x)M ( x) dx dx dx l 2 EI l 2 EI l EI
河南理工大学土木工程学院
材料力学
第十二章 能量法与超静定
材料力学
第十二章 能量法与超静定
第十二章 能量法与超静定问题
§12-1 概述
§12-2 杆件变形能的计算 §12-3 单位荷载法 §12-4 能量法解超静定问题
河南理工大学土木工程学院
材料力学
第十二章 能量法与超静定
§12-1 概述
一、能量方法
能量法是求位移的普遍方法，可以求结构上任意点沿任意 方向的位移。
F
C
1
C A x
A x
a B b
x
x
a
B
b
解：在 C点加竖向单位力 BC:
M ( x ) Fx T ( x) 0 M ( x ) Fx T ( x ) Fb
M ( x) x T ( x) 0 M ( x) x T ( x ) b
AB:
河南理工大学土木工程学院
河南理工大学土木工程学院
材料力学 2、三个力同时作用时
第十二章 能量法与超静定
任意截面的弯矩： M ( x ) M ( x )
变形能：
[ M ( x ) M ( x )]2 V 2 dx L 2 EI
V 1 V 2
[ M ( x ) M ( x )]2 U0 U 1 f A dx l 2 EI
河南理工大学土木工程学院
材料力学
第十二章 能量法与超静定
材料力学第12章 能量方法
9
(2)剪切变形时的应变能及应变能密度 工程中的剪切变形，一般是与其他变形相伴存 在的，且横截面上的切应力是不均匀分布的。在计 算其应变能时，应以单元体为基础。
图12.3
10
剪切变形时的应变能密度为
可见，剪切变形的应变能密度在数值上等于三 角形OAB的面积。 杆件的剪切应变能为
11
(3)圆轴扭转时的应变能 圆轴扭转时，如果材料应力应变关系处于线弹 性范围，则扭矩MT与扭转角φ的关系也是一条直线 ，如图12.4（b）所示。仿照杆件拉伸应变能的证 明，则变形过程中扭矩所做的功在数值上等于三角 形OAB的面积。有
4
那么，在外力从F1增加到F1+dF1的过程中， 外力功的增量为 当外力从零开始逐渐增加到F值时，则外力功 为 代入 ，得
5
图12.1
6
根据功能原理公式（12.1），则应变能为
式（12.3）为等截面直杆在轴力为常量条件下 的应变能计算公式。如果杆件的轴力FN分段为常 量时，应变能应为各段应变能的总和，即
7
积分可得整个杆件的应变能Vε为 为了更全面地了解应变能，还要知道单位体积 内的应变能，即应变能密度（strainenergy dens ity）由式（a）得应变能密度vε
8
显然，应变能密度vε的数值等于如图12.1（c） 所示三角形oab的面积。这样，又可以将上式的应 变能密度和应变能式（12.5）改写为
第12章
第一节 概述
能量方法
在工程结构分析中，经常需要计算结构和构件 的变形。使用一般的方法（如积分法）进行变形计 算时，需要分析结构和构件的具体变形形式，计算 工作量大。特别是对于刚架、桁架和曲杆等变形复 杂的超静定结构，一般方法根本无法完成。工程上 通常采用能量原理完成结构和构件的变形分析。
材料力学第十四章-超静定结构
材料力学第十四章-超静 定结构
欢迎来到材料力学第十四章的学习！本章将介绍超静定结构，我们将一起探 索它的特点、设计方法、力学分析以及应用领域。让我们开始学习吧！
超静定结构的定义
1 什么是超静定结构?
超静定结构是指具有多余约束的结构，其构件由多于所需的约束连接。
超静定结构的特点
1 多余约束的好处
超静定结构具有更高的稳定性和刚度，能够承受更大的荷载。
2 调整性能
通过改变约束条件，可以调整超静定结构的性能。
超静定结构的设计方法
1
力学方法
利用材料力学的知识和结构理论进行设计和分析。
2
优化设计
采用优化算法寻找最佳的结构设计。
3
经验和直觉
通过经验和直觉进行设计和改进。
超静定结构的力学分析
受力分析
通过受力分析了解超静定结构中力的传递和分布。
应力分析
通过应力分析研究超静定结构中的应力分布和变形。
超静定结构的应用领域
桥梁工程
超静定结构可以提高桥梁的稳定性和承载能力。
航空航天
超静定结构可以减轻飞行器的重量，提高性能。
建筑设计
超静定结构可以实现更大跨度和更复杂的建筑形 态。
机械设计
超静定结构可以提高机械设备的稳定性和准确性。
超静定结构的挑战与解决方案
1
挑战
超静定结构的设计和分析复杂，需要考虑多个因素。
2
解决方案
借助计算机辅助设计和模拟技术，提高设计和分析的效率。
3
创新思维
采用创新的方法和理念，寻找超静定结构的新应用。
总结与展望
通过本章的学习，我们了解了超静定结构的定义、特点、设计方法、力学分 析、应用领域以及面临的挑战。希望这些知识能够帮助您深入了解这一领域， 并为未来的设计和研究提供启示。
欢迎来到材料力学第十四章的学习！本章将介绍超静定结构，我们将一起探 索它的特点、设计方法、力学分析以及应用领域。让我们开始学习吧！
超静定结构的定义
1 什么是超静定结构?
超静定结构是指具有多余约束的结构，其构件由多于所需的约束连接。
超静定结构的特点
1 多余约束的好处
超静定结构具有更高的稳定性和刚度，能够承受更大的荷载。
2 调整性能
通过改变约束条件，可以调整超静定结构的性能。
超静定结构的设计方法
1
力学方法
利用材料力学的知识和结构理论进行设计和分析。
2
优化设计
采用优化算法寻找最佳的结构设计。
3
经验和直觉
通过经验和直觉进行设计和改进。
超静定结构的力学分析
受力分析
通过受力分析了解超静定结构中力的传递和分布。
应力分析
通过应力分析研究超静定结构中的应力分布和变形。
超静定结构的应用领域
桥梁工程
超静定结构可以提高桥梁的稳定性和承载能力。
航空航天
超静定结构可以减轻飞行器的重量，提高性能。
建筑设计
超静定结构可以实现更大跨度和更复杂的建筑形 态。
机械设计
超静定结构可以提高机械设备的稳定性和准确性。
超静定结构的挑战与解决方案
1
挑战
超静定结构的设计和分析复杂，需要考虑多个因素。
2
解决方案
借助计算机辅助设计和模拟技术，提高设计和分析的效率。
3
创新思维
采用创新的方法和理念，寻找超静定结构的新应用。
总结与展望
通过本章的学习，我们了解了超静定结构的定义、特点、设计方法、力学分 析、应用领域以及面临的挑战。希望这些知识能够帮助您深入了解这一领域， 并为未来的设计和研究提供启示。
材料力学第十二章动载荷
冲击物对被冲击物作用一 个惯性力Fd ,因而被冲击物 发生变形；被冲击物给冲 击物一个反作用力，使冲 击物的速度减为零。
冲击过程是一个瞬间 过程，难以求得加速 度值，工程中用能量 法来研究。
动画
静止
冲击物为刚性，冲击时冲击 物的变形及变形能不计；冲击过程中，被冲击物始终
处于弹性范围之内；
h
简化假设：
复习
能量法
能量原理：外力功=变形能
拉压： Ul
N 2l 2EA
l
N 2 (x)dx 2EA
扭转： Un
M n2l 2GIp
纯弯曲：
l
M n2 (x)dx 2GI p
U
基本
w
变
形
M 2l
变2E形I能计
M
算l
2 (x)dx 2EI
第十二章 动 载荷
12-1 概述 静载荷 ：载荷由零缓慢增加，到达某值后保持不变； 动载荷 ：引起构件加速度的载荷或冲击载荷； 动变形和动应力 ：在动载荷下产生的变形和应力。 线弹性模型 ：动载荷作用下应力应变保持线形关系。
动载荷问题分类：
惯性力问题：达朗伯原理 冲击问题：能量守衡原理 疲劳问题：（下一次讨论） 振动问题：（不讲）
12-2 惯性力问题 １．等加速度运动时的应力 静内力： 静应力： 静变形： 动内力：
动应力： 动变形：
动荷系数
动荷系数：动内力与静内 力之比； 动应力与静应力之比； 动变形与静变形之比。
由于构件在静载荷作用下 的内力、应力和变形的计 算已经掌握，所以在此基 础上计算出动荷系数，就 可以求解动内力、动应力 和动变形了。所以，解决 动载荷问题的关键是确定 动荷系数。
2．旋转运动
（薄壁圆环的 匀速转动）
冲击过程是一个瞬间 过程，难以求得加速 度值，工程中用能量 法来研究。
动画
静止
冲击物为刚性，冲击时冲击 物的变形及变形能不计；冲击过程中，被冲击物始终
处于弹性范围之内；
h
简化假设：
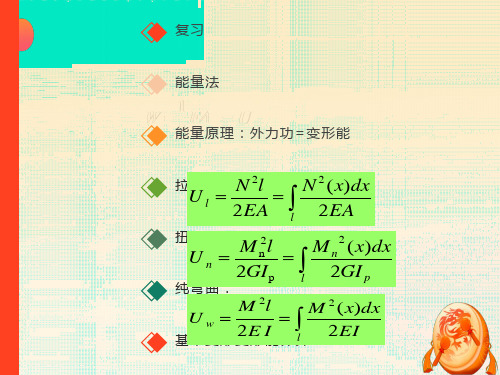
复习
能量法
能量原理：外力功=变形能
拉压： Ul
N 2l 2EA
l
N 2 (x)dx 2EA
扭转： Un
M n2l 2GIp
纯弯曲：
l
M n2 (x)dx 2GI p
U
基本
w
变
形
M 2l
变2E形I能计
M
算l
2 (x)dx 2EI
第十二章 动 载荷
12-1 概述 静载荷 ：载荷由零缓慢增加，到达某值后保持不变； 动载荷 ：引起构件加速度的载荷或冲击载荷； 动变形和动应力 ：在动载荷下产生的变形和应力。 线弹性模型 ：动载荷作用下应力应变保持线形关系。
动载荷问题分类：
惯性力问题：达朗伯原理 冲击问题：能量守衡原理 疲劳问题：（下一次讨论） 振动问题：（不讲）
12-2 惯性力问题 １．等加速度运动时的应力 静内力： 静应力： 静变形： 动内力：
动应力： 动变形：
动荷系数
动荷系数：动内力与静内 力之比； 动应力与静应力之比； 动变形与静变形之比。
由于构件在静载荷作用下 的内力、应力和变形的计 算已经掌握，所以在此基 础上计算出动荷系数，就 可以求解动内力、动应力 和动变形了。所以，解决 动载荷问题的关键是确定 动荷系数。
2．旋转运动
（薄壁圆环的 匀速转动）
超静定问题
ΔA ΔC w B B0 B1 ΔB 2
FN3
ΔA'
A'
F
ΔA
由位移相容 条件 ΔA ΔA ， 利用物理关系(位 移或变形计算公 式)可得补充方程：
A
FN3
FN3 l1 cos 2 E3 A3 2 E1 A1 cos
F FN3 l1
Review
于是可求出多余未知力FN3 。
材料力学
简单的超静定问题
5
e B
材料力学
简单的超静定问题
10
例题 6-5
3. 根据位移相容条件并利用物理关系得补充方程 M ea M B l GI p GI p 求得 M ea MB l 可由平衡方程求得为
M ea M eb M A Me M B Me l l
材料力学
简单的超静定问题
例题 6-7
材料力学
简单的超静定问题
27
例题 6-7
把图d所示外伸梁， 视为由悬臂梁AB(图 e)和简支梁BC(图f) 两部分组成。
( FN a )( 2a ) 2FN a 2 2FN a 3 BM , w A1 B a ( ) 3 EI 3 EI 3 EI 3 3 3 3 FN a 2FN a FN a FN a w A2 ＝ ( ) , w AF＝ ＋ ＝ ( ) 3 EI 3 EI 3 EI EI
材料力学
简单的超静定问题
39
现按如图a中所示各支点沉陷DB >DC > DA的情 况进行分析。此时，支座B相对于支座A 、C 沉陷 后的点A1 、C1 的连线有位移 ΔA ΔC w B B0 B1 ΔB 2
材料力学
材料力学第十二章-考虑材料塑性的极限分析精选全文
M Hi 0 S A a S A 2a Fu 3a 0
极限荷载 Fu S A 容许荷载 [F ] Fu / n
§2-3 等直圆杆扭转时的极限扭矩
S
Mx
S
Mx
S
Mx
O
外力增大
O
外力增大
O
S
S
S
只有弹性区 弹性极限状态
即有弹性区，又有塑性区 弹塑性状态
只有塑性区 塑性极限状态
弹性状态下横截面上 扭矩的最大值
max－S
残余应力
Mu Mr MS
由残余应力分布图知：
max
Mr Wz
最大残余应力发生在截面屈服区与弹性区的交界处；
中性轴上各点的残余应力为零。
作业：
2－2、5； 2－10
第十二章 考虑材料塑性的极限分 析
◆ 塑性变形·塑性极限分析的假设 ◆ 拉、压杆系的极限荷载 ◆ 等直圆杆扭转时的极限扭矩 ◆ 梁的极限弯矩·塑性铰
§2-1 塑性变形·塑性极限分析的假设
在弹性范围内进行强度计算
单向应力状态下采用正应力强度条件： max [ ] 纯切应力状态下采用切应力强度条件： max [ ]
弹性极限状态
弹塑性状态
屈服弯矩 MS ？
在完全塑性状态下
完全塑性状态
极限弯矩 Mu ？
塑性铰 卸载时塑性铰的效应会消失
弹性极限状态
弹塑性状态
完全塑性状态
弹性极限状态下横截面上的最大弯矩 MS ：
max
M Wz
MS
bh2 6
S
完全塑性状态下横截面上的最大弯矩 Mu ？
截面完全屈服时中性轴的位置如何确定？
M xS
Wp S
πd3 16
超静定(静不定)结构概述
材料力学
我们称与多余约束对应的约束力为多余约束力。 求解超静定系统的基本方法是：
解除多余约束，代之以多余约束反力然后 根据多余约束处的变形协调条件建立补充方程 进行求解。
解除多余约束后得到的静定结构，称为原 超静定系统的基本静定系统或相当系统。
材料力学
（本章主要学习用力法解超静定结构）
目录
材料力学
材料力学
材料力学
超静定（静不定）结构概述
在超静定系统中，按其多余约束的情况，可以分为：
外力超静定系统和内力超静定系统。
外力超静定：
支座反力不能全由平衡方程求出； 内力超静定：
支座反力可由平衡方程求出，但杆件 的内力却不能全由平衡方程求出.
材料力学
目录
材料力学
例如
P
Pl
A
B
C
C
Байду номын сангаас
P
a
B
a
A
材料力学
目录
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-能量法(圣才出品)
第12章能量法12.1 复习笔记由于弹性体的变形具有可逆性，因此外力在相应位移上做功在数值上等于在物体内积蓄的应变能。
利用功和能的概念求解可变形固体的位移、变形和内力等的方法，称为能量法。
能量法是有限元法求解固体力学问题的基础。
本章首先介绍了应变能和余能的概念及计算方法，在此基础上讨论了卡氏定理，最后介绍了能量法在求解超静定问题中的应用。
本章应重点掌握卡氏定理内容及能量法求解超静定问题的应用。
一、应变能和余能（见表12-1-1）表12-1-1 应变能和余能二、卡氏定理（见表12-1-2）表12-1-2 卡氏定理三、能量法求解超静定系统（见表12-1-3）表12-1-3 能量法求解超静定系统12.2 课后习题详解12-1 图12-2-1（a）、（b）所示各杆均由同一种材料制成，材料为线弹性，弹性模量为E。
各杆的长度相同。
试求各杆的应变能。
图12-2-1（a）图12-2-1（b ）解：（1）图12-2-1中（a ）杆的应变能为：222112212222222222231842112(2)24478Ni i i F l F l F l V EA EA EA l F F lE d E dF l Ed ==⨯+⎛⎫⋅⋅ ⎪⎝⎭=⨯+⋅⋅=∑επππ（2）图12-2-1中（b ）杆上距离下端x 处截面上的轴力为：F N （x ）＝F ＋fx ＝F ＋（F/l ）x ，故杆件的应变能为：2002220()d d 214d 23llN l F x V V xEAF F x F l l x EA Ed ==⎛⎫+ ⎪⎝⎭==⎰⎰⎰εεπ12-2 拉、压刚度为EA的等截面直杆，上端固定、下端与刚性支承面之间留有空隙Δ，在中间截面B处承受轴向力F作用，如图12-2-2所示。
杆材料为线弹性，当F＞EAΔ/l时，下端支承面的反力为：F C＝F/2－（Δ/l）（EA/2）。
于是，力F作用点的铅垂位移为：ΔB＝（F－F C）l/EA＝Fl/（2EA）＋Δ/2。