中考数学圆与相似综合练习题含详细答案.docx

合集下载

中考数学压轴题专题圆与相似的经典综合题及答案.doc

中考数学压轴题专题圆与相似的经典综合题及答案一、相似1．如图所示，△ ABC 中， AB=AC，∠ BAC=90°， AD⊥ BC， DE⊥ AC，△ CDE 沿直线 BC 翻折到△ CDF，连结 AF 交 BE、 DE、 DC分别于点 G、 H、I．（1）求证： AF⊥ BE；（2）求证： AD=3DI．【答案】（1）证明：∵在△ ABC中， AB=AC，∠ BAC=90°， D 是 BC 的中点，∴AD=BD=CD，∠ ACB=45 ，°∵在△ ADC中， AD=DC，DE⊥ AC，∴A E=CE，∵△ CDE沿直线 BC 翻折到△ CDF，∴△ CDE≌ △CDF，∴C F=CE，∠ DCF=∠ACB=45 ，°∴C F=AE，∠ ACF=∠DCF+∠ACB=90 ，°在△ ABE 与△ ACF中，，∴△ ABE≌ △ ACF（SAS），∴∠ ABE=∠ FAC，∵∠ BAG+∠ CAF=90 ，°∴∠ BAG+∠ ABE=90 ，°∴∠ AGB=90 ，°∴AF⊥BE（2）证明：作IC 的中点 M，连接 EM，由（ 1）∠ DEC=∠ECF=∠ CFD=90°∴四边形 DECF是正方形，∴EC∥ DF， EC=DF，∴∠ EAH=∠ HFD， AE=DF，在△ AEH 与△FDH 中，∴△ AEH≌ △FDH（ AAS），∴EH=DH，∵∠ BAG+∠ CAF=90 ，°∴∠ BAG+∠ ABE=90 ，°∴∠ AGB=90 ，°∴AF⊥BE，∵M 是 IC 的中点， E 是 AC 的中点，∴EM∥AI，∴，∴DI=IM ，∴CD=DI+IM+MC=3DI，∴AD=3DI【解析】【分析】（ 1）根据翻折的性质和SAS 证明△ ABE≌ △ ACF，利用全等三角形的性质得出∠ ABE=∠ FAC，再证明∠ AGB=90°，可证得结论。

中考数学专题复习圆与相似的综合题及答案解析.doc

中考数学专题复习圆与相似的综合题及答案解析一、相似1．如图，在⊙ O 中，直径 AB 经过弦 CD 的中点 E，点 M 在 OD 上， AM 的延长线交⊙ O 于点G，交过 D 的直线于 F，且∠ BDF=∠ CDB，BD 与 CG交于点 N．（1）求证： DF 是⊙ O 的切线；（2）连结 MN，猜想 MN 与 AB 的位置有关系，并给出证明．【答案】（1）证明：∵直径 AB 经过弦 CD 的中点 E，，= ,即是的切线（2）解：猜想： MN∥AB．证明：连结 CB．∵直径 AB 经过弦 CD 的中点 E，∴=,=,∴∵∴∴∵∴∵∵∴∴∴MN ∥ AB．【解析】【分析】（1）要证DF 是⊙ O 的切线，由切线的判定知，只须证∠ODF=即可。

由垂径定理可得 AB⊥ CD，则∠ BOD+∠ODE= ，而∠ ODF=∠ CDF+∠ ODE，由已知易得∠ BOD=∠CDF，则结论可得证；（ 2 ）猜想： MN ∥ AB．理由：连结CB，由已知易证△ CBN∽ △ AOM ，可得比例式，于是由已知条件可转化为，∠ODB是公共角，所以可得△MDN ∽ △ODB，则∠ DMN=∠ DOB，根据平行线的判定可得MN ∥AB。

2．已知抛物线 y＝ ax2＋ bx＋ 5 与 x 轴交于点 A(1， 0)和点 B(5， 0)，顶点为 M．点 C 在 x 轴的负半轴上，且 AC＝ AB，点 D 的坐标为 (0， 3)，直线 l 经过点 C、D．（1）求抛物线的表达式；（2）点 P 是直线 l 在第三象限上的点，联结 AP，且线段 CP是线段 CA、 CB的比例中项，求tan∠ CPA的值；（3）在（ 2）的条件下，联结 AM、 BM，在直线 PM 上是否存在点 E，使得∠ AEM=∠AMB. 若存在，求出点 E 的坐标；若不存在，请说明理由．【答案】（1）解：∵抛物线与x轴交于点A（ 1， 0）， B（5， 0），∴,解得∴ 抛物线的解析式为（2）解：∵ A（1， 0）， B（ 5， 0），∴OA=1， AB=4.∵AC=AB且点 C 在点 A 的左侧，∴ AC=4 .∴CB=CA+AB=8.∵线段 CP 是线段 CA、 CB 的比例中项，∴.∴ CP=.又∵ ∠ PCB是公共角，∴ △ CPA∽ △ CBP .∴ ∠ CPA=∠ CBP.过P 作 PH⊥ x 轴于 H.∵OC=OD=3，∠DOC=90 ，°∴∠ DCO=45 .°∴ ∠ PCH=45 °∴ PH=CH=CP =4，∴H（ -7， 0）， BH=12，∴P（ -7，-4），∴，tan∠ CPA=.（3）解：∵抛物线的顶点是 M （3， -4），又∵ P（ -7，-4），∴PM∥x 轴 .当点 E 在 M 左侧，则∠BAM=∠ AME.∵ ∠ AEM=∠ AMB，∴ △ AEM∽ △ BMA.∴,∴.∴ME=5，∴ E（ -2， -4） .过点 A 作 AN⊥ PM 于点 N，则 N（ 1， -4） .当点 E 在 M 右侧时，记为点，∵ ∠ A N=∠AEN，∴ 点与 E 关于直线 AN 对称，则（4 ，-4） .综上所述， E 的坐标为（ -2， -4）或（ 4，-4） .【解析】【分析】（ 1）用待定系数法即可求解。

中考数学圆与相似综合题含详细答案

中考数学圆与相似综合题含详细答案一、相似1．阅读下列材料，完成任务：自相似图形定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形．例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形．任务：（1）图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为________；（2）如图2，已知△ABC中，∠ACB=90°，AC=4，BC=3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形．已知△ACD∽△ABC，则△ACD与△ABC的相似比为________；（3）现有一个矩形ABCD是自相似图形，其中长AD=a，宽AB=b（a＞b）．请从下列A、B两题中任选一条作答．A：①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a=________（用含b的式子表示）；②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a=________（用含n，b的式子表示）；B：①如图4﹣1，若将矩形ABCD先纵向分割出2个全等矩形，再将剩余的部分横向分割成3个全等矩形，且分割得到的矩形与原矩形都相似，则a=________（用含b的式子表示）；②如图4﹣2，若将矩形ABCD先纵向分割出m个全等矩形，再将剩余的部分横向分割成n 个全等矩形，且分割得到的矩形与原矩形都相似，则a=________（用含m，n，b的式子表示）．【答案】（1）（2）（3）；；或；或【解析】【解答】（解：（1）∵点H是AD的中点，∴AH= AD，∵正方形AEOH∽正方形ABCD，∴相似比为： == ；故答案为：；（ 2 ）在Rt△ABC中，AC=4，BC=3，根据勾股定理得，AB=5，∴△ACD与△ABC相似的相似比为：，故答案为：；（ 3 ）A、①∵矩形ABEF∽矩形FECD，∴AF：AB=AB：AD，即 a：b=b：a，∴a= b；故答案为：②每个小矩形都是全等的，则其边长为b和 a，则b： a=a：b，∴a= b；故答案为：B、①如图2，由①②可知纵向2块矩形全等，横向3块矩形也全等，∴DN= b，Ⅰ、当FM是矩形DFMN的长时，∵矩形FMND∽矩形ABCD，∴FD：DN=AD：AB，即FD： b=a：b，解得FD= a，∴AF=a﹣ a= a，∴AG= = = a，∵矩形GABH∽矩形ABCD，∴AG：AB=AB：AD即 a：b=b：a得：a= b；Ⅱ、当DF是矩形DFMN的长时，∵矩形DFMN∽矩形ABCD，∴FD：DN=AB：AD即FD： b=b：a解得FD= ，∴AF=a﹣ = ，∴AG= = ，∵矩形GABH∽矩形ABCD，∴AG：AB=AB：AD即：b=b：a，得：a= b；故答案为：或；②如图3，由①②可知纵向m块矩形全等，横向n块矩形也全等，∴DN= b，Ⅰ、当FM是矩形DFMN的长时，∵矩形FMND∽矩形ABCD，∴FD：DN=AD：AB，即FD： b=a：b，解得FD= a，∴AF=a﹣ a，∴AG= = = a，∵矩形GABH∽矩形ABCD，∴AG：AB=AB：AD即 a：b=b：a得：a= b；Ⅱ、当DF是矩形DFMN的长时，∵矩形DFMN∽矩形ABCD，∴FD：DN=AB：AD即FD： b=b：a解得FD= ，∴AF=a﹣，∴AG= = ，∵矩形GABH∽矩形ABCD，∴AG：AB=AB：AD即：b=b：a，得：a= b；故答案为： b或 b．【分析】由题意可知，用相似多边形的性质即可求解。

中考数学圆与相似综合经典题附详细答案

∴ 构造的三角形是等腰三角形的概率=
（3）解：存在，
易得 BC 的解析是为 y=﹣2x+4，S△ ABC= AC•OB= ×3×4=6， M 点的坐标为（m，﹣2m+4）（0≤m≤2）， ①当 N 点在 AC 上，如图 1，
∴ △ AMN 的面积为△ ABC 面积的，
∴ （m+1）（﹣2m+4）=2，解得 m1=0，m2=1，当 m=0 时，M 点的坐标为（0，4），N（0，0），则 AN=1，MN=4，
， ∴ AM=
=1 ， ∴ CM=CA ﹣ AM=2 ， ∴ S△ BCM=
×23=3．
（2）解：如图 2 中，连接 EC、CN，作 EQ⊥BC 于 Q，EP⊥BA 于 P．
；
③当 N 点在 AB 上，如图 3，
作 AH⊥BC 于 H，设 AN=t，则 BN= ﹣t，
由②得 AH= ，则 BH=
，
∵ ∠ NBG=∠ HBA，
∴ △ BNM∽ △ BHA，
∴
，即
，
∴ MN=，ຫໍສະໝຸດ ∵ AN•MN=2，即 •（ ﹣t）•
=2，
整理得 3t2﹣3 t+14=0，△ =（﹣3
∴ 点 N 在 AB 上不符合条件，
【答案】（1）解：y=x2+2x+1=（x+1）2 的图象沿 x 轴翻折，得 y=﹣（x+1）2 ，把 y=﹣（x+1）2 向右平移 1 个单位，再向上平移 4 个单位，得 y=﹣x2+4， ∴ 所求的函数 y=ax2+bx+c 的解析式为 y=﹣x2+4
（2）解：∵ y=x2+2x+1=（x+1）2 ， ∴ A（﹣1，0），当 y=0 时，﹣x2+4=0，解得 x=±2，则 D（﹣2，0），C（2，0）；当 x=0 时，y=﹣x2+4=4，则 B（0，4），从点 A，C，D 三个点中任取两个点和点 B 构造三角形的有：△ ACB，△ ADB，△ CDB， ∵ AC=3，AD=1，CD=4，AB= ，BC=2 ，BD=2 ， ∴ △ BCD 为等腰三角形，

中考数学圆与相似综合练习题及详细答案

中考数学圆与相似综合练习题及详细答案一、相似1．如图1，过等边三角形ABC边AB上一点D作交边AC于点E，分别取BC，DE 的中点M，N，连接MN．（1）发现：在图1中， ________；（2）应用：如图2，将绕点A旋转，请求出的值；（3）拓展：如图3，和是等腰三角形，且，M，N分别是底边BC，DE的中点，若，请直接写出的值．【答案】（1）（2）解：如图2中，连接AM、AN，，都是等边三角形，，，，，，，，，，∽，（3）解：如图3中，连接AM、AN，延长AD交CE于H，交AC于O，，，，，，，，，，，，，，，∽，，，，，，≌，，，，，，，，，，【解析】【解答】解：（1）如图1中，作于H，连接AM，，，，时等边三角形，，，，，平分线段DE，，、N、M共线，，四边形MNDH时矩形，，，故答案为：；【分析】（1）作DH ⊥BC 于H，连接AM.证四边形MNDH时矩形，所以MN=DH，则MN：BD=DH：BD=sin60°，即可求解；（2）利用△ABC ，△ADE 都是等边三角形可得AM：AB=AN：AD，易得∠BAD = ∠MAN ，从而得△ BAD ∽△ MAN，则NM：BD=AM：AB=sin60°，从而求解；（3）连接AM、AN，延长AD交CE于H，交AC于O.先证明△BAD ∽△MAN可得NM：BD=AM：AB=sin∠ABC；再证明△ BAD ≌△ CAE，则∠ ABD = ∠ ACE ，进而可得∠ ABC = 45°，可求出答案.2．如图，△ABC内接于⊙O，且AB＝AC.延长BC到点D，使CD＝CA，连接AD交⊙O于点E.（1）求证：△ABE≌△CDE；（2）填空：①当∠ABC的度数为________时，四边形AOCE是菱形；②若AE＝6，BE=8，则EF的长为________.【答案】（1）证明：∵AB=AC，CD=CA，∴∠ABC=∠ACB，AB=CD．∵四边形ABCE是圆内接四边形，∴∠ECD=∠BAE，∠CED=∠ABC．∵∠ABC=∠ACB=∠AEB，∴∠CED=∠AEB，∴△ABE≌△CDE（AAS）（2）60；【解析】【解答】解：（2）①当∠ABC的度数为60°时，四边形AOCE是菱形；理由是：连接AO、OC．∵四边形ABCE是圆内接四边形，∴∠ABC+∠AEC=180°．∵∠ABC=60，∴∠AEC=120°=∠AOC．∵OA=OC，∴∠OAC=∠OCA=30°．∵AB=AC，∴△ABC是等边三角形，∴∠ACB=60°．∵∠ACB=∠CAD+∠D．∵AC=CD，∴∠CAD=∠D=30°，∴∠ACE=180°﹣120°﹣30°=30°，∴∠OAE=∠OCE=60°，∴四边形AOCE是平行四边形．∵OA=OC，∴▱AOCE是菱形；②由（1）得：△ABE≌△CDE，∴BE=DE=8，AE=CE=6，∴∠D=∠EBC．∵∠CED=∠ABC=∠ACB，∴△ECD∽△CFB，∴ = ．∵∠AFE=∠BFC，∠AEB=∠FCB，∴△AEF∽△BCF，∴ = ，∴EF= = ．故答案为：①60°；② ．【分析】（1）由题意易证∠ABC=∠ACB，AB=CD；再由四点共圆和已证可得∠ABC=∠ACB=∠AEB，∠CED=∠AEB，则利用AAS可证得结论；（2）①连接AO、CO.宪政△ABC是等边三角形，再证明四边形AOCE是平行四边形，又AO=CO可得结论；②先证△ECD∽△CFB，可得EC：ED=CF：BC=6:8；再证△AEF∽△BCF，则AE：EF=BC：CF，从而求出EF.3．如图1，以□ABCD的较短边CD为一边作菱形CDEF,使点F落在边AD上，连接BE，交AF于点G.（1）猜想BG与EG的数量关系.并说明理由；（2）延长DE,BA交于点H，其他条件不变，①如图2，若∠ADC=60°，求的值；②如图3，若∠ADC=α（0°<α<90°）,直接写出的值.（用含α的三角函数表示）【答案】（1）解：，理由如下：∵四边形是平行四边形，∴∥， .∵四边形是菱形，∴∥， .∴∥， .∴ .又∵，∴≌ .∴（2）解：方法1：过点作∥，交于点，∴ .∵，∴∽ .∴ .由（1）结论知 .∴ .∴ .∵四边形为菱形，∴ .∵四边形是平行四边形，∴∥ .∴ .∵∥，∴ .∴，即 .∴是等边三角形。

中考数学圆与相似综合题汇编含详细答案

中考数学圆与相似综合题汇编含详细答案一、相似1．如图，在平面直角坐标系xOy中，抛物线y=ax2+bx+c（a＞0）与x轴相交于点A（﹣1，0）和点B，与y轴交于点C，对称轴为直线x=1．（1）求点C的坐标（用含a的代数式表示）；（2）联结AC、BC，若△ABC的面积为6，求此抛物线的表达式；（3）在第（2）小题的条件下，点Q为x轴正半轴上一点，点G与点C，点F与点A关于点Q成中心对称，当△CGF为直角三角形时，求点Q的坐标．【答案】（1）解：∵抛物线y=ax2+bx+c（a＞0）的对称轴为直线x=1，而抛物线与x轴的一个交点A的坐标为（﹣1，0）∴抛物线与x轴的另一个交点B的坐标为（3，0）设抛物线解析式为y=a（x+1）（x﹣3），即y=ax2﹣2ax﹣3a，当x=0时，y=﹣3a，∴C（0，﹣3a）（2）解：∵A（﹣1，0），B（3，0），C（0，﹣3a），∴AB=4，OC=3a，∴S△ACB= AB•OC=6，∴6a=6，解得a=1，∴抛物线解析式为y=x2﹣2x﹣3（3）解：设点Q的坐标为（m，0）．过点G作GH⊥x轴，垂足为点H，如图，∵点G与点C，点F与点A关于点Q成中心对称，∴QC=QG，QA=QF=m+1，QO=QH=m，OC=GH=3，∴OF=2m+1，HF=1，当∠CGF=90°时，∵∠QGH+∠FGH=90°，∠QGH+∠GQH=90°，∴∠GQH=∠HGF，∴Rt△QGH∽Rt△GFH，∴ = ，即，解得m=9，∴Q的坐标为（9，0）；当∠CFG=90°时，∵∠GFH+∠CFO=90°，∠GFH+∠FGH=90°，∴∠CFO=∠FGH，∴Rt△GFH∽Rt△FCO，∴ = ，即 = ，解得m=4，∴Q的坐标为（4，0）；∠GCF=90°不存在，综上所述，点Q的坐标为（4，0）或（9，0）．【解析】【分析】（1）根据抛物线是轴对称图形和已知条件可求得抛物线与x轴的另一个交点B的坐标，再用交点式可求得抛物线的解析式，然后根据抛物线与y轴交于点C可得x=0，把x=0代入解析式即可求得点C的坐标；（2）由（1）的结论可求得AB=4，OC=3a，根据三角形ABC的面积=AB•OC=6可求得a的值，则解析式可求解；（3）设点Q的坐标为（m，0）．过点G作GH⊥x轴，垂足为点H，根据中心对称的性质可得QC=QG，QA=QF=m+1，QO=QH=m，OC=GH=3。

中考数学圆与相似综合经典题及答案解析.docx

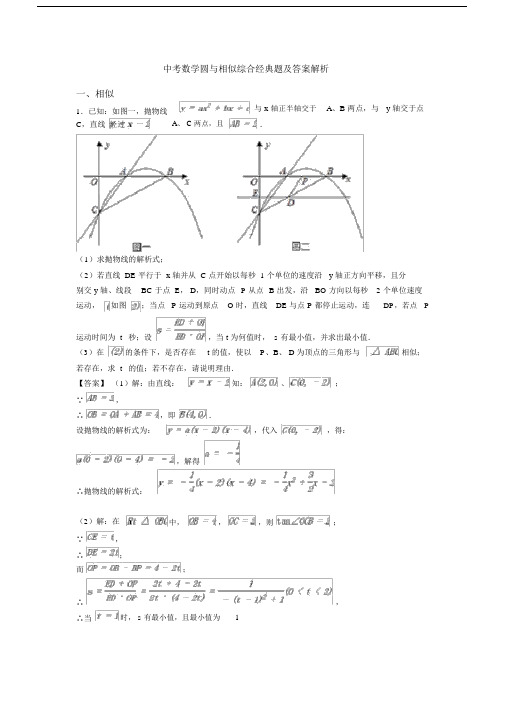
中考数学圆与相似综合经典题及答案解析一、相似1．已知：如图一，抛物线C，直线经过A、 C 两点，且与 x．轴正半轴交于A、B 两点，与y 轴交于点（1）求抛物线的解析式；（2）若直线 DE 平行于 x 轴并从 C 点开始以每秒 1 个单位的速度沿 y 轴正方向平移，且分别交 y 轴、线段BC 于点 E， D，同时动点P 从点运动，如图；当点P 运动到原点O 时，直线B 出发，沿BO 方向以每秒 2 个单位速度DE 与点 P 都停止运动，连DP，若点P运动时间为 t秒；设，当 t 为何值时， s 有最小值，并求出最小值．（3）在的条件下，是否存在t 的值，使以P、B、 D 为顶点的三角形与相似；若存在，求 t的值；若不存在，请说明理由．【答案】（1）解：由直线：知：、；∵，∴，即．设抛物线的解析式为：，代入，得：，解得∴抛物线的解析式：（2）解：在中，，，则；∵，∴；而；∴，∴当时， s 有最小值，且最小值为1（3）解：在中，在中，，∴以 P、 B、 D 为顶点的三角形与；，，则，则相似，已知；；，则有两种情况：，解得；，解得；综上，当或时，以P、B、D为顶点的三角形与相似【解析】【分析】（ 1）由直线与坐标轴相交易求得点A、 C 的坐标，用待定系数法即可求得抛物线的解析式；（2）由题意可将ED、 OP 用含 t 的代数式表示出来，并代入题目中的s 与 OP、 DE 的关系式整理可得s=（0<t<2），因为分子是定值1，所以分母越大，则分式的值越小，则当分母最大时，分式的值越小，即t=1 时， s 有最小值，且最小值为1；（ 3）解直角三角形可得BC 和 CD、 BD 的值，根据题意以P、 B、 D 为顶点的三角形与△ABC相似所得的比例式有两种情况：，，将这些线段代入比例式即可求解。

2．（1）问题发现：如图 1，在等边三角形ABC中，点 M 为 BC 边上异于B、 C 的一点，以AM 为边作等边三角形 AMN ，连接 CN， NC 与 AB 的位置关系为 ________；（2）深入探究：如图 2，在等腰三角形 ABC中， BA=BC，点 M 为 BC边上异于 B、C 的一点，以 AM 为边作等腰三角形 AMN ，使∠ ABC=∠ AMN， AM=MN ，连接 CN，试探究∠ ABC 与∠ACN 的数量关系，并说明理由；（3）拓展延伸：如图 3，在正方形ADBC 中， AD=AC，点 M 为 BC 边上异于B、C 的一点，以AM 为边作正方形 AMEF，点 N 为正方形AMEF 的中点，连接CN，若【答案】（1） NC∥ ABBC=10， CN=，试求EF的长．（2）解：∠ ABC=∠ ACN，理由如下：∵=1 且∠ ABC=∠ AMN ，∴△ ABC～△ AMN∴，∵A B=BC，∴∠ BAC=（180°﹣∠ABC），∵AM=MN∴∠ MAN=（180﹣°∠ AMN），∵∠ ABC=∠ AMN ，∴∠ BAC=∠ MAN ，∴∠ BAM=∠ CAN，∴△ ABM～△ ACN，∴∠ ABC=∠ ACN（3）解：如图3，连接 AB， AN，∵四边形 ADBC， AMEF 为正方形，∴∠ ABC=∠ BAC=45 ，°∠ MAN=45 °，∴∠ BAC﹣∠MAC=∠ MAN ﹣∠ MAC 即∠ BAM=∠ CAN，∵，∴，∴△ ABM～△ ACN∴，∴=cos45 = °，∴，∴B M=2，∴CM=BC﹣ BM=8，在 Rt△ AMC，AM=，∴EF=AM=2．【解析】【解答】解：（1） NC∥ AB，理由如下：∵△ ABC与△ MN 是等边三角形，∴A B=AC， AM=AN，∠BAC=∠MAN=60 °，∴∠ BAM=∠ CAN，在△ ABM 与△ ACN 中，，∴△ ABM≌ △ ACN（ SAS），∴∠ B=∠ACN=60 ，°∵∠ ANC+∠ ACN+∠ CAN=∠ ANC+60 +°∠CAN=180 ，°∴∠ ANC+∠ MAN+∠ BAM=∠ANC+60 +°∠ CAN=∠ BAN+∠ANC=180 ，°∴CN∥ AB；【分析】（1）由题意用边角边易得△ABM≌△ACN，则可得∠B=∠ACN=60°，所以∠BCN+∠B=∠BCA+∠ ACN+∠ B=180 ，°根据平行线的判定即可求解；（2）由题意易得△ABC～△AMN，可得比例式，由三角形内角和定理易得∠BAM=∠ CAN，根据相似三角形的判定可得△ ABM～△ACN，由相似三角形的性质即可求解；（3）要求EF 的值，只须求得CM 的值，然后解直角三角形AMC 即可求解。

中考数学圆与相似综合题汇编含答案.docx

中考数学圆与相似综合题汇编含答案一、相似1．如图，在□ ABCD中，对角线 AC、 BD 相交于点O，点 E、 F 是 AD 上的点，且AE=EF=FD.连结 BE、 BF。

使它们分别与AO 相交于点G、 H（1）求 EG： BG 的值（2）求证： AG=OG（3）设 AG =a ,GH =b，HO =c，求 a : b : c 的值【答案】（1）解：∵四边形 ABCD是平行四边形，∴AO=AC， AD=BC， AD∥ BC，∴△ AEG∽ △CBG，∴==．∵AE=EF=FD，∴BC=AD=3AE，∴GC=3AG， GB=3EG，∴EG： BG=1： 3（2）解：∵GC=3AG（已证），∴AC=4AG，∴AO=AC=2AG，∴GO=AO﹣ AG=AG（3）解：∵ AE=EF=FD，∴BC=AD=3AE，AF=2AE．∵AD∥ BC，∴△ AFH∽ △ CBH，∴===，∴= ，即 AH=AC．∵AC=4AG，∴a=AG=AC，b=AH﹣AG= AC﹣AC=AC，c=AO﹣AH= AC﹣AC=AC，∴a： b： c=：：=5：3： 2【解析】【分析】（ 1）根据平行四边形的性质可得AO= AC， AD=BC， AD∥BC，从而可证得△ AEG∽ △CBG，得出对应边成比例，由 AE=EF=FD可得 BC=3AE，就可证得 GB=3EG，即可求出 EG： BG 的值。

（2）根据相似三角形的性质可得 GC=3AG，就可证得 AC=4AG，从而可得 AO=2AG，即可证得结论。

（3）根据平行可证得三角形相似，再根据相似三角形的性质可得AG= AC， AH= AC，结合AO= AC，即可得到用含AC 的代数式分别表示出a、 b、 c，就可得到a： b： c 的值。

2．如图，在平面直角坐标系中，直线y=﹣x+与x轴、y轴分别交于点B、 A，与直线y=相交于点C．动点 P 从 O 出发在 x 轴上以每秒 5 个单位长度的速度向 B 匀速运动，点Q 从 C 出发在 OC 上以每秒 4 个单位长度的速度，向 O 匀速运动，运动时间为 t 秒（ 0＜ t ＜2）．（1）直接写出点 C 坐标及 OC、 BC 长；（2）连接 PQ，若△ OPQ 与△OBC 相似，求 t 的值；（3）连接 CP、 BQ，若 CP⊥ BQ，直接写出点 P 坐标．【答案】（1）解：对于直线y=﹣x+，令x=0，得到y=，∴A（0，），令 y=0，则 x=10，∴B（ 10，0），由，解得，∴C（，）．∴OC==8，BC==10（2）解：①当时，△ OPQ∽ △OCB，∴，∴t=．②当时，△ OPQ∽ △ OBC，∴，∴t=1 ，综上所述， t 的值为或1s时，△ OPQ与△ OBC相似（3）解：如图作PH⊥ OC于 H．∵OC=8， BC=6， OB=10，∴OC2+BC2=OB2，∴∠ OCB=90 ，°∴当∠ PCH=∠ CBQ时，PC⊥BQ．∵∠PHO=∠BCO=90 ，°∴PH∥ BC，∴，∴，∴P H=3t， OH=4t，∴t an ∠ PCH=tan∠ CBQ，∴，∴t=或0（舍弃），∴t=s 时， PC⊥ BQ．【解析】【分析】（ 1）根据直线与坐标轴交点的坐标特点求出A,B 点的坐标，解联立直线AB,与直线OC 的解析式组成的方程组，求出 C 点的坐标，根据两点间的距离公式即可直接算出 OC,OB的长；（2 ）根据速度乘以时间表示出OP=5t， CQ=4t， OQ=8-4t，①当 OP∶OC=OQ∶ OB 时，△OPQ∽△ OCB，根据比例式列出方程，求解得出t 的值；②当 OP∶ OB=OQ∶OC 时，△OPQ∽△ OBC，根据比例式列出方程，求解得出t 的值，综上所述即可得出t 的值；（ 3 ）如图作PH⊥ OC 于H ．根据勾股定理的逆定理判断出∠ OCB=90°，从而得出当∠PCH=∠CBQ 时， PC⊥ BQ．根据同位角相等二直线平行得出PH∥BC，根据平行线分线段成比例定理得出OP∶ OB=PH∶BC=OH∶ OC,根据比例式得出PH=3t， OH=4t，根据等角的同名三角函数值相等及正切函数的定义，由tan∠ PCH=tan∠ CBQ，列出方程，求解得出t的值，经检验即可得出答案。

中考数学专题复习圆与相似的综合题附答案解析.doc

中考数学专题复习圆与相似的综合题附答案解析一、相似1．如图，在□ ABCD中，对角线 AC、 BD 相交于点O，点 E、 F 是 AD 上的点，且AE=EF=FD.连结 BE、 BF。

使它们分别与AO 相交于点G、 H（1）求 EG ： BG 的值（2）求证： AG=OG（3）设 AG =a ,GH =b，HO =c，求 a : b : c 的值【答案】（1）解：∵四边形 ABCD是平行四边形，∴AO=AC， AD=BC， AD∥ BC，∴△ AEG∽ △CBG，∴==．∵AE=EF=FD，∴BC=AD=3AE，∴GC=3AG， GB=3EG，∴EG： BG=1： 3（2）解：∵ GC=3AG（已证），∴AC=4AG，∴AO=AC=2AG，∴GO=AO﹣ AG=AG（3）解：∵ AE=EF=FD，∴BC=AD=3AE，AF=2AE．∵AD∥ BC，∴△ AFH∽ △ CBH，∴===，∴= ，即 AH=AC．∵AC=4AG，∴a=AG=AC，b=AH﹣AG= AC﹣AC=AC，c=AO﹣AH= AC﹣AC=AC，∴a： b： c=：：=5：3： 2【解析】【分析】（ 1）根据平行四边形的性质可得AO= AC， AD=BC， AD∥BC，从而可证得△ AEG∽ △CBG，得出对应边成比例，由AE=EF=FD可得 BC=3AE，就可证得GB=3EG，即可求出 EG： BG 的值。

（2）根据相似三角形的性质可得 GC=3AG，就可证得 AC=4AG，从而可得 AO=2AG，即可证得结论。

2．已知线段a， b， c 满足，且a＋2b＋c＝26.（1）判断 a， 2b， c，b 2是否成比例；（2）若实数 x 为 a， b 的比例中项，求 x 的值．【答案】（1）解：设，则a=3k， b=2k， c=6k，又∵ a+2b+c=26，∴3k+2 × 2k+6k=26，解得 k=2，∴a=6， b=4，c=12；∴2b=8， b 2=16∵a=6，2b=8 ，c=12， b2=16∴2bc=96， ab2=6× 16=96∴2bc=ab2a， 2b， c，b 2是成比例的线段。

中考数学复习圆与相似专项综合练附答案

中考数学复习圆与相似专项综合练附答案一、相似1．如图，AB是半圆O的直径，AB＝2，射线AM、BN为半圆O的切线.在AM上取一点D，连接BD交半圆于点C，连接AC.过O点作BC的垂线OE，垂足为点E，与BN相交于点F.过D点作半圆O的切线DP，切点为P，与BN相交于点Q.（1）若△ABD≌△BFO，求BQ的长；（2）求证：FQ=BQ【答案】（1）解：∵≌，∴，∵均为半圆切线，∴ .连接 ,则，∴四边形为菱形，∴DQ∥，∵均为半圆切线，∴∥，∴四边形为平行四边形∴，（2）证明：易得∽，∴ = ，∴ .∵是半圆的切线，∴ .过点作于点，则 .在中，，∴，解得：，∴∴【解析】【分析】（1）连接OP,由ΔABD≌ΔBFO可得AD=OB，由切线长定理可得AD=DP，于是易得OP=OA=DA=DP，根据菱形的判定可得四边形DAOP为菱形，则可得DQ∥AB，易得四边形DABQ为平行四边形，根据平行四边形的性质可求解；（2）过Q点作QK⊥AM于点K，由已知易证得ΔABD∽ΔBFO，可得比例式，可得BF与AD的关系，由切线长定理可得AD=DP,QB=QP ，解直角三角形DQK可求得BQ与AD 的关系，则根据FQ=BF−BQ可得FQ与AD的关系，从而结论得证。

2．如图，在平面直角坐标系中，O为原点，四边形ABCD是矩形，点A、C的坐标分别是A（0,2）和C（2,0），点D是对角线AC上一动点（不与A、C重合），连结BD，作，交x轴于点E，以线段DE、DB为邻边作矩形BDEF.（1）填空：点B的坐标为________；（2）是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD的长度；若不存在，请说明理由；（3）①求证：；②设AD=x，矩形BDEF的面积为y，求y关于x的函数关系式（可利用①的结论），并求出y的最小值【答案】（1）（2）解：存在，理由如下：∵OA=2,OC=2，∵tan∠ACO==,∴∠ACO=30°,∠ACB=60°①如图（1）中，当E在线段CO上时，△DEC是等腰三角形，观察图象可知，只有ED=EC，∴∠DCE=∠EDC=30°,∴∠DBC=∠BCD=60°,∴△DBC是等边三角形，∴DC=BC=2，在Rt△AOC中，∵∠ACO=30°，OA=2，∴AC=2AO=4，∴AD=AC-CD=4-2=2，∴当AD=2时，△DEC是等腰三角形，②如图（2）中，当E在OC的延长线上时，△DCE是等腰三角形，只有CD=CE，∠DBC=∠DEC=∠CDE=15°,∴∠ABD=∠ADB=75°,∴AB=AD=2，综上所述，满足条件的AD的值为2或2.（3）①如图，过点D作MN⊥AB于点M，交OC于点N。

中考数学圆与相似综合练习题含详细答案

中考数学圆与相似综合练习题含详细答案一、相似1．已知如图1，抛物线y=﹣ x2﹣ x+3与x轴交于A和B两点（点A在点B的左侧），与y轴相交于点C，点D的坐标是（0，﹣1），连接BC、AC（1）求出直线AD的解析式；（2）如图2，若在直线AC上方的抛物线上有一点F，当△ADF的面积最大时，有一线段MN= （点M在点N的左侧）在直线BD上移动，首尾顺次连接点A、M、N、F构成四边形AMNF，请求出四边形AMNF的周长最小时点N的横坐标；（3）如图3，将△DBC绕点D逆时针旋转α°（0＜α°＜180°），记旋转中的△DBC为△DB′C′，若直线B′C′与直线AC交于点P，直线B′C′与直线DC交于点Q，当△CPQ是等腰三角形时，求CP的值．【答案】（1）解：∵抛物线y=﹣ x2﹣ x+3与x轴交于A和B两点，∴0=﹣ x2﹣ x+3，∴x=2或x=﹣4，∴A（﹣4，0），B（2，0），∵D（0，﹣1），∴直线AD解析式为y=﹣ x﹣1（2）解：如图1，过点F作FH⊥x轴，交AD于H，设F（m，﹣ m2﹣ m+3），H（m，﹣ m﹣1），∴FH=﹣ m2﹣ m+3﹣（﹣ m﹣1）=﹣ m2﹣ m+4，∴S△ADF=S△AFH+S△DFH= FH×|x D﹣x A|=2FH=2（﹣ m2﹣ m+4）=﹣m2﹣m+8=﹣（m+ ）2+ ，当m=﹣时，S△ADF最大，∴F（﹣，）如图2，作点A关于直线BD的对称点A1，把A1沿平行直线BD方向平移到A2，且A1A2= ，连接A2F，交直线BD于点N，把点N沿直线BD向左平移得点M，此时四边形AMNF 的周长最小．．∵OB=2，OD=1，∴tan∠OBD= ，∵AB=6，∴AK= ，∴AA1=2AK= ，在Rt△ABK中，AH= ，A1H= ，∴OH=OA﹣AH= ，∴A1（﹣，﹣），过A2作A2P⊥A2H，∴∠A1A2P=∠ABK，∵A1A2= ，∴A2P=2，A1P=1，∴A2（﹣，﹣）∵F（﹣，）∴A2F的解析式为y=﹣ x﹣①，∵B（2，0），D（0，﹣1），∴直线BD解析式为y=﹣ x﹣1②，联立①②得，x=﹣，∴N点的横坐标为：﹣（3）解：∵C（0，3），B（2，0），D（0，﹣1）∴CD=4，BC= ，OB=2，BC边上的高为DH，根据等面积法得， BC×DH= CD×OB，∴DH= = ，∵A（﹣4，0），C（0，3），∴OA=4，OC=3，∴tan∠ACD= ，①当PC=PQ时，简图如图1，过点P作PG⊥CD，过点D作DH⊥PQ，∵tan∠ACD=∴设CG=3a，则QG=3a，PG=4a，PQ=PC=5a，∴DQ=CD﹣CQ=4﹣6a∵△PGQ∽△DHQ，∴，∴，∴a= ，∴PC=5a= ；②当PC=CQ时，简图如图2，过点P作PG⊥CD，∵tan∠ACD=∴设CG=3a，则PG=4a，∴CQ=PC=5a，∴QG=CQ﹣CG=2a，∴PQ=2 a，∴DQ=CD﹣CQ=4﹣5a∵△PGQ∽△DHQ，同①的方法得出，PC=4﹣，设CG=3a，则PG=4a，从而得出CQ,QG,PQ,DQ的长，由△PGQ∽△DHQ，同①的方法得出，PC的长；③当QC=PQ时，简图如图1过点Q作QG⊥PC，过点C作CN⊥PQ，设CG=3a，则QG=4a，PQ=CQ=5a，∴PG=3a，∴PC=6a∴DQ=CD﹣CQ=4﹣5a，利用等面积法得，CN×PQ=PC×QG，∴CN= a，∵△CQN∽△DQH同①的方法得出PC=④当PC=CQ时，简图如图4，过点P作PG⊥CD，过H作HD⊥PQ，设CG=3a，则PG=4a，CQ=PC=5a，∴QD=4+5a，PQ=4 ，∵△QPG∽△QDH，同①方法得出．CP=综上所述，PC的值为：；4﹣，，=【解析】【分析】（1）根据抛物线与x轴交点的坐标特点，把y=0代入抛物线的解析式，得出一个关于x的一元二次方程，求解得出x的值，进而得出A,B两点的坐标；然后由A,D 两点的坐标利用待定系数法求出直线AD的解析式；（2）过点F作FH⊥x轴，交AD于H，根据函数图像上点的坐标特点，及平行于y轴的直线上的点的坐标特点，设出F,H的坐标，从而得出FH的长度，S△ADF=S△AFH+S△DFH= FH×|x D﹣x A|=2FH,列出关于m的函数解析式，再根据二次函数的性质，由顶点式得出当m=﹣时，S△ADF最大，从而得出F点的坐标；如图2，作点A关于直线BD的对称点A1，把A1沿平行直线BD方向平移到A2，且A1A2= ，连接A2F，交直线BD于点N，把点N沿直线BD向左平移得点M，此时四边形AMNF的周长最小，进而求出点A1，A2坐标，即可确定出A2F的解析式和直线BD解析式联立方程组即可确定出N点的横坐标；（3）根据C,B,D三点的坐标，得出CD,BC,OB的长，BC边上的高为DH，根据等面积法得BC×DH= CD×OB，从而得出DH的长，根据A,C两点的坐标，得出OA,OC的长，根据正切函数的定义得出tan∠ACD= 4∶ 3 ；然后分四种情况讨论：①当PC=PQ时，过点P作PG⊥CD，过点D作DH⊥PQ，由tan∠ACD= 4∶ 3 ，设CG=3a，则QG=3a，PG=4a，PQ=PC=5a，从而由DQ=CD﹣CQ得出DQ的长，根据△PGQ∽△DHQ，得出PG∶DH=PQ∶DQ,从而求出a的值，进而求出PC的值；②当PC=CQ时，简图如图2，过点P作PG⊥CD，tan∠ACD= 4∶3，设CG=3a，则PG=4a，从而得出CQ,QG,PQ,DQ的长，由△PGQ∽△DHQ，同①的方法得出，PC的长；③当QC=PQ时，过点Q作QG⊥PC，过点C作CN⊥PQ，设CG=3a，则QG=4a，PQ=CQ=5a，从而得出PG,PC,DQ的长，利用等面积法得，CN×PQ=PC×QG，从而得出CN，由△CQN∽△DQH同①的方法得出PC的长；④当PC=CQ时，过点P作PG⊥CD，过H作HD⊥PQ，设CG=3a，则PG=4a，CQ=PC=5a，从而得出QD,PQ 的长，由△QPG∽△QDH，同①方法得出．CP的长。

中考数学圆与相似综合练习题附答案

中考数学圆与相似综合练习题附答案一、相似1．设C为线段AB的中点，四边形BCDE是以BC为一边的正方形．以B为圆心，BD长为半径的⊙B与AB相交于F点，延长EB交⊙B于G点，连接DG交于AB于Q点，连接AD．求证：（1）AD是⊙B的切线；（2）AD=AQ；（3）BC2=CF•EG．【答案】（1）证明：连接BD，∵四边形BCDE是正方形，∴∠DBA=45°，∠DCB=90°，即DC⊥AB，∵C为AB的中点，∴CD是线段AB的垂直平分线，∴AD=BD，∴∠DAB=∠DBA=45°，∴∠ADB=90°，即BD⊥AD，∵BD为半径，∴AD是⊙B的切线（2）证明：∵BD=BG，∴∠BDG=∠G，∵CD∥BE，∴∠CDG=∠G，∴∠G=∠CDG=∠BDG= ∠BCD=22.5°，∴∠ADQ=90°﹣∠BDG=67.5°，∠AQB=∠BQG=90°﹣∠G=67.5°，∴∠ADQ=∠AQD，∴AD=AQ（3）证明：连接DF，在△BDF中，BD=BF，∴∠BFD=∠BDF，又∵∠DBF=45°，∴∠BFD=∠BDF=67.5°，∵∠GDB=22.5°，在Rt△DEF与Rt△GCD中，∵∠GDE=∠GDB+∠BDE=67.5°=∠DFE，∠DCF=∠E=90°，∴Rt△DCF∽Rt△GED，∴ ,又∵CD=DE=BC，∴BC2=CF•EG．【解析】【分析】（1）连接BD，要证AD是圆B的切线，根据切线的判定可知，只须证明∠ADB=即可。

由正方形的性质易得BC=CD，∠DCB=∠DCA=，∠DBC=∠CDB=，根据点C为AB的中点可得BC=CD=AC，所以可得∠ADC=，则∠∠ADB=，问题得证；（2）要证AQ=AD，需证∠AQD=∠ADQ。

由题意易得∠AQD=-∠G，∠ADQ=-∠BDG，根据等边对等角可得∠G=∠BDG，由等角的余角相等可得∠AQD=∠ADQ，所以AQ=AD；（3）要证乘积式成立，需证这些线段所在的两个三角形相似，而由正方形的性质可得CD=DE=BC，所以可知BC、CF、EG分别在三角形DCF和三角形GED中，连接DF，用有两对角对应相等的两个三角形相似即可得证。

中考数学复习圆与相似专项综合练附详细答案

中考数学复习圆与相似专项综合练附详细答案一、相似1．如图，在△ABC中，点N为AC边的任意一点，D为线段AB上一点，若∠MPN的顶点P为线段CD上任一点，其两边分别与边BC，AC交于点M、N，且∠MPN+∠ACB=180°．（1）如图1，若AC=BC，∠ACB=90°，且D为AB的中点时，求，请证明你的结论；（2）如图2，若BC=m，AC=n，∠ACB=90°，且D为AB的中点时，则 =________；（3）如图3，若 =k，BC=m，AC=n，请直接写出的值．（用k，m，n表示）【答案】（1）解：如图1中，作PG⊥AC于G，PH⊥BC于H，∵AC=BC，∠ACB=90°，且D为AB的中点，∴CD平分∠ACB，∵PG⊥AC于G，PH⊥BC于H，∴PG=PH，∵∠PGC=∠PHC=∠GCH=90°，∴∠GPH=∠MPN=90°，∴∠MPH=∠NPG，∵∠PHM=∠PGN=90°，∴△PHM∽△PGN，∴ =1（2）（3）解：如图3中，作PG⊥AC于G，PH⊥BC于H，DT⊥AC于T，DK⊥BC于K，易证△PMH∽△PGN，∴，∵，∴，∵DT∥PG，DK∥PH，∴，∴，∴【解析】【解答】解：（2）如图2中，作PG⊥AC于G，PH⊥BC于H，∵∠PGC=∠PHC=∠GCH=90°，∴∠GPH=∠MPN=90°，∴∠MPH=∠NPG，∵∠PHM=∠PGN=90°，∴△PHM∽△PGN，∴，∵△PHC∽△ACB，PG=HC，∴，故答案为：；【分析】（1）作PG⊥AC于G，PH⊥BC于H，根据已知条件可证△PHM和△PGN的两角对应相等，进而可得△PHM∽△PGN，由相似三角形的对应边成比例即可求出。

（2）作PG⊥AC于G，PH⊥BC于H，由两角对应相等，可得△PHM∽△PGN，由相似三角形的对应边成比例可得 = ，由两角对应相等，可得△PHC∽△ACB，又PG=HC，相似三角形的对应边成比例及等量代换即可求出。

中考数学圆与相似综合试题及答案解析

中考数学圆与相似综合试题及答案解析一、相似1．已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB=∠AEC．（1）求证：BD是⊙O的切线；（2）求证：CE2=EH•EA；（3）若⊙O的半径为，sinA= ，求BH的长．【答案】（1）证明：如图，∵∠ODB=∠AEC，∠AEC=∠ABC，∴∠ODB=∠ABC，∵OF⊥BC，∴∠BFD=90°，∴∠ODB+∠DBF=90°，∴∠ABC+∠DBF=90°，即∠OBD=90°，∴BD⊥OB，∴BD是⊙O的切线（2）证明：连接AC，如图2所示：∵OF⊥BC，∴，∴∠CAE=∠ECB，∵∠CEA=∠HEC，∴△CEH∽△AEC，∴，∴CE2=EH•EA（3）解：连接BE，如图3所示：∵AB是⊙O的直径，∴∠AEB=90°，∵⊙O的半径为，sin∠BAE= ，∴AB=5，BE=AB•sin∠BAE=5× =3，∴EA= =4，∵，∴BE=CE=3，∵CE2=EH•EA，∴EH= ，∴在Rt△BEH中，BH= .【解析】【分析】（1）要证BD是⊙O的切线，只需证∠OBD=90°，因为∠OBC+∠BOD=90°，所以只须证∠ODB=∠OBC即可。

由圆周角定理和已知条件易得∠ODB=∠ABC，则∠OBC+∠BOD=90°=∠ODB+∠BOD，由三角形内角和定理即可得∠OBD=90°；（2）连接AC，要证CE2=EH•EA；只需证△CEH∽△AEC，已有公共角∠AEC，再根据圆周角定理可得∠CAE=∠ECB，即可证△CEH∽△AEC，可得比例式求解；（3）连接BE，解直角三角形AEB和直角三角形BEH即可求解。

2．如图，点A、B的坐标分别为（4，0）、（0，8），点C是线段OB上一动点，点E在x轴正半轴上，四边形OEDC是矩形，且OE=2OC．设OE=t（t＞0），矩形OEDC与△AOB 重合部分的面积为S．根据上述条件，回答下列问题：（1）当矩形OEDC的顶点D在直线AB上时，求t的值；（2）当t=4时，求S的值；（3）直接写出S与t的函数关系式（不必写出解题过程）；（4）若S=12，则t=________．【答案】（1）解：由题意可得∠BCD=∠BOA=90°，∠CBD=∠OBA，∴△BCD∽△BOA，∴而CD＝OE＝t，BC＝8−CO＝8− ，OA＝4，则8− ，解得t＝，∴当点D在直线AB上时，t＝（2）解：当t=4时，点E与A重合，设CD与AB交于点F，则由△CBF∽△OBA得，即，解得CF=3，∴S＝ OC(OE+CF)＝ ×2×(3+4)＝7（3）解：①当0＜t≤时，S= t2②当＜t≤4时，S=-t2+10t−16③当4＜t≤16时，S=t2+2t（4）8【解析】【解答】解：（3）①当0﹤t≤时，如图（1），②当<t≤4时，如图（2），∵A（4,0），B（0,8）∴直线AB的解析式为y=-2x+8,∴G（t,-2t+8）,F(4-,),∴DF=t-4,DG=t-8，∴S=S矩形COED-S△DFG=t·③当4＜t≤16时，如图（3）∵CD∥OA，∴△BCF∽△BOA，∴∴,∴CF=4-,∴S=S△BOA-S△BCF=（4）由题意可知把S=12代入S= t2+2t中, . t2+2t=12,整理，得t2-32t+192=0.解得 t1=8,t2=24>16（舍去）当S=12时，t=8【分析】（1）首先判断出△BCD∽△BOA，根据相似三角形对应边成比例得出BC ∶BO=CD ∶OA ，根据矩形的性质及线段的和差得出CD＝OE＝t，BC＝8−CO＝8- ，OA＝4，利用比例式即可得出方程，求解得出t的值；（2）当t=4时，点E与A重合，设CD与AB交于点F，则由△CBF∽△OBA得CF ：CB=OA ∶OB ，根据比例式得出方程，求解得出CF的长，根据梯形的面积公式即可算出答案；（3）①当0﹤t≤ 时，如图（1），其重叠部分的面积就是矩形的面积，根据矩形的面积公式即可得出函数关系式；②当<t≤4时，如图（2），利用待定系数法，求出直线AB 的解析式，根据和坐标轴平行的直线上的点的坐标特点及直线上的点的坐标特点分别表示出G,F的坐标，进而表示出DF的长，DG的长，根据S=S矩形COED-S△DFG即可得出函数关系式；③当4＜t≤16时，如图（3）根据矩形的性质得出CD∥OA，根据平行于三角形一边的直线截其它两边，所截得的三角形与原三角形相似得出△BCF∽△BOA，由相似三角形的对应边成比例得出BC：BO=CF：OA,根据比例式表示出CF的长，再根据S=S△BOA-S△BCF即可得出函数关系式。

中考数学专题《圆与相似》综合检测试卷含详细答案

中考数学专题《圆与相似》综合检测试卷含详细答案一、相似1．已知二次函数y＝ax2＋bx－2的图象与x轴交于A，B两点，与y轴交于点C，点A的坐标为(4，0)，且当x＝－2和x＝5时二次函数的函数值y相等．（1）求实数a，b的值；（2）如图①，动点E，F同时从A点出发，其中点E以每秒2个单位长度的速度沿AB边向终点B运动，点F以每秒个单位长度的速度沿射线AC方向运动．当点E停止运动时，点F随之停止运动．设运动时间为t秒．连接EF，将△AEF沿EF翻折，使点A落在点D处，得到△DEF.①是否存在某一时刻t，使得△DCF为直角三角形？若存在，求出t的值；若不存在，请说明理由；②设△DEF与△ABC重叠部分的面积为S，求S关于t的函数关系式．【答案】（1）解：由题意得：，解得：a= ，b=（2）解：①由（1）知二次函数为 .∵A（4，0），∴B（﹣1，0），C （0，﹣2），∴OA=4，OB=1，OC=2，∴AB=5，AC= ，BC= ，∴AC2+BC2=25=AB2，∴△ABC为直角三角形，且∠ACB=90°．∵AE=2t，AF= t，∴ .又∵∠EAF=∠CAB，∴△AEF∽△ACB，∴∠AEF=∠ACB=90°，∴△AEF沿EF翻折后，点A落在x轴上点D处；由翻折知，DE=AE，∴AD=2AE=4t，EF= AE=t．假设△DCF为直角三角形，当点F在线段AC上时：ⅰ）若C为直角顶点，则点D与点B重合，如图2，∴AE= AB= t= ÷2= ；ⅱ）若D为直角顶点，如图3．∵∠CDF=90°，∴∠ODC+∠EDF=90°．∵∠EDF=∠EAF，∴∠OBC+∠EAF=90°，∴∠ODC=∠OBC，∴BC=DC．∵OC⊥BD，∴OD=OB=1，∴AD=3，∴AE= ，∴t= ；当点F在AC延长线上时，∠DFC＞90°，△DCF为钝角三角形．综上所述，存在时刻t，使得△DCF为直角三角形，t= 或t= ．②ⅰ）当0＜t≤ 时，重叠部分为△DEF，如图1、图2，∴S= ×2t×t=t2；ⅱ）当＜t≤2时，设DF与BC相交于点G，则重叠部分为四边形BEFG，如图4，过点G作GH⊥BE于H，设GH=m，则BH= ，DH=2m，∴DB= ．∵DB=AD﹣AB=4t﹣5，∴ =4t﹣5，∴m= （4t﹣5），∴S=S△DEF﹣S△DBG= ×2t×t﹣（4t﹣5）× （4t﹣5）= ；ⅲ）当2＜t≤ 时，重叠部分为△BEG，如图5．∵BE=DE﹣DB=2t﹣（4t﹣5）=5﹣2t，GE=2BE=2（5﹣2t），∴S= ×（5﹣2t）×2（5﹣2t）=4t2﹣20t+25．综上所述：．【解析】【分析】（1）根据已知抛物线的图像经过点A，以及当x=-2和x=5时二次函数的函数值y相等两个条件，列出方程组求出待定系数的值即可。

中考数学圆与相似的综合题试题含详细答案

中考数学圆与相似的综合题试题含详细答案一、相似1．如图，抛物线过点，．为线段OA上一个动点（点M与点A不重合），过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N．（1）求直线AB的解析式和抛物线的解析式；（2）如果点P是MN的中点，那么求此时点N的坐标；（3）如果以B，P，N为顶点的三角形与相似，求点M的坐标．【答案】（1）解：设直线的解析式为（）∵，∴解得∴直线的解析式为∵抛物线经过点，∴解得∴（2）解：∵轴，则，∴，∵点是的中点∴∴解得，（不合题意，舍去）∴（3）解：∵，，∴，∴∵∴当与相似时，存在以下两种情况：∴解得∴∴ ,解得∴【解析】【分析】（1）运用待定系数法解答即可。

（2）由（1）可得直线AB的解析式和抛物线的解析式，由点M（m,0）可得点N，P用m 表示的坐标，则可求得NP与PM，由NP=PM构造方程，解出m的值即可。

（3）在△BPN与△APM中，∠BPN=∠APM，则有和这两种情况，分别用含m的代数式表示出BP，PN，PM，PA，代入建立方程解答即可。

2．如图，Rt△AOB在平面直角坐标系中，已知：B（0，），点A在x轴的正半轴上，OA=3，∠BAD=30°，将△AOB沿AB翻折，点O到点C的位置，连接CB并延长交x轴于点D.（1）求点D的坐标；（2）动点P从点D出发，以每秒2个单位的速度沿x轴的正方向运动，当△PAB为直角三角形时，求t的值；（3）在（2）的条件下，当△PAB为以∠PBA为直角的直角三角形时，在y轴上是否存在一点Q使△PBQ为等腰三角形？如果存在，请直接写出Q点的坐标；如果不存在，请说明理由.【答案】（1）解：∵B（0，），∴OB= .∵OA= OB，∴OA=3，∴AC=3.∵∠BAD=30°，∴∠OAC=60°.∵∠ACD=90°，∴∠ODB=30°，∴ = ，∴OD=3，∴D（﹣3，0）；（2）解：∵OA=3，OD=3，∴A（3，0），AD=6，∴AB=2 ，当∠PBA=90°时.∵PD=2t，∴OP=3﹣2t.∵△OBA∽△OPB，∴OB2=OP•OA，∴3﹣2t= =1，解得t=1，当∠APB=90°时，则P与O重合，∴t= ；（3）解：存在.①当BP为腰的等腰三角形.∵OP=1，∴BP= =2，∴Q1（0， +2），Q3（0. ﹣2）；②当PQ2=Q2B时，设PQ2=Q2B=a，在Rt△OPQ2中，12+（﹣x）2=x2，解得x= ，∴Q2（0，）；③当PB=PQ4时，Q4（0，﹣）综上所述：满足条件的点Q的坐标为Q1（0， +2），Q2（0，），Q3（0. ﹣2），Q4（0，﹣）.【解析】【分析】（1）根据已知得出OA、OB的值以及∠DAC的度数，进而求得∠ADC，即可求得D的坐标；（2）根据直角三角形的判定，分两种情况讨论求得；（3）求得PB 的长，分四种情形讨论即可解决问题.3．在平面直角坐标系中，抛物线与轴的两个交点分别为A （-3，0）、B（1，0），与y轴交于点D(0，3)，过顶点C作CH⊥x轴于点H.（1）求抛物线的解析式和顶点C的坐标；（2）连结AD、CD，若点E为抛物线上一动点（点E与顶点C不重合），当△ADE与△ACD面积相等时，求点E的坐标；（3）若点P为抛物线上一动点（点P与顶点C不重合），过点P向CD所在的直线作垂线，垂足为点Q，以P、C、Q为顶点的三角形与△ACH相似时，求点P的坐标.【答案】（1）解：设抛物线的解析式为，∵抛物线过点A(-3，0),B(1，0)，D(0，3)，∴，解得，a=-1，b=-2，c=3，∴抛物线解析式为，顶点C（-1,4）；（2）解：如图1，∵A(-3，0)，D(0，3),∴直线AD的解析式为y=x+3，设直线AD与CH交点为F，则点F的坐标为(-1，2)∴CF=FH，分别过点C、H作AD的平行线，与抛物线交于点E，由平行间距离处处相等，平行线分线段成比例可知，△ADE与△ACD面积相等，∴直线EC的解析式为y=x+5，直线EH的解析式为y=x+1，分别与抛物线解析式联立，得，，解得点E坐标为(-2，3)，，；（3）解：①若点P在对称轴左侧（如图2），只能是△CPQ∽△ACH，得∠PCQ=∠CAH，∴，分别过点C、P作x轴的平行线，过点Q作y轴的平行线，交点为M和N，由△CQM∽△QPN，得 =2，∵∠MCQ=45°，设CM=m，则MQ=m，PN=QN=2m，MN=3m，∴P点坐标为(-m-1，4-3m)，将点P坐标代入抛物线解析式，得，解得m=3，或m=0(与点C重合，舍去)∴P点坐标为(-4，-5)；②若点P在对称轴右侧（如图①），只能是△PCQ∽△ACH，得∠PCQ=∠ACH，∴，延长CD交x轴于M，∴M(3，0)过点M作CM垂线，交CP延长线于点F，作FN x轴于点N，∴，∵∠MCH=45°，CH=MH=4∴MN=FN=2，∴F点坐标为(5，2)，∴直线CF的解析式为y= ，联立抛物线解析式，得，解得点P坐标为( ， )，综上所得，符合条件的P点坐标为(-4，-5)，( ， ).【解析】【分析】（1）将A（-3，0）、B（1，0）、D(0，3)，代入y=ax2+bx+3求出即可；(2)求出直线AD的解析式，分别过点C、H作AD的平行线，与抛物线交于点E，利用△ADE与△ACD面积相等，得出直线EC和直线EH的解析式，联立出方程组求解即可;(3) （3）分两种情况讨论：①点P在对称轴左侧；②点P在对称轴右侧.4．如图1，抛物线平移后过点A（8，,0）和原点，顶点为B，对称轴与轴相交于点C，与原抛物线相交于点D．（1）求平移后抛物线的解析式并直接写出阴影部分的面积；（2）如图2，直线AB与轴相交于点P，点M为线段OA上一动点，为直角，边MN与AP相交于点N，设，试探求：① 为何值时为等腰三角形；② 为何值时线段PN的长度最小，最小长度是多少．【答案】（1）解：设平移后抛物线的解析式，将点A（8，,0）代入，得 = ，所以顶点B（4,3），所以S阴影=OC•CB=12（2）解：设直线AB解析式为y=mx+n，将A（8，0）、B（4，3）分别代入得，解得：，所以直线AB的解析式为，作NQ垂直于x轴于点Q，①当MN＝AN时， N点的横坐标为，纵坐标为，由三角形NQM和三角形MOP相似可知 ,得，解得（舍去）.当AM＝AN时，AN＝ ,由三角形ANQ和三角形APO相似可知，，MQ＝，由三角形NQM和三角形MOP相似可知得：，解得：t＝12（舍去）；当MN＝MA时，故是钝角，显然不成立,故；②由MN所在直线方程为y= ，与直线AB的解析式y=﹣x+6联立，得点N的横坐标为X N= ，即t2﹣x N t+36﹣x N=0，由判别式△=x2N﹣4（36﹣）≥0，得x N≥6或x N≤﹣14，又因为0＜x N＜8，所以x N的最小值为6，此时t=3，当t=3时，N的坐标为（6，""），此时PN取最小值为【解析】【分析】（1）平移前后的两个二次函数的a的值相等，平移后的图像经过点原点，因此设函数解析式为：，将点A的坐标代入就可求出b的值，再求出顶点B的坐标，利用割补法可得出阴影部分的面积=以OC，BC为边的矩形的面积。

中考数学圆与相似综合试题含详细答案

中考数学圆与相似综合试题含详细答案一、相似1．如图,在一个长40 m、宽30 m的矩形小操场上,王刚从A点出发,沿着A→B→C的路线以3 m/s的速度跑向C地.当他出发4 s后,张华有东西需要交给他,就从A地出发沿王刚走的路线追赶,当张华跑到距B地2 m的D处时,他和王刚在阳光下的影子恰好落在一条直线上.（1）此时两人相距多少米(DE的长)?（2）张华追赶王刚的速度是多少?【答案】（1）解：在Rt△ABC中：∵AB=40，BC=30，∴AC=50 m.由题意可得DE∥AC，∴Rt△BDE∽Rt△BAC，∴ = ，即 = .解得DE= m.答：此时两人相距 m.（2）解：在Rt△BDE中：∵DB=2，DE=，∴BE=2 m.∴王刚走的总路程为AB+BE=42 m.∴王刚走这段路程用的时间为 =14(s).∴张华用的时间为14-4=10(s)，∵张华走的总路程为AD=AB-BD=40-2=37（m）,∴张华追赶王刚的速度是37÷10≈3.7（m/s）.答：张华追赶王刚的速度约是3.7m/s.【解析】【分析】（1）在Rt△ABC中，根据勾股定理得AC=50 m，利用平行投影的性质得DE∥AC，再利用相似三角形的性质得出对应边的比相等可求得DE长.（2）在Rt△BDE中,根据勾股定理得BE=2 m，根据题意得王刚走的总路程为42 m，根据时间=路程÷速度求得王刚用的时间，减去4即为张华用的时间，再根据速度=路程÷时间解之即可得出答案.2．如图，抛物线y＝x2＋bx＋c经过B(－1，0)，D(－2，5)两点，与x轴另一交点为A，点H是线段AB上一动点，过点H的直线PQ⊥x轴，分别交直线AD、抛物线于点Q、P.（1）求抛物线的解析式；（2）是否存在点P，使∠APB＝90°，若存在，求出点P的横坐标，若不存在，说明理由；（3）连接BQ，一动点M从点B出发，沿线段BQ以每秒1个单位的速度运动到Q，再沿线段QD以每秒个单位的速度运动到D后停止，当点Q的坐标是多少时，点M在整个运动过程中用时t最少？【答案】（1）解：把B（﹣1，0），D（﹣2，5）代入，得：，解得：，∴抛物线的解析式为：（2）解：存在点P，使∠APB=90°．当y=0时，即x2﹣2x﹣3=0，解得：x1=﹣1，x2=3，∴OB=1，OA=3．设P（m，m2﹣2m﹣3），则﹣1≤m≤3，PH=﹣（m2﹣2m﹣3），BH=1+m，AH=3﹣m，∵∠APB=90°，PH⊥AB，∴∠PAH=∠BPH=90°﹣∠APH，∠AHP=∠PHB，∴△AHP∽△PHB，∴，∴PH2=BH•AH，∴[﹣（m2﹣2m﹣3）]2=（1+m）（3﹣m），解得m1= ，m2= ，∴点P的横坐标为：或（3）解：如图，过点D作DN⊥x轴于点N，则DN=5，ON=2，AN=3+2=5，∴tan∠DAB= =1，∴∠DAB=45°．过点D作DK∥x 轴，则∠KDQ=∠DAB=45°，DQ= QG．由题意，动点M运动的路径为折线BQ+QD，运动时间：t=BQ+ DQ，∴t=BQ+QG，即运动的时间值等于折线BQ+QG的长度值．由垂线段最短可知，折线BQ+QG的长度的最小值为DK与x轴之间的垂线段．过点B作BH⊥DK于点H，则t最小=BH，BH与直线AD的交点，即为所求之Q点．∵A（3，0），D（﹣2，5），∴直线AD的解析式为：y=﹣x+3，∵B点横坐标为﹣1，∴y=1+3=4，∴Q（﹣1，4）．【解析】【分析】（1）把点B，D的坐标代入二次函数中组成二元一次方程组，解方程组即可得到抛物线的解析式；（2）先按照存在点P使∠APB＝90°，先根据抛物线的解析式求得点A，B的坐标，设出点P的坐标，根据点P的位置确定m的取值范围，再证△AHP∽△PHB，从而得到PH2=BH•AH，即可列出关于m的方程，解方程即可得到m即点P的横坐标，且横坐标在所求范围内，从而说明满足条件的点P存在；（3）先证明∠DAB=45°，从而证得DQ= 2 QG，那么运动时间t值等于折线BQ+QG的长度值，再结合垂线段最短确定点Q的位置，再求得点Q的坐标即可.3．如图1，在矩形ABCD中，AB=6cm，BC=8cm，E、F分别是AB、BD的中点，连接EF，点P从点E出发，沿EF方向匀速运动，速度为1cm/s，同时，点Q从点D出发，沿DB方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t（0＜t＜4）s，解答下列问题：（1）求证：△BEF∽△DCB；（2）当点Q在线段DF上运动时，若△PQF的面积为0.6cm2，求t的值；（3）当t为何值时，△PQF为等腰三角形？试说明理由．【答案】（1）解：∵四边形ABCD是矩形，∴ AD∥BC，在中，∵别是的中点，∴EF∥AD，∴ EF∥BC，∴∴（2）解：如图1，过点Q作于，∴QM∥BE，∴∴∴（舍）或秒（3）解：当点Q在DF上时，如图2，∴∴ .当点Q在BF上时，，如图3，∴∴时，如图4，∴∴时，如图5，∴∴综上所述，t=1或3或或秒时，△PQF是等腰三角形【解析】【分析】（1）根据题中的已知条件可得△BEF和△DCB中的两角对应相等，从而可证△BEF∽△DCB；（2）过点Q作QM⊥EF 于M ，先根据相似三角形的预备定理可证△QMF ∽△BEF；再由△QM F ∽△BEF可用含t的代数式表示出QM的长；最后代入三角形的面积公式即可求出t的值。

中考数学圆与相似综合试题附答案

中考数学圆与相似综合试题附答案一、相似1．如图，在等腰Rt△ABC中，O为斜边AC的中点，连接BO，以AB为斜边向三角内部作Rt△ABE，且∠AEB=90°，连接EO．求证：（1）∠OAE=∠OBE；（2）AE=BE+ OE．【答案】（1）证明：在等腰Rt△ABC中，O为斜边AC的中点，∴OB⊥AC，∴∠AOB=90°，∵∠AEB=90°，∴A，B，E，O四点共圆，∴∠OAE=∠OBE（2）证明：在AE上截取EF=BE，则△EFB是等腰直角三角形，∴，∠FBE=45°，∵在等腰Rt△ABC中，O为斜边AC的中点，∴∠ABO=45°，∴∠ABF=∠OBE，∵，∴，∴△ABF∽△BOE，∴ = ，∴AF= OE，∵AE=AF+EF，∴AE=BE+ OE．【解析】【分析】（1）利用等腰直角三角形的性质，可证得∠AOB=∠AEB=90°，可得出A，B，E，O四点共圆，再利用同弧所对的圆周角相等，可证得结论。

（2）在AE上截取EF=BE，易证△EFB是等腰直角三角形，可得出BF与BE的比值为，再证明∠ABF=∠OBE，AB与BO的比值为，就可证得AB、BO、BF、BE四条线段成比例，然后利用两组对应边成比例且夹角相等的两三角形相似，可证得△ABF∽△BOE，可证得AF= OE，由AE=AF+EF，可证得结论。

2．如图，正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上（点P与A、C不重合），QP与BC交于E，QP延长线与AD交于点F，连接CQ．（1）①求证：AP=CQ；②求证：PA2=AF•AD；（2）若AP：PC=1：3，求tan∠CBQ．【答案】（1）证明：①∵四边形ABCD是正方形，∴AB=CB，∠ABC=90°，∴∠ABP+∠PBC=90°，∵△BPQ是等腰直角三角形，∴BP=BQ，∠PBQ=90°，∴∠PBC+∠CBQ=90°∴∠ABP=∠CBQ，∴△ABP≌△CBQ，∴AP=CQ;②∵四边形ABCD是正方形，∴∠DAC=∠BAC=∠ACB=45°，∵∠PQB=45°，∠CEP=∠QEB，∴∠CBQ=∠CPQ，由①得△ABP≌△CBQ，∠ABP=∠CBQ∵∠CPQ=∠APF，∴∠APF=∠ABP，∴△APF∽△ABP，(本题也可以连接PD，证△APF∽△ADP)（2）证明：由①得△ABP≌△CBQ，∴∠BCQ=∠BAC=45°，∵∠ACB=45°,∴∠PCQ=45°+45°=90°∴tan∠CPQ= ,由①得AP=CQ,又AP:PC=1:3，∴tan∠CPQ= ，由②得∠CBQ=∠CPQ，∴tan∠CBQ=tan∠CPQ= .【解析】【分析】（1）①利用正方形的性质和等腰直角三角形的性质易证△ABP≌△CBQ，可得AP=CQ；②利用正方形的性质可证得∠CBQ=∠CPQ，再由△ABP≌△CBQ可证得∠APF=∠ABP，从而证出△APF∽△ABP，由相似三角形的性质得证；（2）由△ABP≌△CBQ可得∠BCQ=∠BAC=45°，可得∠PCQ=45°+45°=90°，再由三角函数可得tan∠CPQ=，由AP:PC=1:3，AP=CQ，可得tan∠CPQ=，再由∠CBQ=∠CPQ可求出答案.3．如图，抛物线y=﹣ +bx+c过点A（3，0），B（0，2）．M（m，0）为线段OA上一个动点（点M与点A不重合），过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N．（1）求直线AB的解析式和抛物线的解析式；（2）如果点P是MN的中点，那么求此时点N的坐标；（3）如果以B，P，N为顶点的三角形与△APM相似，求点M的坐标．【答案】（1）解：设直线AB的解析式为y=px+q，把A（3，0），B（0，2）代入得，解得，∴直线AB的解析式为y=﹣ x+2；把A（3，0），B（0，2）代入y=﹣ +bx+c得，解得，∴抛物线解析式为y=﹣ x2+ x+2（2）解：∵M（m，0），MN⊥x轴，∴N（m，﹣ m2+ m+2），P（m，﹣ m+2），∴NP=﹣ m2+4m，PM=﹣ m+2，而NP=PM，∴﹣ m2+4m=﹣ m+2，解得m1=3（舍去），m2= ，∴N点坐标为（，）（3）解：∵A（3，0），B（0，2），P（m，﹣ m+2），∴AB= = ，BP= = m，而NP=﹣ m2+4m，∵MN∥OB，∴∠BPN=∠ABO，当 = 时，△BPN∽△OBA，则△BPN∽△MPA，即 m：2=（﹣ m2+4m）：，整理得8m2﹣11m=0，解得m1=0（舍去），m2= ，此时M点的坐标为（，0）；当 = 时，△BPN∽△ABO，则△BPN∽△APM，即 m： =（﹣ m2+4m）：2，整理得2m2﹣5m=0，解得m1=0（舍去），m2= ，此时M点的坐标为（，0）；综上所述，点M的坐标为（，0）或（，0）【解析】【分析】（1）因为抛物线和直线AB都过点A（3,0）、B（0,2），所以用待定系数法求两个解析式即可；（2）由题意知点P是MN的中点，所以PM=PN；而MN OA交抛物线与点N，交直线AB于点P，所以M、P、N的横坐标相同且都是m,纵坐标分别可用（1）中相应的解析式表示，即P（m,）,N（m,）,PM与PN的长分别为相应两点的纵坐标的绝对值，代入PM=PN即可的关于m的方程，解方程即可求解；（3）因为以B，P，N为顶点的三角形与△APM相似，而△APM是直角三角形，所以分两种情况：当∠PBN=时，则可得△PBN∽△PMA，即得相应的比例式，可求得m的值；当∠PNB=时，则可得△PNB∽△PMA，即得相应的比例式，可求得m的值。