画法几何习题集 第四章答案(大连理工大学版)
解析几何第四版习题答案第四章[1]讲解
![解析几何第四版习题答案第四章[1]讲解](https://img.taocdn.com/s3/m/aa31a9df844769eae109edb3.png)
第四章柱面、锥面、旋转曲面与二次曲面§4.1柱面1、已知柱面的准线为:'(X—1)2+(y+3)2+(z-2)2=25 x+y—z+2=0且(1)母线平行于X轴;(2)母线平行于直线X = y, z = c,试求这些柱面的方程。
解:(1)从方程'(x_1)2 十(y+ 3)2 +(z_2)2=25<x+y-z+2=0中消去X,得到:(Z 一y 一3)2 (y 3)2 (Z-2)2 =25即:y2 z2_ yz _6y _5z「3二02此即为要求的柱面方程。
x = y(2)取准线上一点M 0(x0,y0,z0),过M 0且平行于直线丿'的直线方程为:jZ = CX = X o t X o 二X - t“y = y° +t 二彳y° =y-1z = z°= z而M o在准线上,所以7x_t _1)2 +(y _t +3)2 +(z_2)2=25 、x+y-z-2t+2 = 0上式中消去t后得到:x2 y2• 3z2 -2xy-8x • 8y-8z-26 =0此即为要求的柱面方程。
2而M。
在准线上,所以:厂 2 2』x -t = y +(z + 2t)、x-t = 2(z+2t)消去t,得到:4x225y2 z2 4xz-20x -10z =0此即为所求的方程。
3、求过三条平行直线x=y=乙x ^^^1,与x-1=y /二乙- 2的圆柱面方程。
解:过又过准线上一点M/x^y—zJ,且方向为1,1,1的直线方程为:= x1t X\ =x-ty = y i t 二y i = y -1z = z t z = z -t将此式代入准线方程,并消去t得到:2 2 25( x y - z - xy - yz - zx) 2x 11y - 13z = 0此即为所求的圆柱面的方程。
4、已知柱面的准线为(u) —x(u), y(u), z(u)1,母线的方向平行于矢量S —X,Y,Z?,试证明柱面的矢量式参数方程与坐标式参数方程分别为:x = Y(u) vS与x 二 x(u) Xv« y = y(u)+Yvz = z(u) +Zv式中的u, v为参数。
几何公差第四章习题答案

包容要求
MMB
40
0பைடு நூலகம்
0.015
39.975~40
4-9答案:DM=19.966mm;DL=20.005mm
据包容要求的内容,孔的合格条件为:
①、体外作用尺寸不应超出最大实体尺寸,Dfe≥DM=19.966mm。
②、实际尺寸不应超出最小实体尺寸,Da≤DL=20.005mm。
该孔的体外作用尺寸Dfe=Da-e=19.985-0.025=19.96mm
满足合格条件①;实际尺寸Da=19.985mm,满足合格条件②;所以该孔不合格。
几何公差第四章习题答案几何公差proe几何公差标注几何量公差与检测几何量公差画法几何习题集平面解析几何习题集王几何课后习题课后习题答案网补充习题答案
4-1答案:
4-2答案:
4-3答案:
4-4答案:
4-5答案:
4-6答案:
4-7答案:
4-8答案:
图号
最大实体尺寸(mm)
最小实体尺寸(mm)
采用的
公差原则
边界名称及边界尺寸(mm)
MMC时的形位公差值(mm)
LMC时的形位公差值(mm)
实际尺寸合格范围(mm)
a
40
39.975
(可逆的)最大实体要求
MMVB
40.01
0.01
0.035
39.975~40.01
b
40
40.039
(零形位公差的)最大实体要求
MMVB
40
0
0.039
40~40.039
c
40
画法几何习题集答案
a’
bc于m,作
m’
m’m ∥oz,交
n’
b’c’于m’,连接
b’
a’m’,作c’n’
⊥am交于n’,
b
作nn’ ⊥am交
a
于n,利用直角
mn
三角形求出
倾角β
c
31 判别直线AB是否平行于平面CDEF
• 作法:
c’
b’
f’ • 作e’f’ ∥a’b’,
a’
交c’d’于m’,
e’
m’
作mm’ ∥oz,
b’ p’ o’ n1’’
a’
c’
4’
m’
a c
po
4 m
n1 b
• 做法:
2’ • 延长 ac .34交
于m,求出 m’,
延长2‘1’交点
3’ 为o’,p,’ 在ab
求出p,bc利用
3 定比性求出o, 连接po交21
于n,求出n’,连
2
接mn,m’n’.
42 已知直线AB平行于平面CDE求直线的正面投影
33 过A点作平面平行∆ DEF
a’
d’ a
d
e’
n’ • 作法:
• 作a’m’
f’ ∥e’f’,作am
m’
∥ef, mm
∥oz.
e
• 作a’n’
∥d’f’,作an
n
∥df, nn’
∥oz.
f m
34 过直线AB作平面平行于直线CD
b’
m’ a’
c’
b
a
c
m
• 作法:
• 作am ∥cd,
d’
作a’m’
20mm b1 X2
67用换面法确定两交错直线间的距离返回做出投影
画法几何第四册习题册答案

画法几何第四册习题册答案
《画法几何第四册习题册答案》
在学习画法几何的过程中,习题册答案是我们检验自己学习成果的重要指标。
通过认真完成习题册,我们不仅可以巩固所学知识,还可以发现自己的不足之处,及时进行纠正和提高。
画法几何第四册习题册答案中的每一道题目都是一个学习的挑战,需要我们动脑筋、细心观察和灵活运用所学知识。
通过一道道题目的练习,我们可以逐渐提高自己的绘画技巧和审美能力,培养自己的观察力和思维能力。
在完成习题册的过程中,我们不仅要注重答案的准确性,更要注重过程的思考和方法的探索。
只有通过不断的实践和思考,我们才能真正掌握画法几何的技巧和精髓,从而在绘画的道路上越走越远。
画法几何第四册习题册答案不仅是我们学习的成果,更是我们成长的见证。
通过不断地挑战和突破,我们可以在习题册中找到自己的成长和进步,不断提高自己的绘画水平和艺术修养。
总之,画法几何第四册习题册答案是我们学习的重要标志,也是我们成长的见证。
在学习的道路上,让我们不断挑战自己,不断进步,不断创新,让习题册成为我们成长的伴侣,让答案成为我们成长的见证。
画法几何第四版练习册答案

画法几何第四版练习册答案画法几何是工程图学中的一个重要分支,它涉及到图形的绘制、分析和理解。
本练习册旨在帮助学生通过练习来巩固和深化对画法几何的理解和应用。
以下是《画法几何第四版练习册》的部分答案,以供参考。
第一章:点、线、面的投影1. 问题:如何确定一个点在平面上的投影?答案:首先确定点相对于平面的位置,然后根据点到平面的垂直距离,使用投影规则找到该点在平面上的投影。
2. 问题:给定两条相交线段,如何找到它们的交点?答案:通过分析两条线段的投影,可以确定它们在空间中的交点。
这通常涉及到计算交点的坐标。
第二章:平面图形的绘制1. 问题:如何绘制一个圆的投影?答案:首先确定圆心的投影,然后根据圆的半径,绘制圆的投影。
圆的投影可能是一个椭圆或一个圆,取决于观察的角度。
2. 问题:如何绘制一个多边形?答案:首先确定多边形的顶点,然后依次连接相邻顶点,形成闭合图形。
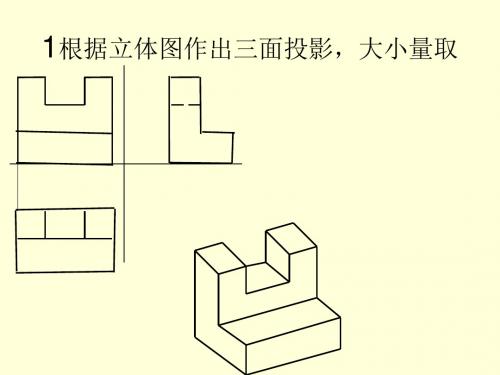
第三章:立体图形的投影1. 问题:如何绘制一个立方体的三视图?答案:立方体的三视图包括正视图、侧视图和俯视图。
正视图显示立方体的前面和后面,侧视图显示立方体的侧面,俯视图显示立方体的顶部。
2. 问题:如何确定一个圆锥的投影?答案:圆锥的投影通常是一个圆和一个三角形。
圆是圆锥底面的投影,三角形是圆锥侧面的投影。
第四章:剖面图和断面图1. 问题:什么是剖面图?答案:剖面图是一种通过假想的切割面来显示物体内部结构的图形表示方法。
2. 问题:如何绘制一个物体的断面图?答案:首先确定切割面的位置,然后根据切割面与物体相交的部分,绘制出断面图。
第五章:轴测图1. 问题:什么是轴测图?答案:轴测图是一种通过改变投影角度来更直观地展示三维物体的图形表示方法。
2. 问题:如何绘制一个物体的轴测图?答案:选择适当的轴测投影方式,然后根据物体的尺寸和形状,绘制出轴测图。
结束语:通过本练习册的练习,希望能够帮助学生更好地理解画法几何的基本概念和应用。
在实际应用中,学生应该结合具体的工程问题,灵活运用所学知识,不断提高自己的绘图和分析能力。
画法几何习题集答案

画法几何习题集答案问题一:如何确定一个平面图形在空间中的投影?答案:确定一个平面图形在空间中的投影,首先需要确定投影面和视图。
通常,我们使用正投影法,将图形投影到三个相互垂直的平面上,即前视图(正视图)、侧视图和俯视图。
通过这三个视图,可以完整地表达出空间图形的形状和尺寸。
问题二:如何绘制一个长方体的三视图?答案:绘制长方体的三视图需要从三个不同的方向观察长方体。
首先,绘制前视图,显示长方体的正面和侧面;然后,绘制侧视图,显示长方体的侧面和背面;最后,绘制俯视图,显示长方体的顶面和底面。
每个视图都应该展示长方体的相应边长和高度。
问题三:如何通过已知的两个视图来恢复第三个视图?答案:通过已知的两个视图来恢复第三个视图,需要利用空间几何关系和已知的尺寸。
首先,分析已知视图中的尺寸和形状,确定缺失视图的轮廓。
然后,根据已知视图中的尺寸和比例,计算缺失视图中的线段长度和角度。
最后,将计算出的数据绘制成缺失的视图。
问题四:如何判断两个平面图形是否平行或垂直?答案:判断两个平面图形是否平行或垂直,可以通过观察它们的投影。
如果两个图形在所有视图中的投影都保持相同的相对位置,并且没有相交线,那么这两个图形是平行的。
如果两个图形在某个视图中的投影相交于一条直线,并且在其他视图中没有相交,那么这两个图形是垂直的。
问题五:如何计算空间中两点之间的距离?答案:计算空间中两点之间的距离,可以使用空间两点距离公式。
设两点的坐标分别为 \( P_1(x_1, y_1, z_1) \) 和 \( P_2(x_2, y_2, z_2) \),则两点之间的距离 \( d \) 可以通过以下公式计算:\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \]结束语:画法几何习题的解答需要对空间图形有深刻的理解,以及对几何原理和绘图技巧的熟练掌握。
通过不断的练习和思考,可以提高解决画法几何问题的能力。
