初中数学竞赛试题之三角形

合集下载

初中数学竞赛专题：三角形

初中数学竞赛专题：三角形§9. 1全等三角形1. 1. 1★已知等腰直角三角形A8C,8C是斜边.々的角平分线交AC于。

，过C作CE与a）垂直且交8。

延长线于邑求证：BD = 2CE.解析如图，延长CE、B4,设交于b・则NF3E = NAb,A8 = AC,得△AB£>gA4b,CF = 8O.乂BE 1.CF, BE 平分/FBC,故BE 平分CF, E为CF 中点、，所以2CE = FC = BD .9. 1. 2★在△ABC中，已知乙4 = 60。

,£、F、G分别为/W、AC、8C的中点,P、Q为AABC形外两点，使总_14从尸£ = ¥，°尸_14。

,0尸=卓,若6尸=1,求尸0的长.解析如图，连结EG、FG ,则EG//AC , FG//AB，故/PEG = 150。

= NQFG . 又QF = -AC = EG , PE 4AB = FG , 故APEG 9AGFQ , 所以2 2PG = GQ , AEGP + ZFGQ = ZFQG + ZFGQ = 30°, 乂ZEGF = 60°,所以NPG0 = 9O。

，于是PQ = 0PG = y/2 .10.1. 3★在梯形A8C0的底边AD上有一点心若八钻石、ABCEx △（7£）七的周长相等，求竺L AD 解析作平行四边形EC8A,则△AB石口\。

£»,若H与A不重合，则H在£4 （或延长线）上，但由三角形不等式易知,A，在E4上时,AABE的周长〉/XAZE的周长；A，在E4延长线上时,AABE的周长<AA f BE周长,均与题设矛盾，故A与H重合,A£〃8C ,同理ED//BC ,£ = =.= = AD 2AA f E11.1.4★★△ABC 内,44。

= 60。

,/4(78 = 40。

初中数学竞赛资料第二辑专题13 三角形的基本知识

专题13三角形的基本知识阅读与思考三角形是最基本的几何图形，是研究复杂几何图形的基础，许多几何问题都可转化为三角形的问题来解.三角形基本知识主要包括三角形基本概念、三角形三边关系定理及推论、三角形内角和定理及推论等，它们在线段和角度的计算、图形的计数等方面有广泛的应用.解与三角形的基本知识相关的问题时，常用到数形结合及分类讨论法，即用代数方法解几何计算题及简单的证明题，对三角形按边或按角进行恰当分类.应熟悉以下基本图形：例题与求解【例1】在△ABC中，∠A=50°，高BE，CF交于O，则∠BOC=________.（“东方航空杯”——上海市竞赛试题）解题思路：因三角形的高不一定在三角形内部，故应注意符合题设条件的图形多样性.【例2】等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分，则这个等腰三角形底边的长为（）A.17cmB.5cmC.5cm或17cmD.无法确定（北京市竞赛试题）解题思路：中线所分两部分不等的原因在于等腰三角形的腰与底的不等，应分情况讨论.【例3】如图，BE 是∠ABD 的平分线，CF 是∠ACD 的平分线，BE 与CF 交于G ，若∠BDC =140°，∠BGC =110°，求∠A 的大小.（“希望杯”邀请赛试题）解题思路：运用凹四边形的性质计算.【例4】在△ABC 中，三个内角的度数均为正数，且∠A ＜∠B ＜∠C ，4∠C ＝7∠A ，求∠B 的度数.（北京市竞赛试题）解题思路：把∠A ，∠C 用∠B 的代数式表示，建立关于∠B 的不等式组，这是解本题的突破口.【例5】（1）周长为30，各边长互不相等且都是整数的三角形共有多少个？（2）现有长为150cm 的铁丝，要截成)2(>n n 小段，每段的长不小于1cm 的整数，如果其中任意3小段都不能拼成三角形，试求n 的最大值.此时有几种方法将该铁丝截成满足条件的n 段.（江苏省竞赛试题）解题思路：对于（1），不妨设三角形三边为a ，b ，c ，且c b a <<，由条件及三角形三边关系定理可确定c 的取值范围，从而可以确定整数c 的值.对于（2），因n 段之和为定值150cm ，故欲使n 尽可能的大，必须使每段的长度尽可能的小.这样依题意可构造一个数列.【例6】在三角形纸片内有2008个点，连同三角形纸片的3个顶点，共有2011个点，在这些点中，没有三点在一条直线上.问：以这2011个点为顶点能把三角形纸片分割成多少个没有重叠部分的小三角形？（天津市竞赛试题）解题思路：本题的解题关键是找到规律：三角形内角每增加1个内点，就增加了2个三角形和3条边.能力训练A 级1.设a ，b ，c 是△ABC 的三边，化简c b a c b a --+++=____________.2.三角形的三边分别为3，a 21-，8，则a 的取值范围是__________.3.已知一个三角形三个外角度数比为2:3:4，这个三角形是_______（按角分类)三角形.4.如图，∠A +∠B +∠C +∠D +∠E 的度数为____________.（“缙云杯“试题）（第4题）（第5题）（第6题）5.如图，已知AB ∥CD ，GM ，HM 分别是∠AGH ，∠CHG 的角平分线，那么∠GMH =_________.（第7题）（第9题）6.如图，△ABC 中，两外角平分线交于点E ，则∠BEC 等于（）A .)90(21A ∠-︒B .A ∠+︒2190C .)180(21A ∠-︒D .A ∠-︒211807.如图，在△ABC 中，BD ，BE 分别是高和角平分线，点F 在CA 的延长线上，FH ⊥BE 交BD 于G ，交BC 于H .下列结论：①∠DBE =∠F ；②2∠BEF =∠BAF +∠C ；③∠F =21（∠BAC -∠C ）；④∠BGH =∠ABE +∠C .其中正确的是（）A .①②③B .①③④C .①②③D .①②③④8.已知三角形的每条边长的数值都是2001的质因数，那么这样的不同的三角形共有（）A .6个B .7个C .8个D .9个9.如图，将纸片△ABC 沿着DE 折叠压平，则（）A .∠A =∠1+∠2B .∠A =21（∠1+∠2）C .∠A =31（∠1+∠2）D .∠A =41（∠1+∠2）（北京市竞赛试题）10.一个三角形的周长是偶数，其中的两条边分别是4和1997，则满足上述条件的三角形的个数是（）A .1个B .3个C .5个D .7个（北京市竞赛试题）11.如图，已知∠3=∠1+∠2，求证：∠A +∠B +∠C +∠D =180°.（河南省竞赛试题）12.平面内，四条线段AB ，BC ，CD ，DA 首尾顺次连接，∠ABC =24°，∠ADC =42°.（1）∠BAD 和∠BCD 的角平分线交于点M （如图1），求∠AMC 的大小.（2）点E 在BA 的延长线上，∠DAE 的平分线和∠BCD 平分线交于点N （如图2），求∠ANC .图1图213.三角形不等式是指一个三角形的两边长度之和大于第三边的长度.在下图中，E 位于线段CA 上，D 位于线段BE 上.（1）证明：AB +AE ＞DB +DE ；（2）证明：AB +AC ＞DB +DC ；（3）AB +BC +CA 与2（DA +DB +DC ）哪一个更大？证明你的结论；（4）AB +BC +CA 与DA +DB +DC 哪一个更大？证明你的结论.（加拿大埃蒙德顿市竞赛试题）B 级1.已知三角形的三条边长均为整数，其中有一条边长是4，但不是最短边，这样的三角形的个数有_______个.（“祖冲之杯”邀请赛试题）2.以三角形的3个顶点和它内部的9个点共12个点为顶点能把原三角形分割成______个没有公共部分的小三角形.3.△ABC 中，∠A 是最小角，∠B 是最大角，且有2∠B =5∠A ，若∠B 的最大值是 m ，最小值是 n ，则=+n m ___________.（上海市竞赛试题）4.如图，若∠CGE =α，则∠A +∠B +∠C +∠D +∠E +∠F =_______.（山东省竞赛试题）（第4题）（第5题）5.如图，在△ABC 中，∠A =96°，延长BC 到D ，∠ABC 与∠ACD 的平分线相交于1A 点，BC A 1∠与CD A 1∠的平分线相交于2A 点，依此类推，BC A 4∠与CD A 4∠的平分线相交于5A 点，则5A ∠的大小是（）A .3°B .5°C .8°D .19.2°6.四边形ABCD 两组对边AD ，BC 与AB ，DC 延长线分别交于点E ，F ，∠AEB ，∠AFD 的平分线交于点P .∠A =64°，∠BCD =136°，则下列结论中正确的是（）①∠EPF =100°；②∠ADC +∠ABC =160°；③∠PEB +∠PFC +∠EPF =136°；④∠PEB +∠PFC =136°.A .①②③B .②③④C .①③④D .①②③④7.三角形的三角内角分别为α，β，γ，且γβα≥≥，βα2=，则β的取值范围是（）A . 4536≤≤βB . 6045≤≤βC . 9060≤≤βD .3245≤≤β（重庆市竞赛试题）8.已知周长小于15的三角形三边的长都是质数，且其中一边的长为3，这样的三角形有（）A .4个B .5个C .6个D .7个（山东省竞赛试题）9.不等边△ABC 的两条高的长度分别为4和12，若第三条高的长也是整数，试求它的长.（第三十二届美国邀请赛试题）10.设m ，n ，p 均为自然数，满足p n m ≤≤且15=++p n m ，试问以m ，n ，p 为三边长的三角形有多少个？11.锐角三角形用度数来表示时，所有角的度数为正整数，最小角的度数是最大角的度数的41，求满足此条件的所有锐角三角形的度数.（汉城国际数学邀请赛试题）12.如图1，A 为x 轴负半轴上一点，B 为x 轴正半轴上一点，C （0，-2），D （-2，-2）.（1）求△BCD 的面积；（2）如图2，若∠BCO =∠BAC ，作AQ 平分∠BAC 交y 轴于P ，交BC 于Q .求证：∠CPQ =∠CQP ；（3）如图3，若∠ADC =∠DAC ，点B 在x 轴正半轴上运动，∠ACB 的平分线交直线AD 于E ，DF ∥AC交y 轴于F ，FM 平分∠DFC 交DE 于M ，EDMF BCF ∠∠-∠2的值是否发生变化？证明你的结论.图1图2图313.如图1，),0(m A ，)0,(n B .且m ，n 满足0)42(32≤-+-n m .图1图2（1）求A ，B 的坐标；（2）C 为y 轴正半轴上一动点，D 为△BCO 中∠BCO 的外角平分线与∠COB 的平分线的交点，问是否存在点C ，使∠D =41∠COB .若存在，求C 点坐标；（3）如图2，C 为y 轴正半轴上A 的上方一动点，P 为线段AB 上一动点，连CP 延长交x 轴于E ，∠CAB 和∠CEB 平分线交于F ，点C 在运动过程中FECO ABO ∠∠+∠的值是否发生变化？若不变求其值；若变化，求其范围.专题13三角形的基本知识例1130°或50°例2B例380°提示：∠A＝2∠BGC－∠BDC例4设∠C＝x°，则∠A＝(47 x)°，∠B＝180°－∠C－∠A＝180°－117 x°由∠A＜∠B＜∠C，得47x＜180－117x＜x．解得70＜x＜84．∵47x是整数，∴x＝77．故∠C＝77°，则∠A＝44°，∠B＝180°－77°－44°＝59°．例5（1）不妨设a＜b＜c，则由30a b ca b c+=-⎧⎨+>⎩，得10＜c＜15．∵c是整数，∴c＝11，12，13，14．当c＝11时，b＝10，a＝9．当c＝12时，b＝11，a＝7；b＝10，a＝8．当c＝13时，b＝12，a＝5；b＝11，a＝6；b＝10，a＝7；b＝19，a＝8．当c＝14时，b＝13，a＝3；b＝12，a＝4；b＝11，a＝5；b＝10，a＝6；b＝9，a＝7．（2）这些小段的长度只可能分别是1，1，2，3，5，8，13，21，34，55，89…但1＋1＋2＋5＋8＋13＋21＋34＋55＝143＜150，1＋1＋2＋3＋5＋8＋13＋21＋34＋55＋89＞150，故n的最大值为10.共有以下7种方式：（1，1，2，3，5，8，13，21，34，62）；（1，1，2，3，5，8，13，21，35，61）；（1，1，2，3，5，8，13，21，36，60）；（1，1，2，3，5，8，13，21，37，59）；（1，1，2，3，5，8，13，22，35，60）；（1，1，2，3，5，8，13，22，36，59）；（1，1，2，3，5，8，14，22，36，58）.例6解法1我们不妨先考察三角形内有1个点、2个点、3个点…的简单情况，有下表所示的关系：三角形内点数1234…连线得到的小三角形个数3579…不难发现，三角形内有一个点时，连线可得到3个小三角形，以后每增加一个点，这个点必落在某一个小三角形内，它与该三角形的三个顶点可得到三个小三角形，从而增加了两个小三角形，于是可以推出，当三角形内有2008个点是，连线可得到小三角形的个数为：3＋2×（2008－1）＝4017（个）.解法2整体核算法设连线后把原三角形分割成n个小三角形，则它们的内角和为180°·n，又因为原三角形内每一个点为小三角形顶点时，能为小三角形提供360°的内角，2008个点共提供内角2008×360°，于是得方程180n ＝360×2008＋180，解得n ＝4017，即这2008个点能将原三角形纸片分割成4017个小三角形.A 级1.2（b ＋c ）2.－5＜a ＜－23.钝角4.180°5.90°6.C7.D8.B9.B 10.B11.提示：过G 作GH ∥EB ，可推得BE ∥CF .12.（1）∠AMC ＝12（∠ABC ＋∠ADC ）＝12×（24°＋42°）＝33°（2）∵AN 、CN 分别平分∠DAE ，∠BCD ，∴可设∠EAN ＝∠DAB ＝x ，∠BCN ＝∠DCN ＝y ，∴∠BAN ＝180°－x ，设BC 与AN 交于S ，∴∠BSA ＝∠CSN ，∴180°－x ＋∠B ＝y ＋∠ANC ，①同理：180°－2x ＋∠B ＝2y ＋∠D ，②由①×2－②得：2∠ANC ＝180°＋∠B ＋∠D .∴∠ANC ＝12（180°＋24°＋42°）＝123°.13.（1）（2）略提示：（3）DA ＋DB ＞AB ，DB ＋DC ＞DC ，DC ＋DA ＞CA ，将三个不等式相加，得2（DA ＋DB ＋DC ）＞AB ＋CB ＋CA .（4）由（2）知AB ＋AC ＞DB ＋DC ，同理BC ＋BA ＞DC ＋DA ，CA ＋CB ＞DA ＋DB ，故AB ＋BC ＋CA ＞DA ＋DB ＋DCB 级1.82.193.175提示：设∠A ＝（2x ）°，∠B ＝（5x ）°，则∠C ＝180°－（7x ）°，由∠A ≤∠C ≤∠B 得15≤x ≤204.2a5.A6.D7.D8.B9.提示：设长度为4和12的高分别是边a ，b 上的，边c 上的高为h ，△ABC 的面积为S ，则24S a =，212S b =，2S c h =，由22222412412S S S S S h -<<+得36h <<，故5h =.10.711.设锐角三角形最小角的度数为x ，最大角的度数为4x ，另一角为y ，则41804490x x y x y x x ++=︒⎧⎪⎨⎪<︒⎩，解得20≤x ≤22.5，故x ＝20或21或22.所有锐角三角形的度数为：(20°，80°，80°)，(21°，75°，84°)，(22°，70°，88°).12.（1）S △BCD ＝2（2）略（3）设∠ABC ＝x ，则∠BCF ＝90°＋x ，可证：∠E ＝12x ，∠DMF ＝45°.∴2(90)245212BCF DMF x E x ∠-∠︒+-⨯︒==∠。

初中数学八年级竞赛培优训练直角三角形含解析

直角三角形【思维入门】1．在一个直角三角形中，有一个锐角等于60°，则另一个锐角的度数是() A．120°B．90°C．60°D．30°2．如图1－5－1，△ABC中，AB＝AC＝10，BC＝8，AD平分∠BAC交BC于点D，点E为AC的中点，连结DE，则△CDE的周长为()A．20 B．12 C．14 D．13图1－5－13．如图1－5－2，Rt△ABC中，∠ACB＝90°，点D为斜边AB的中点，AB＝10 cm，则CD的长为______cm.图1－5－24．将一副三角板拼成如图1－5－3所示的图形，过点C作CF平分∠DCE交DE于点F.(1)求证：CF∥AB；(2)求∠DFC的度数．图1－5－35．如图1－5－4，在△ABC 中，AB ＝CB ，∠ABC ＝90°，D 为AB 延长线上一点，点E 在BC 边上，且BE ＝BD ，连结AE ，DE ，DC . (1)求证：△ABE ≌△CBD ；(2)若∠CAE ＝30°，求∠BDC 的度数．【思维拓展】6．如图1－5－5，在Rt △ABC 中，D ，E 为斜边AB 上的两个点，且BD ＝BC ，AE ＝AC ，则∠DCE 的大小为____°.图1－5－57．如图1－5－6，△ABC 中，AB ＝AC ，DE 垂直平分AB ，BE ⊥AC ，AF ⊥BC ，则∠EFC ＝______．图1－5－68．如图1－5－7，∠ABC ＝90°，D ，E 分别在BC ，AC 上，AD ⊥DE ，且AD ＝DE ，点F 是AE 的中点，FD 与AB 延长线相交于点M . (1)求证：∠FMC ＝∠FCM ； (2)AD 与MC 垂直吗？并说明理由．图1－5－79．如图1－5－8，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点图1－5－8D．CG平分∠ACB交BD于点G，F为AB边上一点，连结CF，且∠ACF＝∠CBG.求证：(1)AF＝CG；(2)CF＝2DE.【思维升华】10．如图1－5－9，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY，XZ分别经过点B，C，若∠A＝40°，则∠ABX＋∠ACX＝()图1－5－9A．25°B．30°C．45°D．50°11．如图1－5－10，直线l平行于射线AM，要在直线l与射线AM上各找一点B和C，使得以A，B，C为顶点的三角形是等腰直角三角形，这样的三角形最多能画____个．图1－5－1012．如图1－5－11，点P在△ABC的BC边上，且PC＝2PB，若∠ABC＝45°，∠APC ＝60°，则∠ACB的度数是____．图1－5－1113．如图1－5－12，在△ABC中，AC＝BC，且∠ACB＝90°，点D是AC上一点，AE⊥BD，交BD的延长线于点E，且AE＝12BD，则∠ABD＝____．图1－5－1214．如图1－5－13，在△ABC中，∠ACB＝90°，M是∠CAB的平分线AL的中点，延长CM交AB于K，BK＝BC，则∠CAB＝____，∠ACK∠KCB＝____．图1－5－1315．如图1－5－14，已知△BAD和△BCE均为等腰直角三角形，∠BAD＝∠BCE＝90°，点M为DE的中点．过点E与AD平行的直线交射线AM于点N.(1)当A，B，C三点在同一直线上时(如图1－5－14①)，求证：M为AN的中点；(2)将图1－5－14①中△BCE绕点B旋转，当A，B，E三点在同一直线上时(如图1－5－14②)，求证：△CAN为等腰直角三角形；(3)将图1－5－14①中△BCE绕点B旋转到图③的位置时，(2)中的结论是否仍然成立？若成立，试证明之；若不成立，请说明理由．图1－5－14第5讲直角三角形【思维入门】1．在一个直角三角形中，有一个锐角等于60°，则另一个锐角的度数是(D) A．120°B．90°C．60°D．30°2．如图1－5－1，△ABC中，AB＝AC＝10，BC＝8，AD平分∠BAC交BC于点D，点E为AC的中点，连结DE，则△CDE的周长为(C) A．20 B．12 C．14 D．13图1－5－1【解析】∵AB＝AC，AD平分∠BAC，BC＝8，∴AD⊥BC，CD＝BD＝12BC＝4，∵点E为AC的中点，∴DE＝CE＝12AC＝5，∴△CDE的周长＝CD＋DE＋CE＝4＋5＋5＝14.3．如图1－5－2，Rt△ABC中，∠ACB＝90°，点D为斜边AB的中点，AB＝10 cm，则CD的长为__5____cm.图1－5－24．将一副三角板拼成如图1－5－3所示的图形，过点C作CF平分∠DCE交DE于点F.(1)求证：CF∥AB；(2)求∠DFC的度数．图1－5－3解：(1)证明：∵∠DCE＝90°，CF平分∠DCE，∴∠DCF ＝45°，∵△ABC 是等腰直角三角形，∴∠BAC ＝45°，∴∠BAC ＝∠DCF ，∴CF ∥AB ； (2)∵∠D ＝30°，∴∠DFC ＝180°－30°－45°＝105°.5．如图1－5－4，在△ABC 中，AB ＝CB ，∠ABC ＝90°，D 为AB 延长线上一点，点E 在BC 边上，且BE ＝BD ，连结AE ，DE ，DC . (1)求证：△ABE ≌△CBD ；(2)若∠CAE ＝30°，求∠BDC 的度数．解：(1)证明：∵∠ABC ＝90°，∴∠DBE ＝180°－∠ABC ＝180°－90°＝90°， ∴∠ABE ＝∠CBD .在△ABE 和△CBD 中，∵⎩⎨⎧AB ＝CB ，∠ABE ＝∠CBD ，EB ＝DB ，∴△ABE ≌△CBD ；(2)∵AB ＝CB ，∠ABC ＝90°， ∴△ABC 是等腰直角三角形， ∴∠ECA ＝45°.∵∠CAE ＝30°，∠BEA ＝∠ECA ＋∠EAC ， ∴∠BEA ＝45°＋30°＝75°. 由①知∠BDC ＝∠BEA . ∴∠BDC ＝75°.【思维拓展】6．如图1－5－5，在Rt △ABC 中，D ，E 为斜边AB 上的两个点，且BD ＝BC ，AE ＝AC ，则∠DCE 的大小为__45__°.图1－5－5【解析】设∠DCE＝x，∠ACD＝y，则∠ACE＝x＋y，∠BCE＝90°－∠ACE＝90°－x－y.∵AE＝AC，∴∠ACE＝∠AEC＝x＋y，∵BD＝BC，∴∠BDC＝∠BCD＝∠BCE＋∠DCE＝90°－x－y＋x＝90°－y.在△DCE中，∵∠DCE＋∠CDE＋∠DEC＝180°，∴x＋(90°－y)＋(x＋y)＝180°，解得x＝45°，∴∠DCE＝45°.7．如图1－5－6，△ABC中，AB＝AC，DE垂直平分AB，BE⊥AC，AF⊥BC，则∠EFC ＝__45°____．图1－5－68．如图1－5－7，∠ABC＝90°，D，E分别在BC，AC上，AD⊥DE，且AD＝DE，点F是AE的中点，FD与AB延长线相交于点M.(1)求证：∠FMC＝∠FCM；(2)AD与MC垂直吗？并说明理由．图1－5－7解：(1)证明：∵△ADE是等腰直角三角形，F是AE的中点，∴DF⊥AE，DF＝AF＝EF.又∵∠ABC＝90°，∠DCF，∠AMF都与∠MAC互余，∴∠DCF＝∠AMF.又∵∠DFC＝∠AFM＝90°，∴△DFC≌△AFM.∴CF＝MF.∴∠FMC＝∠FCM；(2)AD⊥MC.由(1)知∠MFC＝90°，FD＝FE，FM＝FC，∴∠FDE＝∠FMC＝45°，∴DE∥CM，∴AD⊥MC.9．如图1－5－8，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点图1－5－8D．CG平分∠ACB交BD于点G，F为AB边上一点，连结CF，且∠ACF＝∠CBG.求证：(1)AF＝CG；(2)CF＝2DE.证明：(1)∵∠ACB＝90°，CG平分∠ACB，AC＝BC.∴∠BCG＝∠CAB＝45°，又∵∠ACF＝∠CBG，AC＝BC，∴△ACF≌△CBG(ASA)，∴AF＝CG；(2)如答图，延长CG交AB于点H.∵AC＝BC，CG平分∠ACB，∴CH⊥AB，H为AB的中点，又∵AD⊥AB，∴CH∥AD，∴G为BD的中点，∠D＝∠EGC，∵E为AC的中点，∴AE＝EC，又∵∠AED＝∠CEG，∴△AED≌△CEG，∴DE＝EG，∴DG＝2DE，∴BG＝DG＝2DE，由(1)得CF＝BG，∴CF＝2DE.第9题答图【思维升华】10．如图1－5－9，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY，XZ分别经过点B，C，若∠A＝40°，则∠ABX＋∠ACX＝(D)图1－5－9A．25°B．30°C．45°D．50°11．如图1－5－10，直线l平行于射线AM，要在直线l与射线AM上各找一点B和C，使得以A，B，C为顶点的三角形是等腰直角三角形，这样的三角形最多能画__3__个．图1－5－10【解析】如答图．①AC为直角边时，符合的等腰直角三角形有2个，一个是以∠BAC为直角，一个是以∠ACB为直角；②AC为斜边时，符合的等腰直角三角形有1个．∴这样的三角形最多能画3个，12．如图1－5－11，点P在△ABC的BC边上，且PC＝2PB，若∠ABC＝45°，∠APC＝60°，则∠ACB的度数是__75°__．图1－5－11【解析】过C作AP的垂线CD，垂足为点D，连结BD.∵△PCD中，∠APC＝60°，∴∠DCP＝30°，PC＝2PD，∵PC＝2PB，∴BP＝PD，∴△BPD是等腰三角形，∠BDP＝∠DBP＝30°，∵∠ABP＝45°，∴∠ABD＝15°，∵∠BAP＝∠APC－∠ABC＝60°－45°＝15°，∴∠ABD＝∠BAD＝15°，∴BD＝AD，∵∠DBP＝∠DCP＝30°，∴BD＝DC，∴△BDC是等腰三角形，∵BD＝AD，∴AD＝DC，∵∠CDA＝90°，∴∠ACD＝45°，∴∠ACB＝∠DCP＋∠ACD＝75°.13．如图1－5－12，在△ABC中，AC＝BC，且∠ACB＝90°，点D是AC上一点，AE⊥BD，交BD的延长线于点E，且AE＝12BD，则∠ABD＝__22.5°__．第11题答图图1－5－12 第13题答图【解析】延长AE ，BC 交于点F .∵AE ⊥BE ， ∴∠BEF ＝90°，又∵∠ACF ＝∠ACB ＝90°， ∴∠DBC ＋∠AFC ＝∠F AC ＋∠AFC ＝90°， ∴∠DBC ＝∠F AC ，在△ACF 和△BCD 中，⎩⎨⎧∠ACF ＝∠BCD ＝90°，AC ＝BC ，∠F AC ＝∠DBC ，∴△ACF ≌△BCD (ASA )， ∴AF ＝BD . 又∵AE ＝12BD ，∴AE ＝EF ，即点E 是AF 的中点． ∴AB ＝BF ，∴BD 是∠ABC 的角平分线． ∴∠ABD ＝22.5°.14．如图1－5－13，在△ABC 中，∠ACB ＝90°，M 是∠CAB 的平分线AL 的中点，延长CM 交AB 于K ，BK ＝BC ，则∠CAB ＝__45°__，∠ACK ∠KCB＝__13__．图1－5－13【解析】设∠CAB ＝2α.∵AM ＝ML ，且∠ACB ＝90°，∴CM ＝MA ， ∴∠ACM ＝∠MAC ＝α.∴∠CKB ＝∠CAK ＋∠ACM ＝3α， ∠KCB ＝90°－∠ACM ＝90°－α. ∵BK ＝BC ， ∴∠CKB ＝∠KCB .∴3α＝90°－α，即α＝22.5°. ∴∠CAB ＝45°，∠ACK ∠KCB ＝22.5°67.5°＝13.15．如图1－5－14，已知△BAD 和△BCE 均为等腰直角三角形，∠BAD ＝∠BCE ＝90°，点M 为DE 的中点．过点E 与AD 平行的直线交射线AM 于点N .(1)当A ，B ，C 三点在同一直线上时(如图1－5－14①)，求证：M 为AN 的中点； (2)将图1－5－14①中△BCE 绕点B 旋转，当A ，B ，E 三点在同一直线上时(如图1－5－14②)，求证：△CAN 为等腰直角三角形；(3)将图1－5－14①中△BCE 绕点B 旋转到图③的位置时，(2)中的结论是否仍然成立？若成立，试证明之；若不成立，请说明理由．图1－5－14证明：(1)∵点M 为DE 的中点，∴DM ＝ME . ∵AD ∥EN ，∴∠ADM ＝∠NEM ，又∵∠DMA＝∠EMN，∴△DMA≌△EMN，∴AM＝MN，即M为AN的中点；(2)由(1)中△DMA≌△EMN可知DA＝EN，又∵DA＝AB，∴AB＝NE，∵∠ABC＝∠NEC＝135°，BC＝CE，∴△ABC≌△NEC，∴AC＝CN，∠ACB＝∠NCE，∵∠BCE＝∠BCN＋∠NCE＝90°，∴∠BCN＋∠ACB＝90°，∴∠ACN＝90°，∴△CAN为等腰直角三角形．(3)由(2)可知AB＝NE，BC＝CE.又∵∠ABC＝360°－45°－45°－∠DBE＝270°－∠DBE＝270°－(180°－∠BDE－∠BED)＝90°＋∠BDE＋∠BED＝90°＋∠ADM－45°＋∠BED＝45°＋∠MEN＋∠BED ＝∠CEN，∴△ABC≌△NEC，再同(2)可证△CAN为等腰直角三角形，∴(2)中的结论仍然成立.。

数学相似三角形(竞赛题专页)

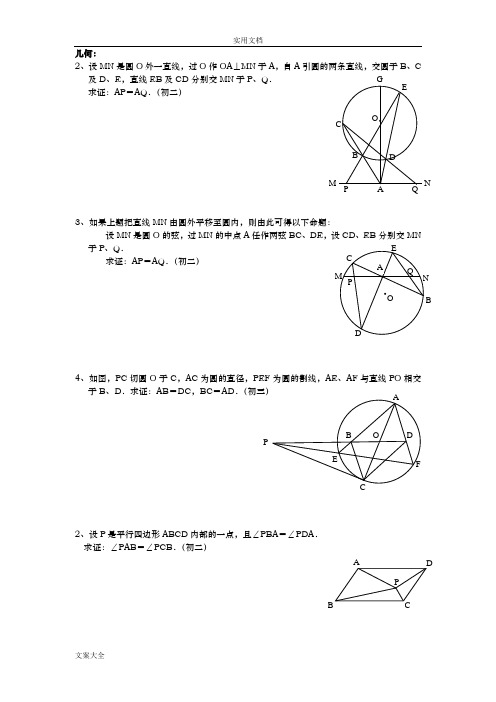
几何：2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）· GAO DB EC Q P NM · O Q PBDEC N M · A OD BFAECP P ADCB4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．1.∠ABC 的顶点B 在⊙O 外，BA 、BC 均与⊙O 相交，过BA 与圆的交点K 引∠ABC 平分线的垂线，交⊙O 于P ，交BC 于M 。

求证：线段PM 为圆心到∠ABC 平分线距离的2倍。

EDCBA2.在△ABC中，AP为∠A的平分线，AM为BC边上的中线，过B作BH⊥AP于H，AM的延长线交BH于Q，求证：PQ∥AB。

3.菱形ABCD的内切圆O与各边分别切于E、F、G、H，在EF与GH上分别作⊙O的切线交AB于M，交BC于N，交CD于P，交DA于Q。

求证：MQ∥NP。

4.ABCD是圆内接四边形，其对角线交于P，M、N分别是AD、BC的中点，过M、N分别作BD、AC的垂线交于K。

求证：KP⊥AB。

5.以△ABC的边BC为直径作半圆，与AB、AC分别交于点D、E。

与三角形的角有关的竞赛题

word 专业资料-可复制编辑-欢迎下载与三角形的角有关的竞赛题.（1996年“希望杯”全国数学邀请赛初二试题）已知：如图23，DO 平分∠ADC ，BO 平分∠ABC ，且∠A=270，∠O=330，则∠C 的大小是 . 2.（1994年四川省初中数学竞赛试题）如图24，已知∠xoy=900，点A 、B 分别在射线ox 、oy 上移动，∠OAB 的内角平分线与∠OBA 的外角平分线交于点C .试问∠ACB 的大小是否变动？证明你的结论.3.（江苏省第十五届初中数学竞赛初二第1试试题）如图25，XK ，ZF 是△XYZ 的高且交于一点H ，∠XHF ＝400，那么∠XYZ ＝度.A BOF X Y图23 图24 图254.在△ABC 中，∠A=70°，∠B=50°，过A 、B 两点分别作BC 和AC 的垂线，这两条垂线相交于O ，则∠AOB 等于( ) A.120° B.60° C.70°或50° D.60°或120°5.（江苏省第十八届初中数学竞赛初一年级第1试）如图26，在一个正方体的两个面上画了两条对角线AB ，AC ，那么这两条对角线的夹角等于（）A 、600B 、750C 、900D 、13506. (2004年富阳市初一数学竞赛试卷)如图27，已知AB ∥ED ，∠C ＝900，∠ABC ＝∠DEF ，∠D ＝1300，∠F ＝1000，求∠E 的大小。

7.（1988年上海市初二数学竞赛）一个六边形的六个内角都是1200,连续四边的长依次是1,3,3,2,则该六边形的周长是____.8.已知空间中有8个点，其中任四点不在同一个平面上，在这8点中间连结21条线段，则这些线段最多能构成的三角形的个数为（） (A)56 (B)35 (C)21 (D)以上都不对9.平面上有n 个点，其中每三个点都是某个正三角形的顶点，则n 的最大值是 .10. (1988年上海市初二数学竞赛试题) ABC ∆中，A ∠是最小角，B ∠是最大角,且25B A ∠=∠,若B ∠的最大的值是m 0最小值是n 0,则m n += .11.如图28所示,四边形ABCD 中,AB=AC=AD,(1) 若∠DAC=2∠BAC,则∠DBC=2∠BDC,说明理由;(2) 试猜想当∠DAC=3∠BAC,∠DAC=4∠BAC,…,∠DAC=n ∠BAC 时,∠DBC 与∠BDC 有何关系?并说明你的理由O D C B A。

数学初中竞赛《三角形的五心》专题训练(含答案) (1)

数学初中竞赛《三角形的五心》专题训练一．选择题1．如图，已知直线MN∥AB，把△ABC剪成三部分，点C在直线AB上，点O在直线MN上，则点O是△ABC的（）A．垂心B．重心C．内心D．外心2．课本第5页有这样一个定义“三角形的三条中线的交点叫做三角形的重心”．现在我们继续定义：①三角形三边上的高线的交点叫做三角形的垂心；②三角形三条内角平分线的交点叫做三角形的内心；③三角形三边的垂直平分线的交点叫做三角形的外心．在三角形的这四“心”中，到三角形三边距离相等的是（）A．重心B．垂心C．内心D．外心3．如图为4×4的网格图，A，B，C，D，O均在格点上，则点O是（）A．△ACD的重心B．△ABC的外心C．△ACD的内心D．△ABC的垂心4．如图，O是△ABC的外心，OD⊥BC，OE⊥AC，OF⊥AB，则OD：OE：OF等于（）A．a：b：c B．：：C．sin A：sin B：sin C D．cos A：cos B：cos C5．在△ABC中，两中线AD与CF相交于点G，若∠AFC＝45°，∠AGC＝60°，则∠ACF的度数为（）A．30°B．45°C．60°D．75°6．如图，已知△ABC的三个顶点分别在反比例函数y＝（k＞0）的图象上，那么△ABC的（）也一定在该函数图象上．A．重心B．内心C．外心D．垂心7．如图，已知H是△ABC的垂心，△ABC的外接圆半径为R，△BHC的外接圆半径为r，则R 与r的大小关系是（）A．R＝r B．R＞r C．R＜r D．无法确定8．以Rt△ABC的两条直角边AB、BC为边，在三角形ABC的外部作等边三角形ABE和等边三角形BCF，EA和FC的延长线相交于点M，则点B一定是三角形EMF的（）A．垂心B．重心C．内心D．外心9．如图，锐角△ABC的垂心为H，三条高的垂足分为D、E、F，则H是△DEF的（）A．垂心B．重心C．内心D．外心10．三个等圆O 1，O 2，O 3有公共点H ，点A 、B 、C 是其他交点，则H 是三角形ABC 的（）A ．外心B ．内心C ．垂心D ．重心二．填空题11．在半径为1的⊙O 中内接有锐角△ABC ，H 是△ABC 的垂心，角平分线AL 垂直于OH ，则BC ＝．12．如图，ADCFBE 是某工厂车间的一种剩余残料，且∠ACB ＝90°，现需要利用这块残料在△ABC 的外部制作3个等边△ADC 、△CBF 、△ABE 的内切圆⊙O 1、⊙O 2、⊙O 3，若其中最大圆⊙O 3的半径为0.5米，可使生产成本节约3元（节约成本与圆面积成正比），照此计算，则10块这样的残料可使生产成本节约元．13．如图，在△ABC 中M 为垂心，O 为外心，∠BAC ＝60°，且△ABC 外接圆直径为10，则AM ＝．14．如图，锐角三角形ABC 内接于半径为R 的⊙O ，H 是三角形ABC 的垂心，AO 的延长线与BC 交于点M ，若OH ⊥AO ，BC ＝10，OA ＝6，则OM 的长＝．15．设凸四边形ABCD 的对角线AC 与BD 相交于O ，△OAB ，△OBC ，△OCD ，△ODA 的重心分别为E ，F ，G ，H ，则S EFGH ：S ABCD ＝．16．如图，I 是Rt △ABC （∠C ＝90°）的内心，过I 作直线EF ∥AB ，分别交CA 、CB 于E 、F ．已知EI＝m，IF＝n，则用m、n表示S△ABC＝．17．已知点I是锐角三角形ABC的内心，A1、B1、C1分别是点I关于边BC，CA，AB的对称点，若点B在△A1B1C1的外接圆上，则∠ABC等于．三．解答题18．如图所示，已知锐角△ABC的外接圆半径R＝1，∠BAC＝60°，△ABC的垂心和外心分别为H、O，连接OH、BC交于点P（1）求凹四边形ABHC的面积；（2）求PO•OH的值．19．如图，AD，BE，CF是△ABC的高，K，M，N分别为△AEF，△BFD，△CDE的垂心，求证：△DEF≌△KMN．20．如图，点H为△ABC的垂心，以AB为直径的⊙O1和△BCH的外接圆⊙O2相交于点D，延长AD交CH于点P，求证：点P为CH的中点．21．如图，△ABC的三边满足关系BC＝（AB+AC），O、I分别为△ABC的外心、内心，∠BAC 的外角平分线交⊙O于E，AI的延长线交⊙O于D，DE交BC于H，求证：（1）AI＝BD；（2）OI＝AE．22．如图，H是锐角△ABC的垂心，O为△ABC的外心，过O作OD⊥BC，垂足为D．（1）求证：AH＝2OD；（2）若AO＝AH，求∠BAC的度数．23．如图，D ，E ，F 分别是△ABC 的边BC ，CA ，AB 上的点，且∠FDE ＝∠A ，∠DEF ＝∠B ．又设△AFE ，△BDF ，△CED 均为锐角三角形，它们的垂心依次为H 1，H 2，H 3，求证：1．∠H 2DH 3＝∠FH 1E ；2．△H 1H 2H 3≌△DEF ．24．如图，△ABC 为锐角三角形，CF ⊥AB 于F ，H 为△ABC 的垂心．M 为AH 的中点，点G 在线段CM 上，且CG ⊥GB ．（1）求证：∠MFG ＝∠GCF ；（2）求证：∠MCA ＝∠HAG ．25．如图，已知H 为锐角△ABC 的垂心，D 是使四边形AHCD 为平行四边形的一点，过BC 的中点M 作AB 的垂线，垂足为N ，K 为MN 的中点，过点A 作BD 的平行线交MN 于点G ，若A ，K ，M ，C 四点共圆．求证：直线BK 平分线段CG ．参考答案一．选择题1．解：如图1，过点O作OD⊥BC于D，OE⊥AC于E，OF⊥AB于F∵MN∥AB，OD＝OE＝OF（夹在平行线间的距离处处相等）如图2，过点O作OD'⊥BC于D'，作OE'⊥AC于E'，作OF'⊥AB于F'，由裁剪知，OD＝OD'，OE＝OE'，OF＝OF'，∴OD'＝OE'＝OF'，∴图2中的点O是三角形三个内角的平分线的交点，∴点O是△ABC的内心，故选：C．2．解：内心是三角形的三条内角平分线的交点，而角平分线上的点到角的两边的距离相等，所以在三角形的四“心”中，到三角形三边距离相等的是内心；到三个顶点的距离相等的是外心．故选：C．3．解：如图，连接OA、OB、OC、OD，设每一个小方格的边长为1，由勾股定理可求得OA＝OB＝OC＝，OD＝2，∴O点在AB、AC、BC的垂直平分线上，∴点O为△ABC的外心，∵OA＝OC≠OD，∴点O即不是△ACD的重心，也不是△ACD的内心，故选：B．4．解：如图，连接OA、OB、OC；∵∠BOC＝2∠BAC＝2∠BOD，∴∠BAC＝∠BOD；同理可得：∠BOF＝∠BCA，∠AOE＝∠ABC；设⊙O的半径为R，则：OD＝R•cos∠BOD＝R•cos∠A，OE＝R•cos∠AOE＝R•cos∠B，OF＝R•cos∠BOF＝R•cos∠C，故OD：OE：OF＝cos∠A：cos∠B：cos∠C，故选：D．5．解：∵点G是△ABC的重心，∴＝2，作CE⊥AG于点E，连接EF，∴△CEG是直角三角形，∵∠EGC＝60°，∴∠ECG＝30°，那么EG＝CG＝GF，∴GE＝GF，∠FGE＝120°，∴∠GFE＝∠FEG＝30°，而∠ECG＝30°，∴EF＝EC，∵∠EFA＝45°﹣30°＝15°，∠FAD＝∠AGC﹣∠AFC＝15°，∴∠FAD＝∠EFA，∴EF＝AE，∴AE＝EC，∵△AEC是等腰直角三角形，∴∠ACE＝45°，∴∠ACF＝∠ACE+∠ECF＝30°+45°＝75°，故选：D．6．解：结论：△ABC的垂心也一定在该函数图象上；理由：∵A、B、C都在y＝上，∴可设A、B、C的坐标依次是：（a，）、（b，）、（c，）．令H的坐标为（x，y）．容易得出：AB的斜率＝＝﹣，BC的斜率＝＝﹣，AH的斜率＝，CH的斜率＝，∵AH⊥BC，CH⊥AB，∴＝，＝，∴a•＝c•，∴（k﹣ay）（c﹣x）＝（k﹣cy）（a﹣x），∴ck﹣kx﹣acy+axy＝ak﹣kx﹣acy+cxy，∴（a﹣c）xy＝（a﹣c）k．显然，a﹣c≠0，∴xy＝k，即：y＝．∴点H（x，y）在反比例函数y＝的图象上．故选：D．7．解：如图，延长AD交△ABC的外接圆于G，连接BG，CG，∴△ABC的外接圆的半径等于△BGC的外接圆的半径，∵△ABC的外接圆半径为R，∴△BGC的外接圆半径为R，∵点H是△ABC的垂心，∴AD⊥BC，BE⊥AC，∴∠ADC＝∠BEC＝90°，∴∠CAD+∠ACB＝90°，∠CBE+∠ACB＝90°，∴∠CAD＝∠CBE，∵∠CBG＝∠CAD，∴∠CBE＝∠CBG，同理：∠BCF＝∠BCG，在△BCH和△BCG中，，∴△BCH≌△BCG（ASA），∴△BHC的外接圆的半径等于△BGC的外接圆的半径，∵△BHC的外接圆半径为r，∴△BGC的外接圆的半径为r，∴R＝r，故选：A．8．解：如图，连接CE，AF，延长EB交MF于G，延长FB交ME于H，∵以Rt△ABC的两条直角边AB，BC为边作等边△ABE和等边△BCF，∴∠CBE＝90°+60°＝150°，∠FBE＝360°﹣90°﹣60°﹣60°＝150°，在△CBE与△FBE中，，∴△CBE≌△FBE（SAS）；∴CE＝FE，∠FEB＝∠CEB，∴BE⊥CF于G，∴EG是△MEF的边FM上的高，同理：FH是△MEF的边EM上的高，∴点B是△MEF的三边的高，即：点B是△MEF的垂心．故选：A．9．解：∵BE丄AC，CF丄AB，∴四点B、C、E、F共圆（以BC为直径），∴∠EBF＝∠FCE，∵HD丄BD，HF丄BF，∴四点B、D、H、F共圆（以BH为直径），∴∠HBF＝∠FDH，同理，四点C、D、H、E共圆，（以CH为直径），∠HDE＝∠HCE，∴∠HDE＝∠HDF，∴DA平分∠EDF即可．同理可证EB平分∠DEF，FC平分∠EFD，∴H是△DEF的角平分线的交点，∴H是△DEF的内心．故选：C．10．解：延长AH交BC于E点，延长CH交AB于F点，如图，∵三个等圆O1，O2，O3有公共点H，∴∠1所对的弧BH与∠4所对的弧BH为等弧；∠2所对的弧CH与∠5所对的弧CH为同弧；∠3所对的弧AH与∠6所对的弧AH为同弧，∴∠1＝∠4，∠2＝∠5，∠3＝∠6，∵∠1+∠2+∠3+∠4+∠5+∠6＝180°，∴2∠2+2∠3+2∠4＝180°，2∠1+2∠3+2∠2＝180°，∴∠2+∠3+∠4＝90°，∠1+∠3+∠2＝90°，∴AE⊥BC，CF⊥AB，∴点H为△ABC的垂心．故选：C．二．填空题（共7小题）11．解：设AL与⊙O交于点D，与OH交于点N，连接OD，交BC于点M，连接CO并延长交⊙O于点G，连接GA、GB、AO，如图所示，∵CG是⊙O的直径，∴∠CBG＝∠CAG＝90°，∴BG⊥BC，AG⊥AC．∵H为△ABC的垂心，∴AE⊥BC，BF⊥AC，∴AE∥BG，AG∥BF，∴四边形AGBH是平行四边形，∴BG＝AH．∵AL平分∠BAC，∴∠BAD＝∠CAD，∴＝，根据垂径定理的推论可得：OD⊥BC．∵AE⊥BC，∴OD∥AE，∴∠ODA＝∠EAD．∵OA＝OD，∴∠ODA＝∠OAD，∴∠OAD＝∠EAD．∵AL垂直于OH，∴∠ANO＝∠ANH＝90°．在△ANO和△ANH中，，∴△ANO≌△ANH（ASA），∴AO＝AH，∴BG＝AH＝AO＝1．在Rt△GBC中，∵BG＝1，GC＝2，∴BC＝＝．故答案为：．12．解：由勾股定理和相似图形的性质可知，⊙O1的面积+⊙O2的面积＝⊙O3的面积，∵⊙O3可使生产成本节约3元，∴1块这样的残料可使生产成本节约6元．则10块这样的残料可使生产成本节约6×10＝60元．故答案为：60．13．解：延长AM交BC于D，延长CM交AB于E，作直径BF，连结AF，如图，∵BF为⊙的直径，∴∠BAF＝90°，∴sin F＝＝，∴AB＝10•sin F＝10•sin∠ACB，又∵点M为△ABC的垂心，∴AD⊥BC，CE⊥AB，∴∠ADB＝∠AEC＝90°，∴△AEM∽△ADB，∴＝，即AM＝，在Rt△AEC中，∠EAC＝60°，AC＝2AE，即AE＝AC，在Rt△ADC中，sin∠ACD＝，即AD＝AC•sin∠ACD，∴AM＝＝5．故答案为5．14．解：如图，连接BO并延长交圆于F，连接CF，AH，连接AF，CH，过点O作ON⊥BC于N，∵BF是⊙O的直径，∴∠BCF＝∠BAF＝90°，∴ON∥FC，∵OB＝OF，∴ON是△BCF的中位线，∴CF＝2ON．∴BN＝CN＝BC＝5，在Rt△OBN中，OB＝OA＝6，BN＝5，∴ON＝＝，∴CF＝2ON＝2，∵H是△ABC的垂心，∴AH⊥BC，∵CF⊥BC，∴AH∥CF，同理可得：CH∥AF，∴四边形AHCF是平行四边形，∴AH＝CF＝2∵H是△ABC的垂心，∴AH⊥BC，∵ON⊥BC，∴AH∥ON，∴∠OAH＝∠NOM，∵OH⊥AM，∴∠AOH＝∠ONM＝90°，∴△AOH∽△ONM，∴，∴，∴OM＝．故答案为．15．解：如图：∵E、F分别是△OAB与△OBC的重心，∴，∴EF∥AC，同理：FG∥BD，HG∥AC，HE∥BD，∴ERUQ，RUSF，USGT，THQU，EFGH是平行四边形，∵，∴，同理：，∴，∴，同理：，，．∴．16．解：如图，过I分别作三边的垂线，垂足为D、F、G，设AB＝c，BC＝a，AC＝b，ID＝IH＝IG＝r，由△ABC∽△EIG∽△IFH，得＝，＝，解得a＝，b＝，由勾股定理，得c2＝a2+b2，得1＝+，解得r＝，又ab＝2S△ABC＝r（a+b+c），∴＝r（++c），解得c＝m+n+＝m+n+，∴S△ABC＝ab＝＝（）2（m+n+）2＝．故答案为：．17．解：∵I是锐角三角形ABC的内心，∴∠DBI＝∠ABC，∵A1、B1、C1分别是点I关于边BC，CA，AB的对称点，∴ID＝A1D＝IA1，∠BDI＝90°，∵点B在△A1B1C1的外接圆上，∴IB＝IA1，∴ID＝IB，∴∠IBD＝30°，∴∠ABC＝60°．故答案为：60°．三．解答题（共8小题）18．解：（1）如图：连接BO并延长交⊙O于点G，连接AG、CG、CO，延长CH交AB于F，延长BH交AC于E，延长AH交BC于N，作OM⊥BC于M．∵BG是直径，∴GA⊥AB，GC⊥BC，∵H为垂心，∴BE⊥AC，CF⊥AB，AN⊥BC，∴GA∥CH，GC∥AH，∴AGCH是平行四边形，∴AG＝GC，∵∠BA C＝60°，OB＝OC，∴∠OBC＝∠OCB＝30°，∴OM＝OB＝，BM＝，∴BC＝，又∵OM＝CG，∴AH＝2OM＝1，设凹四边形的面积为S，则S＝S△AHB+S△AHC＝×AH×BN+×AH×CN＝×AH×BC＝，（2）∵BE⊥AC，CF⊥AB，AN⊥BC，∠BAC＝60°，∴∠ACF＝30°，∴∠CHE＝60°，∴∠BHC＝120°，∴B、C、H、O四点共圆，∵∠OBC＝∠OCB＝30°，∴∠CHP＝∠OBC＝30°，∴∠OHC＝∠OCP＝150°，∴△OHC∽△OCP，∴OH•OP＝OC2＝1．19．证明：如图：∵OD⊥BC，FM⊥BC，∴OD∥FM，∵OF⊥AB，DM⊥AB，∴OF∥DM，∵DMFO是平行四边形，同理OFKE，ODNE均为平行四边形，∴MD∥KE，MD＝KE，∴MDEK也是平行四边形，∴DE＝MK，同理DF＝KN，EF＝MN∴△DEF≌△KMN（SSS）．于点Q，20．证明：如图，延长AP交⊙O2连接AH，BD，QB，QC，QH．因为AB为⊙O的直径，1所以∠ADB＝∠BDQ＝90°．（5分）故BQ为⊙O的直径．2于是CQ⊥BC，BH⊥HQ．（10分）又因为点H为△ABC的垂心，所以AH⊥BC，BH⊥AC．所以AH∥CQ，AC∥HQ，四边形ACQH为平行四边形．（15分）所以点P为CH的中点．（20分）21．证明：（1）作IG⊥AB于G点，连BI，BD，如图，∴AG＝（AB+AC﹣BC），而BC＝（AB+AC），∴AG＝BC，又∵AD平分∠BAC，AE平分∠BAC的外角，∴∠EAD＝90°，∴O点在DE上，即ED为⊙O的直径，而BD弧＝DC弧，∴ED垂直平分BC，即BH＝BC，∴AG＝BH，而∠BAD＝∠DAC＝∠DBC，∴Rt△AGI≌Rt△BHD，∴AI＝BD；（2）∵∠BID＝∠BAI+∠ABI，而∠BAI＝∠DBC，∠ABI＝∠CBI，∴∠DBI＝∠BID，∴ID＝DB，而AI＝BD，∴AI＝ID，∴OI为三角形AED的中位线，∴OI＝AE．22．（1）证明：如图1，连接BH并延长交AC于E，∴BE⊥AC，过O作OF⊥AC于F，则F为AC的中点，连接CH，取CH中点N，连接FN，DN，则FN∥AM，AH＝2FN，DN∥BE，∵AM⊥BC，OD⊥BC，∴OD∥AM，∴FN∥OD，∵BE⊥AC，OF⊥AC，∴BE∥OF，∵OD⊥BC，∴D为BC中点，∵N为CH中点，∴DN∥BE，∴DN∥OF，∴四边形ODNF是平行四边形，∴OD＝FN，∵AH＝2FN，∴AH＝2OD．（2）解：如图2，连接OB，OC，∴OA＝OB，∵OA＝AH，∴OB＝AH，由（1）知，AH＝2OD，∴OB＝2OD，在Rt△ODB中，cos∠BOD＝＝，∴∠BOM＝60°，∵OD⊥BC，∴∠BOC＝2∠BOD＝120°，∴∠BAC＝∠BOC＝60°．23．证明：（1）∵H2是△BDF的垂心，⊥BF，∴DH2DB＝90°﹣∠B，∴∠H2同理：∠H 3DC ＝90°﹣∠C ，∴∠H 2DH 3＝180°﹣∠H 2DB ﹣∠H 3DC ＝∠B +∠C ， ∵H 1是△AEF 的垂心，∴∠H 1EF ＝90°﹣∠AFE ，∠H 1FE ＝90°﹣∠AEF ， ∴∠EH 1F ＝180°﹣∠H 1EF ﹣∠H 1FE ＝180°﹣（90°﹣∠AFE ）﹣（90°﹣∠AEF ）＝180°﹣∠A ＝∠B +∠C ，∴∠H 2DH 3＝∠FH 1E ；（2）如图，由（1）知，∠FH 1E ＝∠B +∠C ， ∵∠FDE ＝∠A ，∠A +∠B +∠C ＝180°， ∴∠FH 1E +∠EDF ＝180°，∴H 1在△DEF 的外接圆上，同理：H 2，H 3也在△DEF 的外接圆上， ∴D ，H 2，F ，H 1，E ，H 3六点共圆，由（1）知，∠EH 1F ＝∠H 2DH 3， ∴EF ＝H 2H 3，同理：DF ＝H 1H 3，DE ＝H 1H 2，∴△DEF ≌△H 1H 2H 3（SSS ）．24．证明：（1）如图延长AH 交BC 于T ． ∵H 是△ABC 的垂心，∴∠THC ＝∠HFA ＝90°，∵∠THC ＝∠AHF ，∴∠HCT ＝∠FAH ，在Rt △AFH 中，∵AM ＝MH ，∴FM＝AM＝MH，∴∠FAH＝∠MFA，∴∠MFA＝∠HCT，∵BG⊥CM，∴∠BFC＝∠BGC＝90°，∴B、C、G、F四点共圆，∴∠AFG＝∠BCG，∴∠AFM+∠MFG＝∠HCT+∠MCF，∴∠MFG＝∠GCF．（2）∵∠FMG＝∠FMC，∠MFG＝∠MCF，∴△MFG∽△MCF，∴＝，∴MF2＝MG•MC，∵MA＝MF，∴MA2＝MG•MC，∴＝，∵∠AMG＝∠AMC，∴△MAG∽△MCA，∴∠MCA＝∠HAG．25．证明：如图，设BK交CG于E，连接AG，AK，∵A，K，M，C四点共圆，∴∠AC B＝∠AKG（外角等于内对角），∵H是△ABC的垂心，∴AH⊥BC，CH⊥AB，∵四边形AHCD是平行四边形，∴CH∥AD，AH∥CD，∴CD⊥BC，AD⊥AB，∴∠BCD＝∠BAD＝90°，∴∠BAD+∠BCD＝180°，∴点A，B，C，D四点共圆，∴∠5＝∠ACB＝∠AKG，∵AH⊥BC，MN⊥AB，AD⊥AB，∴∠1＝∠2＝∠4，∵AG∥BD，∴∠3＝∠4＝∠2，在△ANG和△ANK中，，∴△ANG≌△ANK，∴GN＝KN＝MK，∴MK＝KG，∵直线BKE截得△GMC，由梅涅劳斯定理得：，∵点M是CB中点，∴CB＝2BM，∴GE＝EC，∴直线BK平分线段CG．。

2024全国初中数学竞赛试题

1、已知直角三角形的两条直角边长度分别为3和4，则斜边上的高为：A. 2.4B. 1.2C. 5D. 不能确定（答案）A2、若a、b、c为三角形的三边长，且满足a² + b² + c² + 50 = 10a + 6b + 8c，则此三角形为：A. 直角三角形B. 等腰三角形C. 等边三角形D. 不能确定（答案）A3、解方程组 { x + 2y = 5, 3x - 4y = -2 } 时，若先消去y，则得到的方程是：A. 5x = 14B. 5x = 10C. 7x = 16D. 7x = 22（答案）B4、在平行四边形ABCD中，若∠A : ∠B = 2 : 3，则∠C的度数为：A. 60°B. 90°C. 120°D. 不能确定（答案）C5、已知 |x| = 5，y = 3，则x - y等于：A. 8或-2B. 2或-8C. -2或8D. -8或2（答案）D6、若关于x的一元二次方程x² - (k - 1)x - k = 0有两个相等的实数根，则k的值为：A. -3B. 3C. -1D. 1（答案）D7、在圆O中，弦AB的长度等于半径OA，则∠AOB的度数为：A. 30°B. 60°C. 120°D. 30°或150°（答案）B8、若a > b > 0，c < d < 0，则一定有：A. a² > b²B. c² > d²C. a/d > b/cD. a/d < b/c（答案）A9、已知一次函数y = kx + b的图像经过点(2, 3)和(-1, -3)，则它的图像不经过：A. 第一象限B. 第二象限C. 第三象限D. 第四象限（答案）C10、在△ABC中，若∠A = 60°，∠B = 45°，则∠C的度数为：A. 45°B. 60°C. 75°D. 90°（答案）C。

江苏数学竞赛初中试题及答案

江苏数学竞赛初中试题及答案试题一：代数基础题题目：已知 \( a \) 和 \( b \) 是两个正整数，且 \( a^2 - b^2 = 21 \)，求 \( a \) 和 \( b \) 的值。

答案：根据差平方公式，\( a^2 - b^2 = (a+b)(a-b) \)。

已知\( a^2 - b^2 = 21 \)，我们可以将21分解为两个因数的乘积，即\( 21 = 3 \times 7 \)。

考虑到 \( a \) 和 \( b \) 是正整数，我们可以得出 \( a = 7 \)，\( b = 3 \)。

试题二：几何题题目：在一个直角三角形中，如果一个锐角是另一个锐角的两倍，求这个三角形的三个角度数。

答案：设较小的锐角为 \( x \) 度，则较大的锐角为 \( 2x \) 度。

根据直角三角形的性质，三个角的和为180度，因此有 \( x + 2x + 90 = 180 \)。

解这个方程，我们得到 \( 3x = 90 \)，所以 \( x = 30 \)。

因此，较小的锐角是30度，较大的锐角是60度，直角是90度。

试题三：数列题题目：一个数列的前三项为 \( 2, 4, 7 \)，从第四项开始，每一项都是前三项的和。

求第10项的值。

答案：根据题意，数列的前几项为：2, 4, 7, (2+4+7), (4+7+13), ...即：2, 4, 7, 13, 24, 41, 75, 130, 231, ...第10项的值为 \( 231 \)。

试题四：逻辑推理题题目：有5个盒子，每个盒子里都装有不同数量的球，分别是1个，2个，3个，4个和5个。

现在有5个人，每个人从每个盒子里都拿了一个球，但没有人拿到两个相同数量的球。

每个人拿的球的总数都是6个。

问每个人分别从哪些盒子里拿球？答案：设5个人分别为A、B、C、D、E。

根据题意，每个人拿的球的总数都是6个，且没有人拿到两个相同数量的球。

我们可以列出以下可能的组合：- A: 1, 2, 3- B: 1, 3, 4- C: 1, 4, 5- D: 2, 3, 5- E: 2, 4由于每个人拿的球的总数都是6个，我们可以排除E的组合，因为2+4=6，没有第三个球。

初中数学竞赛——三角形四边形综合

三角形四边形综合1. 如图，已知ABC △中，AD BC AB CD AC BD ⊥+=+，．求证：AB AC =．2. 两个全等的3060︒︒、角的三角板ADE 和三角板ABC 如图所示放置，E A C 、、三点在一条直线上，连接BD ，取BD 的中点M ，连接ME MC 、，试判断EMC △的形状，并说明理由。

3. 如图，已知AD 是ABC △的中线，且1356AB AC AD ===，，，则ABC △的面积为_______．4. □ABCD 中，DE AB ⊥于E 交AC 于F ，且12AD FC =．求证：3DAB ACD ∠=∠． CDBAEF CBADCDBAMBEACD5. 平面上有3个正ABD BCE ACF △、△、△，两两共有一个顶点．求证：CD 与EF 互相平分．6. 在ABC △中，BD 是ABC ∠的平分线．在ABC △外取一点E ，使得EAB ACB ∠=∠，AE DC =，并且线段ED 与线段AB 相交，交点记为K ．求证：KE KD =．7. 正方形ABCD 中，E 为CD 的中点，F 为CD 上的点，且AF CD CF =+．求证：2BAF BAE ∠=∠．8.ABC △是等腰直角三角形，90ACB ∠=，D 是AC 的中点，连结BD ，作ADF CDB ∠=∠，连结 CF 交BD 于E ．求证：BD CF ⊥．F E DCBACFEDBAFE CDBACAKBDE9. 如图，在梯形ABCD 中，//AD BC ，点E 在BC 上，AE BE =，点F 是CD 的中点，且AF AB ⊥，若 2.7AD =，4AF =，6AB =，求CF 的长.10. 如图，梯形ABCD 中，AD BC ∥，AB AD =，2ABC BCD ∠=∠，点E 在DC 上，且BEF A ∠=∠.求证：BE EF =.11. 如图，已知AD 为ABC △的角平分线，AB AC ＜，在AC 上截取CE AB =，M 、N 分别为BC 、AE 的中点．求证：MN AD ∥．NMD CBAEFDC BAEFEDCBA12. 如图，已知ABC △中，D 在AC 上，DC AB =，E 、F 分别是BC 、AD 的中点，连结EF 并延长交BA 的延长线于G ，求证：AF AG =．13. 如图，在ABC △中，D 为AB 的中点，分别延长CA CB 、到E F 、，使得DE DF =，过E F 、分别作CF 、CB 的垂线，相交于点P ．求证：PAE PBF ∠=∠．14. 如图，90BAC DAE ∠=∠=，M 是BE 的中点，AB AC =，AD AE =，求证：AM CD ⊥． DCBAF EG ECD BAMDCB AFMP15. 如图，在ABC ∆中，3AB AC =，BAC ∠的平分线交BC 于点D ，过点B 作BE AD ⊥，垂足为E ，求证：AD DE =．16. ．分别以ABC △的边AC BC 、为一边，在ABC △外作正方形ACDE CBFG 、，点P 是EF 的中点．求证：点P 到边AB 的距离是AB 的一半．17. 在ABC △中，789BC CA AB ===，，，P 为三角形内一点，PD BC ⊥于D ，PE AC ⊥于E ，PF AB ⊥于F ，且12BD CE AF ++=，求BD BF +的值．C DEBACP EDFABQP BCAFGED18. 四边形ABCD 中，135ABC ∠=，120BCD ∠=，6AB =，53BC =-，6CD =，求AD .19. 如图，在四边形ABCD 中，10545ACB BAD ABC ADC ︒︒∠=∠=∠=∠=，，求证：CD AB =。

全等三角形培优竞赛题精选

全等三角形证明1、已知：∠1=∠2，CD=DE ，EF知：AB知：如图所示，AB ＝AD ，BC ＝DC ，E 、F 分别是DC 、BC 的中点，求证： AE ＝AF 。

10．如图，在四边形ABCD 中，E 是AC 上的一点，∠1=∠2，∠3=∠4，求证: ∠5=∠6． 11．如图：BE ⊥AC ，CF ⊥AB ，BM=AC ，CN=AB 。

求证：（1）AM=AN ；（2）AM ⊥AN 。

12.如图所示，△ABC ≌△ADE ，BC 的延长线过点E ，∠ACB=∠AED=105°，∠CAD=10°，∠B=50°，求∠DEF 的度数。

13．如图，AD 是△ABC 的角平分线，DE ⊥AB,DF ⊥AC,垂足分别是E,F ，连接EF,交AD 于G,AD 与EF 垂直吗？证明你的结论。

FAEDC BP DACBDCBAFEBA CDF2 1 EA14.如图所示，在△ABC 中，AD 为∠BAC 的角平分线，DE ⊥AB 于E,DF ⊥AC 于F, △ABC 的面积是28cm 2,AB=20cm,AC=8cm,求DE 的长。

15．如图，在R t △ABC 中，∠ACB=450，∠BAC=900，AB=AC ，点D 是AB 的中点，AF ⊥CD 于H 交BC 于F ，BE ∥AC 交AF 的延长线于E ，求证：BC 垂直且平分DE.16、已知正方形ABCD 中，E 为对角线BD 上一点，过E 点作EF ⊥BD 交BC 于F ，连接DF ，G 为DF 中点，连接EG ，CG ．（1）直接写出线段EG 与CG 的数量关系；（2）将图1中△BEF 绕B 点逆时针旋转45º，如图2所示，取DF 中点G ，连接EG ，CG ．你在（1）中得到的结论是否发生变化？写出你的猜想并加以证明．（3）将图1中△BEF 绕B 点旋转任意角度，如图3所示，再连接相应的线段，问（1）中的结论是否仍然成立？17、已知Rt ABC △中，90AC BC C D ==︒，∠，AB 边的中点，90EDF ∠=， EDF ∠绕D 点旋转，它的两边分别交AC 、CB （或它们的延长线）于E 、F ．当EDF ∠绕D 点旋转到DE AC ⊥于E 时（如图1），易证12CEF ABC S S S +=△△△．当EDF ∠绕D 点旋转到DE AC 和不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，DEF S △、CEF S △、ABC S △又有怎样的数量关系？请写出你的猜想，不需证明．18、在中，将绕点顺时针旋转角得交于点，分别交于两点．（1）如图1，观察并猜想，在旋转过程中，线段与有怎样的数量关系？并证明你的结论；B DCF AE GAEFBDCA DE G图1F A DE G图2 FAE 图3 D AE CFBD图1图3AD FECBA DBCE 图2F（2）如图2，当时，试判断四边形的形状，并说明理由；（3）在（2）的情况下，求的长．19、如图9，若△ABC 和△ADE 为等边三角形，M ，N 分别EB ，CD 的中点，易证：CD=BE ，△AMN 是等边三角形．（1）当把△ADE 绕A 点旋转到图10的位置时，CD=BE 是否仍然成立？若成立请证明，若不成立请说明理由；（4分）（2）当△ADE 绕A 点旋转到图11的位置时，△AMN 是否还是等边三角形？若是，请给出证明，并求出当AB =2AD 时，△ADE 与△ABC 及△AMN 的面积之比；若不是，请说明理由．（6分）20、如图，直角梯形ABCD 中，BC AD ∥，90BCD ∠=°，且2tan 2CD AD ABC =∠=，，过点D 作AB DE ∥，交BCD ∠的平分线于点E ，连接BE ．（1）求证：BC CD =；（2）将BCE △绕点C ，顺时针旋转90°得到DCG △，连接EG.．求证：CD 垂直平分EG . （3）延长BE 交CD 于点P ．求证：P 是CD 的中点．21、如图，四边形ABCD 是正方形，△ABE 是等边三角形，M 为对角线BD （不含B 点）上任意一点，将BM 绕点B 逆时针旋转60°得到BN ，连接EN 、AM 、CM. ⑴ 求证：△AMB≌△ENB；⑵ ①当M 点在何处时，AM ＋CM 的值最小；②当M 点在何处时，AM ＋BM ＋CM22、如图，△ABC 中，D 是BC 的中点，过D 点的直线行线BG 于G 点，DE ⊥DF ，交AB 于点E ，连结EG 、EF.求证：EG=EF;请你判断BE+CF 与EF 23、如图，等腰直角三角形ABC 中，∠ACB ＝90°，AD 为腰CB 上的中线，CE ⊥AD 交AB 于E ．求证∠CDA ＝∠EDB ．24、在Rt △ABC 中，∠A ＝90°，CE 是角平分线，和高AD 相交于F ，作FG ∥BC 交AB 于G ，求证：AE ＝BG ．AD BECFD BECFADGECB图9 图10 图11E A DB C C25、如图，已知∠BAC=90º,AD ⊥BC, ∠1=∠2,EF ⊥BC, FM ⊥AC,说明FM=FD 的理由26、用两个全等的等边三角形△ABC 和△ACD 拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A 重合，两边分别与AB 、AC 重合.将三角尺绕点A 按逆时针方向旋转.（1）当三角尺的两边分别与菱形的两边BC 、CD 相交于点E 、F 时（如图所示），通过观察或测量BE 、CF 的长度，你能得出什么结论？并证明你的结论；（2）当三角尺的两边分别与菱形的两边BC 、CD 的延长线相交于点E 、F 时（如图所示），你在（1）中得到的结论还成立吗？说明理由。

初中数学竞赛全等三角形(含答案)

全等三角形你见过两片完全相同的树叶吗？你见过两个完全相同的事物吗？也许你从未意识到这世界上还有完全相同。

在这里我们将引导你的思路，给你解题技巧：完全相同--全等三角形。

三解形是平面几何中最重要的图形，它的有关知识是今后我们学习四边形、多边形乃至立体几何的重要基础。

三角形全等的判定和性质是证明有关三角形问题的基础，必须熟练掌握。

判定两个三角形全等的方法有：SAS，ASA，AAS，SSS。

全等三角形的性质：全等三角形的对应边、对应角及其它对应元素相等。

例1：如图2-7-1，△ABC和△DCE均是等边三角形，B、C、E三点共线，AE交CD于G，BD交AC于F。

求证：① AE=BD;② CF=CG.思路① 证明△ACE≌△BCD。

证明① ∵ △ABC和△DCE都是等边三角形，∴ CB=CA， CD=CE，∠BCA=∠ECD=，∴∠BCD=∠ACE=，∴△BCD≌△ACE，∴ AE=BD。

思路② 证明△FCD≌△GCE。

证明② 由△BCD≌△DCE都是等边三角形可知∴ CD=CE，∠BCA=∠ECD=∴∠ACD=-∠BCA-∠ECD=∴△FCD≌△GCE，∴ CF=CG说明：证明两条线段相等的重要方法之一就是证明它们所在的两个三角形全等。

例2：如图2-7-2，在正方形ABCD中，M是AB的中点，MN⊥MD，BN平分∠CBE。

求证：MD=MN。

思路：取AD的中点P，连结PM，证明△DMP≌△MNB。

证明：取AD的中点P，连结PM，则有DP=MB。

∵DM⊥MN，∴∠DMA+∠BMN=，又由正方形ABCD 知∠A=，∴∠DMA+∠MDA=，∴∠BMN=∠MDA又∵BN平分∠CBE，∴∠MBN=又由P、M分别为AD、AB的中点，ABCD是正方形，得△PAM是等腰直角三角形，故∠DPM=。

∴∠DPM=∠MBN，∴△DPM≌△MBN，∴ DM=MN。

说明：本题中DM和MN所在的三角形不全等，这时就要考虑作出它们所在的新三角形，证明这两个新三角形全等。

初中数学竞赛教程8三角形的初步知识

2013年暑期初一数学竞赛第八讲：三角形的初步知识【例题解析】例1、在△ABC中，若∠A＝70°－∠B，则∠C等于（）A、35°B、70°C、110°D、140°1、如图．平面上六个点A，B，C，D，E，F构成一个封闭折线图形．求：∠A+∠B+∠C+∠D+∠E+∠F．2、若三角形的一个外角等于160°，另两个外角的比为2:3，则这个三角形的形状是（）A、锐角三角形B、直角三角形C、钝角三角形D、无法确定3、如果α、β、γ分别是△ABC中∠A、∠B、∠C的外角，且α：β：γ=4：2：3，则∠BAC等于（）A、20°B、40°C、60°D、80°4、如图，∠A=10°，∠ABC=90°，∠ACB=∠DCE，∠ADC=∠EDF，∠CED=∠FEG．求∠F的度数．5、在△ABC内有三个点D、E、F，分别以A、B、C、D、E、F这六个点为顶点画三角形，如果每个三角形的顶点都不在另一个三角形的内部，则这个三角形的所有内角之和为（）A、360°B、900°C、1260°D、1440°例2、周长为30，各边长互不相等且都是整数的三角形共有多少个？1、现有长度分别为2cm、3cm、4 cm、5 cm的线段，从中任取三条，能组成三角形的个数是。

2、用9根同样长的火柴棒在桌面上摆一个三角形（不允许火柴棒折断，并且全部用完），能摆出不同形状的三角形的个数是（）A、1个B、2个C、3个D、4个OCBAEBD CA3、一个三角形的周长是偶数，其中的两条边分别是4和1997，则满足上述条件的三角形的个数是（）A 、1个B 、2个C 、3个D 、4个4、已知三角形的每条边长的数值都是2001的质因数，则这样的不同三角形共有（） A 、6个 B 、7个 C 、8个 D 、9个5、三角形三条边a 、b 、c 都是质数，且16a b c ++=，则这个三角形是（） A 、直角三角形 B 、等腰三角形 C 、等边三角形 D 、直角三角形或等腰三角形6、现有11根火柴，用火柴棒首尾连接构成三角形（这11根火柴可以不用完，但不能折断），则可以搭成的互不全等的三角形个数为（） A ．11个 B ．14个 C ．15个 D ．18个例3、在△ABC 中，高BD 和CE 所在直线相较于点O ，若△ABC 不是直角三角形，且∠A=60°，求∠BOC 的度数。

初中数学竞赛指导：《三角形》竞赛专题训练(含答案)

《三角形》竞赛专题训练1 与三角形有关的线段我们来看这样一个问题:如图1所示，AD 是BC 边上的高，若点P 在BC 边上移动，你能判断线段AP 与边AB 或边AC 的大小吗?从直观上我们可以看出，若点P 在线段BD 上移动，则AP AB <，若点P 在线段CD 上移动，则AP AC <.可是遇到这样判断三角形中边与边的大小的问题，我们会想到哪些定理呢?下面我们就通过例题来看看这些定理的运用.经典例题(1)在ABC ∆内，AB AC =，AD 是边BC 上的高，若点P 在ABD ∆内，证明: APB APC ∠>∠.( 2) ABC ∆是等边三角形，P 是ABC ∆内或边上任意一点(不包含端点)，证明:PA PB PC <+. 解题策略(1)如图2，设PC 与AD 交于点E ，连结BE ，延长AP 交BC 于点F ，因为AB AC =，所以ACB ABC ∠=∠，CAD BAD ∠=∠，CE BE =，ECB EBC ∠=∠(由等腰三角形性质)，则ACE ACB ECB ABC CBP ABP ∠=∠-∠>∠-∠=∠，CAP BAP ∠>∠ 所以180APB ABP BAP ∠=︒-∠-∠ 180ACE CAP >︒-∠-∠ APC =∠(2)直接找PA 与PB PC +的关系并不容易，因为它们不在一个三角形中，这时我们要想办法找个中间量，使得PA 小于这条边，而PB PC +大于这条边，由两边之和大于第三边可知PB PC BC +>，我们很自然地想到把BC 作为中间量来证明.如图3，延长AP 交边BC 于点F ，则AP AF ≤，因为AFC B ∠>∠，B C ∠=∠，所以AC AF >，而PB PC BC +≥ (等号成立条件是点P 在边BC 上)，所以AP PB PC <+.画龙点睛判断三角形边与边的大小，我们常用的定理有:(1)在同一个三角形中，两边之和大于第三边，两边之差小于第三边; (2)在同一个三角形中，大角对大边，小角对小边，等角对等边. 举一反三1. 如图，ABC ∆中，D 、E 、F 分别是边BC 、CA 、AB 上的点，证明: DEF ∆的周长小于ABC ∆的周长.2. 如图，在ABC ∆中，AB AC >，AD 是高，P 是线段AD 上任意一点，证明:PB PC BD CD -<-3. 如图，在ABC ∆中有D 、E 两点，求证:BD DE EC AB AC ++<+.融会贯通4. 已知点O 在ABC ∆内部，连结OA ，OB ，OC ，说明:1()2AB AC BC OA OB OC AB AC BC ++<++<++2 与三角形有关的角三角形内角和是180度，这条看似简单的定理在我们求三角形中的角的度数甚至是其他多边形的内角的度数时，却起着不可缺少的作用，这一讲我们就来看几道利用内角和定理的有趣的问题. 经典例题如图所示.平面上六个点A B C D E F 、、、、、构成一个封闭折线图形.求+A B C D E F ∠∠+∠+∠+∠+∠的度数.解题策略所求的六个角中任意三个都不在同一个三角形中，两两成对地分布在三个三角形中，且这三个三角形中第三个角的对顶角在同一个三角形中，于是，我们反复利用内角和定理可求得结果.因为+180A B APB ∠∠+∠=︒ +180E F FRE ∠∠+∠=︒+180C D DQC ∠∠+∠=︒ 且 +180PRQ PQR QPR ∠∠+∠=︒ 即 +180FRE DQC APB ∠∠+∠=︒故 +360A B C D E F ∠∠+∠+∠+∠+∠=︒ 画龙点睛三角形内角和等于180度，在涉及求角度的时候，总要直接或间接地用到这条定理，当然，更多时候，它要结合其他知识，如外角和定理、对顶角相等，平行线性质定理才能使它的作用更大的发挥出来，希望同学们能熟练应用. 举一反三1. 如图，求+A B C D E ∠∠+∠+∠+∠的度数.2. 如图，求+A B C D E ∠∠+∠+∠+∠的度数.3. 如图，BE 平分ABD ∠，CF 平分ACD ∠，BE 与CF 相交于G ，若140BDC ∠=︒，100BGC ∠=︒，求A ∠的度数.融会贯通4. 如图，在ABC ∆中，延长BC 到D ，ABC ∠与ACD ∠的平分线交于1A ，1A CD∠与1A BC ∠的平分线交于2A ，2A BC ∠与2A CD ∠的平分线交于3A ，3A BC ∠与3A CD ∠的平分线交于4A ，若450A ∠=︒，求A ∠的度数.3 多边形的边和角在平面内，由不在同一条直线上的一些线段首尾顺次相接组成的图形叫做多边形.多边形的内角和公式: (2)180n -⨯︒.多边形的外角和等于360︒.经典例题如图1，在六边形ABCDEF 中，=A B C D E F ∠∠=∠=∠=∠=∠，1AB =cm ，3BC CD ==cm ，2DE =cm.求六边形ABCDEF 的周长.解题策略如图2，将BC 、DE 、AF 分别向两边延长交于L 、M 、N 三点.由六边形内角和公式可知=A B C D E F ∠∠=∠=∠=∠=∠(2)1806n =-⨯︒÷120=︒所以=N L M NCD NDC FEM EFM LBA ∠∠=∠=∠=∠=∠=∠=∠LAB =∠60=︒，所以LMN ∆、ALB ∆、CDN ∆、EFM ∆都是等边三角形；所以LN MN LM ==，AB LB AL ==，EM MF FE ==，CD DN CN ==因为1AB =cm ，3BC CD ==cm ，2DE =cm ，所以1AB LB AL ===cm ，3CD DN CN ===cm.因为LN CN BC LB =++，所以3317LN =++=(cm)，所以7LN MN LM === cm.因为EM MN DE DN =--，所以7232ME =--=(cm)，所以2EM MF FE ===cm.因为AF LM LA FM =--，所以7124AF =--=(cm)，因为六边形ABCDEF 的周长AB BC CD DE EF FA =+++++，所以六边形ABCDEF 的周长13322415=+++++=cm.画龙点睛因为每个内角都是120°，所以多边形的每个外角也都相等，且为60°，从而可以通过延长线段构造等边三角形，利用等边三角形的特殊性质解题. 举一反三1. 如图，一个多边形纸片按图示的剪法剪去一个内角后，得到一个内角和为2340°的新多边形，则原多边形的边数为( ).(A)13 (B)14 (C)15 (D)162. 一块正六边形硬纸片，做成一个底面仍为正六边形且高相等的无盖纸盒(侧面均垂直于底面，见图b)，需在每一个顶点处剪去一个四边形，如图a 中的四边形'AGA H ，那么'GA H ∠的大小是度.3. 如图是某广场地面的一部分，地面的中央是一块正六边形的地砖，周围用正三角形和正方形的大理石地砖密铺，从里向外共铺了10层(不包括中央的正六边形地砖)，每一层的外边界都围成一个多边形，若中央正六边形的地砖的边长为0.5m ，则第10层的外边界所围成的多边形的周长是多少?融会贯通4. 在一个多边形中，除了两个内角外，其余的内角和为2002°，求这个多边形的边数.4 图形面积——等积变换对于三角形的面积有以下两个重要性质:1. 两个三角形的面积之比等于它们的底、高乘积的比;2. 等底(高)的两个三角形面积之比等于它们的高(底)之比.作为以上两个性质的一个特例，等底等高的两个三角形面积相等. 经典例题如图，已知P 为ABC ∆内一点，AP 、BP 、CP 分别与对边相交于点D 、E 、F .把ABC ∆分成六个小三角形，其中四个小三角形的面积已经给出.求ABC ∆的面积.解题策略设BPF S x ∆=，APE S y ∆=，由题设404303PBD PCD S BD DC S ∆∆=== 所以8440435303ABD ACD S x S y ∆∆++==++ 化简得34112x y -=- ①又30402351BPC EPC S BP PE S ∆∆+===所以8421ABP APE S x S y ∆∆+== 化简得284x y =- ② 由①、②可得56,70x y == 所以315ABC S ∆=画龙点睛底边相等的两个三角形面积之比等于它们的高之比，高相等的两个三角形面积之比等于它们的底之比，灵活利用这个性质可以帮助我们解决许多问题. 举一反三1. 如图，平行四边形ABCD 中，//EF AC 分别交CD 、AD 于E 、F .连结AE 、BE 、BF 、CF ，问与BCE ∆面积相等的三角形还有几个?分别是哪几个？2. 在ABC ∆中，E 为AC 中点，D 在BC 上，2DC BD =，AD 交BE 于F ，求证::1:5BDF FDCE S S ∆=四边形3. 在ABC ∆内任取一点P ，连结AP 、BP 、CP ，并分别延长交BC 、CA 、AB 于D 、E 、F .求证:1AF BD CEBF CD AE=.融会贯通4. 设P 是ABC ∆内任一点，AD 、BE 、CF 过点P 且分别交边BC 、CA 、AB 于D 、E 、F .求证:1PD PE PFAD BE CF++=.参考答案1 与三角形有关的线段1. 因为,,AE AF EF BD BF DF CE CD DE +>+>+>所以AE AF BD BF CD CE DE EF DF +++++>++ 所以DEF ∆的周长小于ABC ∆的周长.2. 如图，在BD 上取一点E ，使得DE CD =，则BD CD BE -=，PD 既是PEC ∆的高，又是中线，则PEC ∆是等腰三角形，所以PE PC =，因为PB PE BE -<，故PB PC BD CD -<-.3. 延长BD 交AC 于M 点，延长CE 交BD 的延长线于点N .在ABM ∆中AB AM BM +>，在CNM ∆中，NM MC NC +> 所以AB AM NM MC BM NC +++>+ 因为AM MC AC +=，BM BN NM =+ 所以AB AC NM BN NM NC ++>++ 所以AB AC BN NC +>+……①在BNC ∆中，BN NC BD DN NE EC +=+++……② 在DNE ∆中，DN NE DE +>……③由②、③得BN NC BD DE EC +>++……④由①、④得AB AC BN NC BD DE EC +>+>++4. 根据两边之和大于第三边，对于OAB ∆、OBC ∆、OAC ∆，有： OA OB AB +>，OA OC AC +>，OB OC BC +> 因此OA OB OA OC OB OC AB AC BC +++++>++所以1()2AB AC BC OA OB OC ++<++ 延长BO 交AC 于D ，则AB AC AB AD DC BD DC BO OD DC BO OC +=++>+=++>+，即AB AC OB OC +>+同理可得：AB BC OA OC +>+，AC BC OA OB +>+三式相加得：2()2()AB AC BC OA OB OC ++>++ 即AB AC BC OA OB OC ++>++2 与三角形有关的角1. 将CD 延长，交AB 于点F ，AE 于点G ，则AFG B C ∠=∠+∠，AGF D E ∠=∠+∠ 因为180A AFG AGF ∠+∠+∠=︒所以+180A B C D E ∠∠+∠+∠+∠=︒2. 如图，因为CIH D E ∠=∠+∠，CHI A B ∠=∠+∠，180CHI CIH C ∠+∠+∠=︒所以+180A B C D E ∠∠+∠+∠+∠=︒3. 延长CD 交AB 于H ，212123CDB DHB A ∠=∠+∠=∠+∠+∠，224CGB CFB A ∠=∠+∠=∠+∠+∠因为12∠=∠，34∠=∠，且140BDC ∠=︒，100BGC ∠=︒ 所以1340∠+∠=︒，60A ∠=︒4. 因为ACD A ABC ∠=∠+∠（外角和定理）所以111222ACD ABC A ∠-∠=∠ 即112A A ∠=∠以此类推2112A A ∠=∠，3212A A ∠=∠，4312A A ∠=∠所以41680A A ∠=∠=︒3 多边形的边和角1. B2. 60°3. 根据题意分析可得:从里向外的第1层是61612⨯+=边形;第2层是62618⨯+= 边形;此后，每层都比前一层多6条边.依此递推，第10层是610666⨯+=边形，因为边长为0.5m ，所以第10层的外边界所围成的多边形的周长是660.533⨯=(m).4. 设这个多边形的边数为n ，两个内角的和为x ︒.则(2)1802002n x --=解得1802362x n =-因为0360x <<所以01802362360n <-< 解得118113619090n << 所以14n =或15，则多边形的边数是14或15.4 图形面积——等积变换1. BCE CEA S S ∆∆=，ACE AFC S S ∆∆=，AFC ABF S S ∆∆=，，，所以与BCE ∆面积相等的有3个三角形，分别是CEA ∆、AFC ∆、ABF ∆2. 设BDF S a ∆=.连结DE ，取DC 中点G ，连结EG ，由中位线性质可知//EG AD ，所以F 是BE 的中点，于是有BDF EDF S S a ∆∆==，又2GCE DEG BDE S S S a ∆∆∆===，所以225FDE DEG GCE FDCE S S S S a a a a ∆∆∆=++=++=四边形.因此:1:5BDF FDCE S S ∆=四边形3. 因为ACF APF BPF BCFS S AF BF S S ∆∆∆∆== 所以ACF APF ACP BCF BPF BCP S S S AF BF S S S ∆∆∆∆∆∆-==-同理可得APB APC S BD CD S ∆∆=，BCP APB S CE AE S ∆∆= 三式相乘可得1AF BD CE BF CD AE= 4. 设P 到BC 、CA 、AB 的距离分别为a t 、b t 、c t ，BC 、CA 、AB 边上的高分别为a h 、b h 、c h ，因为PDC a PBC ADC a ABCS t S PD AD S h S ∆∆∆∆=== 所以PBC ABCS PD AD S ∆∆= 同理PAC ABC S PE BE S ∆∆=，PAB ABC S PF CF S ∆∆= 三式相加即得1PD PE PF AD BE CF ++=。

【八年级数学几何培优竞赛专题】专题2 全等三角形判定方法的选择【含答案】

专题2 全等三角形判定方法的选择知识解读三角形全等判定方法的选择已知条件可供选择的判定方法一边和这边邻角对应相等选边：只能选角的另一边（SAS ）选角：可选另外两对角中任意一对角（AAS ，ASA ）一边及它的对角对应相等只能再选一角：可选另外两对角中任意一对角（AAS ）两边对应相等选边；只能选剩下的一边（SSS ）选角：只能选两边的夹角（SAS ）两角对应相等只能选边：可选三条边的任意一对对应边（AAS ．ASA ）典例示范一、从变换的角度理解“全等”1．轴对称变换例1如图1－2－1，点D 在AB 上，点E 在AC 上，BE 和CD 相交于点O ，且AB ＝AC ，∠B ＝∠C ，求证：BD ＝CE ．【提示】从结论“BD ＝CE ”来看，有两种思路，思路一：通过证明△BOD ≌△COE 得到对应边相等；思路二：通过证明“△ACD ≌△ABE ”得到AD ＝AE ，然后运用等式性质证得．从题设看，由“AB ＝AC ，∠B ＝∠C ”加上公共角∠A ，可得△ACD ≌△ABE ，所以我们考虑使用思路二给出证明过程．图1-2-1B【技巧点评】哪些情况下，可考虑利用全等的性质来证明线段相等和角相等呢？本题中，这个图形很显然是轴对称图形，而BD 和CE 也是轴对称的，这时候就可以考虑把BD 和CE 置于一对轴对称的三角形中，且BD 和CE 恰好是一对对应边.跟踪训练1．如图1－2－2，已知AB ＝DC ，AE ＝DF ，CE ＝F B ．求证：AF ＝DE ．图1-2-22．旋转变换例2如图1－2－3，AD 是△ABC 的中线，在AD 及其延长线上截取DE ＝DF ，连接CE ，BF ，试判断△BDF 与△CDE 全等吗？BF 与CE 有何位置关系？【提示】若△BDF 与△CDE 全等，需要寻找三个相等的要素，题中已知一对对顶角相等，由中线可得到BD ＝CD ，加上DE ＝DF ，即可根据“SAS ”得到两个三角形全等．图1-2-3B【技巧点评】本题是一个简单的全等证明题，本题意在说明图中△BDF 与△CDE 是中心对称的图形．，其中一个三角形可以看作另一个三角形绕点D 旋转180°得到．从中心对称的角度寻找相等的线段和相等的角，可以为证明全等提供方便．跟踪训练2．如图1－2－4，AB ＝AE ，∠1＝∠2，∠B ＝∠E ，求证：BC ＝E D ．图1-2-4二、线段和角度相等，常考虑证全等例3如图1－2－5，AC 交BD 于点O ，AC ＝BD ，AB ＝CD ，求证：∠C ＝∠B ．【提示】要证明∠C ＝∠B ，可考虑将∠C 和∠B 置于一对三角形中，证明两个三角形全等，由于本题图中△AOB 和ACOD 全等不容易证明，可考虑连接AD ，证明△ACD 与△DBA 全等．图1-2-5跟踪训练3．已知，如图1－2－6，AD ⊥DB ，BC ⊥CA ，AC ，BD 相交于点O ，且AC ＝BD ，求证：AD ＝B C ．图1-2-6B【技巧点评】由于全等三角形的对应角相等，对应边相等，因此证明两个三角形全等是证明两个角相等和两条线段相等常用的方法．利用全等三角形证明线段相等和角相等的思路：对应边（角）相等→两个三角形全等→线段相等或者角相等，可以看出全等三角形类似于一个桥梁，建立起角度相等与线段相等、线段相等与另两条相等的线段、角相等与另一对相等的角之间的联系．跟踪训练4．如图1－2－7，A ，D ，B 三点在同一条直线上，△ADC ，△BDO 均为等腰三角形，AO ，BC 的大小关系和位置关系分别如何？证明你的结论．图1-2-7三、借助“同角的余角相等”寻找相等的角例4如图1－2－8，在△ABC 中，BD ⊥AC 于D ，CE ⊥AB 于E ，F 是BD 上一点，BF ＝AC ，G 是CE 延长线一点，CG ＝AB ，连接AG ，AF ．（1）求证：∠ABD ＝∠ACE ；（2）探求线段AF ，AG 有什么关系，并证明．【提示】（1）∠ABD ，∠ACE 都和∠BAC 互余，根据“同角的余角相等”可证明∠ABD ＝∠ACE ；（2）由已知条件“BF ＝AC ”“CG ＝AB ” “∠ABD ＝∠ACE ”可证明△ABF ≌△GCA ，AF ，AG 恰好是这对全等三角形的对应边，所以这两条线段的大小关系是相等．又由于∠G ＝∠BAF ，∠G ＋∠GAE ＝90°，因此∠GAF ＝90°，所以AF 和AG 的位置关系是垂直．图1-2-8B 【技巧点评】（1）当已知两条边相等，要证明两个三角形全等时，“同角的余角相等”是常用的证明夹角相等的手段．（2）要证明两直线垂直，证明夹角等于90°也是常用思路，当夹角是由两个角的和组成的时候，常考虑证明这两个角的和等于90°．跟踪训练5．如图1－2－9，在△ABC 中，∠ACB ＝90°，CD ⊥AB 于点D ，点E 在AC 上，CE ＝BC ，过E 点作AC 的垂线，交CD 的延长线于点F ．求证：AB ＝F C ．图1-2-9A四、从等腰、等边、正方形中获取全等所需的元素例5如图1－2－10，在Rt △ABC 中，∠ACB ＝90°，AC ＝BC ，D 为BC 的中点，CE ⊥AD ，垂足为E ，BF ∥AC 交CE 的延长线于点F ．求证：DB ＝BF ．【提示】要证明DB ＝BF ，由于D 为BC 的中点，所以CD ＝BD ，因此本题可转证CD ＝BF ，将这两条线段放置到三角形中，可证明△ACD ≌△CBF ．图1-2-10A【技巧点评】本题证明△ACD ≌△CBF 需要的三个要素AC ＝BC ，∠CAD ＝∠BCF ，∠ACD ＝∠CBF 都和△ABC 是等腰直角三角形相关．当题目中出现等边三角形、等腰三角形、正方形、菱形等条件时，往往图形中隐含着一对全等三角形，这对全等三角形的一对对应边往往和等边三角形、等腰三角形、正方形、菱形的边长相等有关．跟踪训练6．如图1－2－11，在Rt △ABC 中，∠BAC ＝90°，AC ＝2AB ，点D 是AC 的中点，将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A ，D 重合，连接BE ，E C ．试猜想线段BE 和EC 的数量关系和位置关系，并证明你的猜想．图1-2-11B拓展延伸五、AAS 华丽变全等例6 如图1-2-12，在△ABC 中，∠DBC ＝∠ECB ＝∠A ，求证：BE ＝CD ．21ABCD E F【提示】要证明BE ＝CD ，一般考虑证明两个三角形全等，而△DCF 和△EBF 显然不全等，本题有三种构造全等的方法，如图1-2-13①②③．图1-2-12GFE D CBAHFE D CBAFE D CBAH G 【技巧点评】本题△BEF 和△CDF 虽然不全等，但是∠BFE ＝∠CFD ，加之可证FB ＝FC 以及待证的BE ＝CD ，可见这两个三角形虽然不全等，但也有3对相等的要素．构造全等三角形可将小三角形补上一部分，或者将大三角形截去一部分．跟踪训练7．如图1-2-14，OC 平分∠AOB ，点D 、E 分别在OA 、OB 上，点P 在OC 上，且有PD ＝PE ，求证：∠PDO ＝∠PEB ．(有三种解法)P OD C BA E竞赛链接图1-2-13图1-2-14②③①例7 (全国初中数学竞赛浙江赛区题)如图1-2-15，在四边形ABCD 中，∠A ＝∠BCD ＝90°，BC ＝CD ，E 是AD 延长线上一点，若DE ＝AB ＝3cm ，CE ＝4cm ，则AD 的长是．2【提示】如图1-2-16，连接CA ，构造△BAC ≌△DEC ，利用勾股定理求出AE 的长．EDCB AAB CDE【技巧点评】勾股定理——如果直角三角形的两直角边长分别为a 、b ，斜边长为c ，那么a 2＋b 2＝c 2．跟踪训练8．(希望杯竞赛题)如图1-2-17，在四边形ABCD 中，AB ∥CD ，AD ∥BC ，AC 与BD 相交于O ，AE ⊥BD 于E ，CF ⊥BD 于F ，那么图中的全等三角形共有()A ．5对B ．6对C ．7对D ．8对F OABCDE 培优训练1．如图1-2-18，AC ，BD 交于点E ，且∠1＝∠2，∠3＝∠4，求证：AC ＝BD ．4321ABCED2．如图1-2-19，已知AD ＝AE ，AB ＝AC ．求证：BF ＝FC ．图1-2-17图1-2-15图1-2-16图1-2-18ABCDEF3．如图1-2-20，已知△ABD 、△AEC 都是等边三角形，AF ⊥CD 于F ，AH ⊥BE 于H ，问：(1)BE 与CD 有何数量关系?为什么?(2)AF 、AH 有何数量关系?O HFEDCBA 4．如图1-2-21，△ACD 和△BCE 都是等腰直角三角形，∠ACD ＝∠BCE ＝90°，AE 交DC 于点F ，BD分别交CE ，AE 于点G ，H 试猜测线段AE 和BD 的位置关系和数量关系，并说明理由．DBCFH AE G 5．将两个全等的直角三角形ABC 和DBE 按图1-2-22①方式摆放，其中∠ACB ＝∠DEB ＝90°，∠A ＝∠D ＝30°，点E 落在AB 上，DE 所在直线交AC 所在直线于点F ．(1)求证：AF ＋EF ＝DE ；(2)若将图1-2-22①中的△DBE 绕点B 按顺时针方向旋转角，且0°＜＜60°，其他条件不变，请在αα图1-2-22②中画出变换后的图形，并直接写出(1)中的结论是否仍然成立．AC BABCE FD①图1-2-19图1-2-20图1-2-21②图1-2-226．如图1-2-23，AD 是△ABC 的高，作∠DCE ＝∠ACD ，交AD 的延长线于点E ，点F 是点C 关于直线AE 的对称点，连接AF ．(1)求证：CE ＝AF(2)在线段AB 上取一点N ，使∠ENA ＝∠ACE ，EN 交BC 于点M ，连接AM 请你判断∠B 与∠MAF 21的数量关系，并说明理由．DBEAF CN M直击中考7．★★(2017江苏常州)如图1-2-24，在四边形ABCD 中，点E 在AD 上，∠BCE ＝∠ACD ＝90°，∠BAC ＝∠D ，BC ＝CE ．(1)求证：AC ＝CD ；(2)若AC ＝AE ，求∠DEC 的度数．ECDBA 8．(凉山州中考题)如图1-2-25，△ABO 与△CDO 关于O 点中心对称，点E 、F 在线段AC 上，且AF ＝CE ．求证：FD ＝BE ．FBECDAO9．(内江中考题)如图1-2-26，△ABC 和△ECD 都是等腰直角三角形，∠ACB ＝∠DCE ＝90°，D 为AB 边上一点．求证：AE ＝BD ．图1-2-23图1-2-24图1-2-25CDEBA10．(重庆中考题)如图1-2-27，在△ABC 中，∠ACB ＝90°，AC ＝BC ，E 为AC 边的中点，过点A 作AD ⊥AB 交BE 的延长线于点D ．CG 平分∠ACB 交BD 于点G ，F 为AB 边上一点，连接CF ，且∠ACF ＝∠CBG ．求证：(1)AF ＝CG ；(2)CF ＝2DE ．GCDFEBA挑战竟赛11．(希望杯竞赛题)如图1-2-28，在△ABC 中，∠ACB ＝60°，∠BAC ＝75°，AD ⊥BC 于D ，BE ⊥AC 于E ，AD 与BE 交于H ，则∠CHD ＝．HBCE ADBGF E ADC12．(希望杯竞赛题)如图1-2-29，在△ABC 中，∠BAC ＝90°，AD ⊥BC 于D ，∠BCA 的平分线交AD 于F ，交AB 于E ，FG ∥BC 交AB 于G ．AE ＝4，AB ＝14，则BG ＝．图1-2-26图1-2-27图1-2-28图1-2-29。

初中数学竞赛专题复习第二篇平面几何第9章三角形试题新人教版

第9章三角形§9．1全等三角形9．1．1★已知等腰直角三角形ABC ,BC 是斜边．B ∠的角平分线交AC 于D ,过C 作CE 与BD 垂直且交BD 延长线于E ,求证.2BD CE =．解析如图,延长CE 、BA ,设交于F ．则FBE ACF ∠=∠,AB AC =,得ABD ACF △△≌,CF BD =．又BE CF ⊥,BE 平分FBC ∠,故BE 平分CF ,E 为CF 中点,所以2CE FC BD ==．9．1．2★在ABC △中,已知60A ∠=︒,E 、F 、G 分别为AB 、AC 、BC 的中点,P 、Q 为ABC △形外两点,使PE AB ⊥,2AB PE =,QF AC ⊥,2ACQF =,若1GP =,求PQ 的长． F AE DBC解析如图,连结EG 、FG ,则EG AC ∥,FG AB ∥,故150PEG QFG ∠=︒=∠．又12QF AC EG ==,12PE AB FG==,故PEG GFQ △△≌,所以PG GQ =,30EGP FGQ FQG FGQ ∠+∠=∠+∠=︒,又60EGF ∠=︒,所以90PGQ ∠=︒,于是PQ ==ACG QPEF9．1．3★在梯形ABCD 的底边AD 上有一点E ,若ABE △、BCE △、CDE △的周长相等,求BCAD．解析作平行四边形ECBA ',则A BE CEB '△△≌,若A '与A 不重合,则A '在EA （或延长线）上,但由三角形不等式易知,A '在EA 上时,ABE △的周长>A BE '△的周长；A '在EA 延长线上时,ABE △的周长A BE '<△周长,均与题设矛盾,故A 与A '重合,AE BC ∥,同理ED BC ∥,12BC AD =．B CEDAA'9．1．4★★ABC △内,60BAC ∠=︒,40ACB ∠=︒,P 、Q 分别在边BC 、CA 上,并且AP 、BQ 分别是BAC ∠、ABC ∠的角平分线．求证.BQ AQ AB BP +=+．解析延长AB 到D ,使BD BP =,连结DP ．易知80ABC ∠=︒,所以40QBC ACB ∠=︒=∠,AC AQ QC AQ QB =+=+．ABCDQP因1402BDP BPD ABC ACB ∠=∠=∠=︒=∠,所以ADP ACP △△≌,AC AD AB BD AB BP ==+=+．于是BQ AQ AB BP +=+．9．1．5★★设等腰直角三角形ABC 中,D 是腰AC 的中点,E 在斜边BC 上,并且AE BD ⊥．求证. BDA EDC ∠=∠．解析如图,作BAD ∠的平分线AF ,F 在BD 上．ABCEFD由于45BAF ACE ∠=︒=∠,AB AC =,ABF CAE ∠=∠,故ABF CAE △△≌,故EC AF =．又45C FAD ∠=∠=︒,AD CD =,于是AFD CED △△≌,于是ADB EDC ∠=∠．9．1．6★★设ABE △、ACF △都是等腰直角三角形,AE 、AF 是各自的斜边,G 是EF 的中点,求证.GBC △也是等腰直角三角形．解析如图,作AQ 、GP 、EM 、FN 分别垂直于直线BC ,垂足为Q 、P 、M 、N ．AE FGMBQ PC由90EBM ABQ BAQ ∠=︒-∠=∠,AB BE =,EMB BQA △△≌,故有EM BQ =,BM AQ =．同理FN QC =,CN AQ =,所以BM CN =, EM FN BQ QC BC +=+=．又EG GF =得BP CP =,且()1122GP EM FN BC =+=,故GP BP CP ==．又由GP BC ⊥,故结论成立．9．1．7★★已知AB AC ⊥,AB AC =,D 、E 在BC 上（D 靠近B ）,求证.222DE BD CE =+的充要条件是45DAE ∠=︒．ABEFC解析如图,作FC BC ⊥,且FC BD =,则45ACF B ∠=︒=∠,又AB AC =,故ABD ACF △△≌,AD AF =,且490D F BAC ∠=∠=︒．若45DAE ∠=︒,则45EAF ∠=︒,因AD AF =,得ADE AFE △△≌,则222222DE EF EC FC EC BD ==+=+．反之,若222DE EC BD =+,由222EF EC FC =+得EF DE =．又AD AF =,故ADE AEF △△≌,又90DAF ∠=︒,于是45DAE ∠=︒．9．1．8★★两三角形全等且关于一直线对称,求证.可以将其中一个划分成3块,每一块通过平移、旋转后拼成另一个三角形．解析如图,设ABC △与A B C '''△关于l 对称,分别找到各自的内心I 、I ',分别向三边作垂线ID 、IE 、 IF 与I D ''、I E ''、I F '',于是6个四边形AFIE ……均为轴对称的筝形,且四边形AFIE ≌四边形A E J F '''',所以两者可通过平移、旋转后重合；同理,另外两对筝形也可通过平移、旋转后重合．AECDF BA'B'C'D'F'E'l l'l9．1．9★★★已知.两个等底等高的锐角三角形,可以将每个三角形分别分成四个三角形,分别涂上红色、蓝色、黄色和绿色,使得同色三角形全等．解析如图,设BC B C ''=,A 至BC 距离等于A '至B C ''距离,取各自的中位线FE 、F E '',则FE FE '=．由ABC △、A B C '''△均为锐角三角形,可在BC 、B C ''上各取一点D 、D ',使图中标相同数字的角相等,于是AEF D E F '''△△≌,DEF A E F '''△△≌,FBD FD B ''△△≌,EDC E C D '''△△≌．评注还有一种旋转而不是对称的构造法．A BC DEF A'B'D'C'E'F'123451465264152432519．1．10★已知ABC △与A B C '''△中,A A '∠=∠,BC B C ''=,ABC A B C S S '''=△△,ABC △与A B C '''△是否一定全等？A B CA'解析如图,让B 与B '重合,C 与C '重合,A 、A '在BC 同侧,若A 与A '重合,则ABC A B C '''△△≌；否则由条件知四边形ABCA '为梯形和圆内接四边形,于是它是一个等腰梯形,于是ABC A CB '∠=∠,AB A C '=,ABC A C B '''△△≌．综上,可知ABC △与A B C '''△全等．评注本题也可以运用三角形面积公式、余弦定理结合韦达定理来证明．9．1．11★★如图所示,已知ABC △、CED △均为正三角形,M 、N 、L 分别为BD 、AC 和CE 的中点,求证.MNL △为正三角形．ABEDM TS CN L解析如图,设BC 、CD 中点分别为S 、T ,连结NS 、SM 、MT 、TL ．则四边形CSMT 为平行四边形,设BCD θ∠=,则60180240NSM LTM θθ∠=︒+︒-=︒-=∠,360120240NCL θθ∠=︒-︒-=︒-,又NC SN SC MT ===,LC LT CT SM ===,故CNL SNM TML △△△≌≌, NL NM ML ==,于是MNL △为正三角形．评注注意有时S 在MN 另一侧,此时120NSM LTM NCL θ∠=∠=∠=︒+,不影响最终结论．9．1．12★★★ABC △中,90A ∠=︒,AB c =．6AC =,BC a =,M 是BC 中点,P 、Q 分别在AB 、AC 上（可落在端点）,满足MP MQ ⊥,求22BP CQ +的最小值（用a 、b 、c 表示）．解析如图,延长QM 至N ,使QM MN =,连结PN 、BN 、PQ 、AM 由于M 是BC 、NQ 的中点,故BN CQ =,BN AC ∥,BN BP ⊥,又PM 垂直平分NQ ,故222222BP CQ BP BN PN PQ +=+==．取PQ 中点K （图中未画出）,则2a PQ AK MK AM =+=≥,于是22BP CQ +的最小值为24a ,取到等号仅当PQ AM =即四边形APMQ 为矩形时．NMP CBQA9．1．13★★★已知P 为ABC △内一点,PAC PBC ∠=∠,由P 作BC 、CA 的垂线,垂足分别是L 、M ．C ABDEFMP L设D 为AB 中点,求证.DM DL =．解析如图所示,取AP 中点E ,BP 中点F ,连ME 、ED 、DF 、FL ．显然四边形DEPF 是平行四边形,所以EP DF =,FP DE =．DEP DFP ∠=∠．又由PM AC ⊥,所以EM EA EP DF ===,2PEM PAC ∠=∠；同理FL DE =,2PFL PBC ∠=∠．由PAC PBC ∠=∠,所以DEM DEP PEM DFP PFL DFL ∠=∠+∠=∠+∠=∠,从而DFM LFD △△≌,所以DM DL =．9．1．14★★在ABC △中,已知60CAB ∠=︒,D 、E 分别是边AB 、AC 上的点,且60AED ∠=︒,ED DB CE +=,2CDB CDE ∠=∠,求DCB ∠的度数．解析如图,延长AB 到F ,使BF ED =,连CF 、EF ．CEA DB F因为60EAB AED ∠=∠=︒,所以60FDA ∠=︒,120EDB CED ∠=∠=︒, AD AE ED BF ===．CE ED DB DB BF DF =+=+=．于是,AC AF =,60ACF AFC ∠=∠=︒．又因为120EDB ∠=︒,2CDB CDE ∠=∠, 所以40CDE ∠=︒,80CDB ∠=︒,18020ECD CED EDC ∠=︒-∠-∠=︒．在CDA △和CBF △中,CA CF =,60CAD CFB ∠=∠=︒,AD BF =,所以CDA CBF △△≌,故 20FCB ACD ∠=∠=︒．于是,6020DCB CDE FCB ∠=︒-∠-∠=︒．9．1．15★★在ABC △中,B ∠、C ∠为锐角,M 、N 、D 分别为边AB 、AC 、BC 上的点,满足AM AN =,BD DC =,且BDM CDN ∠=∠．求证.AB AC =．解析若DM DN >,则在DM 上取一点E ,使DN DE =．连结BE 并延长交AC 于F ,连结EN ．在BED △与CND △中,BD DC =,BDE CDN ∠=∠,DE DN =,故BDE CDN △△≌．于是有EBD NCD ∠=∠,BE NC =,所以FB FC =．又易知EN BC ∥,因此ENF ACB ∠=∠．但另一方面,由DM DN >,知ABC FBC ACB ∠>∠=∠,所以AFM NE BDC1(180)2ANM BAC ∠=︒-∠()12ABC ACB =∠+∠ ()12ACB ACB ACB >∠+∠=∠．从而ENF MNA ACB ∠>∠>∠．矛盾,故假设DM DN >不成立．若DM DN <,同法可证此假设不成立．综上所述DM DN =,于是由BDM CDN △△≌ 知DBM DCN ∠=∠,从而AB AC =．9．1．16★★如图,ABC △为边长是1的等边三角形,BDC △为顶角()BDC ∠是120︒的等腰三角形,以D 为顶点作一个60︒角,角的两边分别交AB 、AC 于M 、N ,连结MN ,形成一个AMN △．求AMN △的周长．AM NBC DE解析延长AC 到E ,使CE BM =,连结DE ．易知在BMD △与CED △中有BD DC =,90MBD ECD ∠=∠=︒,BM CE =,从而MBD ECD △△≌．所以MD DE =,MDB EDC ∠=∠．于是在DMN △与DEN △中有DN DN =,MD DE =,60MDN MDB CDN EDC CDN EDN ∠=︒=∠+∠=∠+∠=∠．从而MDN EDN △△≌,故NE MN =．所以AM MN AN AM NE AN AM NC CE AN AM MB NC AN ++=++=+++=+++= 2AB AC +=．9．1．17★★★ABC △为等腰直角三角形,90C ∠=︒,点M 、N 分别为边AC 和BC 的中点,点D 在射线BM 上,且2BD BM =,点E 在射线NA 上,且2NE NA =,求证.BD DE ⊥．解析取AD 中点F ,连EF ．EADF MBNC在BMC △与DMA △中,AM MC =,12BM BD MD ==,BMC DMA ∠=∠,故AMD CMB △△≌．于是有ADM CBM ∠=∠,AD BC =,AD BC ∥．同样易知BMC ANC △△≌,于是有CBM CAN ∠=∠．在ANC △与EAF △中,12NA NE AE ==,1122AF AD BC NC ===,由AD BC ∥知EAF ANC ∠=∠,所以FAF ANC △△≌．于是有AEF NAC ∠=∠,90EFA ACN EFD ∠=∠=︒=∠．从而在EAF △与EDF △中有AF FD =,EF EF =,故FAF EDF △△≌．于是有EDF EAF ∠=∠, FED FEA ∠=∠．总之,90EDF MDA EDF NAC EDF AEF EDF FED ∠+∠=∠+∠=∠+∠=∠+∠=︒,即 BD DE ⊥．9．1．18★★★已知ABCD ,延长DC 至P ,使DP AD =,连结PA 与BC 交于Q ,O 为PQC △的外心,则B 、O 、C 、D 共圆．ADBC O PQ解析如图连好辅助线,由于DPA BAP PAD CQP ∠=∠=∠=∠,故CQ CP =,设OCP OCQ OQC θ∠=∠=∠=,则180BQO DCO θ∠=︒-=∠,又BQ AB CD ==,QO CO =,故BQO DCO △△≌,于是QOB COD ∠=∠,于是2BOD QOC QPC BCD ∠=∠=∠=∠,因此B 、O 、C 、D 共圆．9．1．19★★★已知ABC △和A B C '''△,A A '∠=∠,且BC B C ''=,D 和D '分别是BC 、B C ''的中点,AD A D ''=,问两个三角形是否必定全等？解析如图,作出ABC △外心O (A B C '''△及相应的O '、D '图中未画出)．若O 在BC 上,则90A A '∠=︒=∠,此时ABC △与A B C '''△未必全等．若O 不与D 重合,则2sin 2sin BC B C AO A O A A ''''===', cos cos OD BO A AO A == cos A O A O D '''''==,AD A D ''=．当A 、O 、D 共线,则AD BC ⊥,A D B C ''''⊥,所以ABD A B D '''△△≌,ACD A C D '''△△≌,从而 ABC A B C '''△△≌．当A 、O 、D 不共线,则AOD A O D '''△△≌,ODA O D A '''∠=∠,于是'ADC A D C ''∠=∠（或A D B '''∠）,于是由三角形全等可得AC A C ''=(或A B ''),AB A B ''=（或A C ''）,故有ABC A B C '''△△≌（或A CB '''△）．评注此题亦可用中线长公式证明．9．1．20★★如果两个三角形满足“ASS ”,它们不一定全等,此时称它们是相近的,现在有一三角形1△,作2△与之“相近”,……一般有1n +△与n △相近,问是否存在一个k ,使1△与k △相做且不全等？解析这是不可能的．因为由正弦定理,1△与2△有等大的外接圆（它们有一对内角相等或互补）,从而推出1△与x k △有等大的外接圆,它们不可能只相似不全等．9．1．21★★★是否存在两个全等的三角形△与'△,△可划分为两个三角形1△与2△,'△可划分成两个三角形1'△与2'△,使12△△≌,2△与2'△却不全等？解析这样的两个三角形是存在的,如图(a)、(b),设不等边三角形ABC A B C '''△△≌,其中22''BC AB AC A B A C B C ''''=⋅=⋅=,不妨设AC A C ''=是各自的最长边,则AB 、A B ''为各自的最短边．在AC 、B C ''上分别找D 、D ',使CD AB =,BA D C ''∠=∠,则由于2BC AB AC CD AC =⋅=⋅,故ABC BDC △∽△,所以'BDC ABC A B C ''∠=∠=∠,又因为C B A D '''∠=∠,CD A B ''=,因此BDC D B A '''△△≌,而ABD △显然不与A C D '''△全等．（若90B B '∠=∠=︒,还可避免相似．） ABCDA'B'D'图(a)图(b)9．1．22★★★已知ABC △中,60A ∠=︒,I 是ABC △内心,AI 的垂直平分线分别交AB 、AC 于M 、N ,E 、F 在BC 上,BE EF FC ==,求证.ME NF ∥．解析如图,连结MI 、BI 、CI 、NI ．易诮AMN △与IMN △为全等之正三角形,120BIC ∠=︒, 180MIB NIC ∠+∠=︒．ANMTB E F CIS两端延长MN 至S 与T ,使SM MN NT ==,则60SMB AMN BMI ∠=∠=∠=︒,于是SMB IMB △△≌,同理NTC NIC △△≌,因此180S T MIB NIC ∠+∠=∠+∠=︒,SB TC ∥．而M 、N 将ST 三等分,E 、F 将BC 三等分,于是由平行线分线段成比例,知ME NF ∥(SB ∥)．评注读者可以考虑.如果ME NF ∥是否有60BAC ∠=︒．9．1．23★★★已知锐角三角形ABC ,60BAC ∠=︒,AB AC >,ABC △的垂心和外心分别为M 和O ,OM 分别与AB 、AC 交于X 、Y ,证明.AXY △的周长为AB AC +,OM AB AC =-．解析如图,连结AO 、BO 、CO 、AM ．由AB AC >可知O 在AB 一侧,M 在AC 一侧．因120BOC ∠=︒,故AO =,而tan BC AM BAC ==∠于是AO AM =,AOM AMO ∠=∠．又90OAB C YAM ∠=︒-∠=∠,故AXY AYX ∠=∠,AXY △为正三角形．又60XOB YOC YOC OCY ∠+∠=︒=∠+∠,故XOB YCO ∠=∠,120BXO CYO ∠=︒=∠,又BO CO =,故XBO YOC △△≌,XY XO YO BX YC =+=+．于是AX XY YA AB AC ++=+．又XO MY YC ==,做()()112233OM XY YC AB AC AC AB AC AB AC ⎡⎤=-=+--+=-⎢⎥⎣⎦．§9．2特殊三角形9．2．1★在直角三角形ABC 中,BC 是斜边,5AC =,D 是BC 中点,E 是AC 上一点,2DE AE ==,求AB ．BADEC解析如图,连结AD ．设AD CD x ==,因2DE =,2AE =,3CE =,则 22223x -=⨯,x =AB ==9．2．2★已知ABC △中,14AB =,16BC =,28CA =,P 为B 在A ∠平分线上的射影,M 为BC 中点,求PM ．解析延长BP 交AC 于Q ．由BAP QAP ∠=∠．AP BQ ⊥知BP QP =,AB AQ =．又BM CM =,故()()11128147222PM CQ AC AQ =-=⨯-=∥．ABCQ P M9．2．3★等腰三角形ABC 中,AB AC =,D 为直线BC 上一点,则22AB AD BD CD -=⋅（D 在BC 上）,22AD AB BD CD -=⋅（D 在BC 外）．解析如图,设D 在BC 上且较靠近B ．作AE BC ⊥于E ,则E 为BC 中点,于是AB D E C()()BD CD BE DE CE DE ⋅=-⋅+2222BE DE AB AD =-=-．当D 在BC 外时的结论同理可证．评注这是斯图沃特定理在等腰三角形的特殊情形,具有十分广泛的用途（例如题9．2．1）,亦可用相交弦定理证明．9．2．4★★已知锐角三角形ABC 中,AD 、CE 是高,H 为垂心,AD BC =,F 是BC 的中点,求证.12FH DH BC +=．AEBFDCH解析如图,连结EF ,则12EF CF BC ==．于是2222FH EF EH CH EF AH HD EF =-⋅=-⋅=- 222AH HD HD HD EF HD AD ⋅-+=-⋅+22222HD EF HD BC HD EF HD =-⋅+=-⋅ ()22EF HD EF HD +=-．由于EF FH HD >>,故12FH EF DH BC DH =-=-． 9．2．5★已知斜边为AC 的直角三角形ABC 中,B 在AC 上的投影为H ．若以AB 、BC 、BH 为三边可以构成一个直角三角形,求AHCH的所有可能值． BHAC解析显然由AB 、BC 、BH 构成的直角三角形中,BH 不是斜边,且AB BC ≠．若AB BC >,则AB 为斜边．设AB c =,BC a =,BH h =,则由ABC △的面积知h ac ,又h =,故4422c a a c -=．易知2222AH AB c kCH BC a ===,则由前式知21k k -=,得k =,故AH CH =同理,若AB BC <,可得AH CH =．所以AHCH9．2．6★★已知ABC △中,AD 为高,D 在BC 上, 以下哪些条件能判定AB AC =. (1)AB CD AC BD +=+. (2)AB CD AC BD ⋅=⋅；(3)1111AB CD AC BD+=+． AB D C解析设BD x =,CD y =,AD h =,则AB ,AC先看条件y x =．若x y =,则AB AC =；否则不妨设x y >,则22x y -==．x y =+,于是0h =,矛盾．故AB AC =．再看见条件（2）.=22222222h y x y h x x y +=+,于是x y =,故AB AC =．最后条件（3）.11y x =+．于是22x y xy -=．若x y ≠,则()xy x y =+,仍有0h =,矛盾,故AB AC =．所以三个条件都能判定AB AC =．9．2．7★已知P 是等腰直角三角形ABC 的斜边BC 上任意一点,求222BP CP AP +．解析如图,作AD BC ⊥于D ．AB D CP不妨设1AD BD CD ===．P 在CD 上,PD a =,则1BP BD PD a =+=+,1CP CD PD a =-=-,于是()()222221122BP CP a a a +=++-=+．又22221AP AD PD a =+=+．故2222BP CP AP +=．评注请读者考虑,若对BC 上任一点P ,有222BP CP AP+为定值,是否可认为ABC △为等腰直角三角形． 9．2．8★★在ABC △中,19AB =,17BC =,18CA =,P 是ABC △内一点,过点P 向ABC △的三边BC 、CA 、AB 分别垂线PD 、PE 、PF ,垂足分别为D 、E 、F ,且27BD CE AF ++=,求BD BF + 的长．解析如图,由于2222220BD CD CE AE AF BF -+-+-=,于是AFEPBDC()()222222(17)18190BD BD CE CE AF AF --+--+--=,此即171819487BD CE AF ++=．而181818486BD CE AF ++=,故1AF BD -=．所以118BD BF BD AB AF AB +=+-=-=． 9．2．9★★已知ABC △中,AB AC =,AE 是BC 的中垂线,AE BC =,3BDC BAC ∠=∠, 求ADDE．AF DBEC解析如图,不妨设1BE CE ==,则2AE =,AB =．作ABD ∠的平分线BF ,由于3BDE BAE ABD BAE ∠=∠=∠+∠,故ABF DBF BAE ∠=∠=∠．因此AF BF =,ABD BFD △∽△, AB AD BD BF BD DF ==,从而2BD DF DA =⋅,DB ADDF AB DB⋅=+,所以()2DA BD BD AB =⋅+．设DE x=,则221BD x =+,2DA x=-,因此()2221x x -=+,()223455x x -=+,2112440x x -+=,211x =（2x =舍）．于是2011AD =,10AD DE =． 9．2．10★★正三角形ABC 内有一点P ,P 关于AB 、AC 的对称点分别为Q 、R ,作平行四边形QPRS ,求证.AS BC ∥．A SMRQBCP解析如图,设QS 与AB 交于M ,连结MP ,则60Q ∠=︒,AB 垂直平分PQ ,QM PM =,MPQ △ 为正三角形,MP PQ SR ==,于是四边形MPRS 为等腰梯形,PR 的中垂线即MS 的中垂线．于是60SAC MAC C ∠=∠==∠,AS BC ∥．9．2．11★★AB 与O 相切于点B ,AC 与O 相交于C 、D ,若45C ∠=︒,60BDA ∠=︒,CD =求AB ．BC D AK T解析如图,由题意可得45ABD ∠=︒,作BK AC ⊥于K ,则BK CK=,又CK CD DK =+=,故32BK =,BD =再作AT BD ⊥于T ,设BT AT x ==,则DT =,x =x =于是6AB ==．9．2．12★已知大小相等的等边ABC △与等边PQR △有三组边分别平行,一个指向上方,一个指向下方,相交部分是一个六边形,则这个六边形的主对角线共点．A D KR QEHBFGCP解析如图,设两个三角形的边的交点依次为D 、E 、F 、G 、H 、K ．设ABC △、PQR △的高为h ,则正ADK △的高h =（RQ 与BC 的距离）=正FPG △的高,于是DK FG ∥,DG 、KF 互相平分,同理DG 、EH 互相平分,于是DG 、EH 、KF 的中点为同一点,结论成立．9．2．13★★★★求证.过正三角形ABC 的中心O 任作一条直线l ,则A 、B 、C 三点至l 的距离平方和为常数．AlB'A'OC'B QC P解析如图,不妨设l 与AB 、AC 相交,且与BC 延长线交于P (平行容易计算)．由中位线及重心性质,知BB CC AA '''+=．故222222()B B C C A A B B C C B B C C '''''''++=++⋅．连结OB 、OC ,作OQ BC ⊥,易知B BP QOP C CP ''△∽△∽△,故C C CP OQ OP '=,B B BPOQ OP'=．对于等腰三角形OBC ,有22OP OC CP BP -=⋅．因此()()222222222223OQ OQ B B C C B B C C CP BP CP BP BC CP BP OP OP ''''++⋅=++⋅=+⋅= ()222222333OQ BC OP OC OQ OP+-=(定值),这里用到了BC =．于是A 、B 、C 三点至l 的距离平方和为22162OQ BC =,结论得证．§9．3三角形中的巧合点9．3．1★已知.H 是ABC △内一点,AH 、BH 、CH 延长后分别交对边于D 、E 、F ,若AH HD BH HE CH HF ⋅=⋅=⋅,则H 是ABC △的垂心,解析如图,由条件知AHE BHD △∽△,故AEH BDH ∠=∠,同理,AFH CDH ∠=∠,故180AFH AEH ∠+∠=︒．A FEHBDC又FBH ECH △∽△,故BFH CEH ∠=∠,这样可得90AFH AEH ∠=∠=︒,故H 为ABC △之垂心．9．3．2★★求证.到三角形三顶点的距离平方和最小的点是三角形的重心．解析设ABC △中,AD 、BE 、CF 是中线,G 是重心,M 是任一点．由斯图沃特定理,并考虑到结论成立． 123DG GA AD =∶∶∶∶,得2222122339MG AM DM AD =+-22212233AM DM GD =+-．① 又由中线长公式,有 ()22221124MD BM CM BC =+-, ()22221124GD BG CG BC =+-．代入式①,得()()222222230MG MA MB MC GA GB GC =++-++≥．结论成立． 9．3．3★★★已知,H 是锐角ABC △的垂心,D 是BC 中点,过H 作DH 的垂线,交AB 、AC 于M 、N ,求证.H 是MN 中点．AQ NMHBD PC解析设ABC △两条高为AP 、CQ ．又不妨设D 在BP 上．由于HAM DCH ∠=∠,90AHM DHP HDC ∠=︒-∠=∠,故AMH CHD △∽△,于是MH AH HD CD =,同理NH AHHD BD=, 又CD BD =,故MH NH =．9．3．4★★★ABC △的边BC 、CA 、AB 上分别有点D 、E 、F ,且BD CE AFDC EA FB==,求证.ABC △的重心与DEF △的重心是同一点．解析在AB 上取一点M ,使MD AC ∥,则MD BD CEAC BC AC==,所以MD CE =,四边形MDCE 为平行四边形,设MC 与DE 交于N ,又设BC 的中点为,P 连结PN 、AP 、FN ,AP 与FN 交于G ,于是由 BM BD CE AF AB BC AC AB ===,得RM AF =,于是1122PN BM AF ∥∥,于是12PG GN PN GA FG AF ===,所以G 为ABC △与DEF △之重心．AFMG EBDPCN9．3．5★★★已知ABC △,60A ∠=︒,G 是ABC △重心,120BGC ∠=︒,求证.ABC △是正三角形．解析设ABC △三条中线分别为AD 、BE 、CF ．连EF 为中位线．于是由条件知A 、F 、G 、E 共圆,故GBD FEG BAD ∠=∠=∠,于是2BD GD DA =⋅．由于12BD BC =,13GD AD =,代入,得AD =．在ABC △外作等腰BCP △,使BP CP =,120BPC ∠=︒,连结DP ,DP BC ⊥．由圆心角与圆周角的关系,211333GP BP AD AD AD GD PD ====+=+,故G 、D 、P 三点共线,故AD BC ⊥,于是AB AC =,又60RAC ∠=︒,故ABC △为正三角形．AFEBD CPG9．3．6★★★已知D 是BC 上一点,ABD △、ECD △、BCF △都是正三角形,A 、E 在BC 同侧,F 在另一侧,求证.以这三个正三角形的中心为顶点的三角形是正三角形,且它的中心在BC 上．又问此题如何推广？A BCEFR R'DQ'P'Q解析如图,设P 、Q 、R 分别为BCF △、DCE △和ABD △的中心,则由题11．2．25知PQR △为正三角形．过P 、Q 、R 分别作BC 的垂线PP '、QQ '、RR ',则RR QQ PP BD CD BC ⎛'''=== ⎝⎭,又BD CD BC +=, 故RR QQ PP '''+=．又设RQ 中点为S （图中未画出）,SS BC '⊥于S ',则SS PP ''∥,且()1122SS RR QQ PP ''''=+=．设SP 与BC 交于G ,则12SG SS GP PP '==',所以G 为PQR 的中点．评注此题不难推广,只需AB DE CF ∥∥,AD CE BF ∥∥,此时ABD DC FCB △∽△∽△, P 、Q 、R 为各自对应的重心,则必有PQR △之重心位于BC 上． 9．3．7★★★ABC △内有一点P ,连结AP 、BP 、CP 并延长,分别与对边相交,把ABC △分成六个小三角形,若这六个小三角形中有三个面积相等,则点P 是否必为ABC △之重心？解析如图,设AD 、BE 、CF 交于P ．由对称性,可分四种情况讨论．AFEPBDC（1）BPD CDP BPF S S S ==△△△．于是BD CD =,2CPPF=,由梅氏定理（或添平行线）,得AF BF =,P 为中心．（2）BPD CDP APF S S S ==△△△．此时FD AC ∥,故D 、F 分别为BC 、AB 中点,P 为重心．（3）BPD BPF APE S S S ==△△△．此时有DE AB ∥,由塞瓦定理,AF BF =,于是APF BPF S S =△△,回到情形（1）．（4）APF BPD CPE S S S ==△△△,见题15．1．58．综上所知,答案是肯定的．9．3．8★★★设有一个三角形三角之比为124∶∶,作两较大角的平分线,分别交对边于M 、N ．求证.这个三角形的重心在MN 上．解析如图(a),设A ∠为最小角,作中线AD ,交MN 于G ,于是只要证明2AG GD =．分别作EB AD CF ∥∥,E 、F 在直线MN 上,则2GD EB CF =+,故问题变成1EB FCAG AG+=,或 1BC BC CM BN CF BEAB AC AM AN AG AG+=+=+=．不妨设A θ∠=,2C θ∠=,4B θ∠=,7180θ=︒,在AC 上找一点P ,使ABP θ∠=,又作PQ BC ∥,Q 在AB 上,则各角大小如图(b)所示．于是BC BP AP BQ ===,故 11BC AP CP BQ BCAC AC AC AB AB==-=1-=-． ABCD E FNMGA QP B C2θ3θ2θ3θ3θθθ图(a)图(b)9．3．9★★★不等边锐角ABC △中,H 、G 分别是其垂心和重心,求证.若112HABHACHBCS S S +=△△△,AG HG ⊥．ABDECGH解析设ABC △的一条中线与高分别为AD 、AE ,则欲证结论等价于AG AD AH AE ⋅=⋅．熟知cot AH BC A =⋅,23AG AD =．于是结论变为22cot cos 3AD BC AE A AB AC A =⋅⋅=⋅⋅．设AB c =,BC a =,CA b =,则由中线长及余弦定理,知欲证式左端()2221226b c a =+-, 右端2222b c a +-=,整理,得2222b c a +=,于是剩下的任务是证明这个等价条件．1cos 2BHC S BH BC C =⋅⋅⋅△1cot cos 2AC BC B C =⋅⋅⋅⋅ cot cot ABC S B C =⋅⋅△,同理有另两式,于是条件变为cot cot 2cot C B A +=,由正弦及余弦定理,知上式即cos cos ab C ac B +=2cos bc A ,或()()22222222262()ac a c b b c a +-++-=+-,化简即得2222b c a +=．9．3．10★★已知凸四边形ABCD 中,2BAC BDC ∠=∠,2CAD CBD ∠=∠,A 是否一定为BCD △之外心？ABDC解析当BCD △固定．由题设BAC ∠、CAD ∠固定,于是BAC △、ACD △外接圆固定,它们的交点 C 、A '固定,又若A 为BCD △外心时,确为BAC △的外接圆和ACD △的外接圆之异于C 的交点,因此A A '=,结论成立．9．3．11★★★已知锐角ABC △的外接圆与内切圆的半径分别为R 、r ,O 是外心,O 至三边距离之和为L ,试用R 、r 表示L ．解析易知()cos cos cos L R A B C =++．设ABC △三边分别为a 、b 、c ,由于cos cos a B b A c +=等,则()()cos cos cos a b c A B C ++⋅++=cos cos cos a b c a A b B c C +++++,于是 cos cos cos 1A B C ++-cos cos cos a A b B c Ca b c++=++．①又1cos 2BOC Ra A S =△等,可得()()11cos cos cos 22ABC R a A b B c C S r a b c ++==++△,故式①的右端r R =．于是L R r =+． 9．3．12★★★★.已知ABC △,D 、E 分别在AC 、AB 上,BD 、CE 交于F ,ED BC ∥,求证.AEF △、ADF △、EFB △、DFC △的外心四点共圆．AED BCOKO 1O 2解析如图,设BEF △、DFC △的外心分别为1O 、2O ,O 为EFD △的外心,于是1OO 垂直平分EF ．2OO 垂直平分DF ．设EFB DFC θ∠=∠=,则由垂径定理知11sin 2OO BD θ=,21sin 2OO CE θ=,于是12OO BD FD OO CE EF ==．易知AF 过ED 中点（由塞瓦定理或面积比）,作KD EF ∥,K 在AF 上,则KD EF =,又 12180KDF EFD O OO ∠=︒-∠=∠,故12O OO FDK △∽△．又设AEF △,ADF △的外心分别为3O 、4O （图中未画出）,于是3O 、4O 分别在直线1O O 与2O O 上, 且34O O AF ⊥,于是4312OO O KFD OO O ∠=∠=∠,于是1O 、2O 、3O 、4O 四点共圆．9．3．13★★★已知.ABC △中,AB AC =,D 是AB 中点,F 为ADC △重心,O 为ABC △外心,求证.FO CD ⊥．解析1如图,延长DF 交AC 于E ,则AE CE =,2DF EF =．连结AO 并延长,分别交CD 、BC 于G 、H ,则G 为ABC △重心,BH CH =,2233DF DE BH ==,易见2323BHDO BH DF AD AH AG AH ===． ADEF OGB H C又OD AB ⊥,90ODF ADE DAG ∠=︒-∠=∠,ODF DAG △∽△,对应边垂直,所以FO CD ⊥．解析2O 为ABC △外心,故22222CO DO AO DO AD -=-=；而由中线公式,CF =DF 于是22222CF DF AD CO DO -==-,于是FO CD ⊥．9．3．14★★★设I 和O 分别是ABC △的内心和外心,求证.90AIO ∠︒≤的充分必要条件是2BC AB AC +≤．解析延长AI 与外接圆交于点D ,连结BD 、CD 、OD ,则 90AIO ∠︒≤ AI ID ⇔≥．2ADDI⇔≤D由内心性质知,DI DB DC ==,结合托勒密定理得 AD BC AB CD AC BD ⋅=⋅+⋅ AB DI AC DI =⋅+⋅, 所以AD AB ACDI BC+=, 所以902AB ACAIO BC+∠︒⇔≤≤, 故90AIO ∠︒≤的充要条件是2BC AB AC +≤．评注本题的关键是先把90AIO ∠︒≤转换为AI ID ≥,然后再用托勒密定理．托勒密定理是.圆内接四边形的对角线的乘积等于对边乘积的和．9．3．15★★★设O 是ABC △的外接圆,G 是三角形重心,延长AG 、BG 、CG ,分别交O 于D 、E 、F ,则3AG BG CGGD GE GF++=． AF ERQGBP DC解析设BC 、CA 、AB 的中点分别为P 、Q 、R ,则由中线长公式及相交弦定理,有（此处ABC △三边分别设为a 、b 、c ） AG AG AGBP CPGD GP PD GP AP==⋅++22223133APAP BP CP AP BP CP AP AP ==⋅+⋅+ 2222222222222122211132244b c a b c a a b c b c a a +-+-==+++-+．同理,有22222222BG c a b GE a b c +-=++ , 22222222CG a b c GF a b c +-=++．三式相加,即得结论．9．3．16★★I 在ABC △内,AI 平分BAC ∠,1902BIC A ∠=︒+∠,求证.I 是ABC △内心．解析如图,作EIF AI ⊥,E 在AB 上,F 在AC 上,则AE AF =,LE IF =,AEF BCI1902BEI IFC A BIC ∠=∠=︒+∠=∠．又1902EBI EIB A EIB FIC ∠+∠=︒-∠=∠+∠,故EBI FIC ∠=∠,于是EBI FIC △∽△,BI BE BEIC IF EI==．而BEI BIC ∠=∠,故BEI BIC △∽△,ABI IBC ∠=∠,所以I 为ABC △内心．9．3．17★★已知.ABC △中,2BC AB AC =+,D 是内心,DE 与BC 垂直于E ,求2DE BE CE⋅的值．解析设ABC △三边长分别为a 、b 、c ,则2a b c =+．易知若设DE r =,()12p a b c =++,则BE p b =-,CE p c =-．r =于是2133DE P a b c a a BE CE p a b c a -+-====⋅++． 9．3．18★★设ABC △中,AB 最长,在其上分别找两点M 、N ,使AN AC =,BM BC =,又设I 为ABC △内心,求MIN ∠（用A ∠、B ∠、C ∠及其组合表示）．解析如图,连结CM 、CN 、CI 、AI ．CABM NI易知ACI ANI △△≌,CI NI =,同理CI MI =,I 为CMN △的外心,因此 MCN ACN BCM C ∠=∠+∠-∠11909022A B C =︒-∠+︒-∠-∠1902C =︒-∠,2180MIN MCN C ∠=∠=︒-∠．9．3．19★★★★ABC △的边BC 上有一点D ,ABD △与ACD △的内心与B 、C 四点共圆,求证. AD BD ABAD CD AC+=+． AMNE FBDCPI 1I 2解析如图,设ABD △与ACD △的内心分别为1I 与2I ．连结1AI 、2AI 、1BI 、2CI 、12I I ,两端延长12I I ,分别交AB 、AC 于E 、F ,则由条件知()1112AEF ABI EI B ABC ACB ∠=∠+∠=∠+∠,同理AFE ∠也是此值,于是AE AF =．又设12I I 与AD 交于P ,则由角平分线性质知1212EI FI AE AF I P AP AP I P ===,故由梅氏定理（直线AB 截1PDI △及直线AC 截2PDI △）,得1212I D I DI M I N=（此处M 、N 分别为1DI 、2DI 延长后与AB 、AC 之交点）,又由角平分线性质,知11I D AD BD I M AB +=,22I D AD CDI N AC+=于是结论成立． 9．3．20★★★已知ABC △中,AB AC =,O 、I 分别为其外心与内心,D 在AC 上,DI AB ∥,求证.OD CI ⊥．解析如图,不妨设O 在ABC △内,且在I “之上”(O 在形外、I 之下类似处理）,连结AOI 、OC ,则IOC BAC IDC ∠=∠=∠,故O 、I 、C 、D 共圆,于是ODC ICD OIK ICD ∠+∠=∠+∠．这里K 为DO 、CI 直线之交点．AD O KIBC由于AOI BC ⊥,故9090OIK ICD BCI ICD ∠+∠=︒-∠+∠=︒,于是90DKC ∠=︒．9．3．21★★设G 为ABC △的重心,已知GA =GB =2GC =,求ABC △的面积．解析1由题意可画出图(a),令D 为AB 中点,GE AB ⊥,垂足为点E ,因G 为重心,可知112GD GC ==．由勾股定理可知222222222GE GB EB GE GA EA GE GD DE ⎧=-⎪=-⎨⎪=-⎩①②③,C ABD E G22322(a)令AD BD c ==．由①与②可得(()(()2222c DE c DE -+=--,化简后可得1c DE ⨯=,即1DE c =,代入③得2211GE c=-,再代入①式可得 22118c c c ⎛⎫1-=-- ⎪⎝⎭, 解方程可得3c =,GE =,故 ABC △的面积=6GBD ⨯△的面积1632=⨯⨯= 解析2由题意可画出图(b),令D 为AB 中点,在GD 的延长线上取E 点使得GD DE =,因此GBD △ 之面积为AEG △之面积的一半．此时因AB 与GE互相平分,可知四边形AEBG 为平行四边形,也因此可知AE GB ==,即AEG △的三边长为2、,故可知AEG △为直角三角形,故GBD △的面积为11222⨯⨯=,所以ABC △的面积6GBD =⨯△的面积=(b)22232GD BAC 22E 119．3．22★★★已知120AFB BFC CFA ∠=∠=∠=︒,P 为异于F 的任一点,求证. PA PB PC FA FB FC ++>++．解析如图,在ABC △外作正三角形ABD ,由于ABC ∠,120BAC ∠<︒,故四边形DBCA 的内角均小于180︒,是凸四边形．ADF F'PP'BC对于ABC △中任一异于F 的点P ,将ABP △、ABF △均以点A 为中心顺时针旋转60︒,至ADP '△ 和ADF '△,则AFF △与APP '△均为正三角形．由全等知AP BP CP PP DP CP CD DF F F FC AF BF CF ''''++=++>=++=++,这是因为DP PC '是一条折线,而120DF A AFC '∠=∠=︒,60AFF AF F ''∠=∠=︒,D 、F '、F 、C 四点共线且仅对于F 满足四点共线．评注当ABC △内角均小于120︒时,满足条件的点F 称为ABC △的费马点（当ABC △有内角比如120A ∠︒≥时,到A 、B 、C 距离之和最小的点正是点A ）．。

竞赛初中数学试题及答案

竞赛初中数学试题及答案一、选择题（每题2分，共10分）1. 已知一个等腰三角形的两边长分别为3cm和5cm，那么这个三角形的周长是（）。

A. 11cmB. 13cmC. 16cmD. 无法确定2. 下列哪个数是无理数（）。

A. 0.5B. √2C. 22/7D. 03. 一个数的相反数是-3，那么这个数是（）。

A. 3B. -3C. 0D. 64. 若a、b、c是等差数列，且a+c=10，b=5，则a、b、c的值分别是（）。

A. 2, 5, 8B. 3, 5, 7C. 4, 5, 6D. 5, 5, 55. 一个圆的半径为2cm，那么这个圆的面积是（）。

A. 4π cm²B. 8π cm²C. 12π cm²D. 16π cm²二、填空题（每题2分，共10分）6. 一个数的平方是25，那么这个数是______或______。

7. 一个数增加20%后是120，那么这个数原来是______。

8. 已知一个直角三角形的两个直角边长分别为3cm和4cm，那么斜边长是______cm。

9. 一个数的绝对值是5，那么这个数是______或______。

10. 一个数除以-2的商是-3，那么这个数是______。

三、解答题（每题5分，共20分）11. 已知一个二次函数y=ax²+bx+c，其中a=1，b=-3，c=2，求当x=1时，y的值。

12. 一个长方形的长是宽的两倍，如果宽增加2cm，长减少2cm，面积不变，求原长方形的长和宽。

13. 一个数列的前三项分别是1，2，3，从第四项开始，每一项都是前三项的和，求数列的第8项。

14. 一个圆的直径是10cm，求这个圆的周长和面积。

答案：一、选择题1. B2. B3. A4. A5. B二、填空题6. ±57. 1008. 59. ±510. 6三、解答题11. 当x=1时，y=1-3+2=0。

初中数学竞赛试卷及答案解析

初中数学竞赛试卷及答案解析一、选择题1.已知函数f(x) = 2x - 3，求f(4)的值。

A. 2B. 5C. 6D. 7答案：C. 6解析：将x = 4代入函数f(x) = 2x - 3，得到f(4) = 2(4) - 3 = 8 - 3 = 5。

因此，答案为C. 6。

2.下列哪个不是三角形的内角？A. 90度B. 120度C. 180度D. 270度答案：C. 180度解析：三角形的内角之和总是等于180度。

因此，180度不是三角形的内角，而是一条直线的内角。

答案为C. 180度。

3.已知a = 3，b = 4，c = 5，求三角形的周长。

A. 6B. 12C. 15D. 20答案：C. 15解析：三角形的周长等于三条边的长度之和。

因此，周长 = a + b +c = 3 + 4 + 5 = 12。

答案为C. 15。

4.若x + 3 = 7，则x的值是多少？A. 2B. 3C. 4D. 5答案：A. 2解析：将x + 3 = 7转化为x = 7 - 3，得到x的值为2。

因此，答案为A. 2。

5.已知正方形的周长为20cm，求正方形的边长。

A. 4cmB. 5cmC. 10cmD. 20cm答案：B. 5cm解析：正方形的周长等于4倍的边长。

因此，边长 = 周长 / 4 = 20 /4 = 5。

答案为B. 5cm。

二、填空题1.已知等差数列的首项a₁ = 2，公差d = 3，求该数列的第10项。

答案：28解析：根据等差数列的通项公式an = a₁ + (n - 1) * d，代入a₁ = 2，d = 3，n = 10，得到a10 = 2 + (10 - 1) * 3 = 2 + 9 * 3 = 2 + 27 = 28。

2.若x² + 3x + k是一个完全平方数，则k的值为多少？答案：9/4解析：对于一个完全平方数，它的因式分解必然是两个相同的因式相乘。

根据已知的二次项系数求平方根的方法，可以得到k = (b/2a)² = (3/2)² = 9/4。

专题35 初中数学竞赛分类汇编(七)三角形(简单) 初中数学学科素养能力培优竞赛试题精选专练含解析卷

专题35 全国初中数学竞赛分类汇编卷（七）三角形（简单）1．如图，BF 是∠ABD 的平分线，CE 是∠ACD 的平分线，BF 与CE 交于点G ，若∠BDC ＝140°，∠BGC ＝110°，则∠A 的度数为（）A ．50°B ．55°C ．70°D ．80°2．如图，在△ABC 中，∠BAC ＝90°，AB ＝8，AC ＝6，AD 为△ABC 的中线，点F 在边AC 上（不与端点重合），BF 与AD 交于点E ，若AF ＝EF ，则AE 的长为（）A ．145 B ．3 C ．165 D ．43．在⊙O 中，AB ，CD 是互相垂直的两条直径，点E 在BĈ上，CF ⊥AE 于点F ．若点F 三等分弦AE ，⊙O 的直径为12，则CF 的长是（）A ．2√55B ．2√105C ．6√55D ．6√1054．平面上任意一点到边长为2√3的等边三角形三顶点距离之和不可能的是（）A．3√3B．6C．4√3D．85．如图，在△ABC中，∠BAC、∠BCA的平分线相交于点I，若∠B＝35°，BC＝AI+AC，则∠BAC的度数为（）A．60°B．70°C．80°D．90°6．如图所示，ABCD是长方形地面，长AB＝20m，宽AD＝10m．中间竖有一堵砖墙高MN ＝2m．一只蚂蚱从A点爬到C点，它必须翻过中间那堵墙，则它至少要走m的路程．7．如图，在四边形ABCD中，∠ABC＝90°，CD⊥AD，AD2+CD2＝2AB2．AB BC （填＝、＞或＜号），当BE⊥AD于E时，BE、AE、CD数量之间等量关系是．8．如图，点C在线段AB上，DA⊥AB，EB⊥AB，FC⊥AB，且DA＝BC，EB＝AC，FC ＝AB，∠AFB＝51°，则∠DFE＝．9．如图，在R t△AOB中，∠AOB＝90°，OA＝3cm，OB＝4cm，以点O为坐标原点建立坐标系，设P、Q分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动，速度均为1cm/秒，设P、Q移动时间为t（0≤t≤4）．（1）求AB的长，过点P作PM⊥OA于M，求出P点的坐标（用t表示）；（2）求△OPQ面积S（cm2）与运动时间t（秒）之间的函数关系式，当t为何值时，S有最大值？最大是多少？（3）当t为何值时，△OPQ为直角三角形？（4）若点P运动速度不变，改变Q的运动速度，使△OPQ为正三角形，求Q点运动的速度和此时t的值．10．在△ABC中，已知D为直线BC上一点，若∠ABC＝x°，∠BAD＝y°．（1）当D为边BC上一点，并且CD＝AB，x＝40，y＝30时，求证：AB＝AC．（2）若CD＝CA＝AB，请写出y与x的关系式及x的取值范围．（不写解答过程，直接写出结果）11．如图，在五边形ABCDE中，∠ABC＝∠AED＝90°，M是CD的中点，BM＝EM，求证：∠BAC＝∠EAD．12．（1）如图1，∠MAN＝90°，射线AE在这个角的内部，点B、C分别在∠MAN的边AM、AN上，且AB＝AC，CF⊥AE于点F，BD⊥AE于点D．求证：△ABD≌△CAF；（2）如图2，点B、C分别在∠MAN的边AM、AN上，点E、F都在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB＝AC，且∠1＝∠2＝∠BAC．求证：△ABE≌△CAF；（3）如图3，在△ABC中，AB＝AC，AB＞BC．点D在边BC上，CD＝2BD，点E、F 在线段AD上，∠1＝∠2＝∠BAC．若△ABC的面积为15，求△ACF与△BDE的面积之和．13．如图，在△ABC中，DM、EN分别垂直平分AC和BC，交AB于M、N两点，DM与EN相交于点F．（1）若△CMN的周长为15cm，求AB的长；（2）若∠MFN＝70°，求∠MCN的度数．14．如图，在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD＝AC，在CF的延长线上截取CG＝AB，连接AD．AG．（1）求证：AD＝AG；（2）AD与AG的位置关系如何．专题35全国初中数学竞赛分类汇编卷（七）三角形（简单）1．如图，BF是∠ABD的平分线，CE是∠ACD的平分线，BF与CE交于点G，若∠BDC ＝140°，∠BGC＝110°，则∠A的度数为（）A．50°B．55°C．70°D．80°【解答】解：连接BC．∵∠BDC＝140°，∴∠DBC+∠DCB＝180°﹣140°＝40°，∵∠BGC＝110°，∴∠GBC+∠GCB＝180°﹣110°＝70°，∵BF是∠ABD的平分线，CE是∠ACD的平分线，∴∠GBD+∠GCD=12∠ABD+12∠ACD＝30°，∴∠ABC+∠ACB＝100°，∴∠A＝180°﹣100°＝80°．故选：D．2．如图，在△ABC中，∠BAC＝90°，AB＝8，AC＝6，AD为△ABC的中线，点F在边AC上（不与端点重合），BF与AD交于点E，若AF＝EF，则AE的长为（）A ．145B ．3C ．165D ．4【解答】解：过点D 作DG ∥AC ，交BF 于点G ，则∠EGD ＝∠EFA ，∵AD 是△ABC 的中线，∴DG 是△BFC 的中位线，设AF ＝x ，则CF ＝6﹣x ，EF ＝x ，∴DG =12（6﹣x ），∵∠EGD ＝∠EFA ，∠GED ＝∠FEA ，∴△EDG ∽△EAF ，∴EG EF =DG AF ，∵AF ＝EF ，∴EG ＝DG =12（6﹣x ），∴FG ＝EG +EF =12（6﹣x ）+x =12（6+x ），∴BF ＝6+x ，∵AB ＝8，AF ＝x ，∠BAF ＝90°，∴BF =√AB 2+AF 2=√82+x 2=√64+x 2，∴√64+x 2=6+x ，解得：x =73，∴EG =116，EF =73，∵AB ＝8，AC ＝6，∠BAC ＝90°，∴BC ＝10，∵AD 是△ABC 的中线，∴AD ＝5，∵△EDG ∽△EAF ，∴AE ED =EF EG ，即AE 5−AE =73116，解得：AE =145．故选：A ．3．在⊙O 中，AB ，CD 是互相垂直的两条直径，点E 在BĈ上，CF ⊥AE 于点F ．若点F 三等分弦AE ，⊙O 的直径为12，则CF 的长是（）A ．2√55B ．2√105C ．6√55D ．6√105【解答】解：如图，连接AC ，EC ．设AE 交OC 于点K ，设EF ＝a ．∵AF ＝2EF ，EF ＝a ，∴AF ＝2a ，∵AB ⊥CD ，∴∠AOC ＝90°，∴∠CEA =12∠AOC ＝45°，∵CF ⊥EF ，∴∠CFE ＝90°，∴∠FCE ＝∠FEC ＝45°，∴CF ＝EF ＝a ，∴AC =√a 2+(2a)2=√5a ，∵OA ＝OC ＝6，∴AC ＝6√2，∴√5a ＝6√2，∴a =6√105∴CF=6√10 5故选：D．4．平面上任意一点到边长为2√3的等边三角形三顶点距离之和不可能的是（）A．3√3B．6C．4√3D．8【解答】解：如图，当点P为等边△ABC的中心时，PA+PB+PC＝6最小，将△APC绕点A逆时针旋转60°得到△ADE，连接PD，∵AP＝AD，∠PAD＝60°，∴△APD是等边三角形，∴∠APD＝∠ADP＝60°，PD＝AP，∵△ABC是等边三角形，∴AB＝BC＝AC＝2√3，∵点P为等边△ABC的中心，∴PA＝PB＝PC，∴△PAB≌△PBC≌△PCA（SSS），∴∠APB＝∠APC＝120°，由旋转得：∠ADE＝∠APC＝120°，∴∠APD+∠APB＝180°，∠ADP+∠ADP＝180°，∴PA+PB+PC＝BP+PD+DE＝BE，即此时PA+PB+PC最小，∵∠ABP＝30°，∠BAC＝60°，∴∠AHB＝90°，∴AH=12AC=√3，∴BH＝AH•tan∠BAC=√3•tan60°＝3，∵AE＝AC＝AB＝2√3，AH⊥BE，∴BE＝2BH＝6，在平面内任取一点P′，连接P′A，P′B，P′C，将△P′AC绕点A逆时针旋转60°得到△AD′E，连接P′D′，∵BP′，P′D′，D′E不在同一条直线上，∴BP′+P′D′+D′E＞PA+PB+PC＝6，∵（3√3）2＝27，62＝36，27＜36，∴3√3＜6，故选：A．5．如图，在△ABC中，∠BAC、∠BCA的平分线相交于点I，若∠B＝35°，BC＝AI+AC，则∠BAC的度数为（）A．60°B．70°C．80°D．90°【解答】解：方法一：如图1，在BC上取CD＝AC，连接BI、DI，∵CI平分∠ACB，∴∠ACI＝∠BCI，在△ACI与△DCI中，{AC=CD∠ACI=∠BCI CI=CI，∴△ACI≌△DCI（SAS），∴AI＝DI，∠CAI＝∠CDI，∵BC＝AI+AC，∴BD＝AI，∴BD＝DI，∴∠IBD＝∠BID，∴∠CDI＝∠IBD+∠BID＝2∠IBD，又∵AI、CI分别是∠BAC、∠ACB的平分线，∴BI是∠ABC的平分线，∴∠ABC＝2∠IBD，∠BAC＝2∠CAI，∴∠CDI＝∠ABC，∴∠BAC＝2∠CAI＝2∠CDI＝2∠ABC，∵∠B＝35°，∴∠BAC＝35°×2＝70°；方法二：如图2，延长CA到D，使AD＝AI，∴∠D＝∠AID，∵BC＝AI+AC，∴BC＝CD，在△BCI与△DCI中，{BC=CD∠BCI=∠DCI CI=CI，∴△BCI≌△DCI（SAS），∴∠D＝∠CBI，∵AI、CI分别是∠BAC、∠ACB的平分线，∴BI是∠ABC的平分线，∴∠ABC＝2∠CBI，又∵∠CAI＝∠D+∠AID＝2∠D，∠BAC＝2∠CAI＝2∠ABC，∵∠B＝35°，∴∠BAC＝2×35°＝70°．故选：B．6．如图所示，ABCD是长方形地面，长AB＝20m，宽AD＝10m．中间竖有一堵砖墙高MN ＝2m．一只蚂蚱从A点爬到C点，它必须翻过中间那堵墙，则它至少要走26m的路程．【解答】解：如图所示，将图展开，图形长度增加2MN，原图长度增加4米，则AB＝20+4＝24m，连接AC，∵四边形ABCD是长方形，AB＝24m，宽AD＝10m，∴AC=√AB2+BC2=√242+102=√676=26m，∴蚂蚱从A点爬到C点，它至少要走26m的路程．故答案为：26m．7．如图，在四边形ABCD中，∠ABC＝90°，CD⊥AD，AD2+CD2＝2AB2．AB＝BC （填＝、＞或＜号），当BE⊥AD于E时，BE、AE、CD数量之间等量关系是BE＝AE+CD．【解答】解：连接AC．∵∠ABC＝90°，∴AB2+BC2＝AC2．∵CD⊥AD，∴AD2+CD2＝AC2．∵AD2+CD2＝2AB2，∴AB2+BC2＝2AB2，∴BC2＝AB2，∵AB＞0，BC＞0，∴AB＝BC；过C作CF⊥BE于F．∵BE⊥AD，CF⊥BE，CD⊥AD，∴∠FED＝∠CFE＝∠D＝90°，∴四边形CDEF是矩形．∴CD＝EF．∵∠ABE+∠BAE＝90°，∠ABE+∠CBF＝90°，∴∠BAE＝∠CBF，∴在△BAE与△CBF中∴{∠AEB =∠BFC∠BAE =∠CBF AB =BC，∴△BAE ≌△CBF ．（AAS ）∴AE ＝BF ．∴BE ＝BF +EF ＝AE +CD ，故答案为：＝，BE ＝AE +CD ．8．如图，点C 在线段AB 上，DA ⊥AB ，EB ⊥AB ，FC ⊥AB ，且DA ＝BC ，EB ＝AC ，FC ＝AB ，∠AFB ＝51°，则∠DFE ＝ 39° ．【解答】解：连接BD 、AE ，∵DA ⊥AB ，FC ⊥AB ，∴∠DAB ＝∠BCF ＝90°，在△DAB 和△BCF 中，{DA =BC ∠DAB =∠BCF AB =FC，∴△DAB ≌△BCF （SAS ），∴BD ＝BF ，∠ADB ＝∠ABF ，∴∠BDF ＝∠BFD ，∵∠DAB ＝90°，∴∠ADB +∠DBA ＝90°，∴∠DBF ＝∠ABD +∠ABF ＝90°，∴∠BFD ＝∠BDF ＝45°，同理∠AFE ＝45°，∴∠DFE ＝45°+45°﹣51°＝39°，故答案为：39°．9．如图，在R t △AOB 中，∠AOB ＝90°，OA ＝3cm ，OB ＝4cm ，以点O 为坐标原点建立坐标系，设P 、Q 分别为AB 、OB 边上的动点它们同时分别从点A 、O 向B 点匀速运动，速度均为1cm /秒，设P 、Q 移动时间为t （0≤t ≤4）．（1）求AB 的长，过点P 作PM ⊥OA 于M ，求出P 点的坐标（用t 表示）；（2）求△OPQ 面积S （cm 2）与运动时间t （秒）之间的函数关系式，当t 为何值时，S 有最大值？最大是多少？（3）当t 为何值时，△OPQ 为直角三角形？（4）若点P 运动速度不变，改变Q 的运动速度，使△OPQ 为正三角形，求Q 点运动的速度和此时t 的值．【解答】解：（1）∵OA ＝3cm ，OB ＝4cm ，∴AB =√OA 2+OB 2=√32+42=5cm ．∵PM ⊥OA 于M ，∠AOB ＝90°，∴PM ∥OB ，∵△APM ∽△ABO ，∴MP AP =OB AB =AM AO ，∴MP =45t ，AM =3t 5，∴P （45t ，3−35t ）．（2）如图：过点P 作PN ⊥OQ 于点N ，则PN ＝3−3t 5，S =12OQ •PN=12t （3−3t 5）=−310t 2+32t ， ∵a =−310＜0，∴当t =−b 2a =52时，S 有最大值，且S 最大值=158．（3）△OPQ 能成为直角三角形．∵∠POQ ＜90°，OQ ＝t ＞ON ，∠OQP ＜90°，∴只有∠OPQ 可能是90°，当∠OPQ ＝90°时，△OPN ∽△PQN ，∴PN ON =NQ PN ，∴PN 2＝ON •NQ即：(3−3t 5)2=45t ×t 5，解得：t 1＝3，t 2＝15，∵OB ＝4＜15，∴t ＝3．（4）要使△OPQ 为正三角形，则OQ ＝2ON =85t ，∴Q 点的速度为85cm /s ，此时3−35t =85t •√32，解得t =20√3−1513．故Q 点运动的速度为85cm /s 时，t 的值为20√3−1513． 10．在△ABC 中，已知D 为直线BC 上一点，若∠ABC ＝x °，∠BAD ＝y °．（1）当D 为边BC 上一点，并且CD ＝AB ，x ＝40，y ＝30时，求证：AB ＝AC ．（2）若CD ＝CA ＝AB ，请写出y 与x 的关系式及x 的取值范围．（不写解答过程，直接写出结果）【解答】（1）证明：如图，在BC 上取点E ，使BE ＝CD ＝AB ，连接AE ，则∠AEB ＝∠EAB =12（180°﹣40°）＝70°，∴∠AEB ＝∠ADE ＝70°，∴AD ＝AE ，∴∠ADB ＝∠AEC ＝180°﹣70°＝110°，∵BD ＝BE ﹣DE ，CE ＝CD ﹣DE ，∴BD ＝EC ，在△ADB 和△AEC 中，{AD =AE∠ADB =∠AEC BD =CE∴△ADB ≌△AEC （SAS ），∴AB ＝AC ．（2）解：①当点D 在边BC 上时，∵∠ABC ＝x °，CA ＝AB ，∴∠C ＝∠ABC ＝x °，∵CD ＝CA ，∴∠ADC ＝∠CAD =180°−∠C 2=90°−12x °，∵∠ADC＝∠B+∠BAD，∴90−12x＝x+y，即：y=−32x+90（0＜x≤60）（取等号时B、D重合）②当点D在BC的延长线上时，如图1，∵AB＝AC，∴∠ACB＝∠B＝x°，∵AC＝CD，∴∠ACB＝2∠D，∴∠D=12∠ACB=12x°，在△ABD中，∠B+∠BAD+∠D＝180°，∴x+y+12x＝180，即：y=−32x+180，（0＜x＜90）③当点D在CB延长线上时，如图2，∵∠BAD＝y°，∠ABC＝x°，∴∠D＝∠ABC﹣∠BAD＝x°﹣y°，∵AB＝AC，∴∠C＝∠ABC＝x°，∵CD＝AC，∴∠CAD＝∠D＝x°﹣y°，在△ACD中，∠D+∠C+∠CAD＝180°，∴x﹣y+x+x﹣y＝180，∴3x﹣2y＝180，∴y=32x﹣90（60＜x＜90）（取等号时B、D重合）．11．如图，在五边形ABCDE中，∠ABC＝∠AED＝90°，M是CD的中点，BM＝EM，求证：∠BAC＝∠EAD．【解答】解：分别取AC、AD的中点F、G，再连接BF、MF、MG、EG，∵F是AC中点，∠ABC＝90°，∴BF=12AC，又∵MG是△ACD的中位线，∴MG=12AC，∴BF＝MG，同理GE＝MF，又∵BM＝EM，∴△BFM≌△MGE，∴∠BFM＝∠MGE，∵∠CFM＝∠CAD＝∠DGM，∴∠BFC＝∠EGD，∴∠BAF+∠ABF＝∠GAE+∠AEG，∵AF＝BF，∴∠BAF＝∠ABF，同理∠GAE＝∠AEG，∴2∠BAF＝2∠EAG，即∠BAC＝∠EAD．12．（1）如图1，∠MAN＝90°，射线AE在这个角的内部，点B、C分别在∠MAN的边AM 、AN 上，且AB ＝AC ，CF ⊥AE 于点F ，BD ⊥AE 于点D ．求证：△ABD ≌△CAF ；（2）如图2，点B 、C 分别在∠MAN 的边AM 、AN 上，点E 、F 都在∠MAN 内部的射线AD 上，∠1、∠2分别是△ABE 、△CAF 的外角．已知AB ＝AC ，且∠1＝∠2＝∠BAC ．求证：△ABE ≌△CAF ；（3）如图3，在△ABC 中，AB ＝AC ，AB ＞BC ．点D 在边BC 上，CD ＝2BD ，点E 、F 在线段AD 上，∠1＝∠2＝∠BAC ．若△ABC 的面积为15，求△ACF 与△BDE 的面积之和．【解答】解：（1）如图①，∵CF ⊥AE ，BD ⊥AE ，∠MAN ＝90°，∴∠BDA ＝∠AFC ＝90°，∴∠ABD +∠BAD ＝90°，∠ABD +∠CAF ＝90°，∴∠ABD ＝∠CAF ，在△ABD 和△CAF 中，{∠ADB =∠CFA ∠ABD =∠CAF AB =AC，∴△ABD ≌△CAF （AAS ）；（2）∵∠1＝∠2＝∠BAC ，∠1＝∠BAE +∠ABE ，∠BAC ＝∠BAE +∠CAF ，∠2＝∠FCA +∠CAF ，∴∠ABE ＝∠CAF ，∠BAE ＝∠FCA ，在△ABE 和△CAF 中，{∠ABE =∠CAFAB =AC ∠BAE =∠ACF，∴△ABE ≌△CAF （ASA ）；（3）∵△ABC 的面积为15，CD ＝2BD ，∴△ABD 的面积是：13×15＝5，由（2）中证出△ABE ≌△CAF ，∴△ACF 与△BDE 的面积之和等于△ABE 与△BDE 的面积之和，即等于△ABD 的面积，是5．13．如图，在△ABC 中，DM 、EN 分别垂直平分AC 和BC ，交AB 于M 、N 两点，DM 与EN 相交于点F ．（1）若△CMN 的周长为15cm ，求AB 的长；（2）若∠MFN ＝70°，求∠MCN 的度数．【解答】解：（1）∵DM 、EN 分别垂直平分AC 和BC ，∴AM ＝CM ，BN ＝CN ，∴△CMN 的周长＝CM +MN +CN ＝AM +MN +BN ＝AB ，∵△CMN 的周长为15cm ，∴AB ＝15cm ；（2）∵∠MFN ＝70°，∴∠MNF +∠NMF ＝180°﹣70°＝110°，∵∠AMD ＝∠NMF ，∠BNE ＝∠MNF ，∴∠AMD +∠BNE ＝∠MNF +∠NMF ＝110°，∴∠A +∠B ＝90°﹣∠AMD +90°﹣∠BNE ＝180°﹣110°＝70°，∵AM ＝CM ，BN ＝CN ，∴∠A ＝∠ACM ，∠B ＝∠BCN ，∴∠MCN ＝180°﹣2（∠A +∠B ）＝180°﹣2×70°＝40°．14．如图，在△ABC 中，BE 、CF 分别是AC 、AB 两边上的高，在BE 上截取BD ＝AC ，在CF 的延长线上截取CG ＝AB ，连接AD ．AG ．（1）求证：AD ＝AG ；（2）AD 与AG 的位置关系如何．【解答】（1）证明：∵BE、CF分别是AC、AB两边上的高，∴∠AFC＝∠BFC＝∠BEC＝∠BEA＝90°∴∠BAC+∠ACF＝90°，∠BAC+∠ABE＝90°，∠G+∠GAF＝90°，∴∠ABE＝∠ACF．在△ABD和△GCA中，{BD=AC∠ABE=∠ACF AB=CG，∴△ABD≌△GCA（SAS），∴AD＝GA，（2）结论：AG⊥AD．理由：∵△ABD≌△GCA（SAS），∴∠BAD＝∠G，∴∠BAD+∠GAF＝90°，∴AG⊥AD．。