椭圆几何性质3 胡红
椭圆的简单几何性质课件

椭圆的简单几何性质课件椭圆的简单几何性质椭圆,作为一种常见的几何形状,具有许多有趣的性质和特点。
在这篇文章中,我们将探讨椭圆的一些简单几何性质,帮助读者更好地理解和应用椭圆。
一、椭圆的定义和基本元素椭圆是指平面上到两个固定点F1和F2的距离之和等于常数2a的点的轨迹。
这两个固定点称为焦点,连接两个焦点的线段称为主轴,主轴的中点称为椭圆的中心。
椭圆的两个焦点与中心之间的距离称为焦距,记为c。
椭圆的长轴长度为2a,短轴长度为2b,其中a大于b。
二、椭圆的离心率和焦半径椭圆的离心率是一个重要的参数,用e表示。
离心率的定义是焦距与长轴长度的比值,即e=c/a。
离心率可以用来描述椭圆的扁平程度,当离心率接近于0时,椭圆趋近于圆形;当离心率接近于1时,椭圆趋近于直线。
与离心率相关的概念是焦半径。
焦半径是指从椭圆上的任意一点到两个焦点的距离之和,记为r。
根据焦半径的定义,我们可以得到一个重要的结论:椭圆上的任意一点到两个焦点的距离之和等于2a,即r=2a。
三、椭圆的方程和参数方程椭圆的方程是描述椭圆上的点的数学表达式。
椭圆的标准方程是(x-h)^2/a^2+(y-k)^2/b^2=1,其中(h,k)是椭圆的中心坐标。
根据椭圆的定义,我们可以得到一个重要的性质:椭圆上的任意一点到中心的距离与椭圆的长轴、短轴长度之间存在一定的关系,即(x-h)^2/a^2+(y-k)^2/b^2=1。
除了标准方程,椭圆还可以用参数方程来表示。
参数方程是通过引入一个参数t,将椭圆上的点的坐标表示为x=a*cos(t)+h,y=b*sin(t)+k。
参数方程的优点是可以方便地描述椭圆上的点的运动和变化。
四、椭圆的性质和应用椭圆具有许多有趣的性质和应用。
首先,椭圆是一个闭合曲线,它的形状稳定且对称。
其次,椭圆上的点到两个焦点的距离之和是常数,这个性质可以应用于天文学中的行星轨道计算、卫星轨道设计等领域。
此外,椭圆还有许多与切线、法线、对称性等相关的性质。
苏教版高考总复习一轮数学精品课件 第九章 平面解析几何 第五节 椭圆-第2课时 椭圆的几何性质

4
4
3
4
3
2
2
2
2
2
2
2
2
C. + = 1或 + = 1D. + = 1或 + = 1
6
3
6
3
16
9
9
16
[解析]因为离心率为 ,则有 = = ,所以 = ,又椭圆的面积为
所以 =
+
,又
= .故选B.
=
+ ,解得
=
,
∴ = ,解得 = ,
∵ = × ,∴ = ,
∴椭圆的标准方程为
+ = ;
+
= > > ,∵椭圆过点 , ,
若焦点在轴上,设方程为
= ,
又 = × ,∴ =
+
=
或
1 = + 0 , 2 = − 0 .
自测诊断
1.椭圆3 2 + 4 2 = 12的长轴长、短轴长分别为() C
A.2, 3B. 3,2C.4,2 3D.2 3,4
[解析]把
+
短轴长为 .
=
化成标准形式为
+
= ,得 = , = ,则长轴长为4,
+
= .
3.若椭圆的两个焦点与短轴的一个端点构成一个正三角形,则该椭圆的离心率为( A )
椭圆的几何性质

1、定义:e=c/a。
2、离心率范围:0<e<1。
3、离心率越大椭圆就越扁,越小则越接近于圆。
面积
S=π×a×b(其中a,b分别是椭圆的长半轴,短半轴的长)。
或S=π×A×B/4(其中A,B分别是椭圆的长轴,短轴的长)。
周长
椭圆周长没有公式,有积分式Fra bibliotek无限项展开式。
椭圆周长的精确计算要用到积分或无穷级数的求和。
chusancom隶属于吉林省春雨秋风科技有限公司其它同名网站均为侵权或假冒
椭圆的几何性质
范围:焦点在x轴上-a≤x≤a,-b≤y≤b;焦点在y轴上-b≤x≤b,-a≤y≤a。对称性:关于x轴对称,关于y轴对称,关于原点中心对称。顶点:(a,0),(-a,0),(0,b),(0,-b)。离心率:e=c/a。离心率范围0<e<1。离心率越大椭圆就越扁,越小则越接近于圆。
椭圆和双曲线的性质

椭圆和双曲线的性质椭圆和双曲线是数学中常见的曲线形状,它们具有一些独特的性质和特点。
本文将介绍椭圆和双曲线的定义、方程、焦点、直径、离心率等基本概念,并探讨它们的性质和应用。
一、椭圆的性质椭圆是平面上一点到两个固定点的距离之和等于常数的轨迹。
这两个固定点称为椭圆的焦点,常数称为椭圆的离心率。
椭圆的方程一般形式为:(x/a)^2 + (y/b)^2 = 1其中a和b分别是椭圆的半长轴和半短轴的长度。
椭圆的中心位于原点(0,0)处。
椭圆的性质有以下几点:1. 椭圆是对称图形,关于x轴和y轴都具有对称性。
2. 椭圆的长轴和短轴分别是直径,且长轴和短轴的长度之比等于椭圆的离心率。
3. 椭圆的焦点到椭圆上任意一点的距离之和等于椭圆的长轴长度。
4. 椭圆的离心率小于1,且越接近于1,椭圆越扁平。
椭圆的应用广泛,例如在天文学中,行星的轨道可以近似看作椭圆;在工程中,椭圆的形状常用于设计汽车、船舶等物体的外形。
二、双曲线的性质双曲线是平面上一点到两个固定点的距离之差等于常数的轨迹。
这两个固定点称为双曲线的焦点,常数称为双曲线的离心率。
双曲线的方程一般形式为:(x/a)^2 - (y/b)^2 = 1其中a和b分别是双曲线的半长轴和半短轴的长度。
双曲线的中心位于原点(0,0)处。
双曲线的性质有以下几点:1. 双曲线是对称图形,关于x轴和y轴都具有对称性。
2. 双曲线的长轴和短轴分别是直径,且长轴和短轴的长度之比等于双曲线的离心率。
3. 双曲线的焦点到双曲线上任意一点的距离之差等于双曲线的长轴长度。
4. 双曲线的离心率大于1,且越接近于1,双曲线越扁平。
双曲线的应用也非常广泛,例如在物理学中,双曲线常用于描述光的折射和反射现象;在经济学中,双曲线常用于描述供需关系和市场变化。
总结:椭圆和双曲线是两种常见的曲线形状,它们具有一些共同的性质,如对称性和焦点到曲线上任意一点的距离关系。
同时,它们也有一些不同的特点,如离心率的大小和形状的扁平程度。
《椭圆的简单几何性质》知识点总结

椭圆的简单几何性质知识点总结椭圆是一种重要的几何图形,具有一些特殊的性质。
在本篇文档中,我们将总结椭圆的一些简单几何性质。
1. 椭圆的定义椭圆可以通过以下定义来描述:对于给定的两个焦点F1和F2,及其到两个焦点的总距离的一半定为常量2a(长轴),椭圆上每一点到两个焦点的距离之和等于常量2a。
椭圆的另一个参数e(离心率)定义为焦点之间的距离与长轴的比值:e = c/a,其中c是焦点之间的距离。
2. 椭圆的焦点和准线椭圆的焦点F1和F2对称分布在长轴上,并且与椭圆的中心O相等。
准线是通过焦点F1和F2垂直于长轴的直线,交于椭圆的中心O。
准线的长度定为2b(短轴)。
椭圆的离心率e= c/a = √(a^2 - b^2)/a。
3. 椭圆的主轴和副轴椭圆的主轴是长轴,长度为2a。
副轴是短轴,长度为2b。
长轴和短轴是椭圆上的两个对称轴。
4. 椭圆的焦准距椭圆上的任意一点P到两个焦点F1和F2的距离之和等于2a,即PF1+PF2=2a。
我们把这个距离之和称为焦准距。
对于同一条主轴上的两个点P1和P2,它们到焦点的距离之和相等。
5. 椭圆的离心率椭圆的离心率是一个反映椭圆形状的重要参数。
离心率e定义为焦点之间的距离与长轴的比值:e = c/a。
当离心率小于1时,椭圆是真椭圆;当离心率等于1时,椭圆是半圆;当离心率大于1时,椭圆是伪椭圆。
离心率越接近于0,椭圆形状越扁。
6. 椭圆的方程椭圆的方程可以通过不同的形式来表示,其中最常用的是标准形式和一般形式。
标准形式的椭圆方程为:x2/a2 + y2/b2 = 1,其中a和b分别为椭圆的长轴和短轴的长度。
一般形式的椭圆方程为:Ax^2 + By^2 + Cx + Dy + E = 0,其中A、B、C、D和E为常数。
7. 椭圆的焦距定理椭圆的焦距定理说明了椭圆上的任意一点P到两个焦点F1和F2的距离之和等于椭圆的主轴长度。
即PF1+PF2=2a。
8. 椭圆的切线椭圆上任意一点P的切线是通过点P且与椭圆仅相交于点P的直线。
椭圆的基本概念与性质

椭圆的基本概念与性质椭圆是一种常见的几何图形,具有许多独特的性质和应用。
本文将介绍椭圆的基本概念和性质,包括定义、标准方程、焦点、直径、离心率、轨道和应用等方面。
1.椭圆的定义椭圆可以定义为平面上到两个固定点(焦点)的距离之和等于常数的点的集合。
这两个固定点称为焦点,常数称为椭圆的离心率。
椭圆也可以视为一个平面上到定点的连线长度之和等于一定长度(主轴)的点的轨迹。
2.椭圆的标准方程以坐标原点为中心的椭圆的标准方程为x²/a² + y²/b² = 1,其中a和b 分别表示椭圆的长短半轴。
可以看出,a表示椭圆离心率对应的焦距长度,b表示椭圆的短半轴长度。
3.焦点和直径椭圆的焦点是椭圆的一个重要属性,它是椭圆离心率定义的核心。
可以通过标准方程中的离心率公式e = c/a(c为焦点到原点的距离),求得焦点的坐标表达式为(c, 0)和(-c, 0)。
椭圆的直径是通过椭圆中心并且同时与椭圆上两个点相交的线段。
对于以坐标原点为中心的椭圆,直径的长度为2a。
4.椭圆的离心率椭圆的离心率是描述椭圆形状的重要指标。
离心率的取值范围为0到1,离心率为0时表示圆形,离心率为1时表示扁平的线段。
椭圆的离心率定义为离心焦距和长半径之比,即e = c/a。
5.椭圆的轨迹椭圆的轨迹是指通过一定规则的运动得到的点所形成的图形。
在天体力学中,行星绕太阳运动的轨迹就是椭圆。
椭圆的轨迹具有许多独特的性质,例如对称性、曲率等。
6.椭圆的应用椭圆在现实生活中有许多重要的应用。
例如,在通信中,为了提高信号传输的质量和距离,卫星轨道通常选择为椭圆轨道。
此外,椭圆也被广泛应用于地理测量、天体力学、光学设计等领域。
总结:椭圆作为几何图形中的重要一员,具有许多独特的概念和性质。
通过本文的介绍,我们了解到椭圆的定义、标准方程、焦点、直径、离心率、轨迹和应用。
对于几何学的学习和实际应用,理解和掌握椭圆的基本概念与性质至关重要。
人教版高中数学课件:8.2椭圆的几何性质3

(c,0)
B2(0,-b)
1.习题8.3 第2题(3) (4)(5)第3题
秦皇岛市职业技术学校 李天乐
一、椭圆的范围
x a
2 2
y b
2 2
1( a b 0 )
x a
2 2
1,
y b
2 2
1
即
x a和 y b
y
B2
A1
F1
O
B1
F2
A2 X
说明:椭圆位于矩形之中。
二、椭圆的对称性
x a
2 2
y b
2 2
1( a b 0 )
y
椭圆关于x轴对称; 椭圆关于y轴对称; 椭圆关于原点对称; 中心:椭圆的对称中心叫做椭圆的中心. o x
四、椭圆的离Βιβλιοθήκη 率离心率:椭圆的焦距与长轴长的比: e y a 叫做椭圆的离心率。 [1]离心率的取值范围: 因为 a > c > 0,所以 0 e 1 o [2]离心率对椭圆形状的影响: 1)e 越接近 1,c 就越接近 a,从而 b就越小,椭圆就 越扁 . 2)e 越接近 0,c 就越接近 0,从而 b就越大,椭圆 就 越圆 . 3)特例:e =0,则 a = b,则 c=0,两个焦点重合, 2 2 2 方程变为 x y a .
由题意,有 2c=8,c=4;2a=10,a=5.
x a
2 2
y b
2 2
1( a b 0 )
又
b2=a2-c2=25-16=9.
故所求方程为x2/25+y2/9=1.
(2)设焦点在y轴上,标准方程为
椭圆的几何性质一览表
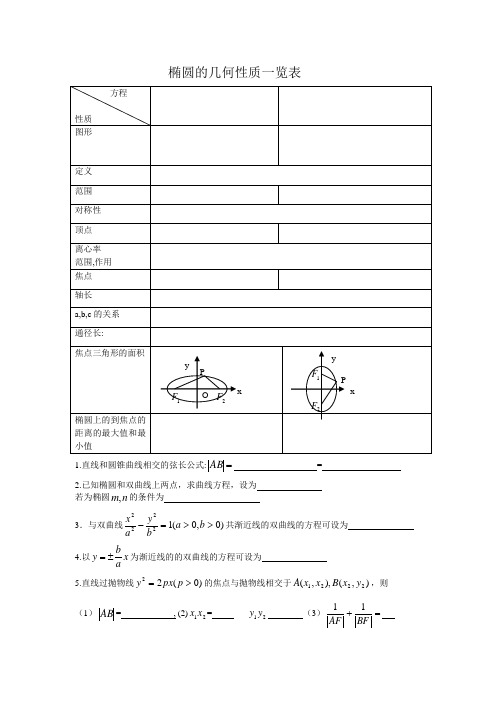
5.直线过抛物线 的焦点与抛物线相交于 ,则
(1) =,(2) = (3)
双曲线的几何性质一览表
方程
性质
图形
范围
对称性
顶点
离心率
对称性
焦点
轴长
的关系
通径长
焦点三角形的面积
渐进线方程
抛物线的几何性质一览表
方程
性质
图形
范围
对称性
顶点
离心率
对称性
焦点
准线方程
焦半径
焦半径的范围
椭圆的几何Leabharlann 质一览表方程性质图形
定义
范围
对称性
顶点
离心率
范围,作用
焦点
轴长
a,b,c的关系
通径长:
焦点三角形的面积
P
x
y
O
x
y
P
O
椭圆上的到焦点的距离的最大值和最小值
1.直线和圆锥曲线相交的弦长公式: =
2.已知椭圆和双曲线上两点,求曲线方程,设为
若为椭圆 的条件为
3.与双曲线 共渐近线的双曲线的方程可设为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x2 y2 1 练习2.无论k为何值,直线y=kx+2和曲线 9 4 交点情况满足( D )
6 6 k< 时没有交点 3 3
A.没有公共点
C.两个公共点
B.一个公共点
D.有公共点
x2 y2 1 , 直线 4 x 5 y 40 0 , 椭圆 例 2: 已知椭圆 25 9 上是否存在一点,到直线 l 的距离最小?最小距离是多少 ? y
椭圆的简单几何性质3
直线与椭圆的位置关系
种类:
相离(没有交点) 相切(一个交点)
相交(二个交点)
直线与椭圆的位置关系的判定
代数方法
Ax By C 0 2 由方程组 x y2 2 2 1 b a
mx 2 nx p 0(m 0)
△=n2 4mp
右焦点F ( 3,0).
y x 3 2 x 2 y 1 4
直线l方程为: y x 3. 消y得: 5x 8 3x 8 0
2
设A( x1, y1 ), B( x2 , y2 )
8 3 8 x1 x2 , x1 x2 5 5
AB 1 k x1 x2 1 k
o
x
.
知识点2:弦长公式
可推广到任意二次曲线
设直线与椭圆交于A(x1,y1),B(x2,y2)两点,直线P1P2的斜率为k.
同理可得
当k=0时,直线平行于x轴所以
当直线斜率不存在时,直线平行于 y 轴所
例3:已知斜率为1的直线L过椭圆 的右焦点,交椭圆于A,B两点,求弦AB之长.
解 :由椭圆方程知 : a2 4, b2 1, c2 3.
解:设直线m平行于l,
则l可写成: 4x 5 y k 0
4 x 5 y k 0 2 2 2 2 消去y,得25x 8kx k - 225 0 由方程组 x y 1 25 9 由 0,得64k 2 - 4 25 (k 2 - 225) 0
题型一:直线与椭圆的位置关系
例1:直线y=x+1与椭圆
x2 y 2 1 m 5
恒有公共点,
求m的取值范围。
变式练习:y=kx+1与椭圆 m的范围( )。 A、(0,1) B、(0,5 ) C、[ 1,5)∪(5,+ ∞ ) D、(1,+ ∞ )
x2 y2 1 恰有公共点,则 5 m
练习1.K为何值时,直线y=kx+2和曲线2x2+3y2=6有两 个公共点?有一个公共点?没有公共点?
2 2
8 ( x1 x2 ) 4 x1 x2 5
2
x y 例 4:已知点 F1 、F2 分别是椭圆 1 的左、右 2 1 焦点,过 F2 作倾斜角为 的直线,求 △F1 AB 的面积. 4 x2
解:∵椭圆
2
2
∴直线 AB 的方程为 y x 1 设 A( x1 , y1 ), B( x2 , y2 )
△ 0
方程组有两解 方程组有一解 方程组无解
两个交点 一个交点 无交点
相交 相切 相离
△=0 △ 0
知识点1.直线与椭圆的位置关系
1.位置关系:相交、相切、相离 2.判别方法(代数法) 联立直线与椭圆的方程 消元得到二元一次方程组 (1)△>0直线与椭圆相交有两个公共点; (2)△=0 直线与椭圆相切有且只有一个公共点; (3)△<0 直线与椭圆相离无公共点. 3.几何法 在平面直角坐标系中画出直线和椭圆,从而观察 直线与椭圆的位置关系。
y x 1 由 x2 消去 y 并化简整理得 2 y 1 2
2
2
y 2 1 的两个焦点坐标 F1 (1, 0), F2 (1, 0)
3x 4x 0
4 2 2 ∴ AB ( x1 x2 )2 ( y1 y2 )2 2( x1 x2 )2 2 = ( x x ) 4 x x 2 1 2 1 3
4 ∴ x1 x2 , x1 x2 0 3
0 ( 1) 1 2
∵点 F1 到直线 AB 的距离 d
∴ S F1 AB
= 2
1 1 4 4 4 d AB = 2 2= . 答: △F1 AB 的面积等于 2 2 3 3 3
解得k1 =25,k 2 =-25
o
x
由图可知k 25.
直线m为: 4 x 5 y 25 0
直线m与椭圆的交点到直线l的距离最近。 15 且d 41 42 52 41 40 25
y
思考:最大的距离是多少?
dmax 65 41 42 52 41 40 25
