浙教版八年级数学上册一学期10月份学习检测 .docx
浙教版八年级第一学期10月阶段性测试数学试卷(word版,含答案)
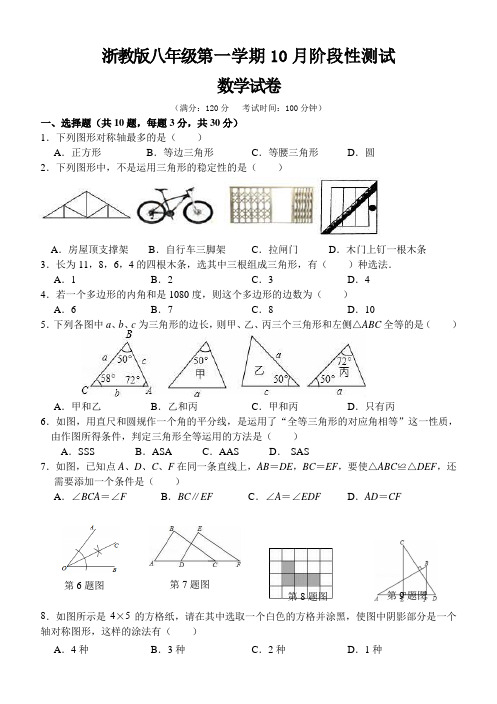
浙教版八年级第一学期10月阶段性测试数学试卷(满分:120分 考试时间:100分钟)一、选择题(共10题,每题3分,共30分) 1.下列图形对称轴最多的是( ) A .正方形 B .等边三角形 C .等腰三角形 D .圆2.下列图形中,不是运用三角形的稳定性的是( )A .房屋顶支撑架B .自行车三脚架C .拉闸门D .木门上钉一根木条 3.长为11,8,6,4的四根木条,选其中三根组成三角形,有( )种选法. A .1 B .2 C .3 D .4 4.若一个多边形的内角和是1080度,则这个多边形的边数为( ) A .6 B .7 C .8 D .10 5.下列各图中a 、b 、c 为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC 全等的是( )A .甲和乙B .乙和丙C .甲和丙D .只有丙6.如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( ) A .SSS B .ASA C .AAS D . SAS7.如图,已知点A 、D 、C 、F 在同一条直线上,AB =DE ,BC =EF ,要使△ABC ≌△DEF ,还需要添加一个条件是( ) A .∠BCA =∠F B .BC ∥EF C .∠A =∠EDF D .AD =CF8.如图所示是4×5的方格纸,请在其中选取一个白色的方格并涂黑,使图中阴影部分是一个轴对称图形,这样的涂法有( ) A .4种B .3种C .2种D .1种第6题第6题图 第7题图 第8题图 第9题图9.如图,AB ⊥CD ,且AB =CD .E 、F 是AD 上两点,CE ⊥AD ,BF ⊥AD .若CE =a ,BF =b ,EF =c ,则AD 的长为( )A .a +cB .b +cC .a ﹣b +cD .a +b ﹣c10.如图,Rt △ACB 中,∠ACB =90°,△ABC 的角平分线AD 、BE 相交于点P ,过P 作PF ⊥AD 交BC 的延长线于点F ,交AC 于点H ,则下列结论:①∠APB =135°;②BF =BA ;③PH =PD ;④连接CP ,CP 平分∠ACB ,其中正确的是( ) A .①②③ B .①②④ C .①③④D .①②③④二、填空题(本大题共8小题,每小题3分,共24分) 11.点P (-1,3)关于x 轴对称的点的坐标是.12.下图是平面镜里看到背向墙壁的电子钟示数,这时的实际时间应该是 ______ .13.在△ABC 中,若∠A =∠B =∠C ,则∠A = ,△ABC 是 三角形.14.如图,在ABC △中,40C ∠=︒,将ABC △沿直线l 折叠,点C 落在点D 的位置,则12∠-∠的度数是__________.15.如图,在Rt △ABC ,∠C=90°,AC=12,BC=6,一条线段PQ=AB ,P 、Q 两点分别在AC第12题图 21lCBAD和过点A 且垂直于AC 的射线AX 上运动,要使△ABC 和△QPA 全等,则AP= ______ .16.在△ABC 中,AD 是高,∠BAD =60°,∠CAD =20°,AE 平分∠BAC ,则∠EAD 的度数为.17.如图,已知OP 平分∠MON ,P A ⊥ON 于点A ,点Q 是射线OM 上的一个动点.若P A =2,则PQ 的最小值为 ,理论根据为 .18.如图所示,图①是边长为1的等边三角形纸板,周长记为C 1,沿图①的底边剪去一块边长为的等边三角形,得到图②,周长记为C 2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的),得图③④…,图n 的周长记为∁n ,若n ≥3,则∁n ﹣C n ﹣1= .第15题图第18题图三.解答题19.(8分)如图,在△ABC 中,DE 是边AB 的垂直平分线,交AB 于E 、交AC 于D ,连接BD .(1)若∠ABC =∠C ,∠A =40°,求∠DBC 的度数;(2)若AB =AC ,且△BCD 的周长为18cm ,△ABC 的周长为30cm ,求BE的长.20.(10分)已知一个等腰三角形的两边长a 、b 满足方程组. (1)求a 、b 的值;(2)求这个等腰三角形的周长.21.(10分)如图,在四边形ABCD 中,∠ABC =150°,∠BCD =30°,点M 在BC 上,AB =BM ,CM =CD ,点N 为AD 的中点,求证:BN ⊥CN 。
浙江省杭州市上学期数学10月月考试卷

八年级上学期数学10月月考试卷一、单项选择题1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是〔〕A. B. C. D.2.以下各组数分别是三根小木棒的长度,将它们首尾相连能摆成三角形的是〔〕A. 3cm,4cm,8cmB. 4cm,4cm,8cmC. 5cm,6cm,8cmD. 5cm,5cm,12cm3.如图,,那么的度数是〔〕A. B. C. D.4.对于命题“如果,那么〞,能说明它是假命题的反例是〔〕A. B.C. D.5.以下命题中,是真命题的是( )A. 成轴对称的两个图形是全等图形B. 面积相等的两个三角形全等C. 三角形的三条高线相交于三角形内一点D. 内错角相等6.如图,点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,依据“SSS〞还需要添加一个条件是( )A. AD=CDB. AD=CFC. BC∥EFD. DC=CF7.如图是尺规作图法作的平分线时的痕迹图,能判定的理由是〔〕A. B. C. D.8.如图,中,边的垂直平分线交于点,,,,那么的周长为〔〕A. 18B. 15C. 10D. 119.小王、小陈、小张当中有一人做了一件好事,另两人也都知道是谁做了这件事.老师在了解情况时,他们三人分别说了下面几句话:小陈:“我没做这件事.〞“小张也没做这件事.〞小王:“我没做这件事.〞“小陈也没做这件事.〞小张:“我没做这件事.〞“我也不知道谁做了这件事.〞他们每人都说了一句假话,一句真话,做好事的人是〔〕A. 小王B. 小陈C. 小张D. 不能确定10.如图,AC平分,于E,,那么以下结论① ;② ;③ ;④ .其中,正确结论的个数〔〕A. 1个B. 2个C. 3个D. 4个二、填空题11.命题“对顶角相等〞的逆命题是一个________命题〔填“真〞或“假〞〕.12.一个等腰三角形的两边长分别为3和6,那么等腰三角形的周长是________.13.如图,是△ABC的外角,假设,,那么________度.14.如图,AE是△ABC的边BC上的中线,假设AB=8cm,△ACE的周长比△AEB的周长多2cm,那么AC=________.15.如图,在中,是边上的高,是边上的高,且,交于点,假设,BD=8,,那么线段的长度为________.16.如图,在中,,分别作其内角与外角的平分线,且两条角平分线所在的直线交于点,那么________度;分别作与的平分线,且两条角平分线交于点,那么________度.三、解答题17.如图,在正方形网格上有一个△ABC.〔 1 〕画出△ABC关于直线l对称的图形;〔 2 〕在直线l上找一点P,使PB+PC的长最短.〔不写作法,保存作图痕迹〕18.如图,为的中线,延长,分别过点,作,.求证:.19.如图,在和中,,,.求证:.20.,的三边长分别为,,,且,满足,为方程的解,求的周长,并判断的形状.21.如图,在中,是边上的高线.〔1〕假设是边上的中线,,.求的长.〔2〕假设是的平分线,,,求的大小.22.在一次数学探究活动中:如图,在△ABC中,AB=5,AC=9,AD是BC边上的中线,求AD的取值范围.小明给出了一种方法,步骤如下:①过点C作一条与AB平行的线;②延长AD交这条平行线于点E;③通过证明得到AD=DE,AB=CE;④利用△ACE三边的数量关系得到AD的取值范围.根据这个方法,请你完成下面两个问题:〔1〕求证:AD=DE,AB=CE;〔2〕求AD的取值范围.23.如图,中,,分别平分和,,相交于点,.〔1〕求的度数;〔2〕判断,,之间的等量关系,并证明你的结论.答案解析局部一、单项选择题1.【解析】【解答】解:A、不是轴对称图形,故A选项不符合题意;B、不是轴对称图形,故B选项不符合题意;C、不是轴对称图形,故C选项不符合题意;D、是轴对称图形,故D选项符合题意.故答案为:D.【分析】如果一个图形沿着一条直线对折后两局部完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴,根据定义即可一一判断得出答案.2.【解析】【解答】解:A选项,3+4<8,不能构成三角形,故A错误;B选项,4+4=8,不能构成三角形,故B错误;C选项,5+6>8,能构成三角形,故C正确;D选项,5+5<12,不能构成三角形,故D错误;应选C.【分析】此题主要考查了三角形的三边关系:任意两边之和大于第三边. 较直接的方法是,判断两条较小的边之和大于第三边,便能构成三角形.3.【解析】【解答】解:∵△ABC≌A′B′C′,∴∠B=∠B′=51°,在△ABC中,∠C=180°−∠A−∠B=180°−56°−51°=73°.故答案为:D.【分析】根据全等三角形对应角相等求出∠B=∠B′,再根据三角形内角和定理列式进行计算即可得解. 4.【解析】【解答】解:A、满足且∠1=∠2,能说明原命题是假命题,本选项正确;B、,不满足,不能说明原命题是假命题,本选项错误;C、,满足但不满足∠1=∠2,不能说明原命题是假命题,本选项错误;D、,不满足,不能说明原命题是假命题,本选项错误.故答案为:A.【分析】要证明一个命题是假命题的反例,需要满足命题的条件,但又不满足命题的结论即可,即只要说明且∠1=∠2,即可,据此逐项判断即可.5.【解析】【解答】解:A、成轴对称的两个图形是全等形,此命题是真命题,故A符合题意;B、面积相等的两个三角形不一定全等,故B不符合题意;C、三角形的三条高线相交于三角形内一点是假命题,只有锐角三角形的三条高线交点在三角形内,故C 不符合题意;D、内错角相等时假命题,两直线平行时,内错角才相等,故D不符合题意;故答案为:A【分析】利用轴对称的性质,可对A作出判断;根据全等三角形的判定,可对B作出判断;三角形的三条高的交点可能在三角形内或三角形外或三角形上,可对C作出判断;两直线平行,内错角才相等,可对D 作出判断,即可得出答案。
最新浙教版八年级数学第一学期10月份阶段性检测及答案解析.docx

第一学期初二年级阶段性检测(10月)数学试题卷一.仔细选一选(本题有10个小题,每小题3分,共30分.)1.小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是()A、B、C、D、2.如右上图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是()A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°3.到△ABC的三个顶点距离相等的点是△ABC的( ).A.三条中线的交点B.三条角平分线的交点C.三条高的交点D.三条边的垂直平分线的交点4. 如图,锐角三角形ABC中,BC>AB>AC,小靖依下列方法作图:(1)作∠A的角平分线交BC于D点.(2)作AD的中垂线交AC于E点.(3)连接DE.根据他画的图形,判断下列关系何者正确?()A 、DE ⊥ACB 、DE ∥ABC 、CD=DED 、CD=BD5. △ABC 中, AC=5, 中线AD=7, 则AB 边的取值范围是( )A. 1<AB<29B. 4<AB<24C. 5<AB<19D. 9<AB<196.若不等式组⎩⎨⎧>-<+m x x x 148的解集是x>3,则m 的取值范围是( ) A 、m ≥3 B 、m=3 C 、m<3 D 、m ≤37.解不等式3211722x x -+≤的过程如下: ①去分母,得3x -2≤11x +7,②移项,得3x -11x ≤7+2,③合并同类项,得-8x ≤9,④系数化为1,得98x -≤. 其中造成错误的一步是( )A .①B .②C .③D .④8.某一个两位数,其个位数字比十位数字大2,已知这个两位数不小于20,不大于40,那么这个两位数是多少?为了解决这个问题,我们可设个位数字为x ,那么可列不等式( )A .20≤10(x -2)+x ≤40B .20<10(x -2)+x <40C .20≤x -2+x ≤40D .20≤10x+x -2≤409.关于x 的不等式x -b >0恰有两个负整数解,则b 的取值范围是( )A.-3<b <-2B.-3<b ≤-2C.-3≤b ≤-2D.-3≤b <-210.有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人。
浙江省八年级上学期数学10月月考试卷

浙江省八年级上学期数学10月月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)已知点P在第三象限,且到x轴的距离为3,到y轴的距离为5,则点P的坐标为()A . (3,5)B . (-5,3)C . (3,-5)D . (-5,-3)2. (2分) (2017七下·宁江期末) 如图,建立适当的直角坐标系后,正方形网格上的点M,N坐标分别为(0,2),(1,1),则点P的坐标为()A . (﹣1,2)B . (2,﹣1)C . (﹣2,1)D . (1,﹣2)3. (2分) (2019七下·许昌期末) 如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动一个单位,依次得到点P1(0,1);P2(1,1);P3(1,0);P4(1,﹣1);P5(2,﹣1);P6(2,0)……,则点P2019的坐标是()A . (672,0)B . (673, 1)C . (672,﹣1)D . (673,0)4. (2分)函数的自变量x的取值范围是()A .B .C .D . 且5. (2分) (2021八上·金台期末) 在平面直角坐标系中,一次函数的图象如图所示,观察图象,可判断一次函数的图象不经过()A . 第一象限B . 第二象限C . 第三象限D . 第四象限6. (2分)下列函数解析式中,不是正比例函数的是()A . xy=﹣2B . y+8x=0C . 3x=4yD .7. (2分) (2020七下·富县期末) 已知点在第一象限或第三象限,则的取值范围是()A .B .C .D . 或8. (2分) (2021八下·咸宁期末) 如图,函数和的图象相交于点,则不等式组的整数解有()个.A . 2B . 3C . 4D . 59. (2分) (2016九上·磴口期中) 已知反比例函数y= 的图象如图,则函数y=kx﹣2的图象是图中的()A .B .C .D .10. (2分) (2019八上·昌平月考) 一次函数y=-2x+m的图象经过点P(-2,3),且与x轴.y轴分别交于点A ,B ,则△AOB的面积是()A .B .C . 2D . 1二、填空题 (共5题;共10分)11. (1分)如图,某雷达探测器显示在A,B,C处有目标出现,其中,目标A的位置为(2,90°),目标B 的位置为(4,210°),则目标C的位置为12. (5分) (2019七下·海淀期中) 将点A(﹣1,4)向上平移三个单位,得到点A′,则A′的坐标为.13. (2分) (2021八下·钦州期末) 一次函数y=x﹣5的图象与y轴的交点坐标为 .14. (1分) (2016七上·长兴期末) 如图,天平左边放着3个乒乓球,右边放5.4g的砝码和1个乒乓球,天平恰好平衡.如果设1个乒乓球的质量为x(g),请你列出一个含有未知数x的方程15. (1分) (2020八上·温州期末) 已知一次函数y=(k-4)x+2,若y随x的增大而增大,则k的值可以是(写出一个答案即可)三、解答题 (共9题;共92分)16. (5分) (2020八上·淮北期末) 已知一次函数的自变量与函数之间的部分对应值如下表:123…1-1-3…求这个一次函数的解析式.17. (10分) (2015七下·泗阳期中) 如图,在边长为1个单位长度的小正方形组成的网格中(1)把△ABC平移至A′的位置,使点A与A'对应,得到△A′B′C′;(2)线段AA′与BB′的关系是:;(3)求△ABC的面积.18. (5分)将等腰直角△ABC斜放在平面直角坐标系中,使直角顶点C与点(1,0)重合,点A的坐标为(﹣2,1).(1)求△ABC的面积S;(2)求直线AB与y轴的交点坐标.19. (5分)抛物线y=ax2+2x+c与其对称轴相交于点A(1,4),与x轴正半轴交于点B.(1)求这条抛物线的函数关系式;(2)在抛物线对称轴上确定一点C,使△ABC是等腰三角形,求出所有点C的坐标.20. (7分)(2019·渝中模拟) 小明根据学习函数的经验,对函数y=x+ 的图象与性质进行了探究.下面是小明的探究过程,请补充完整:(1)函数y=x+ 的自变量x的取值范围是.(2)下表列出了y与x的几组对应值,请写出m,n的值:m=,n=;x…﹣3﹣2﹣1﹣﹣1234…y…﹣﹣﹣2﹣﹣m2n…(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;(4)结合函数的图象,请完成:①当y=﹣时,x=.②写出该函数的一条性质.③若方程x+ =t有两个不相等的实数根,则t的取值范围是.21. (15分) (2019八下·闽侯期中) 如图,已知点A(﹣3,0),点B(0,m),直线l:x=1.直线AB与直线l交于点C ,连结OC .(1)△OBC的面积与△O AC的面积比是否是定值?如果是,请求出面积比;如果不是,请说明理由.(2)若m=2,点T在直线l上且TA=TB ,求点T的坐标.22. (10分) (2020九上·银川期末) 某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;(2)求销售单价为多少元时,该文具每天的销售利润最大;(3)商场的营销部结合上述情况,提出了A、B两种营销方案方案A:该文具的销售单价高于进价且不超过30元;方案B:每天销售量不少于10件,且每件文具的利润至少为25元请比较哪种方案的最大利润更高,并说明理由23. (15分) (2020八下·邹平期末) 某果园计划新购进两个品种的果树苗,若计划购进这两种果树苗共棵,其中A种苗的单价为元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.(1)当时,求y与x的函数关系式;(2)当时,求y与x的函数关系式;(3)若在购买计划中,B种苗的数量不少于棵但不超过棵,请设计购买方案,使总费用最低,并求出最低费用.24. (20分)(2018·衡阳) 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量(件与销售价(元/件)之间的函数关系如图所示.(1)求与之间的函数关系式,并写出自变量的取值范围;(2)求每天的销售利润W(元与销售价(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?参考答案一、单选题 (共10题;共20分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:二、填空题 (共5题;共10分)答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:三、解答题 (共9题;共92分)答案:16-1、考点:解析:答案:17-1、答案:17-2、答案:17-3、考点:解析:考点:解析:答案:19-1、考点:解析:答案:20-1、答案:20-2、答案:20-3、答案:20-4、考点:解析:答案:21-1、答案:21-2、考点:解析:答案:22-1、答案:22-2、答案:22-3、考点:解析:答案:23-1、答案:23-2、答案:23-3、考点:解析:答案:24-1、答案:24-2、考点:解析:。
浙教版八年级数学上册10月月考试卷含答案

,
分三种情况:
①当 时,如图 所示:
,
,
, ,
,
,
,
,
.
②当 时,如图 所示:
则 ,
.
③当 时,如图 所示:
过 点作 于点 ,
,
,
,
,
.
由上可知,当运动时间为 秒或 秒或 秒时, 为等腰三角形.
依题意得
解得
答:A,B 两种型号电风扇的销售单价分别为 元、 元.
(2) 设采购 A 种型号电风扇 台,则采购 B 种型号电风扇 台.
依题意得
解得
答:超市最多采购 A 种型号电风扇 台时,采购金额不多于 元.
(3) 依题意有
解得
此时 .
所以在(2)的条件下超市不能实现利润 元的目标.
21. (1) ;
A. ①②④B. ①②③C. ②③D. ①③
10. 已知:四边形 是正方形,在平面内找一点 满足 , , , 均为等腰三角形,这样的点 有
A. 个B. 个C. 个D. 个
二、填空题(共6小题;共29分)
11. 已知图中的两个三角形全等,则 的度数是.
12. 等腰三角形的周长为 ,其一边长为 ,那么它的底边长度为.
A. B. C. D.
7. 如图,把 纸片的 沿 折叠,点 落在四边形 外,则 , 与 的关系是
A. B. C. D.
8. 如图, 为 内一点, 平分 , , .若 , ,则 的长为
A. B. C. D.
9. 如图, 中, , 是斜边 上的高,角平分线 交 于 , 于 ,下列结论:① ;② ;③ ;④ .其中正确的结论为
A. B. C. D.
5. 一块三角形玻璃被小红碰碎成四块,如图,小红只带其中的两块去玻璃店,买了一块和以前一样的玻璃,你认为她带了哪两块去玻璃店
浙教版八年级数学上册10月份模考练习卷(解答卷)

浙教版八年级数学上册10月份模考练习卷(解答卷)一、选择题(本大题共有10个小题,每小题3分,共30分)1.下列地方银行的标志中,既不是轴对称图形,也不是中心对称图形的是( )A .B .C .D .【答案】D2.下列每组数分别是三根木棒的长度,能用它们摆成三角形的是( )A .3,4,8B .4,4,9C .5,7,12D .7,8,9【答案】D3. 如图,12∠=∠,下列条件中不能使...ABD ACD ∆≅∆的是( )A .AB AC = B .B C ∠=∠ C .ADB ADC ∠=∠D .DB DC =【答案】D4.下列命题中的假命题是( )A .互余两角的和是90°B .全等三角形的面积相等C .相等的角是对顶角D .两直线平行,同旁内角互补【答案】C5. 将一副三角板按如图方式重叠,则1∠的度数为( )A .45°B .60°C .75°D .105°【答案】C6. 如图,小颖按下面方法用尺规作角平分线:在已知的AOB ∠的两边上,分别截取,OC OD ,使OC OD =.再分别以点C ,D 为圆心、 大于12CD 的长为半径作弧,两弧在AOB ∠内交于点P , 作射线OP ,则射线OP 就是AOB ∠的平分线.其作图原理是:OCP ODP ≌,这样就有AOP BOP ∠=∠,那么判定这两个三角形全等的依据是( )A .SASB .ASAC .AASD .SSS【答案】D7. 如图,ABC 中,,BF CF 分别平分ABC ∠和ACB ∠,过点F 作//DE BC 交AB 于点D ,交AC 于点E ,那么下列结论:①DFB DBF ∠=∠; ②ECF EFC ∠=∠;③ADE 的周长等于BFC △的周长; ④1902BFC A ∠=°+∠.其中正确的有( )A .①②B .①②③C .①②④D .②③④【答案】C8 .如图,EB 交AC 于点M ,交CF 于点D ,AB 交FC 于点N ,90E F ∠=∠=°,B C ∠=∠,AE AF =.下列结论:①12∠=∠;②CD BD =;③AFN BDN ≌;④AM AN =.其中所以正确结论的序号是( )A .①②③B .①②④C .①③④D .②③④【答案】B9. 如图,有一张直角三角形的纸片,两直角边AC =6cm ,BC =8cm ,现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上且与AE 重合,则BD 的长为( )A.5cm B.4cm C.3cm D.2cm【答案】A10 . 如图,在△ABC与△AEF中,AB=AE,BC=EF,∠ABC=∠AEF,∠EAB=40°,AB交EF于点D,连接EB.下列结论:①∠FAC=40°;②AF=AC;③∠EBC=110°;④AD=AC;⑤∠EFB=40°,其中正确的个数为()个.A.1 B.2 C.3 D.4【答案】C二、填空题(本大题共有8个小题,每小题3分,共24分)11.如图,分别以直角三角形各边为一边向三角形外部作正方形,其中两个正方形的面积分别为34和25,则正方形A的面积是.【答案】9.12.如图,∠B=60°,∠ACD=100°,那么∠A=________【答案】 40°13.如图,ABC DEF ≌△△,若5BC =,3EC =,则CF 的长为 .【答案】214.如图,在△ABC 中,AB 的垂直平分线l 交BC 于点D ,BC=7,AC=4,则△ACD 的周长为 .【答案】1115 . 如图,AB AC =,AD AE =,BAC DAE ∠=∠,125∠=°,230∠=°,【答案】55°16 .在直角ABC 中,∠C=90°,AD 平分∠BAC 交BC 于点D ,若CD=4,则点D 到斜边AB 的距离为 .【答案】417.如图,△ABC 是等边三角形,点B 、C 、D 、E 在同一直线上,且CG =CD ,DF =DE ,则∠E = 度.【答案】1518.如图,在ABC 中,BAC ∠为钝角,边AB ,AC 的垂直平分线分别交BC 于点D ,E , 连接AD ,AE ,若45B C ∠+∠=°,12BD =,5CE =,则DE = .【答案】13三、解答题(本大题共有6个小题,共46分)19.如图,AC 和BD 相交于点O ,OA =OC ,DC ∥AB .求证DC =AB .证明:∵DC ∥AB ,∴∠D =∠B ,在△COD 与△AOB 中,D B DOC BOA OC OA ∠=∠ ∠=∠ =, ∴△COD ≌△AOB (AAS ), ∴DC =AB .20.如图,在长度为1个单位的小正方形组成的网格中,点A 、B 、C 在小正方形的顶点上.(1)在图中画出与ABC 关于直线l 成轴对称的AB C ′′△;(2)ABC 的面积为___________.解:(1)ABC 关于直线l 成轴对称的AB C ′′△如下图,;(2)ABC 的面积为:1115241114232222ABC S =×−××−××−××= . 故答案为:52.21.如图,在四边形ABCD 中,3AB =,4BC =,12CD =,13AD =,∠B=90°,求四边形ABCD 的面积.解:90B ∠=° ,3AB =,4BC =,5AC ∴,在ACD 中,22225144169AC CD AD +=+== ,ACD ∴是直角三角形,且=90ACD ∠°,ABC ACD ABCD S S S ∴=+ 四边形1122AB BC AC CD =⋅+⋅ 11630=+36=.22 .麒麟某数学兴趣小组的同学用数学知识测一池塘的长度,他们所绘如图,点B ,F ,C (点F ,C 之间不能直接测量,为池塘的长度),点A ,D 在l 的异侧, 且AB DE ∥,A D ∠=∠,测得AB DE =.(1) 求证:ABC DEF ≌△△;(2)若100m 30m BE BF ==,,求池塘FC 的长. 解:(1)证明:∵AB DE ∥,∴ABC DEF ∠=∠, 在ABC 与DEF 中,ABC DEF AB DEA D ∠=∠ = ∠=∠∴(ASA)ABC DEF ≌ ;(2)解:∵ABC DEF ≌△△∴BF FC EC FC +=+,∴BF EC =,∵100m30m BE BF ==, ∴100303040FC =−−=m .答:FC 的长是40m23.已知,如图,在ABC 中,AD ,AE 分别是ABC 的高和角平分线,(1)若∠B=30°,∠C=50°.求∠DAE 的度数;(2)试写出∠DAE 与∠C ,∠B 有何关系?并证明你的结论. 解:(1)∵∠B=30°,∠C=50°,∴∠BAC=180°-∠B-∠C=100°,又∵AE 是△ABC 的角平分线,∴∠BAE=12∠BAC=50°,∵AD 是△ABC 的高,∴∠BAD=90°-∠B=90°-30°=60°,则∠DAE=∠BAD-∠BAE=10°;(2)∠DAE=12(∠C-∠B),理由如下:∵AD是△ABC的高,∴∠ADC=90°,∴∠DAC=180°-∠ADC-∠C=90°-∠C,∵AE是△ABC的角平分线,∴∠EAC=12∠BAC,∵∠BAC=180°-∠B-∠C∴∠DAE=∠EAC-∠DAC,=12∠BAC-(90°-∠C),=12(180°-∠B-∠C)-90°+∠C,=90°-12∠B-12∠C-90°+∠C,=12(∠C-∠B).24.如图, ABC是等腰直角三角形,∠BCA=90°,AC=BC,AD⊥CD,BE⊥CD,连接BD.(1)求证:AD=CE;(2)BE平分∠DBC,①试判断 DBC的形状,并给出证明的过程;解:(1)证明:∵AD ⊥CD ,BE ⊥CD , ∴∠ADC =∠BEC =90°,∵∠ACB =90°,∴∠ACD +∠BCE =90°,∠ACD +∠CAD =90°, ∴∠CAD =∠BCE ,在△ACD 和△CBE 中,ADC BEC CAD BCE AC BC ∠=∠ ∠=∠ =, ∴△ACD ≌△CBE (AAS ).∴AD =CE(2)①解:△DBC 为等腰三角形,理由如下: ∵BE ⊥CD ,∴∠BEC =∠BED =90°,∵∠EBC =∠EBD ,∠EBC +∠BCE =90°,∠EBD +∠BDC =90°, ∴∠BCD =∠BDC ,∴△DBC 为等腰三角形; ②∵△ACD ≌△CBE , ∴AD =EC =4,EB =CD =8,∴AC =BC =∴S △ADB =S △ADC +S △BDC ﹣S △ACB =12×4×8+12×8×8﹣128. 故答案为:8.。
浙教版八年级数学上册一学期10月份学习检测 .docx

朝晖初中 2015学年第一学期10月份八年级学习检测数学试题卷 分值120分 时间90分钟2015.10.10一、仔细选一选(本题有10个小题,每小题3分,共30分) 1.如果a 与-3互为相反数,那么a 等于( ).(A )3 (B )-3 (C )31 (D )31- 2.如图,已知△ABC ≌△DAE ,BC =2,DE =5,则CE 的长为( )A.2B.2.5C.3D.3.5 3. 下列命题中,正确的是( ) A . 同角的余角相等 B . 两直线平行,同旁内角相等 C . 三角形的外角一定大于它的任一内角 D . 相等的角是对顶角 4. 一个三角形三个内角的度数之比为2∶3∶7,这个三角形一定是( ) A .直角三角形 B .有两个角相等的三角形 C .锐角三角形 D .钝角三角形 5. 如图,在ABC △与DEF △中,已有条件AB DE =,还需添加两个条件才能使ABC DEF △≌△,不能添加的一组条件是( ) A .B E ∠=∠,BC EF = B .BC EF =,AC DF = C .A D ∠=∠,B E ∠=∠ D .A D ∠=∠,BC EF = 6. 如图,在△ABC 中,AB=a,AC=b,BC 边上的垂直平分线DE 交BC 、BA 分别于点D 、E ,则△AEC 的周长等于 A. a+b B. a-b C. 2a+b D. a+2b7. 甲、乙两人连续7年调查某县养鸡业的情况,提供了两方面的 信息图(如图).甲调查表明:养鸡场的平均产鸡数从第1年的1万只上升到第7年的2.8万只;乙调查表明:养鸡场的个数由第1年的46个减少到第 7年的22个.现给出下列四个判断:①该县第2年养鸡场产鸡的数量为1.3万只;②该县 第2年养鸡场产鸡的数量低于第1年养鸡场产鸡的数量;③该县这7年养鸡场产鸡的数 量逐年增长;④这7年中,第5年 该县养鸡场出产鸡的数量最多.根据 甲、乙两人提供的信息,可知其中 正确的判断有( )A.3个B.2个C.1个D.0个 8.若(+)•w=1,则w= ( ) A . a +2B . ﹣a+2C . a ﹣2D . ﹣a ﹣29. 若∠α的两边与∠β的两边分别平行,且210,x α∠=+ 320x β∠=-,则∠α的度数为: A)70OB)86OC)70O或86OD)30O或38O10. 如图,在四边形ABCD 中,对角线AC 平分∠BAD ,AB>AD ,下列结论中正确的是: A .AB -AD>CB -CD B .AB -AD =CB —CD C .AB —AD<CB —CDD .AB -AD 与CB —CD 的大小关系不确定.二、认真填一填(本题共6个小题,每小题4分,共24分)11.2012年末统计,杭州市常住人口是880.2万人,用科学记数法表示为 人. 12. 把代数式244ax ax a -+分解因式得 。
浙教版八年级数学上册一学期初二十月份质量检测试卷 .docx

2016年第一学期初二数学十月份质量检测试卷一、选择题1、下列各组长度的线段能构成三角形的是( )A 、2.5cm 4.9cm 2.3cmB 、4.5cm 8.1cm 3.6cmC 、8cm 2cm 8cmD 、5cm 12cm 3cm 2、下列各图中,正确画出AC 边上的高的是( )A B C D3、在下列条件中①∠A =∠C-∠B ,②∠A ∶∠B ∶∠C=1∶1∶2,③∠A=90°-∠B ,④∠A=∠B=21∠C ,○5C B A ∠=∠=∠3121中,能确定△ABC 是直角三角形的条件有 ( )A 、2个;B 、3个;C 、4个;D 、5个4、如图,工人师傅砌门时,常用木条EF 固定长方形门框ABCD ,使其不变形,这样做的根据是( )A 、两点之间的线段最短;B 、三角形具有稳定性;C 、长方形是轴对称图形;D 、长方形的四个角都是直角; 5、下列语句是命题的是( ) A .作直线AB 的垂线 B .在线段AB 上取点C C .同旁内角互补D .垂线段最短吗?6、下列说法中:①三边对应相等的两个三角形全等;②三角对应相等的两个三角形全等;③两边和它们的夹角对应相等的两个三角形全等;④两角及其中一角的对边对应相等的两个三角形全等;⑤两边及其中一边的对角对应相等的两个三角形全等;不正确的是( )A 、 ①②B 、 ②④C 、 ④⑤D 、②⑤第7题图 第8题图 第9题图7、如图,三条直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A. 一处B. 两处C. 三处D. 四处8、工人师傅常用角尺平分一个任意角.作法如下:如图所示,∠AOB 是一个任意角,在边OA ,OB 上分别取OM=ON ,移动角尺,使角尺两边相同的刻度分别与M ,N 重合,过角尺顶点C 的射线OC 即是∠AOB 的平分线.这种作法的道理是( )A .SSAB .SSSC .SASD .ASA9、如图所示,在△ABC 中,已知点D ,E ,F 分别为边BC ,AD ,CE 的中点,且S △ABC =4cm 2,则S 阴影等于( ) A .1cm 2B .2cm 2C . cm 2D . cm 210、如图,在△ABC 中,∠C=90°,∠B=30°,以点A 为圆心,任意长为半径画弧分别交AB ,AC 于点M 和N ,再分别以点M ,N 为圆心画弧,两弧交于点P ,连结AP 并延长交BC 于点D ,则下列说法中正确的个数是( )①AD 是∠BAC 的平分线 ②∠ADC=60° ③∠BAD=∠B④点D 到直线AB 的距离等于CD 的长度.第10题图 第12题图 第14题图 A .1 B .2 C .3 D .4二、填空题11、 命题“同角的余角相等”改写成如果 ,那么 . 12、如图,∠A =50°,∠ABO =28°,∠ACO =32°,则∠BDC = ,∠BOC = .第15题图 第16题图 13、已知三角形的三边长分别是3、x 、9,则化简135-+-x x =14、如图,△ABC 的两边AB 和AC 的垂直平分线分别交BC 于D 、E ,若边BC 长为5cm ,则△ADE 的周长为__________cm .15、如图,点P 是∠BAC 的平分线上一点,PB ⊥AB 于B ,且PB=5cm ,AC=12,则△APC 的面积是________cm 216、如图所示,点B 、C 、E 在同一条直线上,AC=BC,CD=CE ,∠ACB=∠DCE=60°则下列结论①△ACE ≌△BCD ②CG=CF ③.若连接GF ,则GF ∥BE ④△ADB ≌△CEA 一定成立的有 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
朝晖初中 2015学年第一学期10月份八年级学习检测
数学试题卷 分值120分 时间90分钟
2015.10.10
一、仔细选一选(本题有10个小题,每小题3分,共30分)
1.如果a 与-3互为相反数,那么a 等于( ).
(A )3 (B )-3 (C )
31 (D )3
1
- 2.如图,已知△ABC ≌△DAE ,BC =2,DE =5,则CE 的长为( )
A.2
B.2.5
C.3
D.3.5 3. 下列命题中,正确的是( ) A . 同角的余角相等 B . 两直线平行,同旁内角相等 C . 三角形的外角一定大于它的任一内角 D . 相等的角是对顶角 4. 一个三角形三个内角的度数之比为2∶3∶7,这个三角形一定是( ) A .直角三角形 B .有两个角相等的三角形 C .锐角三角形 D .钝角三角形 5. 如图,在ABC △与DEF △中,已有条件AB DE =,还需添加两个条件才能使ABC DEF △≌△,不能添加的一组条件是( ) A .B E ∠=∠,BC EF = B .BC EF =,AC DF = C .A D ∠=∠,B E ∠=∠ D .A D ∠=∠,BC EF = 6. 如图,在△ABC 中,AB=a,AC=b,BC 边上的垂直平分线DE 交BC 、
BA 分别于点D 、E ,则△AEC 的周长等于 A. a+b B. a-b C. 2a+b D. a+2b
7. 甲、乙两人连续7年调查某县养鸡业的情况,提供了两方面的 信息图(如图).甲调查表明:养鸡场的平均产鸡数从第1年的
1万只上升到第7年的2.8万只;乙调查表明:养鸡场的个数由第1年的46个减少到第 7年的22个.现给出下列四个判断:①该县第2年养鸡场产鸡的数量为1.3万只;②该县 第2年养鸡场产鸡的数量低于第1年养鸡场产鸡的数量;③该县这7年养鸡场产鸡的数 量逐年增长;④这7年中,第5年 该县养鸡场出产鸡的数量最多.根据
甲、乙两人提供的信息,可知其中 正确的判断有( )
A.3个
B.2个
C.1个
D.0个 8.若(
+
)•w=1,
则w= ( )
A . a +2
B . ﹣a+2
C . a ﹣2
D . ﹣a ﹣2
9. 若∠α的两边与∠β的两边分别平行,且210,x α∠=+ 320x β∠=-,则∠α的度数为: A)70O
B)86O
C)70O
或86O
D)30O
或38O
10. 如图,在四边形ABCD 中,对角线AC 平分∠BAD ,AB>AD ,下列结论中正确的是: A .AB -AD>CB -CD
B .AB -AD =CB —CD
C .AB —AD<CB —CD
D .AB -AD 与CB —CD 的大小关系不确定.
二、认真填一填(本题共6个小题,每小题4分,共24分)
11.2012年末统计,杭州市常住人口是880.2万人,用科学记数法表示为 人. 12. 把代数式244ax ax a -+分解因式得 。
13. 三角形一边上的高与另两边的夹角分别为62°和28°,则这边所对的角的度数为 。
14. 观察下列给出的方程, x 3+x 2-3x +4=0,x 3+x -1=0,x 3-2x 2+3=x , y 3+2y 2-5y -1=0.找出它们的共同特征后,试给出这种方程的名称 ,并作出定义 . 15. 考查下列命题:(1)全等三角形的对应边上的中线、高、角平分线对应相等;(2)两边和其中一边上的中线对应相等的两个三角形全等;(3)两角和其中一角的角平分线对应相等的两个三角形全等;(4)两边和第三边上的高对应相等的两个三角形全等.其中正确的命题是(填序号) 。
16. .“三角形的两条边长分别是3cm 和4cm ,一个内角为40°”,那么满足这一条件,且彼此不全等的三角形共有 个.
三、全面答一答(本题共7小题,共66分)解答应写出文字说明,证明过程或演算步骤,如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.
17.(6分)设实数x 、y 满足方程组,求x+y 的值。
18. (8分)若代数式(x 2
﹣y 2
)(4x 2
﹣y 2
)+3x 2
(4x 2
﹣y 2
)能化简为y 4
,且0≠x 。
求x
y 的值。
19.(8分)如图,AD 是△ABC 的边BC 上的中线,AB=BC ,且AD 把△ABC 的周长分成3和4的两部分,求AC 边的长.
20.(10分)把一条12个单位长度的线段分成三条线段,其中一条线段成为4个单位长度,另两条线段长都是单位长度的整数倍.
(1)若不同分段得到的三条线段能组成三角形且每两边都不相等,用直尺和圆规作此三
角形(用给定的单位长度,不写作法,保留作图痕迹); (2)用直尺和圆规作出此三角形最大边上的高。
21.(10分)平面上有△ACD 与△BCE ,其中AD 与BE 相交于P 点,若AC =BC ,CD =CE ,∠ACB=∠ECD 。
(1)求证:AD=BE ;
(2)∠ACE =55︒,∠BCD =155︒,求∠BPD 的度数。
22.(12分)(1)如图,在△ABC 中,BD 是角平分线,BD 交AC 于点D ,已知∠ABC =∠C = ∠BDC . 求∠A 和∠C 的度数.
(2)天津市奥林匹克中心体育场——“水滴”位于天津市西南部的奥 林匹克中心内,某校九年级学生由距“水滴”10千米的学校出发前往 参观,一部分同学骑自行车先走,过了20分钟后,其余同学乘汽车
D
C B A
出发,结果他们同时到达.已知汽车的速度是骑车同学速度的2倍,
求骑车同学的速度.
(3)解了以上两题后,你发现以上两小题有什么共同点?请简单地
写出.
23.(12分)如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB。
(1)求∠AOC的度数;
(2)求证:AC=AE+CD.
(3)图中还有相等的线段吗?请找出来(不用说明理由)。
朝晖初中2015学年第一学期10月份八年级学习检测
数学答题卷
一、仔细选一选(本题有10个小题,每小题3分,共30分)
1 2 3 4 5 6 7 8 9 10
二、认真填一填(本题共6个小题,每小题4分,共24分)
11. ; 12. ; 13. ;
14. , ;
15. ; 16. 。
三、全面答一答(本题共7小题,共66分)解答应写出文字说明,证明过程或演算步骤,如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.
17.(6分)设实数x 、y 满足方程组,求x+y 的和的立方根。
18. (8分)若代数式(x 2
﹣y 2
)(4x 2
﹣y 2
)+3x 2
(4x 2
﹣y 2
)能化简为y 4
,且0 x 。
求x
y 的值。
19.(8分)
D
C
B
A
20.(10分)把一条12个单位长度的线段分成三条线段,其中一条线段成为4个单位长度,另两条线段长都是单位长度的整数倍.
(1)若不同分段得到的三条线段能组成三角形且每两边都不相等,用直尺和圆规作此三角形(用给定的单位长度,不写作法,保留作图痕迹);
(2)用直尺和圆规作出此三角形最大边上的高。
21.(10分)
(1)
(2)
22.(12分)
(1)
(2)
(3)23.(12分)
(1)
(2)
(3)
朝晖初中2015学年第一学期10月份八年级学习检测
数学参考答案
一、仔细选一选(本题有10个小题,每小题3分,共30分)
1 2 3 4 5 6 7 8 9 10
A C A D D A
B D
C A
二、认真填一填(本题共6个小题,每小题4分,共24分)
11. 8.802×106 ; 12. a(x-2)2 ; 13. 90O 或34O
;
14. 一元三次方程 , 含有一个未知数且未知数的最高次数是三次的整式方程 ;
15. (1)(2)(3) ; 16. 4 。
三、全面答一答(本题共7小题,共66分)解答应写出文字说明,证明过程或演算步骤,如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以. 17.(6分)
解得:x=9,y=-1(4分),则x+y 的和的立方根为2(2分) 18. (8分)
解:化简得:16x 4-8x 2y 2+y 4(4分),由16x 4-8x 2y 2+y 4= y 4,得16x 4=8x 2y 2.(1分)由0≠x ,
得222=x y (1分)则x
y
=2±(2分) 19.(8分)
解:AC=3或5/3.(每个答案4分)具体过程酌情给分. 20.(10分)
解:三边为3,4,5(2分),画出三角形(4分),画出高(4分). 21.(10分)
解:(1)用边角边证明全等得4分,得结论得1分.
(2) ∠BPD 的度数为130度(5分,具体小分自己组长定) 22.(12分)
解: (1)∠A 和∠C 的度数分别是36和72度.(4分) (2)每小时15千米(4分) (3)都用了方程思想(4分) 23.(12分)
(1)∠AOC 的度数是120度(4分); (2)求证:AC=AE+CD(6分).
(3)OE=OD(2分)。
初中数学试卷
鼎尚图文**整理制作。
