点线面之间的位置关系
空间点、线、面之间的位置关系

空间点、线、面之间的位置关系1.线与线的位置关系:平行、相交、异面(特别注意一下:垂直只是相交与异面当中的特殊情况,我们说相交有相交垂直,异面有异面垂直)2.线与面的位置关系:线在面内(选择题时一定要考虑)、线面平行、线面相交3.如何确定一个平面?方法(1)三个不共线的点可以确定一个平面方法(2)两条相交线可以确定一个平面方法(3)两条平行线可以确定一个平面4.如何证明三点共线?具体的做法:就是把其中两点确定的直线作为两个面的交线,证明剩下这一点是这两个面的交点,那么交点必在交线上,则三点共线。
5.如何证明线线平行?方法(1)利用三角形或梯形的中位线方法(2)利用平行四边形方法(3)利用线段对应成比例(通常题目中会出现三等份点或四等份点)方法(4)垂直于同一个面的两条直线互相平行方法(5)借助一个性质:两个面相交,其中一个面内的一条直线平行于另一个面,则这条线平行于两个面的交线(利用这个性质来证明在以往的高考中出现过若干次,同学们需要注意一下)6.如何证明线面平行?方法(1)只需证明这条直线与平面内的一条直线平行即可,简称线线平行推出线面平行。
方法(2)只需把这条直线放入一个合适的平面内,然后证明这个平面与已知平面平行即可,简称面面平行推出线面平行。
特别注意:直线平行于平面,可以得出直线与平面内无数条直线平行,但得不出与平面内任意一条直线平行。
7.如何证明面面平行?只需证明其中一个面内的两条相交线分别平行于另一个面即可。
8.如何证明线面垂直?只需证明这条直线分别与平面内的两条相交线互相垂直即可。
特别注意:直线垂直于平面,可以得出直线与平面内任意一条直线都垂直。
9.如何证明面面垂直?只需证明其中一个面内的一条直线垂直与另一个面即可。
特别注意:面面垂直,既得不出两个面内的任意两条直线互相垂直,也得不出其中一个面内的任意一条直线都垂直于另一个面。
10.异面直线的夹角范围是多少?如何求出异面直线的夹角?夹角范围是:0°~ 90°在求异面直线的夹角时,要把两条异面直线平移使它们出现交点,有时只需平移一条,有时两条都需要平移,这个过程中用得比较多的是中位线,当平移后两条直线出现交点时,复杂些的在三角形中利用余弦定理来求。
点线面间的位置关系知识点总结(含题)(

点线面间的位置关系知识点总结一、三个公理公理1如果一条直线上的两点在一个平面内,那么_________________________________________公理2:过________________________ 的三个点,有且只有一个平面公理3:如果两个不重合的平面有一个公共点,那么它们有且只有_____________________________二、空间两条直线间的位置关系分类为:______________ , ______________ ,_______________ ;其中__________ , _________ 合称为______________三、空间直线与平面间的位置关系分类为:__________________ ,____________ ,__________________ ;其中__________ , _________ 合称为______________四、空间平面与平面间的位置关系分类为:______________ ,当两个平面成90。
时,属于____________ 关系常用证明技巧一、线面平行列1 (2IH1年怀化楓蝌)如图所示*已知几0是单位止方WABCn-A^.C^的面A^BA和面』肮2>的中心*求证:卩总〃平面ncr^n.练习1. 正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q且AP = DQ. 求证:PQ//平面BCE.2・妇匿,四棱链/一乩噸一平面所裁*截面为平厅四边形吕他求证,m/zz面日捌3* (加10年彌考■陕丙雜)如图’在四棱饰P ABCD中.底血ABCD^矩形「只4 丄平SLUJC/h .lP-.Ltf, BP-IiC-1, E, F分别&l f B T PC 的中点.门)证明* EF//平血知";卩)求二棱锥E—.【号「的休枳匚(2)1/3二、线面垂直1、(2006年北京卷)如图,在底面为平行四边形的四棱锥P ABCD中,AB 点E是PD的中点•(I)求证:AC PB ; (n)求证:PB〃平面AEC ;2、( 2006年浙江卷)如图,在四棱锥P-ABCD中,底面为直角梯形BAD=90 ° ,PA丄底面ABCD,且PA= AD=AB=2BC,M、N 分别为PC、PB 求证:PB丄DM;3、(2006年福建卷)如图,四面体ABCD中,0、E分别是BD、BC的中点,CA(I)求证:AO 平面BCD;AC , PA 平面ABCD,且PA AB , CB CD BD 2, AB AD . 2.,AD // BC, /的中点•ADOE4、( 2006年重庆卷)如图,在四棱锥P—ABCD中,PA 底面ABCD, PC、DAB 为直角,AB II CD,AD=CD=24B,E、F 分另U为CD的中点.(I)试证:CD 平面BEF;5、(全国H ?理?9题)如图,在四棱锥SCS-ABCD中,底面ABCD为正方形,侧棱SD丄底面ABCD , E、F分别是AB、的中点。
点线面的位置关系

点线面的位置关系在几何学中,点、线和面是基本的几何元素。
它们之间的位置关系是我们研究几何学的基础。
本文将详细探讨点线面之间的位置关系,并从几何学的角度解释这些关系。
一、点与线的位置关系在平面几何中,点是最简单的几何元素。
它没有长度、面积和方向。
而线则是由无数个点组成的,具有长度但没有宽度。
点与线之间有以下几种位置关系:1. 点在线上:当一个点正好在一条线上时,我们说这个点在这条线上。
这意味着点与线上的所有点重合。
2. 点在线的两侧:如果一个点不在一条线上,并且离线的两侧距离都不为零,则我们说这个点在这条线的两侧。
3. 点在线的延长线上:如果一个点不在一条线上,并且它在这条线的延长线上,则我们说这个点在线的延长线上。
延长线是指将线无限延长的线段。
二、点与面的位置关系与点与线的位置关系类似,点与面之间也有几种不同的位置关系:1. 点在面上:当一个点正好在一个平面上时,我们说这个点在这个平面上。
这意味着点与面上的所有点重合。
2. 点在面的上方或下方:如果一个点不在一个平面上,并且它在这个平面的上方或下方,则我们说这个点在这个平面的上方或下方。
3. 点在面的边界上:如果一个点在一个平面的边界上,则我们说这个点在这个平面的边界上。
三、线与面的位置关系线与面之间的位置关系也是几何学中重要的内容,它们之间有以下几种位置关系:1. 线在面上:当一条线正好在一个平面上时,我们说这条线在这个平面上。
这意味着线上的所有点都在这个平面上。
2. 线与面相交:如果一条线与平面有一个或多个公共点,则我们说这条线与这个平面相交。
3. 线平行于面:如果一条线与平面上的所有点都不相交,则我们说这条线平行于这个平面。
4. 线垂直于面:如果一条线与平面的交点为一点,并且与平面上的所有其他点都垂直,则我们说这条线垂直于这个平面。
综上所述,点线面之间的位置关系是几何学的重要内容,它们的不同位置关系可以通过几何学的方法进行判断和描述。
通过研究这些位置关系,我们可以更好地理解几何学的基本概念,并应用于实际生活和工作中。
点、线、面之间的位置关系

结束
同一条直线
面内
平行 相交
课 前 ·双 基 落 实
课 堂 ·考 点 突 破
课后· 三维演练
点、线、面之间的位置关系
结束
[小题体验]
1.已知 a,b 是两条不同的直线,α,β,γ 是三个不同的平面, 给出下列命题: ①若 α∥β,a⊂α,则 a∥β; ②若 a,b 与 α 所成的角相等,则 a∥b; ③若 α⊥β,β⊥γ,则 α∥γ; ④若 a⊥α,a⊥β,则 α∥β. 其中正确命题的序号是________.
课 前 ·双 基 落 实
课 堂 ·考 点 突 破
课后· 三维演练
点、线、面之间的位置关系
结束
[小题纠偏]
1.(2017· 南京名校联考)已知直线 a 和平面 α,β,α∩β=l, a⊄α,a⊄β,且 a 在 α,β 内的射影分别为直线 b 和 c,则 直线 b 和 c 的位置关系是________.
课 前 ·双 基 落 实
课 堂 ·考 点 突 破
课后· 三维演练
点、线、面之间的位置关系
结束
解析:由 α∥β,a⊂α,结合面面平行的定义可得 a∥β,所 以①正确;由 a,b 与 α 所成角相等,可得 a 与 b 平行或相 交或异面,所以②不正确;由 α⊥β,β⊥γ,得 α 与 γ 平行 或相交,所以③不正确;由垂直于同一条直线的两个平面 平行,知④正确. 答案:①④
结束
(2)CE,D1F,DA三线共点.
证明:因为 EF∥CD1,EF<CD1, 所以 CE 与 D1F 必相交,设交点为 P, 则由 P∈CE,CE⊂平面 ABCD, 得 P∈平面 ABCD. 同理 P∈平面 ADD1A1. 又平面 ABCD∩平面 ADD1A1=DA, 所以 P∈直线 DA. 所以 CE,D1F,DA 三线共点.
点、线、面之间的位置关系

点、线、面之间的位置关系点线面之间的位置关系(一)平面:1、平面的两个特征:①无限延展②平的(没有厚度)2、平面的画法:通常画平行四边形来表示平面3、平面的表示:(1)用一个小写的希腊字母α、β、γ等表示,如平面α、平面β;(2)用表示平行四边形的两个相对顶点的字母表示,如平面AC 考点一、点线面的位置关系表示点A 在直线a 上(或直线a 经过点A )A ∈a 元素与集合间的关系点A 在直线a 外(或直线a 不经过点A )A ?a 点A 在平面α内(或平面α经过点A )A ∈α点A 在平面α外(或平面α不经过点A )A ?α例1 如图10,用符号语言表示下列图形中点、直线、平面之间的位置关系.变式训练1.画图表示下列由集合符号给出的关系:(1)A ∈α,B ?α,A ∈l,B ∈l;(2)a ?α,b ?β,a ∥c,b∩c=P,α∩β=c.例6.A 、B 、C 表示不同的点,a 、l 表示不同的直线,α、β表示不同的平面,下列推理不正确的是()()A ααα??∈∈∈∈l B l B A l A ,,,()B βα∈∈A A ,,AB B B =?∈∈βαβα ,直线()C αα??∈?A l A l , ()D α∈C B A ,,,β∈C B A ,,且C B A ,,不共线α?与β重合考点2.直线与直线的位置关系1.空间两条直线的位置关系:(1)相交直线——有且仅有一个公共点;(2)平行直线——在同一平面内,没有公共点;(3)异面直线——不同在任何一个平面内,没有公共点。
相交直线和平行直线也称为共面直线.异面直线的画法常用的有下列三种:2. 平行直线:在平面几何中,平行于同一条直线的两条直线互相平行,这个结论在空间也是成立的。
即公理4:平行于同一条直线的两条直线互相平行。
3.等角定理等角定理:如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等.a b a b ab βααα推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.4.异面直线定理:连结平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线推理模式:,,,A B a B a ααα?∈AB 与a 是异面直线例1.若直线a 与b 是异面直线,直线b 与c 是异面直线,则直线a 与c 的位置关系是 .例2.已知a ,b 是异面直线,直线c ∥直线a,则c 与b 的位置关系. ①一定是异面直线②一定是相交直线③不可能是平行直线④不可能是相交直线例3.若P 是两条异面直线l 、m 外的任意一点,则说法错误的有(填序号). ①过点P 有且仅有一条直线与l 、m 都平行②过点P 有且仅有一条直线与l 、m 都垂直③过点P 有且仅有一条直线与l 、m 都相交④过点P 有且仅有一条直线与l 、m 都异面例4. 如图6,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.图6求证:四边形EFGH是平行四边形.例5.如图6,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点且AC=BD. 求证:四边形EFGH是菱形.例4 如图7,已知正方体ABCD—A′B′C′D′.图7(1)哪些棱所在直线与直线BA′是异面直线?(2)直线BA′和CC′的夹角是多少?(3)哪些棱所在直线与直线AA′垂直?例5.如图8,已知正方体ABCD —A′B′C′D′.图8(1)求异面直线BC ′与A′B′所成的角的度数; (2)求异面直线CD′和BC′所成的角的度数.例6.在正三棱柱111C B A ABC -中,若12BB AB =,则1AB 与B C 1所成的角的大小.变式训练1.下列四个命题:(1)分别在两个平面内的两条直线是异面直线(2)和两条异面直线都垂直的直线有且只有一条(3)和两条异面直线都相交的两条直线必异面(4)若a 与b 是异面直线,b 与c 是异面直线,则a 与c 也异面其中真命题个数为()()A 3 ()B 2 ()C 1 ()D 02.在正方体-ABCD ''''D C B A 中,M 、N 分别是棱'AA 和AB 的中点,P 为上底面ABCD 的中心,则直线PB 与MN 所成的角为()()A 300 ()B 450 ()C 600 ()D3.已知直线a ,如果直线b 同时满足条件:①a 、b 异面②a 、b 所成的角为定值③a 、b 间的距离为定值,则这样的直线b 有()()A 1条 ()B 2条 ()C 4条 ()D 无数条4.正四棱柱ABCD-A 1B 1C 1D 1中,AA 1=2AB ,则异面直线A 1B 与AD 1所成角的余弦值为 .考点三.直线与平面的位置关系(二)三公理三推论:公理1:若一条直线上有两个点在一个平面内,则该直线上所有的点都在这个平面内.A l ∈,B l ∈,A α∈,B α∈?α?l公理2:如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
空间点线面之间的位置关系
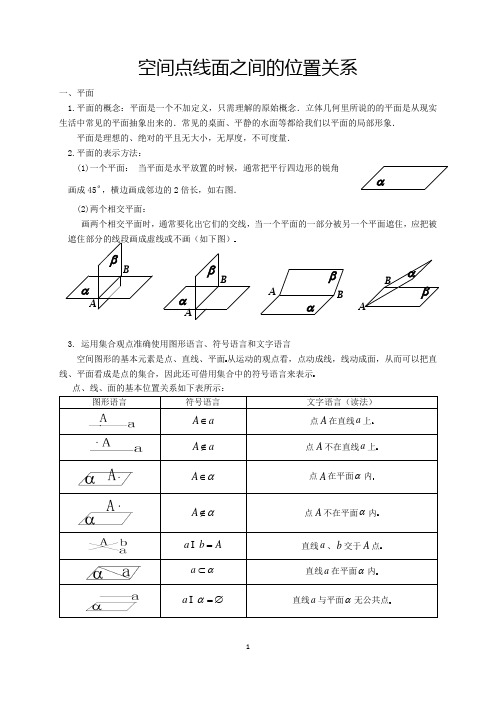
空间点线面之间的位置关系一、平面1.平面的概念:平面是一个不加定义,只需理解的原始概念.立体几何里所说的的平面是从现实生活中常见的平面抽象出来的.常见的桌面、平静的水面等都给我们以平面的局部形象.平面是理想的、绝对的平且无大小,无厚度,不可度量. 2.平面的表示方法:(1)一个平面: 当平面是水平放置的时候,通常把平行四边形的锐角 画成45,横边画成邻边的2倍长,如右图. (2)两个相交平面:画两个相交平面时,通常要化出它们的交线,当一个平面的一部分被另一个平面遮住,应把被遮住部分的线段画成虚线或不画(如下图)3. 运用集合观点准确使用图形语言、符号语言和文字语言空间图形的基本元素是点、直线、平面从运动的观点看,点动成线,线动成面,从而可以把直线、平面看成是点的集合,因此还可借用集合中的符号语言来表示点、线、面的基本位置关系如下表所示:b A =a α⊂α=∅ αBAβαABαβαβBAAβαBAα=l β= 二、平面的基本性质1. 公理1 如果一条直线的两点在一个平面内,那么这条直线在这个平面内推理模式:A AB B ααα∈⎫⇒⊂⎬∈⎭. 如图示: 或者:∵,A B αα∈∈,∴AB α⊂ 公理1的作用:①判定直线是否在平面内;②判定点是否在平面内; ③检验面是否是平面.2. 公理2 经过不在同一条直线上的三点,有且只有一个平面推理模式:,, ,,,,A B C A B C A B C ααβ⎫⎪∈⇒⎬⎪∈⎭不共线与β重合或者:∵,,A B C 不共线,∴存在唯一的平面α,使得,,A B C α∈. 推论1:经过一条直线和这条直线外的一点,有且只有一个平面; 推论2:经过两条相交直线,有且只有一个平面; 推论3:经过两条平行直线,有且只有一个平面.(1)以上是确定平面的四个不同的条件,是判断两个平面重合的依据,是证明点线共面的依据,也是作截面、辅助面的依据.(2)“有且只有一个”的含义要准确理解.这里的“有”是说图形的存在,“只有一个”是说图形唯一.因此,在证明有关这类语句的命题时,要从“存在性”和“唯一性”两方面来论证. 2. 公理3 如果两个不重合的平面有一个公共点,有且只有一条过该点的公共直线推理模式:A A l A ααββ∈⎫⇒∈=⎬∈⎭如图示:或者:∵,A A αβ∈∈,∴,l A l αβ=∈公理3的作用:(1)判断两个平面是否相交及交线位置; (2)判断点是否在线上 1、证明空间三点共线问题通常证明这些点都在两个平面的交线上,即先确定出某两点在两个平面的交线上,再证明第三点既在第一个平面内,又在第二个平面内。
点线面的位置关系

点线面的位置关系点、线、面是几何学中的基本概念,它们之间存在着重要的位置关系。
通过研究它们的位置关系,我们可以更好地理解和应用几何学知识。
本文将详细探讨点、线、面的位置关系,并对其应用进行讨论。
一、点、线、面的定义1. 点:几何学中最基本的元素,没有大小和形状,只有位置。
可以用坐标表示,例如(x, y)。
2. 线:由无数个点按照一定规律连接而成,具有长度但没有宽度。
可以用两个点的坐标表示,例如(1, 2)和(3, 4)之间的线段。
3. 面:由无数个线按照一定规律连接而成,具有长度和宽度。
可以用多边形的边界来表示,例如三角形、矩形等。
二、点、线、面的位置关系1. 点与线的位置关系:a. 在线上:如果一个点恰好在一条线上,则称该点在线上。
b. 在线内:如果一个点在一条线的两个端点之间,则称该点在线内。
c. 在线外:如果一个点既不在线上,也不在线内,则称该点在线外。
2. 点与面的位置关系:a. 在面上:如果一个点恰好在一个面上,则称该点在面上。
b. 在面内:如果一个点在一个面的边界之内,则称该点在面内。
c. 在面外:如果一个点既不在面上,也不在面内,则称该点在面外。
3. 线与线的位置关系:a. 相交:如果两条线有公共的一个或多个点,则称这两条线相交。
b. 平行:如果两条线的方向相同,但没有公共的点,则称这两条线平行。
c. 重合:如果两条线有无数个公共的点,则称这两条线重合。
4. 线与面的位置关系:a. 相交:如果一条线与一个面有公共的一个或多个点,则称这条线与该面相交。
b. 平行:如果一条线的方向与一个面平行,且线上没有与该面有公共的点,则称这条线与该面平行。
c. 重合:如果一条线与一个面重合,即线上的所有点都在该面上,则称这条线与该面重合。
5. 面与面的位置关系:a. 相交:如果两个面有公共的一条或多条线段,则称这两个面相交。
b. 平行:如果两个面的法向量平行,则称这两个面平行。
c. 重合:如果两个面有无数个公共的点,则称这两个面重合。
点、线、面的位置关系

点、线、面的基本位置关系如下表所示:公理1:文字语言:如果一条直线的两点在一个平面内,那么这条直线上的所有点都在这个平面内. 符号语言:A AB B ααα∈⎫⇒⊂⎬∈⎭.图形语言:公理2:文字语言:如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线. 符号语言:A A l A ααββ∈⎫⇒∈=⎬∈⎭图形语言:应用:①确定两相交平面的交线位置;②判定点在直线上说明:①公理2揭示了两个平面相交的主要特征,是判定两平面相交的依据,提供了确定两个平面交线的方法.②指出:今后所说的两个平面(或两条直线,如无特殊说明,均指不同的平面(直线). 公理3:文字语言:经过不在同一条直线上的三点,有且只有一个平面. 符号语言:,, ,,,,A B C A B C A B C ααβ⎫⎪∈⇒⎬⎪∈⎭不共线与β重合图形语言:应用:①确定平面;②证明两个平面重合说明:①“有且只有一个”的含义分两部分理解:“有”说明图形存在,但不唯一,“只有一个”说明图形如果有顶多只有一个,但不保证符合条件的图形存在,“有且只有一个”既保证了图形的存在性,又保证了图形的唯一性.②在数学语言的叙述中,“确定一个”,“可以作且只能作一个”与“有且只有一个”是同义词,因此,在证明有关这类语句的命题时,要从“存在性”和“唯一性”两方面来论证. 推论1:经过一条直线和直线外的一点有且只有一个平面. 推论2:经过两条相交直线有且只有一个平面. 推论3:经过两条平行直线有且只有一个平面.图形符号语言文字语言(读法)AaA a ∈ 点A 在直线α上 AaA a ∉点A 不在直线a 上BA αAαA α∈ 点A 在平面α内AαA α∉点A 不在平面α内b a Aa b A = 直线a 、b 交于A 点aαa α⊂ 直线a 在平面α内aαa α=∅ 直线a 与平面α无公共点a Aαa A α= 直线a 与平面α交于点Al αβ=平面α、β相交于直线l【典型例题分析】例1、将下列符号语言转化为图形语言:()1,,,;A B A l B l αβ∈∈∈∈()2,,//,,.a b a c b c p c αβαβ⊂⊂==例2、将下列文字语言转化为符号语言: ⑴ 点A 在平面α内,但不在平面β内; ⑵ 直线a 经过平面α外一点M ;⑶ 直线l 在平面α内,又在平面β内.(即平面α和β相交于直线l )例3、求证:三角形是平面图形. 已知:三角形ABC求证:三角形ABC 是平面图形例4、点A ∉平面BC D ,,,,E F G H 分别是,,,AB BC CD DA 上的点,若E H 与F G 交于P . 求证:P 在直线BD 上.1、试用集合符号表示下列各语句,并画出图形: (1)点A 在平面α内,但不在平面β内;(2)直线a 经过不属于平面α的点A ,且a 不在平面α内; (3)平面α与平面β相交于直线l ,且l 经过点P ; (4)直线l 经过平面α外一点P ,且与平面α相交于点M .2、 在正方体1111ABCD A B C D -中,①1A A 与1C C 是否在同一平面内? ②点1,,B C D 是否在同一平面内?③画出平面1AC 与平面1BC D 的交线,平面1AC D 与平面1BD C 的交线.GH A BC D EPFA 1D 1C 1CD AB B 13、已知直线a //b //c ,直线d 与a 、b 、c 分别相交于A 、B 、C ,求证:a 、b 、c 、d 四线共面.c'badc αC B A4、求证:一个平面和不在这个平面内的一条直线最多只有一个公共点.推论1: 经过一条直线和直线外的一点有且只有一个平面. 已知:直线l ,点A 是直线l 外一点. 求证:过点A 和直线l 有且只有一个平面推论2: 经过两条相交直线有且只有一个平面. 已知:直线P b a = .求证:过直线a 和直线b 有且只有一个平面.推论3:经过两条平行直线有且只有一个平面. 已知:直线//a b .求证:过直线a 和直线b有且只有一个平面【小结】认清点、线、面的位置关系,注意各种关系的定义【课堂练习】1.在空间中,下列命题不正确的是()错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 平面与平面 若有公共点,就不止一个.
3 因为平面型斜屋面与地面不相交,所以屋 面所在的平面与地面不相交.
推论1 经过一条直线和这条直线外一点,有且只有
一个平面. 已知:点A a.
A B aC
求证:过点A和直线a可以确定一个平面.
要证各线共面,先确定一个平面, 再证明其他直线也在这个平面内
证法三:
B
A
C
因为A,B,C三点不在一条直线上,
所以过A,B,C三点可以确定平面.(公理3) 因为A∈,B∈,所以AB .(公理1)
同理BC ,AC , 所以AB,BC,CA三直线共面.
平面的基本性质
推论2 经过两条相交直线,有且只有一个平面.
a
α
b
推论3 经过两条平行直线,有且只有一个平面.
a
b
α
P22例1.已知 : A, B,C l,D l 求证:直线AD,BD,CD共面
A
l
B
D C
证明: D l. l与D确定平面.
又 A, B,C l, l A, B,C .
平面图形与立体图形比较
平面图形
立体图形
直线是向两方无限延伸 直线用线段加想象表示
平面是向四周无限延伸, 无比平整的
平面用封闭平面图形加以想 象表示
平面几何研究平面图形
立体几何研究空间图形
最简单、最基本的图形是: 最简单、最基本的图形是:
点、直线
点、直线、平面
点、线、面的表示
•字母表示:
点(元素):大写字母A、B、C、D……
直线(点的集合):小写英文字母l, m, n
平面(点的集合):用希腊字母, , 或用平行四边形ABCD相对两字母表示,即AC
• 点、线、面之间的关系表示
用集合中的关系符号
元素与集合关系:,
集合与集合关系:, ;
平面的特征: (1) 平展性 (2) 无限延展性 (3) 没有厚度 平面的画法: 通常用平行四边形来表示平面。
所以直线AB,AC确定一个平面.(推论2)
因为B∈AB,C∈AC,所以B∈,C∈,
故BC.(公理1)
因此直线AB,BC,CA共面.
证法二:
B
因为A 直线BC上,
A
C
所以过点A和直线BC确定平面.(推论1)
因为A∈, B∈BC,所以B∈. 故AB ,同理AC ,
所以AB,AC,BC共面.
(2)B1_ , D_ A
(3) A1B1
O
C
B
(4) BB1
D1
(5)A1B1 __, A1B1 _ A1
O1
(6)平面A1C1CA∩平面D1B1BD= oo1
B1
C1
练习
2.根据下列符号表示的语句,说出有关 点、线、面的关系,并画出图形.
(1)A, B
l
符号语言
P AB Q AB
M 平面AC A1 平面AC
AB 平面AC AA1 平面AC
AB BC=B
l A
l
练习
1.正方体的各顶点如图所示,正方体的三个面所在平
面 A1C1, A1B , B1C ,分别记作、、 ,试用适当的符号填
空.
(1)A1_, A_ D
公理2:
1.文字语言:若两个平面有一个公共点, 则它们还有其它公共点,且所有这些公 共点的集合是一条过这个公共点的直线。
2.符号语言:
P,P 3.图形语言:
l且P l
Pl
公理3
平面的基本性质
过一点可以做几条直线?两点呢?
过平面内一点可以做几个平面?两点呢?三点呢?
平面基本性质
公理3:
1.文字语言:经过不在同一直线上的三点, 有且只有一个平面。
2.符号语言: A
, B ,C
A, B,C不共线
唯一
A, B,C不共线 A, B,C确定一平面
3.图形语言:
A
B C
P23练习:(1)为什么自行车后轮只安装一支脚?
(2)用符号表示" A在直线l, l在平面外",正确的是( ) A.A l, l B.A l, l C.A l, l D.A l,l (3)若A , B , A l, B l,那么直线l与平面有
A.∵A∈α,B∈α,∴AB∈α. B.∵a∈α,a∈β,∴α∩β=a.
其中命题和叙述方法都正确的是[ D ]
2.下列推断中,错误的是[ C ]
D.A、B、C∈α,A、B、C∈β,且A、B、C 不共
例题讲解
例1 两两相交且不同点的三条直线必在同一个平面内
B
A
C
已知:AB∩AC=A,AB∩BC=B,AC∩BC=C 求证:直线AB,BC,AC共面. 证法一: 因为AB∩AB=A
两个相交平面的画法:
三种语言转换
图形语言
Q A
P
B
D A1
A
M
C B
A1 D
A
B
A
C
B
A
BC
文字语言
点P在直线AB上 点Q不在直线AB上 点M在平面AC内 点A1不在平面AC内
直线AB在平面AC内 直线AA1不在平面AC内
直线AB与直线BC交于点B
l A
直线l和平面α交于A
平面α和平面β交于直线l
B
(2)l ,m
(3) l
A
(4)Pl, P,Ql,Q
P
l
Q
平面基本性质
公理1:
1.文字语言:若一条直线 上的两点在同一 个平面内,则这条直线上所有的点都在 这个平面内。
2.符号语言:Al, B l, A, B l
3.图形语言:
平面基本性质
证明:存在性.
因为A a,在a上任取两点B,C.
所以过不共线的三点A,B,C有一个平面.(公理3)
因为B∈,C∈,所以a .(公理1)
故经过点A和直线a有一个平面. 唯一性. 因为B,C在a 上, 所以过直线a和点A的平面一定经过点A,B,C。 根据公理3,经过不共线三点A,B,C的平面只有一个, 所以过直线a和点A的平面只有一个。
D BD,CD, AD ,即AD, BD,CD共面
P 例2 23
.
在长方体A
C1中,
P为棱BB1的中点,画出
由A1,C1,P三点所确定的平面与长方体
表面的交线.
D1
C1
A1
B1
D
C
P
A
B
D1
C1
A1
B1
D
C
P
AA、B表示点, a表示直线,α、β表示平面)
