计算机软件基础 第3章 非线性数据结构精品PPT课件
非线性结构课件PPT

案例二:基于图状结构的社交网络分析
总结词
揭示关系、挖掘信息、广泛应用
VS
详细描述
图状结构是一种描述对象之间关系的非线 性结构,广泛应用于社交网络、生物信息 学等领域。社交网络分析基于图状结构, 能够揭示用户之间的联系和社交行为模式 ,挖掘出有价值的信息,如影响力传播、 社区发现等。
案例三:基于网状结构的网络流量预测模型
总结词
实时预测、优化资源、保障网络性能
详细描述
网状结构是一种复杂的非线性结构,用于描 述网络流量等复杂系统的动态变化过程。网 络流量预测模型基于网状结构,能够实时预 测网络流量变化趋势,为网络资源优化配置 提供依据,保障网络性能稳定和高效。
案例四:基于链状结构的图像分割算法
总结词
分割准确、计算效率高、应用广泛
03
非线性结构的设计方法
确定结构的初始状态
确定初始条件
在非线性结构设计中,需要明确结构的初始状态 ,包括位置、速度和加速度等物理量。这些初始 条件是结构演化的基础。
选择合适的模型
根据问题的性质和目标,选择适合的非线性模型 进行结构设计。需要考虑模型的稳定性、收敛性 和计算效率等因素。
设定结构的演化规则
非线性结构课件
目录
• 非线性结构概述 • 常见非线性结构类型 • 非线性结构的设计方法 • 非线性结构的优化策略 • 非线性结构在机器学习中的应用 • 非线性结构课件案例分析
01
非线性结构概述
定义与特点
01
02
定义:非线性结构是指 信息之间不是严格的按 照线性关系进行排列和 组织的一种结构形式, 也称为非顺序结构、网 状结构或链接结构。
优化结构的参数设置
总结词
合理设置参数,提高性能
计算机软件技术基础3-1_数据结构及算法(概述+线性表)

幻灯片1第三章常用数据结构及其运算37 幻灯片23.1.1 数据结构的概念●数值型与非数值型数据●数值型:整型、实型、布尔型等●非数值型:文献检索、金融管理、商业系统等数据处理●数据结构●研究非数值运算的程序设计问题。
●数据结构就是相互之间存在一种或多种特定关系的数据元素的集合。
●如线性关系、层次关系、网状关系等。
37 幻灯片33.1.1 数据结构的概念3. 基本概念和术语数据(data)——是信息的载体,指所有能输入到计算机中并被计算机程序处理的符号的总称。
如数、字符、符号等的集合。
分为数值型和非数值型数据两类。
数据元素(data element)——是数据的基本单位。
如数据集合N={ 1,2,3,4,5 }中整数1至5均为数据元素。
数据元素不一定是单个的数字或字符,也可能是若干个数据项的组合,如学生信息。
数据元素有时也称结点或记录。
37 幻灯片43.1.1 数据结构的概念数据对象(data object)——性质相同的数据元素的集合。
如大写字母字符的数据对象是集合:C={ ‘A’,’B’,...,’Z’}。
数据类型——程序设计语言中允许的变量类型基本数据类型(原子类型):变量值不可分,如整型、实型、字符型等结构类型:变量值可分,如数组、结构体等37 幻灯片53.1.1 数据结构的概念数据结构(data structure)——是指同一数据对象中各数据元素间存在的关系。
数据结构与算法——程序=算法+数据结构算法指解决特定问题的有限运算序列37 幻灯片63.1.2 数据的逻辑结构和物理结构1.逻辑结构:研究数据元素及其关系的数学特性,即数据元素间的逻辑关系。
二元组 S =(D,R)D--数据元素的非空有限集合R--D上关系的非空有限集合。
37 幻灯片73.1.2 数据的逻辑结构和物理结构四类基本结构:举例37 幻灯片83.1.2 数据的逻辑结构和物理结构例1:linearity = (D, R),其中D = {1,2,3,4,5,6,7,8,9,10}R = {r}r = {<7,2>, <2,1>, <1,6>, <6,10>, <10,8>, <8,4>, <4,5>, <5,3>, <3,9>}例2:Tree= (D, R),其中D = {1,2,3,4,5,6,7,8,9,10}R = {r}r = {<1,2>, <2,3>, <2,4>, <1,5>, <5,6>, <1,7>, <7,8>, <7,9>, <7,10>}37 幻灯片93.1.2 数据的逻辑结构和物理结构例3:Graph= (D, R),其中D = {1,2,3,4,5}; R = {r}r = {<1,2>, <1,4>, <1,3>, <3,5>, <2,3>}例4:S = (D, R),其中D = {1,2,3,4,5,6}R = {r1, r2}r 1= {<3,2>, <3,5>, <2,1>, <5,4>, <5,6>}r2={<1,2>,<2,3>,<3,4>,<4,5>,<5,6>}37 幻灯片103.1.2 数据的逻辑结构和物理结构2.物理结构(存储结构):是逻辑结构在计算机中的映象,即具体实现。
软件技术基础第三章(2)

交换排序
逆序:在数组A[n]中, 存在i<j,且A[i]>A[j]则 称A[i]和A[j]构成一个 逆序
交换排序的思想是通过交换元素以达到消除逆序的目的
冒泡排序
(1)从表头开始往后扫描线性表,在扫描过程中逐次比较相邻两个 元素的大小。若相邻两个元素中,前面的元素大于后面的元素,则 将它们互换,称之为消去了一个逆序。显然,在扫描过程中,不断 地将两相邻元素中的大者往后移动,最后就将线性表中的最大者换 到了表的最后。 (2)除去最后已经冒出的元素,对剩下的线性表重复上述过程,直到 剩下的线性表变空为止,此时冒出的元素构成的线性表已经变为有 序。
0
1
2
3
4
5
6
7
8
49
38
65
97
76
13
27
49
49
27
38
65 i
97
76
13
j
49
界点
14
e.g: 将序列 49、38、65、97、76、13、27、49 用 快速排序的方法进行排序。
0
1
2
3
4
5
6
7
8
49
38
65
97
76
13
27
49
49
27
38
i
97
76
13
65 j
49
界点
15
e.g: 将序列 49、38、65、97、76、13、27、49 用 快速排序的方法进行排序。
0
1
2
3
4
5
6
7
8
13
27
38
计算机软件基础第3章
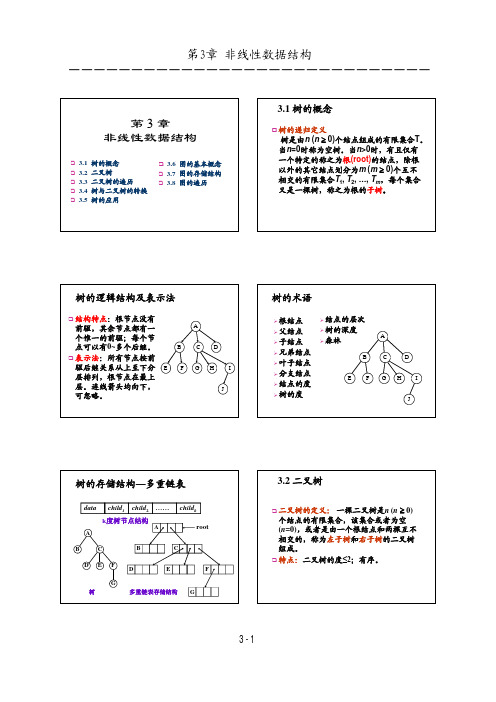
data child brother 节点结构
树,T’为T所对应的二叉树,则有: Ø T中结点与T’中的结点一一对应; Ø 若在T中d1是其父结点d 的第一个子结 点,则在T’中d1是d 的左子结点; Ø 若在T中di是其父结点d 的第i个子结点 (i>1), di-1是d 的第i-1个子结点,则在T’ 中di是di-1的右子结点。
二叉树的遍历示例
•
前序遍历的递归算法
A B E F G H I J C D
前序遍历序列为: ABEFCGDHIJ 中序遍历序列为: EFBGCHIJDA 后序遍历序列为: FEGJIHDCBA
•
•
void preorder(TNODE *bt) { if (bt != NULL) { printf("%d ", bt->data); preorder(bt->lchild); preorder(bt->rchild); } }
3-6
第3章 非线性数据结构 —————————————————————————————
Huffman树的构造过程 Huffman树节点定义
typedef struct { char data; int weight; int lchild; int rchild; } huffnode; //字符值 //权重 //左子结点 //右子结点
二叉树称为满二叉树。 q 定义:若一棵深度为k的二叉树,每层结 点个数满足: Ø 第i 层(1≤i ≤k-1)上有2i-1个结点; Ø 第k 层只在右边连续缺若干结点; 则称此树为完全二叉树。 q 满二叉树也是完全二叉树。
完全二叉树的性质
q 性质4
完全二叉树的性质
q 性质5':对一棵含有n个结点的完全二叉树的
全国计算机等级考试二级_公共基础知识精品PPT课件

14
三、线性表 线性表是最简单的、最常用的一种线性结构。 1.线性表的定义:线性表是n个元素的有限序列,它们
之间的关系可以排成一个线性序列:a1,a2,…… ,ai,…… ,an ,其中n称作表的长度,当n=0 时,称作空表。 线性表(非空线性表)必须同时满足以下3个条件: (1)有且只有一个根结点a1,它无前件。 (2)有且只有一个终端结点an,它无后件。 (3)除根结点与终端结点外,其他所有结点有且只 有一个前件,也有且只有一个后件。
线性表的定义、线性表的顺序存储结构及其插入与删除运算。
栈和队列的定义、栈和队列的顺序存储结构及其基本运算。
线性单链表、双向链表与循环链表的结构及其基本运算。
树的基本概念,二叉树的定义及其存储结构,二叉树的前序、 中序和后序遍历。
顺序查找与二分法查找算法、基本排序算法(交换类排序、选 择类排序与插入类)。
8
A.二元关系表示方法:一个数据结构可以表示为B=( D、R),其中R用二元组来表示(a、b)。 a表示前 件, b表示后件。 例如,一年四季的数据结构可以表示成: B=(D、R) D={春,夏,秋,冬} R={(春,夏),(夏,秋),(秋,冬)}
B.在图形表示方法中,用中间标有元素值的方框来表示 数据元素,称为数据结点,简称为结点;用一条有 向线段从前件结点指向后件结点(注意:有时可以 省略箭头)来表示元素之间的前后关系。
16
例:正确表示线性表(A1,A2,A3,A4)的顺序结 构是( )
二级公共基础知识
二级公共基础知识
第一章 算法与数据结构 第二章 程序设计基础 第三章 软件工程基础 第四章 数据库设计基础
2
本章要求
计算机软件技术基础-第三章算法与数据结构

返回
类C、类Pascal、类VB之类的伪代码,也不尽相同,但 程序员必须记住“用伪代码写算法,编程语言写程序” 还是应该遵循的! 本书约定的算法描述语言是VC语言的变体,称为类VC 语言。 这里还需要说一说流程图(Flow Chart)。因为它在历史上 有过巨大的影响,在20世纪50—70年代结构化编程语 言尚未风行时,流程图一直是表达算法的设计工具。 美国国家标准协会(ANSI)还把它定为标准。为了帮助 读者阅读历史的软件文档,这里做一点简单说明。
返回
图3.1 常用流程图符号
返回
如图3.1所示,其中: • 带圆弧的框是起止框,表示算法的起始、终止。框内填写文字。 • 圆圈一般是连接框,连接多个流向箭头。大圈中写文字标号,无文字 时是句号大小的圈。 • 平行四边形的输入输出框表示输入数据和输出计算结果。框内应填写 需要输入或输出的量。有的标准将输出画成打印纸形状。 • 菱形的判断框根据条件判断执行的走向。框内应填上条件。 • 矩形的处理框表示执行计算表达式和赋值操作。框内用文字或符号表 明具体实现的操作。 • 双立边矩形框是调用/引用框。框内写函数/过程名。 • 注释框表示对操作或数据做必要的说明, 框内用文字说明注释信息。 • 流向线表示算法中控制的流向,向下向右可不画箭头,其他方向必画。 画流程图时,主流程必须在一条垂直的轴线上,特别是起止框要对齐, 切勿因有多次分支而将主流程画成台阶形或横宽大于纵长。
返回
计算机容许的动作是: • 为变量赋值(包括初值); • 计算表达式(在变量上做四则或逻辑运算); • 计算过程的选择、循环、转移控制; • 调用函数/子程序。 再看如何写出计算机的辗转相除法。 令变量x为被除数,y为除数,z为余数。计算机中有求余函数mod,则: z = x mod y 然后x←y, y←z就换过来了,x依然是被除数,y是除数。于是写出GCD(Greatest Common Divisor最大公约数)算法: 1.设定x, y, z 2.输入x, y 3.if y>x then z←y; y←x; x←z fi 4.while y< >0 do A.z←y B.y←x mod y; C.x←z od 5.输出z,即最大公约数□
计算机软件基础课件-2017-第3章-2-图
简单路径:表示路径的顶点序列中的顶点各不相同。 简单回路:除了第一个和最后一个顶点外,其余各顶点均不重复 出现的回路。
2
4
5
1
3
6
路径:1,2,3,5,6,3 路径长度:5 简单路径:1,2,3,5 回路:1,2,3,5,6,3,1 简单回路:3,5,6,3
最后一个邻接点,则返回“空”。
(8) Insertvex(&G, v):在G中增加的顶点v。
初始条件:图G存在,v和G中顶点有相同特征。 操作结果:在G中增添新顶点v。
(9)DeleteVex(&G,v):删除G中的顶点v。
初始条件:图G存在,v是G中的某个顶点。 操作结果:删除G中顶点v及相关的边。
初始条件:V是图的顶点集,E是图中边的集合。 操作结果:按V和VR的定义创建图G。
(2)DestoryGraph(&G):销毁图G。
初始条件:图G存在。 操作结果:销毁图G。
(3)LocateVex(G,v):确定v在图G中的位置。
初始条件:图G存在,v和G中顶点有相同特征。 操作结果:若顶点v在G中,则返回v在G中的位置;
4
B 7
C (a)
A1 B2 C3
2 43 1 34
37
(b)
邻接表
#define VTXUNM n #define ETXUNM e typedef char vextype; struct arcnode {
int adjvex; float data; struct arcnode *nextarc; }; typedef struct arcnode ARCNODE; struct headnode { vextype vexdata; ARCNODE *firstarc; }adjlist[VTXUNM];
软件技术基础第3章 算法与数据结构(一)精品PPT课件
13
3.1.2 基本概念和术语
• 数据
➢ 是对客观事物的符号表示。在计算机科学中其含义是指所 有能够输入到计算机中并被计算机程序处理的符号集合
• 数据元素
➢ 是数据集合中的一个实体,是计算机程序中加工处理的基 本单位(记录、结构体)
• 数据项
➢ 组成数据元素的有特定意义的最小的不可分割的单位。
《软件技术基础》电子教案
• 数据结构的形式定
义
数据结构是一个二元组:Data_Structures = (D, R)
其中:D是数据元素的有限集,R是D上关系的有限集。
• 数据结构分为四大类:
➢ 表:元素是线性关系(连接)
➢ 图:元素间是非线性关系(连接)
➢ 树:元素间是非线性关系,连接不得有回路
➢ 文件:记录的序列
《软件技术基础》电子教案
(字符、表格、图像) • 对非数值数据的处理:分析数据的逻辑特征
→抽象出合适的数学模型→合理地存储到计 算机→设计出算法→编写出程序
《软件技术基础》电子教案
5
例1 学生信息查询系统
首先要构造学生信息表,表3-1表达出学生数据的逻辑关系,
它就是一个数学模型,这张表如何构造、在计算机内如何 存储将直接影响查找算法的设计以及算法的效率
......
表3-1
《软件技术基础》电子教案
6
学生信息表的特点
• 每个学生的信息占据一行,所有学生的信息 按学号顺序依次排列构成一张表格
• 表中每个学生的信息依据学号的大小存在着 一种前后关系,这就是我们所说的线性结构, 现实中这类关系的数据有很多。
• 通常的操作
➢ 插入某个学生的信息 ➢ 删除某个学生的信息 ➢ 更新某个学生的信息 ➢ 按条件查找某个学生的信息
计算机软件基础ppt
3
2
rear
1
0
front (a)
rear =4
e4
e3
e3
e2
front
e1
(b)
(c)
rear=front=0(队空) (b)e1,e2,e3入队 (c) e1,e2出队,e4入队
栈和队列
循环队列:首尾相接的队列,逻辑上形成一个环状。
a1 , a2 , a3 , a4 , ………… an-1 , an
服务特 权
共享文档下载特权
VIP用户有效期内可使用共享文档下载特权下载任意下载券标价的文档(不含付费文档和VIP专享文档),每下载一篇共享文
档消耗一个共享文档下载特权。
年VIP
月VIP
连续包月VIP
享受100次共享文档下载特权,一次 发放,全年内有效
赠每的送次VI的发P类共放型的享决特文定权档。有下效载期特为权1自个V月IP,生发效放起数每量月由发您放购一买次,赠 V不 我I送 清 的P生每 零 设效月 。 置起1自 随5每动 时次月续 取共发费 消享放, 。文一前档次往下,我载持的特续账权有号,效-自
栈和队列
栈和队列是两种运算时要受到某些特殊限制的线性 表,故也称为限定性的数据结构。
栈:限定只能在表的一端进行插入和删除的特殊的线性表,此
种结构称为后进先出。
进栈 出栈
设栈s=(a1,a2,…,ai,…,an)
其中a1是栈底元素, an是栈顶元素。
栈顶(top):允许插入和删除的一端; 栈顶
E
F
G
D
HI
J
现实K 世界中L,能用树的结T构2 表示M:学校的T行3 政关 系、书的层次结构、人类的家族血缘关系等。
软件技术ppt第3章 数据结构3(树和图)
E
K
F
L
3.3.4 树的应用
应用于分类、检索、数据库及人工智能等多个方面。
哈夫曼树
是一类带权路径最短的树。如用于通讯及数据传送中构造传送
效率最高的二进制编码(哈夫曼编码),用于编程中构造平均执 行时间最短的最佳判断过程。
例:
A
1) 哈夫曼树的有关概念
B
C
• 结点间的路径长度:从树中 一个结点到另一个结点之 间的分支个数。
A:10, B:9, C:21, D:2
• 树的带权路径长度:树中所有带权结 点的路径长度之和,常记作WPL。
树的带权路径长度:
(a) WPL = 10+9+21+2 = 42 (b) WPL = 10+6+14+4 = 34 (c) WPL = 7+10+9+6 = 32
例:
D2 A5
B3 C 7 (a)
5 3 72 A BCD
57 AC
5 BD
10 7 CA
BD
C A BD
哈夫曼树的应用:
在解决某些判定问题时的最佳判定算法。
例: 将学生百分成绩按分数段分级的程序。
若学生成绩分布是均匀的,可用二叉树结构来
实现。
a<60
Y
N
输入10000个
不及格 a<70
Y
N
数据,则需进 行28000次比
较。
及格
a<80
A 5 B 3 C7 D 2
(b)
• 哈夫曼树:设有n个权值{w1,w2,…, wn},构造一棵有n个叶子结点的二叉树 ,每个叶子结点带权为wi,1≤i≤n,则带权 路径长度最小的二叉树称哈夫曼树,也 称最优二叉树。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章 非线性数据结构
3.1 树及其基本概念 3.2 二叉树
3.2.1 二叉树的定义及其性质 3.2.2 二叉树的存储结构
3.3 二叉树的遍历 3.4 树的存储结构和遍历
第3章 非线性数据结构
3.1 树及其基本概念
树型结构是一种应用十分广泛的非线性数据结构, 它很类似自然界中的树,直观地讲,树型结构是以分 支关系定义的层次结构。
第3章 非线性数据结构 A
B
C
D
E
F
G
H
I
J
图3-1 树型结构
第3章 非线性数据结构
下面结合图3-1,给出树型结构中的一些基本术语。 结点的度:一个结点拥有的子树数目。如A结点的 度为3,它有三个子树T1、T2和T3。E、F结点的度为0, 它们没有子树。 叶子:度为零的结点称叶子或终端结点。 树的度:一棵树上所有结点的度的最大值就是这 棵树的度。
第3章 非线性数据结构
3.2 二 叉 树
3.2.1 二叉树的定义及其性质 1.二叉树的定义 一个二叉树是一个有限结点的集合,该集合或者
为空,或由一个根结点和两棵互不相交的被称为该根 的左子树和右子树的二叉树组成。二叉树中每个结点 最多只能有两棵子树,并且有左右之分,即有序。 二叉树有下面两个主要特点:
第3章 非线性数据结构 A
B
C
D
E
F
G
H
I
J
图3-1 树型结构
第3章 非线性数据结构
结点的层次:根结点的层数为1,其它任何结点的 层数等于它的父结点的层数加1。
树的深度:一棵树中,结点的最大层次值就是树 的深度。图3-1中树的深度为4。
森林:森林是m(m≥0)棵互不相交的树的集合。 孩子(child):某结点子树的根称为该结点的孩子结 点。 如B、C、D是A的孩子。
性质4:具有n个结点的完全二叉树的深度为
⌊log2n⌋+1 。
第3章 非线性数据结构
性质5:如果对一棵有n个结点的完全二叉树的结点按 层序编号(从第1层到第⌊log2n⌋+1层,每层从左到右),则 对任一结点i(1≤i≤n),有
(1) 如果i=1,则i是二叉树的根,无双亲;如果i>1,则 其双亲是结点i/2。
第3章 非线性数据结构
双亲(parent):一个结点是它的那些子树的根的双 亲结点。如A是B、C、D的双亲。
兄弟(sibling):同一个双亲的孩子之间互为兄弟。B、 C、D是A的孩子;B、C、D互为兄弟。
堂兄弟(cousins):其双亲在同一层的结点互为堂兄 弟。如G与E、F、H、I互为堂兄弟。
k
2 i 1 = 2k−1
i1
第3章 非线性数据结构
下面介绍两种特殊形态的二叉树,满二叉树和完全二叉树。 如果一棵二叉树的深度为k,并且含有2k–1个结点,则称此
二叉树为满二叉树。图3-6是一棵深度为4的满二叉树。
A
B
C
D
E
F
G
H
I
J
K L MN O
图3-6 深度为4的满二叉树
第3章 非线性数据结构
(2) 如果2i>n,则结点i无左孩子;否则其左孩子是2i。 (3) 如果2i+1>n,则结点i无右孩子;否则其右孩子是结 点2i+1。 证明从略。
第3章 非线性数据结构 A
B
C
D
E
F
G
H
I
J
图3-1 树型结构
第3章 非线性数据结构
这是一个递归定义,即在树的定义中又用到了树, 即一棵树是由若干棵子树构成的,而子树又可由若干 棵更小的子树构成。树中的每一个结点都是该树中某 一棵子树的根。
如图3-1所示的树中,A为根结点,其余的结点分 为三个互不相交的有限集合:T1={B,E,F},T2={C, G,J},T3={D,H,I}。T1、T2和T3都是A的子树,而 它们本身也是一棵树。例如,T1是一棵以B为根的树, 其余结点分为互不相交的两个集合{E}和{F},而{E}和 {F}本身又是仅有一个根结点的树。
2.二叉树的性质
二叉树具有下列重要特性。
性质1:在二叉树中,第i层的结点数最多有2i-1(i≥1)个。
例如:层次i
第i层最多结点数
1
20=1
2
21=2
22=4
k
2k−1
此性质可以用数学归纳法证明。
第3章 非线性数据结构
性质2:在深度为k的二叉树中结点总数最多有2k–1个。 由性质1可见,深度为k的二叉树的最大结点数为:
第3章 非线性数据结构
(1) 每个结点最多只能有两个孩子,即二叉树中不 存在度大于2的结点。
(2) 二叉树的子树有左、右之分,其次序不能任意 颠倒。二叉树可以有五种基本形态,如图3-2所示。
第3章 非线性数据结构
(a)
(b)
(c)
(d)
(e)
图3-2 二叉树的五种基本形态
第3章 非线性数据结构
第3章 非线性数据结构
有序树:若将树中每个结点的各子树看成是从左 到右有次序的(即不能互换的),则称该树为有序树,否 则为无序树。作为有序树,图6.26中的两棵树是不同的, 因为结点A的两个孩子在两棵树中的左右次序不同。以 后若不特别指明,所讨论的树都是有序树。
A
A
B
CC
B
图6.26 两棵不同的有序树
树(Tree)是n(n≥0)个结点的有限集合。在树形图中, 结点常用圆圈表示,结点的名字一般写在圆圈旁边, 有时亦可写在圆圈内。当n=0时称为空树,否则在任一 非空树中:
第3章 非线性数据结构
(1) 有且仅有一个称为该树之根的结点; (2) 除根结点之外的其余结点可分为m(m≥0)个互不 相交的集合T1,T2,…,Tm,且其中每一个集合本身 又是一棵树,并且称为根的子树(SubTree)。
结点都与深度为k的满二叉树中的编号从1到n的结点一
一对应时,称之为完全二叉树。如图3-8所示是一棵深
度为4的完全二叉树。
1
2
4
5
3
6
7
8
9
10 11 12
图3-8 深度为4的完全二叉树
第3章 非线性数据结构
完全二叉树是一个十分重要的概念,在许多算法和算 法分析中,都明显或隐含地用到了完全二叉树的概念。 下面介绍完全二叉树的两个重要特性。
可以看出这种树的特点是每一层的结点数都是最大 结点数。
对满二叉树的结点进行连续编号:从根结点起,自 上而下逐层从左到右给每个结点编一个从1开始的顺序 号。图3-6就成为图3-7。
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15
图3-7 深度为4的满二叉树
第3章 非线性数据结构
深度为k,有n个结点的二叉树,当且仅当其每一个
