高等数学-函数全微分
合集下载
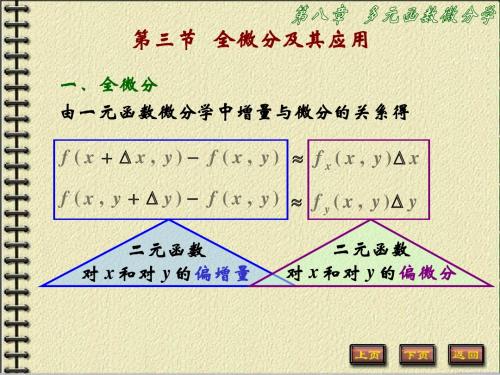
《高等数学B》第八章 多元函数微分学 第三节 全微分及其应用
P ′( x + ∆ x , y + ∆ y ) ∈ P 的某个邻域
∆ z = A∆ x + B∆ y + o( ρ ) 总成立 ,
上式仍成立， 当 ∆ y = 0 时，上式仍成立，此时 ρ = | ∆ x | ,
f ( x + ∆ x , y ) − f ( x , y ) = A ⋅ ∆ x + o(| ∆ x |) ,
所求全微分 dz = e 2dx + 2e 2dy .
y yz 例2 计算函数 u = x + sin + e 的全微分 . 2
y ∂u 1 ∂u ∂u yz yz 解 = ye , =1, = cos + ze , ∂y 2 2 ∂z ∂x
所求全微分
1 y yz yz du = dx + ( cos + ze )dy + ye dz . 2 2
例4 试证函数
1 , ( x , y ) ≠ ( 0 , 0) , xy sin 2 2 x +y f ( x , y) = 0, ( x , y ) = ( 0 , 0) .
在点 (0 , 0) 连续且偏导数存在，但偏导数在点 (0 , 0) , 0) 可微 . 不连续， (证明略) 证明略)
∂u ∂u ∂u du = dx + dy + dz . ∂x ∂y ∂z
例1 计算函数 z = e x y在点 ( 2 , 1) 处的全微分 . 解
∂z = ye xy , ∂x
∂z = e2 , ∂x ( 2 , 1 )
∂z = xe xy , ∂y
∂z = 2e 2 , ∂y ( 2 , 1 )
∆ z ≈ dz = f x ( x , y )∆ x + f y ( x , y )∆ y .
∆ z = A∆ x + B∆ y + o( ρ ) 总成立 ,
上式仍成立， 当 ∆ y = 0 时，上式仍成立，此时 ρ = | ∆ x | ,
f ( x + ∆ x , y ) − f ( x , y ) = A ⋅ ∆ x + o(| ∆ x |) ,
所求全微分 dz = e 2dx + 2e 2dy .
y yz 例2 计算函数 u = x + sin + e 的全微分 . 2
y ∂u 1 ∂u ∂u yz yz 解 = ye , =1, = cos + ze , ∂y 2 2 ∂z ∂x
所求全微分
1 y yz yz du = dx + ( cos + ze )dy + ye dz . 2 2
例4 试证函数
1 , ( x , y ) ≠ ( 0 , 0) , xy sin 2 2 x +y f ( x , y) = 0, ( x , y ) = ( 0 , 0) .
在点 (0 , 0) 连续且偏导数存在，但偏导数在点 (0 , 0) , 0) 可微 . 不连续， (证明略) 证明略)
∂u ∂u ∂u du = dx + dy + dz . ∂x ∂y ∂z
例1 计算函数 z = e x y在点 ( 2 , 1) 处的全微分 . 解
∂z = ye xy , ∂x
∂z = e2 , ∂x ( 2 , 1 )
∂z = xe xy , ∂y
∂z = 2e 2 , ∂y ( 2 , 1 )
∆ z ≈ dz = f x ( x , y )∆ x + f y ( x , y )∆ y .
高等数学 第八章 第3节 全微分及其应用(中央财经大学)
第三节 全微分及其应用一、全微分二、全微分在近似计算中的应用d d tan xy=α沿此曲线计算的函数在点P 处的增量为偏增量z x∆多元函数的全增量运用多元函数的全增量概念,将一元函数的微分概念推广到多元函数中.应用的某一个线性函数表示二元函数的全增量y x ∆∆ ,:z ∆α+∆+∆=−∆+∆+=∆y b x a y x f y y x x f z ),() ,(, ,无关的常数和是与y x b a ∆∆.应该是一个无穷小量α二元函数全微分的定义全微分概念的极限形式函数在区域上的可微性如果函数)f在区域Ω中的(X每一点均可微, 则称函数在区域Ω上可微 .可微连续可导连续：0lim 00=∆→∆→∆z y x 可微：+∆=∆x a z +∆y b )o(22y x ∆+∆什么?可微连续可导可微连续可导可微连续可导逆命题?可 微连续可导连 续可 导连续可导Okf,0(),(≠y xf二、全微分在近似计算中的应用例5 计算的近似值. 解.),(y x y x f =设函数.02.0,04.0,2,1=∆=∆==y x y x 取,1)2,1(=f ∵,),(1−=y x yx y x f ,ln ),(x x y x f yy =,2)2,1(=x f ,0)2,1(=y f 由公式得02.0004.021)04.1(02.2×+×+≈.08.1=谢谢大家！。
高等数学全微分方程精品PPT课件
dx x
dy y
0
即 d 1 d( ln x ) d( ln y ) 0
xy
1
因此通解为 1 ln x ln C , 即 x C e xy
xy y
y
因 x = 0 也是方程的解 , 故 C 为任意常数 .
练习题 解方程 y d x ( y x) d y 0.
解法1 积分因子法. 原方程变形为
2
3
因此方程的通解为
y (x, y)
x5 3 x2 y2 xy3 1 y3 C
2
3
o (x,0) x
例2. 求解
(
x
y x2
)
dx
1 x
dy
0
解:
P y
1 x2
Q , x
∴ 这是一个全微分方程 .
用凑微分法求通解. 将方程改写为
x
dx
x
d
y x2
y
dx
0
即
d 1 x2 d y 0, 或 d 1 x2 y 0
为全微分方程 ( 又叫做恰当方程 ) .
判别: P, Q 在某单连通域D内有连续一阶偏导数, 则
① 为全微分方程 求解步骤:
P Q , (x, y) D y x
1. 求原函数 u (x, y)
方法1 凑微分法;
方法2 利用积分与路径无关的条件.
2. 由 d u = 0 知通解为 u (x, y) = C .
第二节 一阶微分方程
第十二章
一、可分离变量方程 二、齐次型微分方程 三、可化为齐次型的微分方程 四、一阶线性微分方程 五、全微分方程
五、全微分方程
若存在 u(x, y) 使 d u(x, y) P (x, y) dx Q (x, y) dy
高等数学常用公式大全
高等数学常用公式大全1.微分学公式：- 导数的定义：若函数y=f(x)在点x0处可导，则其导数为f'(x0)=lim(x→x0)(f(x)-f(x0))/(x-x0)-基本导数公式：- (1) 常数函数的导数：d(C)/dx = 0，其中C为常数- (2) 幂函数的导数：d(x^n)/dx = n*x^(n-1)，其中n为实数- (3) 指数函数的导数：d(e^x)/dx = e^x- (4) 对数函数的导数：d(ln(x))/dx = 1/x- (5) 三角函数的导数：d(sin(x))/dx = cos(x)，d(cos(x))/dx = -sin(x)，d(tan(x))/dx = sec^2(x)，d(cot(x))/dx = -csc^2(x)，d(sec(x))/dx = sec(x)*tan(x)，d(csc(x))/dx = -csc(x)* cot(x)2.积分学公式：- 不定积分的性质：∫(f(x)+g(x))dx = ∫f(x)dx + ∫g(x)dx，∫k*f(x)dx = k*∫f(x)dx，其中f(x)和g(x)是可积函数，k是常数-基本积分公式：- (1) 幂函数的不定积分：∫x^n dx = (1/(n+1))*x^(n+1) + C，其中n不等于-1- (2) 指数函数的不定积分：∫e^x dx = e^x + C，其中C为常数- (3) 对数函数的不定积分：∫1/x dx = ln，x， + C- (4) 三角函数的不定积分：∫sin(x) dx = -cos(x) + C，∫cos(x) dx = sin(x) + C，∫tan(x) dx = -ln，cos(x)， + C，∫cot(x) dx = ln，sin(x)， + C，∫sec(x) dx = ln，sec(x)+tan(x)， + C，∫csc(x) dx = ln，csc(x)-cot(x)， + C3.微分方程公式：- 一阶线性微分方程：dy/dx + p(x)y = q(x)，其中p(x)和q(x)是已知函数，分别称为系数函数和非齐次项函数。
高等数学教学： 偏导数与全微分
轮换对称性
f
x
(0,0,0)
3
x cos
x
x
0
1 4
利用轮换对称性 , 可得
f y (0,0,0)
f z (0,0,0)
1 4
d f (0,0,0) f y (0,0,0) d x f y (0,0,0) d y f z (0,0,0) d z
1 (d x d y d z) 4
例 7. 求所有的二阶偏导数： 两个混合偏导数：是否总相等
例8. 设
f(x,y)=
xy
x2 x2
y2 y2
,
0 ,
x2 y2 0 x2 y2 0
证明: fxy (0, 0) f yx (0, 0)
在什么条件下才能保证两者相等呢？
定理16.4 这个定理可以推广到 n阶偏导数的情形： 即若函数 f 具有直到 n 阶的连续偏导数，则求偏导数与变量的顺序
z
2
2ze
x2
y2
z
2
2
x
sin
y
u
2 x (1 2 x2 sin2 y) ex2 y2 x4 sin 2 y
xyz
u y
f y
f z
z y
2ye x2 y2 z2 2ze x2 y2 z2 x2 cos y
2 ( y x4 sin y cos y ) ex2 y2 x4 sin 2 y
x y
x f x
y
s f
同理 y
t
例4. 设 u f (xy, y ) 求 u 2u 2u
f
x
(0,0,0)
3
x cos
x
x
0
1 4
利用轮换对称性 , 可得
f y (0,0,0)
f z (0,0,0)
1 4
d f (0,0,0) f y (0,0,0) d x f y (0,0,0) d y f z (0,0,0) d z
1 (d x d y d z) 4
例 7. 求所有的二阶偏导数： 两个混合偏导数：是否总相等
例8. 设
f(x,y)=
xy
x2 x2
y2 y2
,
0 ,
x2 y2 0 x2 y2 0
证明: fxy (0, 0) f yx (0, 0)
在什么条件下才能保证两者相等呢？
定理16.4 这个定理可以推广到 n阶偏导数的情形： 即若函数 f 具有直到 n 阶的连续偏导数，则求偏导数与变量的顺序
z
2
2ze
x2
y2
z
2
2
x
sin
y
u
2 x (1 2 x2 sin2 y) ex2 y2 x4 sin 2 y
xyz
u y
f y
f z
z y
2ye x2 y2 z2 2ze x2 y2 z2 x2 cos y
2 ( y x4 sin y cos y ) ex2 y2 x4 sin 2 y
x y
x f x
y
s f
同理 y
t
例4. 设 u f (xy, y ) 求 u 2u 2u
高等数学11.2多元函数的偏导数和全微分-精选文档
河北工业职业技术学院
高等数学
主讲人 宋从芝
11.2
多元函数的偏导数与全微分
本讲概要 偏导数的概念 高阶偏导数
全微分
一、偏导数的概念
１.偏导数的定义
定义1 设函数 z = f(x , y) 在点 P0(x0 , y0)及其近旁 有定义. 若极限
f ( x xy ,0 ) f ( x ,y ) 0 0 0 l i m x 0 x
2 z z z ; (x fyx ,y ) z yx y x y y x x
z z 2z y y y 2 y y
. (x fyy ,y ) z yy
(x, y) 称为二阶混合偏导数. (x, y) 及 fyx 其中 fxy
类似的，可以定义三阶、四阶、… 、n 阶偏导数，
而 f ( x ,y ) , 二阶及二阶以上的偏导数称为高阶偏导数， x f ( x , y ) 称为函数 f ( x , y ) 的一阶偏导数. y
偏导数都存在， 那么这个偏导数是 x , y 的函数，此函 数称为函数 z = f ( x , y ) 对自变量 x 的偏导函数， 记作
z , f ( x, y), z (x fx ,y ). x 或 x x 可以定义函数 z = f (x , y) 对自变量 y 的偏导 类似地，
代入等式左边得
u u u x y z
2 2 2
2
2
2
4 x y z 4 u 4 x 4 y 4 z
2 2 2
3.偏导数的几何意义
我们知道 一元 函数 y = f (x) 的导数的几何 意义是曲线 y = f (x) 在点 (x0 , y0) 处切线的斜率， 而二元函数 z = f ( x , y ) 在点( x0 , y0) 处的偏导数， 实际上就是一元函数 z = f ( x , y0) 及 z = f (x0 , y ) 分别在点 x = x0 及 y = y0 处的导数． 因此二元函 数 z = f (x , y) 的偏导数的几何意义 也是曲线切线 的斜率.
高等数学
主讲人 宋从芝
11.2
多元函数的偏导数与全微分
本讲概要 偏导数的概念 高阶偏导数
全微分
一、偏导数的概念
１.偏导数的定义
定义1 设函数 z = f(x , y) 在点 P0(x0 , y0)及其近旁 有定义. 若极限
f ( x xy ,0 ) f ( x ,y ) 0 0 0 l i m x 0 x
2 z z z ; (x fyx ,y ) z yx y x y y x x
z z 2z y y y 2 y y
. (x fyy ,y ) z yy
(x, y) 称为二阶混合偏导数. (x, y) 及 fyx 其中 fxy
类似的，可以定义三阶、四阶、… 、n 阶偏导数，
而 f ( x ,y ) , 二阶及二阶以上的偏导数称为高阶偏导数， x f ( x , y ) 称为函数 f ( x , y ) 的一阶偏导数. y
偏导数都存在， 那么这个偏导数是 x , y 的函数，此函 数称为函数 z = f ( x , y ) 对自变量 x 的偏导函数， 记作
z , f ( x, y), z (x fx ,y ). x 或 x x 可以定义函数 z = f (x , y) 对自变量 y 的偏导 类似地，
代入等式左边得
u u u x y z
2 2 2
2
2
2
4 x y z 4 u 4 x 4 y 4 z
2 2 2
3.偏导数的几何意义
我们知道 一元 函数 y = f (x) 的导数的几何 意义是曲线 y = f (x) 在点 (x0 , y0) 处切线的斜率， 而二元函数 z = f ( x , y ) 在点( x0 , y0) 处的偏导数， 实际上就是一元函数 z = f ( x , y0) 及 z = f (x0 , y ) 分别在点 x = x0 及 y = y0 处的导数． 因此二元函 数 z = f (x , y) 的偏导数的几何意义 也是曲线切线 的斜率.
《高等数学》第三节 全微分
z 称为函数 z xy 的全增量， 记 (x) 2 (y ) 2
当 0 时,即 x 0 ,且
y 0
xy 是比 时，
高阶的无穷小. 则 z yx xy
z z z z ,y 其中 x ，从而有 z x y x y x y
第三节
全微分
一、全微分的定义 二、全微分在近似计算中的应用
一、全微分的定义
1、引例 一矩形金属片,长为 x ,宽为 y ,则面积 z xy 当边长 x, y 分别有增量 x, y 时,面积的增量为
z ( x x)( y y) xy yx xy xy
dz = 34dx + 12dy
极限, 连续, 偏导存在, 可微的关系:
极限
连续
+
偏导存在
连续
+
可微
二、全微分在近似计算中的应用 设函数
z f ( x, y) 在点 ( x, y )处可微，当 x, y
分别取得增量 x, y 时，
z f ( x x, y y) f ( x, y) dz f x( x, y)x f y ( x, y)y
yx y 1 d x x y ln x d y
注：关于二元函数全微分的定义及可微分的充 分条件可以完全类似地推广到三元和三元以上 的多元函数. y yz 例２：计算 u x sin 2 e 的全微分． 解
u 1, x u ye yz z
y u 1 yz cos ze y 2 2
15.47
y 1 dz dx ( cos ze yz ) dy ye yz dz 2 2
例３: 求 z = x4 y3 +2x 在点 (1, 2)的全微分.
当 0 时,即 x 0 ,且
y 0
xy 是比 时，
高阶的无穷小. 则 z yx xy
z z z z ,y 其中 x ，从而有 z x y x y x y
第三节
全微分
一、全微分的定义 二、全微分在近似计算中的应用
一、全微分的定义
1、引例 一矩形金属片,长为 x ,宽为 y ,则面积 z xy 当边长 x, y 分别有增量 x, y 时,面积的增量为
z ( x x)( y y) xy yx xy xy
dz = 34dx + 12dy
极限, 连续, 偏导存在, 可微的关系:
极限
连续
+
偏导存在
连续
+
可微
二、全微分在近似计算中的应用 设函数
z f ( x, y) 在点 ( x, y )处可微，当 x, y
分别取得增量 x, y 时，
z f ( x x, y y) f ( x, y) dz f x( x, y)x f y ( x, y)y
yx y 1 d x x y ln x d y
注：关于二元函数全微分的定义及可微分的充 分条件可以完全类似地推广到三元和三元以上 的多元函数. y yz 例２：计算 u x sin 2 e 的全微分． 解
u 1, x u ye yz z
y u 1 yz cos ze y 2 2
15.47
y 1 dz dx ( cos ze yz ) dy ye yz dz 2 2
例３: 求 z = x4 y3 +2x 在点 (1, 2)的全微分.
高等数学第八章第三讲 多元函数的全微分
元函数全微分的概念； ２．多元函数全微分的求法； ３．多元函数连续、可导、可微的关系．
作业： 28; 29; 30.
Yu lin Polytechnic（Shen Mu Campus）
Yu lin Polytechnic（Shen Mu Campus）
上页 下页 返回
第八章
证 如果函数 z f ( x , y ) 在点P ( x , y ) 可微分,
P ( x x , y y ) P 的某个邻域
z Ax By o( )
总成立,
当y 0 时，上式仍成立，此时 | x | ,
z z 2 x 1, 2 y y ( 1,2 )
所求全微分
dz 5dx 2dy.
Yu lin Polytechnic（Shen Mu Campus）
第八章
y yz À2 Æ ¼ ã Ë ¯ º ý Ê u x sin e Ä µ « È ¢ Î · Ö . 2
[ f ( x , y y ) f ( x , y )],
Yu lin Polytechnic（Shen Mu Campus）
第八章
在第一个方括号内，应用拉格朗日中值定理
f ( x x , y y ) f ( x , y y )
f x ( x 1x, y y )x
Yu lin Polytechnic（Shen Mu Campus）
第八章
函数若在某区域 D 内各点处处可微分， 则称这函数在 D 内可微分.
如果函数z f ( x , y ) 在点( x , y ) 可微分, 则 函数在该点连续.
事实上 z Ax By o( ), lim z 0,
作业： 28; 29; 30.
Yu lin Polytechnic（Shen Mu Campus）
Yu lin Polytechnic（Shen Mu Campus）
上页 下页 返回
第八章
证 如果函数 z f ( x , y ) 在点P ( x , y ) 可微分,
P ( x x , y y ) P 的某个邻域
z Ax By o( )
总成立,
当y 0 时，上式仍成立，此时 | x | ,
z z 2 x 1, 2 y y ( 1,2 )
所求全微分
dz 5dx 2dy.
Yu lin Polytechnic（Shen Mu Campus）
第八章
y yz À2 Æ ¼ ã Ë ¯ º ý Ê u x sin e Ä µ « È ¢ Î · Ö . 2
[ f ( x , y y ) f ( x , y )],
Yu lin Polytechnic（Shen Mu Campus）
第八章
在第一个方括号内，应用拉格朗日中值定理
f ( x x , y y ) f ( x , y y )
f x ( x 1x, y y )x
Yu lin Polytechnic（Shen Mu Campus）
第八章
函数若在某区域 D 内各点处处可微分， 则称这函数在 D 内可微分.
如果函数z f ( x , y ) 在点( x , y ) 可微分, 则 函数在该点连续.
事实上 z Ax By o( ), lim z 0,
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
d z e2 d x 2e2 d y
(2,1)
9
例3. 设
解: f (x,0,0) x 3 cos x
注意: x , y , z 具有 轮换对称性
f
x
(0,0,0)
3
x cos
x
x
0
1 4
利用轮换对称性 , 可得
f y (0,0,0)
f z (0,0,0)
1 4
d f (0,0,0) f y (0,0,0) d x f y (0,0,0) d y f z (0,0,0) d z
z x
z u z v u x v x
f11
f21
z
uv
z z u z v y u y v y
f12 f2 2
x yx y
3、 中间变量只有一个的情形
例如: z f u u x, y
z dz u x du x
z dz u y du y
z u xy
注: 由于 z f u 是一元函数,则它对u 的导数应该
fv
f2
2z u 2
fuu (u, v)
fuu
f11
2z v2
fvv (u, v)
fvv
f22
2z uv 2z vu
fuv (u, v) fvu (u, v)
f
fuv f12 vu f21
称为混合偏导数
当 f12 和 f21 均连续时有 f12 f21
在计算时注意合并同类项!
推广: 设下面所涉及的函数都可微 .
求
解
2z x y
2z yx
2y x2
f2
2y( x
y2 x2
f22 )
例4 已知 Z f (x y, x ) g y
求
2z .
y x
yx
其中 f , g 二阶连续可导
解:
z y
x
f1
x y2
f 2
1 g x
2z yx
f1 x[ y
f11
1 y
f12]
1 y2
f2
x y2
[
du dx udy udz u
8
例1. 计算函数
在点 (2,1) 处的全微分.
解法1:
z yexy , x
z xexy y
z x
(2,1) e2 ,
z y
(2,1) 2e2
d z e2 d x 2e2 d y
(2,1)
解法2:
z
e2 ,
x (2,1)
z
2e2 ,
y (2,1)
u
u2v 2 v
2
,
0,
u2 v2 0 u2 v2 0
易知:
但复合函数 z f (t, t ) t 2
d z 1 z du z dv 0 1 0 1 0
d t 2 u dt v dt
常用导数符号
设 z f (u, v)
z u
fu (u, v)fuf1z vfv (u, v)
定理. 若函数 处偏导数连续, 则复合函数
在点 t 可导, 且有链式法则
d z z d u z dv d t u d t v d t 此式是 Z 对t的导数 dz 称为全导数.
dt
z f (u,v)
z
uv tt
说明: 若定理中
偏导数连续减弱为
偏导数存在, 则定理结论不一定成立.
例如: z f (u, v) ut, vt
下面两个定理给出了可微与偏导数的关系:
(1) 函数可微
偏导数存在
(2) 偏导数连续
函数可微
4
定理1(必要条件) 若函数 z = f (x, y) 在点(x, y) 可微 ,
则该函数在该点偏导数
必存在,且有
d z z x z y x y
证: 由全增量公式
得到对 x 的偏增量
x x
x
z lim x z A x x0 x
例1
已知 f
可微，求
u,u ,u. x y z
u x
f1(
x y
,
y) z
u y
f1 f2
u z
f 2
例2
z
f
(x
y2 ) 已知
x
f (u)
连续,求
解
2y x2
f
(x
y2 ) x
2y x
(1
y2 x2
)
f (x
y2 ) x
例3 已知 z f (x , y2 ) f 具有二阶连续偏导数, x
1 (d x d y d z) 4
11
例4
证明函数
在点 (0,0) 连续且偏导数存在, 但偏导数在点 (0,0) 不连
续, 而 f (x, y) 在点 (0,0) 可微 .
证: 1) 因
xy sin
1 x2 y2
xy x2 y2 2
所以
lim f (x, y) 0 f (0,0)
z Ax B y o( ) ,
可表示成
其中 A , B 不依赖于 x , y , 仅与 x , y 有关，则称函数
f ( x, y ) 在点( x, y) 可微，Ax By 称为函数f (x, y)
在点 (x, y) 的全微分, 记作 dz d f Ax By
若函数在域 D 内各点都可微, 则称此函数在D 内可微.
x
y
例4
z x yez
求 z , z . x y
解: 利用微分形式的不变性有
dz d x yez d x ezd y yezdz
(1 yez )dz d x ezd y
dz
1 1 yez
d x ez 1 yez
dy
z x
1 1 yez
z y
ez 1 yez
作业
习题册 第八章第三节
fx (x,
y)
lim( x sin 1
x0
2|x| 2
x3 2 | x |3 cos
1) 2|x|
极限不存在 , fx (x, y) 在点(0,0)不连续 ;
同理 , f y (x, y) 在点(0,0)也不连续
13
4) 下面证明 f (x, y) 在点 (0,0)可微 :
令 (x)2 (y)2 , 则
r2 h2
[2rhr r2h 2rrh hr2 r2h]
r, h 的一个线性函数 的高阶无穷小
当 r , h 很小时 V [2rhr r2h]
与一元函数类似此式称为函数V的全微分.
2
定义: 如果函数 z = f ( x, y )在定义域 D 的内点( x , y )
处全增量
同样可证z B , 因此有 y
令y 0, Ax o ( x )
5
注意: 定理1 的逆定理不成立 . 即:
偏导数存在函数 不一定可微 !
反例: 函数 f (x, y)
xy , x2 y2 0 x2 y2
0,
x2 y2 0
易知 fx (0, 0) f y (0, 0) 0 , 但
f f x (0,0)x f y (0,0)y
说明: 此题表明, 偏导数连续只是可微的充分条件. 14
作业
习题册 第八章第二节
第四节
第九章
多元复合函数的求导法则
一元复合函数
求导法则
微分法则
本节内容: 一、多元复合函数求导的链式法则
二、多元复合函数的全微分
一、多元复合函数求导的链式法则
中间变量是一元函数的情形
高等数学(下)
第七讲
三、函数全微分
二元函数
当x, y 取得增量x, y 时如何方便
求出全增量 Z f x x, y y f x, y
引例:设有一圆柱体,受压后方式变形,它的底面半径由
r 变化到 r r, 高度由 h 变化到 h h. 问圆柱体体积
V 改变了多少.
解: 圆柱体的体积 V r2h V [(r r)2 (h h) r2h]
z [ fx ( 0, 0)x f y ( 0, 0)y]
x y (x)2 (y)2
x y (x)2 (
y)
2
0
o( ) 因此,函数在点 (0,0) 不可微 .
注: 此为证明二元函数可微的方法!
6
定理2 (充分条件) 若函数
的偏导数
z x
,
z y
在点 (x, y) 连续, 则函数在该点可微分.且
dz z dx z dy x y
7
推广: 类似可讨论三元及三元以上函数的可微性问题.
例如, 三元函数 u f (x, y, z)的全微分为 d u u x u y u z x y z
习惯上把自变量的增量用微分表示, 于是
du
u d z z
记作
dz u
d x u , d y u , d z u 称为偏微分. 故有下述叠加原理
采用一元函数的导数记号 dz f (u). du
又如, z f (x,v), v (x, y)
当它们都具有可微条件时, 有
z x
f x
f1 f21
注意:
这里 z 与 f 不同, x x
z x表示固定 y 对 x 求导,
f 表示固定 v 对 x 求导 x
z y
f2 2
口诀 : 分段用乘, 分叉用加, 单路全导, 叉路偏导
注: 对x 的偏增量
x x
x Ax o ( x )
其中 Ax 称为对 x 的偏微分 3
由微分定义 :
lim z lim (Ax By ) o ( ) 0
x0
0