19秋福师《数学分析选讲》在线作业二参考答案
福建师范大学《数学分析选讲》考试大纲
《数学分析选讲》考试大纲一、单项选择题1．设243)(-+=x x x f ，则当0→x 时，有（ ）.A ．)(x f 与x 是等价无穷小B ．)(x f 与x 同阶但非是等价无穷小C ．)(x f 是比x 高阶的无穷小D ．)(x f 是比x 低阶的无穷小 答案：B 2. 设函数111()1xx e f x e -=+，则0x =是()f x 的（ ）A ．可去间断点B ．第二类间断点C ．跳跃间断点D ．连续点 答案：C3. 22lim (1)n nn→∞+等于( ).A ． 221ln xdx ⎰B ．212ln xdx ⎰C ．212ln(1)x dx +⎰ D ．221ln (1)x dx +⎰答案：B4. (,)z f x y =在点(,)x y 处偏导数连续是(,)f x y 在该点连续的（ ）条件.A ．充分非必要 B.必要非充分 C.充分必要 D.既不充分也不必要 答案：A5. 如果级数1n n u ∞=∑和1n n v ∞=∑均发散，则以下说法正确的是（ ）.A. 1()n n n u v ∞=±∑一定都收敛 B. 1()n n n u v ∞=±∑一定都发散C. 1()n n n u v ∞=-∑可能收敛，但1()n n n u v ∞=+∑一定发散D. 1()n n n u v ∞=±∑都可能收敛答案：D6. 设232)(-+=x x x f ，则当0→x 时，有（ ）A ．)(x f 与x 是等价无穷小 B. )(x f 与x 是同阶但非等价无穷小 C. )(x f 是比x 高阶的无穷小 D. )(x f 是比x 低阶的无穷小答案;B 7. 设arctan (),xf x x=则0x =是()f x 的（ ） A. 连续点 B. 可去间断点 C.跳跃间断点 D. 第二类间断点 答案：B8. 下列极限计算中，正确的是（ ）A ．01lim(1)x x e x +→+= B. 01lim(1)1x x x +→+= C. 1lim(1)x x e x →∞-=- D. 1lim(1)x x e x -→∞+=答案：B9. 设函数)(x f 在0x 处可导，且2)(0'=x f ，则=--→hx f h x f h )()(lim000（ ）A.21 B. 2 C. 21- D. -2 答案：D10. 下列反常积分中收敛的是 （ ） A. 211x dx x +∞+⎰B. 1+∞⎰12011sin dx x x ⎰ D. 10ln xdx ⎰答案：D11. 函数()y f x =，若0000()(2)3,|limx x h f x f x h dy h=→--==则（ ）A. 32dx B.32dx - C.3dx D.3dx -答案：A12. 已知函数(,)f x y 在点(0,0)的某个邻域内连续，且224(,)(0,0)(,)lim1()x y f x y xyx y →-=+，则下述四个选项中正确的是 ( ). A ．点(0,0)不是(,)f x y 的极值点 B. 点(0,0)是(,)f x y 的极小值点 C. 点(0,0)是(,)f x y 的极大值点D. 根据所给条件无法判断点(0,0)是否是(,)f x y 的极值点 答案：A13. lim →∞n 等于( ) A. 1ln ⎰xdx B. 0ln +∞⎰xdx C. 1⎰xdx D. 0+∞⎰xdx .答案：A14.设)(x f 在],[b a 上连续，则0[()]xd f t dt dx -⎰等于( )A. ()f x -B. ()f x -C. ()f x --D. ()f x 答案：A15.下列结论正确的是（ ）.A. 若0()f x dx +∞⎰和0()f x dx -∞⎰均发散，则()f x dx +∞-∞⎰一定发散；B. 若0()f x dx +∞⎰发散，0()g x dx +∞⎰发散，则0[()()]f x g x dx +∞+⎰一定发散； C. 若0()f x dx +∞⎰发散，0()g x dx +∞⎰发散，则0()()f x g x dx +∞⎰一定发散； D. 若0()f x dx +∞⎰收敛，0()g x dx +∞⎰发散，则0()()f x g x dx +∞⎰一定发散.答案：A16.lim →∞n 等于( ) A. 1ln ⎰xdx B. 0ln +∞⎰xdx C. 1⎰xdx D. 0+∞⎰xdx .答案：A 17. 函数2ln(1)y x =+单调增加且图形为凹的区间是（ ）.A. (,1)-∞-B. (1,0)-C. (0,1)D. (1,)+∞答案：C18. 设二元函数(,)f x y 存在偏导数，则00000(2,)(,)lim x f x x y f x x y x∆→+∆--∆=∆（ ）.A. 0B. 00(,)x f x x y +∆C. 002(,)x f x yD. 003(,)x f x y 答案;D19. 若24()f x dx x C '=+⎰，则)(x f =（ ）A ．2x C + B. 33x C + C.5285x C + D. 4x C +答案：C20. 部分和数列}{n S 有界是正项级数∑∞=1n n u 收敛的( )条件A. 充分非必要B. 必要非充分C.充分必要D.非充分非必要 答案：C21．当0→x 时，x x sin -与x 比较是（ ）.A.等价无穷小B.高阶无穷小C.低阶无穷小D.同阶无穷小 答案：B22. 设32()431f x x x x =+--，则方程()0f x =（ ）. A.在(0,1)内没有实根 B.在(1,0)-内没有实根C.在(,0)-∞内有两个不同的实根D.在(0,)+∞内有两个不同的实根 答案：C23. 设32,1()3,1x x f x x x ⎧≤⎪=⎨⎪>⎩，则()f x 在1x =处的（ ）.（A ）左右导数都存在（B ）左导数存在，右导数不存在 （C ）左右导数都不存在（D ） 左导数不存在，右导数存在 答案：B24. 0()0f x '=是()f x 在0x x =取得极值的（ ）. A ．充分非必要条件 B ．必要非充分条件 C ．充分且必要条件 D ．既非充分又非必要条件 答案：D25. 设()f x 和()g x 均为区间I 内的可导函数，则在I 内，下列结论正确的是（ ）.A ．若()()f x g x =, 则()()f x g x ''= B. 若()()f x g x ''=，则()()f x g x = C. 若()()f x g x >，则 ()()f x g x ''> D. 若()()f x g x ''>，则()()f x g x > 答案：A26．()f x 在[,]a b 有界是()f x 在[,]a b 可积的（ ）.A. 充分非必要条件B. 必要非充分条件C. 充分且必要条件D. 既非充分又非必要条件 答案：B27. 设()f x 为可导函数，且满足0(1)(1)13lim x f f x x →--=，那么曲线()y f x =在点(1,(1))f 处的切线斜率为 ( )A. 3B. 3-C. 1D. 1-答案：A二、判断题：以下各题若正确请在（ ）内填“√”, 若错误填“×”. 1. 若{}n x 不是无穷大量，则{}n x 必存在收敛子列. （ ） 答案：√2.)(x f 在],[b a 上连续是⎰ba dx x f )(存在的充要条件 . （ ）答案：×3. 若()f x 是初等函数，其定义域为(,)a b ，0(,)x a b ∈，则00lim ()()x x f x f x →= .（ ） 答案：√4. 若(1,2)n n u v n ≤=，级数1n n v ∞=∑收敛，则1n n u ∞=∑不一定收敛.（ ）答案：√5. 已知函数(,)f x y 在点(0,0)的某个邻域内连续，且224(,)(0,0)(,)lim1()x y f x y xyx y →-=+，则点(0,0)是(,)f x y 的极小值点. （ ） 答案：×6.若{}n x 不是无穷大量，则{}n x 任一子列均不是无穷大量. （ ） 答案：×7. 若函数()f x 在[,]a b 上可积，则()f x 在[,]a b 上也可积. （ ） 答案：×8. 当0x x →时，()f x 不以A 为极限，则存在00{},(1,2),()n n n x x x n x x n ≠=→→∞，使{()}n f x 不以A 为极限.（ ） 答案：√9. 若lim 0n n u →∞=，则级数1n n u ∞=∑收敛但和不一定是0 . （ ）答案：×10. 对),(y x f z =, 偏导数连续,则全微分存在. （ ） 答案：√11.若{}n x 不是无穷大量，则{}n x 必存在有界子列. （ ） 答案：√12. 若函数()f x 在[,]a b 上可积，而()g x 只在有限个点上与()f x 的取值不相同，则()g x 在[,]a b 上也可积，且有()()bbaaf x dxg x dx =⎰⎰.（ ）答案：√13.若()f x 在点0x 连续，则()f x 在0x 既是右连续，又是左连续. （ ） 答案：×14. 函数21xx-展开成x 的幂级数为210,1n n x x ∞+=<∑. （ ）答案：√15.二元函数22220(,)0,0x y f x y x y +≠=+=⎩，在点(0,0)处连续，偏导数存在.（ ） 答案：√ 三、填空题1、若20(23)0kx x dx -=⎰，则k 的值为 .答案：0或12、设21(2021)n n x ∞=-∑收敛，则lim n n x →∞= .答案：20213、级数1nn ∞=的收敛区间是 .答案：（2，4）或[2,4）4.设21(10)n n x ∞=-∑收敛，则lim n n x →∞= .答案：105.(,)(0,0)limx y →= .答案：46.级数21nn ∞=的收敛区间是_____________.答案：（1，3）7.广义积分20110k dx x π+∞=+⎰，则1k= . 答案：58.1lim 1+xx x →∞⎛⎫= ⎪⎝⎭. 答案：e9.设21,0()0,0x x f x x x e ⎧--⎪≠=⎨⎪=⎩，则(0)f '= . 答案：1四、计算题1. 2+3200lim (sin )x x x t dtt t t dt→-⎰⎰.解 原式=++320026lim lim 12(sin )1cos xx x x x x x x x→→⋅==--2.求sin cos cos 2x x y x e π+=+ 的导数.解：cos sin ()'=-x x xe e esin sin ln sin sin ()cos n ()l ()'='=+xx x x xex x x xx cos 02'π⎛⎫= ⎪⎝⎭sin sin cos ln '()sin 所以+=-x x x xe xy x x x e . 3.求积分cot 1sin xdx x+⎰.解：cot 1sin xdx x+⎰=()sin sin 1sin d x x x +⎰=11sin sin 1sin d x x x ⎛⎫- ⎪+⎝⎭⎰=ln sin ln 1sin x x c -++ 4.将函数1()12f x x=+展成1-x 的幂级数. 解：1001111()21232(1)31(1)312(1)2()(1)(1),333nn n n n n n f x x x x x x ∞∞+=====++-+--=-=--∑∑收敛域为15 (,)22 -.五、综合题.1.241lim cos1nnnn→∞-+！. （请说明理由）答：原式＝０（有界量乘以无穷小量）2. 叙述一元函数可导，可微，连续的关系.答：一元函数可导与可微是等价的，可导推出连续，连续不一定可导.（温馨提示：照抄答案，没有加入自己的答案，一律不给分。
数学分析(Ⅱ)试题与参考答案
数学分析（2）期末试题课程名称 数学分析（Ⅱ） 适 用 时 间 试卷类别 1 适用专业、年级、班 应用、信息专业一、单项选择题（每小题3分，3×6＝18分）1、 下列级数中条件收敛的是（ ）．A ．1(1)nn ∞=-∑ B ． 1nn ∞= C ．21(1)nn n∞=-∑ D ． 11(1)nn n ∞=+∑2、 若f 是(,)-∞+∞内以2π为周期的按段光滑的函数, 则f 的傅里叶（Fourier ）级数在它的间断点x 处 （ ）．A ．收敛于()f xB ．收敛于1((0)(0))2f x f x -++ C ． 发散 D ．可能收敛也可能发散3、函数)(x f 在],[b a 上可积的必要条件是（ ）．A ．有界B ．连续C ．单调D ．存在原函数4、设()f x 的一个原函数为ln x ，则()f x '=（ ）A ．1x B ．ln x x C ． 21x- D ． x e 5、已知反常积分20 (0)1dxk kx +∞>+⎰收敛于1，则k =（ ）A ． 2πB ．22πC ． 2D ． 24π6、231ln (ln )(ln )(1)(ln )n nx x x x --+-+-+ 收敛，则（ ）A ． x e <B ．x e >C ． x 为任意实数D ． 1e x e -<<二、填空题（每小题3分，3×6＝18分）1、已知幂级数1nn n a x∞=∑在2x =处条件收敛，则它的收敛半径为 ．2、若数项级数1n n u ∞=∑的第n 个部分和21n nS n =+，则其通项n u = ，和S = ． 3、曲线1y x=与直线1x =，2x =及x 轴所围成的曲边梯形面积为 ． 4、已知由定积分的换元积分法可得，1()()bxxaef e dx f x dx =⎰⎰，则a = ，b = ．5、数集(1)1, 2 , 3, 1nn n n ⎧⎫-=⎨⎬+⎩⎭的聚点为 ． 6、函数2()x f x e =的麦克劳林（Maclaurin ）展开式为 ．65三、计算题（每小题6分，6×5＝30分） 1、(1)dx x x +⎰． 2、2ln x x dx ⎰． 3、 0 (0)dx a >⎰． 4、 2 0cos limsin xx t dt x→⎰．5、dx ⎰．四、解答题（第1小题6分，第2、3 小题各8分，共22分）1、讨论函数项级数21sin n nxn ∞=∑在区间(,)-∞+∞上的一致收敛性． 2、求幂级数1nn x n ∞=∑的收敛域以及收敛区间内的和函数．3、设()f x x =, 将f 在(,)ππ-上展为傅里叶（Fourier ）级数．五、证明题（每小题6分，6×2＝12分）1、已知级数1nn a∞=∑与1nn c∞=∑都收敛，且, 1, 2, 3 n n n a b c n ≤≤= ，证明：级数1nn b∞=∑也收敛．2、证明：22 0sin cos nn x dx x dx ππ=⎰⎰．66试题参考答案与评分标准课程名称 数学分析(Ⅱ) 适 用 时 间 试卷类别 1 适用专业、年级、班 应用、信息专业一、 单项选择题（每小题3分，3×6＝18分）⒈ B ⒉ B ⒊ A ⒋ C ⒌ D ⒍ D二、 填空题（每小题3分，3×6＝18分）⒈ 2 ⒉ 2, =2(1)n u S n n =+ ⒊ ln 2⒋ 1, a b e == ⒌ 1± ⒍ 201, (,)!nn x x n ∞=∈-∞+∞∑三、 计算题（每小题6分，6×5＝30分）1. 解111(1)1x x x x=-++ 1(1)dx x x ∴+⎰ （3分）11()1dx x x =-+⎰ln ln 1.x x C =-++ （3分）2. 解 由分部积分公式得231ln ln 3x xdx xdx =⎰⎰ 3311ln ln 33x x x d x =-⎰ （3分） 33111ln 33x x x dx x =-⋅⎰ 3211ln 33x x x dx =-⎰ 3311ln 39x x x C =-+ （3分） 3. 解 令sin , [0, ]2x a t t π=∈ 由定积分的换元积分公式，得⎰2220cos a tdt π=⎰ （3分）6768220(1cos 2)2a t dt π=+⎰221(sin 2)22a t t π=+2.4a π=（3分）4. 解 由洛必达(L ＇Hospital)法则得200cos limsin xx tdtx →⎰20cos limcos x xx →= （4分） 0lim cos x x →=1= （2分）5. 解= （2分）20 sin cos x xdx π=-⎰4204(cos sin ) (sin cos )x x dx x x dx πππ=-+-⎰⎰ （2分）244(sin cos )(sin cos )x x x x πππ=+-+2.= （2分）四、 解答题（第1小题6分，第2、3小题各8分，共22分）1. 解 (, ), x n ∀∈-∞∞∀+（正整数）22sin 1nx n n ≤ （3分） 而级数211n n ∞=∑收敛，故由M 判别法知，21sin n nxn ∞=∑在区间(,)-∞+∞上一致收敛． （3分）2. 解 幂级数1nn x n∞=∑的收敛半径1R ==，收敛区间为(1,1)-． （2分）易知1nn x n∞=∑在1x =-处收敛，而在1x =发散，故1nn x n∞=∑的收敛域为[1,1)-． （2分） 01, (1, 1)1n n x x x ∞==∈--∑ （2分）逐项求积分可得0001, (1,1)1xx nn dt t dt x t ∞==∈--∑⎰⎰． 即101ln(1), (1,1).1n nn n x x x x n n+∞∞==--==∈-+∑∑ （2分） 3. 解 函数f 及其周期延拓后的图形如下函数f 显然是按段光滑的，故由收敛性定理知它可以展开为Fourier 级数。
19秋福师《复变函数》在线作业二[2]答案
![19秋福师《复变函数》在线作业二[2]答案](https://img.taocdn.com/s3/m/dcd9b70627d3240c8547ef15.png)
【奥鹏】19秋福师《复变函数》在线作业二
试卷总分:100 得分:100
一、单选题（共30题，60分）
1、
AA
BB
CC
DD
[仔细分析上述题目，并作出选择]
正确答案是：C
2、
AA
BB
CC
DD
[仔细分析上述题目，并作出选择]
正确答案是：B
3、
AA
BB
CC
DD
[仔细分析上述题目，并作出选择]
正确答案是：A
4、
AA
BB
CC
DD
[仔细分析上述题目，并作出选择]
正确答案是：D
5、关于泰勒级数和洛朗级数的区别，下列说法错误的是（）A收敛区域形状一定不同
B泰勒级数能表示的解析函数类型不如洛朗级数广
C泰勒级数是洛朗级数的特例
D洛朗级数是泰勒级数的推广
[仔细分析上述题目，并作出选择]
正确答案是：A。
数学分析选讲习题答案。我们学校自己编的《数学分析选讲》讲义习题解答,不要乱评论。OK？
27. 28. 29. 30. 31. 32. 33. 34. 35.
Burkill, J.C., and Burkill,H., A Second Course in Mathematical Analysis, London, Cambridge, 1970. Gelbaum, B., Problems in Analysis, New York, Springer-Verlag, 1982. Klambauer, G., Problems and Propositions in Analysis, New York, Marcel Dekker, 1979. Lang, S., Undergraduate Analysis, New York, Springer-Verlag, 1983. Pö lya, G. and Szegö , G., Problems and Theorems in Analysis, Vol.1, Berlin, Springer-Verlag, 1972. Smith, K. T., Primer of Modern Analysis, New York, Springer-Verlag, 1983. Stromberg, K.R., An Introduction to Classical Analysis, Belmont, Wadsworth, 1981. Van Rooij, A. C. M., and Schikhof, W. H. A Second Course on Real Functions, London, Cambridge, 1982. Lewin, J. W., Amer. Math. Monthly, 93(1986), 395 397.
< 1 (x12 + x1+ 1) | x n 1 | ,极限为 1. 7 n n n 14. 由平均不等式, 1 kak n !( ak )1 / n . n k 1 k 1 15. 由 F (1, y) = ½ f (y 1) = ½ y2 y + 5 得 f (t ) = t + 9, 故 xn+1 =
西南大学《数学分析选讲》网上作业及参考答案
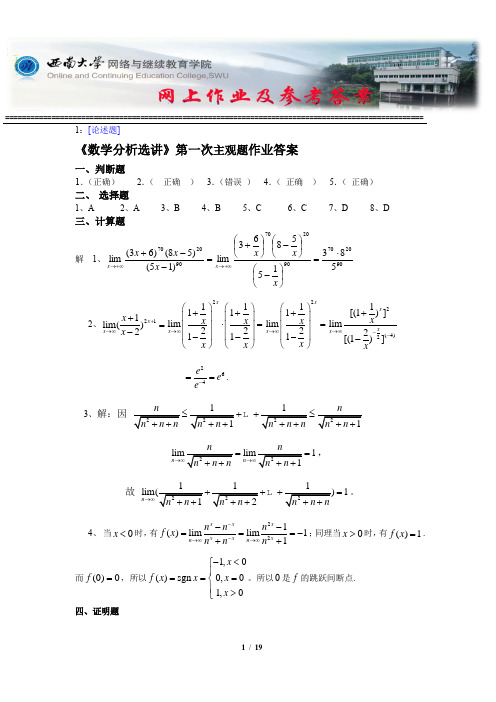
===================================================================================================1：[论述题]《数学分析选讲》第一次主观题作业答案一、判断题 1．（正确） 2．（ 正确 ） 3．（错误 ） 4．（ 正确 ） 5．（ 正确） 二、 选择题1、A2、A3、B4、B5、C6、C7、D8、D三、计算题解 1、902070902070902070583155863lim )15()58()63(lim⋅=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+=--++∞→+∞→x x x x x x x x 2、211lim()2x x x x +→∞+=-21111lim 2211xx x x x x →∞⎛⎫⎛⎫++ ⎪ ⎪⋅= ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭211lim 21xx x x →∞⎛⎫+ ⎪= ⎪ ⎪-⎝⎭2(4)21[(1)]lim 2[(1)]x x x x x→∞--+- 264e e e-==. 3、解：因2n ≤++≤+1n n==， 故 21n n →∞++=+。
4、 当0x <时，有221()lim lim 11x x x x x x n n n n n f x n n n --→∞→∞--===-++；同理当0x >时，有()1f x =.而(0)0f =，所以1,0()sgn 0,01,0x f x x x x -<⎧⎪===⎨⎪>⎩。
所以0是f 的跳跃间断点.四、证明题===================================================================================================证 由b a <，有b b a a <+<2. 因为2lim ba a a n n +<=∞→，由保号性定理，存在01>N ，使得当1N n >时有2b a a n +<。
【奥鹏】2019秋福师《微积分》在线作业二[2]答案
![【奥鹏】2019秋福师《微积分》在线作业二[2]答案](https://img.taocdn.com/s3/m/1ffe1c530b4c2e3f56276342.png)
19秋福师《微积分》在线作业二
试卷总分:100 得分:100
一、判断题（共50题，100分）
1、若f(x)在x0处可导，则f(x)在x0处可微。
（）
A错误
B正确
[仔细阅读以上题目后，并运用所学知识完成作答]
正确的选择是：B
2、若函数在某一点的极限存在，则它在这点的极限惟一。
（）
A错误
B正确
[仔细阅读以上题目后，并运用所学知识完成作答]
正确的选择是：B
3、所有初等函数及其复合而得到的函数都是连续函数。
（）
A错误
B正确
[仔细阅读以上题目后，并运用所学知识完成作答]
正确的选择是：B
4、极值点一定包含在区间内部驻点或导数不存在的点之中。
（）A错误
B正确
[仔细阅读以上题目后，并运用所学知识完成作答]
正确的选择是：A
5、图像法表示函数的特点是形象直观，一目了然。
（）
A错误
B正确
[仔细阅读以上题目后，并运用所学知识完成作答]
正确的选择是：B
6、多元函数u=xyz+2008的全微分du=2008+yzdx+xzdy+xydz（）A错误
B正确
[仔细阅读以上题目后，并运用所学知识完成作答]
正确的选择是：A
7、隐函数的导数表达式中不可含有y。
（）
A错误
B正确
[仔细阅读以上题目后，并运用所学知识完成作答]。
福师1203考试批次《数学分析选讲》复习题及参考答案
福师1203考试批次《数学分析选讲》复习题及参考答案本课程复习题所提供的答案仅供学员在复习过程中参考之用，有问题请到课程论坛提问。
本复习题页码标注所用教材为：教材名称 单价 作者版本 出版社 数学分析41华东师范大学数学系第三版高等教育出版社如学员使用其他版本教材，请参考相关知识点福师1203考试批次《数学分析选讲》复习题及参考答案一一、（12分）选择题（将符合要求的结论题号，填在题末的括号内，每题至多选两个题号）： 1. 与lim n n x a →∞=的定义等价的是：（ ）A 、0,ε∀> 总有n x a ε-<；B 、0,ε∀> 至多只有{}n x 的有限项落在(,)a a εε-+之外；C 、存在自然数N ，对0,ε∀>当n N >，有n x a ε-<；D 、0(01),εε∀><<存在自然数N ，对,n N ∀>有n x a ε-<； 答案：B,D2．下列命题中正确的是：（ ）A 、若函数()f x 在[,]a b 内无界，则()f x 在[,]a b 上不可积；B 、若函数()f x 在[,]a b 上不连续，则()f x 在[,]a b 上不可积；C 、若函数()f x 在[,]a b 上可积，则[()]()xaf t dt f x '=⎰;D 、若函数()f x 在[,]a b 上可积，则()f x 在[,]a b 上也可积，反之不然. 答案：AD3.函数()f x 在[a,b]上可积的必要条件是( )A 、有界B 、连续C 、单调D 、存在原函数 答案：A二、填空题：（共10分，每题2分）1.设21(1)nn x∞=-∑收敛，则lim n n x →∞= 。
考核知识点：级数的收敛性。
参见教材（下册）P1-5 提示：利用P3页的推论进行计算。
2.(,)limx y →= 。
考核知识点：二元函数的极限。
参见教材（下册）P93-96.提示：)(,)(,)(0,0)(,)(0,0)1limlimlim1x y x y x y xy→→→==3.设3()sin F x x '=，则()F x = 。
39882福建师范大学19秋福师《数学分析选讲》在线作业二答案
20.如图所示 A.A B.B C.C D.D 答案：D
21.
如题 A.A B.B C.C D.D 答案：C
22.
如题 A.A B.B C.C D.D 答案：D
23.
如题 A.A B.B C.C D.D 答案：A
24.
如题 A.A B.B C.C
福师《数学分析选讲》在线作业二
单选题 1.
如题 A.A B.B C.C D.D 答案：B
2. A.A B.B C.C D.D 答案：A
3. A.A B.B C.C D.D 答案：D
4.如图所示 A.A B.B C.C D.D 答案：D
5.
如题 A.A B.B C.C D.D 答案：C
6.
如题 A.A B.B C.C D.D
37.
如题 A.A B.B C.C D.D 答案：B
38. A.A B.B C.C D.D 答案：C
39.
如题 A.A B.B C.C D.D 答案：C
40.
如题 A.A B.B C.C D.D 答案：D
41.题面见图片 A.A B.B C.C D.D 答案：A
42.
如题 A.A B.B
C.C D.D 答案：D
13. A.A B.B C.C D.D 答案：C
14. A.A B.B C.C D.D 答案：B
15.
如题 A.A B.B C.C D.D 答案：B
16.题目如图 A.A B.B C.C D.D 答案：C
17.
如题 A.A B.B C.C D.D 答案：B
18.
如题 A.A B.B C.C D.D
答案：A
西南大学《数学分析选讲》网上作业题及答案
（0088）《数学分析选讲》网上作业题答案1：第一次作业2：第二次作业3：第三次作业4：第四次作业5：第五次作业1：[判断题]两个无穷小量的和一定是无穷小量参考答案：正确1、应注意写出要点；2、注意检查语法和拼写错误；3、文理通顺，中心突出。
2：[判断题]两个无穷大量的和一定是无穷大量参考答案：错误1、应注意写出要点；2、注意检查语法和拼写错误；3、文理通顺，中心突出。
3：[单选题]设f,g在（-a,a)上都是奇函数，则g(f(x))与f(g(x))A：都是奇函数B：都是偶函数C：一是奇函数，一是偶函数D：都是非奇、非偶函数参考答案：A社会实践是检验认识是否具有真理性的唯一标准，这是由真理的本性和实践的特点所决定的。
第一，真理的本性是主观同客观相符合。
要判明认识是否具有真理性的标准，只能通过一种能够把主观同客观联系、沟通起来的桥梁，这就是人们的社会实践，舍此别无它路。
它成为“实践是检验真理的唯一标准”的内在根据。
第二，实践的过程是一个主体能动地使自己的目的物化或对象化的过程，因而它具有直接现实性。
因此实践可以使主观与客观相对照，从而直接检验出主观认识是否与客观相符合以及符合的程度。
4：[判断题]闭区间上的连续函数是一致连续的参考答案：正确1、应注意写出要点；2、注意检查语法和拼写错误；3、文理通顺，中心突出。
5：[单选题]设数列{An}收敛，数列{Bn}发散，则数列{AnBn}A：收敛B：发散C：是无穷大D：可能收敛也可能发散参考答案：D马克思主义认为，劳动创造了人本身，同时也就创造了人类社会。
因此，只有实践，才是社会生活的真正本质。
说实践是社会的本质，主要理由是：首先，实践是社会关系的发祥地。
其次，实践构成了社会生活的基本领域。
最后，实践构成了社会发展的动力。
6：[判断题]最大值若存在必是上确界参考答案：正确1、应注意写出要点；2、注意检查语法和拼写错误；3、文理通顺，中心突出。
7：[判断题]若f,g在区间I上一致连续，则fg在I上也一致连续。
数学分析选讲习题答案。我们学校自己编的《数学分析选讲》讲义习题解答,不要乱评论。OK？
pk / (p1+…+pn) < / 2. 故 n > N + m 时 | n k 1 pk ak / (p 1 +…+p n ) a | < s1 + ( / 2) ((p N+1 +…+pn ) / (p 1 +…+p n )) < . 8. 设 bn→b 〖若 . an→a, 则 b = 3a〗 设 a = b/3, n > N 时| bn b | < / 2, 则 | an a | = ½ | (bn b) (an1 a) | ½ | bn b | + ½ |an1 a | < ¼ + ½ |an1 a | <…< ½ + 2 (n N) |an1 a | < . 9. 设各式为 an . (1) n 1 a n n (n 3), a n→1; (2) 分子分母各式均分解因式, a n =
参 考 文 献
1. 庄亚栋, 王慕三 数学分析, 北京, 高等教育出版社, 1990.
2. Rudin, w., Principles of Mathematical Analysis, 3-d. New York, McGraw-Hill, 1976. 中译 本, 数学分析原理(上册), 赵慈庚、蒋铎译， 3. G. 克莱鲍尔, 数学分析, 庄亚栋译, 上海 , 上海科学技术出版社, 1981. 4. Birkhoff, G., and MacLane, S., A Survey of Modern Algebra, 4-d. New York, Macmillan, 1977. 中译本: G. 伯克霍夫, S. 麦克莱恩 , 近世代数概论(上册), 王连祥、徐广善译, 人 民教育出版社, 1979. 5. 杨宗磐, 数学分析入门 , 北京, 科学出版社 , 1958. 6. 华东师范大学数学系 , 数学分析(第二版), 北京, 高等教育出版社, 1990. 7. 庄亚栋, 方洪锦, 姚林, 基础数学试题选解 , 南京 , 江苏科学技术出版社, 1986 8. Dieudonne, J., Foundations of Morden Analysis, New York, Academic, 1969. 中译本: J. 狄厄多尼, 现代分析基础 , 苏维宜译, 科学出版社, 1982. 9. 方企勤, 数学分析, 第一册 , 北京, 高等教育出版社, 1986. 10. 沈燮昌, 数学分析, 第二册, 北京, 高等教育出版社, 1986. 11. 廖可人, 李正元 , 数学分析, 第三册 , 北京 , 高等教育出版社 , 1986. 12. 陈传璋, 金福临 , 朱学炎, 欧阳光中 数学分析(第二版), 北京, 高等教育出版社, 1983. 13. 14. 15. 16. 17. 18. Г .М .菲赫金哥尔茨 , 微积分学教程 , 第二卷二、 三分册 , 北京大学高等数学教研室译, 北京, 高等教育出版社 , 1954. 强文久, 李元章 , 黄雯荣, 数学分析的基本概念与方法, 北京, 高等教育出版社, 1989. 汪林, 数学分析中的问题与反例, 昆明, 云南科技出版社, 1990. 裴礼文, 数学分析中的典型问题与方法, 北京 , 高等教育出版社 , 1993. 周家云, 刘一鸣 , 解际太, 数学分析的方法, 济南, 山东教育出版社, 1991.
数学分析选讲参考答案
《数学分析选讲》A/B 模拟练习题参考答案一、选择题:(共18题,每题3分） 1、下列命题中正确的是（ Ａ B ）A 、若'()()F x f x =，则()F x c +是()f x 的不定积分，其中c 为任意常数B 、若()f x 在[,]a b 上无界，则()f x 在[,]a b 上不可积C 、若()f x 在[,]a b 上有界,则()f x 在[,]a b 上可积D 、若()f x 在[,]a b 上可积,则()f x 在[,]a b 上可积 2、设243)(-+=x x x f ,则当0→x 时，有( Ｂ ） A ．)(x f 与x 是等价无穷小 B ．)(x f 与x 同阶但非是等价无穷小 C.)(x f 是比x 高阶的无穷小 Ｄ．)(x f 是比x 低阶的无穷小3、若f 为连续奇函数，则()x f sin 为（ A ) A 、奇函数 Ｂ、偶函数Ｃ、非负偶函数 Ｄ、既不是非正的函数,也不是非负的函数． 4、函数()f x 在[,]a b 上连续是()f x 在[,]a b 上可积的（ Ａ ）条件 A ． 充分非必要 B 。
必要非充分C 。
充分必要条件D ． 非充分也非必要条件。
5、若f 为连续奇函数，则()x f cos 为（ B ） A 、奇函数 Ｂ、偶函数Ｃ、非负偶函数 D 、既不是非正的函数，也不是非负的函数。
6、设arctan (),xf x x=则0x =是()f x 的（ B ) A 。
连续点 B. 可去间断点 Ｃ.跳跃间断点 D. 第二类间断点7、设+N ∈∃N ,当N n >时,恒有n n b a >,已知A a n n =∞→lim ，B b n n =∞→lim .则正确的选项是（ A ）A 、B A ≥ B 、B A ≠C 、B A > Ｄ、A 和B 的大小关系不定． 8、函数f （x,ｙ) 在点00(,)x y 连续是它在该点偏导数都存在的( Ａ ） A 。
数学分析选讲习题答案。我们学校自己编的《数学分析选讲》讲义习题解答,不要乱评论。OK？
参 考 文 献
1. 庄亚栋, 王慕三 数学分析, 北京, 高等教育出版社, 1990.
2. Rudin, w., Principles of Mathematical Analysis, 3-d. New York, McGraw-Hill, 1976. 中译 本, 数学分析原理(上册), 赵慈庚、蒋铎译， 3. G. 克莱鲍尔, 数学分析, 庄亚栋译, 上海 , 上海科学技术出版社, 1981. 4. Birkhoff, G., and MacLane, S., A Survey of Modern Algebra, 4-d. New York, Macmillan, 1977. 中译本: G. 伯克霍夫, S. 麦克莱恩 , 近世代数概论(上册), 王连祥、徐广善译, 人 民教育出版社, 1979. 5. 杨宗磐, 数学分析入门 , 北京, 科学出版社 , 1958. 6. 华东师范大学数学系 , 数学分析(第二版), 北京, 高等教育出版社, 1990. 7. 庄亚栋, 方洪锦, 姚林, 基础数学试题选解 , 南京 , 江苏科学技术出版社, 1986 8. Dieudonne, J., Foundations of Morden Analysis, New York, Academic, 1969. 中译本: J. 狄厄多尼, 现代分析基础 , 苏维宜译, 科学出版社, 1982. 9. 方企勤, 数学分析, 第一册 , 北京, 高等教育出版社, 1986. 10. 沈燮昌, 数学分析, 第二册, 北京, 高等教育出版社, 1986. 11. 廖可人, 李正元 , 数学分析, 第三册 , 北京 , 高等教育出版社 , 1986. 12. 陈传璋, 金福临 , 朱学炎, 欧阳光中 数学分析(第二版), 北京, 高等教育出版社, 1983. 13. 14. 15. 16. 17. 18. Г .М .菲赫金哥尔茨 , 微积分学教程 , 第二卷二、 三分册 , 北京大学高等数学教研室译, 北京, 高等教育出版社 , 1954. 强文久, 李元章 , 黄雯荣, 数学分析的基本概念与方法, 北京, 高等教育出版社, 1989. 汪林, 数学分析中的问题与反例, 昆明, 云南科技出版社, 1990. 裴礼文, 数学分析中的典型问题与方法, 北京 , 高等教育出版社 , 1993. 周家云, 刘一鸣 , 解际太, 数学分析的方法, 济南, 山东教育出版社, 1991.
数学分析选讲复习资料参考答案
数学分析选讲复习资料参考答案一、选择题（将符合要求的结论题号，填在题末的括号内，每题至多选两个题号）：1、下列命题中，正确的是：A 、若()f x 在点0x 连续，则()f x 在0x 连续；B 、若 ()f x 在(,)a b 上连续；则对0,()f x ε∀>在[,]a b εε+-上连续；C 、若()f x 是初等函数，其定义域为(,)a b ，则()f x 在(,)a b 有界；D 、函数()y f x =在0x 点连续的充要条件是()f x 在0x 点的左、右极限存在. 答：（ B ） 2、当0x x →时，()f x 以B 为极限，则A 、0,0,εδ∀>∀>存在x 满足00,x x δ<-<有()f xB ε-<; B 、0,0,εδ∀>∃>00x x δ<-<当时，有()f x B ε-<；C 、存在00{},(1,2),()n n n x x x n x x n ≠=→→∞L ，使{()}n f x 不以B 为极限；D 、0x x →时，()f x 的极限存在. 答：（ B D ）3、设函数()f x 在[,]a b 上连续，则在[,]a b 上有A 、()()ba d f x dx f x dx =⎰； B 、()()xad f t dt f x dx =⎰；C 、；()f x 在[,]a b 上单调；D 、()f x 在[,]a b 上未必有最大值. 答：（ B ） 4、设级数n u ∑收敛，则A 、0,N ∃> 当n m N >>时，11/2m m n u u u ++++<L .B 、{}1n n u =∞有界；C 、绝对收敛；D 、 lim n n u →∞未必存在答：（ AB ） 5、若数列{}1n n a =∞满足lim nn a a →∞=，则下列说法正确的是（ B ）A 、0,ε∀> 0,N ∀>当n N >时，都有n a a ε-<。
福师《数学分析选讲》在线作业一-0003.0B58938
A:A B:B C:C D:D 答案：A
如题
A:A B:B C:C D:D 答案：B
A:A B:B C:C D:D 答案：B
如题
A:A B:B C:C D:D 答案：C
如题
A:A B:B C:C D:D 答案：D
如题
A:A B:B C:C D:D 答案：D
如题
A:A B:B C:C D:D 答案：C
如题
A:A B:B C:C D:D 答案：D 题目如图 A:0 B:1 C:2 D:3 答案：C
题目如图
A:A B:B C:C D:D 答案：C
如题
A:A B:B C:C D:D 答案：A
A:A B:B C:C D:D 答案：A
如题
A:A B:B C:C D:D 答案：C A:A B:B C:C D:D 答案：B 如图所示 A:A B:B C:C D:D 答案：D
如题
A:A B:B C:C D:D 答案：B
如题
A:A B:B C:C D:d 答案：D
如题
A:A B:B C:C D:D 答案：B
如题
A:A B:B C:C D:D 答案：B
A:A B:B C:C D:D 答案：C
如题
A:A B:B C:C D:D 答案：D
如题
A:A B:B C:C D:D 答案：D
福师《数学分析选讲》在线作业一-0003
如题
A:A B:B C:C D:D 答案：B 如图所示 A:A B:B C:C D:D 答案：C
如题
A:A B:B C:C D:D 答案：A
如题
A:A B:B D 答案：B
如题
A:A B:B C:C D:D 答案：B 如图所示 A:A B:B C:C D:D 答案：D
福师《数学分析选讲》模拟试题及答案(一)
《数学分析选讲》试题一一、单项选择题1．设243)(-+=x x x f ，则当0→x 时，有（ ）.A ．)(x f 与x 是等价无穷小B ．)(x f 与x 同阶但非是等价无穷小C ．)(x f 是比x 高阶的无穷小D ．)(x f 是比x 低阶的无穷小 答案：B 2. 设函数111()1xx e f x e -=+，则0x =是()f x 的（ ）A ．可去间断点B ．第二类间断点C ．跳跃间断点D ．连续点 答案：C3. 22lim (1)n nn→∞+等于( ).A ． 221ln xdx ⎰B ．212ln xdx ⎰C ．212ln(1)x dx +⎰ D ．221ln (1)x dx +⎰答案：B4. (,)z f x y =在点(,)x y 处偏导数连续是(,)f x y 在该点连续的（ ）条件.A ．充分非必要 B.必要非充分 C.充分必要 D.既不充分也不必要 答案：A5. 如果级数1n n u ∞=∑和1n n v ∞=∑均发散，则以下说法正确的是（ ）.A. 1()n n n u v ∞=±∑一定都收敛B. 1()n n n u v ∞=±∑一定都发散C. 1()n n n u v ∞=-∑可能收敛，但1()n n n u v ∞=+∑一定发散D. 1()n n n u v ∞=±∑都可能收敛答案：D6. 设232)(-+=x x x f ，则当0→x 时，有（ ）A ．)(x f 与x 是等价无穷小 B. )(x f 与x 是同阶但非等价无穷小 C. )(x f 是比x 高阶的无穷小 D. )(x f 是比x 低阶的无穷小答案;B 7. 设arctan (),xf x x=则0x =是()f x 的（ ） A. 连续点 B. 可去间断点 C.跳跃间断点 D. 第二类间断点 答案：B8. 下列极限计算中，正确的是（ ）A ．01lim(1)x x e x +→+= B. 01lim(1)1x x x +→+= C. 1lim(1)x x e x →∞-=- D. 1lim(1)x x e x -→∞+=答案：B9. 设函数)(x f 在0x 处可导，且2)(0'=x f ，则=--→hx f h x f h )()(lim000（ ）A. 21B. 2C. 21- D. -2答案：D10. 下列反常积分中收敛的是 （ ） A. 211x dx x +∞+⎰B. 1+∞⎰12011sin dx x x ⎰ D. 10ln xdx ⎰ 答案：D11. 函数()y f x =，若0000()(2)3,|limx x h f x f x h dy h=→--==则（ ）A. 32dx B.32dx - C.3dx D.3dx -答案：A12. 已知函数(,)f x y 在点(0,0)的某个邻域内连续，且224(,)(0,0)(,)lim1()x y f x y xyx y →-=+，则下述四个选项中正确的是 ( ).A ．点(0,0)不是(,)f x y 的极值点 B. 点(0,0)是(,)f x y 的极小值点 C. 点(0,0)是(,)f x y 的极大值点D. 根据所给条件无法判断点(0,0)是否是(,)f x y 的极值点 答案：A13. lim ln→∞n n等于( ) A. 1ln ⎰xdx B. 0ln +∞⎰xdx C. 1⎰xdx D. 0+∞⎰xdx .答案：A14.设)(x f 在],[b a 上连续，则[()]xd f t dt dx -⎰等于( ) A. ()f x - B. ()f x - C. ()f x -- D. ()f x 答案：A二、判断题：以下各题若正确请在（ ）内填“√”, 若错误填“×”. 1. 若{}n x 不是无穷大量，则{}n x 必存在收敛子列. （ ） 答案：√2.)(x f 在],[b a 上连续是⎰ba dx x f )(存在的充要条件 . （ ）答案：×3. 若()f x 是初等函数，其定义域为(,)a b ，0(,)x a b ∈，则00lim ()()x x f x f x →= .（ ）答案：√4. 若(1,2)n n u v n ≤=，级数1n n v ∞=∑收敛，则1n n u ∞=∑不一定收敛.（ ）答案：√5. 已知函数(,)f x y 在点(0,0)的某个邻域内连续，且224(,)(0,0)(,)lim1()x y f x y xyx y →-=+，则点(0,0)是(,)f x y 的极小值点. （ ） 答案：×6.若{}n x 不是无穷大量，则{}n x 任一子列均不是无穷大量. （ ） 答案：×7. 若函数()f x 在[,]a b 上可积，则()f x 在[,]a b 上也可积. （ ）答案：×8. 当0x x →时，()f x 不以A 为极限，则存在00{},(1,2),()n n n x x x n x x n ≠=→→∞，使{()}n f x 不以A 为极限.（ ） 答案：√9. 若lim 0n n u →∞=，则级数1n n u ∞=∑收敛但和不一定是0 . （ ）答案：×10. 对),(y x f z =, 偏导数连续,则全微分存在. （ ） 答案：√ 三、填空题1、若20(23)0kx x dx -=⎰，则k 的值为 .答案：0或12、设21(2021)n n x ∞=-∑收敛，则lim n n x →∞= .答案：20213、级数1nn ∞=的收敛区间是 .答案：（2，4）或[2,4）4.设21(10)n n x ∞=-∑收敛，则lim n n x →∞= .答案：105.(,)limx y →= .答案：46.级数2nn ∞=_____________.答案：（1，3）7.广义积分2110k dx x π+∞=+⎰，则1k= . 答案：58.1lim 1+xx x →∞⎛⎫= ⎪⎝⎭. 答案：e9.设21,0()0,0x x f x x x e ⎧--⎪≠=⎨⎪=⎩，则(0)f '= . 答案：1 四、计算题1. 2+3200lim (sin )x x x t dtt t t dt→-⎰⎰.解 原式=++320026lim lim 12(sin )1cos x x x x x x x x x→→⋅==--2.求sin cos cos 2x x y x e π+=+ 的导数.解：cos sin ()'=-x x xe e esin sin ln sin sin ()cos n ()l ()'='=+xx x x xex x x x xcos 02'π⎛⎫= ⎪⎝⎭sin sin cos ln '()sin 所以+=-x x x xe xy x x x e . 五、综合题.1.241lim cos 1n n n n →∞-+！. （请说明理由）答： 原式＝０（有界量乘以无穷小量） 2. 叙述一元函数可导，可微，连续的关系.答：一元函数可导与可微是等价的，可导推出连续，连续不一定可导。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
试卷总分:100 得分:100
一、单选题 (共 50 道试题,共 100 分)
1.{图}
如题
A.A
B.B
C.C
D.D
答案:A
2.{图}
如题
A.A
B.B
C.C
D.D
答案:D
3.{图}
如题
A.A
B.B
C.C
D.D
答案:D
4.{图}
如题
A.A
B.B
C.C
D.D
答案:D
A.A
B.B
C.C
D.D
答案:D
30.{图}
如题
A.A
B.B
C.C
D.D
答案:B
31.{图}
如题
A.A
B.B
C.C
D.D
答案:D
32.{图}
如题
A.A
B.B
C.C
D.D
答案:C
33.{图}
如题
A.A
B.B
C.C
D.D
答案:D
34.{图} {图}
A.A
B.B
C.C
D.D
答案:B
35.{图}
A.A
B.B
17.{图}
如题
A.A
B.B
C.C
D.D
答案:D
18.{图}
A.A
B.B
C.C
D.D
答案:D
19.如图所示{图}
A.A
B.B
C.C
D.D
答案:D
20.{图}
如题
A.A
B.B
C.C
D.D
答案:B
21.{图}
如题
A.A
B.B
C.C
D.D
答案:A
22.{图}
如题
A.A
B.B
C.C
D.D
答案:D
23.{图}
第一种情况，对于双方当事人都是既知道有违反婚姻生效的法定事由，又对此事由有过错的，适用现行的规定，即双方协商，协商不成的，由法院裁判。第二种情况，对于仅知道有违反婚姻生效事由但没有过错的当事人，在财产分配过程中应当少分，而不论是否属于弱国一方。因为这种情形下，当事人对社会公共利益和法律秩序的挑衅太严重，应当予以更加不利的法律后果。第三种情况，对于不知道存在违反婚姻生效法定事由但是有过错的当事人，境如当事人婚前不知自己患有禁止结婚的疾病而后导致婚姻可撤销，可以适用离婚时财产分割的相关规定。第四种情况，对于既不知道存在违反婚姻生效要件存在，对此又没有过错责任的当事人应当适用离婚时的财产分割规定。因为以上情形中，当事人对社会公益和法律秩序的破坏很小，甚至是无辜的，应当适用更为有利的法律制度。但是需要注意的时，当事人不知的状态需要一直持续到婚姻被确认无效或者被撤销，否者将构化为第一种或者第二种情况。最后，对于子女抚养在题一律适用与离婚时一样的对子女保护的相关规定。
D.D
答案:C
48.{图}
如题
A.A
B.B
C.C
D.D
答案:C
49.{图}
如题
A.A
B.B
C.C
D.D
答案:D
50.{图}
A.A
B.B
C.C
D.D
答案:A
以下内容可以删除：
我们知道立法活动的论后是立法者对不同利益间的衡量。无效婚姻和可撤销婚姻制度衡量的是公共利益、道德秩序与个人的意思自治，其法律结果应当衡量的是当事人对利益的危害程度和当事人的责任程度以及其应适当承受的不利后果。但是法律结果却被规定在同一个条文里适用同样的结果，这显然是不合无的。如果不区分两者的法律后果，那么二者的法定情形的重构从现实层面上来讲也就毫无意义了。
5.{图}
如题
A.A
B.B
C.C
D.D
答案:B
6.{图}
如题
A.A
B.B
C.C
D.D
答案:D
7.{图}
如题
A.A
B.B
C.C
D.D
答案:C
8.如图所示{图}{图}
A.A
B.B
C.C
D.D
答案:D
9.{图}
如题
A.A
B.B
C.C
D.D
答案:C
10.{图}
如题
A.A
B.B
C.C
Dห้องสมุดไป่ตู้D
答案:B
11.{图}
D.D
答案:D
42.如图所示{图}{图}
A.A
B.B
C.C
D.D
答案:D
43.题面见图片{图}
A.A
B.B
C.C
D.D
答案:C
44.{图}
如题
A.A
B.B
C.C
D.D
答案:D
45.{图}
A.A
B.B
C.C
D.D
答案:D
46.{图}
如题
A.A
B.B
C.C
D.D
答案:A
47.{图}
如题
A.A
B.B
C.C
{图}{图}
A.A
B.B
C.C
D.D
答案:B
12.{图}
如题
A.A
B.B
C.C
D.D
答案:A
13.题目如图{图}{图}
A.A
B.B
C.C
D.D
答案:C
14.{图}
如题
A.A
B.B
C.C
D.d
答案:D
15.如图所示{图}{图}
A.A
B.B
C.C
D.D
答案:C
16.{图}
如题
A.A
B.B
C.C
D.D
答案:B
如题
A.A
B.B
C.C
D.D
答案:D
24.{图}
如题
A.A
B.B
C.C
D.D
答案:B
25.{图}
如题
A.A
B.B
C.C
D.D
答案:B
26.题面见图片{图}
A.A
B.B
C.C
D.D
答案:A
27.题目如图{图}
A.0
B.1
C.2
D.3
答案:C
28.{图}
如题
A.A
B.B
C.C
D.D
答案:A
29.{图}
如题
其次，笔者认为对婚姻无效与被撤销后的财产分割应方式当加以丰富。我国现在的无效婚姻与可撤销婚姻制度的法律后果中对财产的规定非常单一，忽略了当事人在该婚姻因违法导致无效过程中的主观意志和责任程度，采取各打五十大板的做法不利于发挥法律惩恶扬善的功能。笔者认为在婚姻被撤销或被确认无效后的财产分配中应当参虑双方当事人的主观意志和责任程度，以此作出与之相匹配的分割方案。换句话说主要从“是否知道存在婚姻无效和可撤销的法定事由”和“对法定事由是否有过错”这两个维度来参虑财产的划分。
C.C
D.D
答案:C
36.{图}
如题
A.A
B.B
C.C
D.D
答案:C
37.{图}
A.A
B.B
C.C
D.D
答案:C
38.{图}
A.A
B.B
C.C
D.D
答案:C
39.{图}
如题
A.A
B.B
C.C
D.D
答案:B
40.题面见图片{图}
A.A
B.B
C.C
D.D
答案:A
41.如图所示{图}{图}
A.A
B.B
C.C
首先，笔者认为应当调整现行婚姻无效与可撤销规定的溯及力在题。溯及力涉及到对之前婚姻事实的法律认可状况。如果溯及既往，那么婚姻关系自成立起无效，从而导致因夫妻身份关系产生的其他一切行为也将陷入纠纷，对于与之有交易的第三人来讲将面临不可预测的法律法风险，不利于交易安全。笔者认为应当根据无效婚姻与可撤销婚姻中不同法定情形的违法程度区分为无效婚姻和可撤销婚姻的溯及力。在笔者对于无效婚姻法定情形重构之后，只剩下重婚、近亲婚姻以及未满十六周岁未成年人婚姻三种，本以为可以完全适用的无效婚姻被确认无效后自始无效的规定，但是在引入责任要素之后，笔者发现其中可能存在无辜方的情况，如重婚情形中被重婚的一方不知对方已有配偶，在婚姻被宣告无效之后，被重婚者依然与造成婚姻无效的一方当事人共同承担婚姻自始无效一样的结果，这样的规定对被重婚者不公平，也不利于保护子女的利益。笔者认为应参虑双方当事人的责任区分不同的溯及力，由造成婚姻无效的一方承担婚姻自始无效的后果，无辜一方则自法院宣告无效之日起婚姻开始无效。实际生活中造成婚姻无效的责任人可能是当事人一方，也可能是双方，可统一适用上无规则，笔者认为更加公平。笔者对可撤销婚姻的法定情形重构之后扩充了未达法定婚龄的婚姻、患禁婚疾病的婚姻、欺诈的婚姻与重大误解的婚姻。笔者认为此部分也不可以完全重构为“婚姻被撤销的，自撤销之日起生效”。因为尽管重构后的可撤销婚姻制度所保护的个人私益要件，但是其中当事人还是有过错方与无辜方的区分，适用同种法律后果依然不公平，应当根据造成婚姻无效的责任有无、大小区别对待，重构为“对婚姻被撤销有责任的，适用婚姻自始无效规定，无责任的适用撤销之日起无效。”