四年级几何巧求周长与面积学生版
巧求周长与面积

巧求周长与面积办法技巧:经由过程扭转.平移.朋分等办法,然后本身着手绘图,可以或许奇妙地在简略平面图形周长与面积的基本上求较为庞杂的平面图形的周长与面积.【例1】下图是一座衡宇的平面图,求这座衡宇平面图的周长.【例2】有一块长方形广场,沿着它不合的两条边各划出2米预备种树,剩下的部分仍是长方形,且周长为280米.问:种树的面积是若干平方米?【例3】一块花圃如图所示,梯形ABCD中有个直角三角形,AD=10米,BC=14米,AE=6米,DE=8米.暗影部分的面积是若干平方米?闯关演习:1.有一块纸板外形如图(单位:厘米),这块纸板的周长是若干厘米?2.一块长方形木板,把长和宽各锯去6厘米,锯失落的面积为396平方厘米.如今这块木板的周长是若干厘米?3.图中三角形AED的面积是28平方厘米,长方形ABCD中,AD=7厘米,CF=3厘米.求梯形ABCF的面积.4.(选做题)在一个长方形花圃中有个走道(图中的暗影部分),长方形的面积是216平方米,长18米,走道的宽1.2米,走道的面积是若干平方米?填补题1.在一块正方形的地盘上计划出一块长方形的地(暗影部分)用来建活动场,剩下的面积是123200平方米,相邻的双方剩下的长度是40米和120米.求本来正方形地盘的面积是若干平方米?(640000平方米)2. 将一个长方形和一个正方形按如图方法拼接成一个大长方形,已知拼接后的大长方形的长是25厘米,求本来小长方形的周长.. 50厘米3. 如右下图所示,一个腰长是20厘米的等腰三角形的面积是140平方厘米,在底边上随意率性取一点,这个点到两腰的垂线段的长分离是a 厘米和b 厘米.求a + b 的长.14厘米4. 如下图,一个平行四边形被分成甲.乙两部分,甲的面积比乙大80平方米,甲的上底是若干米?10米6. 如图,三角形ABC 的面积是48平方分米,AD = DE = EC,F 是BC 的中点,FG=GC,暗影部分的面积是若干平方厘米?28平方厘米7. 如右图,把一个三角形的底边延伸2厘米后,面积增长了2.4平方厘米,你知道原三角形的面积是若干吗?例题1:一个等腰直角三角形,最长的边是10厘米,这个三角形的面积是若干平方厘米?【巩固演习1】:如图正方形中套着一个长方形,正方形的边长是12厘米,长方形的四个角的极点把正方形的四条边各分成两段,个中长的一段是短的2倍.求中央长方形的面积.例题2: 求右面平行四边形的周长.【巩固演习2】:求右面三角形的AB 上的高.例题3:求右图等腰直角三角形中暗影部分的面积.(单位:厘米)【巩固演习3】:求四边形ABCD 的面积.(单位:厘米) 例题4:有一种将正方形内接于等腰直角三角 米米410C A 43形.已知等腰直角三角形的面积是72平方厘米,正方形的面积分离是若干?【巩固演习4】:有一种将正方形内接于等腰直角三角形.已知等腰直角三角形的面积是72平方厘米,正方形的面积分离是若干?例题5:图中两个正方形的边长分离是10厘米和6厘米,求暗影部分的面积.【巩固演习5】:图中两个正方形的边长分离是6厘米和4厘米,求暗影部分的面积.【巩固演习6】求右图等腰直角三角形中暗影部分的面积.(单位:厘米)名校真题体验:【例1】下图中甲和乙都是正方形,求暗影部分的面积.(单位:厘米)【练一练】求图中暗影部分的面积.(单位:厘米)【例2】如图所示,甲三角形的面积比乙三角形的面积大6平方厘米,求CE的长度.【练一练】平行四边形ABCD的边长BC=10厘米,直角三角形BCE的直角边EC长8厘米,已知暗影部分的面积比三角形EFG的面积大10平方厘米.求CF的长.【例3】两条对角线把梯形ABCD朋分成四个三角形.已知两个三角形的面积(如图所示),求另两个三角形的面积各是若干?(单位:厘米)B【练一练】下面的梯形ABCD中,下底是上底的2倍,E是AB的中点,求梯形ABCD的面积是三角形EDB面积的若干倍?。
四年级奥数几何问题:巧求周长【三篇】

【导语】成功根本没有秘诀可⾔,如果有的话,就有两个:第⼀个就是坚持到底,永不⾔弃;第⼆个就是当你想放弃的时候,回过头来看看第⼀个秘诀,坚持到底,永不⾔弃,学习也是⼀样需要多做练习。
以下是为⼤家整理的《四年级奥数⼏何问题:巧求周长【三篇】》供您查阅。
【第⼀篇】
下图中是⼀个⽅形螺线.已知两相邻平⾏线之间的距离均为l厘⽶,求螺线的总长度.
【第⼆篇】
有10张长3厘⽶,宽2厘⽶的纸⽚,将它们按照下图的样⼦摆放在桌⾯上,那么这10张纸⽚所盖住的桌⾯的⾯积是多少平⽅厘⽶?
每多盖⼀张,遮住的⾯积增加2×1,所以这10张纸⽚所盖住的桌⾯的⾯积是3×2+2×1×9=24cm2.
【第三篇】
有红、黄、绿三块⼤⼩⼀样的正⽅形纸⽚,放在⼀个正⽅形盒内,它们之间相互叠合(如右图),已知露在外⾯部分中,红⾊⾯积是20,黄⾊⾯积是12,绿⾊⾯积是8,那么正⽅形盒的底⾯积是多少?
黄⾊纸⽚露出部分与绿⾊纸⽚露出部分⾯积不同,把黄⾊纸⽚向左移动,在这个移动过程中,黄⾊纸⽚露出部分减少的⾯积等于绿⾊纸⽚纸⽚露出部分增加的⾯积,它们露出的⾯积和不变,所以图2中黄⾊露出部分⾯积为10,绿⾊⾯积也为10。
红、黄、绿三个长⽅形的⾯积已经求出,因为长⽅形中对⾓的⾯积乘积相等,故有:黄×绿=红×⽩。
空⽩长⽅形的⾯积应为10×10÷20=5,纸盒的底⾯积为20+10+10+5=45。
解答此题的关键是让黄⾊正⽅形纸⽚移动,使复杂的图形变为基本图形。
四年级奥数专题 图形周长和面积

第一讲图形周长和面积知识导航亲爱的同学们,我们已经学会长方形、正方形的周长与面积的计算,利用公式很容易算出它们的面积与周长。
但在遇到一些较复杂的有关长方形和正方形的周长和面积计算时,一些同学就会感到棘手。
这一讲我们将学习用平移、转化、分解、合并等技巧解决难题,使大家在解题中能顺利地找到突破口,化难为易,化繁为简。
精典例题例1:下图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是多少厘米?思路点拨每个正方形的面积为:400÷16=25(平方厘米),所以每个正方形的边长是5厘米。
从上下方向来看有14条边是周长的一部分,从左右方向来看有20条边是周长的一部分,所以……模仿练习计算右面图形的周长(单位:厘米)。
例2:有9个小长方形,它们的长和宽分别相等,用这9个小长方形拼成的大长方形(如图)的面积是45平方厘米,求这个大长方形的周长。
思路点拨从图上可以知道,小长方形的长的4倍等于宽的5倍,所以长是宽的5÷4=1.25倍。
每个小长方形的面积为45÷9=5平方厘米,所以1.25×宽×宽=5,所以宽为2厘米,长为2.5厘米。
模仿练习下图的长方形被分割成5个正方形,已知原长方形的面积为120平方厘米,求原长方形的长与宽。
例3:一块正方形的苗圃(如右图实线所示),若将它的边长各增加30米,则面积增加9900平方米,问原来这块正方形苗圃的面积是多少平方米?思路点拨通过画图可以算出:小正方形的面积为:30×30=900平方米。
用增加的面积减去小正方形的面积就得到增加的两个长方形的面积之和,9900-900=9000平方米。
而增加的两个长方形的面积相等,于是其中一个长方形的面积为9000÷2=4500平方米。
模仿练习喜阳阳小学的操场长90米,宽45米。
改造后,长增加10米,宽增加5米。
现在操场面积比原来增加了多少平方分米?例4:如下图,用标号为1,2,3,4,5的五种大小不同的正方形拼成一个大长方形,大长方形的长和宽分别是18,14,则标号为5的正方形的面积是多少?(2006年“希望杯”第二试)思路点拨如果标号为5的正方形的边长是a ,那么1号比2号大a ,2号比3号大a ,所以1号比3号大2a ,又因为2号和3号的边长之和是14,1号和2号的边长之和是18,所以1号比3号大18-14=4。
小学四年级数学面积与周长的计算

小学四年级数学面积与周长的计算小学四年级数学:面积与周长的计算数学对于小学四年级的学生来说是一门重要且基础的学科。
在数学的学习过程中,面积和周长的计算是一个关键的概念,对于帮助学生理解几何形状和解决实际问题非常重要。
本文将讨论小学四年级学生如何计算面积和周长,以及如何应用这些概念来解决实际问题。
一、面积的计算方法在数学中,面积是指平面图形所占据的空间单位。
小学四年级学生需要学习如何计算各种形状的面积,如正方形、长方形和三角形。
1. 正方形的面积计算正方形是四个边长相等的四边形。
计算正方形的面积非常简单,只需要将正方形的边长相乘即可。
例如,一个正方形的边长为3厘米,则其面积为3厘米乘以3厘米,即9平方厘米。
2. 长方形的面积计算长方形是两个对边相等且四个角都是直角的四边形。
计算长方形的面积也很简单,只需要将长方形的长度乘以宽度即可。
例如,一个长方形的长度为5厘米,宽度为2厘米,则其面积为5厘米乘以2厘米,即10平方厘米。
3. 三角形的面积计算三角形是一个三边都相连的三边形状。
计算三角形面积的方法是将底边长度乘以三角形的高,然后除以2。
例如,一个三角形的底边长为4厘米,高为3厘米,则其面积为4厘米乘以3厘米,再除以2,即6平方厘米。
二、周长的计算方法周长是指一个封闭图形的边长总和。
小学四年级学生需要学习如何计算正方形、长方形和三角形的周长。
1. 正方形的周长计算正方形的周长计算非常简单,只需要将正方形的边长乘以4即可。
例如,一个正方形的边长为5厘米,则其周长为5厘米乘以4,即20厘米。
2. 长方形的周长计算长方形的周长计算方法是将长方形的长度和宽度相加后再乘以2。
例如,一个长方形的长度为6厘米,宽度为3厘米,则其周长为(6+3)乘以2,即18厘米。
3. 三角形的周长计算三角形的周长计算需要将三个边长相加。
例如,一个三角形的三边长分别为3厘米、4厘米和5厘米,则其周长为3厘米加4厘米加5厘米,即12厘米。
四年级秋-第6讲-长正方形周长和面积(二)-学生版
长正方形周长和面积(二)知识纵横特殊图形计算方法:平移法1、角上去掉长方形,周长不变。
2、边上去掉长方形,还要加上两条短线段。
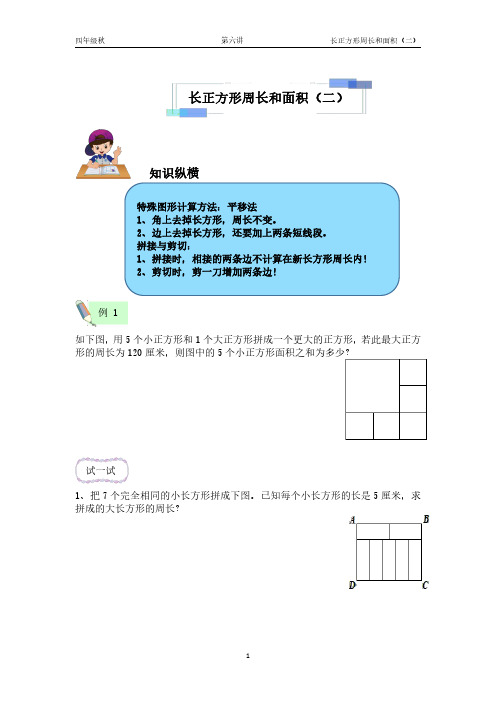
拼接与剪切:1、拼接时,相接的两条边不计算在新长方形周长内!2、剪切时,剪一刀增加两条边!例1如下图,用5个小正方形和1个大正方形拼成一个更大的正方形,若此最大正方形的周长为120厘米,则图中的5个小正方形面积之和为多少?试一试1、把7个完全相同的小长方形拼成下图。
已知每个小长方形的长是5厘米,求拼成的大长方形的周长?将边长是24厘米的大正方形剪成4个相同的小正方形,那么这4个小正方形的周长之和比原来的大正方形的周长增加了多少厘米?2、如下图所示,沿虚线将这个大长方形分成了九个小长方形,如果这九个小长方形的周长之和比大长方形的周长多34厘米,那么,大长方形的周长是多少厘米?下图所示阴影部分的面积是66平方厘米。
则图中正方形的面积是多少平方厘米?3、如图,长方形草坪长和宽各增加8米,面积就增加208平方米,求原草坪的周长?例2试一试例3试一试如下图,从长方形纸片ABCD 上剪去正方形ADFE,剩下的长方形EFCB 的周长是100厘米,线段AB 长多少厘米?4、下图中的阴影部分BCGF 是正方形,线段FH 长18厘米,线段AC 长24厘米,则长方形ADHE 的周长是多少厘米?如下图,正方形花坛(阴影部分)边长增加3米,面积就增加69平方米,求原花坛边长。
例4试一试例51、如图所示,用5个小正方形和1个大正方形拼成一个更大的正方形,若此最大正方形的周长为120厘米。
则图中的5个小正方形周长之和为多少厘米?2、下图的长方形长15厘米,宽10厘米,沿直线剪两刀,将其剪成三个或四个长方形,那么被剪成的若干个长方形的周长之和最大是多少?3、下图阴影部分是正方形,面积是64平方厘米,大长方形周长是50厘米。
大长方形的长为多少厘米?4、如图,正方形花坛(阴影部分)边长增加4米,则面积增加80平方米,求原花坛边长。
巧求周长及面积B版(四年级)

5 / 10
优能一对一小学数学组
【随堂练】 6 个相同的长方形围成了大小两个正方形,已知小正方形的面积是 36 平方厘米,则每个小长方形的面积是多少平方厘米?(第四届希望杯试题)
2、 求不规则图形面积的方法:割补法、转化、整体 - 局部 中心思想:将不规则图形通过上述三种方法转化成规则图形,利用规 则图形的面积求法求不规则图形的面积。
【例题】
一、 周长 【例 1】求右图中一座楼房平面的周长( a 50 米, b 30 米, c 10 米)。(第 三届“走进美妙数学花园“试题)
二、 面积
【例 6 】有一块菜地长 37 米,宽 25 米。菜地中间留了 1 米宽的路,把菜地平
均分成四块,每一块地的面积是多少?(广东省中山市竞赛试题)
1米
1米
25 米
37 米
【随堂练】一块儿菜地长 16 米,宽 8 米,中间有两条路,一条是长方形的,一
条是平行四边形的,问种菜的面积是多少平方米?
巧求周长及面积
优能一对一小学数学组
【教学目标】
1、 培养观察能力、操作能力、空间想象能力、推理能力、巧算能力 2、 训练比较、平移、转化、恒等、代换等思想 3、 掌握求不规则图形周长的方法 4、 掌握求不规则图形面积的方法
【知识梳理】
1、 求不规则图形周长的方法: ① 公式法:包括周长公式及其变式 ② 图形转化法:将某个图形转变为标准的长方形或正方形 ③ 线段平移法:通过平移,将不规则线段整合成比较规则的线段
8 / 10
优能一对一小学数学组
小学数学竞赛:巧求周长.学生版解题技巧 培优 易错 难

一、基本概念①周长:封闭图形一周的长度就是这个图形的周长.②面积:物体的表面或封闭图形的大小,叫做它们的面积.二、基本公式:①长方形的周长2=⨯(长+宽),面积=长⨯宽.②正方形的周长4=⨯边长,正方形的面积=边长⨯边长.三、常用方法:(1)对于基本的长方形和正方形图形,可以直接用公式求出它们的周长和面积,对于一些不规则的比较复杂的几何图形,我们可以采用转化的数学思想方法割补成基本图形,利用长方形、正方形周长及面积计算的公式求解.(2)转化是一种重要的数学思想方法,在转化过程中要抓住“变”与“不变”两个部分.转化后的图形虽然形状变了,但其周长和面积不应该改变,所以在求解过程中不能遗漏掉某些线段的长度或某部分图形的面积.转化的目标是将复杂的图形转化为周长或面积可求的图形.(3)寻求正确有效的解题思路,意味着寻找一条摆脱困境、绕过障碍的途径.因此,我们在解决数学问题时,思考的着重点就是要把所需解决的问题转化为已经能够解决的问题.也就是说,在直接求解不容易或很难找到解题途径的问题时,我们往往转化问题的形式,从侧面或反面寻找突破口,知道最终把它转化成一个或若干个能解决的问题.这种解决问题的思想在数学中叫“化归”,它是数学思维中重要的思想和方法.(4)在几何中,有许多图形是由一些基本图形组合、拼凑而成的.这样的图形我们称为不规则图形.不规则图形的面积往往无法直接应用公式计算.那么,不规则图形的面积怎样去计算呢?对称、旋转、平移这几种几何变换就是解决这类面积问题的手段.四、几个重要的解题思想 (1)平移在平面图形的计算中,常常要将一个平面图形移动到平面上的另一个位置进行计算.其中,将图形沿一个固定方向的移动叫做平移,一个图形经过平行移动不改变其形状与大小,所以图形面积是保持不变的.利用图形的平移,可以使面积计算问题的解法简捷明快,颇有新意.(2)割补割补法在我国古代叫“出入相补原理”,我国古代魏晋时期著名的数学家刘徽在《九章算术注》中就明确地提出“出入相补,各从其类”的出入相补原理.这个原理的内容是几何图形经过分、合、移、补所拼凑成的新图形,它的面积不变.知识点拨4-2-2.巧求周长(3)旋转在平面图形的割补中,有时要将一个图形绕定点旋转到一个新的位置,产生一种新的图形结构,图形在转动过程中形状大小不发生改变.利用这种新的图形结构可以帮我们解决面积的计算问题.(4)对称平面图形中有许多简单漂亮的图形都是轴对称图形.轴对称图形沿对称轴折叠,轴两侧可以完全重合.也就是说,如果一个图形是轴对称图形,那么对称轴平分这个图形的面积.熟悉轴对称图形这个性质,对面积计算会有很大帮助.(5)代换在几何计算中,对有关数量进行适当的等量代换也是解决问题的已知技巧.小结:本讲主要通过求一些不规则图形的周长,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求周长的技巧,提高学生的观察能力、动手操作能力、综合运用能力.例题精讲模块一、图形的周长和面积——割补法【例 1】求图中所有线段的总长(单位:厘米)【例 2】如图所示,点B是线段AD的中点,由A、B、C、D四个点所构成的所有线段的长度均为整数,若这些线段的长度之积为10500,则线段AB的长度是。
巧求周长与面积(五升六分班考)

教学内容概要学生:初中数学备课组教师:王老师年级:小五日期上课时间:学生上课情况:主课题:巧求周长与面积教学目标:1、复习巩固小学阶段平面几何的相关知识2、针对特殊的图形进行几何图形的周长和面积的拓展训练教学重点:1.组合图形的周长的巧妙求法2.组合图形面积的巧妙求法教学难点:1.组合图形的周长的巧妙求法2.组合图形面积的巧妙求法家庭作业1.讲义上相关练习考点及考试要求:1.直线型图形面积及周长教学内容【前课回顾】 上节课作业评讲。
【知识精要】一、知识回顾:我们以前学过哪些几何图形?主要考察哪几个方面的知识?具体的计算公式有哪些? 二、例题精讲:(巧求周长)【例1】 (2007年“希望杯”第一试)右图中的阴影部分BCGF 是正方形,线段FH 长18厘米,线段AC 长24厘米,则长方形ADHE 的周长是__________厘米。
【分析】 由于图中阴影部分BCGF 是个正方形,其四条边的边长都相等,且等于长方形ADHE 的宽。
FH AC +的和应为长方形ADHE 的长加上正方形BCGF 的边长,所以等于长方形ADHE 的长与宽之和。
所以长方形ADHE 的周长为:(1824)284+⨯=厘米。
【例2】 如右图所示,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲,和L 形区域乙和丙。
甲的边长为4厘米,乙的边长是甲的边长的1.5倍,丙的边长是乙的边长的1.5倍,那么丙的周长为多少厘米?EF 长多少厘米?【分析】 乙的周长实际上是正方形AHJE 的周长(我们可将乙与甲重合的两条线段分别向左、向下平移),同样的,丙的周长也就是正方形ABCD 的周长。
由于4 1.56AE =⨯=,6 1.59AD =⨯=,所以丙的周长为9436⨯=厘米,642EF AE AF =-=-=(厘米)。
【例3】 用若干个边长都是2厘米的平行四边形与三角形(如右图)拼接成一个大的平行四边形,已知大平行四边形的周长是244厘米,那么平行四边形和三角形各有多少个?【分析】 大平行四边形上、下两边的长为(24422)2120-⨯÷=厘米,观察上边,每6厘米有两个平行四边形的边,所以共有小平行四边形1206240÷⨯=个,三角形的数量与小平行四边形的数量相等,也是40个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识要点巧求周长【例 1】 如图所示,在一个大长方形的右上角挖去一个小长方形。
如果大长方形的长是7厘米,宽是5厘米。
小长方形的长是5厘米,宽是3厘米。
那么该图形的周长是多少厘米?3575巧求周长与面积巧求周长长方形周长公式:长方形周长=(长+宽)2⨯,记作:C 长方形()2a b =+⨯; 正方形周长公式:正方形周长=边长4⨯,记作:C 正方形4a =⨯; 巧求周长时,常用到“平移线段法”和“标向法”。
巧求面积长方形面积公式:长方形面积=长⨯宽,记作:S 长方形a b =⨯; 正方形面积公式:正方形面积=边长⨯边长,记作:S 正方形2a a a =⨯=; 巧求面积时,常用到“割补法”(将图形平移、对称、旋转)。
【例 2】如图所示,这个多边形任意相邻的两条边都互相垂直。
请根据图中所给出的数,求出这个多边形的周长。
(单位:分米)【例 3】如图所示,这个多边形任意相邻的两条边都互相垂直。
请根据图中所给出的数,求出这个多边形的周长。
(单位:厘米)68【例 4】如图所示,将3个边长为8厘米的正方形叠放在一起。
后一个正方形的顶点恰好落在前一个正方形的正中心。
那么它们覆盖住的图形周长是多少厘米?【例 5】(2010年3月14日第八届小学“希望杯”全国数学邀请赛四年级第1试第9题)将边长为10厘米的五张正方形纸片如图那样放置,每张小正方形纸片被盖住的部分是一个较小的正方形,它的边长是原正方形边长的一半,则图中的图形外轮廓(图中粗线条)的周长为_______厘米。
【例 6】 如图是由10个边长为4厘米的小正方形组成.每个小正方形的顶点恰在另一个正方形的中心,且边相互平行,求这个图形的周长。
【例 7】 如图所示,从一个大正方形的边上挖去一个正方形得到一个多边形。
大长方形的长是6厘米,宽是4厘米,正方形的边长是2厘米。
这个图形的周长是多少厘米?462【例 8】 如图所示,四个长方形组成了一个多边形,如果图中所标数值的单位都是厘米,那么这个多边形的周长是多少厘米?836512【例 9】 如图,某人从点A 走到点B 所走的路程是多少?【例 10】如图,把长为2厘米、宽为1厘米的6个长方形摆成3层。
摆成的图形周长是多少厘米?【例 11】把一块长20厘米,宽12厘米的长方形纸按右下图所示方法一层、二层、三层的摆下去,共要摆十层,摆好后图形周长是多少厘米?【例 12】如图是一个零件的平面图,图中每一条最短线段均长5厘米。
零件长35厘米,高30厘米,这个零件周长是多少厘米?【例 13】用一块长8分米,宽4分米的长方形纸板与两块边长4分米的正方形纸板拼成一个正方形。
拼成的正方形的周长是多少分米?【例 14】两个大小相同的正方形拼成了一个长方形,长方形的周长比原来的两个正方形周长的和减少了6厘米,原来一个正方形的周长是多少厘米?【例 15】 (2007年湖北省“创新杯”数学邀请赛四年级初赛第15题)有两个一样大小的长方形,可拼成两种大长方形,如图,大长方形⑴的周长是240厘米,大长方形⑵的周长是258厘米,原长方形的面积是_______平方厘米。
(2)(1)【例 16】 如图所示,一个边长10厘米的正方形纸片,被横着剪了一刀,竖着剪了两刀,分成了6个小长方形。
这6个小长方形的周长总和等于多少厘米?【例 17】 有一个长20厘米、宽15厘米的长方形,用2条平行于长方形边界的直线可以将其划分成3个或4个小长方形。
这些小长方形周长之和最大是多少厘米?【例 18】 从一张长15厘米、宽9厘米的长方形纸片上剪下一个边长尽可能大的正方形,剩下了一块长方形。
然后从剩下的长方形中再剪下一个边长尽可能大的正方形……按此方式不断重复,直到剩下一个正方形无法再继续剪为止。
请问:所有剪下的正方形的周长之和是多少厘米?【例 19】 如图,这个多边形任意相邻的两条边都互相垂直。
这个多边形的周长是多少?1226326352【例 20】 在图中,至少要测量几条线段,才能求出这个图形的周长?67548123【例 21】 如图所示,共有16条线段,每2条相邻的线段都是互相垂直。
为了计算出这个图形的周长,最少要量出多少条线段的长度?巧求面积【例 22】 有一块菜地长16米,宽8米,菜地中间留了宽2米的路,把菜地平均分成四块,每一块地的面积是多少?2m2m8m 16m【例 23】 有一块边长是18厘米的白色正方形手帕,手帕上横竖各有二道宽是2厘米的红条(图中阴影部分),这块手帕白色部分的面积是多少?【例 24】在一个正方形的小花园周围,环绕着宽5米的水池,水池面积为300平方米,那么正方形花园的面积是多少平方米?【例 25】在一个正方形中放入一个四个顶点与大正方形相接的一个小正方形(如图),如果两个正方形的周长相差16厘米,面积相差96平方厘米,求小正方形的面积。
【例 26】如图所示,大正方形边长为40厘米,中间是一个小正方形,A、B、C、D是大正方形各边的中点,求中间阴影部分小正方形的面积。
【例 27】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形。
求第五个正方形的面积。
?【例 28】(2010年5月3日第三届“学而思·乐加乐”杯综合素质测评B卷第10题)如图所示,最大的正方形的面积是最小的正方形的面积的_______倍。
图10【例 29】(2005年春武汉明心奥数入学测试题四年级第13题)7个完全相同的长方形拼成了图中阴影部分,图中空白部分的面积是多少平方厘米?【例 30】如图所示,在长方形中放入六个形状,大小相同的长方形,图中阴影部分的面积是多少?【例 31】(2001年第十届日本小学数学奥林匹克大赛预赛第2题)如图所示,图中的大长方形分成了四个面积相等的图形。
请问:“?”处的长度是多少厘米??9cm2cm巧求周长与面积【例 32】 如图所示,图中的ABEFGD 是由一个长方形ABCD 及一个正方形CEFG 拼成的,线段的长度如图所示(单位:厘米),求ABEFGD 的周长和面积。
10104GF ED CB A【例 33】 如图所示,4个相同的长方形和一个小正方形拼成一个大的正方形,大正方形的面积是100平方分米,小正方形的面积是36平方分米,求一个小长方形的面积及周长。
一课一练【练习1】 (2007年香港圣公会数学竞赛应用题第3题)如图所示,直线上依次分布着A ,B ,C ,D ,E 5个点,已知1998AB =,2007CE =,AC BD =,那么DE _______=。
ABCD E【练习2】 边长是15厘米的3个正方形拼成一个长方形,这个长方形的周长是多少?【练习3】(2007年天津“陈省身杯”国际青少年数学邀请赛四年级第7题)如图所示(单位:厘米),里面正方形的周长为30厘米,并且外面正方形的各边分别平行于正方形的四条边,根据图中给出的数据,计算长方形周长是_______厘米。
【练习4】如图所示,内部正方形的周长为24厘米。
请根据图中给出的数,求出长方形的周长。
(单位:厘米)【练习5】如图,有一个八边形,任意相邻的两条边都互相垂直,已知其中3条边的长度,这个八边形的周长是多少厘米?(单位:厘米)8412【练习6】如图所示,在一个长为8厘米、宽为6厘米的长方形纸片上剪去一个边长为3厘米的正方形。
⑴如果剪去的正方形在右上角,那么剩下的图形周长是多少厘米?⑵如果剪去的正方形在右边,那么剩下的图形周长是多少厘米?368【练习7】一个正方形与一个长方形的周长相等,长方形长与宽的和是12分米,求正方形的周长和面积。
【练习8】(2007年湖北省“创新杯”数学邀请赛四年级初赛第2题)两个正方形的纸片盖住桌面上,位置与尺寸如图所示(单位:厘米),则它们一共盖住桌面_______平方厘米。
. D.1225.. B.1125A.1075. C.1175322【练习9】有一块长方形土地,长是宽的2倍,中间有一座雕塑,雕塑的底面是一个正方形,周围是草坪(如图所示),草坪的面积是多少平方米?【练习10】有一个正方形水池(图中阴影部分),在它的周围修一个宽是8米的草地,草地的面积为480平方米,求水池的边长?【练习11】如图是学校操场一角,请计算它的面积(单位:米)30403020【练习12】一块长方形钢板,长截下4分米,宽截下1分米后,成了一块正方形钢板,如图所示,面积比原来减少了49平方分米。
求原长方形钢板的面积及裁下钢板的周长。
1【练习13】如图,用16个周长为8厘米的小正方形拼成了一个大正方形。
大正方形的周长是多少厘米?【练习14】(2007年第五届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛四年级第2题)用6张边长为3厘米的正方形纸片拼成一个长方形,这个长方形的周长是_______厘米。
补充【补充1】 如图,在一个长方形中有一段阴影部分。
如果阴影部分恰好是正方形,那么图中大长方形的周长是多少厘米?9厘米6厘米【补充2】 (2007年第五届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛四年级第5题)一个周长是20厘米的正方形,剪下一个周长是6厘米的正方形,剩下的图形的周长是_______。
(写出所有可能的结果)【补充3】 (1989年第一届“华罗庚金杯”少年数学邀请赛小学组团体决赛口试第5题)正方形树林每边长1000米,里面有白杨树和榆树。
小明从树林的西南角走入树林,,碰见一珠白杨树就往正北走,碰到一株榆树就往正东走,最后他走到了东北角。
问:小明一共走了多少米的距离?【补充4】 (2004年4月11日第二届小学“希望杯”全国数学邀请赛四年级第2试第19题)将若干个边长为1的正六边形(即单位六边形)拼接起来,得到一个拼接图形。
例如:周长=14周长=12周长=10周长=6那么,要拼接成周长等于18的拼接图形,需要多少个单位六边形?画出对应的一种图形。
