2018版高中数学第三章导数及其应用3.3.3最大值与最小值学案苏教版选修1_120180309421
3．3.3 最大值与最小值学习目标 1.理解函数最值的概念，了解其与函数极值的区别与联系.2.会求某闭区间上函数的最值．知识点函数的最大值与最小值如图为y＝f(x)，x∈[a，b]的图象．思考1 观察[a，b]上函数y＝f(x)的图象，试找出它的极大值、极小值．思考2 结合图象判断，函数y＝f(x)在区间[a，b]上是否存在最大值，最小值？若存在，分别为多少？思考3 函数y＝f(x)在[a，b]上的最大(小)值一定是某极值吗？思考4 怎样确定函数f(x)在[a，b]上的最小值和最大值？梳理(1)函数的最大(小)值的存在性一般地，如果在区间[a，b]上函数y＝f(x)的图象是一条________________的曲线，那么它必有最大值与最小值．(2)求函数y ＝f (x )在闭区间[a ，b ]上的最值的步骤 ①求函数y ＝f (x )在(a ，b )内的________；②将函数y ＝f (x )的____________与________处的函数值f (a )，f (b )比较，其中最大的一个是____________，最小的一个是____________．类型一 求函数的最值命题角度1 不含参数的函数求最值 例1 求下列函数的最值： (1)f (x )＝2x 3－12x ，x ∈[－2,3]； (2)f (x )＝12x ＋sin x ，x ∈[0,2π]．反思与感悟 求解函数在固定区间上的最值，需注意以下几点： (1)对函数进行准确求导，并检验f ′(x )＝0的根是否在给定区间内； (2)研究函数的单调性，正确确定极值和端点函数值； (3)比较极值与端点函数值大小，确定最值．跟踪训练1 求函数f (x )＝e x (3－x 2)，x ∈[2,5]的最值．命题角度2 含参数的函数求最值例2 已知a 是实数，函数f (x )＝x 2(x －a )，求f (x )在区间[0,2]上的最大值．反思与感悟 由于参数的取值不同会导致函数在所给区间上的单调性的变化，从而导致最值的变化．所以解决这类问题常需要分类讨论，并结合不等式的知识进行求解． 跟踪训练2 在例2中，将区间[0,2]改为[－1,0]，结果如何？类型二 由函数的最值求参数例3 已知函数f (x )＝ax 3－6ax 2＋b ，x ∈[－1,2]的最大值为3，最小值为－29，求a ，b 的值．反思与感悟 已知函数在某区间上的最值求参数的值(范围)是求函数最值的逆向思维，一般先求导数，利用导数研究函数的单调性及极值点，探索最值点，根据已知最值列方程(不等式)解决问题．其中注意分类讨论思想的应用．跟踪训练3 设f (x )＝－13x 3＋12x 2＋2ax .当0<a <2时，f (x )在[1,4]上的最小值为－163，求f (x )在该区间上的最大值．类型三 函数最值的综合应用例4 设函数f (x )＝tx 2＋2t 2x ＋t －1(x ∈R ，t ＞0)． (1)求f (x )的最小值h (t )；(2)若h (t )＜－2t ＋m 对t ∈(0,2)恒成立，求实数m 的取值范围．反思与感悟 (1)“恒成立”问题向最值问题转化是一种常见的题型，一般地，可采用分离参数法进行转化．λ≥f (x )恒成立⇔λ≥[f (x )]max ；λ≤f (x )恒成立⇔λ≤[f (x )]min .对于不能分离参数的恒成立问题，直接求含参函数的最值即可．(2)此类问题特别要小心“最值能否取得到”和“不等式中是否含等号”的情况，以此来确定参数的范围能否取得“＝”．跟踪训练4 已知2x ln x ≥－x 2＋ax －3对一切x ∈(0，＋∞)恒成立，求a 的取值范围．1．函数f (x )＝x 3－3x (|x |<1)，则下列说法正确的是________．(填序号) ①有最大值，但无最小值；②有最大值，也有最小值； ③无最大值，但有最小值；④既无最大值，也无最小值．2．函数y ＝x －sin x ，x ∈⎣⎢⎡⎦⎥⎤π2，π的最大值是________．3．函数f (x )＝x 3－x 2－x ＋t 在区间[0,2]上的最小值为3，则函数在[0,2]上的最大值为________．4．已知函数y ＝－x 2－2x ＋3在区间[a,2]上的最大值为154，则a ＝________.5．函数f (x )＝x 3－12x 2－2x ＋5，若对于任意x ∈[－1,2]，都有f (x )<m ，则实数m 的取值范围是______________．1．求函数在闭区间上的最值，只需比较极值和端点处的函数值即可；若函数在一个开区间内只有一个极值，则这个极值就是最值．2．已知最值求参数时，可先确定参数的值，用参数表示最值时，应分类讨论．3．“恒成立”问题可转化为函数最值问题．提醒：完成作业第3章§3.3 3.3.3答案精析问题导学 知识点思考1 极大值为f (x 1)，f (x 3)，极小值为f (x 2)，f (x 4)． 思考2 存在，f (x )min ＝f (a )，f (x )max ＝f (x 3)．思考3 不一定，也可能是区间端点的函数值．思考4 比较极值与区间端点的函数值，最大的是最大值，最小的是最小值． 梳理 (1)连续不断 (2)①极值 ②各极值 端点 最大值 最小值 题型探究例1 解 (1)f (x )＝2x 3－12x ，所以f ′(x )＝6x 2－12＝6(x ＋2)(x －2)， 令f ′(x )＝0，解得x ＝－2或x ＝ 2. 因为f (－2)＝8，f (3)＝18，f (2)＝－82， f (－2)＝82；所以当x ＝2时，f (x )取得最小值－82； 当x ＝3时，f (x )取得最大值18. (2)f ′(x )＝12＋cos x ，令f ′(x )＝0，又x ∈[0,2π]， 解得x ＝23π或x ＝43π.计算得f (0)＝0，f (2π)＝π，f (23π)＝π3＋32， f (43π)＝23π－32. 所以当x ＝0时，f (x )有最小值f (0)＝0； 当x ＝2π时，f (x )有最大值f (2π)＝π. 跟踪训练1 解 ∵f (x )＝3e x －e x x 2， ∴f ′(x )＝3e x －(e x x 2＋2e xx ) ＝－e x(x 2＋2x －3)＝－e x(x ＋3)(x －1)． ∵在区间[2,5]上，f ′(x )＝－e x (x ＋3)(x －1)<0，∴函数f (x )在区间[2,5]上单调递减，∴当x ＝2时，函数f (x )取得最大值f (2)＝－e 2； 当x ＝5时，函数f (x )取得最小值f (5)＝－22e 5. 例2 解 令f ′(x )＝0， 解得x 1＝0，x 2＝2a3.当2a3≤0，即a ≤0时，f (x )在[0,2]上单调递增， 从而f (x )max ＝f (2)＝8－4a .当2a3≥2，即a ≥3时，f (x )在[0,2]上单调递减， 从而f (x )max ＝f (0)＝0. 当0<2a3<2，即0<a <3时，f (x )在⎣⎢⎡⎦⎥⎤0，2a 3上单调递减，在⎣⎢⎡⎦⎥⎤2a 3，2上单调递增，从而f (x )max ＝⎩⎪⎨⎪⎧8－4a ，0<a ≤2，0， 2<a <3，综上所述，f (x )max ＝⎩⎪⎨⎪⎧8－4a ，a ≤2，0， a >2.跟踪训练2 解 令f ′(x )＝0， 解得x 1＝0，x 2＝23a .①当23a ≥0，即a ≥0时，f (x )在[－1,0]上单调递增，从而f (x )max ＝f (0)＝0；②当23a ≤－1，即a ≤－32时，f (x )在[－1,0]上单调递减，从而f (x )max ＝f (－1)＝－1－a ； ③当－1<23a <0，即－32<a <0时，f (x )在⎣⎢⎡⎦⎥⎤－1，23a 上单调递增；在⎣⎢⎡⎦⎥⎤23a ，0上单调递减，则f (x )max ＝f ⎝ ⎛⎭⎪⎫23a ＝－427a 3. 综上所述，f (x )max＝⎩⎪⎨⎪⎧－1－a ，a ≤－32，－427a 3，－32<a <0，0，a ≥0.例3 解 由题设知a ≠0，否则f (x )＝b 为常函数，与题设矛盾． 求导得f ′(x )＝3ax 2－12ax ＝3ax (x －4)， 令f ′(x )＝0，得x 1＝0，x 2＝4(舍去)． ①当a >0时，f ′(x )，f (x )的变化情况如下表：由表可知，当x ＝0时，f (x )取得极大值b ，也是函数f (x )在[－1,2]上的最大值，∴f (0)＝b ＝3.又f (－1)＝－7a ＋3，f (2)＝－16a ＋3<f (－1)，∴f (2)＝－16a ＋3＝－29，解得a ＝2. ②当a <0时，同理可得，当x ＝0时，f (x )取得极小值b ，也是函数在[－1,2]上的最小值，∴f (0)＝b ＝－29.又f (－1)＝－7a －29，f (2)＝－16a －29>f (－1)，∴f (2)＝－16a －29＝3，解得a ＝－2. 综上可得，a ＝2，b ＝3或a ＝－2，b ＝－29.跟踪训练3 解 f ′(x )＝－x 2＋x ＋2a ， 令f ′(x )＝0，得两根x 1＝1－1＋8a2， x 2＝1＋1＋8a2. 当x ∈(－∞，x 1)，(x 2，＋∞)时，f ′(x )<0；当x ∈(x 1，x 2)时，f ′(x )>0，所以f (x )在(－∞，x 1)，(x 2，＋∞)上单调递减，在(x 1，x 2)上单调递增． 当0<a <2时，有x 1<1<x 2<4，所以f (x )在[1,4]上的最大值为f (x 2)． 又f (4)－f (1)＝－272＋6a <0，即f (4)<f (1)，所以f (x )在[1,4]上的最小值为f (4)＝8a －403＝－163，故a ＝1，x 2＝2，从而f (x )在[1,4]上的最大值为f (2)＝103.例4 解 (1)∵f (x )＝t (x ＋t )2－t 3＋t －1(x ∈R ，t ＞0)， ∴当x ＝－t 时，f (x )取最小值f (－t )＝－t 3＋t －1， 即h (t )＝－t 3＋t －1. (2)令g (t )＝h (t )－(－2t ＋m ) ＝－t 3＋3t －1－m ，由g ′(t )＝－3t 2＋3＝0，得t ＝1，t ＝－1(不合题意，舍去)．当t 变化时g ′(t )、g (t )的变化情况如下表：∴对t ∈(0,2)，当t ＝1时，g (t )max ＝1－m ，h (t )<－2t －m 对t ∈(0,2)恒成立，也就是g (t )<0对t ∈(0,2)恒成立， 只需g (t )max ＝1－m <0，∴m >1. 故实数m 的取值范围是(1，＋∞)． 跟踪训练4 解 由2x ln x ≥－x 2＋ax －3， 则a ≤2ln x ＋x ＋3x .设h (x )＝2ln x ＋3x＋x (x >0)． 则h ′(x )＝ x ＋3 x －1x2，令h ′(x )＝0，得x ＝1，当x ∈(0,1)时，h ′(x )<0，h (x )单调递减； 当x ∈(1，＋∞)时，h ′(x )>0，h (x )单调递增． ∴h (x )min ＝h (1)＝4. ∴a ≤h (x )min ＝4.∴a 的取值范围是(－∞，4]． 当堂训练1．④ 2.π 3.6 4.－125.(7，＋∞)。
高中数学第三章导数及其应用3.1导数的概念3.1.2瞬时变化率—导数学案苏教版选修1-1(2021
（江苏专用）2018-2019学年高中数学第三章导数及其应用3.1 导数的概念3.1.2 瞬时变化率—导数学案苏教版选修1-1编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（江苏专用）2018-2019学年高中数学第三章导数及其应用3.1 导数的概念3.1.2 瞬时变化率—导数学案苏教版选修1-1）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（江苏专用）2018-2019学年高中数学第三章导数及其应用3.1 导数的概念3.1.2 瞬时变化率—导数学案苏教版选修1-1的全部内容。
3.1。
2 瞬时变化率—导数学习目标：1。
理解导数的概念和定义及导数的几何意义．(重点） 2.理解运动在某时刻的瞬时变化率(瞬时速度）．（难点)[自主预习·探新知］1．曲线上一点处的切线设曲线C上的一点P，Q是曲线C上的另一点，则直线PQ称为曲线C的割线；随着点Q沿曲线C向点P运动，割线PQ在点P附近越来越逼近曲线C。
当点Q无限逼近点P时，直线PQ 最终就成为在点P处最逼近曲线的直线l，这条直线l称为曲线在点P处的切线．2．瞬时速度运动物体的位移S(t）对于时间t的导数，即v（t）＝S′（t）．3．瞬时加速度运动物体的速度v（t）对于时间t的导数,即a(t)＝v′（t)．4．导数设函数y＝f(x）在区间(a，b)上有定义,x0∈(a，b），当Δx无限趋近于0时，比值错误!＝错误!无限趋近于一个常数A，则称f(x)在点x＝x0处可导，并称常数A为函数f（x）在点x＝x处的导数,记作f′（x0）．5．导函数若函数y＝f（x)对于区间(a,b)内任一点都可导，则f(x)在各点的导数也随自变量x的变化而变化,因而也是自变量x的函数，该函数称为f(x）的导函数，记作f′（x）．6．函数y＝f(x）在点x＝x0处的导数f′(x0）的几何意义是曲线y＝f(x）在点(x0，f(x0）)处的切线的斜率．[基础自测］1．判断正误：(1)函数y＝f（x）在x＝x0处的导数值与Δx值的正、负无关．（)(2）在导数的定义中，Δx，Δy都不可能为零．( )（3）在导数的定义中，错误!＞0.( ）【解析】(1）√。
高中数学第三章导数及其应用3.3.3最大值与最小值作业苏教版选修1-1(2021年整理)
2018-2019学年高中数学第三章导数及其应用3.3.3 最大值与最小值作业苏教版选修1-1编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018-2019学年高中数学第三章导数及其应用3.3.3 最大值与最小值作业苏教版选修1-1）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018-2019学年高中数学第三章导数及其应用3.3.3 最大值与最小值作业苏教版选修1-1的全部内容。
3.3.3 最大值与最小值［基础达标]1．函数f（x)＝x3－3x＋1在[－3，0］上的最大值,最小值分别为________．解析:f′(x)＝3x2－3,令f′（x)＝0,解得x＝－1或x＝1，f（－3）＝－17，f(－1)＝3，f（1)＝－1，f(0)＝1.比较可得f（x）max＝f（－1）＝3，f(x）min＝f(－3)＝－17.答案：3，－172．函数f（x）＝x ln x在(0,＋∞)上的最小值为________．解析：f′(x）＝（x ln x)′＝x′·ln x＋x·（ln x)′＝ln x＋1.由f′（x)>0，得x>1e ；由f′（x）<0，得x〈错误!.∴f（x）＝x ln x在x＝错误!处取得极小值f(错误!）＝－错误!，∴－错误!就是f（x）在（0，＋∞）上的最小值．答案:－错误!3．函数y＝x＋2cos x在区间［0，错误!］上的最大值是________．解析：令y′＝1－2sin x＝0,得x＝错误!，比较0，错误!，错误!处的函数值，得y max＝错误!＋错误!.答案：错误!＋错误!4．若函数f(x）＝ax2＋4x－3在[0，2]上有最大值f(2）,则a的取值范围是________．解析：f′(x)＝2ax＋4，由f(x）在[0，2]上有最大值f(2)，则要求f(x）在[0,2］上单调递增,则2ax＋4≥0在［0，2］上恒成立．当a≥0时，2ax＋4≥0恒成立；当a〈0时，要求4a＋4≥0恒成立，即a≥－1.∴a的取值范围是a≥－1.答案：a≥－15．已知函数f(x)＝错误!x4－2x3＋3m，x∈R，若f(x)＋9≥0恒成立，则实数m的取值范围是________．解析：因为函数f(x）＝错误!x4－2x3＋3m，所以f′（x）＝2x3－6x2，令f′（x）＝0,得x＝0或x＝3，经检验知x＝3是函数的一个最小值点,所以函数的最小值为f（3)＝3m－错误!，因为不等式f(x)＋9≥0恒成立，即f（x)≥－9恒成立，所以3m－错误!≥－9，解得m≥错误!.答案：m≥错误!6．函数f(x)＝ax4－4ax2＋b(a〉0,1≤x≤2）的最大值为3，最小值为－5，则a＝________，b＝________。
高级中学高中数学(苏教版)选修1-1导学案：3.3.3最大值与最小值
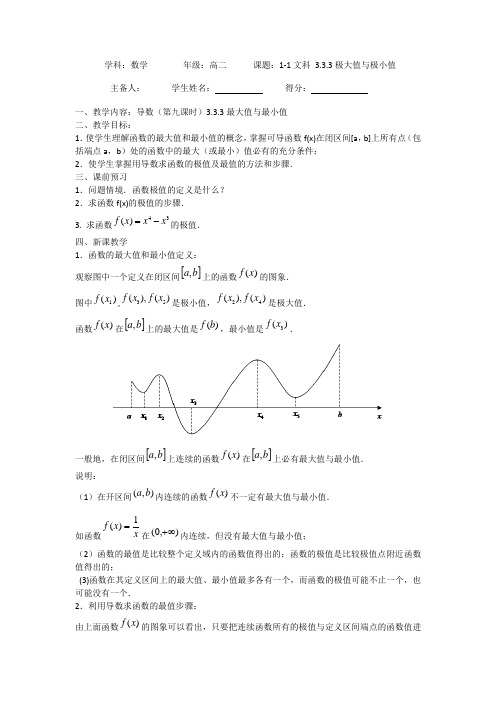
学科：数学 年级：高二 课题：1-1文科 3.3.3极大值与极小值主备人： 学生姓名： 得分：一、教学内容：导数（第九课时）3.3.3最大值与最小值二、教学目标：1．使学生理解函数的最大值和最小值的概念，掌握可导函数f(x)在闭区间[a ，b]上所有点（包括端点a ，b ）处的函数中的最大（或最小）值必有的充分条件；2．使学生掌握用导数求函数的极值及最值的方法和步骤．三、课前预习1．问题情境．函数极值的定义是什么？2．求函数f(x)的极值的步骤．3. 求函数43()f x x x =-的极值．四、新课教学1．函数的最大值和最小值定义：观察图中一个定义在闭区间[]b a ,上的函数)(x f 的图象． 图中)(1x f ,35(),()f x f x 是极小值，24(),()f x f x 是极大值． 函数)(x f 在[]b a ,上的最大值是)(b f ，最小值是3()f x ．一般地，在闭区间[]b a ,上连续的函数)(x f 在[]b a ,上必有最大值与最小值．说明：（1）在开区间(,)a b 内连续的函数)(x f 不一定有最大值与最小值． 如函数x x f 1)(=在),0(+∞内连续，但没有最大值与最小值；（2）函数的最值是比较整个定义域内的函数值得出的；函数的极值是比较极值点附近函数值得出的；(3)函数在其定义区间上的最大值、最小值最多各有一个，而函数的极值可能不止一个，也可能没有一个．2．利用导数求函数的最值步骤：由上面函数)(x f 的图象可以看出，只要把连续函数所有的极值与定义区间端点的函数值进行比较，就可以得出函数的最值了．设函数)(xf在[]b a,上连续，在(,)a b内可导，则求)(xf在[]b a,上的最大值与最小值的步骤如下：（1）求)(xf在(,)a b内的极值；（2）将)(xf的各极值与)(af、)(bf比较得出函数)(xf在[]b a,上的最值．3、有关例题例1求函数f(x)＝x2－4x＋3在区间[－1，4]内的最大值和最小值．例2求函数f(x)＝12x＋sinx在区间[0，2π]上的最值．例3．已知函数f(x)＝2x＋ln x.(1)求函数f(x)在[1，e]上的最大值和最小值；(2)求证：当x∈(1，＋∞)时，函数f(x)的图像在g(x)＝23x3＋12x2的下方．五、课堂练习2.求下列函数的最大值与最小值：（1）];3,1[,23)(-∈+=x x x f （2）];3,31[,1)(∈+=x x x x f3.求函数,(0,1]x y e x x =-∈的值域. 六、课堂小结七、课后作业1.求下列函数在所给区间上的最大值与最小值：（1）]2,0[,21∈+-=x x x y ； （2）]2,2[,cos 21ππ-∈-=x x x y2.求下列函数的值域：（1）]3,1[,11∈++=x x x y ； ；（3）22ln y x x =-3．已知函数f(x)＝ax2＋bln x 在x ＝1处有极值12.(1)求a ，b 的值；(2)判断函数y ＝f(x)的单调性并求出单调区间．。
201x-201x学年高中数学 第三章 导数及其应用 3.3.3 最大值与最小值 苏教版选修1 -1
列表：
x 0 (0,1) 1 (1,3) 3 (3,4) 4
f′(x)
－ 0 ＋0－
f(x) 0
↘ －43 ↗
0
↘ －43
由上表可知,函数在区间[0,4]上的最大值是 0，最小值是－43.
若函数f(x)在闭区间[a，b]上连续，在开区间(a，b)上可导， 则f(x)在[a，b]上必有最大值和最小值，其最值一定在极值点 处或区间端点处取得，因此在求闭区间[a，b]上连续，开区间 (a，b)内可导的函数的最值时，可将过程简化，即不用判断导 数为零的点是极大值点还是极小值点，直接将极值点与端点 的函数值进行比较,就可判定最大(小)的函数值．对于开区间 (a,b)内可导的函数(定义域为开区间或半开半闭区间)求最值， 除求出函数的极大值、极小值外,还应考虑函数在区间端点处 的函数值或画出函数的大致图象,再判定函数的最大(小) 值，否则会犯错误，但定义在开区间(a，b)上的可导函数，如 果只有一个极值点，该极值点必为最值点．
大值与最小值．函数的最值必在端点处或极值点处取得．
注意：开区间(a，b)上连续函数y＝f(x)的最值有如下几种 情况： 图①中的函数y＝f(x)在开区间(a，b)上有最大值无最小值; 图②中的函数y＝f(x)在开区间(a，b)上有最小值无最大值; 图③中的函数y＝f(x)在开区间(a，b)上既无最大值也无最 小值； 图④中的函数y＝f(x)在开区间(a，b)上既有最大值也有最 小值．
3．求函数y＝f(x)在区间[a，b]上的最值的步骤 第一步，求f(x)在区间(a，b)上的_____极__值_____； 第二步，将函数y＝f(x)的各极值与端点处的函数值f(a)，f(b) 比较，其中最大的一个是最大值，最小的一个是最小值． 注意：(1)若函数在闭区间[a，b]上连续单调，则最大、最小 值在端点处取得． (2)当连续可导函数f(x)在开区间(a，b)内只有一个导数为零的 点时，若在这一点处f(x)有极大值(或极小值)，则可以判定 f(x)在该点处取得最大值(或最小值)，这里(a，b)也可以是无 穷区间．
2018-2019数学苏教版选修1-1课件：第3章3.3.2 极大值与极小值
1．函数极值的概念
(1)极大值与极小值的直观解释 如图，函数图象在点P处从左侧到右侧由“____上__升______”变
为“_____下__降_____”(函数由单调递增变为单调递减)，这时
在点P附近，点P的位置最高，也就是说f(x1)比它附近点的函 数值都要______大______．我们称f(x1)为函数f(x)的极 _____大_______值．类似地，图中f(x2)为函数f(x)的极小值．函 数的极大值、极小值统称为函数的_____极__值_____．
(2)由(1)得 f(x)＝－23ln x－16x2＋x.f(x)的定义域为(0，＋∞)，f′(x)
＝－32x－13x＋1，
f′(x)，f(x)的变化情况如下表：
x (0,1) 1 (1,2)
2
(2，＋∞)
f′(x) － 0 ＋
0
－
f(x)
↘5 6
↗ 43－23ln 2
↘
因此，当 x＝1 时，f(x)有极小值56；当 x＝2 时，f(x)有极大值43－
(1)求可导函数f(x)的极值的步骤： ①由函数f(x)的解析式确定定义域，求出f′(x)并通过因 式分解化为积(商)形式； ②令f′(x)＝0解方程求根； ③由f′(x)＝0的根顺次将函数定义域划分成若干开区间, 并列成表格(f′(x)＝0只有一个根时可以不列表格)； ④根据表格指出极值及相应极值点(同时也可以得到单调 区间)． (2)函数解析式或给定的定义域中含有字母常数时要注意 分类讨论．
第3章 导数及其应用
3．3.2 极大值与极小值
第3章 导数及其应用
学习导航
1.了解函数极大值与极小值概念．(重点) 学习 2.理解区分极值与极值点，极值点与导数为零的点 目标 之间的关系．
高中数学新苏教版精品教案《苏教版高中数学选修1-1 3.3.3 最大值与最小值》9
探究二：求函数 的极值．
任务三：掌握运用导数求函数的最值的方法
利用导数求函数的最值步骤：
设函数 在 上连续，在 内可导，则求 在 上的最大值与最小值的步骤如下：
（1）求 在 内的极值；
（2）将 的各极值与 、 比较得出函数 在 上的最值．
探究三：设 在区间［－1，2］上的最大值为3，最小值为－29，且a＞b，求a，b的值．
【课堂小结】通过本节课的学习，你学到了哪些知识？能解决哪些问题？本节课我们还用到了哪些数学思想方法？
【总体记悟】能熟练运用导数研究函数的性质。
【评价】
【作业练习】
1．确定下列函数的单调区间：
（1）＝3－92＋24；（2）＝－3．
2求下列函数的极值：
（1）＝3－27； ．
3．已知方程 有三个不同的实数解，求实数 的取值范围．
主题：导数在研究函数中的应用
课时数
1课时
授课者
学习目标
1．掌握运用导数方法判断函数的单调性；
2．掌握求可导函数的极值的步骤；
3．掌握利用导数求函数的最值的方法．
评价任务
1．能够理解并掌握运用导数方法判断函数的单调性；
2．能够理解并掌握求可导函数的极值的步骤；
3．能够运用导数求函数的最值．来自自学过程复习回顾
（1）如何运用导数方法判断函数的单调性；
（2）求可导函数的极值的一般步骤有哪些；
（3）如何利用导数求函数的最值．
自主解答
1.确定函数 的单调区间。
2.求函数 的极值．
3.
课中过程
第一课时
教学过程
任务一：理解并掌握运用导数方法判断函数的单调性
导数与函数的单调性的关系：
一般地，对于函数＝f（），
选修1-1-第三章-《导数及其应用》教案
第三章 导数及其应用备课人 周志英3.1 导数的概念教学目的1.了解导数形成的背景、思想和方法；正确理解导数的定义、几何意义；2.使学生在了解瞬时速度的基础上抽象出变化率，建立导数的概念；掌握用导数的定义求导数的一般方法3.在教师指导下，让学生积极主动地探索导数概念的形成过程，锻炼运用分析、抽象、归纳、总结形成数学概念的能力,体会数学知识在现实生活中的广泛应用。
教学重点和难点导数的概念是本节的重点和难点 教学过程一、前置检测(导数定义的引入)1．什么叫瞬时速度？(非匀速直线运动的物体在某一时刻t0的速度) 2．怎样求非匀速直线运动在某一时刻t0的速度？在高台跳水运动中，如果我们知道运动员相对于水面的高度h （单位：m ）与起跳后的时间t （单位：s ）存在关系()105.69.42++-=t t t h ，那么我们就会计算任意一段的平均速度v ，通过平均速度v 来描述其运动状态，但用平均速度不一定能反映运动员在某一时刻的瞬时速度，那么如何求运动员的瞬时速度呢？问题：2秒时的瞬时速度是多少？我们现在会算任意一段的平均速度，先来观察一下2秒附近的情况。
先计算2秒之前的t ∆时间段内的平均速度v ，请同学们完成表格1左边部分，（事先准备好的），再完成表格的右边部分〉表格1 格 20<∆t 时，在[]2,2t ∆+这段时间内0>∆t 时，在[]t ∆+2,2这段时间内()()()1.139.41.139.422222-∆-=∆-∆+∆=∆+-∆+-=t tt t t t h h v ()()()1.139.41.139.422222-∆-=∆∆-∆-=-∆+-∆+=t tt t t h t h v 当-=∆t 0.01时，-=v 13.051； 当=∆t 0.01时，-=v 13.149； 当-=∆t 0.001时，-=v 13.095 1； 当=∆t 0.001时，-=v 13.104 9； 当-=∆t 0.000 1时，-=v 13.099 51；当=∆t 0.000 1时，-=v 13.100 49；当-=∆t 0.000 01时，-=v 1 3.099 951；当=∆t 0.000 01时，-=v 13.100 049； 当-=∆t 0.000 001时，-=v 13.099 995 1；当=∆t 0.000 001时，-=v 13.100 004 9；。
【新】版高中数学第三章导数及其应用3.3.3最大值与最小值学案苏教版选修1_1
3．3.3 最大值与最小值学习目标 1.理解函数最值的概念，了解其与函数极值的区别与联系.2.会求某闭区间上函数的最值．知识点函数的最大值与最小值如图为y＝f(x)，x∈[a，b]的图象．思考1 观察[a，b]上函数y＝f(x)的图象，试找出它的极大值、极小值．思考2 结合图象判断，函数y＝f(x)在区间[a，b]上是否存在最大值，最小值？若存在，分别为多少？思考3 函数y＝f(x)在[a，b]上的最大(小)值一定是某极值吗？思考4 怎样确定函数f(x)在[a，b]上的最小值和最大值？梳理(1)函数的最大(小)值的存在性一般地，如果在区间[a，b]上函数y＝f(x)的图象是一条________________的曲线，那么它必有最大值与最小值．(2)求函数y ＝f (x )在闭区间[a ，b ]上的最值的步骤 ①求函数y ＝f (x )在(a ，b )内的________；②将函数y ＝f (x )的____________与________处的函数值f (a )，f (b )比较，其中最大的一个是____________，最小的一个是____________．类型一 求函数的最值命题角度1 不含参数的函数求最值 例1 求下列函数的最值： (1)f (x )＝2x 3－12x ，x ∈[－2,3]； (2)f (x )＝12x ＋sin x ，x ∈[0,2π]．反思与感悟 求解函数在固定区间上的最值，需注意以下几点： (1)对函数进行准确求导，并检验f ′(x )＝0的根是否在给定区间内； (2)研究函数的单调性，正确确定极值和端点函数值； (3)比较极值与端点函数值大小，确定最值．跟踪训练1 求函数f (x )＝e x (3－x 2)，x ∈[2,5]的最值．命题角度2 含参数的函数求最值例2 已知a 是实数，函数f (x )＝x 2(x －a )，求f (x )在区间[0,2]上的最大值．反思与感悟 由于参数的取值不同会导致函数在所给区间上的单调性的变化，从而导致最值的变化．所以解决这类问题常需要分类讨论，并结合不等式的知识进行求解． 跟踪训练2 在例2中，将区间[0,2]改为[－1,0]，结果如何？类型二 由函数的最值求参数例3 已知函数f (x )＝ax 3－6ax 2＋b ，x ∈[－1,2]的最大值为3，最小值为－29，求a ，b 的值．反思与感悟 已知函数在某区间上的最值求参数的值(范围)是求函数最值的逆向思维，一般先求导数，利用导数研究函数的单调性及极值点，探索最值点，根据已知最值列方程(不等式)解决问题．其中注意分类讨论思想的应用．跟踪训练3 设f (x )＝－13x 3＋12x 2＋2ax .当0<a <2时，f (x )在[1,4]上的最小值为－163，求f (x )在该区间上的最大值．类型三 函数最值的综合应用例4 设函数f (x )＝tx 2＋2t 2x ＋t －1(x ∈R ，t ＞0)． (1)求f (x )的最小值h (t )；(2)若h (t )＜－2t ＋m 对t ∈(0,2)恒成立，求实数m 的取值范围．反思与感悟 (1)“恒成立”问题向最值问题转化是一种常见的题型，一般地，可采用分离参数法进行转化．λ≥f (x )恒成立⇔λ≥[f (x )]max ；λ≤f (x )恒成立⇔λ≤[f (x )]min .对于不能分离参数的恒成立问题，直接求含参函数的最值即可．(2)此类问题特别要小心“最值能否取得到”和“不等式中是否含等号”的情况，以此来确定参数的范围能否取得“＝”．跟踪训练4 已知2x ln x ≥－x 2＋ax －3对一切x ∈(0，＋∞)恒成立，求a 的取值范围．1．函数f (x )＝x 3－3x (|x |<1)，则下列说法正确的是________．(填序号) ①有最大值，但无最小值；②有最大值，也有最小值； ③无最大值，但有最小值；④既无最大值，也无最小值．2．函数y ＝x －sin x ，x ∈⎣⎢⎡⎦⎥⎤π2，π的最大值是________．3．函数f (x )＝x 3－x 2－x ＋t 在区间[0,2]上的最小值为3，则函数在[0,2]上的最大值为________．4．已知函数y ＝－x 2－2x ＋3在区间[a,2]上的最大值为154，则a ＝________.5．函数f (x )＝x 3－12x 2－2x ＋5，若对于任意x ∈[－1,2]，都有f (x )<m ，则实数m 的取值范围是______________．1．求函数在闭区间上的最值，只需比较极值和端点处的函数值即可；若函数在一个开区间内只有一个极值，则这个极值就是最值．2．已知最值求参数时，可先确定参数的值，用参数表示最值时，应分类讨论．3．“恒成立”问题可转化为函数最值问题．提醒：完成作业第3章§3.3 3.3.3答案精析问题导学 知识点思考1 极大值为f (x 1)，f (x 3)，极小值为f (x 2)，f (x 4)． 思考2 存在，f (x )min ＝f (a )，f (x )max ＝f (x 3)．思考3 不一定，也可能是区间端点的函数值．思考4 比较极值与区间端点的函数值，最大的是最大值，最小的是最小值． 梳理 (1)连续不断 (2)①极值 ②各极值 端点 最大值 最小值 题型探究例1 解 (1)f (x )＝2x 3－12x ，所以f ′(x )＝6x 2－12＝6(x ＋2)(x －2)， 令f ′(x )＝0，解得x ＝－2或x ＝ 2. 因为f (－2)＝8，f (3)＝18，f (2)＝－82， f (－2)＝82；所以当x ＝2时，f (x )取得最小值－82； 当x ＝3时，f (x )取得最大值18. (2)f ′(x )＝12＋cos x ，令f ′(x )＝0，又x ∈[0,2π]， 解得x ＝23π或x ＝43π.计算得f (0)＝0，f (2π)＝π，f (23π)＝π3＋32， f (43π)＝23π－32. 所以当x ＝0时，f (x )有最小值f (0)＝0； 当x ＝2π时，f (x )有最大值f (2π)＝π. 跟踪训练1 解 ∵f (x )＝3e x －e x x 2， ∴f ′(x )＝3e x －(e x x 2＋2e xx ) ＝－e x(x 2＋2x －3)＝－e x(x ＋3)(x －1)． ∵在区间[2,5]上，f ′(x )＝－e x (x ＋3)(x －1)<0，∴函数f (x )在区间[2,5]上单调递减，∴当x ＝2时，函数f (x )取得最大值f (2)＝－e 2； 当x ＝5时，函数f (x )取得最小值f (5)＝－22e 5. 例2 解 令f ′(x )＝0， 解得x 1＝0，x 2＝2a3.当2a3≤0，即a ≤0时，f (x )在[0,2]上单调递增， 从而f (x )max ＝f (2)＝8－4a .当2a3≥2，即a ≥3时，f (x )在[0,2]上单调递减， 从而f (x )max ＝f (0)＝0. 当0<2a3<2，即0<a <3时，f (x )在⎣⎢⎡⎦⎥⎤0，2a 3上单调递减，在⎣⎢⎡⎦⎥⎤2a 3，2上单调递增，从而f (x )max ＝⎩⎪⎨⎪⎧8－4a ，0<a ≤2，0， 2<a <3，综上所述，f (x )max ＝⎩⎪⎨⎪⎧8－4a ，a ≤2，0， a >2.跟踪训练2 解 令f ′(x )＝0， 解得x 1＝0，x 2＝23a .①当23a ≥0，即a ≥0时，f (x )在[－1,0]上单调递增，从而f (x )max ＝f (0)＝0；②当23a ≤－1，即a ≤－32时，f (x )在[－1,0]上单调递减，从而f (x )max ＝f (－1)＝－1－a ； ③当－1<23a <0，即－32<a <0时，f (x )在⎣⎢⎡⎦⎥⎤－1，23a 上单调递增；在⎣⎢⎡⎦⎥⎤23a ，0上单调递减，则f (x )max ＝f ⎝ ⎛⎭⎪⎫23a ＝－427a 3. 综上所述，f (x )max＝⎩⎪⎨⎪⎧－1－a ，a ≤－32，－427a 3，－32<a <0，0，a ≥0.例3 解 由题设知a ≠0，否则f (x )＝b 为常函数，与题设矛盾． 求导得f ′(x )＝3ax 2－12ax ＝3ax (x －4)， 令f ′(x )＝0，得x 1＝0，x 2＝4(舍去)． ①当a >0时，f ′(x )，f (x )的变化情况如下表：由表可知，当x ＝0时，f (x )取得极大值b ，也是函数f (x )在[－1,2]上的最大值，∴f (0)＝b ＝3.又f (－1)＝－7a ＋3，f (2)＝－16a ＋3<f (－1)，∴f (2)＝－16a ＋3＝－29，解得a ＝2. ②当a <0时，同理可得，当x ＝0时，f (x )取得极小值b ，也是函数在[－1,2]上的最小值，∴f (0)＝b ＝－29.又f (－1)＝－7a －29，f (2)＝－16a －29>f (－1)，∴f (2)＝－16a －29＝3，解得a ＝－2. 综上可得，a ＝2，b ＝3或a ＝－2，b ＝－29.跟踪训练3 解 f ′(x )＝－x 2＋x ＋2a ， 令f ′(x )＝0，得两根x 1＝1－1＋8a2， x 2＝1＋1＋8a2. 当x ∈(－∞，x 1)，(x 2，＋∞)时，f ′(x )<0；当x ∈(x 1，x 2)时，f ′(x )>0，所以f (x )在(－∞，x 1)，(x 2，＋∞)上单调递减，在(x 1，x 2)上单调递增． 当0<a <2时，有x 1<1<x 2<4，所以f (x )在[1,4]上的最大值为f (x 2)． 又f (4)－f (1)＝－272＋6a <0，即f (4)<f (1)，所以f (x )在[1,4]上的最小值为f (4)＝8a －403＝－163，故a ＝1，x 2＝2，从而f (x )在[1,4]上的最大值为f (2)＝103.例4 解 (1)∵f (x )＝t (x ＋t )2－t 3＋t －1(x ∈R ，t ＞0)， ∴当x ＝－t 时，f (x )取最小值f (－t )＝－t 3＋t －1， 即h (t )＝－t 3＋t －1. (2)令g (t )＝h (t )－(－2t ＋m ) ＝－t 3＋3t －1－m ，由g ′(t )＝－3t 2＋3＝0，得t ＝1，t ＝－1(不合题意，舍去)．当t 变化时g ′(t )、g (t )的变化情况如下表：∴对t ∈(0,2)，当t ＝1时，g (t )max ＝1－m ，h (t )<－2t －m 对t ∈(0,2)恒成立，也就是g (t )<0对t ∈(0,2)恒成立， 只需g (t )max ＝1－m <0，∴m >1. 故实数m 的取值范围是(1，＋∞)． 跟踪训练4 解 由2x ln x ≥－x 2＋ax －3， 则a ≤2ln x ＋x ＋3x .设h (x )＝2ln x ＋3x＋x (x >0)． 则h ′(x )＝x ＋x －x2，令h ′(x )＝0，得x ＝1，当x ∈(0,1)时，h ′(x )<0，h (x )单调递减； 当x ∈(1，＋∞)时，h ′(x )>0，h (x )单调递增． ∴h (x )min ＝h (1)＝4. ∴a ≤h (x )min ＝4.∴a 的取值范围是(－∞，4]． 当堂训练1．④ 2.π 3.6 4.－125.(7，＋∞)。
高中数学第3章导数及其应用第10课时函数的最大值与最小值教案苏教版选修1_1
第三章 导数及其应用第10课时 函数的最大值与最小值教学目标：1.理解函数的最大值和最小值的概念；2.掌握用导数求函数的极值及最值的方法和步骤.教学重点：利用导数求函数的最大值和最小值的方法教学难点：函数的最大值、最小值与函数的极大值和极小值的区别与联系教学过程：Ⅰ.问题情境Ⅱ.建构数学1.最大值：2.最小值：3.利用导数求函数的最值步骤：Ⅲ.数学应用例1：求函数243y x x =-+在区间[]1,4-上的最大值与最小值变式练习：求下列函数在所给区间上的最大值和最小值（1）()32f x x =+ []1,3x ∈-（2）1()f x x x =+ 1,33x ⎡⎤∈⎢⎥⎣⎦（3）3y x x =- []0,2x ∈例2：求1()sin 2f x x x =+在区间[]0,2π上的最大值与最小值.变式练习：已知()c x bx ax x f +-+=223在2-=x 时有极大值6，在1=x 时有极小值，求c b a ,,的值；并求()x f 在区间[]3,3-上的最大值和最小值.Ⅳ.课时小结:Ⅴ.课堂检测Ⅵ.课后作业书本P 80 练习2(2),31.下列说法正确的是A.函数的极大值就是函数的最大值B.函数的极小值就是函数的最小值C.函数的最值一定是极值D.在闭区间上的连续函数一定存在最值2.函数y =x 3－3x 2－8x +5在区间[－4, 4]上的最大值是 .3.求下列函数在所给区间上的最大值和最小值（1）22y x x =- [0,3]x ∈（2）12x y x -=+ [0,2]x ∈（3）1cos 2y x x =- [,]22x ππ∈-4.把长度为L cm 的线段分成四段，围成一个矩形，问怎样分法，所围成矩形的面积最大?精美句子1、善思则能“从无字句处读书”。
读沙漠，读出了它坦荡豪放的胸怀；读太阳，读出了它普照万物的无私；读春雨，读出了它润物无声的柔情。
读大海，读出了它气势磅礴的豪情。
高中数学 3.3.3最大值与最小值同步练习(含解析)苏教版高二选修1-1数学试题
3.3.3 最大值与最小值课时目标 1.理解函数最值的概念.2.了解函数最值与极值的区别和联系.3.会用导数求在给定区间上不超过三次的多项式函数的最大值、最小值．1．最大值：如果在函数定义域I 内存在x 0，使得对任意的x ∈I ，总有_____________，则称f (x 0)为函数在______________的最大值．2．一般地，如果在区间[a ，b ]上的函数的图象是一条连续不断的曲线，那么f (x )必有最大值和最小值．此性质包括两个条件：(1)给定函数的区间是闭区间；(2)函数图象在区间上的每一点必须连续不间断．函数的最值是比较整个定义域的函数值得出的，函数的极值是比较极值点附近的函数值得到的．3．一般地，求f (x )在[a ，b ]上的最大值与最小值的步骤如下： (1)求f (x )在(a ，b )上的________；(2)将(1)中求得的极值与f (a )，f (b )比较，得到f (x )在区间[a ，b ]上的最大值与最小值．一、填空题1．给出下列四个命题：①若函数f (x )在[a ，b ]上有最大值，则这个最大值一定是[a ，b ]上的极大值； ②若函数f (x )在[a ，b ]上有最小值，则这个最小值一定是[a ，b ]上的极小值； ③若函数f (x )在[a ，b ]上有最值，则最值一定在x ＝a 或x ＝b 处取得； ④若函数f (x )在(a ，b )内连续，则f (x )在(a ，b )内必有最大值与最小值． 其中真命题共有________个．2．函数f (x )＝x (1－x 2)在[0,1]上的最大值为______．3．已知函数f (x )＝ax 3＋c ，且f ′(1)＝6，函数在[1,2]上的最大值为20，则c ＝________.4．若函数f (x )、g (x )在区间[a ，b ]上可导，且f ′(x )>g ′(x )，f (a )＝g (a )，则在区间[a ，b ]上有f (x )与g (x )的大小关系为____________．5．已知函数y ＝－x 2－2x ＋3在[a,2]上的最大值为154，则a ＝________.6．函数f (x )＝ln x －x 在(0，e]上的最大值为________．7．函数f (x )＝12e x (sin x ＋cos x )在区间⎣⎢⎡⎦⎥⎤0，π2上的值域为________．8．若函数f (x )＝x 3－3x －a 在区间[0,3]上的最大值、最小值分别为M 、N ，则M －N 的值为________． 二、解答题9．求下列各函数的最值．(1)f (x )＝12x ＋sin x ，x ∈[0,2π]；(2)f (x )＝x 3－3x 2＋6x －2，x ∈[－1,1]．10．已知f (x )＝x 3－x 2－x ＋3，x ∈[－1,2]，f (x )－m <0恒成立，某某数m 的取值X 围．能力提升11．设函数f (x )＝12x 2e x.(1)求f (x )的单调区间；(2)若当x ∈[－2,2]时，不等式f (x )>m 恒成立，某某数m 的取值X 围．12．若f (x )＝ax 3－6ax 2＋b ，x ∈[－1,2]的最大值为3，最小值是－29，求a 、b 的值．1．求闭区间上函数的最值也可直接求出端点函数值和导数为零时x对应的函数值，通过比较大小确定函数的最值．2．在求解与最值有关的函数综合问题时，要发挥导数的解题功能，同时也要注意对字母的分类讨论；而有关恒成立问题，一般是转化为求函数的最值问题．3．可以利用导数的实际意义，建立函数模型，解决实际生活中的最大值最小值问题．3．3.3 最大值与最小值知识梳理1．f(x)≤f(x0) 定义域上3．(1)极值作业设计 1．0解析 因为函数的最值可以在区间[a ，b ]的两端取得，也可以在内部取得，当最值在端点处取得时，其最值就一定不是极值，故命题①与②不真．由于最值可以在区间内部取得，故命题③也不真．对于命题④，我们只要考虑在(a ，b )内的单调函数，它在(a ，b )内必定无最值(也无极值)，因此命题④也不真．综上所述，四个命题均不真． 2.239解析 ∵f (x )＝x －x 3，∴f ′(x )＝1－3x 2，令f ′(x )＝0，得x ＝±33，∵f (0)＝0，f (1)＝0，f ⎝⎛⎭⎪⎫33＝239，f ⎝ ⎛⎭⎪⎫－33＝－239. ∴f (x )max ＝239.3．4解析 ∵f ′(x )＝3ax 2，∴f ′(1)＝3a ＝6，∴a ＝2.当x ∈[1,2]时，f ′(x )＝6x 2>0，即f (x )在[1,2]上是增函数，∴f (x )max ＝f (2)＝2×23＋c ＝20，∴c ＝4. 4．f (x )≥g (x )解析 ∵f ′(x )>g ′(x )，∴f (x )－g (x )单调递增． ∵x ≥a ，∴f (x )－g (x )≥f (a )－g (a )， 即f (x )－g (x )≥0.5．－12解析 y ′＝－2x －2，令y ′＝0，得x ＝－1.当a ≤－1时，最大值为f (－1)＝4，不合题意．当－1<a <2时，f (x )在[a,2]上单调递减，最大值为f (a )＝－a 2－2a ＋3＝154，解得a ＝－12或a ＝－32(舍去)．6．－1解析 f ′(x )＝1x －1＝1－xx，令f ′(x )>0得0<x <1，令f ′(x )<0得x <0或x >1，∴f (x )在(0,1]上是增函数，在(1，e]上是减函数． ∴当x ＝1时，f (x )有最大值f (1)＝－1.7. 211,22e π⎡⎤⎢⎥⎣⎦解析 ∵x ∈⎣⎢⎡⎦⎥⎤0，π2，∴f ′(x )＝e xcos x ≥0，∴f (0)≤f (x )≤f ⎝ ⎛⎭⎪⎫π2.即12≤f (x )≤122e π.8．20解析 f ′(x )＝3x 2－3，令f ′(x )＝0， 得x ＝1，(x ＝－1舍去)．∵f (0)＝－a ，f (1)＝－2－a ，f (3)＝18－a . ∴M ＝18－a ，N ＝－2－a .∴M －N ＝20.9．解 (1)f ′(x )＝12＋cos x .令f ′(x )＝0，又∵0≤x ≤2π，∴x ＝2π3或x ＝4π3.∴f ⎝ ⎛⎭⎪⎫2π3＝π3＋32，f ⎝ ⎛⎭⎪⎫4π3＝2π3－32，又∵f (0)＝0，f (2π)＝π.∴当x ＝0时，f (x )有最小值f (0)＝0， 当x ＝2π时，f (x )有最大值f (2π)＝π.(2)f ′(x )＝3x 2－6x ＋6＝3(x 2－2x ＋2)＝3(x －1)2＋3，∵f ′(x )在[－1,1]内恒大于0， ∴f (x )在[－1,1]上为增函数． 故x ＝－1时，f (x )最小值＝－12； x ＝1时，f (x )最大值＝2.即f (x )在[－1,1]上的最小值为－12，最大值为2. 10．解 由f (x )－m <0，即m >f (x )恒成立， 知m >f (x )max ，f ′(x )＝3x 2－2x －1，令f ′(x )＝0，解得x ＝－13或x ＝1.因为f (－13)＝8627，f (1)＝2，f (－1)＝2，f (2)＝5. 所以f (x )的最大值为5，故m 的取值X 围为(5，＋∞)．11．解 (1)f ′(x )＝x e x＋12x 2e x ＝e x2x (x ＋2)．由ex 2x (x ＋2)>0，解得x >0或x <－2， ∴(－∞，－2)，(0，＋∞)为f (x )的增区间， 由ex 2x (x ＋2)<0，得－2<x <0， ∴(－2,0)为f (x )的减区间．∴f (x )的单调增区间为(－∞，－2)，(0，＋∞)； 单调减区间为(－2,0)．(2)令f ′(x )＝0，得x ＝0或x ＝－2，∵f (－2)＝2e 2，f (2)＝2e 2，f (0)＝0，∴f (x )∈[0,2e 2]，又∵f (x )>m 恒成立，∴m <0. 故m 的取值X 围为(－∞，0)．12．解 ∵f (x )＝ax 3－6ax 2＋b ，∴f ′(x )＝3ax 2－12ax .令f ′(x )＝0，解得x ＝0或4. ∵4D ∈/[－1,2]，故舍去，∴f (x )取最大值，最小值的点在x ＝－1、0、2上取得，f (－1)＝－7a ＋b ，f (0)＝b ， f (2)＝－16a ＋b .当a >0时，最大值为b ＝3， 最小值为－16a ＋b ＝－29，解得⎩⎪⎨⎪⎧a ＝2，b ＝3，当a <0时，最大值为－16a ＋b ＝3，b ＝－29， 解得⎩⎪⎨⎪⎧a ＝－2b ＝－29，综上所述：⎩⎪⎨⎪⎧a ＝2b ＝3或⎩⎪⎨⎪⎧a ＝－2b ＝－29.§3.4 导数在实际生活中的应用课时目标 通过用料最省、利润最大、效率最高等优化问题，使学生体会导数在解决实际问题中的作用，会利用导数解决简单的实际生活中的最值问题．1．解决实际应用问题时，要把问题中所涉及的几个变量转化成函数关系，这需通过分析、联想、抽象和转化完成．函数的最值要由极值和端点的函数值确定，当定义域是开区间，而且其上有惟一的极值，则它就是函数的最值． 2．解决优化问题的基本思路是：上述解决优化问题的过程是一个典型的数学建模的过程．一、填空题1．随着人们生活水平的提高，汽车的拥有量越来越多，据有关统计数据显示，从上午6点到9点，车辆通过某一路段的用时y (分钟)与车辆进入该路段的时刻t 之间的关系可近似表示为y ＝－18t 3－34t 2＋36t －6294.则在这段时间内，通过该路段用时最多的时刻是________． 2．若底面为等边三角形的直棱柱的体积为V ，则其表面积最小时，底面边长为________． 3．要做一个圆锥形的漏斗，其母线长为20 cm ，要使其体积最大，则高为________ cm.4．某厂生产某种产品x 件的总成本：C (x )＝1 200＋275x 3，又产品单价的平方与产品件数x 成反比，生产100件这样的产品的单价为50元，总利润最大时，产量应定为________件． 5.如图所示，一窗户的上部是半圆，下部是矩形，如果窗户面积一定，窗户周长最小时，x 与h 的比为________．6．某公司生产某种产品，固定成本为20 000元，每生产一件产品成本增加100元，已知总收益R 与年产量x 的关系式为R ＝⎩⎪⎨⎪⎧400x －12x 2 0≤x ≤400，80 000 x >400.则总利润最大时，每年生产的产品件数是________．7．某公司租地建仓库，每月土地占用费y 1与仓库到车站的距离成反比，而每月库存货物的运费y 2与到车站的距离成正比，如果在距离车站10千米处建仓库，这两项费用y 1和y 2分别为2万元和8万元．那么，要使这两项费用之和最小，仓库应建在离车站________千米处．8．做一个无盖的圆柱形水桶，若需使其体积是27π，且用料最省，则圆柱的底面半径为________． 二、解答题9．某地建一座桥，两端的桥墩已建好，这两墩相距m 米，余下工程只需建两端桥墩之间的桥面和桥墩．经测算，一个桥墩的工程费用为256万元，距离为x 米的相邻两墩之间的桥面工程费用为(2＋x )x 万元．假设桥墩等距离分布，所有桥墩都视为点，且不考虑其它因素．记余下工程的费用为y 万元． (1)试写出y 关于x 的函数关系式；(2)当m ＝640米时，需新建多少个桥墩才能使y 最小？10.某商品每件成本9元，售价30元，每星期卖出432件．如果降低价格，销售量可以增加，且每星期多卖出的商品件数与商品单价的降低值x (单位：元，0≤x ≤30)的平方成正比，已知商品单价降低2元时，一星期多卖出24件． (1)将一个星期的商品销售利润表示成x 的函数； (2)如何定价才能使一个星期的商品销售利润最大？能力提升 11．某单位用2 160万元购得一块空地，计划在该块地上建造一栋至少10层、每层2 000平方米的楼房．经测算，如果将楼房建为x (x ≥10)层，则每平方米的平均建筑费用为560＋48x (单位：元)．为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？(注：平均综合费用＝平均建筑费用＋平均购地费用，平均购地费用＝购地总费用建筑总面积)12．已知某商品生产成本C 与产量q 的函数关系式为C ＝100＋4q ，价格p 与产量q 的函数关系式为p ＝25－18q ，求产量q 为何值时，利润L 最大．利用导数解决生活中的优化问题的一般步骤．(1)分析实际问题中各变量之间的关系，建立实际问题的数学模型，写出实际问题中变量之间的函数关系y ＝f (x )；(2)求函数的导数f ′(x )，解方程f ′(x )＝0；(3)比较函数在区间端点和f ′(x )＝0的点的函数值的大小，最大(小)者为最大(小)值；(4)写出答案．§3.4 导数在实际生活中的应用作业设计 1．8解析 由题意知，所求的量为当y 为最大值时的自变量t 的取值，y ′＝－38t 2－32t ＋36，令y ′＝0，得3t 2＋12t －36×8＝0， ∴t 1＝8，t 2＝－12(舍)．当t ∈(6,8)时．y ′>0，t ∈(8,9)时，y ′<0， 所以t ＝8时，y 有最大值．2.34V解析 设底面边长为a ，直三棱柱高为h .体积V ＝34a 2h ，所以h ＝4V3a 2， 表面积S ＝2·34a 2＋3a ·4V 3a2＝32a 2＋43Va ， S ′＝3a －43V a2，由S ′＝0，得a ＝34V . 当a ＝34V 时，表面积最小． 3.2033解析 设高为x cm ，则底面半径为202－x 2cm ，体积V ＝π3x ·(202－x 2) (0<x <20)，V ′＝π3(400－3x 2)，由V ′＝0，得x ＝2033或x ＝－2033(舍去)．当x ∈⎝ ⎛⎭⎪⎫0，2033时，V ′>0，当x ∈⎝ ⎛⎭⎪⎫2033，20时，V ′<0，所以当x ＝2033时，V 取最大值． 4．25解析 设产品单价为a 元，又产品单价的平方与产品件数x 成反比，即a 2x ＝k ，由题知k ＝250 000，则a 2x ＝250 000，所以a ＝500x.总利润y ＝500x －275x 3－1 200 (x >0)，y ′＝250x －225x 2，由y ′＝0，得x ＝25，x ∈(0,25)时，y ′>0，x ∈(25，＋∞)时，y ′<0，所以x ＝25时，y 取最大值． 5．1∶1解析 设窗户面积为S ，周长为L ，则S ＝π2x 2＋2hx ，h ＝S 2x －π4x ，所以窗户周长L ＝πx ＋2x ＋2h ＝π2x ＋2x ＋S x ，L ′＝π2＋2－Sx 2.由L ′＝0，得x ＝2S π＋4，x ∈⎝⎛⎭⎪⎫0， 2S π＋4时，L ′<0， x ∈⎝⎛⎭⎪⎫2S π＋4，＋∞时，L ′>0， 所以当x ＝2Sπ＋4时，L 取最小值， 此时h x ＝2S －πx 24x 2＝2S 4x 2－π4＝π＋44－π4＝1. 6．300解析 设总成本为C ，则C ＝20 000＋100x ， 所以总利润 P ＝R －C ＝⎩⎪⎨⎪⎧300x －x 22－20 000 0≤x ≤400，60 000－100x x >400.P ′＝⎩⎪⎨⎪⎧300－x0≤x ≤400，－100 x >400.令P ′＝0，得x ＝300，易知当x ＝300时，总利润最大． 7．5解析 依题意可设每月土地占用费y 1＝k 1x，每月库存货物的运费y 2＝k 2x ，其中x 是仓库到车站的距离．于是由2＝k 110，得k 1＝20；由8＝10k 2，得k 2＝45.因此两项费用之和为y ＝20x ＋4x 5，y ′＝－20x 2＋45，令y ′＝－20x 2＋45＝0得x ＝5(x ＝－5舍去)，经验证，此点即为最小值点．故当仓库建在离车站5千米处时，两项费用之和最小． 8．3解析 设半径为r ，则高h ＝27ππr 2＝27r2.∴水桶的全面积S (r )＝πr 2＋2πr ·27r2＝πr 2＋54πr.S ′(r )＝2πr －54πr2，令S ′(r )＝0，得r ＝3.∴当r ＝3时，S (r )最小．9．解 (1)设需新建n 个桥墩，则(n ＋1)x ＝m ，即n ＝mx－1 (0<x <m )，所以y ＝f (x )＝256n ＋(n ＋1)(2＋x )x＝256⎝ ⎛⎭⎪⎫m x －1＋mx (2＋x )x＝256m x＋m x ＋2m －256 (0<x <m )．(2)由 (1)知，f ′(x )＝－256m x 2＋12m 12x -＝m 2x 2(32x －512)．令f ′(x )＝0，得32x ＝512，所以x ＝64.当0<x <64时，f ′(x )<0，f (x )在区间(0,64)内为减函数；当64<x <640时，f ′(x )>0，f (x )在区间(64,640)内为增函数，所以f (x )在x ＝64处取得最小值，此时n ＝m x －1＝64064－1＝9. 故需新建9个桥墩才能使y 最小．10．解 (1)设商品降低x 元时，多卖出的商品件数为kx 2，若记商品在一个星期的销售利润为f (x )，则依题意有f (x )＝(30－x －9)·(432＋kx 2)＝(21－x )·(432＋kx 2)，又由已知条件24＝k ·22，于是有k ＝6，所以f (x )＝－6x 3＋126x 2－432x ＋9 072，x ∈[0,30]．(2)根据(1)，有f ′(x )＝－18x 2＋252x －432＝－18(x －2)(x －12)．当x 变化时，f (x )与f ′(x )的变化情况如下表：故x ＝12时，f (x )达到极大值．因为f (0)＝9 072，f (12)＝11 664，所以定价为30－12＝18(元)能使一个星期的商品销售利润最大．11．解 设楼房每平方米的平均综合费用为f (x )元，则f (x )＝(560＋48x )＋2 160×10 0002 000x＝560＋48x ＋10 800x(x ≥10，x ∈N *)， f ′(x )＝48－10 800x2，令f ′(x )＝0得x ＝15. 当x >15时，f ′(x )>0；当0<x <15时，f ′(x )<0.因此，当x ＝15时，f (x )取最小值f (15)＝2 000.所以为了使楼房每平方米的平均综合费用最少，该楼房应建为15层．12．解 收入R ＝q ·p ＝q ⎝⎛⎭⎪⎫25－18q ＝25q －18q 2. 利润L ＝R －C ＝⎝⎛⎭⎪⎫25q －18q 2－(100＋4q ) ＝－18q 2＋21q －100 (0<q <200)， L ′＝－14q ＋21， 令L ′＝0，即－14q ＋21＝0，解得q ＝84. 因为当0<q <84时，L ′>0；当84<q <200时，L ′<0，所以当q ＝84时，L 取得最大值．所以产量q为84时，利润L最大．。