分析力学第一章作业答案【精选】
分析力学参考答案

分析力学参考答案分析力学参考答案引言:分析力学是物理学的一个重要分支,研究物体在力的作用下的运动规律。
在学习分析力学的过程中,参考答案是一个非常重要的工具,可以帮助学生巩固知识,理解问题的解决方法。
本文将分析力学的一些典型问题,并给出参考答案,帮助读者更好地掌握分析力学的基本原理和解题技巧。
一、牛顿第二定律问题牛顿第二定律是分析力学的基础,描述了物体在力的作用下的加速度。
以下是一个典型的牛顿第二定律问题:问题:一个质量为m的物体在水平面上受到一个恒定的力F作用,求物体的加速度和受力大小的关系。
解答:根据牛顿第二定律的公式F=ma,我们可以得到物体的加速度a等于受力F除以物体的质量m,即a=F/m。
因此,物体的加速度与受力大小成反比。
二、动量守恒问题动量守恒是分析力学中的一个重要原理,描述了系统在没有外力作用下动量的守恒。
以下是一个典型的动量守恒问题:问题:两个质量分别为m1和m2的物体在水平面上碰撞,碰撞前物体1的速度为v1,物体2的速度为v2,碰撞后物体1的速度为v'1,物体2的速度为v'2,求碰撞前后两个物体的动量是否守恒。
解答:根据动量守恒定律,系统在没有外力作用下,动量守恒。
即m1v1 +m2v2 = m1v'1 + m2v'2。
因此,两个物体的动量在碰撞前后保持不变,动量守恒。
三、角动量问题角动量是分析力学中的一个重要概念,描述了物体绕某一点旋转的特性。
以下是一个典型的角动量问题:问题:一个质量为m的物体绕固定点O以角速度ω旋转,求物体的角动量L 与角速度ω的关系。
解答:根据角动量的定义L=Iω,其中I为物体对固定点O的转动惯量。
对于一个质量为m的物体,其转动惯量I等于mr^2,其中r为物体到固定点O的距离。
因此,物体的角动量L与角速度ω成正比,L=mr^2ω。
结论:通过以上的分析力学问题及其参考答案,我们可以看出分析力学的基本原理和解题技巧。
牛顿第二定律描述了物体在力的作用下的加速度,动量守恒原理描述了系统在没有外力作用下动量的守恒,角动量则描述了物体绕某一点旋转的特性。
大学物理习题解力学1234910
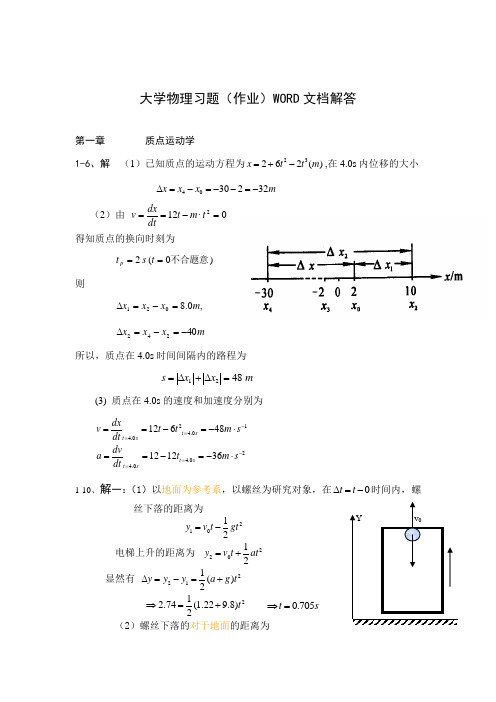
大学物理习题(作业)WORD 文档解答第一章 质点运动学1-6、解 (1)已知质点的运动方程为23262()x t t m =+-,在4.0s 内位移的大小 4030232x x x m ∆=-=--=- (2)由 0·122=-==t m t dtdxv 得知质点的换向时刻为)0(2不合题意==t s t p则,0.8021m x x x =-=∆ m x x x 40242-=-=∆所以,质点在4.0s 时间间隔内的路程为 m x x s 4821=∆+∆=(3) 质点在4.0s 的速度和加速度分别为214.04.024.04.012648121236t s t st s t sdxv t t m s dt dv a t m s dt -==-====-=-⋅==-=-⋅1-10、解一:(1)以地面为参考系,以螺丝为研究对象,在0t t ∆=-时间内,螺丝下落的距离为21012y v t gt =-电梯上升的距离为22012y v t at =+显然有 2211()2y y y a g t ∆=-=+212.74(1.229.8)2t ⇒=+ 0.705t s ⇒=(2)螺丝下落的对于地面的距离为2210112.440.7059.8(0.705)0.71622y v t gt m =-=⨯-⨯⨯=- 解二:(1)以电梯为参考系,螺丝对于电梯的加速度为()a g j -+,而初速度为零,因此有21()2y a g t ∆=+ 212.74(1.229.8)0.7052t t s ⇒=+⇒= (2)螺丝下落的对于地面的距离为2210112.440.7059.8(0.705)0.71622y v t gt m =-=⨯-⨯⨯=-1-11 一质点P 沿半径m R 00.3=的圆周作匀速速率运动,运动一周所需时间为20.0s ,设t=0时,质点位于O 点,按图1-5(a)中所示Oxy 坐标系,求(1)质点P 在任意时刻的位矢;(2)5 s 时的速度和加速度。
理论力学第一章题及解答(文末)

第一章 思考题1.1平均速度与瞬时速度有何不同?1.2 在极坐标系中,r v r =,θθ r v =.为什么2θ r r a r-=而非r ?为什么θθ r r a 20+=而非θθ r r +?你能说出r a 中的2θ r -和θa 中另一个θ r 出现的原因和它们的物理意义吗?1.3 在内禀方程中,n a 是怎样产生的?为什么在空间曲线中它总沿着主法线方向?当质点沿空间运动时,副法线方向的加速度b a 等于零,而作用力在副法线方向的分量b F 一般不等于零,这是不是违背了牛顿运动定律呢?1.4 在怎样的运动中只有τa 而无n a ?在怎样的运动中又只有n a 而无τa ?在怎样的运动中既有n a 而无τa ?1.5dt r d 与dt dr 有无不同?dt v d与dtdv 有无不同?试就直线运动与曲线运动分别加以讨论. 1.6人以速度v 向篮球网前进,则当其投篮时应用什么角度投出?跟静止时投篮有何不同?1.7雨点以匀速度v 落下,在一有加速度a 的火车中看,它走什么路经?1.8某人以一定的功率划船,逆流而上.当船经过一桥时,船上的渔竿不慎落入河中.两分钟后,此人才发现,立即返棹追赶.追到渔竿之处是在桥的下游600米的地方,问河水的流速是多大?1.9物体运动的速度是否总是和所受的外力的方向一致?为什么?1.10在那些条件下,物体可以作直线运动?如果初速度的方向和力的方向一致,则物体是沿力的方向还是沿初速度的方向运动?试用一具体实例加以说明.1.11质点仅因重力作用而沿光滑静止曲线下滑,达到任一点时的速度只和什么有关?为什么是这样?假如不是光滑的将如何?1.12为什么被约束在一光滑静止的曲线上运动时,约束力不作功?我们利用动能定理或能量积分,能否求出约束力?如不能,应当怎样去求?1.13质点的质量是1千克,它运动时的速度是k j i v 323++=,式中i 、j 、k 是沿x 、y 、z 轴上的单位矢量。
理论力学习题解答第一章

第一章 静力学基本概念
1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量
B.自由矢量
C.定位矢量
1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相反,则其合力可表为( C )。
A.1F –2F
B.2F - 1F
C.1F +2F
图1-18 图1-19 1-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小 x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6
B. 70.0
C. 136.6
D.25.9
1-4 力的可传性只适用于 A 。
A. 刚体
B. 变形体
1-5 加减平衡力系公理适用于 C 。
A. 刚体;
B. 变形体;
C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0
B. F/2
C. F/6
D.-F/3
1-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为:
Fx Fy Fz
图1-20 图1-21。
(完整版)第一章答案
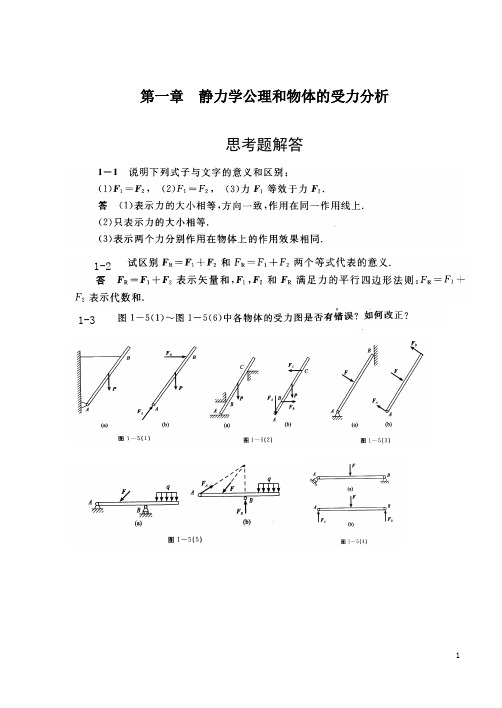
第一章静力学公理和物体的受力分析思考题解答1-21-31-4 刚体上A点受力F作用,如图1-24所示,问能否在B点加一个力使刚体平衡?为什么?答:不能。
1-5 如图l-25所示结构,若力F作用在B点,系统能否平衡?若力F仍作用在B点,但可任意改变力F的方向,F在什么方向上结构能平衡?答:若力F作用在B点,系统不能平衡;F 在指向A方向上结构能平衡。
1-6 将如下问题抽象为力学模型,充分发挥你们的想象、分析和抽象能力,试画出它们的力学简图及受力图。
(1)用两根细绳将日光灯吊挂在天花板上;(2)水面上的一块浮冰;(3)一本打开的书静止于桌面上;(4)一个人坐在一只足球上。
答:(1)(2)(3)(4)1-7 图1-26中力F作用于三铰拱的铰链C处的销钉上,所有物体重量不计。
(1)试分别画出左、右两拱及销钉C的受力图;(2)若销钉C属于AC,分别画出左、右两拱的受力图;(3)若销钉C属于BC,分别画出左、右两拱的受力图。
习题b c g h i j k分离体1.分布载荷在受力分析时,不要用其合力代替2.B点约束?C 点约束?简图太简,表现不出约束类型和构件基本形状1.整体?2.没有C F3.三力汇交没表示AB三力汇交,AD二力杆。
1-31.ACE虽然三力汇交,但C、A点力的方向不确定2.没有A3.搞清楚铰链在与谁一体。
(e)1.AD是二力杆2. A三个杆件铰链3.轮的自重不计4.不一定要用三力汇交,三力汇交只有二个力的方向确定才能确定第三个力的方向。
力学参考答案解析

力学参考答案解析力学参考答案解析力学是物理学的一个重要分支,研究物体在受到外力作用下的运动和相互作用。
学习力学需要掌握一系列的基本概念和定律,并能够应用这些知识解决实际问题。
在学习过程中,参考答案解析是一个重要的辅助工具,它能够帮助我们理解问题的解题思路和方法。
首先,我们来看一个力学问题的例子:一个质量为m的物体以初速度v0沿着水平方向匀速运动,经过时间t后速度变为v。
求物体受到的合外力F。
解答这个问题的关键在于应用牛顿第二定律,即F=ma,其中F表示物体受到的合外力,m表示物体的质量,a表示物体的加速度。
根据题目中给出的条件,物体在时间t内的加速度为a=(v-v0)/t。
将这个加速度代入牛顿第二定律的公式中,可以得到F=m(v-v0)/t。
通过这个例子,我们可以看出参考答案解析的作用。
首先,它告诉我们解答这个问题的关键在于应用牛顿第二定律,这是我们解决力学问题的基本原理。
其次,它给出了具体的计算步骤和公式,帮助我们进行问题的求解。
最后,它给出了最终的答案,即物体受到的合外力为F=m(v-v0)/t。
在学习力学的过程中,参考答案解析不仅仅是为了得到正确的答案,更重要的是理解解题的思路和方法。
通过分析解答过程,我们可以看到问题的关键点和解题思路。
在解答问题的过程中,我们需要注意以下几点。
首先,要仔细阅读问题,理解问题的要求和条件。
在解答问题之前,我们需要明确问题的目标和所给的限制条件。
只有明确了问题的要求,我们才能有针对性地选择合适的解题方法和公式。
其次,要善于运用物理学的基本原理和定律。
力学是建立在牛顿力学定律基础上的,所以我们在解答力学问题时,需要熟练掌握牛顿力学的基本原理和定律。
只有掌握了这些基本概念和定律,我们才能够正确地应用它们解决实际问题。
再次,要注意问题的逻辑推理和计算过程。
在解答问题的过程中,我们需要进行逻辑推理和计算。
逻辑推理是为了找到问题的解题思路和方法,计算过程是为了得到最终的答案。
分析力学答案

K FV
m 448浒 421122 - Ík 4- 4 行mg crank
代入⻮ 器 器 - 0中 可得
mki zmisinzeuttkicq 4.1 mg2Sin4 0 mEsin244 0 4 0 运动微分方程 miii miisiuqcose mg2siuqtkRi9-线 0
C2
0 时零解渐近稳定
1.8 试利用李雅普诺夫直接方法讨论系数在取不同值时判断
系统的零解稳定性
X X2
X十 a 3 加
解 选择正定李雅诺夫函数 比吅 二 水 水
计算 治 方程解曲线的全导数 V 荪义 器加二 zxixztzxzEXitlaih I
E 2 G 37 X22
则当 以 3时 V为负定 零解渐近稳定 a 3 时 V为零 零解稳定 a 3时 V为正定 零解不稳定
讨论是否存在初积分
i
䚡 取摇杆0A的转⻆为0 则系统的动能
T 士 加 以 04 Ìmi 旰士 Ìmhyo
二 Gmt Ém EG
取系统平衡位置为零势能 则运动时系统势能为
V kid 4 Ütmlglsin0
6 -sins
则L T V
且出售了一
是
tmtimtEG 二日 mini
zkdkcitmlgl sino tkdtimsglll cme
则 fm2以g外3tmlzmxitomtmiiiomy
f 去㗊㗊 a
i riiig 二his
3 8 质量为 m的均质摇杆0A 铰接 质量为 以的匀质圆盘A 在13 处联结刚度系数为人的弹簧 当系统平衡时 以处于水平位置 弹
簧处于铝垂位置如图所示 已知 非1.013 a 若圆盘沿固定圆弧形
分析力学第一章作业答案

FT
C
W
坐标系:两根钉连线的中点为坐标原点,连线 所在直线为x轴(向右为正),垂直连线为y轴 (向下为正),并取 为广义坐标。
x l s i n D a C点的y坐标: y 2 lc o s C ta n F r ( F r ) W r 0 T B T D C
a yC (2l sin 2 ) sin
最后可得:
2 2 F l c o s2 + W l s i n W a c s c 0 T
2
s in s in s in
3
a Fa W / ( 2 l s i n c o s ) W t a n = W t a n ( 1 ) 即有: T 3 2 l s i n
B、D点的x坐标: x l s i n B
Fi x i y ( Fi x i y T ( B B j) T )( D Dj) W j ( x i y 0 C C j) F x F x W y 0 T B T D C xB l cos xD l cos
作业参考答案
2013年9月
1.设质点在势能场U(r)中运动,在笛卡尔坐 标系中写出其拉格朗日方程。
解:拉格朗日方程为:
d L L 0 d t q q ( 1 , 2 , 3 )
L为拉格朗日函数
L T U
笛卡尔坐标中的坐标变量为 x1 , x 2 , x3 ,那么
T mxi2 / 2
i 1 3
2 L T U m x U ( xx ,2 ,x ) 所以, i /2 1 3 i 1
3
3 L 2 m x 2 U ( xxx ,2 ,3 ) m x i/ 1 i x x i 1 i i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t2 t1
平均值大 于υ平均 值的平方。
m 2(t2 t1)
t2 t1
dt
2
m(b a)2 2(t2 t1)
S0
解:由柱坐标和笛卡尔坐标的关系可知
dr ed e d ezdz
z
等式两边同时除以dt
r e e ez z
r z
那么,系统的动能为
y
T = 1 mr 2 1 m( 2 2 2 z2 ) x
2
2
那么,系统的拉格朗日函数为
所以
L T U = 1 m( 2 2 2 z2 ) U ()
t2
S0 L(x, x,t)dt m2/2dt m2 (t2 t1) / 2
t1
t1
将 (x2 x1) /(t2 t1) 带入得到
S0
m( x2 2(t2
x1)2 t1)
将 (x2 x1) /(t2 t1) 带入得到
S0
m( x2 2(t2
系统的总能量
E 1 m( X x cos )2
2
1 MX 2 1 mx2 sin2
2
2
mgx sin
E 1 m( X +x cos V )2
2
1 M ( X V )2 1 mx2 sin2
2
2
mgx sin
系统的能量在k系和 k系之间的变换方程
带入拉格朗日方程得到
mxi
U xi
Fi
(i 1, 2,3)
这就是笛卡尔坐标系中的拉格朗日方程
即牛顿第二定律
2.已知柱坐标 (,, z) 与笛卡尔坐标的关系是
x cos, y= sin, z z
如图.设质点在轴对称势能场 U () 中运动,
写出其拉格朗日方程。
以无摩擦的改变顶角的菱形ABCD,AB和AD
两棒无摩擦的支于处于同一水平线上且相距
2a的两根钉上,BD之间用一根轻质棒连接,
在连接点(B和D处),各棒之间可以无摩擦
的转动,C点上系有一重物W,C点和重物受
到约束,只能上下运动,设A点两棒之间的
夹角为2 ,试用虚功原理求平衡时联结棒BD
中的张力 FT ,讨论FT 的方向 与 的大小的关系。问:在 什么情况下有 FT 0,说明其 意义。
dr 和 r 的区别如图所示:
l
m z
M
M
l
r
m
x3
l
dr
m
x3
虚位移和实际位移的主要区别在于
虚位移只和约束有关,某一时刻约束所允许 的位移。
实际位移除了和约束有关以外,还和物体 当前的运动状态有关;运动方程和约束允许, 在时间间隔内所发生的位移。
4. 长度同为l 的轻棒四根,相互连接成一个可
f
q, t
t
s
q
1
f q,t
q
Lq,q,t
f
q, t
t
s
+ q
1
f q,t
q
那么
L ' L 2 f q,t
2 f q,t
q q tq
q
q q
L ' L
作业参考答案
2013年9月
1.设质点在势能场U(r)中运动,在笛卡尔坐 标系中写出其拉格朗日方程。
解:拉格朗日方程为:
d L L 0 dt q q
( 1, 2,3)
L为拉格朗日函数
L T U
笛卡尔坐标中的坐标变量为 x1, x2, x3,那么
3
T mxi2 / 2 i 1
2
L m 2 U ()
L 0
L 0 z
L m
L m 2 L mz
z
带入拉格朗日方程,则有:
m m 2 dU () , d
d (m 2) 0
dt
z0
3.长度为l的细绳系一小球,悬挂点按照 X Asin (t t0)方式运动,如图所示,小球被限 制在 (x, z)平面内运动,t t0时悬线竖直向下。
坐标系:两根钉连线的中点为坐标原点,连线
所在直线为x轴(向右为正),垂直连线为y轴
(向下为正),并取 为广义坐标。
B、D点的x坐标:xB l sin
xD l sin
C点的y坐标:
yC
2l
cos
a
tan
FT rB (FT rD ) W rC 0
FT i ( xBi yB j ) (FT i ) ( xDi yD j )
Wj ( xCi yC j ) 0
FT xB FT xD W yC 0
xB l cos
xD l cos
yC
(2l
sin
即有:
m( X x cos ) MX 0 mx mX cos mg sin
m( X x cos ) MX 0
解之得:
X
mg sin cos M msin2
x
(M M
m)g sin msin2
P37 第5题
x
O
X
K系(桌面坐标系)
10.直接用拉格朗日方程[ 1.1.2 (2.21) 式 ]证明,
由相差一广义坐标和时间的函数的时间全导数 的两个拉格朗日函数L` 和L [1.1.3 (3.13)式 ] 得 到的运动方程相同。
证明:L和L’相差一个广义坐标和时间的全微分
L'
Lq,q,t
df
q, t
dt
Lq,q,t
dt q dt q q
d L
dt q
2 f q,t
tq
q
2 f q,t
q q
将拉格朗日方程 d L L
dt q q 得到 d L L
dt q q
代入上两式
由L` 和L 得到的运动方程相同。
12.已知一维运动自由质点的拉氏量是 L m2 / 2
a
sin2
)
最后可得:
2FTl cos + 2Wl sin Wa csc2 0
即有:FT
Wa / (2l sin2 cos ) W
tan =W
tan
(
2l
a sin
3
-1)
FT 0
sin 3 a
2l
杠对B的作用力向内
FT 0
sin 3 a
(a)求悬线和竖直线偏离 所对应的虚位移 r
(b)已知在这一时刻的角速度为 ,求经过 dt
时间后的位移 dr。问:当 dt 0时,dr 与 r
有何差别? 解:(a)在任意时刻,约束所
x M
容许的位移为虚位移,途中
的小球,受到细绳的和自身 重力的约束,在这个时刻,
l
m z
小球只能围绕O点作圆周运动,当偏离角为 时,对应的虚位移为 l 。
q q
2 f q,t
tq
q
Байду номын сангаас f q,t
q q
L '
q
L q
q
f [
q, t
t
s
q
1
f q,t
] q
L q
f q,t
q
那么
d
L '
d [ L
f
q, t
]
A l 2 l
2a
B
D
l
l
C
W
解:由虚功原理,在平衡状态下可得
l
F主( ) r 0
B
为了求棒中的张力,可将棒的约
FT
l
A
2 l
2a
D
FT l
束予以“释放”,以张力 FT 作为
C
主动力代替棒。此时系统的自由度
W
为1,系统受3个外力作用:作用于
B的张力FT ,作用于D的张力 FT , 作用于C点的W。
2l
杠对B的作用力向外
FT 0
sin 3 a
2l
杠对B无作用力
9.质量为M的斜面可以无摩擦地在水平桌面 上滑动。斜面上无摩擦地放一滑块 m,如图所 示。写出拉格朗日方程,并求斜面的加速度 X 和滑块相对于斜面的加速度 x 。
解:系统的拉格朗日函数为
x
L 1 m( X x cos )2 1 mx2 sin2 O
x1)2 t1)
(b)假设自由质点不做匀速直线运动,则速
度为时间的函数 (t),且满足:
t2
那么
υ平方的
b a (t)dt t1
S1
t2 1 m 2dt 1 m t2 2dt
2 t1
2 t1
t2 2dt
t2 dt
t1
( t1
)2
t2 t1
(b)小球经过 dt 时间后的位移,可以看作由 两部分组成:
(1)小球绕O点作圆周运动所产生的位移 ldte
(2)小球随O点一起作简谐运动所产生的位
移 Xdt A cos(t t0 )dteX 所以,小球的位移为
