2017秋季班尖子班第2讲讲义
第二讲--秋季竞赛班补充讲义-吴桐老师

巧填算符基本方法:✓试算法(列小算式):最基本、最常用的方法,考察口算能力。
但切记:不要瞎试,要动脑思考,边分析边尝试。
✓倒推法(从最后一个符号往前填):适合于数字比较少,结果也比较小的问题。
✓凑数法:先找接近结果的数进行试算,适用于等式两边数字相差大的算式。
✓凑0法:适用于结果非常容易凑出的算式,凑出后,将其它“多余”数变0。
(可利用结论:0乘任何数都是0)✓综合方法:综合运用上述几种方法,真正做题时往往都不是只死板地用一种方法,我们要学会灵活运用。
1.在下列算式的□中,添入加好和减号,使等式成立(1)1□23□4□5□6□78□9=100(2)12□3□4□5□6□7□89=1002.在下列合适位置,添入加好和减号,使等式成立(1)9 8 7 6 5 4 3 2 1=21(2)9 8 7 6 5 4 3 2 1 =233. 只添加一个加号和两个减号,使算式成立1 2 3 4 5 6 7 8 9=1004.在下列算式中适当的地方添加+、—、×,使等式成立(比较难哦!加油!) (1)4 4 4 4 4 4 4 4 4 4 4 4 4 4 =1996(2)6 6 6 6 6 6 6 6 6 6 6 6 6 6 =19925. 在下列算式中添加适当的()、[],使等式成立(1)1+3×5+7×9+11×13+15=401(2)15-13×11-9×7-5×3-1=86、在各数之间添上适当的:“+、-、×、÷”符号,也可以使用小括号,使算式成立。
(1)321=0(2)321=1(3)321=2(4)321=3(5)321=4(6)321=57、在下面的算式中,增添运算符号(+、-、×、÷)和括号,使等式成立。
(填出五种为满分)99999=08、改变一个符号使下列等式成立。
1+2+3+4+5+6+7+8+9+10=459、请在下面的11个数字8之间添上一些四则运算符号,使计算式子,能够成立。
学而思初一数学秋季班第1讲.有理数与数轴.尖子班.学生版

1初一秋季·第1讲·尖子班·学生版长度单位实数5级 有理数综合运算实数4级 有理数与数轴 实数3级 有理数的混合运算 满分晋级阶梯漫画释义1有理数与数轴2初一秋季·第1讲·尖子班·学生版知识点切片(3个)2+1+1知识点目标有理数与数轴(2) 1、点表示数;2、比较大小 相反数与数轴(1) 1、相反数的几何意义 绝对值与数轴(1)1、绝对值的几何意义题型切片(6个)对应题目题型目标用数轴表示数 例1、练习1数轴上点、线段的移动 例2、例3、练习2 利用数轴比较大小例4、练习3 利用数轴性质建立方程求点对应的数 例5、练习4 数轴折叠 例6、练习5 周期问题与数轴例7、练习6数轴:规定了原点、正方向和单位长度的直线叫做数轴;原点、正方向、单位长度称为数轴的三要素,三者缺一不可.有理数与数轴的关系:一切有理数都可以用数轴上的点表示出来.在数轴上,右边的点所对应的数总比左边的点所对应的数大.正数都大于0,负数都小于0,正数大于一切负数. 注意:数轴上的点不都代表有理数,如π.相反数:只有符号不同的两个数,互称为相反数.特别地,0的相反数是0.数轴上,位于原点两侧且到原点距离相等的点表示的数互为相反数.绝对值:一个数a 的绝对值就是数轴上表示数a 的点与原点的距离.数a 的绝对值记作a .正数的绝对值是它本身,0的绝对值是0,负数的绝对值是它的相反数.数轴上的点,对应的数绝对值越大,离原点越远.【例1】 ⑴在数轴上画出表示12.540252--,,,,各数的点,并按从小到大的顺序重新排列,用“<”连接起来.⑵如图,数轴上表示数2-的相反数的点是( ) A .点P B .点Q C .点M D .点N ⑶数轴的单位长度为1,点A ,B 表示的数的绝对值相等,那么点A 表示的数是( ) A .4- B .2- C .0 D .4【例2】 ⑴数轴上有一点A ,它表示的有理数是3-,将点A 向左移动3个单位得到点B ,再向3210﹣1﹣2P Q M BA3初一秋季·第1讲·尖子班·学生版右移动8个单位,得到点C ,则点B 表示的数是 ,点C 表示的数是 .⑵在数轴上,坐标是整数的点称为“整点”.设数轴的单位长度是1厘米,若在这个数轴上随意画出一条长2013厘米的线段AB ,则线段AB 盖住的整点至少有 个, 至多有 个.【例3】 ⑴一个机器人从数轴原点出发,沿数轴正方向以每前进3步后退2步的程序运动,设该机器人每秒钟前进或后退1步,并且每步的距离为1个单位长,n x 表示第n 秒时机器人在数轴上的位置所对应的数. ①求3x 、5x 的值.②比较2013x 与2014x 的大小.⑵电子跳蚤在数轴上的某一点0K ,第一步由点0K 向左跳1个单位到点1K ,第二步由点1K 向右跳2个单位到点2K ,第三步由点2K 向左跳3个单位到点3K ,第四步由点3K 向右跳4个单位到点4K ,…,按以上规律跳了100步时,电子跳蚤落在数轴上的点100K 所表示的数恰好是19.94.求电子跳蚤的初始位置点0K 所表示的数.【例4】 ⑴有理数a b ,在数轴上的对应点如图,试比较a a b b a b a b --+-,,,,,的大小.4初一秋季·第1讲·尖子班·学生版0ba⑵已知a b ,是不为0的有理数,且a a b b a b =-=>,,,那么用数轴上的点来表示a b ,,正确的应该是哪一个( )DCB A a bab 0abb a【例5】 ⑴如图,数轴上标出若干点,每相邻的两点相距一个单位长度,点A 、B 、C 、D 对应的数分别为整数a 、b 、c 、d ,且24d a -=.试问:数轴上的原点在哪一点上?A B C D MNabcd⑵如图,数轴上标出若干个点,每相邻的两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d .①若2a b c d +++=-,那么与数轴原点最接近的点是( )A .A 点B .B 点C .C 点D .D 点② 若7a b +=,那么与数轴原点最接近的点是( )A .A 点B .B 点C .C 点D .D 点⑶如图,在数轴上有若干个点,每相邻两个点之间的距离是一个单位长,有理数a 、b 、c 、d 所表示的点是这些点中的4个,且在数轴上的位置如图所示,已知343a b =-,求2c d +的值.A5初一秋季·第1讲·尖子班·学生版dc b a【例6】 已知在纸面上有一数轴(如图),折叠纸面.1⑴ 若1表示的点与1-表示的点重合,则2-表示的点与数 表示的点重合: ⑵ 若1-表示的点与3表示的点重合,则5表示的点与数 表示的点重合;⑶ 若数轴上A 、B 两点之间的距离为c 个单位长度,点A 表示的有理数是a ,并且A 、B 两点经折叠后重合,请写出此时折线与数轴的交点表示的有理数是多少?【例7】 如图所示,数轴被折成90︒,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3.先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2013将与圆周上的数字 重合?初一秋季·第1讲·尖子班·学生版987654312367初一秋季·第1讲·尖子班·学生版训练1. 已知a b +与a b -互为相反数,求2000200020032003a b a b ++-训练2. 在数轴上任取一条长度为119999的线段,则此线段在这条数轴上最多能盖住的整数点的个数为 .训练3. 设a 是大于1的有理数,若a ,23a +,213a +在数轴上对应的点分别记作A ,B ,C ,则A ,B ,C 三点在数轴上自左至右的顺序是 .训练4. ⑴ a 、b 、c 、d 分别为有理数,a 是绝对值最小的有理数,b 是最小的正整数,c 的相反数是其本身,d 为负数且它的倒数是本身.求:①ab 的值;②a b c d ++-的值.⑵ 非零整数m ,n 满足||||50m n +-=,所有这样的有序(即()(),,m n n m 和不同)整数组()m n ,共有 组.8初一秋季·第1讲·尖子班·学生版用数轴表示数【练习1】 一辆货车从超市出发,向东走了3km 到达小彬家,继续向前走了1.5km 到达小颖家,然后向西走了9.5km 到达小明家,最后回到超市⑴以超市为原点,向东作为正方向,用1个单位长度表示1km ,在数轴上表示出小明,小彬,小颖家的位置. ⑵小明家距离小彬家多远? ⑶货车一共行驶了多少千米?数轴上的点、线段的移动【练习2】 ⑴在数轴上,点A 和点B 都在与154-对应的点上,若点A 以每秒3个单位长度的速度 向动,点B 以每秒2个单位长度的速度向左运动,则7秒之后,点A 和点B 所处的位置对应的数是什么?这时线段AB 的长度是多少?⑵在数轴上表示整数的点称为整数点,某数轴的单位长度是1cm ,若在这个数轴上随意画出一条长2007cm 的线段AB .被线段AB 盖住的整数有( )个.A .2005或2006B .2006或2007C .2007或2008D .2008或2009利用数轴比较大小 【练习3】 数a b c d ,,,所对应的点A B C D ,,,在数轴上的位置如图所示,那么a c +与b d +的大小关系为 .利用数轴性质建立方程求点对应的数9初一秋季·第1讲·尖子班·学生版【练习4】 如图,数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的整数a 、b 、c 、d ,且29b a -=,那么数轴的原点对应点是( ).A .A 点B .B 点C .C 点D .D 点DCB A数轴折叠【练习5】 已知在纸面上有一数轴(如图),折叠纸面.1⑴ 若1-表示的点与5表示的点重合,则7表示的点与数 表示的点重合; ⑵ 若数轴上A 、B 两点之间的距离为8个单位长度,点A 表示的有理数是10-,并且A 、B 两点经折叠后重合,请写出此时折线与数轴的交点表示的有理数是多少?周期问题与数轴【练习6】 如图,圆的周长为3,在圆的三等分点处标上数字0、1、2. 圆从图示的位置向右滚动,那么数轴上的2013将与圆上哪个数字重合?120…201321﹣1数轴是谁最先发现的?勒内·笛卡儿1596年3月31日生于法国安德尔-卢瓦尔省的图赖讷(现笛卡尔,因笛卡儿得名),1650年2月11日逝世于瑞典斯德哥尔摩,是世界著名的法国哲学家、数学家、物理学家。
初二数学秋季尖子班讲义第2章 全等模型综合别册

第二章全等模型综合第一部分:补救练习第一关:证全等模型关卡1-1 证明手拉手模型中的全等1. 已知:如图,点C为线段BD上一点,以BC,CD分别为边作等边△ABC和等边△CDE,连接BE与AC交于点M,连接AD与BE交于点O,与CE交于点N.求证:(1)CM=CN;(2)MN∥BD.2. 已知:如图,在△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE,点E在BC 上.过点D作DF∥BC,连接DB.求证:(1)△ABD≌△ACE;(2)DF=CE.关卡1-2 证明垂直模型中的全等1. 把等腰直角三角形ABC按如图所示的方式立在桌子上,顶点A顶着桌面,若另外两个顶点分别距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,求垂足之间的距离DE 的长.2. 已知:如图,在△ABC中,∠C=90°,点E在AC上,且AE=BC,ED⊥AB于点D,过点A作AC的垂线,交ED的延长线于点F.求证:AB=FE.3. 如图,在△ABC中,∠ABC=∠BAC=45°,点P在AB上,AD⊥CP于点D,BE垂直于CP的延长线于点E.求证:CD=BE.1. 如图,已知在△ABC中,AD是BC边上的中线,E是AD上一点,连接BE并延长交AC 于点F,AF=EF,求证:AC=BE.2.如图,在△ABC中,AD交BC于点D,点E是BC的中点,EF∥AD交CA的延长线于点F,交EF与于点G.若BG=CF,求证:AD为△ABC的角平分线.1. 在正方形ABCD中,点E是BC上的一动点(不与点B、C重合),点F是CD上的一动点(不与点B、C重合).(1)如图1,若AE=AF,求证:CE=CF.(2)如图2,若∠BAE=30°,∠DAF=15°,试猜想EF、BE、DF之间的数量关系,并给出证明.第二部分超级挑战1.(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E.证明:DE=BD+CE;(2)如图2,将第(1)题中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE 是否依然成立?若成立,请证明;若不成立,请说明理由;(3)拓展与应用:如图3,D,E是D,A,E三点所在的直线m上的两个动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.。
第1-7讲 尖子班合订版

Page 2 of 87
一元二次方程—— 含参问题
模块一
课前检测
1.一元二次方程 x2-3x-8=0 的两根分别为 x1、x2,则 x1x2=(
A.2
B.-2
C.8
) D.-8
2.若关于 x 的一元二次方程(k-1)x2+4x+1=0 有两个不相等的实数根,则 k 的取值范围是( )
A.k<5
B.k<5 且 k≠1
Page 4 of 87
(4)已知关于 x 的一元二次方程(m+1)x2-2(m-1)x+m=0 有实根,求 m 的取值范围 _______.
【巩固】(1)已知关于 x 的一元二次方程 ax2+bx+c=0 有一个根为 1,则 a+b+c= __________
(2)已知(x-3y)2+3(x-3y)-4=0,则 x-3y 的值等于___________
Page 5 of 87
(4)已知关于 x 的一元二次方程 x2-(3m+1)x+2m2+m=0 ①求证:无论 k 取何值,这个方程总有实数根 ②若△ABC 的两边 AB、AC 的长是这个方程的两个实数根,第三边 BC 的长为 3,当△ABC 是 等腰三角形时,求 m 的值
【巩固】(1)若 x 的方程 kx2+2x-1=0 有两个不相等的实数根,则实数 k 的取值范围是
(2)已知 a 是方程 x2-2016x+1=0 个一个根,求代数式 a2-2017a+ a 2 1 的值 2016
Page 3 of 87
模块二 方程的根与判别式
知识点睛
对于 ax2 bx c 0 的解题相关注意事项: ①确定 a 0 ; ②若已知方程的根,直接代入; ③关注代数式处理方法:整体代入法、降次法; ④任何含参方程必须计算△ = b2 - 4ac 。
秋季班讲义(1-2讲)

第一讲词语/句子能否去掉1.学会理解作者的写作意图,掌握相关的阅读解题技巧,提高语言的运用能力;2.积累文学常识和词语。
阅读宝典词语/句子能否去掉1.某句话中某个词换成另一个行吗?为什么?答:动词:不行。
因为该词准确生动具体地写出了……形容词:不行。
因为该词生动形象地描写了……副词(如都,大都,非常只有等):不行。
因为该词准确地说明了……的情况(表程度,表限制,表时间,表范围等),换了后就变成……,与事实不符。
2.一句话中某两三个词的顺序能否调换?为什么?答:不能。
因为(1)与人们认识事物的(由浅入深、由表入里、由现象到本质)规律不一致(2)该词与上文是一一对应的关系(3)这些词是递进关系,环环相扣,不能互换。
3.句子的调换,总之首先指出这两句有什么关系,再分析调换后产生的不同意思,所以不能调换(若是说明文则看是时间顺序或空间顺序或逻辑顺序;若是其他文体则看是并列式或层进式或总分式)。
【实战演练】(一)从母亲住进我们医院的那一刻起,我就后悔自己当初选择的职业了。
曾经有那么多的患者能在我的手上康复,母亲的病,却让我无能为力。
面对越来越消瘦的母亲,我除了强颜欢笑地安慰她,就只能偷偷躲到某个角落抹眼泪。
那个时候,她的癌细胞已扩散到整个胸部。
整夜整夜的疼痛让她无法入睡,可她却从来不吱一声。
每次进去看她的时候,她都装作很平静的样子,面带微笑地看着我:“我觉得比先前好多了。
你工作忙,不用老来看我。
”我扭过头,眼泪无声地掉下来。
午后的阳光照在洁白的病床上,我轻轻地梳理着母亲灰白的头发。
母亲唠叨着她的身后事,她说她早在来之前就已准备好了自己的送老衣,可惜还少一条裙子,希望我们能尽快给她准备好。
说这些的时候,母亲的脸上始终挂着平静的微笑,不像是谈死,倒像去赴一个美丽的宴会。
母亲一生爱美,临终,都不忘记要完美地离去。
我的泪,再也忍不住,一滴又一滴地落到母亲的头发里。
母亲的病房,离我的办公室仅有几步之遥,可她从来没有主动要求我去她的病房。
秋季尖子第二讲家长版讲义
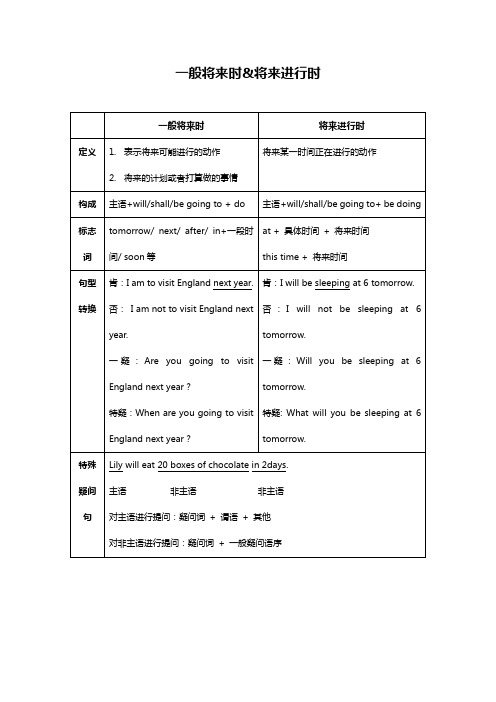
Lily will eat 20 boxes of chocolate in 2days. 主语 非主语 非主语
对主语进行提问:疑问词 + 谓语 + 其他 对非主语进行提问:疑问词 + 一般疑问语序
注意
1. 区分:will& shall;be going to& will Shall:第一人称, Will:任何人称。 be going to:有计划、或者有意图要做的某件事,或者有某种迹象要发生的事情, will:客观情况。 2. 一现表将来 当 come/arrive/leave/go/move/begin/start/stop/die 等词出现时, 可以用现在进行 时表将来。 eg. Tom is leaving for France next Sunday. 3. 主将从现 当引导词 if/unless/as soon as/ not… until/when/before/after 引导从句时,主句一 般将来时(或祈使句、或含有情态动词) 。
将来进行时
将来一时间正在进行的动作
主语+will/shall/be going to+ be doing at + 具体时间 + 将来时间 this time + 将来时间 肯:I will be sleeping at 6 tomorrow. 否 : I will not be sleeping at 6 tomorrow. 一 疑 : Will you be sleeping at 6 tomorrow. 特疑: What will you be sleeping at 6 tomorrow.
一般将来时&将来进行时
一般将来时
定义 1. 表示将来可能进行的动作 2. 将来的计划或者打算做的事情 构成 标志 词 句型 转换 主语+will/shall/be going to + do tomorrow/ next/ after/ in+一段时 间/ soon 等 肯:I am to visit England next year. 否: I am not to visit England next year. 一 疑 : Are you going to visit England next year? 特疑:When are you going to visit England next year? 特殊 疑问 句
2017七年级秋季讲义汇总1-7讲—尖子班

成长手册
第 1 页 共 101 页
让进步看得见
目录
课程 1 有理数的应用.........................................................................................5 课程 2 整式..........................................................................................................21 课程 3 绝对值化简.............................................................................................34 课程 4 含参数的一元一次方程.......................................................................47 课程 5 找规律、程序运算与新定义.............................................................59 课程 6 数轴动点(一)......................................................................................69 课程 7 数轴动点(二)......................................................................................83
第 4 页 共 101 页
让进步看得见
有理数的应用
尖子班必修2讲义1

博闻强识
——尖子班必修2
教师:王文博
温馨提示:本讲义为A4大小,如需打印请注意用纸尺寸
爱护环境,从我做起,提倡使用电子讲义
习题1 弹力
习题2 摩擦力
习题3 力的合成分解
习题4 共点力平衡
习题5 匀变速直线运动
习题6 运动图象
习题7 运动的合成和分解
习题8 平抛
习题9 牛顿运动定律
习题10 牛顿运动定律的应用
习题11 圆周运动
习题12 万有引力定律
习题13 人造卫星
习题14 功和功率
习题15 动能定理
习题16 机械能守恒定律
习题17 功和能
习题18 动量定理
习题19 动量守恒定律
习题20 力学综合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【分析】 因为关于 x 的方程 mx 2 − 4 x + 4 = 0 有实数根; 所以
m≠0 , 2 ∆1 = ( −4 ) − 4 × m × 4 = 16 (1 − m ) ≥ 0 m ≠ 0 x 的方程 ;因为关于 m ≤1 0 有实数根; x 2 − 4mx + 4m 2 − 4m − 5 =
∆ 2 = ( −4m ) − 4 × 1 × ( 4m 2 − 4m − 5 ) 5 = 4 ( 4m + 5 ) ≥ 0 , m ≥ − ; 4 5 所以 − ≤ m ≤ 1且 m ≠ 0 ; 4 因为 m 取整数, 所以 m = −1或 m = 1.
2
所以
当 m = −1时,方程 − x 2 − 4 x + 4 = 0的 两个根 x1 =−2 + 2 2 , x2 =−2 − 2 2
八年级尖子班第二讲 一元二次方程 整数解问题(一) 【例 1】★★☆☆☆ 已知 a 是正整数, 如果关于 x 的方 程 x 2 + ( a + 18 ) x + 56 = 0 的根都是整 数,求 a 的值及方程的整数根. 【分析】 因为关于 x 的方程 x 2 + ( a + 18 ) x + 56 = 0 的根都是整数, 且 a 为正整数,∴ a + 18 > 0 利用十字相乘:因为
【例 8】★★★★☆ ⑴已知关于 x 的方程 x 2 + ( m − 1) x + m + 1 = 0 的两根均为 整数,试求整数 m 的值. ⑵已知 k 是正整数, 关于 x 的一元 二次方程 x 2 + x + 10 = k ( k − 1) 有一 个正整数根,求这个根及 k 的值. 【分析】⑴因为关于 x 的二次方 程 x 2 + ( m − 1) x + m + 1 = 0 的两根均 为整数;所以
又因为 m − 3 − k , m −3− k ≤m −3+ k;
m − 3 + k 同奇偶; 2 m − 3 − k = −6 m − 3 − k = 所以 或 ; 6 m − 3 + k = −2 m − 3 + k = m = 7 m = −1 所以 或 ; k = 2 k = 2
或 −5 ; 综上所述, a = 1或 −1或 3或 −3或 5 或 −5 . 【例 5】★★★☆☆ ⑴若 m 为整数,且关于 x 的方程 求m m 2 x 2 + (m + 1) x + 1 = 0 有有理根, 的值. ⑵设关于 x 的方程 mx 2 − (m − 2) x + (m − 3) = 0 有整数解, 试确定整数 m 的值,并求出这时 方程所有的整数解. 【分析】⑴当 m = 0 时, x + 1 = 0, 解得, x = −1,符合题意, 当 m ≠ 0 时,由 ∆ = (m + 1) 2 − 4m 2 = −3m 2 + 2m + 1 ≥ 0 ,
x1 = x2 = −1 ∴ a = −2
【例 3】★★★☆☆ 若关于 x 的方程
(6 − k )(9 − k ) x 2 − (117 − 15k ) x + 54 = 0
的解都是整数,则符合条件的整 数 k 的值有哪些? 【分析】 当6 − k = 0 时,即 k = 6 ,则原方程 为 −(117 − 15 × 6) x + 54 = 0 ,解得 x = 2 ; 当9 − k = 0 时,即 k = 9 ,则原方程 为 −(117 − 15 × 9) x + 54 = 解得 x = −3; 0, 当 6 − k ≠ 0 ,9 − k ≠ 0 时,即 k ≠ 6 且
56 = 1 × 56 =2 × 28 =4 × 14 = 8× 7 所以 a + 18 = (舍) , 1 + 56 , 2 + 28, 4 + 14 8 + 7 (舍)
即 a = 39 或12 . 当 a = 39 时,方程的整数根为 −1,
−56 ;
当 a = 12 时,方程的整数根为 −2 , −28. 【例 2】★★☆☆☆ ⑴ 若 k 为正整数,且关于 x 的方 程 ( k 2 − 1) x 2 − 6 ( 3k − 1) x + 72 = 0 有两 个相异正整数根,求 k 的值. ⑵已知关于 x 的方程 (a 2 − 1) x 2 − 2(5a + 1) x + 24 = 0 有两个 不等的负整数根,则整数 a 的值 是________. 【分析】 ⑴根据题意得: k ≠ ±1 利用因式分解: 0, ( k + 1)( k − 1) x 2 − 6 ( 3k − 1) x + 72 = 0 .即 ( k + 1) x − 12 ( k − 1) x − 6 =
1 解得, − ≤ m ≤ 1, 3 因为 m 为整数,所以 m = 1.
经检验: m = 1,方程两根为 x = x= 1,符合题意. 1 2 ⑵若 m = 0 ,则 2 x − 3 = 0 ,此时方程 无整数解; 若 m ≠ 0 ,∵方程有整数根,则 ∆ = (m − 2) 2 − 4m(m − 3) ≥ 0 , 即 3m 2 − 8m − 4 ≤ 0 ,解得
2 2k − 1 − m = 所以 或 20 2k − 1 + m = 4 2k − 1 − m = k = 6 k = 4 ; 所以 或 ; 10 2k − 1 + m = m = 9 m = 3
当 k = 6 时,原方程的正整数根 x = 4; 当 k = 4 时,原方程的正整数根 x = 1.
6 4 x1 = , x2 = a −1 a +1 −1, −3, −6 , −2 , 即a = 0, 当a −1 = −1, −2 , −5 时, x1为负整数.
−1, −3, −2 , −4 , 当a + 1 = 即 a = −2 , −5 时, x2 为负整数;
∴ a = −5 , −2 .但当 a = −5时,
不为有理数, 不符合题意;当 m = 1时,方程 = x= 2, x2 − 4 x + 4 = 0 的两个根 x 1 2 方程 x 2 − 4 x − 5 = 0 的两个根 x1 = 5 , x2 = −1,符合题意; 关于 x 的两个 综上所述当 m = 1时, 一元二次方程的根是整数. 【例 7】★★☆☆☆ 设 m 为整数, 且 4 < m < 40 , 关于 x 的 方程 x 2 − 2 ( 2m − 3) x + 4m 2 − 14m + 8 = 0有 两个整数根,求 m 的值及方程的 根. 【分析】 = ∆ 4(2m + 1) 为完全平方 数,又 m 为 4 < m < 40 的整数,则 m = 12 或 24 .当 m = 12 时, x1 = 16 , 当 m = 24 时, x2 = 26 ; x3 = 38, x4 = 52 .
有一整数根,求 a 的值. 【分析】 当 a 2 = 0 , a = 0 时,原方程无解. 当 a 2 ≠ 0 ,a ≠ 0 时,原方程是关于 x 的一元二次方程; 利用因式分解: 0 ,所以 ( ax − 2a + 3)( ax − a + 5) =
2a − 3 a −5 x1 = , x2 = ; a a 2a − 3 3 = 2 − 时,a = 1或 −1或 3 当 x= a a 或 −3; a −5 5 = 1 − 时, a = 1或 −1或 5 当 x= a a
= k≠ 9 , x1 9 6 = , x2 ; 6−k 9−k
若方程的解都是整数,则 6−k = ±1, ± 3, ± 9 且
9−k = ±1, ± 2, ± 3, ± 6,
即 k = 3, 7,15 . 【例 4】★★★☆☆ 已知关于 x 的方程
a 2 x 2 − ( 3a 2 − 8a ) x + 2a 2 − 13a + 15 = 0
12 6 x1 = , x2 = . k +1 k −1
12 由 为正整数得:正整数 k = 1、 k +1 2 、 3 、 5 、11; 6 由 为正整数得:正整数 k = 2 、 k −1 3、 4 、7. 所以 k = 2 , 3使得 x1, x2 同时为正
整数, = x= 3,与题目不 但当 k = 3时,x 1 2 符,所以,只有 k = 2 为所求. ⑵根据题意得: a ≠ ±1 利用因式分解: 0 得: ( a + 1) x − 4 ( a − 1) x − 6 =
经检验 m = 7 , m = −1均符合题意. 2 ⑵ △= ( 2k − 1) − 40 是完全平方数; 2 m 2(不妨令 m 为自 设 ( 2k − 1) − 40 = 然数); 2 k − 2 1 40 , ) − m2 = 所以 ( 40 ; ( 2k − 1 − m )( 2k − 1 + m ) = 因为 k 是正整数,m 是自然数;所 以 2k − 1 + m 是正整数;所以 2k − 1 − m 是正整数; 因为 2k − 1 − m 、 2k − 1 + m 同奇偶, 且 2k − 1 − m ≤ 2k − 1 + m ;
∆ =
( m − 1)
2
− 4 × 1× ( m + 1 = ) m 2 − 6m − 3
为完全平方数; 设 m 2 − 6m − 3 = k 2(不妨令 k 为自然 数); 2 2 m − − k = 3 12 , ) ( 12 ; ( m − 3 − k )( m − 3 + k ) = 因为 k 为自然数,所以
4−2 7 4+2 7 ≤m≤ 1时,方程有整数解 −2 和1; 当 m = 2 时,方程无整数解; 当 m = 3时,方程有整数解 0 . 【例 6】★★★☆☆ 当 m 是何整数时, 关于 x 的一元二 次方程 mx 2 − 4 x + 4 = 0与 x 2 − 4mx + 4m 2 − 4m − 5 = 0 的根是整 数?
