构建几何模型求解最值问题
2023年中考数学常见几何模型之最值模型瓜豆原理

专题13 最值模型-瓜豆原理动点轨迹问题是中考的重要题型,受学生解析几何知识的局限和思维能力的束缚,该压轴点往往成为学生在中考中的一个坎,致使该压轴点成为学生在中考中失分的集中点。
掌握该压轴题型的基本图形,构建问题解决的一般思路,是中考专题复习的一个重要途径。
本专题就最值模型中的瓜豆原理(动点轨迹基本类型为直线型和圆弧型)进行梳理及对应试题分析,方便掌握。
【模型解读】瓜豆原理:若两动点到某定点的距离比是定值,夹角是定角,则两动点的运动路径相同。
主动点叫瓜,从动点叫豆,瓜在直线上运动,豆也在直线_上运动;瓜在圆周上运动,豆的轨迹也是圆。
古人云:种瓜得瓜,种豆得豆.“种”圆得圆,“种”线得线,谓之“瓜豆原理”。
模型1、运动轨迹为直线模型1-1如图,P是直线BC上一动点,连接AP,取AP中点Q,当点P在BC上运动时,Q点轨迹是?解析:当P点轨迹是直线时,Q点轨迹也是一条直线.理由:分别过A、Q向BC作垂线,垂足分别为M、N,在运动过程中,因为AP=2AQ,所以QN始终为AM的一半,即Q点到BC的距离是定值,故Q点轨迹是一条直线.模型1-2如图,在△APQ中AP=AQ,∠P AQ为定值,当点P在直线BC上运动时,求Q点轨迹?解析:当AP 与AQ 夹角固定且AP :AQ 为定值的话,P 、Q 轨迹是同一种图形。
理由:当确定轨迹是线段的时候,可以任取两个时刻的Q 点的位置,连线即可,比如Q 点的起始位置和终点位置,连接即得Q 点轨迹线段。
【最值原理】动点轨迹为一条直线时,利用“垂线段最短”求最值。
1)当动点轨迹确定时可直接运用垂线段最短求最值;2)当动点轨迹不易确定是直线时,可通过以下三种方法进行确定:①观察动点运动到特殊位置时,如中点,端点等位置时是否存在动点与定直线的端点连接后的角度不变,若存在该动点的轨迹为直线;②当某动点到某条直线的距离不变时,该动点的轨迹为直线;③当一个点的坐标以某个字母的代数式表示时,若可化为一次函数,则点的轨迹为直线;④若动点轨迹用上述方法都合适,则可以将所求线段转化为其他已知轨迹的线段求值。
中考数学几何模型之阿氏圆最值模型(解析版)

中考数学几何模型:阿氏圆最值模型名师点睛拨开云雾开门见山在前面的“胡不归”问题中,我们见识了“kPA+PB”最值问题,其中P点轨迹是直线,而当P点轨迹变为圆时,即通常我们所说的“阿氏圆”问题.【模型来源】“阿氏圆”又称为“阿波罗尼斯圆”,如下图,已知A、B两点,点P满足PA:PB=k(k≠1),则满足条件的所有的点P的轨迹构成的图形为圆.这个轨迹最早由古希腊数学家阿波罗尼斯发现,故称“阿氏圆”.A B P O【模型建立】如图1 所示,⊙O 的半径为R,点A、B 都在⊙O 外,P为⊙O上一动点,已知R=25 OB,连接PA、PB,则当“PA+25PB”的值最小时,P 点的位置如何确定?解决办法:如图2,在线段OB 上截取OC使OC=25R,则可说明△BPO与△PCO相似,则有25PB=PC。
故本题求“PA+25PB”的最小值可以转化为“PA+PC”的最小值,其中与A与C为定点,P为动点,故当A、P、C 三点共线时,“PA+PC”值最小。
【技巧总结】计算PA k PB +的最小值时,利用两边成比例且夹角相等构造母子型相似三角形问题:在圆上找一点P 使得PA k PB +的值最小,解决步骤具体如下: 1. 如图,将系数不为1的线段两端点与圆心相连即OP ,OB2. 计算出这两条线段的长度比OPk OB = 3. 在OB 上取一点C ,使得OC k OP =,即构造△POM ∽△BOP ,则PCk PB=,PC k PB =4. 则=PA k PB PA PC AC ++≥,当A 、P 、C 三点共线时可得最小值典题探究 启迪思维 探究重点例题1. 如图,在Rt △ABC 中,∠C=90°,AC=4,BC=3,以点C 为圆心,2为半径作圆C ,分别交AC 、BC于D 、E 两点,点P 是圆C 上一个动点,则12PA PB +的最小值为__________.EABC DPMPDCBA【分析】这个问题最大的难点在于转化12PA ,此处P 点轨迹是圆,注意到圆C 半径为2,CA=4,连接CP ,构造包含线段AP 的△CPA ,在CA 边上取点M 使得CM=2,连接PM ,可得△CPA ∽△CMP ,故PA :PM=2:1,即PM=12PA .问题转化为PM+PB ≥BM 最小值,故当B ,P ,M 三点共线时得最小值,直接连BM 即可得13.变式练习>>>1.如图1,在RT △ABC 中,∠ACB=90°,CB=4,CA=6,圆C 的半径为2,点P 为圆上一动点,连接AP ,BP , 求①BP AP 21+,②BP AP +2,③BP AP +31,④BP AP 3+的最小值.[答案]:①=37,②=237,③=3372,④=37例题2. 如图,点C 坐标为(2,5),点A 的坐标为(7,0),⊙C 的半径为10,点B 在⊙C 上一动点,AB OB 55的最小值为________.[答案]:5.变式练习>>>2.如图,在平面直角坐标系xoy 中,A(6,-1),M(4,4),以M 为圆心,22为半径画圆,O 为原点,P 是⊙M 上一动点,则PO+2PA 的最小值为________.[答案]:10.例题3. 如图,半圆的半径为1,AB为直径,AC、BD为切线,AC=1,BD=2,P为上一动点,求PC+PD 的最小值.【解答】解:如图当A、P、D共线时,PC+PD最小.理由:连接PB、CO,AD与CO交于点M,∵AB=BD=4,BD是切线,∴∠ABD=90°,∠BAD=∠D=45°,∵AB是直径,∴∠APB=90°,∴∠P AB=∠PBA=45°,∴P A=PB,PO⊥AB,∵AC=PO=2,AC∥PO,∴四边形AOPC是平行四边形,∴OA=OP,∠AOP=90°,∴四边形AOPC是正方形,∴PM=PC,∴PC+PD=PM+PD=DM,∵DM⊥CO,∴此时PC+DP最小=AD﹣AM=2﹣=.变式练习>>>3.如图,四边形ABCD为边长为4的正方形,⊙B的半径为2,P是⊙B上一动点,则PD+PC的最小值为5;PD+4PC的最小值为10.【解答】解:①如图,连接PB、在BC上取一点E,使得BE=1.∵PB2=4,BE•BC=4,∴PB2=BE•BC,∴=,∵∠PBE=∠CBE,∴△PBE∽△CBE,∴==,∴PD+PC=PD+PE,∵PE+PD≤DE,在Rt△DCE中,DE==5,∴PD+PC的最小值为5.②连接DB ,PB ,在BD 上取一点E ,使得BE =,连接EC ,作EF ⊥BC 于F .∵PB 2=4,BE •BD =×4=4,∴BP 2=BE •BD ,∴=,∵∠PBE =∠PBD ,∴△PBE ∽△DBP , ∴==,∴PE =PD ,∴PD +4PC =4(PD +PC )=4(PE +PC ),∵PE +PC ≥EC ,在Rt △EFC 中,EF =,FC =,∴EC =,∴PD +4PC 的最小值为10.故答案为5,10.例题4. 如图,已知正方ABCD 的边长为6,圆B 的半径为3,点P 是圆B 上的一个动点,则12PD PC 的最大值为_______.AB CDP【分析】当P 点运动到BC 边上时,此时PC=3,根据题意要求构造12PC ,在BC 上取M 使得此时PM=32,则在点P 运动的任意时刻,均有PM=12PC ,从而将问题转化为求PD-PM 的最大值.连接PD ,对于△PDM ,PD-PM <DM ,故当D 、M 、P 共线时,PD-PM=DM 为最大值152. ABCD P MMPDCBAABCDPMMPDCBA变式练习>>>4.(1)如图1,已知正方形ABCD的边长为9,圆B的半径为6,点P是圆B上的一个动点,那么PD+的最小值为,PD﹣的最大值为.(2)如图2,已知菱形ABCD的边长为4,∠B=60°,圆B的半径为2,点P是圆B上的一个动点,那么PD+的最小值为,PD﹣的最大值为.图1 图2【解答】解:(1)如图3中,在BC上取一点G,使得BG=4.∵==,==,∴=,∵∠PBG=∠PBC,∴△PBG∽△CBP,∴==,∴PG=PC,∴PD+PC=DP+PG,∵DP+PG≥DG,∴当D、G、P共线时,PD+PC的值最小,最小值为DG==.∵PD﹣PC=PD﹣PG≤DG,当点P在DG的延长线上时,PD﹣PC的值最大,最大值为DG=.故答案为,(2)如图4中,在BC上取一点G,使得BG=1,作DF⊥BC于F.∵==2,==2,∴=,∵∠PBG=∠PBC,∴△PBG∽△CBP,∴==,∴PG=PC,∴PD+PC=DP+PG,∵DP+PG≥DG,∴当D、G、P共线时,PD+PC的值最小,最小值为DG,在Rt△CDF中,∠DCF=60°,CD=4,∴DF=CD•sin60°=2,CF=2,在Rt△GDF中,DG==∵PD﹣PC=PD﹣PG≤DG,当点P在DG的延长线上时,PD﹣PC的值最大(如图2中),最大值为DG=.故答案为,.例题5. 如图,抛物线y=﹣x2+bx+c与直线AB交于A(﹣4,﹣4),B(0,4)两点,直线AC:y=﹣12x﹣6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.(1)求抛物线y=﹣x2+bx+c的表达式;(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标;(3)①在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F,H为顶点的四边形是矩形?求出此时点E,H的坐标;②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求12AM+CM它的最小值.【解答】解:(1)∵点A(﹣4,﹣4),B(0,4)在抛物线y=﹣x2+bx+c上,∴,∴,∴抛物线的解析式为y=﹣x2﹣2x+4;(2)设直线AB的解析式为y=kx+n过点A,B,∴,∴,∴直线AB的解析式为y=2x+4,设E(m,2m+4),∴G(m,﹣m2﹣2m+4),∵四边形GEOB是平行四边形,∴EG=OB=4,∴﹣m2﹣2m+4﹣2m﹣4=4,∴m=﹣2,∴G(﹣2,4);(3)①如图1,由(2)知,直线AB的解析式为y=2x+4,∴设E(a,2a+4),∵直线AC:y=﹣12x﹣6,∴F(a,﹣12a﹣6),设H(0,p),∵以点A,E,F,H为顶点的四边形是矩形,∵直线AB的解析式为y=2x+4,直线AC:y=﹣12x﹣6,∴AB⊥AC,∴EF为对角线,∴12(﹣4+0)=12(a+a),12(﹣4+p)=12(2a+4﹣12a﹣6),∴a=﹣2,P=﹣1,∴E(﹣2,0).H(0,﹣1);②如图2,由①知,E(﹣2,0),H(0,﹣1),A(﹣4,﹣4),∴EH=5,AE=25,设AE交⊙E于G,取EG的中点P,∴PE=52,连接PC交⊙E于M,连接EM,∴EM=EH=,∴525PEME==12,∵525MEAE==12,∴PE MEME AE==12,∵∠PEM=∠MEA,∴△PEM∽△MEA,∴PE MEME AE==12,∴PM=12AM,∴12AM+CM的最小值=PC,设点P(p,2p+4),∵E(﹣2,0),∴PE2=(p+2)2+(2p+4)2=5(p+2)2,∵PE=52,∴5(p+2)2=54,∴p=52-或p=﹣32(由于E(﹣2,0),所以舍去),∴P(52-,﹣1),∵C(0,﹣6),∴PC==552,即:12AM+CM=552.变式练习>>>5.如图1,抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB 于点M.(1)求a的值和直线AB的函数表达式;(2)设△PMN的周长为C1,△AEN的周长为C2,若=,求m的值;(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E′A、E′B,求E′A+E′B的最小值.【解答】解:(1)令y=0,则ax2+(a+3)x+3=0,∴(x+1)(ax+3)=0,∴x=﹣1或﹣,∵抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),∴﹣=4,∴a=﹣.∵A(4,0),B(0,3),设直线AB解析式为y=kx+b,则,解得,∴直线AB解析式为y=﹣x+3.(2)如图1中,∵PM⊥AB,PE⊥OA,∴∠PMN=∠AEN,∵∠PNM=∠ANE,∴△PNM∽△ANE,∴=,∵NE∥OB,∴=,∴AN=(4﹣m),∵抛物线解析式为y=﹣x2+x+3,∴PN=﹣m2+m+3﹣(﹣m+3)=﹣m2+3m,∴=,解得m=2.(3)如图2中,在y轴上取一点M′使得OM′=,连接AM′,在AM′上取一点E′使得OE′=OE.∵OE′=2,OM′•OB=×3=4,∴OE′2=OM′•OB,∴=,∵∠BOE′=∠M′OE′,∴△M′OE′∽△E′OB,∴==,∴M′E′=BE′,∴AE′+BE′=AE′+E′M′=AM′,此时AE′+BE′最小(两点间线段最短,A、M′、E′共线时),最小值=AM′==.达标检测 领悟提升 强化落实1. 如图,在RT △ABC 中,∠B=90°,AB=CB=2,以点B 为圆心作圆与AC 相切,圆C 的半径为2,点P 为圆B 上的一动点,求PC AP 22的最小值.[答案]:5.2. 如图,边长为4的正方形,内切圆记为⊙O ,P 是⊙O 上一动点,则2PA+PB 的最小值为________.[答案]:25.3. 如图,等边△ABC 的边长为6,内切圆记为⊙O ,P 是⊙O 上一动点,则2PB+PC 的最小值为________.[答案]37.4. 如图,在Rt △ABC 中,∠C=90°,CA=3,CB=4,C 的半径为2,点P 是C 上的一动点,则12AP PB+的最小值为?5. 如图,在平面直角坐标系中,()2,0A ,()0,2B ,()4,0C ,()3,2D ,P 是△AOB 外部第一象限内的一动点,且∠BPA=135°,则2PD PC +的最小值是多少?[答案]426. 如图,Rt△ABC,∠ACB=90°,AC=BC=2,以C为顶点的正方形CDEF(C、D、E、F四个顶点按逆时针方向排列)可以绕点C自由转动,且CD=,连接AF,BD(1)求证:△BDC≌△AFC;(2)当正方形CDEF有顶点在线段AB上时,直接写出BD+AD的值;(3)直接写出正方形CDEF旋转过程中,BD+AD的最小值.【解答】(1)证明:如图1中,∵四边形CDEF是正方形,∴CF=CD,∠DCF=∠ACB=90°,∴∠ACF=∠DCB,∵AC=CB,∴△FCA≌△DCB(SAS).(2)解:①如图2中,当点D,E在AB边上时,∵AC=BC=2,∠ACB=90°,∴AB=2,∵CD⊥AB,∴AD=BD=,∴BD+AD=+1.②如图3中,当点E,F在边AB上时.BD=CF=,AD==,∴BD+AD=+.(3)如图4中.取AC的中点M.连接DM,BM.∵CD=,CM=1,CA=2,∴CD2=CM•CA,∴=,∵∠DCM=∠ACD,∴△DCM∽△ACD,∴==,∴DM=AD,∴BD+AD=BD+DM,∴当B,D,M共线时,BD+AD的值最小,最小值==.7. (1)如图1,在△ABC中,AB=AC,BD是AC边上的中线,请用尺规作图做出AB边上的中线CE,并证明BD=CE:(2)如图2,已知点P是边长为6的正方形ABCD内部一动点,P A=3,求PC+PD的最小值;(3)如图3,在矩形ABCD中,AB=18,BC=25,点M是矩形内部一动点,MA=15,当MC+MD 最小时,画出点M的位置,并求出MC+MD的最小值.【解答】解:(1)如图1中,作线段AB的垂直平分线MN交AB于点E,连接EC.线段EC即为所求;∵AB=AC,AE=EC,AD=CD,∴AE=AD,∵AB=AC,∠A=∠A,AD=AE,∴△BAD≌△CAE(SAS),∴BD=CE.(2)如图2中,在AD上截取AE,使得AE=.∵P A2=9,AE•AD=×6=9,∴P A2=AE•AD,∴=,∵∠P AE=∠DAP,∴△P AE∽△DAP,∴==,∴PE=PD,∴PC+PD=PC+PE,∵PC+PE≥EC,∴PC+PD的最小值为EC的长,在Rt△CDE中,∵∠CDE=90°,CD=6,DE=,∴EC==,∴PC+PD的最小值为.(3)如图3中,如图2中,在AD上截取AE,使得AE=9.∵MA2=225,AE•AD=9×25=225,∴MA2=AE•AE,∴=,∵∠MAE=∠DAM,∴△MAE∽△DAM,∴===,∴ME=MD,∴MC+MD=MC+ME,∵MC+ME≥EC,∴MC+MD的最小值为EC的长,在Rt△CDE中,∵∠CDE=90°,CD=18,DE=16,∴EC==2,∴MC+MD的最小值为2.。
专题02 几何最值之费马点模型(解析版)
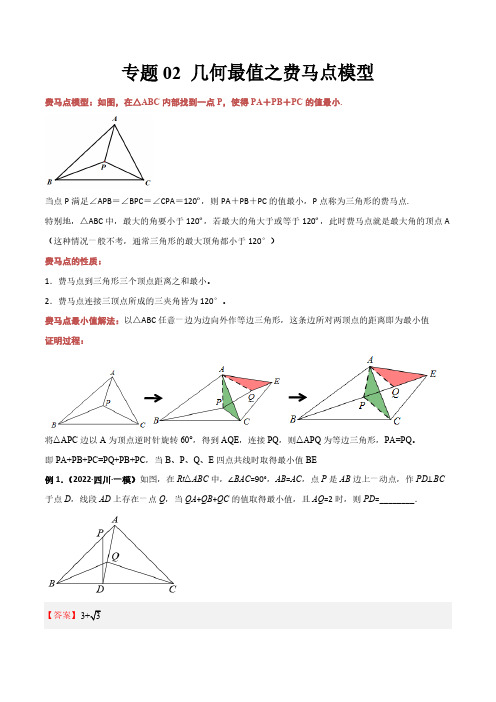
专题02 几何最值之费马点模型费马点模型:如图,在△ABC内部找到一点P,使得PA+PB+PC的值最小.当点P满足∠APB=∠BPC=∠CPA=120º,则PA+PB+PC的值最小,P点称为三角形的费马点.特别地,△ABC中,最大的角要小于120º,若最大的角大于或等于120º,此时费马点就是最大角的顶点A (这种情况一般不考,通常三角形的最大顶角都小于120°)费马点的性质:1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
费马点最小值解法:以△ABC任意一边为边向外作等边三角形,这条边所对两顶点的距离即为最小值证明过程:将△APC边以A为顶点逆时针旋转60°,得到AQE,连接PQ,则△APQ为等边三角形,PA=PQ。
即PA+PB+PC=PQ+PB+PC,当B、P、Q、E四点共线时取得最小值BE例1.(2022·四川·一模)如图,在Rt△ABC中,∠BAC=90°,AB=AC,点P是AB边上一动点,作PD⊥BC 于点D,线段AD上存在一点Q,当QA+QB+QC的值取得最小值,且AQ=2时,则PD=________.【详解】解:如图1,将△BQC绕点B顺时针旋转60°得到△BNM,连接QN,∴BQ=BN,QC=NM,∠QBN=60°,∴△BQN是等边三角形,∴BQ=QN,∴QA+QB+QC=AQ+QN+MN,∴当点A,点Q,点N,点M共线时,QA+QB+QC值最小,此时,如图2,连接MC∵将△BQC绕点B顺时针旋转60°得到△BNM,∴BQ=BN,BC=BM,∠QBN=60°=∠CBM,∴△BQN是等边三角形,△CBM是等边三角形,∴∠BQN=∠BNQ=60°,BM=CM,例2.(2021·四川·成都实外九年级阶段练习)如图,在ABC V 中,901CAB AB AC Ð=°==,,P 是ABC V 内一点,求PA PB PC ++的最小值为______.2【变式训练1】(2022·全国·九年级专题练习)如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为______.【答案】4+33易证△AMD≌△AGF,∴MD∴ME+MA+MD=ME+EG过F作FH⊥BC交BC于H【变式训练2】(2019·湖北武汉·中考真题)问题背景:如图,将ABC D 绕点A 逆时针旋转60°得到ADE D ,DE与BC 交于点P ,可推出结论:PA PC PE+=问题解决:如图,在MNG D 中,6MN =,75M Ð=°,MG =O 是MNG D 内一点,则点O 到MNG D 三个顶点的距离和的最小值是___________【变式训练3】(2021·全国·九年级专题练习)如图,△ABC中,∠BAC=30°且AB=AC,P是底边上的高AH上一点.若AP+BP+CP的最小值为,则BC=_____.课后训练1.(2022·全国·九年级专题练习)如图,四边形ABCD是菱形,AB=4,且∠ABC=∠ABE=60°,G为对角线BD (不含B点)上任意一点,将△ABG绕点B逆时针旋转60°得到△EBF,当AG+BG+CG取最小值时EF的长( )A.B.C.D.【答案】D【详解】解:如图,∵将△ABG绕点B逆时针旋转60°得到△EBF,∴BE=AB=BC,BF=BG,EF=AG,∴△BFG是等边三角形.∴BF=BG=FG,.∴AG+BG+CG=FE+GF+CG.根据“两点之间线段最短”,∴当G点位于BD与CE的交点处时,AG+BG+CG的值最小,即等于EC的长,过E点作EF⊥BC交CB的延长线于F,∴∠EBF=180°-120°=60°,∵BC=4,2.(2022·全国·九年级专题练习)如图,四边形ABCD是菱形,A B=6,且∠ABC=60° ,M是菱形内任一点,连接AM,BM,CM,则AM+BM+CM的最小值为________.3.(2021·全国·九年级专题练习)如图,△ABC中,∠BAC=45°,AB=6,AC=4,P为平面内一点,求+最小值3PC4.(2022·福建三明·八年级期中)【问题背景】17世纪有着“业余数学家之王”美誉的法国律师皮耶·德·费马,提出一个问题:求作三角形内的一个点,使它到三角形三个顶点的距离之和最小后来这点被称之为“费马点”.如图,点P 是ABC V 内的一点,将APC △绕点A 逆时针旋转60°到AP C ¢¢V ,则可以构造出等边APP ¢V ,得AP PP ¢=,CP CP ¢=,所以PA PB PC ++的值转化为PP PB P C +¢+¢¢的值,当B ,P ,P ¢,C 四点共线时,线段BC 的长为所求的最小值,即点P 为ABC V 的“费马点”.(1)【拓展应用】如图1,点P 是等边ABC V 内的一点,连接PA ,PB ,PC ,将PAC △绕点A 逆时针旋转60°得到AP C ¢¢V .①若3PA =,则点P 与点P ¢之间的距离是______;②当3PA =,5PB =,4PC =时,求AP C Т的大小;(2)如图2,点P 是ABC V 内的一点,且90BAC Ð=°,6AB =,AC =PA PB PC ++的最小值.②∵△ABC 为等边三角形,∴AB =AC 又∵APP ¢V 是等边三角形,∴∠PAC 在△ABP 与ACP ¢△中,AB AC BAP AP AP =ìïÐ=Ðíï=î′则,60ACP A CP ACP ACP Ð=ÐÐ+Ð=°′′′,在Rt ABC V 中,(22262BC AB AC =+=+1,30,602AC BC ABC ACB =\Ð=°Ð=°Q ,5.(2021·江苏·苏州工业园区星湾学校八年级期中)背景资料:在已知ABC V 所在平面上求一点P ,使它到三角形的三个顶点的距离之和最小.这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的,所求的点被人们称为“费马点”.如图1,当ABC V 三个内角均小于120°时,费马点P 在ABC V 内部,当120APB APC CPB Ð=Ð=Ð=°时,则PA PB PC ++取得最小值.(1)如图2,等边ABC V 内有一点P ,若点P 到顶点A 、B 、C 的距离分别为3,4,5,求APB Ð的度数,为了解决本题,我们可以将ABP V 绕顶点A 旋转到ACP ¢△处,此时ACP ABP ¢V V ≌这样就可以利用旋转变换,将三条线段PA 、PB 、PC 转化到一个三角形中,从而求出APB Ð=_______;知识生成:怎样找三个内角均小于120°的三角形的费马点呢?为此我们只要以三角形一边在外侧作等边三角形并连接等边三角形的顶点与ABC V 的另一顶点,则连线通过三角形内部的费马点.请同学们探索以下问题.(2)如图3,ABC V 三个内角均小于120°,在ABC V 外侧作等边三角形ABB ¢V ,连接CB ¢,求证:CB ¢过ABC V 的费马点.(3)如图4,在RT ABC V 中,90C Ð=°,1AC =,30ABC Ð=°,点P 为ABC V 的费马点,连接AP 、BP 、CP ,求PA PB PC ++的值.(4)如图5,在正方形ABCD 中,点E 为内部任意一点,连接AE 、BE 、CE ,且边长2AB =;求AE BE CE ++的最小值.(3)解:将△APB 逆时针旋转60°,得到∵∠PAP′=∠BAB′=60°,∴△APP′和△∵PA PB PC PP P B PC¢¢¢++=++∴点C ,点P ,点P′,点B′四点共线时,∵90C Ð=°,1AC =,30ABC Ð=6.(2022·内蒙古·科尔沁左翼中旗教研室八年级期中)如图,在△ABC 中,∠BAC =90°,AB =AC =1,P 是△ABC 内一点,求PA +PB +PC 的最小值.【答案】22+62由旋转可得,△AMN≌△ABP∴△PAM、△ABN都是等边三角形,(3)当AC=BC=1时,AB=2当C、P、M、N四点共线时,由∴AQ=12AB=22=CQ,NQ=(1)如图1,将△ADE绕点D逆时针旋转90°得到△DCF,连接EF;①把图形补充完整(无需写画法);②求2EF的取值范围;(2)如图2,求BE+AE+DE的最小值.②∵四边形ABCD是正方形,∴BC=AB=22,∠B=90°由旋转的性质可知,△AEG 是等边三角形,∴AE =EG ,∵DF≤FG +EG +DE ,BE =FG ,∴AE +BE +DE 的最小值为线段DF 的长.在Rt △AFH 中,∠FAH =30°,AB =8.(2021·全国·九年级专题练习)如图,在平面直角坐标系xoy 中,点B (0,2),点D 在x 轴的正半轴上,30ODB Ð=°,OE 为△BOD 的中线,过B 、E 两点的抛物线2y ax c =+与x 轴相交于A 、F 两点(A 在F 的左侧).(1)求抛物线的解析式;(2)等边△OMN的顶点M、N在线段AE上,求AE及AM的长;=++,请直接写出m的最小值,以及m取得最小值时,线(3)点P为△ABO内的一个动点,设m PA PB PO段AP的长.3。
2024专题4.3圆---利用“胡不归”模型求最值-中考数学二轮复习必会几何模型剖析(全国通用)

F
由勾股定理可求得OD= 2 ,∴ D(0, 2 )
B
4
4
D
D
O
C
x
典例精讲
胡不归模型
知识点一
【例3】如图,菱形ABCD的对角线AC上有一动点P,BC=6,△ABC=150º,
则线段AP+BP+PD的最小值为___.
E
A
M
F
D
P
C
B
解析:根据对称性,AP+BP+PD=AP+2PB=2(0.5AP+PB),所以只需求0.5AP+PB
胡不归模型
知识点一
“已知在驿道和沙砾道行走的速度分别为v1和v2,显然v1<v2,在BC上求
一定点D,使从点A至点D、再从点D至点B的行走时间最短”
不妨假设在AD上行走的速度为1个单位长度/s,在BD上行走的速度为2
A
个单位长度/s,总共用时为:t= AD1+D1H=AD1+BD1sin30º
第一步:在速度快的线段与起点相异的一侧,
1
AF
DF
点M运动的时间为
2
9
1
AF
DF
的最小值.
.即求
2
9
接下来问题便是如何构造DF/2,考虑BD与x轴夹角
y
为30º,且DF方向不变,故过点D作DM∥x轴,过点F
作FH⊥DM交DM于H点,则任意位置均有FH=DF/2.当
9
D
H
M
F F
A、F、H共线时取到最小值,根据A、D两点坐标可
2022年中考数学几何模型之动点最值之瓜豆模型(讲+练)(解析版)

专题16 动点最值之瓜豆模型模型一、运动轨迹为直线问题1:如图,P 是直线BC 上一动点,连接AP ,取AP 中点Q ,当点P 在BC 上运动时,Q 点轨迹是?解析:当P 点轨迹是直线时,Q 点轨迹也是一条直线.理由:分别过A 、Q 向BC 作垂线,垂足分别为M 、N ,在运动过程中,因为AP=2AQ ,所以QN 始终为AM 的一半,即Q 点到BC 的距离是定值,故Q 点轨迹是一条直线. 问题2:如图,点C 为定点,点P 、Q 为动点,CP=CQ ,且∠PCQ 为定值,当点P 在直线AB 上运动,Q 的运动轨迹是?解析:当CP 与CQ 夹角固定,且AP =AQ 时,P 、Q 轨迹是同一种图形,且PP 1=QQ 1 理由:易知△CPP 1≌△CPP 1,则∠CPP 1=CQQ 1,故可知Q 点轨迹为一条直线. 模型总结:条件:主动点、从动点与定点连线的夹角是定量; 主动点、从动点到定点的距离之比是定量.结论:① 主动点、从动点的运动轨迹是同样的图形; ② 主动点路径做在直线与从动点路径所在直线的夹角等于定角③当主动点、从动点到定点的距离相等时,从动点的运动路径长等于主动点的运动路径长;例1.如图,在平面直角坐标系中,A(-3,0),点B是y轴正半轴上一动点,点C、D在x正半轴上,以AB为边在AB的下方作等边△ABP,点B在y轴上运动时,求OP的最小值.【答案】【解析】求OP最小值需先作出P点轨迹,根据△ABP是等边三角形且B点在直线上运动,故可知P点轨迹也是直线.取两特殊时刻:(1)当点B与点O重合时,作出P点位置P1;(2)当点B在x轴上方且AB与x轴夹角为60°时,作出P点位置P2.连接P1P2,即为P点轨迹.根据∠ABP=60°,可知:与y轴夹角为60°,作OP⊥,所得OP长度即为最小值,OP2=OA=3,所以.例2.如图,已知点A是第一象限内横坐标为的一个定点,AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是________.【分析】∵∠PAB=90°,∠APB=30°,∴可得:AP:AB=,故B点轨迹也是线段,且P点轨迹路径长与B,P点轨迹长ON,故B【变式训练1】如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,求CG的最小值是多少?【解析】同样是作等边三角形,区别于上一题求动点路径长,本题是求CG最小值,可以将F点看成是由点B向点A运动,由此作出G点轨迹:考虑到F点轨迹是线段,故G点轨迹也是线段,取起点和终点即可确定线段位置,初始时刻G点在位置,最终G点在位置(不一定在CD边),即为G点运动轨迹.CG最小值即当CG⊥的时候取到,作CH⊥于点H,CH即为所求的最小值.根据模型可知:与AB夹角为60°,故⊥.过点E作EF⊥CH于点F,则HF==1CG的最小值为【变式训练2】如图,△ABC是边长为6的等边三角形,点E在AB上,点D为BC的中点,△EDM为等边三角形.若点E从点B运动到点A,则M点所经历的路径长为6.【解答】解:当点E在B时,M在AB的中点N处,当点E与A重合时,M的位置如图所示,所以点E从点B运动到点A,则M点所经历的路径为MN的长,△△ABC是等边三角形,D是BC的中点,△AD△BC,△BAD=30°,△AB=6,△AD==3,△△EDM是等边三角形,△AM=AD=3,△DAM=60°,△△NAM=30°+60°=90°,△AN=AB=3,在Rt△NAM中,由勾股定理得:MN===6,则M点所经历的路径长为6,故答案为:6.【变式训练3】如图,在矩形ABCD中,AB=4,△DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作△DFE=30°的直角三角形DEF,使点E和点A位于DF 两侧,点F从点A到点C的运动过程中,点E的运动路径长是.【解答】解:E的运动路径是线段EE'的长;△AB=4,△DCA=30°,△BC=,当F与A点重合时,在Rt△ADE'中,AD=,△DAE'=30°,△ADE'=60°,△DE'=,△CDE'=30°,当F与C重合时,△EDC=60°,△△EDE'=90°,△DEE'=30°,在Rt△DEE'中,EE'=;故答案为.【变式训练4】如图,已知线段AB =12,点C 在线段AB 上,且△ACD 是边长为4的等边三角形,以CD 为边的右侧作矩形CDEF ,连接DF ,点M 是DF 的中点,连接MB ,则线段MB 的最小值为 .【答案】6【解析】如图所示,∵∠FCB =30º,∴F 的路径是定射线DF ,又∵点M 是DF的中点,∴∵D 点为定点,F 点为主动点,M 点为从动点,由瓜豆原理内容可知M 点的路径亦是一条射线,取CD 的中点N ,连接NM 并延长,则射线NM 就是M 点的路径,且NM ∥CF , 作BG ⊥NM 于点G ,交CF 于点H ,则BG ⊥CF ,故BG =BH +HG =BH +CN =4+2=6, ∴线段BM 的最小值即为BG ,最小值为6. 模型二、运动轨迹为圆问题1.如图,P 是圆O 上一个动点,A 为定点,连接AP ,Q 为AP 中点.当点P 在圆O 上运动时,Q 点轨迹是?解析:Q 点轨迹是一个圆QPOM理由:Q 点始终为AP 中点,连接AO ,取AO 中点M ,则M 点即为Q 点轨迹圆圆心,半径MQ 是OP 一半,任意时刻,均有△AMQ △△AOP ,1=2QM AQ PO AP . 问题2.如图,△APQ 是直角三角形,∠PAQ=90°且AP=2AQ ,当P 在圆O 运动时,Q 点轨迹是?解析:Q 点轨迹是一个圆理由:∵AP △AQ ,∴Q 点轨迹圆圆心M 满足AM △AO ;又∵AP :AQ =2:1,∴Q 点轨迹圆圆心M 满足AO :AM =2:1.即可确定圆M 位置,任意时刻均有△APO △△AQM ,且相似比为2. 模型总结: 条件:两个定量主动点、从动点与定点连线的夹角是定量(∠PAQ 是定值); 主动点、从动点到定点的距离之比是定量(AP:AQ 是定值).结论:(1)主、从动点与定点连线的夹角等于两圆心与定点连线的夹角:∠PAQ=∠OAM ; (2)主、从动点与定点的距离之比等于两圆心到定点的距离之比:AP:AQ=AO:AM ,也等于两圆半径之比.例1.如图,点P (3,4),圆P 半径为2,A (2.8,0),B (5.6,0),点M 是圆P 上的动点,点C 是MB 的中点,则AC 的最小值是_______.OPQM A【答案】1.5【解析】由题意可知M 点为主动点,C 点为从动点,B 点为定点.∵C 是BM 中点,可知C 点轨迹为取BP 中点F ,以F 为圆心,FC 为半径作圆,即为点C 轨迹,如图所示:由题中数据可知OP =5,又∵点A 、F 分别是OB 、BP 的中点,∴AF 是△BPO 的中位线,∴AF =2.5,当M 运动到如图位置时,AC 的值最小,此时A 、C 、O 三点共线,∴AC =2.5-1=1.5. 例2.如图,A 是⊙B 上任意一点,点C 在⊙B 外,已知AB =2,BC =4,⊙ACD 是等边三角形,则BCD △的面积的最大值为( )A .4 B .4 C .8 D .6【答案】A【详解】解:如图,以BC 为边向上作等边三角形BCM ,连接DM ,⊙60DCA MCB ∠=∠=︒,⊙DCA ACM MCB ACM ∠-∠=∠-∠,即DCM ACB =∠∠ 在DCM △和ACB △中,DC AC DCM ACB MC BC =⎧⎪∠=∠⎨⎪=⎩,⊙()DCM ACB SAS ≅,⊙2DM AB ==,⊙点D 的运动轨迹是以点M 为圆心,DM 长为半径的圆, 要使BCD △面积最大,则求出点D 到线段BC 的最大距离, ⊙BCM 是边长为4的等边三角形,⊙点M 到BC的距离是⊙点D 到BC的最大距离是2,⊙BCD △的面积最大值是()14242⨯⨯=.故选:A .例3.如图,正方形ABCD中,AB O 是BC 边的中点,点E 是正方形内一动点,OE =2,连接DE ,将线段DE 绕点D 逆时针旋转90°得DF ,连接AE 、CF .求线段OF 长的最小值.【解析】E 是主动点,F 是从动点,D 是定点,E 点满足EO =2, 故E 点轨迹是以O 为圆心,2为半径的圆.考虑DE △DF 且DE =DF ,故作DM △DO 且DM =DO ,F 点轨迹是以点M 为圆心,2为半径的圆.直接连接OM ,与圆M 交点即为F 点,此时OF 最小.可构造三垂直全等求线段长,再利用勾股定理求得OM ,减去MF 即可得到OF的最小值.答案为【变式训练1】如图,在等腰Rt △ABC 中,AC =BC=P 在以斜边AB 为直径的半圆上,M 为PC 的中点,当半圆从点A 运动至点B 时,点M 运动的路径长为________.OABCDE F【答案】π【解析】当点P 位于弧AB 的中点时,M 为AB 的中点,,设分别为AC 、BC 的中点,连接交CP 于点O ,如图所示:∵,当点P 沿半圆从点A 运动至点B 时 ,点M 的运动路径是以O 为圆心,1为半径的半圆,如图蓝色半圆,∴点M 的运动路径长为π.【变式训练2】如图,AB 为O 的直径,C 为O 上一点,其中6AB =,120AOC ∠=︒,P 为O 上的动点,连AP ,取AP 中点Q ,连CQ ,则线段CQ 的最大值为( )A .B .32+C .2+D .32【答案】D【详解】如图,连接OQ ,作CH⊙AB 于H .⊙AQ =QP ,⊙OQ⊙PA ,⊙⊙AQO =90°,⊙点Q 的运动轨迹为以AO 为直径的⊙K ,连接CK ,当点Q 在CK 的延长线上时,CQ 的值最大,⊙120AOC ∠=︒⊙⊙COH =60°在Rt⊙OCH 中,⊙⊙COH =60°,OC=12AB=3,⊙OH =12OC =32,CH在Rt⊙CKH 中,CK =⊙CQ 的最大值为32,故选:D . 【变式训练3】如图, ABC 中, ,6,AB AC BC AD BC ==⊥ 于点 ,4,D AD P = 是半径为2的A 上一动点, 连结 PC , 若E 是PC 的中点, 连结DE , 则DE 长的最大值为( )A .3B .3.5C .4D .4.5【答案】B【详解】解:如图,可知P 在BA 延长线与A 的交点时此时DE 长的最大,证明如下:连接BP ,⊙,6,AB AC BC AD BC ==⊥,⊙BD =DC , ⊙E 是PC 的中点, ⊙DE //BP , 12DE BP =, 所以当BP 的长最大时,DE 长的最大, 由题意可知P 在BA 延长线与A 的交点时BP 的长最大此时DE 长的最大,⊙BC =6,AD =4,⊙BD =DC =3,BA =5, ⊙A 的半径为2,即AP =2,⊙BP =5+2=7, ⊙13.52DE BP ==. 故选:B. 课后训练1.如图,在△ABC 中,∠ACB =90º,∠A =30º,BC =2,D 是AB 上一动点,以DC 为斜边向右侧作等腰Rt △DCE ,使∠CED =90º,连接BE ,则线段BE 的最小值为 .【解答】【解析】由题意可知C 为定点,D 点为主动点,路径为线段AB ,点E 为从动点,∵△DCE 是等腰直角三角形,∴∠DCE =45º,,结合瓜豆原理内容可知从动点E 的路径为一条线段,可以看成是由线段AB 先绕着定点C 逆时针旋转45º,再以定点C 为位似比缩小来的,如图,将BE 的最小距离转化为点到线的最小距离(点B 到的最短距离),,,中,有,则,∴线段BE 的最小值为.3.如图,6AB =,点O 在线段AB 上,2AO =,O 的半径为1,点P 是O 上一动点,以BP 为一边作等边BPQ ,则AQ 的最小值为_____.【答案】1【详解】解:如图,在AB 上方以OB 为一边作等边OBC ,连接,,OP CQ AC ,OBC 和BPQ 都是等边三角形,,,60OB CB BP BQ OBC PBQ ∴==∠=∠=︒,OBC PBC PBQ PBC ∴∠-∠=∠-∠,即OBP CBQ ∠=∠,在OBP 和CBQ △中,OB CB OBP CBQ BP BQ =⎧⎪∠=∠⎨⎪=⎩,()OBP CBQ SAS ∴≅,1CQ OP ∴==,∴点Q 在以点C 为圆心,CQ 长为半径的圆上,如图,设AC 与C 交于点D ,过点C 作CM AB ⊥于点M ,则1CD =,则当点Q 与点D 重合时,AQ 取得最小值,最小值为AD , 2,6AO AB ==,4OB AB AO ∴=-=,OBC 是等边三角形,CM AB ⊥,14,22OC OB OM OB ∴====,4CM AM AO OM ∴=+=, 在Rt ACM △中,AC1AD AC CD =-=,即AQ的最小值为1,故答案为:1.4.点A 是双曲线在第一象限上的一个动点,连接AO 并延长交另一交令一分支点B ,以AB 为斜边作等腰Rt △ABC ,点C 在第二象限,随着点A 的运动,点C 的位置也在不断变化,但始终在某函数图像上运动,则这个函数的解析式为 .【答案】 【解析】连接OC ,作CD ⊥轴于点D ,AE ⊥轴于点E ,如图所示:设点A 的坐标为,∵A 、B 两点是正比例函数图像与反比例函数图像的交点,∴点A 与点B 关于原点对称,∴OA =OB ,∵△ABC 为等腰直角三角形,∴OC =OA ,OC ⊥OA ,∴∠DOC +∠AOE =90º,∵∠DOC +∠DCO =90º,∴∠DCO =∠AOE ,在△COD 与△OAE 中,,∴△COD ≌△OAE (AAS ),,∴点C 在反比例函数的图像上.7.如图,AB 为⊙O 的直径,C 为⊙O 上一点,其中AB =2,⊙AOC =120°,P 为⊙O 上的动点,连AP ,取AP 中点Q ,连CQ ,则线段CQ 的最大值为____________.【详解】解:如图,连接OQ ,作CH⊙AB 于H .⊙AQ=QP ,⊙OQ⊙PA ,⊙⊙AQO=90°⊙点Q 的运动轨迹为以AO 为直径的⊙K ,连接CK当点Q 在CK 的延长线上时,CQ 的值最大,在Rt OCH 中,⊙⊙COH=60°,OC=1,⊙OH=1122OC =,CH =在Rt CKH 中,CK =,⊙CQ . 8.如图,已知点M (0,4),N (4,0),开始时,△ABC 的三个顶点A 、B 、C 分别与点M 、N 、O 重合,点A在y轴上从点M开始向点O滑动,到达点O结束运动,同时点B沿着x轴向右滑动,则在此运动过程中,点C的运动路径长4.【解答】解:过点C'作C'D△x轴,C'E△y轴△点M(0,4),N(4,0),△OM=ON,△△CA'C'+45°=△EAB+△MGB=45°+△MGB,△△EA'C'=△B'GB,△△B'GB+△GB'B=45°,△GB'B+△DB'C'=45°,△△EA'C'=△DB'C',又△A'C'=B'C',△Rt△A'C'E△Rt△B'C'D(HL),△EC'=DC',△C'在第四象限的角平分线上,△C的运动轨迹是线段AC,△C的运动路径长为4;故答案为4;9.如图,已知在扇形AOB中,OA=3,∠AOB=120º,C是在上的动点,以BC为边作正方形BCDE,当点C从点A移动至点B时,求点D运动的路径长?【解析】将圆O补充完整,延长BO交圆O于点F,取的中点H,连接FH、HB、BD,如图所示:由题意可得△FHB是等腰直角三角形,HF=HB,∠FHB=90º,∵∠FDB=45º∠FHB,∴点D在圆H上运动,轨迹如图中蓝色虚线,∴∠HFG=∠HCF=15º,∴∠FHG=150º,∴∠CHB=120º,∴∴点D。
2022年全国中考数学经典几何模型解题策略专题 最值之费马点问题
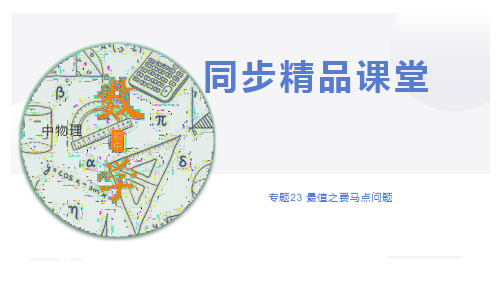
PA 解得: PA 2 3 ,则 PM 3 ,
故 QP 3 3 ,同法可得 PD 2 3 , 则 PA PD PQ 2 2 3 3 3 3 3 3 , 点 P 到点 A 、点 D 、点 Q 的距离之和的最小值为 3 3 3 , 故答案为 3 3 3 .
解:如图:过点 D 作 DM EF 于点 M ,在 BDE 内部过 E 、 F 分别作 MEP MFP 30 ,则 EPF FPD EPD 120 ,点 P 就是费马 点,
在等腰 RtDEF 中, DE DF可得 PF 2 3
3
3
中物理
同步精品课堂
专题23 最值之费马点问题
一、方法突破
皮耶·德·费马,17 世纪法国数学家,有“业余数学家之王”的美誉,之所以叫业余并非段位 不够,而是因为其主职是律师,兼职搞搞数学.费马在解析几何、微积分等领域都有卓越 的贡献,除此之外,费马广为人知的是以其名字命名的“费马小定理”、“费马大定理”等. 今天的问题不是费马提出来的,是他解决的,故而叫费马点.
若点 P 满足∠PAB=∠BPC=∠CPA=120°,则 PA+PB+PC 值最小,P 点称为该三角 形的费马点.
为什么 P 点满足∠PAB=∠BPC=∠CPA=120°,PA+PB+PC 值就会最小呢?
考虑到∠APB=120°,∴∠APE=60°,则可以 AP 为边,在 PE 边取点 Q 使得 PQ=AP,则△APQ 是等边三角形. △APQ、△ACE 均为等边三角形,且共顶点 A,故△APC≌△AQE,PC=QE. 以上两步分别转化 PA=PQ,PC=QE,故 PA+PB+PC=PB+PQ+QE=BE.
几何中的最值问题的解决策略

几何中的最值问题的解决策略
在几何中,最值问题通常是要找到一个几何对象的最大值或最小值。
以下是几何中解决最值问题的一些常用策略:
1. 利用性质或定理:利用已知的几何性质或定理来推导出最值问题的解。
例如,利用三角形的角度和性质来证明某个角度或边长的最大值或最小值。
2. 利用几何画图法:通过绘制几何图形,并观察图形的性质来解决最值问题。
例如,通过绘制直角三角形来找到两条边长之和固定时,两条边长的乘积的最大值。
3. 利用代数方法:将几何问题转化为代数问题,并通过求导、求解方程等代数方法来求解最值问题。
例如,通过代数方法来证明一个函数的极值点是函数的最大值或最小值。
4. 利用不等式:通过建立合适的不等式关系来限制几何对象的取值范围,并通过求解不等式来解决最值问题。
例如,通过利用三角不等式来推导出三角函数的最值问题。
5. 利用等式的极值性质:利用等式的极值性质来解决最值问题。
例如,通过证明函数的取值范围,并找到函数在取值范围边界处的最大值或最小值。
综上所述,解决几何中的最值问题需要运用几何性质和定理,绘制几何图形观察性质,以及运用代数方法、不等式关系和极
值性质等。
同时,解决最值问题还需要对几何对象的性质有深刻的理解和运用。
2022年全国中考数学几何经典模型解题策略专题 最值之阿氏圆问题(解析版)

专题21 最值之阿氏圆问题一、方法突破在前面的“胡不归”问题中,我们见识了“kPA+PB”最值问题,其中P 点轨迹是直线,而当P 点轨迹变为圆时,即通常我们所说的“阿氏圆”问题.所谓“阿氏圆”,是指由古希腊数学家阿波罗尼奥斯提出的圆的概念,在平面内,到两个定点距离之比等于定值(不为1)的点的集合叫做圆.如下图,已知A 、B 两点,点P 满足PA :PB=k (k≠1),则满足条件的所有的点P 构成的图形为圆. B O“阿氏圆”的一些性质:(1)PA MA NA k PB MB NB===. 应用:根据点A 、B 的位置及k 的值可确定M 、N 及圆心O .(2)△OBP ∽△OPA ,即OB OP OP OA=,变形为2OP OA OB =⋅. 应用:根据圆心及半径和A 、B 其中一点,可求A 、B 另外一点位置.(3)OP OB PA k OA OP PB===. 应用:已知半径及A 、B 中的其中一点,即可知道PA :PB 的值.α+ββαβαM NO PB A二、典例精析1.如图,在Rt ABC ∆中,90C ∠=︒,9AC =,4BC =,以点C 为圆心,3为半径做C ,分别交AC ,BC 于D ,E 两点,点P 是C 上一个动点,则13PA PB +的最小值为 .解:在AC 上截取1CQ =,连接CP ,PQ ,BQ ,9AC =,3CP =, ∴13CP AP =, 3CP =,1CQ =, ∴13CQ CP =, ACP PCQ ∴∆∆∽,13PQ AP ∴=, ∴13PA PB PQ PB BQ +=+, ∴当B 、Q 、P 三点共线时,13PA PB +的值最小,在Rt BCQ ∆中,4BC =,1CQ =,17QB ∴= ∴13PA PB +17 172.如图,O 与y 轴、x 轴的正半轴分别相交于点M 、点N ,O 半径为3,点(0,1)A ,点(2,0)B ,点P 在弧MN 上移动,连接PA ,PB ,则3PA PB +的最小值为 85 .解:如图,在y 轴上取点(0,9)H ,连接BH ,点(0,1)A ,点(2,0)B ,点(0,9)H ,1AO ∴=,2OB =,9OH =,1339OA OP OP OH===,AOP POH ∠=∠, AOP POH ∴∆∆∽,∴13AP OP HP OH ==, 3HP AP ∴=,3PA PB PH PB ∴+=+,∴当点P 在BH 上时,3PA PB +有最小值为HB 的长, 2248185BH OB OH ∴=+=+=,故答案为:85.3.如图,在ABC ∆中,6BC =,60BAC ∠=︒,则2AB AC +的最大值为 .解:122()2AB AC AB AC +=+, ∴求2AB AC +的最大值就是求12()2AB AC +的最大值, 过C 作CE AB ⊥于E ,延长EA 到P ,使得AP AE =,60BAC ∠=︒,12EA AC AP ∴==, 12AB AC AB AP ∴+=+, 3EC AE =,2PE AE =,由勾股定理得:7PC AE =,321sin 77CE AE P CP AE∴===, P ∴∠为定值,6BC =是定值,∴点P 在CBP ∆的外接圆上,AB AP BP +=,∴当BP 为直径时,AB AP +最大,即BP ',21sin sin 7BC P P BP '∴===', 解得221BP '=,221AB AP ∴+=,22()421AB AC AB AP ∴+=+=,故答案为:421.4.【新知探究】新定义:平面内两定点A ,B ,所有满足(PA k k PB=为定值)的P 点形成的图形是圆,我们把这种圆称之为“阿氏圆”【问题解决】如图,在ABC ∆中,4CB =,2AB AC =,则ABC ∆面积的最大值为 .解:以A 为顶点,AC 为边,在ABC ∆外部作CAP ABC ∠=∠,AP 与BC 的延长线交于点P ,CAP ABC ∠=∠,BPA APC ∠=∠,2AB AC =,APC BPA ∴∆∆∽,12AP CP AC BP AP AB ===, 2BP AP ∴=,12CP AP =, 4BP CP BC -==,1242AP AP ∴-=,解得:83AP =,163BP ∴=,43CP =,即点P 为定点, ∴点A 的轨迹为以点P 为圆心,83为半径的圆上,如图,过点P 作BC 的垂线,交圆P 与点1A ,此时点1A 到BC 的距离最大,即ABC ∆的面积最大,11181642233ABC S BC A P ∆=⋅=⨯⨯=. 故答案为:163. 5.如图,已知菱形ABCD 的边长为8,60B ∠=︒,圆B 的半径为4,点P 是圆B 上的一个动点,则12PD PC -的最大值为 .解:连接PB ,在BC 上取一点G ,使得2BG =,连接PG ,DG ,过点D 作DH BC ⊥交BC 的延长线于H .4PB =,2BG =,8BC =,2PB BG BC ∴=⋅,∴PB BC BG PB=, PBG CBP ∠=∠,PBG CBP ∴∆∆∽,∴12PG PB PC BC ==, 12PG PC ∴=, 四边形ABCD 是菱形,//AB CD ∴,8AB CD BC ===,60DCH ABC ∴∠=∠=︒,在Rt CDH ∆中,cos604CH CD =⋅︒=,sin 6043DH CD =⋅︒=, 6410GH CG CH ∴=+=+=,222210(43)237DG GH DH ∴=+=+=,12PD PC PD PG DG -=-, 12372PD PC ∴-, 12PD PC ∴-的最大值为237. 三、真题演练1.如图,正方形ABCD 的边长为4,E 为BC 的中点,以B 为圆心,BE 为半径作B ,点P 是B 上一动点,连接PD 、PC ,则12PD PC +的最小值为 .解:如图,在BC 上取一点T ,使得1BT =,连接PB ,PT ,DT .四边形ABCD 是正方形,90DCT ∴∠=︒,4CD =,3CT =,2222435DT CD CT ∴=++,2PB =,1BT =,4BC =,2PB BT BC ∴=⋅,∴PB BC BT PB=, PBT PBC ∠=∠,PBT CBP ∴∆∆∽,∴12PT PB PC CB ==, 12PT PC ∴=, 152PD PC PD PT DT +=+=, 12PD PC ∴+的最小值为5, 故答案为:5.2.如图,扇形AOB 中,90AOB ∠=︒,6OA =,C 是OA 的中点,D 是OB 上一点,5OD =,P 是AB 上一动点,则12PC PD +的最小值为 .解:如图,延长OA 使AE OB =,连接EC ,EP ,OP ,6AO OB ==,C ,D 分别是OA ,OB 的中点,12OE ∴=,6OP =,3OC AC ==,∴12OP OC OE OP ==,且COP EOP ∠=∠ OPE OCP ∴∆∆∽ ∴12PC OP PE OE ==, 2EP PC ∴=,111(2)()222PC PD PC PD PD PE ∴+=+=+, ∴当点E ,点P ,点D 三点共线时,12PC PD +的值最小, 222251213DE OD OE =+=+=,13PD PE DE ∴+=,PD PE ∴+的最小值为13,12PC PD ∴+的值最小值为132.故答案为:132.3.如图所示的平面直角坐标系中,(0,4)A,(4,0)B,P是第一象限内一动点,2OP=,连接AP、BP,则12BP AP+的最小值是.解:如图,取点(0,1)T,连接PT,BT.(0,1)T,(0,4)A,(4,0)B,1OT∴=,4OA=,4OB=,2OP =,2OP OT OA ∴=⋅, ∴OP OA OT OP =, POT AOP ∠=∠, POT AOP ∴∆∆∽,∴12PT OP PA OA ==, 12PT PA ∴=, 12PB PA PB PT ∴+=+, 221417BT =+=,17PB PT∴+, 1172BP AP ∴+12BP PB ∴+的最小值为17. 故答案为:17.4.阅读以下材料,并按要求完成相应的任务. 已知平面上两点A 、B ,则所有符合(0PA k k PB=>且1)k ≠的点P 会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆. 阿氏圆基本解法:构造三角形相似.【问题】如图1,在平面直角坐标系中,在x 轴,y 轴上分别有点(,0)C m ,(0,)D n ,点P 是平面内一动点,且OP r =,设OP k OD=,求PC kPD +的最小值.阿氏圆的关键解题步骤:第一步:如图1,在OD 上取点M ,使得::OM OP OP OD k ==;第二步:证明kPD PM =;第三步:连接CM ,此时CM 即为所求的最小值. 下面是该题的解答过程(部分):解:在OD 上取点M ,使得::OM OP OP OD k ==, 又POD MOP ∠=∠,POM DOP ∴∆∆∽. 任务:(1)将以上解答过程补充完整.(2)如图2,在Rt ABC ∆中,90ACB ∠=︒,4AC =,3BC =,D 为ABC ∆内一动点,满足2CD =,利用(1)中的结论,请直接写出23AD BD +的最小值.解(1)在OD 上取点M ,使得::OM OP OP OD k ==, 又POD MOP ∠=∠, POM DOP ∴∆∆∽.:MP PD k ∴=, MP kPD ∴=,PC kPD PC MP ∴+=+,当PC kPD +取最小值时,PC MP +有最小值,即C ,P ,M 三点共线时有最小值,利用勾股定理得2222222()CM OC OM m kr m k r =+=+=+. (2)4AC m ==,23CD BC =,在CB 上取一点M ,使得2433CM CD ==,∴23AD BD +2244104()3+. 5.如图,在ABC ∆ 与DEF ∆中,90ACB EDF ∠=∠=︒,BC AC =,ED FD =,点D 在AB 上.(1)如图1,若点F 在AC 的延长线上,连接AE ,探究线段AF 、AE 、AD 之间的数量关系,并证明你的结论;(2)如图2,若点D 与点A 重合,且32AC =,4DE =,将DEF ∆绕点D 旋转,连接BF ,点G 为BF 的中点,连接CG ,在旋转的过程中,求32CG BG +的最小值;(3)如图3,若点D 为AB 的中点,连接BF 、CE 交于点M ,CE 交AB 于点N ,且::7:9:10BC DE ME =,请直接写出NDCN的值.解:(1)线段AF 、AE 、AD 之间的数量关系:2AE AD AF +=,证明如下: 过F 作FH AB ⊥于H ,过E 作EG AB ⊥于G ,如图:FH AB ⊥,EG AB ⊥,90EDF ∠=︒,90FHD DGE ∴∠=∠=︒,90FDH EDG DEG ∠=︒-∠=∠,且DF DE =,()FHD DGE AAS ∴∆≅∆, FH DG AD AG ∴==+,90ACB EDF ∠=∠=︒,BC AC =,ED FD =,45FAB FED ∴∠=∠=︒,∴点F 、D 、A 、E 四点共圆,90FAE FDE ∴∠=∠=︒,45EAG DFE ∠=∠=︒,FH AB ⊥,EG AB ⊥,45BAC ∠=︒, FAH ∴∆和EAG ∆为等腰直角三角形,2AF FH ∴=,2AE AG =,2()222AF AD AG AD AG AD AE ∴=+=+=+;(2)取AB 的中点O ,连接OG ,在OB 上取43OH =,连接GH ,如图:G 为BF 的中点,O 为AB 中点,OG ∴是ABF ∆的中位线,1112222OG AF DF DE ∴====, 32AC =,26AB ∴==,132OB AB ==, ∴23OG OB =, 而42323OH OG ==, ∴OG OHOB OG=, 又HOG GOB ∠=∠, HOG GOB ∴∆∆∽,∴23HG OG BG OB ==, 23HG BG ∴=, ∴3323()()2232CG BG CG BG CG HG +=+=+, 要使32CG BG +的最小,需CG HG +最小,∴当H 、G 、C 三点共线时,32CG BG +的最小,32CG BG +的最小值是32CH ,如图:132OC AB ==,43OH =,22973CH OH OC ∴=+=, ∴32CG BG +的最小值是3397972232CH =⨯=. (3)过点C 作BF 平行线,点F 作BC 平行线交于点G ;过点G 作GH BF ⊥于点H ,过点K 作KI FG ⊥;如图:90BDC FDE ∠=∠=︒,BDC CDF FDE CDF ∴∠+∠=∠+∠,即BDF CDE ∠=∠,且CD BD =,DE DF =, ()BDF CDE SAS ∴∆≅∆, BF CE ∴=,DEC DFB ∠=∠,90DEC DPE ∠+∠=︒,DPE MPF ∠=∠, 90DFB MPF ∴∠+∠=︒, 90FME ∴∠=︒由::7:9:10BC DE ME =,设7BC t =,则9DE t =,10ME t =; 292EF DE t ∴=,//CG BF ,//FG BC ,∴四边形BFGC 为平行四边形,CE BF CG ∴==,90ECG FME ∠=∠=︒, ECG ∴∆为等腰直角三角形,45CGE GKH ∴∠=︒=∠, GKH ∴∆为等腰直角三角形,∴2GE CE2FG BC CD CD ==,2EFDE = ∴GE FG EFCE CD DE==, CDE GFE ∴∆∆∽, DCE FGE ∴∠=∠,∴sin sin NDDCE FGE CN=∠=∠; Rt MFE ∆中,2262MF EF ME t =-,1062FK MK MF ME MF t t ∴=-=-=,7FG BC t ==,设GFH α∠=,KGI NCD β∠=∠=,∴sin ,sin GH KI DNFG KG CNαβ===, Rt FKI ∆中,sin KIFKα=, ∴sin GHKI FK FK FGα=⋅=⋅, 2KG GH =,22KI FK FG∴==106252312sin 227KI t t FG KG FG tβ--∴===⋅, ∴5231ND CN -=6.在ABC ∆中,90CAB ∠=︒,AC AB =.若点D 为AC 上一点,连接BD ,将BD 绕点B 顺时针旋转90︒得到BE ,连接CE ,交AB 于点F .(1)如图1,若75ABE ∠=︒,4BD =,求AC 的长;(2)如图2,点G 为BC 的中点,连接FG 交BD 于点H .若30ABD ∠=︒,猜想线段DC 与线段HG 的数量关系,并写出证明过程;(3)如图3,若4AB =,D 为AC 的中点,将ABD ∆绕点B 旋转得△A BD '',连接A C '、A D ',当22A D A C '+'最小时,求A BCS '.解:(1)过D 作DG BC ⊥,垂足是G ,如图1:将BD 绕点B 顺时针旋转90︒得到BE , 90EBD ∴∠=︒, 75ABE ∠=︒, 15ABD ∴∠=︒, 45ABC ∠=︒, 30DBC ∴∠=︒,∴在直角BDG ∆中有122DG BD ==,323BG DG == 45ACB ∠=︒,∴在直角DCG ∆中,2CG DG ==,223BC BG CG ∴=+=+2262AC BC ∴== (2)线段DC 与线段HG 的数量关系为:3HG =,证明:延长CA ,过E 作EN 垂直于CA 的延长线,垂足是N ,连接BN ,ED ,过G 作GM AB ⊥于M ,如图:90END ∴∠=︒,由旋转可知90EBD ∠=︒, 45EDB ∴∠=︒90END EBD ∴∠=∠=︒,E ∴,B ,D ,N 四点共圆,45BNE EDB ∴∠=∠=︒,180NEB BDN ∠+∠=︒ 180BDC BDN ∠+∠=︒,45BCD ∠=︒, BEN BDC ∴∠=∠,45BNE BCD ∴∠=︒=∠,在BEN ∆和BDC ∆中, BNE BCD BEN BDC BE BA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()BEN BDC AAS ∴∆≅∆, BN BC ∴=, 90BAC ∠=︒,在等腰BNC ∆中,由三线合一可知BA 是CN 的中线, 90BAC END ∠=∠=︒, //EN AB ∴,A 是CN 的中点, F ∴是EC 的中点,G 是BC 的中点,FG ∴是BEC ∆的中位线,//FG BE ∴,12FG BE =, BE BD ⊥,FG BD ∴⊥, 30ABD ∠=︒, 60BFG ∴∠=︒,45ABC ∠=︒, 75BGF ∴∠=︒,设AC a =,则AB a =, 在Rt ABD ∆中,3AD =,23BD BE =, 12FG BE ∴=, 3FG ∴=, GM AB ⊥,BGM ∴∆是等腰三角形,2212112222222MG MB BG BC a ∴===⨯==, 在Rt MFG ∆中,60MFG ∠=︒,∴3MF MG =,3MF ∴=, 33BF BM MF +∴=+=, 在Rt BFH ∆中,60BFG ∠=︒, 1332FH BF +∴==, 3331(31)4HG FG FH a +∴=-==, 又33(31)CD a a =, ∴3CD HG =, 3HG ∴=; (3)设AB a =,则2BC a ,取BC 的中点N ,连接A D ',A C ',A N ',连接DN ,如图3,由旋转可知A B AB a'==,222A B aBNa'==,22BC aA B a==',∴2A B BCBN A B'==',又A BN CBA''∠=∠,∴△A BN CBA'∆'∽,∴22A N A BA C BC''==',22A N A C''∴=,根据旋转和两点之间线段最短可知,22A D A C''+最小,即是A D A N''+最小,此时D、A'、N共线,即A'在线段DN上,设此时A'落在A''处,过A''作A F AB''⊥于F,连接AA'',如图4,D,N分别是AC,BC的中点,DN∴是ABC∆的中位线,//DN AB∴,AB AC⊥,DN AC∴⊥,90A A FA A DA''''∠=∠=∠=︒,∴四边形A FAD ''是矩形,AF A D ''∴=,2A F AD ''==,又4A B AB ''==, 设AF x =,在直角三角形A FB ''中,222A B A F BF ''''=+,22242(4)x ∴=+-, 解得423x =-∴此时11111144424(423)434222222A BCABC AA BA ACSS SSAB AC AB A F AC A D ''''''∆''''=--=⋅-⋅-⋅=⨯⨯-⨯⨯-⨯⨯-=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,
% ! +
$$$$$$$$$
+
%
" ! &
% "& !
+
%
!
"
&
% * ) $ .$ ! $ % ( %
$$ $$ $$
(
$$$
$$ $$$
$$$
$$$
$$$
’ ’ %/ ! ) !
$$$$$$$$$
"
&
%% %! 图.
%
图!
万方数据
%
图0
%
图1
%
・ !"# ・
广西师范学院学报 (自 然 科 学 版)
文章编号: ( !##$) (##! % "*.$ / % #!"" % #$
构建几何模型
叶 秀
求解最值问题
芳
$!+.## ,
’ 温州师范学院 第二初等教育学院, 浙江 温州
摘
要: 通过挖掘问题的几何意义, 构造出问题的几何模型, 以形助数, 便于探求问题的简捷解法 文献标识码: 1
关键词: 几何模型; 最值问题; 二次曲线; 函数图象; 直角三角形; 数轴 中图分类号: 0&$$- &
收稿日期: !##$ % #! % !& 作者简介: 叶秀芳 ’ ()*+ % , , 女, 浙江平阳县人, 助讲 -
万方数据
增刊
叶秀芳: 构建几何模型
求解最值问题
・ !"# ・
几何意义是动点 ’ & , 用数形结合的方法研究它们的取值范围是常用的一 % ) 与定点 ’ &( , %( ) 连线的斜率, 种方法 2 以上两题若采用代数方法求解都相当复杂 2
万方数据
构建几何模型求解最值问题
作者: 作者单位: 刊名: 英文刊名: 年,卷(期): 叶秀芳 温州师范学院,第二初等教育学院,浙江,温州,325400 广西师范学院学报(自然科学版) JOURNAL OF GUANGXI TEACHERS COLLEGE(NATURAL SCIENCE EDITION) 2003,20(z1)
"! 3 ’ ! % $ , ! 3 #’ " % ! , ! 3 ’ ! % ( , ! 的几何意义是椭圆 ."! 2 " % !! # 上的动点 ’ " , ! , 分别到定点 ’ #, $ , 和 ’ !, ( , 的距离之和 解 由已知: 即 ."! 2 " % !! , "! !! 3 2 (! "
-
% 2 !
% 所以函数 % - & $ #% $ !& 的值域为 ’ $ 3 , 4 2 ! 评注 此题很多人都采用判别式法来解, 不仅繁琐、 也易产生失误, 本解法不仅简捷、 明快, 而且准 确无误 2 例0 范围 2 分析 用二次函数的图像研究根的分布问题, 再研究所得不等式和式子 实系数一元二次方程 &! , "& , !! - ( 的一根在 ’ (, 另一根在 ’ %, 求 % ) 上, ! ) 上, !$! 的取值 "$%
" , !! , % - (
, , ,
解得为 ( ’ $ ., %) 解得为 ) ’ $ !, () 解得为 * ’ $ %, ()
" , !! , % - (
!$! 的几何意义是点 ’ " / ! ) 与交点 ’ %, ! ) 连线的斜率 2 "$% ! % % !$ ( 因为 /(’ - $ , /*’ - %2 %, . 0 %, % !$! !$! % 由图知 /(’ + + /*’ 2 所以 + +% 0 "$% "$% 评注 本题解法中两次用到数形结合, 一是研究方程根的分布, 利用了二次函数的图像, 二是在研 !$! 究 的取值范围时, 根据其几何意义为斜率, 列出不等式 2 "$% % % % %
求解最值问题, 方法颇多 - 但是, 有些题目采用纯代数方法求解往往演算过程繁琐冗长, 或者无从 着手; 如果注意观察题设中的数式结构特征, 构造出相应的几何图形, 问题便会迎刃而解 -
(
构建二次曲线
关于二元二次方程的最值问题常可借助于建立二次曲线模型而转化为几何问题解决 例( 分析 已知 " , 试求 # ! 满足 ."! 2 " % !! , "! 3 ’ ! % $ , ! 3 #’ " % ! , ! 3 ’ ! % ( , ! 的最小值 -
!$! 的几何意义 2 "$% 解 由 &! , "& , !! - ( 的二根分别在区间 ’ (, % ) 与 ’ %, ! ) 上的几何意义为 % - # ’ & ) - &! , "& , !! 与 ’ %, 有 & 轴的两交点的横坐标分别在区间 ’ (, %) , ! ) 内 ’ 如图 0 ) ,
!
则
则!& %& & ) , " + #& & $ "! ’ -) , 作# $%’ , 使 012# $%’ &
%& #& - $ ’ & . %& ’ #& / 。 ) % -# )
$. 作 &( " %’ + ( 为垂足, $%’ 为锐角 / , % # $ 则 &( & %& 012# $%’ & %& , 所以 ! & . &( ’ #& / 。 % ) 所以要使 ! 最小, 只需 &( ’ #& 最小即可, 显然, 当 #、 这时 #( " %’ , &、 ( 三点共线, #& ’ &( 最 短,所以 3 也最小 . 若 & 在 & 4处,显然 #& 4 ’ & 4 ( 4 ( #& ’ &( / ,这时 # $#& & # (&% ,所以 012# $ * $ $#& & + 560# $#& & + 782# $#& & + % % * 所以 $& & #$ ・ 782# $#& & $。 -9 。 -% 评注 通过分析式子的几何意义, 构造出图形, 使问题得到极为简捷的解法。否则, 仅从代数的方 法考虑, 用两边平方和判别式法解, 或者设参数 ) & * 782 * 去解, 都比较复杂。 所以 " & $ 时, ! 有最小值为 ! &
%・ $ ・ $ "
!
!
建立椭圆模型: 焦点在 ! 轴上且长轴长为 . # ! 的 & ’ ", ! , 为中心在原点, ’ " % ! , ! 3 ’ ! % ( , ! 为点 & ’ " , 椭圆上的点, 如图 (- 又 # "! 3 ’ ! % $ , ! 3 # ! ,到 两点 % ’ #, $, 、 $ ’ !, ( , 的距离之和 易知 % 、 $ 均在椭圆外 直线 ’%$ : " 3 ! % $ 2 # 与椭圆: ."! 3 !! 2 " 有两个交点 &( 、 &! - 要使椭圆上 的点 & 到点 % 、 需且只需 & 取 &( 或 &! $ 距离之和最小,
*
构建数轴
例 ) 求函数 ! & : " , - : ’ : " , ! : ’ : " , $ : 的最小值。 分析 利用数轴, 根据 : "- , "! : 的几何意义是表示有向线段的长度进行研究。 解 在数轴上研究 " 所对应的动点 & 与 -、 如图 9。 !、 $ 所对应的点 # 、 %、 $ 的相对位置, 因为 : " , - : & : #& : + : " , ! : & : %& : + : " , $ : & : $& : + 所以 ! & : #& : ’ : %& : ’ : $& : , 当 & 与 % 点重合时, ! & : #& : ’ : %& : ’ : $& : & : #$ : & ! 为最小。 评注 形如 : " , "# : 的几何意义是数轴上动点 ; 到定点 ;# 的距离, 利用它的几何意义来研究这类 绝对值问题, 十分直观、 简捷。
!##$ 年
$
构建直角三角形
例% 分析 求函数 ! &
! ), " $" ’ -) 的最小值。 ’ -# )
显然当 " ! # 时, 所以只需考察 " ( # 的情形, 分析式子的几何意义, 由 ! 不能取得最小值, 从而想到构造直角三角形。 " ’ -) 想到勾股定理, $ 解 构造图形如图 ), #$ & *+ %$ & )+ #$ " $% , $& & " ,
#
# & $ &+ ( %
% ! # -
$ $ % !
& " $ $
# & %
$ $ $ $
%
- " #
! %.&/ !. " /
