信号与线性系统分析__第三讲
合集下载
信号与线性系统分析第三章
系统描述 分析方法
连续系统 微分方程 卷积积分 变换域（傅氏、s） 系统函数
离散系统 差分方程 卷积和 变换域（离散傅氏、z） 系统函数
第 2页
§2.1 LTI离散系统的响应
• 差分与差分方程 —前向差分、后向差分以及差分方程
• 差分方程解 —数值解、经典解，以及不同特征根对应的齐 次解和不同激励对应的特解
yzi (-2) = y(-2)
-----------
yzi (n) = ？
----------------yzi (-n) = y(-n)
第 13 页
零输入举例
例1：系统方程为 y(k) + 3y(k –1) + 2y(k –2) = f(k) 已知激励f(k)=2k , k≥0；初始状态 y(–1)=0, y(–2)=1/2 求系统的零输入响应
解：yzi(k)零输入响应满足：
yzi(k) + 3yzi(k –1)+ 2yzi(k –2)= 0
yzi(–1)= y(–1)= 0 yzi(–2) = y(–2) = 1/2 递推求 yzi(0)、 yzi(1) yzi(k)= – 3yzi(k –1) –2yzi(k –2)
yzi(0)= –3yzi(–1) –2yzi(–2)= –1
yzs(0)、yzs(1)、---yzs(n)=？ 借助微分方程
n
若其特征根均为单根： yzk (k ) Czsjkj y p (k ) j 1
第 16 页
零状态举例
例1：系统方程为 y(k) + 3y(k –1) + 2y(k –2) = f(k) 已知激励f(k)=2k , k≥0；求系统的零状态响应 解：零状态响应yzs(k) 满足
信号与线性系统分析--第三章
信号与线性系统分析
第三章 离散系统的时域分析
本章概述
离散时间域的方程求解
连续时间域 时间函数 微分方程 卷积积分 离散时间域 离散序列 差分方程 卷积求和
求解方法
迭代法 经典法 卷积法
连续时间信号、连续时间系统
连续时间信号
f(t)是连续变化的t的函数，除若干不连续点之外 对于任意时间值都可以给出确定的函数值。函数 的波形一般具有平滑曲线的形状，一般也称模拟 信号
f (n) .... f (1) (n 1) f (0) (n) f (1) (n 1) ...
i
f (i) (n i)
f(k ) f(2) f(-1) f(1) f(0) … 1 2 i f(i) … k
可推出：离散系统的零状态响应
y zs (n)
m
f (m) (n m)
单位阶跃序列
与阶跃函数的不同？
延时的单位阶跃序列
用单位样值序列来表示
u( n) ( n) ( n 1) ( n 2) ( n 3) (n k )
k 0
( n) u(n) u( n 1)
题目中 y0 y1 0 ,是激励加上以后的,不是初始状 态,需迭代求出 y 1, y 2 。
n 1 y1 3 y0 2 y 1 2u 1 2 u 0
0
0 0 2 y1 2 1 1
1 y 1 2
n0
y0 3 y 1 2 y 2 2 u 0 2 u 1
0 1
0 3 y 1 2 y 2 1
y 2 5 4
将初始状态代入方程求系数
第三章 离散系统的时域分析
本章概述
离散时间域的方程求解
连续时间域 时间函数 微分方程 卷积积分 离散时间域 离散序列 差分方程 卷积求和
求解方法
迭代法 经典法 卷积法
连续时间信号、连续时间系统
连续时间信号
f(t)是连续变化的t的函数，除若干不连续点之外 对于任意时间值都可以给出确定的函数值。函数 的波形一般具有平滑曲线的形状，一般也称模拟 信号
f (n) .... f (1) (n 1) f (0) (n) f (1) (n 1) ...
i
f (i) (n i)
f(k ) f(2) f(-1) f(1) f(0) … 1 2 i f(i) … k
可推出：离散系统的零状态响应
y zs (n)
m
f (m) (n m)
单位阶跃序列
与阶跃函数的不同？
延时的单位阶跃序列
用单位样值序列来表示
u( n) ( n) ( n 1) ( n 2) ( n 3) (n k )
k 0
( n) u(n) u( n 1)
题目中 y0 y1 0 ,是激励加上以后的,不是初始状 态,需迭代求出 y 1, y 2 。
n 1 y1 3 y0 2 y 1 2u 1 2 u 0
0
0 0 2 y1 2 1 1
1 y 1 2
n0
y0 3 y 1 2 y 2 2 u 0 2 u 1
0 1
0 3 y 1 2 y 2 1
y 2 5 4
将初始状态代入方程求系数
信号与线性系统题解第三章
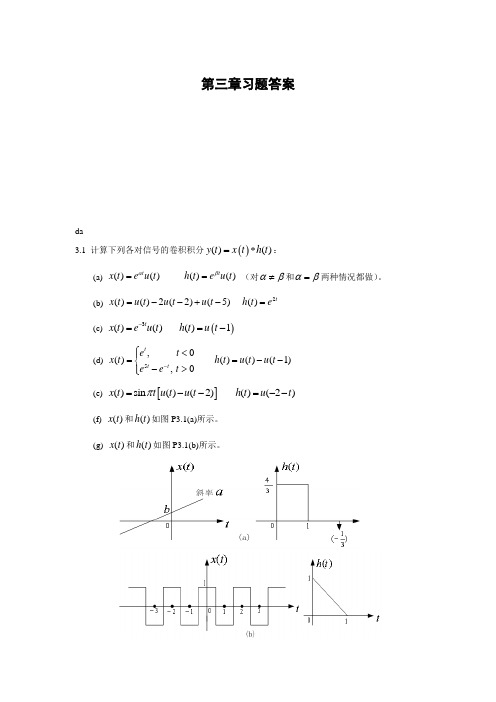
第三章习题答案da3.1 计算下列各对信号的卷积积分()()()y t x t h t =*：(a) ()()()()t tx t e u t h t e u t αβ==（对αβ≠和αβ=两种情况都做）。
(b) 2()()2(2)(5)()tx t u t u t u t h t e =--+-=(c) ()3()()()1tx t eu t h t u t -==-(d) 5,0()()()(1),0tt t e t x t h t u t u t e e t -⎧<⎪==--⎨->⎪⎩(e) []()sin ()(2)()(2)x t t u t u t h t u t π=--=--(f) ()x t 和()h t 如图P3.1(a)所示。
(g) ()x t 和()h t 如图P3.1(b)所示。
图P3.1 解：(a) ()()0()()()(0)t ttty t x t h t eed eed t βτατβαβτττ------=*==>⎰⎰当αβ≠时，()1()()ttey t e u t αβββα----=-当αβ=时，()()t y t te u t α-=(b) 由图PS3.1(a)知， 当1t ≤时，252()2()22(2)2(5)021()22t t t t t y t ed ed e e e ττττ----⎡⎤=-=-+⎣⎦⎰⎰ 当13t ≤≤时，252()2()22(2)2(5)121()22t t t t t y t ed ed e e e ττττ-----⎡⎤=-=-+⎣⎦⎰⎰ 当36t ≤≤时，52()2(5)211()2t t t y t ed e e ττ---⎡⎤=-=-⎣⎦⎰ 当6t >时，()0y t =(c) 由图PS3.1(b)知，当1t ≤时，()0y t = 当1t >时，133(1)01()13t t y t ed e ττ----⎡⎤==-⎣⎦⎰3(1)1()1(1)3t y t e u t --⎡⎤∴=--⎣⎦(d) 由图PS3.1(d)知： 当0t ≤时，11()tt t t y t e d e eττ--==-⎰当01t <≤时，055(1)1014()(2)255t ttt t y t e d e e d e eeτττττ-----=+-=+--⎰⎰当1t >时，555(1)(1)111()(2)2255t tt tt t y t e ed eeeeτττ------=-=-+-⎰(e) 如下图所示：(f) 令()11()(2)3h t h t t δ⎡⎤=+--⎢⎥⎣⎦，则11()()()(2)3y t x t h t x t =*-- 由图PS3.1(h)知，11424()()()()(21)333t t y t x t h t a b d a t b ττ-=*=+=-+⎰2411()(21)(2)()3333a y t tb a t b a t b x t ∴=-+---=+= (g) ()x t 是周期信号，由此可推知()()()y t x t h t =*也是周期的，且周期也为2。
03第三讲：高斯过程、窄带过程
正交分量：
现在我们需要求 Zc(t)和Zs(t)的统计特性，即 f(Zc,Zs)＝?
对于窄带高斯过程来说，同相分量和正交分量是不相关的，或 者也可以说是统计独立的，而对于正弦波+窄带高斯过程来说, 它仍然属于窄带的范畴，所以其同相分量和正交分量也是相互 独立的，而且也是高斯过程。
对于同相分量:
由此可得同相分量Zc(t)的概率密度函数，
（2）y1、y2是x1、x2的函数：y1＝f1(x1,x2)，y2＝f2(x1,x2)， 反函数:x1＝g1(y1,y2)， x2＝g2(y1,y2)，
如果已知x1,x2的pdf为f(x1,x2)， 求：y1,y2的pdf，f(y1,y2)=? 解决此问题时，利用以下结论： f(y1,y2)＝|J|f(x1,x2) |J|是Jacobi行列式，
窄带随机过程的带宽 固定不变，载波频率 变大时，频谱图向高 频处搬移，对应样函数的包络频率不变，但样函数波形的频率 变 大。载波频率 变小时，频谱图向低频处搬移，对应样函数的包络 频率不变，但样函数波形的频率 变小。
二、窄带过程的数学表示
1、用包络和相位的变化表示
窄带过程是功率谱限制在ωc附近的很窄范围内的一个随机过程, 过程中的
2
或erfc(x) 2 2( 2x)
2.6 窄带随机过程
一、引言
1.必要性：任何通信系统都有发送机和接收机，为了提高系 统的可靠性，即输出信噪比，通常在接收机的输入端接有一 个带通滤波器，信道内的噪声构成了一个随机过程，经过该 带通滤波器之后，则变成了窄带随机过程，因此，讨论窄带 随机过程的规律是重要的。
为了能够借助于数表(误差函数表，概率积分表) 来计算高斯分布 ,需要引入概率积分函数或者误 差函数(互补误差函数)
现在我们需要求 Zc(t)和Zs(t)的统计特性，即 f(Zc,Zs)＝?
对于窄带高斯过程来说，同相分量和正交分量是不相关的，或 者也可以说是统计独立的，而对于正弦波+窄带高斯过程来说, 它仍然属于窄带的范畴，所以其同相分量和正交分量也是相互 独立的，而且也是高斯过程。
对于同相分量:
由此可得同相分量Zc(t)的概率密度函数，
（2）y1、y2是x1、x2的函数：y1＝f1(x1,x2)，y2＝f2(x1,x2)， 反函数:x1＝g1(y1,y2)， x2＝g2(y1,y2)，
如果已知x1,x2的pdf为f(x1,x2)， 求：y1,y2的pdf，f(y1,y2)=? 解决此问题时，利用以下结论： f(y1,y2)＝|J|f(x1,x2) |J|是Jacobi行列式，
窄带随机过程的带宽 固定不变，载波频率 变大时，频谱图向高 频处搬移，对应样函数的包络频率不变，但样函数波形的频率 变 大。载波频率 变小时，频谱图向低频处搬移，对应样函数的包络 频率不变，但样函数波形的频率 变小。
二、窄带过程的数学表示
1、用包络和相位的变化表示
窄带过程是功率谱限制在ωc附近的很窄范围内的一个随机过程, 过程中的
2
或erfc(x) 2 2( 2x)
2.6 窄带随机过程
一、引言
1.必要性：任何通信系统都有发送机和接收机，为了提高系 统的可靠性，即输出信噪比，通常在接收机的输入端接有一 个带通滤波器，信道内的噪声构成了一个随机过程，经过该 带通滤波器之后，则变成了窄带随机过程，因此，讨论窄带 随机过程的规律是重要的。
为了能够借助于数表(误差函数表，概率积分表) 来计算高斯分布 ,需要引入概率积分函数或者误 差函数(互补误差函数)
信号与线性系统第三章2
有始信号通过线性电路的瞬态分析
例1：已知 e(t ) 2 t t ，求零状态响应 u 0 t 。
uR ( t )
I j
e(t )
R
uo (t )
I ( j ) jcUБайду номын сангаас0 ( j )
C
E ( j )
1 r (t ) 2
R j e d
jt
1
2
0
H j E ( j )e jt d
将无穷多项e jt 信号分量作用于系统所 得的响应取和（叠加）
频域分析法：也是建立在线性系统具有叠加性、齐次性基础上，与时 域分析法不同处在于信号分解的单元函数不同。
称为系统函数（或传递函数）
此方法称为频域分析法，另外还有复频域分析法、Z域 分析法等都是属于变换域分析法。
1 e(t ) 2
E j e d
jt
1
0
| E j | cos[t ]d
将任意激励信号分解为无穷多项 e jt 信号的叠加 （或无穷多项正弦分量的叠加）
1 1 j j (1) E ( j ) 2[ ( ) ( )e e ] j j
j j j j 2 2 (1 e j ) (e 2 .e 2 e 2 .e 2 ) j j 解：
2 j 2 j 2 ( tSa )( E ()e j ) 1 e 2 S a 2 1 求 Fe e j 2 1 2 U1 1 j C 0 ( j ) ( 2) 求系统函数 H（j） j c 1 1 ， 电1压 j ) 传 j输 RC 比 2 求 系 统 函 数 H ( j ) E ( 1 R 1 j R c R 电压传输比 j C j c
信号与线性系统课件(第5版)管致中 第2章2-3及应用
得齐次解 (自由响应)为： y(t) =12e−t −11e−2t t ≥0
得全解(全响应)为： y(t) =12e−t −11e−2t +2e−3t
14
t ≥0
(4)零输入响应，特征根为：λ1 = −1, λ2 = −2
∴ yzi (t ) = A1e −t + A2e−2t
代入初始值，得
⎧A1 + ⎩⎨− A1
11
例
已知系统的转移算子 H ( p)
=
p2
p +2p+1
，初始条件为
r(0) = 1, r′(0) = 2, 试求系统的零输入响应 rzi(t)。并画出草图。
解：令 p2 + 2 p +1 = 0 得：p1 = p2 = −1
∴ rzi (t) = (C1 + C2t)e− t 代入初值得：
⎧r(0) = C1 = ⎩⎨r′(0) = −C1
一.冲激响应的定义
定义：当激励为单位冲激函数δ (t)时，系统的零状态响应称 为单位冲激响应，简称冲激响应，用h(t)表示。
h(t)
δ(t)
(1)
δ(t)
h(t)
LTI
0
t
零状态
0
t
冲激响应的一般形式：
δ (t)
h (t)
22
冲激响应的求法 � 直接求解法 � 间接求解法 � 转移算子法 � 拉普拉斯变换
� 受迫响应（强迫响应）
� 有输入激励时系统的响应。
� 对应于特解（只含外加激励频率项） 。
� 形式由微分方程的自由项或外加激励信号决定。
2
零输入响应与零状态响应
� 一个连续系统的完全响应，可以根据引起响应的不同原 因，将它分解为零输入响应和零状态响应两部分。 � 零输入响应
信号与线性系统分析课件
04 线性系统的响应
系统的冲激响应
冲激响应定义
01
冲激响应是线性系统对单位冲激函数的响应，反映了系统对瞬
时作用的响应特性。
冲激响应计算
02
通过求解线性系统的微分方程或差分方程，可以得到系统的冲
激响应。
冲激响应的物理意义
03
冲激响应可以理解为系统内部能量的传播和分布，是分析系统
动态特性的重要手段。
卷积积分定义
卷积积分是信号处理中常用的一种运算，用于描述两个函数的相互作用。在线性系统中 ，卷积积分用于描述系统的输出与输入之间的关系。
卷积积分的计算
卷积积分的计算涉及到函数乘积的积分，常用的计算方法包括离散卷积和离散化卷积等 。
卷积积分的物理意义
卷积积分可以理解为系统对输入信号的处理和转换能力，是分析系统动态特性的重要手 段。在信号处理中，卷积积分常用于信号滤波、预测和控制系统设计等领域。
03 信号的傅里叶分析
傅里叶级数
傅里叶级数定义
将周期信号表示为无穷多个正弦和余弦函数 的线性组合。
复指数形式
使用复指数函数来表示周期信号。
三角函数形式
使用正弦和余弦函数来表示周期信号。
傅里叶级数的应用
用于分析信号的频率成分和幅度变化。
傅里叶变换
01
02
03
傅里叶变换定义
将时域信号转换为频域信 号，表示信号的频率分布 。
傅里叶变换的性质
线性、时移、频移、共轭 、对称等性质。
傅里叶变换的应用
用于信号处理、图像处理 、通信等领域。
频域分析
频域分析定义
通过分析信号的频率成分 来理解信号的特征和性质 。
频域分析的应用
用于信号滤波、调制解调 、频谱分析等领域。
信号与线性系统ppt课件
⑸ 深刻理解单位冲激响应h(t)的意义，并会求解。
⑹ 深刻理解卷积积分的定义、运算规律及主要性质，能会求解卷积积分。
⑺ 会应用卷积积分法求线性时不变系统的零状态响应rzs(t)。
第二章 连续时间系统的时域分析
§2.1 引 言 §2.2 系统方程的算子表示法 §2.3 系统的零输入响应 § 2.4 奇异函数 §2.5 信号的脉冲分解 §2.6 阶跃响应和冲激响应 §2.7 叠加积分 §2.8 卷积及其性质 §2.9 线性系统响应时域求解
零输入响应和零状态响应分量；
暂态响应分量和稳态响应分量。
2. 变换域法
系统方程为高阶微分方程或激励信号是较为复杂的函数，利 用时域法求解方程十分困难。为求解方程常采用变换域的方法。
即将自变量从时间变量变换为频率变量、复频率变量等. 如：傅氏变换、拉氏变化等
将求系统的微分方程转换求代数方程
零输入响应和零状态响应的求解
§2.1 引 言
系统分析的基本任务是在给定系统和输入的条件下，求解系统的输出响应。
连续时间系统的分析方法: 时域分析法;变换域分析法
连续时间系统的时域分析法：
在系统的整个分析过程都在连续时间域进行，即所涉及的函 数自变量均为连续时间 t 的一种分析方法。
连续时间系统的变换域分析法：
为便于求解方程而将时间变量变换成其他变量。
绪论 第一章
连续时域 第二章
离散时域 第七章
信号分解 第三章
付氏变换 第四章
拉普拉斯 变换
第五章
系统函数 第六章
状态变量 第十一章
付氏变换 Z变换 第八~九章
基本概念引导
核心内容
应用和拓宽 加深部分
第二章 连续时间系统的时域分析
⑹ 深刻理解卷积积分的定义、运算规律及主要性质，能会求解卷积积分。
⑺ 会应用卷积积分法求线性时不变系统的零状态响应rzs(t)。
第二章 连续时间系统的时域分析
§2.1 引 言 §2.2 系统方程的算子表示法 §2.3 系统的零输入响应 § 2.4 奇异函数 §2.5 信号的脉冲分解 §2.6 阶跃响应和冲激响应 §2.7 叠加积分 §2.8 卷积及其性质 §2.9 线性系统响应时域求解
零输入响应和零状态响应分量；
暂态响应分量和稳态响应分量。
2. 变换域法
系统方程为高阶微分方程或激励信号是较为复杂的函数，利 用时域法求解方程十分困难。为求解方程常采用变换域的方法。
即将自变量从时间变量变换为频率变量、复频率变量等. 如：傅氏变换、拉氏变化等
将求系统的微分方程转换求代数方程
零输入响应和零状态响应的求解
§2.1 引 言
系统分析的基本任务是在给定系统和输入的条件下，求解系统的输出响应。
连续时间系统的分析方法: 时域分析法;变换域分析法
连续时间系统的时域分析法：
在系统的整个分析过程都在连续时间域进行，即所涉及的函 数自变量均为连续时间 t 的一种分析方法。
连续时间系统的变换域分析法：
为便于求解方程而将时间变量变换成其他变量。
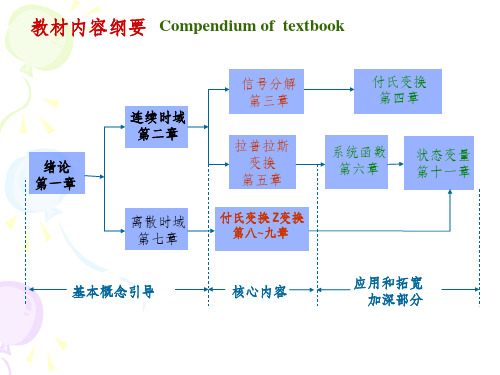
绪论 第一章
连续时域 第二章
离散时域 第七章
信号分解 第三章
付氏变换 第四章
拉普拉斯 变换
第五章
系统函数 第六章
状态变量 第十一章
付氏变换 Z变换 第八~九章
基本概念引导
核心内容
应用和拓宽 加深部分
第二章 连续时间系统的时域分析
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
8
例题
• 例3：设 F ( s)
1 ，求 L1[ F ( s)] ( s 2 1)
9
例题
• 例4：设 F ( s)
s ，求 L1[ F ( s)] ( s 2 1) 2
10
例题
• 例5：设 F ( s) ln(1
1 )，求 L1[ F ( s)] s2
s2
11
es • 例6：设 F ( s ) ，求 L1[ F (s)] ( s 1) 2
2
留数定理
若F(s)在复平面上除有限个孤立奇点 s1 , s2 , , sn 外处处解 析，且存在 0 使 s1 , s2 , , sn 均在 Re(s) 内，并设 lim F ( s ) 0 ，则在 f (t ) 的连续点 t 有
s
1 i st f (t ) L [ F ( s)] i F (s)e ds 2i
R
图 F(s)的围线积分途径
4
用留数定理求拉氏逆变换
用留数定理求拉普拉斯逆变换的公式为:
L1[ F (s)] [ F(s)est的留数]
极点
设极点S=pi处有留数为ri，并设 F(s)est 在围线内共有n 个极点，则
L1[ F(s)] ri
i 1 n
若pi为一阶极点，则
ri ( s pi ) F(s)est
例题
s2
12
小结
通过上面几个例子，我们可以看出： 留数法的要点是求各极点所对应的留数。
13
1 d ri [ 2 ( s pi )3 F(s)est ] s pi 2 ds
6
当k=3
2
例题
• 例1：设 F ( s)
1 1 ，求 L [ F ( s)] s( s 2 1)
7
例题
s2 • 例2：设 F ( s ) 2 ，求 L1[ F ( s)] ( s 1)
s pi
5
用留数定理求拉氏逆变换 n
L1[ 阶极点，则
1 d k 1 ri [ k 1 ( s pi ) k F(s)est ] s pi (k 1)! ds
当k=2
d ri [ ( s pi ) 2 F(s)est ] s pi ds
第三章
拉普拉斯逆变换 ——留数法
1
用留数定理求逆变换（围线积分法）
拉氏变换对中逆变换的定义式：
1 i st f (t ) i F (s)e ds t 0 2i
上式给出了从已知像函数F(s)求它的像原函数f(t)的一般公 式，右端的积分为拉氏反演积分，计算较为困难。
当F(s)满足一定条件时，我们可以由复变函数理论中的留 数法来计算这个反演积分。
1
Re s[ F ( s )e , sk ] (t 0)
st k 1
n
即在s平面沿一不通过被积分函数极点的封闭曲线C进行的围
线积分等于此围线C中被积函数各极点pi的留数之和。
3
用留数定理求拉氏逆变换
要利用留数定理求拉氏反变换，需要补充一条积分路线以 构成一条积分围线C，所补充的积分路线为从积分限 i 至 i 的直线。如下图所示。