自动控制原理试卷2
自动控制原理练习题2
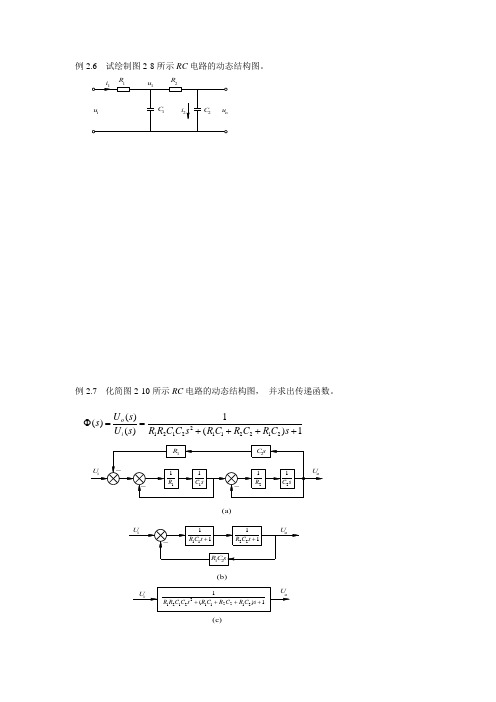
例2.6 试绘制图2-8所示RC 电路的动态结构图。
例2.7 化简图2-10所示RC 电路的动态结构图, 并求出传递函数。
R R 1)(1)()()(21221122121++++==Φs C R C R C R s C C R R s U s U s i o(a)(b)(c)例2.8 试绘制图2-22所示RC 电路的动态结构图对应的信号流图。
例2.9 试用梅逊公式求图2-23所示RC 电路的信号流图的传递函数。
例2.10 试用梅逊公式求图2-24所示动态结构图的传递函数。
o例3.1 一阶系统的结构如图3-7所示,其中KK为开环放大倍数,KH为反馈系数。
设KK=100,KH=0.1,试求系统的调节时间ts(按±5%误差带)。
如果要求ts=0.1 s,求反馈系数。
例3.3 已知系统的特征方程s4+2s3+3s2+4s+5=0试判断该系统的稳定性。
例3.4 系统如图3-15所示。
为使系统稳定,试确定放大倍数K的取值范围。
例3.5 已知系统的特征方程s3+2s2+s+2=0试判断系统的稳定性。
例3.6 设系统的特征方程为s3-3s+2=0试用劳斯判据确定该方程的根在s平面上的分布。
例3.7 某控制系统的特征方程为s6+2s5+8s4+12s3+20s2+16s+16=0试判断系统的稳定性。
例3.8 已知系统的结构如图3-23所示。
求 时系统的稳态误差。
例 3.9 设系统结构如图3-19所示, 其中 又设r (t )=2t , n (t )=0.5×1(t )求系统的稳态误差。
例4.1 设某负反馈系统的开环传递函数 试绘制该系统的根轨迹图。
211)(s s s R +=s s H s s G s s G 2)(,135)(,510)(21=+=+=)2)(1()()(++=s s s k s H s G例4.9 设某正反馈系统的开环传递函数为 试绘制该系统的根轨迹图。
例4.10 设某反馈系统的开环传递函数为试绘制该系统的根轨迹图2)4)(1)(1()()(+-+=s s s k s H s G )22)(73.2()()(2+++=s s s s k s H s G统的根轨迹图。
自动控制原理试卷、习题及答案2套
第 7 页 共 32 页
2-5 求图示运算放大器构成的网络的传递函数。
题 2-5 图
2-6 已知系统方框图如图所示,试根据方框图简化规则,求闭环传递函数。
题 2-6 图
2-7
分别求图示系统的传递函数 C1 (s) 、 C2 (s) 、 C1 (s) 、 C2 (s) R1 (s) R1 (s) R2 (s) R2 (s)
第 1 页 共 32 页
自动控制 (A )试卷
一、系统结构如图所示,u1 为输入, u2 为输出,试求
1.求网络的传递函数 G(s)=U1(s)/U2(s)
2. 讨论元件 R1,R2,C1,C2 参数的选择对系统的稳定性是否有影响。(15 分)
i2
i1
C1
R1
U1
R2
U2
C2
二、图示系统,试求,
(1) 当输入 r(t)=0,n(t)=1(t)时,系统的稳态误差 ess; (2) 当输入 r(t)=1(t),n(t)=1(t)时,系统的稳态误差 ess; (3) 若要减小稳态误差,则应如何调整 K1,K2?(15 分)
(2) 三阶系数的一对主导极点为 s1,2 1 j2 ,求同时满足上述条件的开环传递函 数G(s) 。
3 – 10 系统结构图如图所示,试求当 0 时,系统的 和
n 之值,如要求 =0.7,试确定参数 。
题 3-10 图
3 – 11 设单位反馈系统的开环传递函数如下,试确定系统稳定时 K 的取值范围。
输入信号 r(t)=1 作用下,能使给定系统成为最少拍系统的数字控制器的
答案参见我的新浪博客:/s/blog_3fb788630100muda.html
第 4 页 共 32 页
自动控制原理试题库完整(2)

⾃动控制原理试题库完整(2)⼀、选择题1. 在伯德图中反映系统抗⾼频⼲扰能⼒的是( C )A. 低频段B. 中频段C. ⾼频段D. ⽆法反映2. 对于⼀、⼆阶系统来说,系统特征⽅程的系数都是正数是系统稳定的( C )A. 充分条件B. 必要条件C. 充分必要条件D. 以上都不是3. 开环传递函数G(s)H(s)=)p s )(p s ()z s (K 211+++,其中p 2>z 1>p 1>0,则实轴上的根轨迹为(A )A.(-∞,-p 2] [-z 1,-p 1]B. (- ∞,-p 2]C. [-p 1,+ ∞)D. [-z 1,-p 1]4. ⼆阶振荡环节的相频特性θ(ω) ,当ω→∞ 时,其相位移θ(ω) 为( B )A .-270°B .-180°C .-90°D .0°5. ⽤频域法分析控制系统时,最常⽤的典型输⼊信号是( D )A. 脉冲函数B. 斜坡函数C. 阶跃函数D. 正弦函数 6. 确定根轨迹与虚轴的交点,可⽤(A)A .劳斯判据B .幅⾓条件C .幅值条件D .dk/ds=07. 设⼀单位反馈控制系统的开环传递函数为)2(4s (G 0+=s s K ),要求20K v =,则K=( A )A .10B .20C .30D .408. 过阻尼系统的动态性能指标是调整时间s t 和( C )A .峰值时间p tB .最⼤超调量σC .上升时间r tD .衰减⽐σ/σ′ 9. 设某系统开环传递函数为)1)(10s s (10s (G 2+++=s ),则其频率特性奈⽒图起点坐标为( C ) A .(-10,j0) B .(-1,j0) C .(1,j0) D .(10,j0)10. ⼀阶系统1TS K S (G +=)的时间常数T 越⼤,则系统的输出响应达到稳态值的时间( A ) A .越长 B .越短 C .不变 D .不定11. 当⼆阶系统的根分布在根平⾯的虚轴上时,系统的阻尼⽐为( B )A .ξ<0B .ξ=0C .0<ξ<1D .ξ≥ 112. 同⼀系统,不同输⼊信号和输出信号之间传递函数的特征⽅程(A )A .相同B .不同C .不存在D .不定13. 传递函数反映了系统的动态性能,它与下列哪项因素有关?(C )A. 输⼊信号B. 初始条件C. 系统的结构参数D. 输⼊信号和初始条件14. 奈奎斯特稳定性判据是利⽤系统的( C ) 来判断闭环系统稳定性的⼀个判别准则。
《自动控制原理》试题(卷)与答案解析(A26套)

《⾃动控制原理》试题(卷)与答案解析(A26套)⾃动控制原理试卷A(1)1.(9分)设单位负反馈系统开环零极点分布如图所⽰,试绘制其⼀般根轨迹图。
(其中-P 为开环极点,-Z ,试求系统的传递函数及单位脉冲响应。
3.(12分)当ω从0到+∞变化时的系统开环频率特性()()ωωj j H G 如题4图所⽰。
K 表⽰开环增益。
P 表⽰开环系统极点在右半平⾯上的数⽬。
v 表⽰系统含有的积分环节的个数。
试确定闭环系统稳定的K 值的范围。
4.(12分)已知系统结构图如下,试求系统的传递函数)(,)(s E s C,3==p v (a ),0==p v (b )2,0==p v (c )题4图题2图5.(15分)已知系统结构图如下,试绘制K 由0→+∞变化的根轨迹,并确定系统阶跃响应分别为衰减振荡、单调衰减时K 的取值范围。
6.(15分)某最⼩相位系统⽤串联校正,校正前后对数幅频特性渐近线分别如图中曲线(1)、(2)所⽰,试求校正前后和校正装置的传递函数)(),(),(21s G s G s G c ,并指出Gc (S )是什么类型的校正。
7.(15分)离散系统如下图所⽰,试求当采样周期分别为T=0.1秒和T=0.5秒输⼊)(1)23()(t t t r ?+=时的稳态误差。
8.(12分)⾮线性系统线性部分的开环频率特性曲线与⾮线性元件负倒数描述曲线如下图所⽰,试判断系统稳定性,并指出)(1x N -和G (j ω)的交点是否为⾃振点。
参考答案A(1)1、根轨迹略,2、传递函数)9)(4(36)(++=s s s G ;单位脉冲响应)0(2.72.7)(94≥-=--t e3、 21,21,21><≠K K K 4、6425316324215313211)()(G G G G G G G G G G G G G G G G G G s R s C ++++= 642531632421653111)()(G G G G G G G G G G G G G G G G G s R s E +++-= 5、根轨迹略。
自动控制原理试卷及答案

1《自动控制原理》试卷(A 卷)一、 用运算放大器组成的有源电网络如图所示,试采用复数阻抗法写出它的传递函数。
(10分)(1图 )(3图)二、假设某系统对于单位阶跃输入信号的响应为t t e e t y 10602.12.01)(---+= 。
(a) 求该系统的闭环传递函数。
(b) 确定该系统的阻尼系数。
(10分)三、试用梅逊增益公式求图中系统的闭环传递函数。
(写出步骤)(10分)四、控制系统的结构如图所示,设 r(t ) = t ⋅ 1(t ) ,p (t ) = 1(t )定义e (t ) = r(t ))(t y -,试求系统的稳态误差。
(10分)(4图)五、试确定题图所示系统参数K 和ξ的稳定域。
(写步骤)(10分)(5图)六、设单位反馈控制系统的开环传递函数为(1) 绘制根轨迹,并加以简要说明。
(2) 当系统的阻尼振荡频率s rad /1d =ω时试确定闭环主导极点的值与相应的增益值。
(15分)七、最小相位系统的开环对数幅频特性的渐近线如图所示,确定系统的开环传递函数。
(10分)八、已知最小相位系统校正前后系统的折线对数幅频特性如图所示,其中Lo(ω)为校正前特性,L开(ω)为校正后特性。
(1)试作出校正装置的对数幅频特性Lc(ω)(折线);(2)试写出校正装置的传递函数Gc(s);(3)计算校正后系统的相位裕度γ。
(15分)cp为s右半平面上的开环根的个数,v为开九、设开环系统的奈氏曲线如下图所示,其中,环积分环节的个数,试判别闭环系统的稳定性。
(10分)(a)(b)2《自动控制原理》试卷(B 卷)一、 求下图所示系统的传递函数)(/)(0s U s U i 。
(10分)(1图) (3图)二、假设某系统对于单位阶跃输入信号的响应为t t e e t y 10602.12.01)(---+= 。
(a) 求该系统的闭环传递函数。
(b) 确定该系统的阻尼系数。
(10分)三、系统的信号流图如图所示,求输出C (S )的表达式。
自动控制原理(二)

离散系统闭环脉冲传递函数的极点,则动态响应为(已知,则有的拉氏变换为,则判断题图中系统是否稳定非线性系统的及的轨迹如下图所示,试问)已知非线性系统的微分方程是,两输入,两输出的系统,其模拟结构图如图所示,其状态空间表达式为:()B.C.已知系统传递函数,则系统的约旦标准型的实现为∙B.∙C.D.∙A.∙B.∙C.∙D.正确答案:B19已知系统:已知,下列有关该系统稳定性说法正确的是()闭环脉冲传递函数分别为,输出为已知计算机控制系统如下图所示,采用数字比例控制,其中,,系统的闭环脉冲传递函数为的取值范围是系统的开环脉冲传递函数为的取值范围是已知,,。
符合系统描述的系统稳定系统稳定系统的闭环脉冲传递函数设离散系统如图所示,设,时,若要求其稳态误差,,该系统的闭环脉冲传递函数为该系统的开环脉冲传递函数为对于响应斜坡输入信号统(取F(z)=1),下列选项正确的是()变换为数字控制器的脉冲传递函数为变换为变换为非线性系统的及的轨迹如下图所示,以下说法正确的是求下图中以电压为输入量,以电感中的电流和电容上的电压作为状态变量的状态方程为___,以电阻上的电压作为输出量的输出方程为___。
()∙A.∙B.∙C.D.现用进行状态变换B.C.D.已知系统的传递函数为B. C.对线性系统作状态反馈 , A.某离散控制系统(单位反馈该系统稳态误差为代表时域中的延迟算子系统状态空间表达式中,若离散控制系统(单位反馈,则动态响应为的拉氏变换为,A.C.下图所示为某一闭环离散系统,则该系统的脉冲传递函数为()离散系统闭环脉冲传递函数的极点,的的拉氏变换为,则。
大学期末考试自动控制原理题集( 附带答案)

自动控制原理1一、 单项选择题(每小题1分,共20分)1. 系统和输入已知,求输出并对动态特性进行研究,称为( C )A.系统综合B.系统辨识C.系统分析D.系统设计2. 惯性环节和积分环节的频率特性在(A )上相等。
A.幅频特性的斜率B.最小幅值C.相位变化率D.穿越频率3. 通过测量输出量,产生一个与输出信号存在确定函数比例关系值的元件称为( C )A.比较元件B.给定元件C.反馈元件D.放大元件4. ω从0变化到+∞时,延迟环节频率特性极坐标图为(A )A.圆B.半圆C.椭圆D.双曲线5. 当忽略电动机的电枢电感后,以电动机的转速为输出变量,电枢电压为输入变量时,电动机可看作一个( B )A.比例环节B.微分环节C.积分环节D.惯性环节6. 若系统的开环传 递函数为2)(5 10+s s ,则它的开环增益为(C ) A.1 B.2 C.5 D.107. 二阶系统的传递函数52 5)(2++=s s s G ,则该系统是(B ) A.临界阻尼系统 B.欠阻尼系统 C.过阻尼系统 D.零阻尼系统8. 若保持二阶系统的ζ不变,提高ωn ,则可以(B )A.提高上升时间和峰值时间B.减少上升时间和峰值时间C.提高上升时间和调整时间D.减少上升时间和超调量9. 一阶微分环节Ts s G +=1)(,当频率T1=ω时,则相频特性)(ωj G ∠为(A ) A.45° B.-45° C.90° D.-90°10.最小相位系统的开环增益越大,其( D )A.振荡次数越多B.稳定裕量越大C.相位变化越小D.稳态误差越小11.设系统的特征方程为()0516178234=++++=s s s s s D ,则此系统 ( A )A.稳定B.临界稳定C.不稳定D.稳定性不确定。
12.某单位反馈系统的开环传递函数为:())5)(1(++=s s s k s G ,当k =( C )时,闭环系统临界稳定。
大工17春《自动控制原理》在线作业2满分标准答案

大工17春《自动控制原理》在线作业2试卷总分:100 得分:100一、单选题(共10 道试题,共60 分)1. PID调节器中的D指的是()。
A. 比例B. 积分C. 微分D. 比例积分满分:6 分正确答案:C2. 在分析中常将同频率下输出信号相位与输入信号相位之差称为()。
A. 相位差B. 信号差C. 频率差D. 相差满分:6 分正确答案:A3. 一阶滞后环节的最大滞后相角为()。
A. 0°B. 60°C. 90°D. 180°满分:6 分正确答案:C4. ()是相位滞后环节,它的低通性能好。
A. 比例环节B. 微分环节C. 积分环节D. 振荡环节满分:6 分正确答案:C5. 用直接求解闭环特征根绘制根轨迹的办法,对于()是不适用的。
A. 一阶系统B. 二阶系统C. 三阶系统D. 高阶系统满分:6 分正确答案6. 当根轨迹分支在实轴上某点相遇又向复平面运动时,该交点称为根轨迹的()。
A. 会合点B. 分离点C. 相遇点D. 分离极点满分:6 分正确答案:B7. 如果开环零点数目m小于开环极点数目n,则有()条根轨迹终止于无穷远处。
A. nB. mC. n-mD. m-n满分:6 分正确答案:C8. ()是用来确定根轨迹上某点的相应增益值。
A. 辐角条件B. 幅值条件C. 开环增益D. 开环零点满分:6 分正确答案:B9. ()的对数相频特性恒为0°。
A. 比例环节B. 惯性环节C. 积分环节D. 振荡环节满分:6 分正确答案:A10. 为了减少校正装置的输出功率,以降低成本和功耗,()装置通常被安置在前向通道的前端。
A. 串联校正B. 反馈校正C. 并联校正D. 前馈校正满分:6 分正确答案:A二、判断题(共10 道试题,共40 分)1. 以开环根轨迹增益为可变参数绘制的根轨迹称做参变量根轨迹。
A. 错误B. 正确满分:4 分正确答案:A2. 利用超前网络进行串联校正的基本原理是利用其相角的超前特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
γ = 180 0 + ϕ (ω c ) = 180 0 + (−90 0 − arctg 0.5 × 10 − arctg 0.05 × 10)
= 180 0 − (90 0 − 78.7 0 − 26.6 0 ) = −15.30 < 0 0
可以判断闭环系统不稳定。 (3)由 ϕ (ω g ) = −180 0 ⇒ −90 0 − arctg 0.5ω g − arctg 0.05ω g = −180 0 ,求得 ω g = 6.32(rad / s )
由于阻尼比 0 < ξ < 1 ,所以可以判定为欠阻尼系统。 二、电网络图如下所示,其中电压 u i (t ) 为输入、电压 u 0 (t ) 为输出,试 (1)列写以 u i (t ) 为输入、 u 0 (t ) 为输出的微分方程; (2)求传递函数 G ( s) = 抗法) 。 (本题 12 分)
自动控制原理样卷 2 答案
一、基本概念题(解题过程尽量简单,每小题 6 分,共 36 分) 1.下图为是发电机端电压 U 的自动控制系统,试画出其控制框图。 解:
负载
Ur
U ab
放大器
电动机
变阻器
发电机
U
− 1、 −3, 2. 已知单位反馈系统的闭环根轨迹的起点为 0、 求其开环传递函数的极点, 并说明理由。
1 1 40 40 − )= = 2 s + 2 s + 10 ( s + 2)( s + 10) s + 12 s + 20
频率特性 G ( jω ) =
40 ( jω + 2)( jω + 10)
幅频特性: A(ω ) =
40
ω 2 + 4 ω 2 + 100
,相频特性: ϕ (ω ) = − arctg
(2)求传递函数方法一:方程两侧同时求 Laplace 变换,得到传递函数:
G (s) =
求传递函数方法二:采用电路中的复阻抗法:
G (s) =
三、已知系统的单位冲激(脉冲)响应 g (t ) = 5(e −2t − e −10t ) (t ≥ 0) ,试求该系统的传递函数 G ( s ) 和幅频函数 A(ω ) 、相频函数 ϕ (ω ) 。 (本题 12 分) 解:传递函数 G ( s ) = L[ g (t )] = 5(
K 1 1 s ( s + 1)( s + 1) 2 20
=
K s (0.5s + 1)(0.05s + 1)
由 20 lg K = 33.98 ,求得 K = 50 ,则传递函数为: G K ( s ) =
50 s (0.5s + 1)(0.05s + 1)
K ω<2 L(ω ) = 20 lg ω , K (2) L(ω ) = 20 lg 2 < ω < 20 求得截止频率 ω c = 10(rad / s ) , 0.5ω 2 K L(ω ) = 20 lg 0.5 × 0.05ω 3 , ω > 20 由相位稳定裕度
5.已知单位负反馈控制系统的开环传递函数为 GK (s) =
K(s + 1) ,试判别闭环系统的稳 s + 2s 2 + 3s + 8
3
定性( K > 0 ) 。 解:由给定的系统开环传递函数,可以得到闭环特征方程式:
DB ( s ) = s 3 + 2 s 2 + (3 + K ) s + 8 + K = 0 ,根据 Routh 稳定判据三阶系统稳定的充分必要条件为
解:由于控制系统的闭环根轨迹起始开环传递函数的极点,所以该系统的开环传递函数极点分 别为 0、-1、-3。 3.已知控制系统的闭环传递函数为 Φ(s) =
10 ,求其主导极点并说明理由。 (s + 8)(s 2 + 2s + 2)
解:由闭环特征方程式 DB ( s ) = ( s + 8)( s 2 + 2 s + 2) = 0 ,求得闭环极点分别为 p1 = −8 、
K g (s + 2) s(s + 1)
五、某单位负反馈系统的开环传递函数为: G K (s) =
(1)画出根轨迹草图; (2)求出分离会合点; (3)求当闭环特征根为 s = −2 + j 2 时的根轨迹增益 K g 值。 (本题 15 分) 解:开环传递函数零点、极点: z1 = −2、p1 = 0、p 2 = −1 实轴上根轨迹分布: ( − 1, 0)、( − ∞, − 2) 根轨迹草图
A(ω g ) = 50 6.32 × (0.5 × 6.32) 2 + 1 (0.05 × 6.32) 2 + 1 ≈ 2.5
幅值稳定裕度 L g = −20 lg A(ω g ) = −20 lg 2.5 = −7.95dB ,由此可见对数幅频特性沿纵轴向下平移
7.95dB 后,闭环系统刚好处于临界稳定状态。
2(3 + K ) > 8 + K ,及 K > 0 ,该闭环系统稳定的条件为 K > 2 。
6.设二阶系统的闭环传递函数为 Φ ( s ) =
10 ,求阻尼比 ξ ,并确定该系统的阻尼特性。 s + 4s + 10
2Байду номын сангаас
2 解:比照二阶系统的标准形式,有 ω n = 10 , 2ξω n = 4 ,求得: ω n = 3.16(rad / s ) , ξ = 0.63 ,
闭环特征方程式
DB ( s ) = K g ( s + 2) + s ( s + 1) = 0 ⇒ K g = −
dK g s ( s + 1) s 2 + 4s + 2 ⇒ =− =0 s+2 ds ( s + 2) 2
求得 s1 = −0.586,s 2 = −3.414 ,代入求得 K g1 = 0.172,K g 2 = 5.82 ,可以判断所求得的
K s + 14s + 50
2
, 若要使其闭环系统在单位阶跃信号作
用下的稳态误差 e ss = 0.83 ,求放大倍数 K 值。 解:该系统的静态位置误差系数 K p = K 50 ,由其单位阶跃信号作用下的稳态误差
ess =
1 1 = = 0.83 ,可以求得 K = 10.24 1 + K p 1 + K 50
95dB,对闭环系统的稳定性有什么影响? (本题 (3)若将开环对数幅频特性沿纵轴向下平移 7.
15 分)
L(ω )dB −20dB dec −40dB dec
33.98
0
1
2
ωc
20
−60dB dec
lgω
解: (1)由给定的开环对数频率特性(折线图) ,可以得到开环传递函数
G K ( s) =
s1 = −0.586,s 2 = −3.414 为会合分离点。
由幅值方程可以求得闭环特征根为 s = −2 + j 2 所对应的根轨迹增益:
Kg = − 2 + j 2 − 2 + j 2 +1 −2+ j 2 +2 =3
六、设某单位反馈最小相位系统的开环对数幅频特性分段渐近折线图如下所示,试 (1)求系统的开环传递函数 G K (s) ; (2)用系统的相位稳定裕度 γ 判断闭环系统的稳定性;
ω
2
− arctg
ω
10
四、求用结构图等效变换方法求下图传递函数 G ( s ) =
C (s ) R (s )
。 (本题 10 分)
G 4 ( s)
R (s ) G 1 ( s) G 2 (s)
G 3 (s)
C(s)
解:传递函数 G ( s ) =
G ( s )G 3 ( s ) + G 1 ( s )G 4 ( s ) + G 2 ( s )G 3 ( s ) + G 2 ( s )G 4 ( s ) C (s ) = 1 R (s ) 1 + G1 ( s )G 3 ( s ) + G 2 ( s )G 3 ( s )
C
U 0 ( s) (可用复阻 U i (s)
u i (t )
R
L
u 0 (t )
解: (1)设流过电感的电流为 i (t ) ,列写原始方程组 u i (t ) − u 0 (t ) i= R ,消去中间变量 i (t ) ,得到微分方程: u (t ) = L di (t ) 0 dt
p 2 = −1 + j 、 p3 = −1 − j ,根据闭环主导极点条件:极点为一对共轭复数,周围没有零点且其
它极点离开虚轴的距离是主导极点离开虚轴距离 5 倍以上,可以确定 p 2 = −1 + j 、 p3 = −1 − j 为一对主导极点。 设单位负反馈系统的开环传递函数 G K (s) = 4.
