11.2全等三角形的判定(共103张PPT)
合集下载
人教版八年级数学上册《十一章 全等三角形. 11.2 三角形全等的判定. 全等与全等三角形.》公开课课件_0

②只给一个角:
60°
60°
可以发现按这 些条件画的三 角形都不能保 证一定全等。
60°
2.给出两个条件:
①一边一内角:
30° ②两内角:
30°50° ③两边:
2cm 4cm
30°
30°
可以发现按这 些条件画的三 30° 50° 角形都不能保 证一定全等。
2cm 4cm
探究2
想想该如何画?
已知三角形三条边分别是 4cm,5cm,7cm, 画出这个三角形,把所画的三角形分别剪下来, 并与同伴比一比,发现什么?
3、证明是由题设(已知)出发,经过一步步 的推理,最后推出结论正确的过程。
独立 作业
A 教材P15 -1.2.9 B 教材P15 -1.2
径画弧,交O′A′于点C′;
3、以点C′为圆心,CD长为半径画弧,与第2步中
所画的弧交于点D′;
4、过点D′画射线O′B′,则∠A′O′B′=∠AOB
解惑
全等三角形证明的基本步骤:
①分析已有条件,准备所缺条件: 证全等时要用的间接条件要先证好; ②三角形全等书写三步骤:
• 写出在哪两个三角形中
• 摆出三个条件用大括号括起来
证明:∵点E,F分别是AB,CD的中点
1
1
∴AE= AB, CF = CD
2
2
∵AB=CD ∴AE=CF
DF C A EB
在△ADE与△CBF中 AE=CF AD=CB
∴△ADE≌△CBF ∴∠A=∠C
DE=BF
小结归纳
1. 三边对应相等的两个三角形全等 (边边边或SSS);
2.证明全等三角形书写格式:①准备条件; ②三角形全等书写的三步骤。
• 写出全等结论
完整版三角形全等的判定PPT课件

(1) 三个角 不能! (2) 三条边 SSS (3) 两边一角 ?
(4) 两角一边
继续探讨三角形全等的条件: 两边一角
思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?
A
A
B
C
图一
在图一中, ∠A
是AB和AC的夹角,
符合图一的条件,它 可称为“两边夹角”。
B
图二
A
B
∴ △ABC ≌△DEC(SAS).
∴ AB =DE
1 C
(全等三角形的对应边相等).
2
E
D
例1 如图,点D 在AB上,点E 在AC上,BA =AC, ∠B =∠C.求证:AD =AE.
证明:在△ABE 和△ACD 中,
A
∠B =∠C,
AB =AC ,
∠A =∠A ,
∴ △ABE ≌△ACD(ASA). D
C
符合图二的条件, 通常 说成“两边和其中一边的对角”
1.在下列图中找出全等三角形
30º
Ⅰ
Ⅱ
ⅢⅢ
ⅣⅣ
5 cm
30º
Ⅴ
Ⅵ
30º
Ⅶ
Ⅷ
探索边边角
两边及其中一边的对角对应相等的两个三角形全等吗?
已知:AC=10cm,BC=8cm, ∠A=45 °.
C
△ABC的形状与大小是唯 一确定的吗?
10cm 8cm
=∠EAC.求证:AB =AC. A
证明: ∠DAC =∠EAB,
∠D =∠E, CD =BE,
D
E
∴ △ADC ≌△AEB(AAS).
∴ AC =AB.
B
C
练习 如图,E,F 在线段AC上,AD∥CB,AE = CF.若∠B =∠D,求证:DF =BE.
(4) 两角一边
继续探讨三角形全等的条件: 两边一角
思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?
A
A
B
C
图一
在图一中, ∠A
是AB和AC的夹角,
符合图一的条件,它 可称为“两边夹角”。
B
图二
A
B
∴ △ABC ≌△DEC(SAS).
∴ AB =DE
1 C
(全等三角形的对应边相等).
2
E
D
例1 如图,点D 在AB上,点E 在AC上,BA =AC, ∠B =∠C.求证:AD =AE.
证明:在△ABE 和△ACD 中,
A
∠B =∠C,
AB =AC ,
∠A =∠A ,
∴ △ABE ≌△ACD(ASA). D
C
符合图二的条件, 通常 说成“两边和其中一边的对角”
1.在下列图中找出全等三角形
30º
Ⅰ
Ⅱ
ⅢⅢ
ⅣⅣ
5 cm
30º
Ⅴ
Ⅵ
30º
Ⅶ
Ⅷ
探索边边角
两边及其中一边的对角对应相等的两个三角形全等吗?
已知:AC=10cm,BC=8cm, ∠A=45 °.
C
△ABC的形状与大小是唯 一确定的吗?
10cm 8cm
=∠EAC.求证:AB =AC. A
证明: ∠DAC =∠EAB,
∠D =∠E, CD =BE,
D
E
∴ △ADC ≌△AEB(AAS).
∴ AC =AB.
B
C
练习 如图,E,F 在线段AC上,AD∥CB,AE = CF.若∠B =∠D,求证:DF =BE.
全等三角形的判定课件ppt

两个三角形只有一组对应元素相等一边对应相等一角对应相等7cm
7cm
不全等
32° 32°
不全等
互动交流 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
互动2:如果两个三角形有两组对应相等的
元素(边或角),这两个三角形全等吗?
任务一:讨论分类
第二组:画一个三角形,要求三角形的两边分别为3cm和5cm;
第三组:画一个三角形,要求三角形的一个内角为60°,一条边
为3cm,且这条长3cm的边是60°角的邻边;
第四组:画一个三角形,要求三角形的一个内角为60°,一
条边为3cm,且这条长3cm的边是60°角的对边;
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
A
A′
C′
B
C B′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
联想?
使△ABC 与△A′B′C′全等的条 件能否再减少一些呢?
A
A′
B
? C B′
? C′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
至少要满足几组元素对应相等,两个 三角形才会全等呢?
A
A′
C′
B
C B′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
7cm
不全等
32° 32°
不全等
互动交流 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
互动2:如果两个三角形有两组对应相等的
元素(边或角),这两个三角形全等吗?
任务一:讨论分类
第二组:画一个三角形,要求三角形的两边分别为3cm和5cm;
第三组:画一个三角形,要求三角形的一个内角为60°,一条边
为3cm,且这条长3cm的边是60°角的邻边;
第四组:画一个三角形,要求三角形的一个内角为60°,一
条边为3cm,且这条长3cm的边是60°角的对边;
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
A
A′
C′
B
C B′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
联想?
使△ABC 与△A′B′C′全等的条 件能否再减少一些呢?
A
A′
B
? C B′
? C′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
至少要满足几组元素对应相等,两个 三角形才会全等呢?
A
A′
C′
B
C B′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
全等三角形判定(ASA和AAS)PPT课件

分析:能否转化为ASA?
证明:∵ ∠A=∠D, ∠B=∠E(已知)
∴∠C=∠F(三角形内角和定理) 在△ABC和△DEF中
∠B=∠E BC=EF
∠C=∠F ∴△ABC≌△DEF(ASA)
两角及你能一从角上的题对中边得对到什应么相结等论的? 两个三角形全等(AAS)。
.
6
如
C
C′
何
用 符
A
B A′
B′
B
CF E
∴ △ABC≌△DEF(ASA)
.
20
知识梳理: 三角形全等判定方法4
思考:在△ABC和△DFE中,当∠A=∠D ,
∠C=∠F和AB=DE时,能否得到 △ABC≌△DFE?
有两角和其中一个 角的对边对应相等的两
A
D
个三角形全等(可以
简写成“角边角”或 B
CF
E
“AAS”)。
.
21
知识要点: (1) 两角和它们的夹边对应相等的两个三角形全等.
C
两角和夹
边对应相
A
等
O
B
D
.
15
例3
如图:已知∠ABC=∠DCB,
∠3=∠4,求证:
A
(1)△ABC≌△DCB。
3
(2)∠1=∠2
D
4
O
1
B
2
C
.
16
练习1 已知:如图,AB=A′ C ,∠A=∠A′,
∠B=∠C
求证:△ABE≌ △ A′ CD
A
证明:在 △ABE 和 △A’CD 中
A'
∠__A__=_∠__A_’ ( 已知 )
A
D
E
1
证明:∵ ∠A=∠D, ∠B=∠E(已知)
∴∠C=∠F(三角形内角和定理) 在△ABC和△DEF中
∠B=∠E BC=EF
∠C=∠F ∴△ABC≌△DEF(ASA)
两角及你能一从角上的题对中边得对到什应么相结等论的? 两个三角形全等(AAS)。
.
6
如
C
C′
何
用 符
A
B A′
B′
B
CF E
∴ △ABC≌△DEF(ASA)
.
20
知识梳理: 三角形全等判定方法4
思考:在△ABC和△DFE中,当∠A=∠D ,
∠C=∠F和AB=DE时,能否得到 △ABC≌△DFE?
有两角和其中一个 角的对边对应相等的两
A
D
个三角形全等(可以
简写成“角边角”或 B
CF
E
“AAS”)。
.
21
知识要点: (1) 两角和它们的夹边对应相等的两个三角形全等.
C
两角和夹
边对应相
A
等
O
B
D
.
15
例3
如图:已知∠ABC=∠DCB,
∠3=∠4,求证:
A
(1)△ABC≌△DCB。
3
(2)∠1=∠2
D
4
O
1
B
2
C
.
16
练习1 已知:如图,AB=A′ C ,∠A=∠A′,
∠B=∠C
求证:△ABE≌ △ A′ CD
A
证明:在 △ABE 和 △A’CD 中
A'
∠__A__=_∠__A_’ ( 已知 )
A
D
E
1
数学11.2三角形全等的判定第3课时课件人教新课标八年级上ppt

证明:连接AC
D
2
C ∵ AB∥CD,AD∥BC(已知 )
∴ ∠1=∠2 ∠3=∠4
4 3
1
A
B
在△ABC与△CDA中 ∠1=∠2 (已证)
AC=AC (公共边)
用数字标出角 书写证明时方便
∠3=∠4 (已证)
∴ △ABC≌△CDA(ASA) ∴ AB=CD BC=AD
(全等三角形对应边相等)
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
创设情景,实例引入
怎么办?可以帮帮 我吗?
一张教学用的三角形硬纸板不小心
被撕坏了,如图,你能制作一张与原来
同样大小的新教具?能恢复原来三角形
的原貌吗?
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
探究1
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B 。把画好的△A/B/C/剪下,放到 △ABC上,它们全等吗?
例题讲解:
例1. 已知:点D在AB上,点E在AC上,BE和CD相 交于点O,AB=AC,∠B=∠C。
求证: △ABE≌△ACD
A
D O
B
E C
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
1.如图,应填什么就有 △AOC≌ △BOD
画法: 1、画A/B/=AB;
2、在 A/B/的同旁画∠DA/ B/ =∠A , ∠EB/A/ =∠B, A/ D,B/E交于点C/。
D
2
C ∵ AB∥CD,AD∥BC(已知 )
∴ ∠1=∠2 ∠3=∠4
4 3
1
A
B
在△ABC与△CDA中 ∠1=∠2 (已证)
AC=AC (公共边)
用数字标出角 书写证明时方便
∠3=∠4 (已证)
∴ △ABC≌△CDA(ASA) ∴ AB=CD BC=AD
(全等三角形对应边相等)
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
创设情景,实例引入
怎么办?可以帮帮 我吗?
一张教学用的三角形硬纸板不小心
被撕坏了,如图,你能制作一张与原来
同样大小的新教具?能恢复原来三角形
的原貌吗?
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
探究1
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B 。把画好的△A/B/C/剪下,放到 △ABC上,它们全等吗?
例题讲解:
例1. 已知:点D在AB上,点E在AC上,BE和CD相 交于点O,AB=AC,∠B=∠C。
求证: △ABE≌△ACD
A
D O
B
E C
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
1.如图,应填什么就有 △AOC≌ △BOD
画法: 1、画A/B/=AB;
2、在 A/B/的同旁画∠DA/ B/ =∠A , ∠EB/A/ =∠B, A/ D,B/E交于点C/。
全等三角形的判定ppt课件
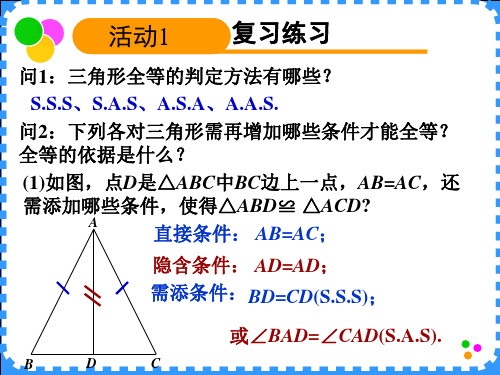
隐含条件: ∠COD=∠AOB 等;.
C
A
O
需添条件: OD=OB (A.A.S);
或OC=OA (A.S.A);
B
或 CD=AB(A.A.S).
活动2
探究新知
例题1 如图,在△ABC中,已知∠BAC=90°,AB=AC,
点A在DE上,∠D=90 ° ,∠E=9吗?
A
解:联结BD.
D
1
∵AD//BC(已知)
2
B
∴∠1=∠2(两直线平行,内错角相等)
C
在△ABD与△CDB中,
AD CB(已知), 1 2(已知), BD DB(公共边),
∴△ABC≌△CDA(S.A.S).
∴AB=DC(全等三角形的对应边相等).
活动4 拓展延伸
已知在△ABC中,AB=5cm,AC=3cm,AD是BC边的 中线,则AD的长x(cm)的取值范围是 1<AD <4 .
(1)直接条件;(2)隐含条件;(3)间接条件.
3.利用三角形全等可以解决: (1)线段相等;(2)角相等;(3)线段之间位置关系.
有时需构造全等三角形.
D E(已证), 1 (2 已证), ∴△ABBDCAA(≌已△知AE)C,(A.A.S).
活动2
探究新知
例题2 如图,已知点B是线段AC的中点,BD=BE, ∠1=∠2.试说明∠D=∠E的理由.
E
D
问:如何证明两个角相等?
? △ABD与△CBE全等
3
12
AB
C
∠1=∠2
∠1+∠3= ∠2+∠3 ∠ABD=∠CBE
直接条件: BD=BE; 易得条件:AB=CB ; 可证条件: ∠ABD=∠CBE(S.A.S).
