全等三角形判定复习 PPT(公开课)
合集下载
三角形全等判定复习ppt课件
N 明方法与前题基本相同,只
须证明⊿ABN≌⊿BCM
A
C
B
变式4:如图,⊿ABD,⊿ACE都是正三角形, 求证CD=BE
D
A
E
B
C
分析:此题实质上是把题目中的条件B,A,C三点改为 不共线,证明方法与前题基本相同.
变式6:如图,分别以⊿ABC的边AB,AC为一边 画正方形AEDB和正方形ACFG,连结CE,BG.
求证BG=CE
E
分析:此题是把两个三
角形改成两个正方形而
D
A
G 以,证法类同
FBBiblioteka C小结:1.证明两个三角形全等，要结合题目的条件 和结论，选择恰当的判定方法
2.全等三角形，是证明两条线段或两个角相 等的重要方法之一，证明时
①要观察待证的线段或角，在哪两个可能全等的三 角形中。
②分析要证两个三角形全等，已有什么条件，还缺 什么条件。
AB=CB
A
AD=CD
BD=BD
_
=
P
∴ △ABD≌△CBD(SSS)
B
D
∴∠ABD=∠CBD
_
=
在△ABP和△CBP中
C
AB=BC
∠ABP=∠CBP
BP=BP
∴ △ABP ≌ △CBP(SAS)
∴PA=PC
例4。已知:如图AB=AE,∠B=∠E，BC=ED AF⊥CD 求证：点F是CD的中点
分析：要证CF=DF可以考虑CF 、 DF所在的两个三角形全等，为此可 添加辅助线构建三角形全等 ，如何 添加辅助线呢?
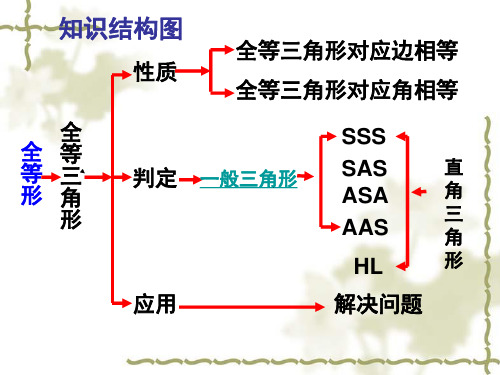
知识结构图
性质
全等三角形对应边相等 全等三角形对应角相等
全 全等 等三 形角
形
全等三角形的判定教学课件公开课获奖课件省赛课一等奖课件
例2(2023金华):如图,
A,E,B,D在同一直线上,
AB=DE,AC=DF,AC ∥ DF,
在ΔABC和ΔDEF,
(1)
求证: ΔABC≌ΔDEF;
F
AB=DE(已知) ∠A=∠D(已证) AC=DF (已知) ∴ΔABC≌ΔDEF(SAS)
A
E
B
D
C
经典例题:
证明:∵AC=2DB,AE=EC (
B
准备条件 指出范围 列举条件 得出结论
例讲解1：
如图，已知AD∥ BC，AD=BC.你能阐明△ABC与 △CDA全等吗？你能阐明AB=CD，AB∥CD吗？ 为何?
证明：∵ AD∥ BC，（已知）
∴ ∠DAC=∠BCA。
D
C
（两直线平行，内错角相等）
在△ADC和△CBA中，
∵ AD=BC（已知）
A B
A
C
2 1
B
D
E
C
第2题
D
想一小想明：旳设计方案：先在池塘旁取一种能 如直图接线到段达AAB和是B处一旳种点池C塘，连旳结长A度C并，延长至
目D前点想，测使A量C这=D个C池，塘连结旳B长C并度延，长在至E点，
水使上BC测=量EC不，以连便结，ED你，有用什米尺么测好出旳DE旳长， 措这施个较长以度便就地等于把A池，塘B两旳点长旳度距测离量。请你阐 出明来理吗由？。想想看。AC=DC
D
C A
∴∠B＝∠C（全等三角形
相应角相等）
B
DE C
3.如图，∠B＝∠E，AB＝EF，BD＝
EC，那么△ABC与 △FED全等吗？ F
为何？ AC∥FD吗？为何？
C 42
B 13 D
全等三角形的判定总复习PPT课件
例子1：如图，在△AEC和△ADB中，已 知AE=AD，AC=AB，请说明△AEC ≌ △ADB的理由。
解：在△AEC和△ADB中
C
_A_E__=__A_D_(已知)
D
∠A= ∠A( 公共角)
A
E
B
_A_C___=_A__B_(已知)
∴ △AEC≌△ADB（ SAS ）
例2：如图，AC=BD，∠CAB= ∠DBA，
第十二章 全等三角形
三角形全等的判定（3）
— ASA AAS
一、知识梳理: 三角形全等判定方法1
三边对应相等的两个三角形全等（可以简写
为“边边边”或“SSS”）。
A
用符号语言表达为：
在△ABC和△ DEF中
B
C
AB=DE
D
BC=EF
CA=FD
∴ △ABC ≌△ DEF（SSS） E
F
例1：如图．△ＡＢＣ是一个钢架，ＡＢ＝ＡＣ， ＡＤ是连接Ａ与ＢＣ中点Ｄ的支架．
1O
B
2
∠A= ∠B (已知）
D OA=OB (已证）
∠1= ∠2 (对顶角相等） ∴ △AOC≌△BO（ASA）
例2： 已知：点D在AB上，点E在AC上，BE 和CD相交于点O,AB=AC, ∠B= ∠C
求证： ∴△ADC≌△AEB AD=AE.
证明：在△ADC和△AEB中
A
∠A= ∠A (公共角）
∴ Rt△ACB≌Rt△ADB (HL). ∴BC=BD
(全等三角形对应边相等).
小结
一般三角形 全等的识别 S.S.S S.A.S A.S.A A.A.S 直角三角形 H.L 全等的识别 灵活运用各种方法证明直角三角形全等
公开课判定三角形全等判定复习.ppt
全等三角形的性质
1.全等三角形对应边相等，对应角相等
2.全等三角形的面积相等，周长相等 3.全等三角形对应边上的高线、中线、角 平分线分别相等
考点精炼
2、ＢＥ与ＣＤ相交于Ｏ，已知ＡＤ＝ＡＥ， ∠ＡＤＣ＝∠ＡＥＢ，图中有几对全等三角 形，说明理由。
Ａ
△ AEB ≌ △ADC （ASA）
Ｂ
Ｄ
Ｏ
2图
Ｅ Ｃ
Ａ Ｄ Ｂ Ｃ
SAS
1图
Ｅ
考点精炼
2、ＢＥ与ＣＤ相交于Ｏ，已知ＡＤ＝ＡＥ，∠ＡＤＣ＝ ∠ＡＥＢ，图中有几对全等三角形，说明理由。
Ａ
△BOD≌ △COE （AAS）
Ｂ
Ｄ
Ｏ
2图
Ｅ Ｃ
考点精炼
1、ＢＥ与ＣＤ相交于Ｏ，已知ＡＤ＝ＡＥ，∠ＡＤＣ＝ ∠ＡＥＢ，图中有几对全等三角形，说明理由。
Ａ △BDC≌ △CEB
A Eห้องสมุดไป่ตู้B
O
D
F
C
二：利用全等三角形证明线的垂直关系
例：如图：BF是Rt△ABC的角平分线，∠ACB=90°， CD是高，BF与CD交于点E，EG∥AC交AB于G 求证：FG⊥AB
证明：∵BF平分∠ABC
A G F
C 3 E 4 D 1 2 B
∴∠1＝∠2 ∵CD⊥AB ∴∠3+∠ABC=90° ∴BG=BC （全等三角形的对应边相等） 又 ∵∠ACB＝90° ∴∠A+∠ABC=90° 在△BFG与△BFC中 ∴∠3＝∠A BG=BC 又∵EG∥AC ∠1＝∠2 ∴∠A＝∠4 BF=BF ∴∠3＝∠4 ∴△BFG≌△BFC （SAS） 在△BEG与△BEC中 ∠1＝∠2 ∴∠FGB=∠FCB=90° ∠3＝∠4 （全等三角形的对应角相等） BE＝BE ∴FG⊥AB ∴△BEG≌△BEC （AAS）
用全等三角形的判定总复习ppt课件
7.如图（5）∠CAE=∠BAD，∠B=∠D，
AC=AE，△ABC与△ADE全等吗？为什么？
B
解：∵ ∠CAE=∠BAD(已知)
E
D
∴ ∠CAE+∠BAE=∠BAD+∠BAE
C
A
(等量加等量，和相等) 即∠BAC=∠DAE
在△ABC和△ADE中，
∠B=∠D(已知)
∠BAC=∠DAE(已证)
AC=AE(已知)
典型例题:
例1 :如图,点B在AE上, ∠CAB=∠DAB,要使 ΔABC≌ΔABD,可补充的 一个条件是∠ACB=B=∠AEA=DC∠D.BEA
C
A
B E
D
分析：现在我们已知 A→∠CAB=∠DAB
S→ AB=AB(公共边) .
①用SAS,需要补充条件 AB=AC, ②用ASA,需要补充条件 ∠CBA=∠DBA, ③用AAS,需要补充条件 ∠C=∠D, ④此外,补充条件 ∠CBE=∠DBE也可以(?)
要使△ABD≌△ACD， • 根据“SAS”需要添加条件 AB=AC ； • 根据“ASA”需要添加条件∠BDA=∠CDA • 根据“AAS”需要添加条件 ∠B=∠C
D
C
； ；
友情提示：添加条件的题目.首先要 找到已具备的条件,这些条件有些是 题目已知条件 ,有些是图中隐含条件.
8
认 识 到 了 贫 困户贫 困的根 本原因 ，才能 开始对 症下药 ，然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视，已 经展开 了“精 准扶贫 ”项目
12
D
E
M
N
B
C
创造条件！ ？ 6
认 识 到 了 贫 困户贫 困的根 本原因 ，才能 开始对 症下药 ，然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视，已 经展开 了“精 准扶贫 ”项目
全等三角形判定复习课(精品公开课)ppt课件
1 A
2
下列条件:①A①BA=BA=EA,②E
D
BC=ED,③∠C=∠D,④
在ΔABC和ΔAED中
∠B=∠E,其中能使
AC=AD
ΔABC≌ΔAED的条件有
∠BAC=∠EAD
( )个. A.4 B.3 C.2 D.1
AB=AE
∴ΔABC≌ΔAED(SAS)
可编辑课件PPT
12
C
E
例2 (2006湖北十堰):如图, 已知∠1=∠2,AC=AD,增加 B
1 A
2
下列条件:①AB=AE,②
D
BC=ED,③∠C=∠D,④
在ΔABC和ΔAED中
∠∠BB=∠=∠EE,其, 中能使
AC=AD
ΔABC≌ΔAED的条件有
∠BAC=∠EAD
( )个.
A.4 B.3 C.2 D.1
∠B=∠E
∴ΔABC≌ΔAED(AAS)
可编辑课件PPT
15
例3 (2007金华):如图,
AB=A’B’
BC=B’C’
B
C B’
C’
AC=A’C’
全等三角形对应边相等，对应角相等
可编辑课件PPT
3
三、全等三角形的判定
1、判定1：两边和它们的夹角对应 相等的两个三角形全等。简称“边 角边 ”（SAS）。 2、判定2：两角和它们的夹边对应 相等的两个三角形全等。简称“角 边 角”（ASA）
可编辑课件PPT
16
∵AB=CD(已知) ∴ AB+BC=CD+BC, 即
AC=BD.
知,AB=CD,CE=DF,AE=BF, 在ΔACE和ΔBDF中
则AE∥BF吗?为A 什么?
2024版全等三角形判定复习(公开课)ppt课件
复习目的与意义
加深对全等三角形判 定定理的理解和掌握
为后续学习相似三角 形、三角函数等知识 点打下基础
2024/1/29
提高运用全等三角形 判定定理解决问题的 能力
4
复习内容与范围
01
02
03
04
全等三角形的定义和性 质
2024/1/29
全等三角形的五种判定 方法：SSS、SAS、ASA、 AAS、HL
角边角（ASA）和角角边（AAS） 判定法
2024/1/29
14
角边角（ASA）和角角边（AAS）判定法原理
角边角（ASA）原理
两个三角形中，如果两个角及它们所 夹的一边分别相等，那么这两个三角 形全等。
角角边（AAS）原理
两个三角形中，如果两个角及其中一个 角的对边分别相等，那么这两个三角形 全等。
2024/1/29
应试技巧指导
总结中考中解答全等三角 形相关问题的应试技巧， 如审题、画图、标注和检 查等。
模拟试题训练
提供针对中考的全等三角 形模拟试题，进行实战演 练和巩固提高。
25
07
总结回顾与展望未来
2024/1/29
26
பைடு நூலகம்
本次复习内容总结回顾
全等三角形的定义和性质
全等三角形是指两个三角形在形状和大小上完全相同。全等三角形的对应边相等，对应角相 等。
2024/1/29
解决问题的策略
掌握观察、分析、归纳和猜想等解 决问题的基本策略，并能够灵活运 用。
创新思维的培养
通过一题多解、多题一解和变式训 练等方式，培养创新思维和发散性 思维。
24
历年中考真题解析与应试技巧指导
中考真题解析
《三角形全等的判定》全等三角形PPT课件
好的△ ′′′剪下来，放到△ 上，它们全等吗？
画一个△ ′′′，使′′ = ，′’ =
，∠′ = ∠：
（1）画∠′ = ∠；
（2）在射线′上截取′′ = ，在
射线′上截取′′ = ；
（3）连接′′.
【结论】两边和它们的夹角分别相等的三角形全等。也就是说，三角形的两
⫽ .
∠4. 求证：∠5 = ∠6.
∵ ∠1 = ∠2，∠3 = ∠4， = ，
根据易证△ ≌△ ，
∴有 = ，
又∵ ∠3 = ∠4， = ，
则可根据判定△ ≌△ ，
故∠5 = ∠6.
知识梳理
例4：如图，、交于点，、为上两点， = ， =
就全等了.如果满足斜边和一条直角边分别相等，这两个直
角三角形全等吗？
教学新知
探索5：任意画出一个△，使∠=90°.再画一个 △ ′’’，使
∠′=90°，′′=，′′=.把画好的△′′′剪下来，放
到△上，它们全等吗？
画 一 个 △ ′′′ ， 使 ∠′ = 90° ， ′′ =
求证 = .
∵⊥，⊥
∴∠与∠都是直角
在R △ 和Rt △ 中，
=
=
∴ △ ≌ △ （）
∴ = .
知识梳理
知识点1：“边边边”（或“SSS”）
1.三边分别相等的两个三角形全等（可以简写成“边边边”
两个三角形全等吗？上述六个条件中，有些条件是相关的.
能否在上述六个条件中选择部分条件，简捷地判定两个三角
形全等呢？
探索1：先任意画出一个△ ABC.再画一个△ A′B′C′，使△ ABC与
△ A′B′C′满足上述六个条件中的一个（一边或一角分别
相等）或两个（两边、一边一角或两角分别相等）.你
画一个△ ′′′，使′′ = ，′’ =
，∠′ = ∠：
（1）画∠′ = ∠；
（2）在射线′上截取′′ = ，在
射线′上截取′′ = ；
（3）连接′′.
【结论】两边和它们的夹角分别相等的三角形全等。也就是说，三角形的两
⫽ .
∠4. 求证：∠5 = ∠6.
∵ ∠1 = ∠2，∠3 = ∠4， = ，
根据易证△ ≌△ ，
∴有 = ，
又∵ ∠3 = ∠4， = ，
则可根据判定△ ≌△ ，
故∠5 = ∠6.
知识梳理
例4：如图，、交于点，、为上两点， = ， =
就全等了.如果满足斜边和一条直角边分别相等，这两个直
角三角形全等吗？
教学新知
探索5：任意画出一个△，使∠=90°.再画一个 △ ′’’，使
∠′=90°，′′=，′′=.把画好的△′′′剪下来，放
到△上，它们全等吗？
画 一 个 △ ′′′ ， 使 ∠′ = 90° ， ′′ =
求证 = .
∵⊥，⊥
∴∠与∠都是直角
在R △ 和Rt △ 中，
=
=
∴ △ ≌ △ （）
∴ = .
知识梳理
知识点1：“边边边”（或“SSS”）
1.三边分别相等的两个三角形全等（可以简写成“边边边”
两个三角形全等吗？上述六个条件中，有些条件是相关的.
能否在上述六个条件中选择部分条件，简捷地判定两个三角
形全等呢？
探索1：先任意画出一个△ ABC.再画一个△ A′B′C′，使△ ABC与
△ A′B′C′满足上述六个条件中的一个（一边或一角分别
相等）或两个（两边、一边一角或两角分别相等）.你
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
全等三角形判定
SAS ASA SSS AAS综合运用
黄渡中心初中 许和睦
教学目标
熟练掌握全等三角形四种判定方法。 能灵活运用各种判定方法。 通过例题讲解，培养学生有条理的分析、推理能力，并进行简单的证明
。
教学重难点
教学重点：能让学生选择适当判定方法 判定两三角形全等。
教学难点：培养学生有条理的分析、推 理能力，并写出证明过程。
前面的知识你忘记了吗？
让我们一起来 复习一下吧
我们学过几种三角形的全等判定呢？（4种）
边角边公理 角边角公理 边边边公理 角角边定理
边角边公理（SAS）
有两边和它们的夹角对应 有两个角和它们的夹边对 应相等的两个三角形全等
小结
边边边（SSS）公理 有三边对应相等的 两个三角形全等
小结
角角边公理（AAS）
有两角和其中一角的对边对 应相等的两个三角形全等
小结
课前热身
已知：如图，AB=DC，AD=BC. 求证： ∠A= ∠C.
例1
已知：如右图，AB、CD相交于点O， AC∥DB,OC = OD, E、F为 AB上两点，
且AE = BF. 求证：CE=DF.
A EB
C OF
D
B
.
例2 A
如右图 已知：AB=AD，CB=CD.
，求证：AC⊥BD.
B
O
D
C
已知：△ABC的顶点和△DBC 的顶点A和D在BC的同旁, AB =DC, AC = DB, AC和DB相交 于点O.
求证：OA =OD.
练习一
继再 续接 学再 习厉 新， 知让 识我 吧们
课堂小结
边角边公理 角边角公理 边边边公理 角角边公理
作业：课本P115 1~8
SAS ASA SSS AAS综合运用
黄渡中心初中 许和睦
教学目标
熟练掌握全等三角形四种判定方法。 能灵活运用各种判定方法。 通过例题讲解，培养学生有条理的分析、推理能力，并进行简单的证明
。
教学重难点
教学重点：能让学生选择适当判定方法 判定两三角形全等。
教学难点：培养学生有条理的分析、推 理能力，并写出证明过程。
前面的知识你忘记了吗？
让我们一起来 复习一下吧
我们学过几种三角形的全等判定呢？（4种）
边角边公理 角边角公理 边边边公理 角角边定理
边角边公理（SAS）
有两边和它们的夹角对应 有两个角和它们的夹边对 应相等的两个三角形全等
小结
边边边（SSS）公理 有三边对应相等的 两个三角形全等
小结
角角边公理（AAS）
有两角和其中一角的对边对 应相等的两个三角形全等
小结
课前热身
已知：如图，AB=DC，AD=BC. 求证： ∠A= ∠C.
例1
已知：如右图，AB、CD相交于点O， AC∥DB,OC = OD, E、F为 AB上两点，
且AE = BF. 求证：CE=DF.
A EB
C OF
D
B
.
例2 A
如右图 已知：AB=AD，CB=CD.
，求证：AC⊥BD.
B
O
D
C
已知：△ABC的顶点和△DBC 的顶点A和D在BC的同旁, AB =DC, AC = DB, AC和DB相交 于点O.
求证：OA =OD.
练习一
继再 续接 学再 习厉 新， 知让 识我 吧们
课堂小结
边角边公理 角边角公理 边边边公理 角角边公理
作业：课本P115 1~8