More Meta-Stable Brane Configurations without D6-Branes
LTE信令流程详解
L T E信令流程详解集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#LTE信令流程目录概述本文通过对重要概念的阐述，为信令流程的解析做铺垫，随后讲解LTE中重要信令流程，让大家熟悉各个物理过程是如何实现的，其次通过异常信令的解读让大家增强对异常信令流程的判断，再次对系统消息的解析，让大家了解系统消息的特点和携带的内容。
最后通过实测信令内容讲解，说明消息的重要信元字段。
第一章协议层与概念1.1控制面与用户面在无线通信系统中，负责传送和处理用户数据流工作的协议称为用户面；负责传送和处理系统协调信令的协议称为控制面。
用户面如同负责搬运的码头工人，控制面就相当于指挥员，当两个层面不分离时，自己既负责搬运又负责指挥，这种情况不利于大货物处理，因此分工独立后，办事效率可成倍提升，在LTE网络中，用户面和控制面已明确分离开。
1.2接口与协议接口是指不同网元之间的信息交互时的节点，每个接口含有不同的协议，同一接口的网元之间使用相互明白的语言进行信息交互，称为接口协议，接口协议的架构称为协议栈。
在LTE中有空中接口和地面接口，相应也有对应的协议和协议栈。
信令流数据流图1 子层、协议栈与流图2 子层运行方式LTE系统的数据处理过程被分解成不同的协议层。
简单分为三层结构：物理层、数据链路层L2和网络层。
图1阐述了LTE系统传输的总体协议架构以及用户面和控制面数据信息的路径和流向。
用户数据流和信令流以IP包的形式进行传送，在空中接口传送之前，IP包将通过多个协议层实体进行处理，到达eNodeB后，经过协议层逆向处理，再通过S1/X2接口分别流向不同的EPS实体，路径中各协议子层特点和功能如下：1.2.1NAS协议（非接入层协议）处理UE和MME之间信息的传输，传输的内容可以是用户信息或控制信息（如业务的建立、释放或者移动性管理信息）。
它与接入信息无关，只是通过接入层的信令交互，在UE和MME之间建立起了信令通路，从而便能进行非接入层信令流程了。
stablediffusion 删除采样方法
stablediffusion 删除采样方法稳定扩散：删除采样方法
稳定扩散是一种采样方法，其目的是通过删除一部分样本来提高采样效率。
这种方法可以在大规模数据集上提供更有效的采样策略，从而减少计算资源的消耗。
在稳定扩散中，删除采样方法是一种重要的技术手段。
它通过识别和删除一些不重要或重复的样本，以减少采样的冗余性。
这样做既可以节省存储空间，又可以提高采样过程的效率。
删除采样方法的实现方式可以是基于样本的重要性度量。
它使用一些算法或模型来评估每个样本的重要性，然后根据重要性进行排序并删除一部分低重要性的样本。
这种方法通常需要使用一些特征选择或特征提取的技术来帮助确定样本的重要性。
另一种实现删除采样的方法是基于聚类分析。
聚类将相似的样本分组在一起，然后可以从每个组中删除一些样本。
这种方法的优点是能够处理大规模数据，并且可以在提供足够代表性的样本的同时减少数据维度。
删除采样方法在很多领域都有应用。
在机器学习和数据挖掘领域，它可以用于构建更高效的模型训练和特征工程流程。
在社交网络分析和推荐系统中，它可以帮助提高信息过滤和推荐算法的性能。
在图像和视频处理中，它可以应用于图像压缩和视频编码等方面。
总而言之，删除采样方法是稳定扩散中的一项重要技术，它可以通过删除一些不重要或冗余的样本来提高采样效率。
这种方法在各个领域都有广泛的应用，并且可以有效地优化数据处理和分析的过程。
stable diffusion wenui 原理
Stable Diffusion是一种潜在扩散模型（LDM），它可以从文本描述生成高质量的图像。
其工作原理可以总结为以下步骤：
1. Stable Diffusion由变分自编码器（V AE）、U-Net和一个可选的文本编码器组成。
2. V AE编码器将图像从像素空间压缩到一个更小维度的潜在空间，捕捉图像的更本质的语义含义。
3. U-Net是一个卷积神经网络，它可以从潜在空间重建图像，并去除高斯噪声。
4. 文本编码器是一个预训练的模型，它可以将文本描述转换为一个向量，用来指导图像生成的过程。
5. Stable Diffusion的生成过程是一个迭代的去噪过程。
它从一个随机噪声开始，然后逐步减少噪声的强度，同时根据文本编码器的输出调整图像的内容，直到达到预设的步数为止，最终得到想要的图像。
希望以上信息对你有帮助。
stable diffusion embedding训练 -回复
stable diffusion embedding训练-回复什么是stable diffusion embedding（稳定扩散嵌入）？如何进行stable diffusion embedding的训练？首先，稳定扩散嵌入是一种用于对高维数据进行降维的方法。
它通过在数据上执行扩散过程来寻找数据的低维结构。
稳定扩散嵌入被广泛应用于图像处理、文本分析、生物信息学和社交网络分析等领域。
本文将逐步解释稳定扩散嵌入的训练过程。
首先，让我们了解一下稳定扩散嵌入的基本原理。
稳定扩散嵌入是基于扩散过程的嵌入方法。
扩散过程是指在给定的数据集上执行随机游走，并通过在数据集中滤波来传播信息。
这个过程在数据集中传播信息的同时，也可以将数据的低维结构捕捉到中，从而实现降维的效果。
稳定扩散嵌入的训练过程可以概括为以下几个步骤：1. 构建相似度矩阵：首先，我们需要根据给定的数据集构建一个相似度矩阵。
相似度矩阵用于度量数据点之间的相似程度。
常用的相似度度量方法包括欧几里得距离、余弦相似度和高斯核函数等。
构建好相似度矩阵后，可以将其视为描述数据点之间关系的图。
2. 构建转移矩阵：接下来，根据相似度矩阵构建一个转移矩阵。
转移矩阵用于描述数据集上的扩散过程。
构建转移矩阵的一种常用方法是将相似度矩阵的每一行除以相似度矩阵对应行的和，以保证每一行的和为1。
3. 进行扩散过程：通过多次迭代转移矩阵，可以在数据集上执行扩散过程。
每一次迭代将会使扩散过程在数据上进一步传播。
扩散过程可以通过将转移矩阵与初始的数据进行相乘来实现。
迭代的次数可以根据需要进行设置，一般情况下，经过足够多次的迭代后，扩散过程会收敛到一个稳定状态。
4. 提取低维嵌入结果：一旦扩散过程达到稳定状态，可以通过提取扩散过程的结果来得到数据的低维嵌入。
通常情况下，扩散过程的结果可以通过提取转移矩阵的特征向量来获得。
将特征向量按照对应的特征值大小进行排序，选择前几个特征向量作为数据的低维表示。
Discovery Studio官方教程--基于MODELER构建蛋白酶模型
基于蛋白序列构建同源蛋白模型（MODELER）教程介绍蛋白质结构的解析对其功能的理解至关重要。
然而，由于技术手段的限制，利用实验方法（主要为X-ray，NMR）解析蛋白质结构投入大、周期长、风险大。
对于某些膜蛋白，只利用现有技术条件，其结构甚至无法解析。
另一方面，随着分子生物学技术的成熟及高通量测序技术的发展，越来越多的基因序列可以被轻松找到。
这造成了现代蛋白质科学中一个奇怪的现象：蛋白质序列数据的累积量及积累速度远远超过蛋白质结构的解析。
这种序列与结构间不平衡的现象极大地限制了我们对蛋白质功能及其相关作用机理的理解。
因此，我们需要一种能够简单、快速且相对准确的技术来预测蛋白质的空间结构。
同源建模技术可以很好的解决上面的问题。
该方法利用信息技术的手段，可以直接从蛋白的一级结构（氨基酸序列）预测蛋白质的高级结构（主要为三级结构）。
根据最新一届国际建模大赛（CASP）的分类，目前主要的蛋白质建模方法包括两种：基于模板的建模（Template-based Modeling）和自由建模（Free Modeling）。
前者又包括两种方法：同源建模法（Homology Modeling）和“穿线法”（Threading）。
后者主要以从头计算法（ab initio）为主。
所有的建模方法中，以同源建模法(Homology Modeling)使用最为广泛，预测结果的准确性最为可靠。
同源建模的理论基础为蛋白质三级结构的保守性远远超过一级序列的保守性。
因此，人们可以通过使用一个或多个已知结构的蛋白（模板蛋白，template）来构建未知结构蛋白（目标蛋白，target）的空间结构。
Discovery Studio为用户提供了一整套利用Homology Modeling方法自动预测蛋白质空间结构的工具。
用户只需要提供蛋白质的氨基酸序列就可以轻松完成同源模型的构建及模型可信度评估的工作。
DS的Homology Modeling主要基于MODELER程序。
stable_diffusion_prompt更改提示词权重原理__概述及解释说明
stable diffusion prompt更改提示词权重原理概述及解释说明1. 引言1.1 概述本文旨在探讨稳定扩散模型中更改提示词权重的原理，并对其进行解释和说明。
稳定扩散模型是一种常用的模型，在自然语言处理、机器学习等领域中有着广泛的应用。
而提示词权重的调整则可以提高模型性能，使得生成的结果更加准确和可靠。
因此，研究和理解如何修改提示词权重的影响因素对于进一步优化稳定扩散模型具有重要意义。
1.2 文章结构本文将从以下几个方面展开论述：首先，介绍stable diffusion prompt更改提示词权重原理的背景和概述；其次，阐明提示词权重在该原理中的重要性；随后，详细探讨修改提示词权重可能产生的影响因素；最后，通过数值实验来验证并解读这些理论。
1.3 目的本文的目标是清晰地描述stable diffusion prompt更改提示词权重原理以及其在稳定扩散模型中的作用。
通过对这一主题的深入分析和解释，我们希望能够增加人们对该原理的理解，并为进一步研究和应用提供有价值的参考。
笔者准备从背景概述、重要性和影响因素三个方面详细论述stable diffusion prompt更改提示词权重原理。
同时，还将通过数值实验来验证这一原理，并对结果进行解读。
最后，本文将对所得结论进行总结，并提出未来研究的建议。
2. stable diffusion prompt更改提示词权重原理：2.1 原理概述在NLP模型中，prompt工程是指为了优化生成结果而对输入进行调整的一种方法。
其中，stable diffusion prompt是一种有效的提示建设技术，可以通过调整生成过程中不同单词或短语的权重来指导模型生成更准确、有逻辑性的结果。
2.2 提示词权重的重要性在NLP任务中，给定一个输入序列作为提示信息，模型需要根据这些提示来合理地生成输出结果。
而不同单词或短语在提示信息中的位置和权重往往对生成结果产生显著影响。
stable diffusion webui的原理
稳定的扩散WebUI原理1. 简介稳定的扩散WebUI是一种用于管理和监控分布式系统的界面，它提供了一种可视化的方式来查看和操作系统的各个组件。
它的原理是基于稳定的扩散算法，该算法通过使用网络连接来实现系统的自动调节和平衡，从而确保系统的稳定性和可靠性。
2. 稳定的扩散算法稳定的扩散算法是一种用于管理分布式系统的方法，它通过使用网络连接来实现系统的自动调节和平衡。
该算法的原理是通过将系统的各个组件连接在一起，形成一个稳定的网络。
这样，当一个组件出现故障或负载过高时，其他组件可以自动接管其工作，从而实现系统的自动平衡和稳定。
3. WebUI界面稳定的扩散WebUI提供了一个用户友好的界面，用户可以通过该界面来监控系统的各个组件。
界面通常包括系统的整体状态、各个组件的负载情况、以及系统的运行日志等信息。
用户可以通过界面来进行系统的操作，例如重新分配组件的负载、重启故障组件等。
4. 工作原理稳定的扩散WebUI的工作原理是将系统的各个组件连接在一起，形成一个稳定的网络。
当一个组件出现故障或负载过高时，其他组件可以自动接管其工作。
系统会根据各个组件的负载情况自动调节和平衡，以确保系统的稳定性和可靠性。
用户可以通过WebUI界面来监控和操作系统的各个组件，从而实现对系统的实时管理和监控。
5. 应用领域稳定的扩散WebUI广泛应用于各种分布式系统的管理和监控中，例如云计算、大数据处理等领域。
它为用户提供了一种可视化的方式来管理和监控系统，极大地简化了操作流程，提高了工作效率。
6. 总结稳定的扩散WebUI是一种基于稳定的扩散算法的管理和监控界面，它通过将系统的各个组件连接在一起，形成一个稳定的网络，从而实现了系统的自动调节和平衡。
用户可以通过WebUI界面来监控和操作系统的各个组件，从而实现对系统的实时管理和监控。
该技术在各种分布式系统中得到了广泛的应用，并为用户带来了极大的便利。
稳定的扩散WebUI在现代分布式系统中起着非常重要的作用，它为用户提供了一种直观简便的方式来管理和监控系统的各个组件。
清华大学研究生学位论文格式模版与要求
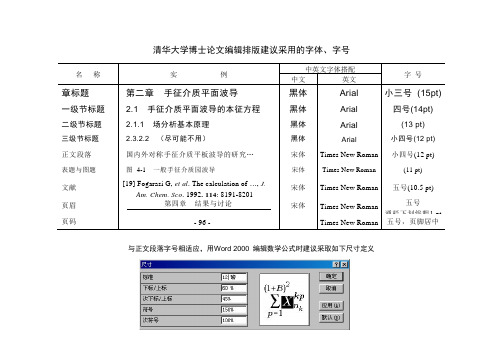
清华大学博士论文编辑排版建议采用的字体、字号与正文段落字号相适应，用Word 2000 编辑数学公式时建议采取如下尺寸定义清华大学博士论文格式样例：芳杂环高分子的高温水解特性与量子化学研究(申请清华大学理学博士学位论文)培养单位：清华大学化学系Array专业：物理化学研究生：易某某指导教师：某甲甲教授某乙乙教授副指导教师：芳杂环高分子的高温水解特性与量子化学研究易某某三号仿宋或华文仿宋请将中文封面左边Experimental and Theoretical Investigations of HydrolyticStability of Aromatic Heterocyclic Polymers in High TemperatureDissertation Submitted toTsinghua Universityin partial fulfillment of the requirementfor the degree ofDoctor of Natural SciencebyDong-ming YI( Physical Chemistry )Dissertation Supervisor : Professor Yong-chang TANG Associate Supervisor : Professor Da-long WUApril, 2001中文摘要摘要论文采用共振多光子电离和Ion-dip两种检测手段对碱土金属单卤化物的里德堡态进行了实验研究。
主要成果是：⑴首次观测到中等有效主量子数的CaCl 预解离里德堡态：在n*=5-7区域内，有5个文献未报导过的2∑+实贯穿里德堡态，填补了CaCl分子此一区域里德堡态研究的空白，对CaCl里德堡态结构的完整分析和其电子态完整的图像的建立具有重要意义；⑵通过理论分析，论证了这些态是因为和一个2∑+连续态的相互作用而导致强烈的预解离。
由实验测定的预解离线宽拟合出45000-47500cm-1范围内的2∑+连续态势能曲线，它能很好地解释这些里德堡态的预解离行为；⑶还观测到若干转动常数值反常小的里德堡态，它们可能是实非贯穿里德堡态的片段。
stable diffusion 背景移除 参数
标题：稳定扩散背景移除参数的研究与分析1. 背景移除技术的重要性背景移除是图像处理领域中非常重要的一项技术，它能够将目标物体从背景中提取出来，使得图像更加清晰和易于分析。
在许多应用中，如计算机视觉、医学影像处理、卫星图像分析等领域中，背景移除都扮演着关键的角色。
2. 稳定扩散背景移除算法稳定扩散背景移除算法是一种基于稳定扩散方程的图像分割算法，其核心思想是根据图像中像素的灰度值和梯度信息来进行像素分类，从而实现背景和前景的分割。
3. 背景移除参数的选择在稳定扩散背景移除算法中，参数的选择对算法的性能具有重要影响。
参数的选择需要考虑到图像的特性、目标物体的大小和形状等因素，并且需要经过一定的实验验证才能确定最优参数值。
4. 影响参数选择的因素（1）图像噪声对于含有噪声的图像，需要选择合适的参数来平衡对噪声的抑制和对目标物体的保留。
（2）目标物体的大小和形状不同大小和形状的目标物体对参数的选择也会有影响，需要根据实际情况进行调整。
（3）背景复杂度图像中背景的复杂度也会影响参数的选择，需要根据背景的复杂程度来调整参数值。
5. 参数选择的方法（1）经验选择通过经验和实践积累，可以逐步调整参数值，找到最优的参数组合。
（2）实验验证可以通过一系列的实验验证，比较不同参数组合下的处理效果，从而确定最优的参数值。
（3）自动参数选择算法也可以通过自动参数选择算法来寻找最优的参数组合，这种方法需要建立数学模型来自动确定参数的取值范围和最优值。
6. 最优参数的确定通过以上的方法，最终确定了稳定扩散背景移除算法的最优参数组合，并在实际应用中取得了良好的效果。
7. 结语稳定扩散背景移除算法在图像处理领域有着广泛的应用前景，选择合适的参数对算法的性能至关重要。
通过本文的研究和分析，希望可以为相关领域的研究和实践提供一定的参考和帮助。
稳定扩散背景移除算法在图像处理领域中是一项非常重要的技术，它能够有效地分离目标物体和背景，提取出清晰的目标物体图像，在计算机视觉、医学影像处理、卫星图像分析等领域具有广泛的应用前景。
基于邻居信息聚合的子图同构匹配算法
2021⁃01⁃10计算机应用,Journal of Computer Applications 2021,41(1):43-47ISSN 1001⁃9081CODEN JYIIDU http ：//基于邻居信息聚合的子图同构匹配算法徐周波，李珍，刘华东*，李萍（广西可信软件重点实验室（桂林电子科技大学），广西桂林541004）（∗通信作者电子邮箱ldd@ ）摘要：图匹配在现实中被广泛运用，而子图同构匹配是其中的研究热点，具有重要的科学意义与实践价值。
现有子图同构匹配算法大多基于邻居关系来构建约束条件，而忽略了节点的局部邻域信息。
对此，提出了一种基于邻居信息聚合的子图同构匹配算法。
首先，将图的属性和结构导入到改进的图卷积神经网络中进行特征向量的表示学习，从而得到聚合后的节点局部邻域信息；然后，根据图的标签、度等特征对匹配顺序进行优化，以提高算法的效率；最后，将得到的特征向量和优化的匹配顺序与搜索算法相结合，建立子图同构的约束满足问题（CSP ）模型，并结合CSP 回溯算法对模型进行求解。
实验结果表明，与经典的树搜索算法和约束求解算法相比，该算法可以有效地提高子图同构的求解效率。
关键词：子图同构；约束满足问题；图卷积神经网络；信息聚合；图匹配中图分类号：TP391文献标志码：ASubgraph isomorphism matching algorithm based on neighbor informationaggregationXU Zhoubo ，LI Zhen ，LIU Huadong *，LI Ping（Guangxi Key Laboratory of Trusted Software （Guilin University of Electronic Technology ），Guilin Guangxi 541004，China ）Abstract:Graph matching is widely used in reality ，of which subgraph isomorphic matching is a research hotspot and has important scientific significance and practical value.Most existing subgraph isomorphism algorithms build constraints based on neighbor relationships ，ignoring the local neighborhood information of nodes.In order to solve the problem ，a subgraph isomorphism matching algorithm based on neighbor information aggregation was proposed.Firstly ，the aggregated local neighborhood information of the nodes was obtained by importing the graph attributes and structure into the improved graph convolutional neural network to perform the representation learning of feature vector.Then ，the efficiency of the algorithm was improved by optimizing the matching order according to the characteristics such as the label and degree of the graph.Finally ，the Constraint Satisfaction Problem （CSP ）model of subgraph isomorphism was established by combining the obtained feature vector and the optimized matching order with the search algorithm ，and the model was solved by using the CSP backtracking algorithm.Experimental results show that the proposed algorithm significantly improves the solving efficiency of subgraph isomorphism compared with the traditional tree search algorithm and constraint solving algorithm.Key words:subgraph isomorphism;Constraint Satisfaction Problem (CSP);graph convolutional neural network;information aggregation;graph matching0引言图匹配技术被广泛地应用于社交网络、网络安全、计算生物学和化学等领域［1］中。
discovery studio libdock打分 -回复
discovery studio libdock打分-回复在药物研发的过程中，从候选化合物中发现有潜力的药物分子是一项非常重要的任务。
分子对接（molecular docking）是一种常用的药物设计方法，可以预测小分子（如药物）与生物大分子（如蛋白质）之间的结合趋势和亲和性。
而Discovery Studio的LibDock是其中一种流行的分子对接工具，它能够用于评估候选化合物与特定蛋白质靶点的结合能力，并预测它们的亲和力。
在使用Discovery Studio LibDock进行打分时，可以按照以下步骤进行操作。
第一步，准备蛋白质和配体文件。
在进行LibDock打分之前，需要准备好目标蛋白质和候选化合物的分子结构文件。
蛋白质的结构可以通过晶体学实验或者通过计算方法得到，而候选化合物的分子结构可以通过化学实验或者计算方法生成。
第二步，设置LibDock参数。
在开始进行分子对接时，需要设置相应的参数来控制计算过程和结果的精度。
Discovery Studio LibDock提供了一系列的参数设置选项，如收敛时迭代次数、搜索空间的大小、分子内的氢键等。
不同的参数设置可能会对结果产生影响，因此需要根据具体情况进行调整。
第三步，运行LibDock分子对接。
当参数设置好之后，可以运行LibDock 分子对接来评估候选化合物与蛋白质之间的亲和性。
LibDock会将候选化合物在蛋白质上进行位置和取向的搜索，并给出每个候选化合物的打分。
较高的分数表示较好的结合亲和性。
第四步，分析和解释结果。
分析和解释LibDock分子对接的结果是非常关键的一步。
可以通过分子对接得分、结合位点的残基相互作用和空间构型等来评估候选化合物与蛋白质之间的结合趋势和亲和力。
根据这些信息，可以选择潜在的药物分子进行进一步的验证和优化。
总结起来，Discovery Studio LibDock是一种常用的分子对接工具，能够用于评估候选化合物与特定蛋白质靶点的结合能力，并预测它们的亲和力。
虎杖解毒颗粒抗病毒的药效物质探究
-药业专论•Monograph on Pharmaceutical Industry2021年4月5日 第30卷第7期Vol. 30, No. 7, April 5, 2021China Pharmaceuticalsdoi ：10. 3969/j. issn. 1006 -4931. 2021. 07. 301虎杖解毒颗粒抗病毒的药效物质探究*唐荣霜1,石 洲1，帅小翠1 12潼荣生1,2,李晋奇1 ,让(1.电子科技大学医学院•个体化药物治疗四川省重点实验室，四川成都610072； 2.四川省医学科学院•四川省人民医院药学部，四川成都610072)摘要：目的探讨虎杖解毒颗粒防治新型冠状病毒肺炎的药效物质及作用机制。
方法以"虎杖""抗病毒”"冠状病毒机制”等为关键 词，检索国内外相关文献，总结虎杖解毒颗粒抗病毒的药效物质、抗冠状病毒的药效物质、抗新型冠状病毒的潜在药效物质,并运用Cytoscape 3. 2. 2软件进行分析。
结果 虎杖解毒颗粒抗病毒的药效物质包括板蓝根多糖、大黄素、野鸢尾苷元等50个成分，抗冠状病毒 的药效物质包括白藜芦醇、大黄素、芦荟大黄素等89个成分，抗新型冠状病毒的潜在药效物质包括白藜芦醇、青蒿素、大黄素等19个 成分。
抗新型冠状病毒的潜在作用机制包括促进I 型干扰素抗病毒、抑制NF-k B 、胞外信号调节激酶(ERK )/促分裂原活化的蛋白激酶(MAPK )、磷脂酰肌醇3激酶(PI3K//AKT 信号通路等。
结论虎杖解毒颗粒中的多种成分具有抗病毒作用，其抗病毒和抗冠状病毒的机制可能与促进I 型干扰素抗病毒，以及抑制NF-k B,ERK/MAPK,PI3K/AKT 信号通路有关，但需通过相关试验进行验证。
关键词:虎杖解毒颗粒;新型冠状病毒;新型冠状病毒肺炎;抗病毒;抗冠状病毒；药效物质中图分类号：R932;R285. 5;R254. 2 文献标志码：A 文章编号:1006 -4931 (2021 )07 -0001 -08Antivirus Pharmacodynamic Materials of Huzhang Jiedu GranulesTANG Rongshuang ；, SHI Zhou 1, SHUAI Xiaocui 1 ■2, TONG Rongsheng 1,2, LI Jinqi 1 ■ 2(1. ScUool of Mentciqn , University of Electronic Science and, TechcCogy of Chino • Penonaim Drug Thnapy Ken Laboratory of SicUuoo Prouiqce , Chengda , SicUuaq, Chino610072; 2. DepaOmeni of Phaonocy , SicUuag Acudemy of Medcol Scienceo • SicUuoo Provincial People's Hospital , Chengda , SicUuoo ,CCino 610077)Abstract ： Objective To investigate the pharmacodynamic materialn and mechanism of Huzhapg Jiedu Grapulen in the preventioo andtreatment of coronavirut Uiseasn 2019(C0VID - 19). Methods The releveai literature ai home aad aproap was searcheV with the key-worUt of Pfygomm cuspinamm , antiviral , coronavirus mechaaism aad se on. The aativirun pharmaconynamic materialn , the aatt - coron avirut pharmaconynamic materialn , aad the potential anh - SARS - CoV - 2 pharmacodynamic materialn of Huzhang JieVu Graaulet weresnmmarizeV , and they were apalyzen by Cytoscape 3.3.2 software. Results The aativirun pharmaconynamic materialn of Huzhang JieUrGrapulvt i 0011x 161 53 componentr, such at Radin Isatinio polysaccharinv, emonia and wild irisia. The anh - coronavirut pharmaconynamicmateuak of Huzhana JieVu Granulet incluCeV 99 components , such at resveratroO , emoUn and aloe emoUn. The potentian anti - SARS -CoV - 2 pharmaconynamic matenalv of Huzhana Jiedu Granulev iucluUen 19 components , such at resveratren , artemisinin and emoUn. The potevtial mechanisms o S anti - SARS - CoV - 2 incluUen promotina antiviral effecto Stype I interferon - indiOiOna uucleae factoe - k B(NF-k B ), extracellulae 8X0011 - renulaten kinase (ERK )/mi 1x 011 - achvaten protein kinase (MAPK ), phosphatinypnosnol 3 kinase(PI3K )/AKT sianaPnu pathwan and se on. Conclusion Mann 1111906x 0 in Huzhana Jiedu Granulee have a antivird effect. The mechanism ofantivird and anti - coronavirue man be relaten he promotina antivird effeet of type I interferon and inhiOitina NF - k B , ERK/MAPKand PI3K/AKT siauaVna pathwanCuh O ueene h be verifien bn relevedt experimente.Key words ： Huzhana JOV u GrauUes ; SARS - CoV-2; coronavOue yisease 2219; antmirue ; anti - coronavirue; pharmaconynamic materials新型冠状病毒肺炎（COVID - 19）是由新型冠状病 毒（SARS -CoV -2）感染引起的疾病,具有传染性强、人 群普遍易感等特点，临床表现以发热、干咳、乏力为主， 少数患者伴有鼻塞、流涕、肌痛、腹泻等;重症患者多在发病1周后出现呼吸困难和（或）低氧血症，严重者可快 速进展为急性呼吸窘迫综合征、脓毒症休克、难以纠正的代谢性酸中毒、凝血功能障碍等犤犦目前尚无治疗的 特效药。
stable difusion 的采样器和调度算法
stable difusion 的采样器和调度算法随着科技的发展，采样器和调度算法在各个领域中发挥着越来越重要的作用。
在稳定扩散（stable diffusion）领域，采样器和调度算法的应用更是具有深远的影响。
本文将探讨稳定扩散的采样器和调度算法，以期为相关领域的研究和实践提供参考。
一、采样器采样器是稳定扩散过程中不可或缺的一部分，其主要作用是从一个大的数据集中抽取样本。
采样器的性能直接影响到最终的扩散结果。
为了提高采样器的效率，需要考虑到样本的分布、数据集的大小以及采样策略等多个因素。
近年来，一些新型的采样器算法如贪婪采样、随机采样等在稳定扩散中得到了广泛应用，并取得了良好的效果。
二、调度算法调度算法是稳定扩散过程中的另一个关键因素，它决定了样本抽取和扩散的顺序。
一个好的调度算法能够充分利用资源，提高扩散效率，同时减少资源浪费。
常见的调度算法包括优先级调度、时间片轮转调度等。
此外，还有一些新型的调度算法，如人工智能调度算法，能够根据样本的特征和需求自动选择合适的调度策略。
三、优化策略在实际应用中，采样器和调度算法的优化是提高稳定扩散效果的重要手段。
通过调整采样器的抽样策略和数据集的分布，以及优化调度算法的执行顺序和资源分配，可以进一步提高稳定扩散的效果和效率。
此外，还可以结合实际需求，对采样器和调度算法进行联合优化，以达到最佳的扩散效果。
四、总结稳定扩散的采样器和调度算法在很大程度上决定了扩散效果和效率。
本文对采样器和调度算法进行了深入探讨，并提出了优化策略。
未来，随着科技的发展，相信采样器和调度算法将在稳定扩散领域发挥更加重要的作用。
stable diffusion 指令的高级用法
稳定扩散（Stable Diffusion）指令是在计算机科学领域中常用的术语，用于描述数据在系统中保持良好稳定状态的能力。
它在各种领域中都有广泛的应用，包括物理学、计算机科学、生物学和经济学等。
在本文中，我们将深入探讨稳定扩散指令的高级用法，以及它在不同领域中的应用。
1. 稳定扩散指令的概念和基本原理稳定扩散指令是一种用于保持数据在系统中稳定状态的功能。
它通过一系列的算法和技术来确保数据在传输、存储和处理过程中不会发生丢失、篡改或损坏。
这种指令通常包括数据校验、纠错和备份等功能，以确保系统的稳定性和数据的完整性。
2. 高级用法和技巧在实际的系统开发和运维中，稳定扩散指令有许多高级用法和技巧。
其中包括但不限于：- 数据冗余：利用冗余数据来实现数据的纠错和恢复功能，提高系统的容错性和稳定性。
- 分布式存储：将数据分布在多个节点上，通过稳定扩散指令来确保数据在不同节点间的一致性和完整性。
- 异地备份：将数据备份到不同地理位置的存储设备上，以防止自然灾害或意外事件对数据的影响。
3. 稳定扩散指令在不同领域中的应用稳定扩散指令在不同领域中都有广泛的应用。
在物理学中，它可以用来描述分子在溶液中的扩散过程；在计算机科学中，它可以用来确保数据在网络传输过程中不会丢失或错位；在生物学中，它可以用来研究细胞内物质的扩散行为；在经济学中，它可以用来描述市场信息的传播和流通。
稳定扩散指令的高级用法和技巧对于这些领域都具有重要意义。
4. 个人观点和理解在我看来，稳定扩散指令是现代信息技术发展中非常重要的一部分。
它不仅可以帮助我们构建稳定、安全的系统，还可以为各种领域的科学研究和实践提供有力支持。
我相信随着技术的不断发展，稳定扩散指令的高级用法和技巧将会越来越受到重视，并在各个领域中发挥更加重要的作用。
总结：稳定扩散指令的高级用法和技巧是一个非常丰富和重要的话题，它涉及到计算机科学、物理学、生物学、经济学等多个领域。
通过对稳定扩散指令的深入理解和应用，我们可以构建更稳定、安全的系统，并推动各个领域的科学研究和发展。
stable diffusion 劳拉路径
稳定扩散（stable diffusion）在物理学和数学中是一个重要的概念，指的是一种在随机过程中出现的稳定性和可预测性。
这个概念在各个领域都有着重要的应用，例如在生态学、金融学和地理学中都有着广泛的应用。
接下来，我将从简单到深入的角度来探讨稳定扩散的含义、特点以及其在不同领域的应用。
1. 稳定扩散的含义稳定扩散是一个在随机过程中出现的现象，指的是粒子或信息在空间中以稳定的速率扩散。
与一般随机扩散不同的是，稳定扩散具有一定的稳定性和可预测性，其扩散过程呈现出一定的规律性，使得我们可以对其进行较为准确的预测和分析。
2. 稳定扩散的特点稳定扩散具有几个显著的特点：它的扩散速率是稳定的，不会因外部环境的变化而产生剧烈波动；它的扩散路径呈现出一定的规律性，可以通过数学模型进行描述和分析；稳定扩散具有一定的局部性，扩散前后的状态之间存在着一定的联系和相似性。
3. 稳定扩散在生态学中的应用在生态学领域，稳定扩散常常被用来描述物种在生态系统中的扩散过程。
我们可以通过稳定扩散模型来研究种群在不同环境中的扩散速率和扩散路径，以及其对生态系统的影响和稳定性。
通过对稳定扩散的研究，我们可以更好地理解生态系统的演变和变化规律。
4. 稳定扩散在金融学中的应用在金融学领域，稳定扩散常常被用来描述金融资产价格的波动和扩散过程。
我们可以通过稳定扩散模型来研究股价、汇率等金融资产的价格扩散路径和波动规律，以及其对金融市场的影响和稳定性。
通过对稳定扩散的研究，我们可以更好地理解金融市场的波动和风险管理。
5. 稳定扩散在地理学中的应用在地理学领域，稳定扩散常常被用来描述土地利用、城市扩张等空间过程的扩散规律。
我们可以通过稳定扩散模型来研究城市的扩张路径和速率，以及其对周边环境和资源的影响和稳定性。
通过对稳定扩散的研究，我们可以更好地理解城市化过程中的空间变化和规划。
总结回顾：稳定扩散是一个在随机过程中出现的重要现象，具有稳定性和可预测性。
stable diffusion使用手册
stable diffusion使用手册摘要：一、前言二、稳定扩散技术的背景与原理三、稳定扩散技术的应用领域四、稳定扩散技术的操作步骤1.准备阶段2.实验阶段3.数据处理与分析阶段五、稳定扩散技术的优点与局限性六、稳定扩散技术的未来发展趋势七、总结正文：【前言】稳定扩散技术作为一种广泛应用于材料科学、生物医学、化学工程等领域的技术，对我国科技进步具有重要意义。
本文旨在介绍稳定扩散技术的背景与原理，应用领域，操作步骤，优缺点以及未来发展趋势。
【稳定扩散技术的背景与原理】稳定扩散技术是一种基于物质扩散原理的分析方法，主要通过测量物质在固定时间内通过特定面积的扩散量，从而获得物质的扩散系数。
这种技术具有测量过程简单、快速、准确等优点，因此在科研和工业生产中得到了广泛应用。
【稳定扩散技术的应用领域】稳定扩散技术在材料科学中的应用主要体现在研究材料的微观结构、相变过程、扩散机制等方面；在生物医学领域，稳定扩散技术可以用于研究药物在生物体内的分布、代谢和排泄等过程；在化学工程领域，稳定扩散技术可用于研究化学反应动力学、催化剂活性等。
【稳定扩散技术的操作步骤】稳定扩散技术的操作步骤主要包括：准备阶段、实验阶段、数据处理与分析阶段。
准备阶段主要是准备实验样品和设备；实验阶段包括将样品放入实验设备，设定实验条件，进行扩散实验；数据处理与分析阶段主要是通过测量和计算，得到物质的扩散系数。
【稳定扩散技术的优点与局限性】稳定扩散技术的优点在于测量过程简单、快速、准确，适用于多种样品和材料。
然而，稳定扩散技术也存在一定的局限性，例如，对于高分子材料，由于高分子链的缠结和运动，扩散系数会受到较大影响，导致测量结果偏差较大。
【稳定扩散技术的未来发展趋势】随着科技的发展，稳定扩散技术有望在测量精度、测量范围、数据处理速度等方面得到进一步优化。
此外，结合其他分析方法，如核磁共振、红外光谱等，稳定扩散技术有望在材料科学、生物医学等领域发挥更大的作用。
stable diffusion使用手册
stable diffusion使用手册
【最新版】
目录
1.稳定扩散的概念
2.稳定扩散的应用
3.稳定扩散的步骤
4.稳定扩散的注意事项
正文
稳定扩散，是指在物质传输过程中，由于分子热运动引起的物质浓度的平均传播过程。
它是一种常见的物理现象，广泛应用于化学、物理、生物等多个领域。
稳定扩散的应用十分广泛。
在化工产业中，稳定扩散被用于控制反应过程，提高产率和选择性；在生物科学中，稳定扩散被用于研究生物膜的通透性，揭示生物膜的功能；在环境科学中，稳定扩散被用于预测污染物在大气、水体中的传播过程，为环境保护提供科学依据。
进行稳定扩散实验，一般需要以下步骤：
首先，需要准备一个扩散池，扩散池由一个装满扩散介质的容器和一个可以容纳扩散介质的容器组成。
扩散介质可以是气体、液体或固体。
其次，将扩散介质装入容器中，然后通过改变容器的温度、压力等条件，引发扩散过程。
最后，通过检测扩散介质的浓度变化，计算出扩散系数，从而揭示扩散过程的规律。
在进行稳定扩散实验时，需要注意以下几点：
首先，扩散介质的选择应根据实验目的进行，以保证实验结果的准确
性。
其次，扩散池的设计应保证扩散过程的稳定性，以防止扩散过程中的异常现象。
最后，实验条件的控制应精确，以保证实验结果的可靠性。
总的来说，稳定扩散作为一种重要的物质传输方式，其在多个领域的应用都取得了显著的成果。
stable diffusion中的采样迭代步数
稳定的扩散（Stable diffusion）是一种常见的数值计算方法，在许多科学和工程领域都有着广泛的应用。
在采用稳定的扩散方法时，迭代的步数对于计算结果的精度和稳定性至关重要。
本文将就稳定扩散中的采样迭代步数进行讨论，以便更好地理解和应用这一重要的数值计算方法。
一、稳定扩散方法简介稳定扩散是一种用于解决偏微分方程问题的数值方法。
在使用稳定扩散方法时，我们需要对空间进行离散化处理，将连续空间上的问题转化为离散空间上的问题。
时间上也需进行离散化处理，将连续时间上的问题转化为离散时间上的问题。
在进行离散化处理后，我们可以利用数值计算方法对问题进行求解。
在稳定扩散方法中，迭代步数是非常重要的参数之一。
迭代步数的选取对于计算结果的收敛性和计算量都有着很大的影响。
合理选择迭代步数对于稳定扩散方法的应用至关重要。
二、采样迭代步数的影响因素1. 空间离散化程度在稳定扩散方法中，空间的离散化程度对采样迭代步数有着直接的影响。
一般来说，空间离散化程度越细致，需要的迭代步数就越多。
在应用稳定扩散方法时，需要根据具体问题的要求和计算资源的限制来确定空间的离散化程度，进而确定采样迭代步数。
2. 时间步长除了空间离散化程度外，时间步长也是影响采样迭代步数的另一个重要因素。
时间步长的选取直接关系到计算结果的精度和稳定性。
通常来说，较小的时间步长会导致较多的迭代步数，但会提高计算结果的精度和稳定性。
在确定时间步长时，需要综合考虑迭代步数和计算结果的精度，从而选择合适的时间步长，进而确定采样迭代步数。
3. 计算资源计算资源也是影响采样迭代步数的一个重要因素。
在计算资源有限的情况下，需要根据实际情况来确定采样迭代步数。
一般来说，计算资源越充足，可以选择的迭代步数就越多，从而提高计算结果的精度和稳定性。
在确定采样迭代步数时，需要综合考虑计算资源的限制，从而选择合适的迭代步数。
三、确定采样迭代步数的方法1. 理论分析在确定采样迭代步数时，可以通过理论分析的方法来确定。
stable diffusion wenui 使用综述 -回复
stable diffusion wenui 使用综述-回复关于稳定扩散wenui的综述稳定扩散（stable diffusion）是一种常用的数学模型，用来描述材料中粒子、能量、化学物质如何在空间中以稳定的、连续的方式扩散。
这种模型在各个领域中都有广泛的应用，包括材料科学、生物学、环境工程等。
其中，稳定扩散在涉及到颗粒的集体行为、物质变化规律以及动态平衡时发挥着重要的作用。
为了深入理解稳定扩散wenui的概念和应用，我们将从以下几个方面展开介绍。
1. 稳定扩散的基本概念与原理（200字）稳定扩散是指在稳态下，粒子从高浓度区域向低浓度区域不断地自发扩散，直到浓度均匀分布。
其背后的基本原理可以通过费克定律来描述，即扩散通量与浓度梯度成正比。
稳定扩散模型通常根据物质的特性和扩散介质的性质来选择适当的方程进行建模和求解。
2. 稳定扩散在材料科学中的应用（400字）稳定扩散在材料科学中起着重要的作用。
例如，在半导体材料和涂层工件的制备过程中，稳定扩散模型可以用来预测材料的组分分布和扩散速率，以及优化制备工艺。
此外，稳定扩散还可以应用于材料的长期稳定性和寿命预测，有助于设计出更具可靠性和耐久性的材料。
3. 稳定扩散在生物学中的应用（400字）稳定扩散在生物学研究中也有广泛的应用。
生物体内许多生物活动都与分子的扩散有关，如细胞内的物质转运、神经元中的离子传导以及微生物群体中的信号传递等。
稳定扩散模型可以帮助研究人员理解这些生物过程背后的物质转运机制，以及对它们进行调控和优化。
4. 稳定扩散在环境工程中的应用（400字）在环境工程领域，稳定扩散模型有助于预测和控制污染物在大气、水体和土壤中的扩散传播。
通过建立扩散方程和数值模拟方法，可以预测事故排放物的传播范围、影响范围和污染物的浓度分布。
这对于环境风险评估、污染源定位以及环境治理决策具有重要意义。
结论（100字）稳定扩散wenui是一种常用的数学模型，可以描述材料中粒子、能量、化学物质的稳定、连续扩散。
stable diffusion embedding训练 -回复
stable diffusion embedding训练-回复什么是稳定扩散嵌入（Stable Diffusion Embedding）？怎样进行稳定扩散嵌入训练？稳定扩散嵌入（Stable Diffusion Embedding，简称SDE）是一种数据降维技术，可以将高维数据映射到低维空间中，同时保留数据的相对距离关系。
SDE的主要目标是找到一个稳定扩散嵌入矩阵，用于产生稳定的低维表示。
稳定扩散嵌入训练是一个迭代的过程，主要包含以下步骤：1. 数据预处理：首先，需要对原始数据进行预处理。
这包括去除异常值、缺失值处理、数据标准化等步骤。
预处理可以确保数据质量，减少对嵌入结果的影响。
2. 构建相似度矩阵：接下来，需要构建原始数据的相似度矩阵。
相似度矩阵反映了数据点之间的相似度或距离关系。
常用的相似度度量方式包括欧氏距离、余弦相似度等。
构建相似度矩阵时，可以根据具体问题选择合适的相似度度量方式。
3. 归一化相似度矩阵：在得到相似度矩阵后，需要将其标准化以使其满足稳定扩散嵌入的要求。
常用的归一化方式是将相似度矩阵转化为概率转移矩阵，使得每行和为1。
这样可以将相似度转化为概率表示。
4. 计算扩散矩阵：根据归一化后的相似度矩阵，可以计算得到扩散矩阵。
扩散矩阵代表数据点之间的累积相似度。
在SDE中，扩散矩阵采用了与自然扩散过程类似的思想，通过迭代计算来使得相似度得到传播和累积。
5. 特征值分解与降维：对扩散矩阵进行特征值分解，得到特征值与特征向量。
根据特征值大小，可以选择保留最重要的特征，进一步实现数据的降维。
特征值较大的特征表示数据中的重要信息。
6. 得到稳定嵌入矩阵：最后，根据选择的特征值与特征向量，可以构建稳定嵌入矩阵。
稳定嵌入矩阵代表了数据在低维空间中的表达形式，可以用于后续的数据分析与可视化。
需要注意的是，稳定扩散嵌入训练中的超参数选择对结果有较大影响。
例如，相似度矩阵的构建方法、相似度度量方式、扩散矩阵的迭代次数等都需要根据具体的数据特点进行选择和调优。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
a r X i v :0707.0092v 2 [h e p -t h ] 21 S e p 2007More Meta-Stable Brane Configurations without D6-Branes Changhyun Ahn Department of Physics,Kyungpook National University,Taegu 702-701,Korea ahn@knu.ac.kr Abstract We describe the intersecting brane configurations,consisting of NS-branes,D4-branes(and anti-D4-branes),in type IIA string theory corresponding to the meta-stable nonsupersymmet-ric vacua of N =1SU (N c )×SU (N ′c )×SU (N ′′c )gauge theory with bifundamentals.By adding the orientifold 4-plane to these brane configurations,we also discuss the meta-stable brane configurations for other gauge theory with bifundamentals.Furthermore,we study the inter-secting brane configurations corresponding to the nonsupersymmetric meta-stable vacua of other gauge theory with bifundamentals,by adding the orientifold 6-plane.1IntroductionIn the standard type IIA brane configuration,the quark masses correspond to the relative dis-placement of the D6-branes(0123789)and D4-branes(01236)along the45directions geomet-rically.Then the eigenvalues of quark mass matrix correspond to the positions of D6-branes in45directions.See the review paper[1]for the gauge theory and the brane dynamics.The Seiberg duality in the classical brane picture can be accomplished by exchanging the locations of the NS5-brane(012345)and NS5’-brane(012389)along x6direction each other.The geometric misalignment of D4-branes connecting both NS5’-brane and D6-branes in the magnetic brane configuration can be interpreted as a nontrivial F-term condition in the gauge theory with massiveflavors.Then the F-term equations can be partially cancelled by both recombination offlavor-D4-branes with the color-D4-branes and then movement of those D4-branes into the45directions.This phenomenon in magnetic brane configuration corresponds to the fact that some entries in the magnetic dual quarks acquire nonzero vacuum expectation values to minimize the F-term in the dual gauge theory side.Moreover,the remainingflavor-D4-branes that do not move to45directions,connecting to NS5’-brane,can move along89directions freely since D6-branes and NS5’-brane are parallel and this geometric freedom of mesonfield corresponds to the classical pseudomoduli space of nonsupersymmetric vacua of the gauge theory.On the other hand,it is known that the NS-brane configuration in type IIA string theory, where there exist only two types of NS5-brane and NS5’-brane,preserves N=2supersym-metry in four dimensions[1].The geometry[2]of the coincident NS5-branes is characterized by the metric,the dilaton,and thefield strength and is useful to construct the DBI action for D4-branes.In order to break the supersymmetry,one adds D4-branes and anti-D4-branes[3]. By adding D4-branes suspending between the NS5-brane and the NS5’-brane,and anti-D4-branes(a quadratic term of bifundamentals in an electric theory.Also the linear term in a meson appears in this magnetic superpotential.Then the F-term equation for this mesonfield leads to the supersymmetry breaking.Onefinds that supersymmetry is broken classically but is re-stored quantum mechanically.It turns out the classical nonsupersymmetric vacuum becomes long-lived state[3].As the distance between the two NS5’-branes along the45directions becomes zero,this brane configuration with D4-and1A replacement of D6-branes with NS5’-brane corresponds to the gauging of theflavor group(global sym-metry)of the gauge theory realized on the D4-branes and this replacement might be useful to construct the phenomenological model building.the number of NS-branes is increased for a given gauge theory with matters since the role of D6-branes is replaced by NS5’-brane.Some of the meta-stable brane configurations lead to the known meta-stable brane configuration corresponding to the gauge theory with less gauge group factors in the literature,by replacing the NS5’-brane with coincident D6-branes. Basically,the gauge group will be a triple product gauge group for four NS-branes with D4-branes.When we add an orientifold4-plane into this brane configuration,the gauge group will be a triple product between symplectic gauge group and an orthogonal gauge group, alternatively,depending on the orientifold4-plane charge.When we add an orientifold6-plane into six NS-branes with D4-branes,one of the gauge group factor will be a symplectic or an orthogonal gauge group depending on the orientifold6-plane charge and the other gauge group factor will be unitary.In section2,we describe the type IIA brane configuration corresponding to the electric theory based on the N=1SU(N c)×SU(N′c)×SU(N′′c)gauge theory with the bifundamentals and deform this theory by adding the mass term for the bifundamental.We construct the three different dual magnetic theories by taking the Seiberg dual for each gauge group factor.Then we consider the nonsupersymmetric meta-stable minimum and present the corresponding intersecting brane configurations of type IIA string theory.In section3,we discuss the type IIA brane configuration,by adding the oreintifold4-plane to the brane onfiguration in section2,corresponding to the electric theory based on the N=1 Sp(N c)×SO(2N′c)×Sp(N′′c)gauge theory with matters and deform this theory by adding the mass term for the bifundamental.Then we construct the corresponding dual magnetic theories by taking the Seiberg dual for each gauge group factor.We consider the nonsupersymmetric meta-stable minimum and present the corresponding intersecting brane configurations of type IIA string theory.We also comment on the case of N=1SO(2N c)×Sp(N′c)×SO(2N′′c) gauge theory with matters.In section4,we discuss the type IIA brane configuration corresponding to the electric theory based on the N=1Sp(N c)×SU(N′c)×SU(N′′c)gauge theory with matters and deform this theory by adding the mass term for the bifundamental.Then we construct the two different dual magnetic theories by taking the Seiberg dual for each unitary gauge group factor.We consider the nonsupersymmetric meta-stable minimum and present the corresponding intersecting brane configurations of type IIA string theory.Moreover,we also discuss the meta-stable brane configurations corresponding to the electric theory based on the N=1SO(N c)×SU(N′c)×SU(N′′c)gauge theory by changing the orientifold6-plane charge.In section5,we make some comments for the future directions.2Meta-stable brane configurations with four NS-branes 2.1Electric theoryThe type IIA brane configuration[10,11]corresponding to N=1supersymmetric gauge theory with gauge groupSU(N c)×SU(N′c)×SU(N′′c)(2.1)and with afield F charged under(N c,N′′c),and their conjugates F and G can be described by the left NS5′L-brane(012389),the left NS5L-brane(012345),the right NS5′R-brane(012389),the right NS5R-brane(012345),N c-,N′c-andN′′c-color D4-branes(01236).Thefields F and F correspond to4-4strings connecting the N c-color D4-branes with N′c-color D4-branes while thefields G and G correspond to4-4strings connecting the N′c-color D4-branes with N′′c-color D4-branes.The left NS5L-brane is located at x6=0and let us denote the x6coordinates for theNS5′L-brane,the NS5′R-brane and the NS5R-brane by x6=−y1,y2,y2+y3respectively. The N c D4-branes are suspended between the NS5′L-brane and the NS5L-brane,the N′c D4-branes are suspended between the NS5L-brane and the NS5′R-brane,and the N′′c D4-branes are suspended between the NS5′R-brane and the NS5R-brane.We draw this brane configuration in Figure1A for the vanishing mass case2.The gauge couplings of SU(N c),SU(N′c)and SU(N′′c)are given by a string coupling constant g s,a string scaleℓs and the x6coordinates y i for three NS-branes throughg2 1=g sℓsy2,g23=g sℓs2There are similar brane configurations in the context of quiver gauge theory[12,13].Figure 1:The N =1supersymmetric electric brane configuration for the gauge groupSU (N c )×SU (N ′c )×SU (N ′′c )and bifundamentals F, F,G and G with vanishing(1A)and non-vanishing(1B)mass for the bifundamentals F and F .The N ′c D4-branes in 1A are decomposedinto (N ′c −N ′′c )D4-branes which are moving to +v direction in 1B and N ′′c D4-branes which are recombined with those D4-branes connecting between NS 5′R -brane and NS 5R -brane in 1B.where the first gauge group indices in F and Fare contracted,each second gauge group index in them is encoded in Φ′and the mass m is given bym =∆xℓ2s .(2.3)The gauge-singlet Φ′for the first dual gauge group is in the adjoint representation forthe second dual gauge group,i.e.,(1,(N ′c −N ′′c )2−1,1)⊕(1,1,1)under the dual gauge group (2.4).Then the Φ′is a (N ′c −N ′′c )×(N ′c −N ′′c )matrix.The NS 5′R -brane together with(N ′c −N ′′c )-color D4-branes is moving to the +v direction for fixed other branes during this massdeformation.In other words,the N ′′c D4-branes among N ′c D4-branes are not participatingin the mass deformation.Then the x 5coordinate(≡x )of NS 5′L -brane is equal to zero while the x 5coordinate of NS 5′R -brane is given by ∆x .Giving an expectation value to the mesonfield Φ′corresponds to recombination of N c -and N ′c -color D4-branes,which will becomeN c -color D4-branes in Figure 1A such that they are suspended between the NS 5′L -brane and the NS 5′R -brane and pushing them into thew ≡x 8+ix 9direction.We assume that the number of colors satisfiesN ′c ≥N c ≥N ′′c .Now we draw this brane configuration in Figure 1B for nonvanishing mass for the fieldsF and F.2.2Magnetic theoryBy applying the Seiberg dual to the SU(N c)factor in(2.1),the two NS5′L,R-branes can be located at the inside of the two NS5-branes,as in Figure2.Starting from Figure1A and moving the NS5′R-brane with(N′c−N′′c)D4-branes to the+v direction leading to Figure1B and interchanging the NS5′L-brane and the NS5L-brane,one obtains the Figure2A.Before arriving at the Figure2A,there exists an intermediate step where the(N′c−N c)D4-branes are connecting between the NS5L-brane and the NS5′L-brane,(N′c−N′′c)D4-branes connecting between the NS5′L-brane and NS5′R-brane,and N′′c D4-branes between the NS5′L-brane and the NS5R-brane.By introducing−N′′c D4-branes and−N′′c anti-D4-branes between the NS5L-brane and NS5′L-brane,reconnecting the former with the N′c D4-branes connecting between NS5L-brane and the NS5′L-brane(therefore N′c−N′′c D4-branes)and moving those combined(N′c−N′′c)D4-branes to+v-direction,one gets thefinal Figure2A where we are left with(N c−N′′c)anti-D4-branes between the NS5L-brane and NS5′L-brane.When two NS5’-branes in Figure2A are close to each other,then it leads to Figure2B by realizing that the number of(N′c−N′′c)D4-branes connecting between NS5L-brane and NS5′R-brane can be rewritten as(N c−N′′c)plus N c.If we ignore N′′c D4-branes and NS5R-brane from Figure2B,then the brane configuration becomes the one in[3].Figure2:The N=1magnetic brane configuration for the gauge group SU( N c=N′c−N c)×SU(N′c)×SU(N′′c)corresponding to Figure1B with D4-andThe matter contents are thefield f charged under( N c,),and their conjugates f and g under the dual gauge group(2.4)and the gauge-N′′csingletΦ′for thefirst dual gauge group in the adjoint representation for the second dual gauge group,i.e.,(1,(N′c−N′′c)2−1,1)⊕(1,1,1)under the dual gauge group(2.4).The cubic superpotential with the mass term(2.2)in the dual theory is given byW dual=Φ′f f+mΦ′.(2.5) Here the magneticfields f and f correspond to4-4strings connecting the N c-color D4-branes(that are connecting between the NS5L-brane and the NS5′R-brane in Figure2B) with N′c-flavor D4-branes(that are a combination of three different D4-branes in Figure2B). Among these N′c-flavor D4-branes,only the strings ending on the upper(N′c−N c)D4-branes and on the tilted middle(N c−N′′c)D4-branes in Figure2B enter the cubic superpotential term.Although the(N′c−N′′c)D4-branes in Figure2A cannot move any directions,the tilted (N c−N′′c)-flavor D4-branes can move w direction in Figure2B.The remaining upper N c D4-branes arefixed also and cannot move any direction.Note that there is a decomposition(N′c−N′′c)=(N c−N′′c)+ N c.The brane configuration for zero mass for the bifundamental,which has only a cubic superpotential,can be obtained from Figure2A by moving the upper NS5′R-brane together with(N′c−N′′c)color D4-branes into the origin v=0.Then the number of dual colors for D4-branes becomes N c between NS5L-brane and NS5′L-brane and N′c between two NS5’-branes as well as N′′c D4-branes between NS5′R-brane and NS5R-brane.Or starting from Figure1A and moving the NS5L-brane to the left all the way past the NS5′L-brane,one also obtains the corresponding magnetic brane configuration for massless case.The brane configuration in Figure2A is stable as long as the distance∆x between the upper NS5’-brane and the lower NS5’-brane is large,as in[3].If they are close to each other, then this brane configuration is unstable to decay and leads to the brane configuration in Figure2B.One can regard these brane configurations as particular states in the magnetic gauge theory with the gauge group(2.4)and superpotential(2.5).The(N′c−N′′c− N c)flavor D4-branes of straight brane configuration of Figure2B bend due to the fact that there exists an attractive gravitational interaction between thoseflavor D4-branes and NS5L-brane from the DBI action,by following the procedure of[3],as long as the distance y3goes to∞because the presence of an extra NS5R-brane does not affect the DBI action.For thefinite and small y3,the careful analysis for DBI action is needed in order to obtain the bending curve connecting two NS5’-branes.When the upper NS5’-brane(or NS5′R-brane)is replaced by coincident(N′c−N′′c)D6-branes and the NS5R is rotated by an angleπy1,g22,mag=g sℓsy3.The dual gauge theory has an adjointΦ′of SU(N′c)and bifundamentals f, f,g and g under the dual gauge group(2.4)and the superpotential corresponding to Figures2A and2B is given byW dual=hΦ′f f−hµ2Φ′,h2=g22,mag,µ2=−∆xwhere the zero of<f>is a(N′c−N′′c− N c)× N c matrix,the zero of< f>is a N c×(N′c−N′′c− N c)matrix and the zeros of<Φ′>are N c× N c, N c×(N′c−N′′c− N c),and (N′c−N′′c− N c)× N c matrices.Then one can expand thesefields around on a point(2.6),as in[4,15,16,17,18]and one arrives at the relevant superpotential up to quadratic order in thefluctuation.At one loop,the effective potential V(1)forΦ′0leads to the positive value foreffimplying that these vacua are stable.m2Φ′02.3Other magnetic theory-ILet us consider other magnetic theory for the same undeformed electric theory given in the subsection2.1.Here we consider the different mass deformation.By applying the Seiberg dual to the SU(N′c)factor in(2.1),the two NS5′L,R-branes can be located at the left hand side of the two NS5-branes,as in Figure4.Figure3:The N=1supersymmetric electric brane configuration for the gauge group SU(N c)×SU(N′c)×SU(N′′c)and bifundamentals F, F,G and G with vanishing(3A)which is identical to Figure1A and nonvanishing(3B)mass for the bifundamentals F and F.This deformation is different from the one(2.2)given previously.In3B,the NS5′L-brane together with N c D4-branes is moving to+v direction.By starting from Figure3A which is the same as Figure1A and moving the NS5′L-brane with N c D4-branes to the+v direction leading to Figure3B and interchanging the NS5L-brane and the NS5′R-brane,one obtains the Figure4A.Before arriving at the Figure 4A,there exists an intermediate step where the N c D4-branes are connecting between the NS5′-brane and the NS5′R-brane,(N′′c−N′c+N c)D4-branes are connecting between the L-brane and NS5L-brane,and N′′c D4-branes are suspended between the NS5L-brane NS5′Rand the NS5R-brane.By moving the combined N c D4-branes,obtained from reconnection of those D4-branes between NS5′L-brane and the NS5′R-brane and those D4-branes betweenthe NS5′R-brane and NS5L-brane(therefore between the NS5′L-brane and the NS5L-brane), to+v-direction,one gets thefinal Figure4A where we are left with(N′c−N′′c)anti-D4-branes between the NS5′R-brane and NS5L-brane.We assume that the number of colors satisfiesN c+N′′c≥N′c≥N′′c.When two NS5’-branes in Figure4A are close to each other,then it leads to Figure4B by realizing that the number of N c D4-branes connecting between NS5′L-brane and NS5L-brane can be rewritten as(N′c−N′′c)plus N′c.Figure4:The N=1magnetic brane configuration for the gauge group SU(N c)×SU( N′c= N c+N′′c−N′c)×SU(N′′c)corresponding to Figure3B with D4-andN′c,1),afield g charged under ,(1, N′3One can also construct the mass deformation by rotating NS5R-brane and moving it to+v direction.Then the brane configuration will look like as the Figure15.where we defineΦasΦ≡F F,the second gauge group indices in F and F are contracted, eachfirst gauge group index in them is encoded inΦand the mass m is given by(2.3)where ∆x refers to the distance between two NS5’-branes along the x5direction in Figure4A.Let us emphasize that although theΦwhich hasfirst gauge group indices looks similar to the previousΦ′which has second gauge group indices in(2.2),the group indices are different.Here the magneticfields f and f correspond to4-4strings connecting the N′c-color D4-branes(that are connecting between the NS5′L-brane and the NS5L-brane in Figure4B)with N c-flavor D4-branes(which are realized as corresponding D4-branes in Figure4A).Although the N c D4-branes in Figure4A cannot move any directions,the tilted(N′c−N′′c)-flavor D4-branes can move w direction in Figure4B.The remaining upper N′c D4-branes arefixed also and cannot move any direction.Note that there is a decompositionN c=(N′c−N′′c)+ N′c.The brane configuration for zero mass for the bifundamental,which has only a cubic superpotential,can be obtained from Figure4A by moving the upper NS5’-brane(or NS5′L-brane)together with N c color D4-branes into the origin v=0.Then the number of dual colors for D4-branes becomes N c between two NS5’-branes, N′c between NS5′R-brane and NS5L-brane and N′′c between NS5L-brane and NS5R-brane.Or starting from Figure3A and moving the NS5L-brane to the right all the way past the NS5′R-brane,one also obtains the corresponding magnetic brane configuration for massless case.The brane configuration in Figure4A is stable as long as the distance∆x between the upper NS5’-brane and the lower NS5’-brane is large.If they are close to each other,then this brane configuration is unstable to decay to the brane configuration in Figure4B.One can regard these brane configurations as particular states in the magnetic gauge theory with the gauge group(2.7)and superpotential(2.8).The(N c− N′c)flavor D4-branes of straight brane configuration of Figure4B bend since there exists an attractive gravitational interaction between thoseflavor D4-branes and NS5L-brane from the DBI action,as long as the distance y3is large because the presence of an extra NS5R-brane does not affect the DBI action.For thefinite and small y3,the careful analysis for DBI action is needed in order to obtain the bending curve connecting two NS5’-branes.Or if y3goes to zero,then this extra NS5R-brane plays the role of enhancing the strength for the NS5-branes and will affect both the energy of bending curve,E curved,which is proportional to1kℓs where k is the number of NS5-branes and∆x which depends on both1similar to the one found in[14]wherethe gauge group was given by SU(n′f+n c−n′c)×SU(n c)with n f multiplets,n′f multiplets,flavor singlets and gauge singlets.Then the present N c corresponds to the n′f,the number N′c corresponds to n′c,and N′′c corresponds to the n c of [14].The low energy dynamics of the magnetic brane configuration can be described by the N=1supersymmetric gauge theory with gauge group(2.7)and the gauge couplings for the three gauge group factors are given byg21,mag=g sℓsy2,g23,mag=g sℓs2πg sℓ3s.Then f f is a N′c× N′c matrix where thefirst gauge group indices for f and f are contracted with those ofΦwhileµ2is a N c×N c matrix.The product f f has the same representation for the product of quarks and moreover,thefirst gauge group indices for thefieldΦplay the role of theflavor indices when there are D6-branes before.Therefore,the F-term equation,the derivative W dual with respect to the mesonfieldΦcannot be satisfied if the N c exceeds N′c.So the supersymmetry is broken.That is,there exist three equations from F-term conditions:f f−µ2=0andΦf=0= fΦ.Then the solutions for these are given by<f>= µ1e N′c0 ,< f>= µ1e N′c0 ,<Φ>= 000Φ01(N c−e N′c)(2.9)where the zero of<f>is a(N c− N′c)× N′c matrix,the zero of< f>is a N′c×(N c− N′c) matrix and the zeros of<Φ>are N′c× N′c, N′c×(N c− N′c)and(N c− N′c)× N′c matrices. Then one can expand thesefields around on a point(2.9),as in[4,15]and one arrives at the relevant superpotential up to quadratic order in thefluctuation.At one loop,the effectivepotential V(1)eff forΦ0leads to the positive value for m2Φimplying that these vacua are stable.2.4Other magnetic theory-IIOne can think of the following dual gauge groupSU(N c)×SU(N′c)×SU( N′′c=N′c−N′′c)(2.10)by performing the magnetic dual for the last gauge group in(2.1).The electric brane configu-ration can be given in terms of Figure1A or Figure1A with an exchange between NS5-brane and NS5’-brane.Then for the latter,the resulting brane configuration is given by NS5L-brane, -brane,NS5R-brane,and NS5′R-brane from the left to the right in the x6direction. NS5′LIn order to obtain the above dual gauge group,we need to interchange between the NS5R-brane and the NS5′R-brane,as we did before.One can do this either by following the previous procedure or by looking at the Figure2from the negative w direction which is an opposite viewpoint,compared with Figure2.In other words,we are looking at the Figure2from the other side of w.Then the resulting brane configuration in this case can be obtained by taking a reflection for all the NS-branes,D4-branes and anti D4-branes with respect to the NS5L-brane(rotating them to the left forfixed NS5L-brane)in Figure2A and Figure2B.Then the N=1magnetic brane configuration for the gauge group SU(N c)×SU(N′c)×SU( N′′c=N′c−N′′c)corresponds to the Figure5A’with D4-andwhich will become NS5′M-brane,mov-2ing it with the(N′c−N c)D4-branes to+v direction where we introduce(N′c−N c)D4-branes and(N′c−N c)anti D4-branes between the NS5R-brane and the NS5′R-brane,one gets the final Figure5A”where we are left with(N′′c−N c)anti-D4-branes between the NS5-brane and the NS5′R-brane.When two NS5’-branes in Figure5A”are close to each other,then it leads to Figure5B”by realizing that the number of(N′c−N c)D4-branes connecting between -brane and NS5-brane can be rewritten as(N′′c−N c)plus N′′c.NS5′MThe brane configuration in Figure5A”is stable as long as the distance∆x between the upper NS5’-brane and the lower NS5’-brane(or NS5′R-brane)is large.If they are close to each other,then this brane configuration is unstable to decay to the brane configuration in Figure 5B”.One can regard these brane configurations as particular states in the magnetic gauge theory with the gauge group and superpotential.The(N′c−N c− N′′c)flavor D4-branes of straight brane configuration of Figure5B”bend since there exists an attractive gravitationalFigure5:The N=1magnetic brane configuration for the gauge group SU(N c)×SU(N′c)×SU( N′′c=N′c−N′′c)with D4-and,1),afield g charged underN′c(1,N′c,and cannot move any direction.Note that there is a decomposition(N′c−N c)=(N′′c−N c)+ N′′c.The brane configuration for zero mass for the bifundamental,which has only a cubicsuperpotential,can be obtained from Figure5A”by moving the upper NS5’-brane together with(N′c−N c)color D4-branes into the origin v=0.Then the number of dual colors for D4-branes becomes N c between the NS5′L-brane and the NS5′M-brane,N′c between theNS5′M-brane and the NS5-brane and N′′c between NS5-brane and NS5′R-brane.Or starting from Figure1A and moving the NS5′R-brane to the right all the way past the NS5R-brane, one also obtains the corresponding magnetic brane configuration for massless case.The low energy dynamics of the magnetic brane configuration can be described by theN=1supersymmetric gauge theory with gauge group(2.10)and the gauge couplings for thethree gauge group factors are given byg21,mag =g sℓs(y2−y3),g23,mag=g sℓs2πg sℓ3s.Then g g is a N′′c× N′′c matrix where the second gauge group indices for g and g are contracted with those ofΦ′whileµ2is a(N′c−N c)×(N′c−N c)matrix.The product g g has the same representation for the product of quarks and moreover,the second gauge group indices for thefieldΦ′play the role of theflavor indices.Therefore,the F-term equation,the derivative W dual with respect to the mesonfieldΦ′cannot be satisfied if the(N′c−N c)exceeds N′′c.So the supersymmetry is broken.That is, there exist three equations from F-term conditions:g g−µ2=0andΦ′g=0= gΦ′.Then the solutions for these are given by<g>= µ1e N′′c0 ,< g>= µ1e N′′c0 ,<Φ′>= 000Φ′01(N′c−N c)−e N′′cwhere the zero of<g>is a(N′c−N c− N′′c)× N′′c matrix,the zero of< g>is a N′′c×(N′c−N c− N′′c)matrix and the zeros of<Φ′>are N′′c× N′′c, N′′c×(N′c−N c− N′′c)and (N′c−N c− N′′c)× N′′c matrices.Then one can expand thesefields around on a point,as in[4,15]and one arrives at the relevant superpotential up to quadratic order in thefluctuation.At one loop,the effective potential V(1)eff forΦ′0leads to the positive value for m2Φ′0implyingthat these vacua are stable.3Meta-stable brane configurations with four NS-branes plus O4-planeIn this section,we add an orientifold4-plane to the previous brane configurations andfind out new meta-stable brane configurations.Or one can realize these brane configurations by inserting the extra NS-brane and O4-planes into the brane configuration[16].3.1Electric theoryThe type IIA brane configuration[19]corresponding to N=1supersymmetric gauge theory with gauge groupSp(N c)×SO(2N′c)×Sp(N′′c)(3.1)and with afield F charged under(2N c,2N′c),afield G charged under(2N′c,2N′′c)can be described by the left NS5′L-brane,the left NS5L-brane,the right NS5′R-brane,the right NS5R-brane,2N c-,2N′c-and2N′′c-color D4-branes as well as an O4±-plane(01236)we should add.The O4±-planes act as(x4,x5,x7,x8,x9)→(−x4,−x5,−x7,−x8,−x9)as usual and they have RR charge±1playing the role of±1D4-brane.We draw this brane configuration in Figure6A for the vanishing mass case.There is no superpotential in Figure6A.Let us deform this theory.Displacing the two NS5’-branes relative each other in the+v direction corresponds to turning on a quadratic mass-deformed superpotential for thefield F as follows:W=mF F≡mΦ′(3.2)where thefirst gauge group indices in F are contracted,each second gauge group index in F is encoded inΦ′and the mass m is given by(2.3).The gauge-singletΦ′for the first dual gauge group is in the adjoint representation for the second dual gauge group, i.e.,(1,(N′c−N′′c)(2N′c−2N′′c−1),1)under the dual gauge group(3.3).Then theΦ′is a2(N′c−N′′c)×2(N′c−N′′c)matrix.The half NS5′R-brane[20]together with(N′c−N′′c)-colorD4-branes is moving to the+v direction(and their mirrors to−v direction)forfixed other branes during this mass deformation.The2N′′c D4-branes among2N′c D4-branes are not。