配合物结构晶体分子
无机化学-配合物结构理论

配位化合物中M与L之间化学健的形成及 配合物的一些性质难以用经典化学健理论来 解释。
1913年Pauling 首先将分子结构中的价健 理论应用于配合物,并经不断修正补充,形 成了近代配合物价健理论。
2019年10月11 日5时28分
一、价键理论的要点
1、中心离子(M)具有空的价电子轨道,配体(L)具 有孤对电子。
2、M的空轨道在成键前必先进行杂化,然后再与 L 形成 配位健。
3、配合物的空间构型和键型取决于M 的杂化轨道。
2019年10月11 日5时28分
二、配合物的空间构型 1、配位数为2的配合物
如:[Ag(NH3) 2]+ Ag+ 4d105s05p0
2019年10月11 日5时28分
(1) 轨道杂化:
[Co(NH3)6]2+等。
2019年10月11 日5时28分
2、内轨配键、内轨型配合物
M以部分次外层的轨道(n-1)d组成杂化轨道, 与配位原子形成的配健称为内轨配键。相应的化 合物称为内轨型配合物。
如:dsp2 、dsp3 、d2sp3等。 内轨型配合物:[Cu(H2O)4]2+、[Co(NH3)6]3+、
2019年10月11 日5时28分
3、配合物的颜色 当dγ轨道(八面体场为例)上填满了电子(d10结构)
或无d电子(d0)时,配合物的电子不能在dγ~dε之 间跃迁。故配合物是无色的。
其余d1~d9情况下,dε上的电子可以吸收能量跃迁 到dγ 上。故要吸收一定谱长的光,而人们看到它们的 补色。此时配合物一般都是有色的。
2019年10月11 日5时28分
例: [Ni(NH3)4]2+ Ni 3d8
配位化合物的结构和性质

2
3
sp
sp2
直线形
平面三角形
[Ag(NH3)2]+
[CuCl3]2-
4
sp3
d3s dsp2
四面体
四面体 平面正方形 三角双锥形 四方锥形
[Ni(NH3)4]2+
MnO4[Ni(CN)4]2Fe(CO)5 [TiF5]2-
5
dsp3 d4s
6
d2sp3
八面体
[Fe(CN)6]3-
6.2 价键理论
(3) 平行正方形场
在平行正方形配合物中,四个配体沿x,y轴正负方向与
中心离子接近。 在平行正方形配合物中,dx2-y2轨道的电子云极大值方向 指向配体,因此能级最高,高于Es能级;dxy 轨其也在xy平面上,所以
也要受到较大的排斥故能级也高于Es能级;dz2 轨道的能级 较低,低于Es能级;dyz和dxz轨道受到的排斥作用相同,是 简并的,能级最低。这样,在平面正方形场中,能级分裂为 四组。
由于△值通常从光谱确定,故称这个顺序为光谱化学序列。
分裂能和成对能
b) 当配体固定时,分裂能随中心离子的不同而不同,其
大小次序为:
Pt 4 Ir 3 Pd 4 Rh3 Mo3 Ru3 Co3 Cr 3 Fe 3 V 2 Co2 Ni 2 Mn2
中正负离子的静电作用;
中心离子在配体的静电作用下,使原来简并的d轨道分 裂成能级不同的几组轨道;
d电子在分裂的d轨道上重新排布,优先占据能量较低
的轨道,往往使体系的总能量有所降低,形成强场低自 旋、弱场高自旋的配合物。
二、d轨道在晶体场中的分裂
d原子轨道的角度分布图
配体配合物的合成、晶体结构及性质

d,降至室温。过滤,得到浅黄色块状透明晶体。 配合物2的合成:称取0.2 mmol苯氨.2.5一二
磺酸单钠盐、0.4 mmol l。lO一邻菲咯啉溶于20 mL 乙醇中.用2 mol·L—NaOH溶液调节该混合溶液的
为中心,2,6.萘二磺酸(2,6.H2NDS)、1,3.Z-(4.吡啶 基)丙烷(BPP)为配体和以Ni2+为中心。苯氨.2,5.二 磺酸似.2,5.H2DSA)、1。10.邻菲咯啉(phen)为配体, 得到了2个新的配合物[Zn(BPP)2(H20)。1(2,6.NDS)· 0.5H20(1)和[Ni(phen)2(820)2】0—2,5一DSA)·3H20
pH约为6。然后将0.2 mmol NiCl2"6H:O的水溶液 慢慢加入.加热搅拌约2 h后过滤,滤液室温放置。3 周后.得到蓝色单晶体。 1.3配合物的晶体结构测定
选取尺寸为0.18 mmx0.14 mmx0.10 mm(1)和
(2)。在此我们报道配合物的合成、晶体结构、荧光 和热稳定性。
O.35 mmx0.30 mmx0.18 mm(2)的配合物单晶,在 Bruker Smart 1000 CCD X一射线单晶衍射仪上.使用
第26卷第8期 2010年8月
无机
化
学
学
报
CHINESE JOURNAl.OF INORGANIC CHEMISTRY
V01.26 No.8 1457—1462
单核Zn(Ⅱ)烈i(Ⅱ)含氮配体配合物的合成、晶体结构及性质
宋金浩顾雅琨李 夏★ (首都师范大学化学系,北京 100048)
摘要:合成了2个新的配合物[Zn(BPP)2(}{20)。1(2,6-NDS)·O.5H20(1)和[Ni(phen):(H20):1(A一2,5一DSA)·3H20(2)(2,6-NDS=2,6一萘二 磺酸根,A.2,5-DSA=苯氨.2,5-二磺酸根,RPP=l,3---(4.吡啶基)丙烷,phen=1,10.邻菲略啉),用X.射线单晶衍射结构分析方法 测定了配合物的晶体结构。配合物l是单核分子.Zn2*离子与2个1,3--2(4.吡啶基)丙烷的2个N原子及4个水分子配位,形 成单核配位阳离子。相邻配位阳离子通过配位水分子与氮原子的氧键作用联接成一维双螺旋阳离子链。双螺旋阳离子链与未配 位的2。6.萘二磺酸根阴离子通过氖键作用形成■维超分子网。配合物2是单核分子,Niz+离子与2个l,10.邻菲咯啉分子中的4 个N原子及2个水分子配位。形成单核配位阳离子。配位阳离子与游离的水分子及苯氨.2,5.二磺酸根阴离子通过氢键作用构 筑成二维超分子网。
配合物结构

2 Eeg + 3Et2 g = 0 ∴ Eeg Et2 g = 10 Dg
那
Eeg = 6 Dg Et2 g = 4 Dg
3、正四面体场的作用:配体从四面体的四个顶点接近中心离子
L
L
一种 d xy , d yz , d zx
L
L L
指向四面体棱的中点,
L
受一定斥力,能量有所 上升;
L
L
d xy , d yz , d zx
2+ 4
[Fe ( H 2O )6 ] ,[Fe ( CN )6 ]
Q Fe2+ : kk 3d 6 , p = 19150cm 1 H 2O = 10400cm 1 , CN = 33000cm 1 ∴ H 2O < p ,
[Fe ( H 2O )6 ]2+ 中Fe2+的 d电子排布
eg 2 t2 g 3+1
正八面体
dsp , d sp L 杂化
一般,共价配合物多是低自旋态。如 [Fe(CN)6]3-等
晶体场理论(CFT) §6-2 晶体场理论(CFT)
M
n+与L n-的作用是L n-形成的力场对M n+的作用,使M n+
的d轨道分裂, d电子重排。
一、中心离子 轨道能级的分裂: 中心离子d轨道能级的分裂 中心离子 轨道能级的分裂: 1、球对称场的作用:5个d轨道受到的作用是相同的,轨道整 体能量上升,但不发生分裂。 Es
依光谱序列
I < Br <L< OH < F < H2O <L< py< NH3 <L< en< NO < CN,CO 2
物质结构与性质高考热点归纳 配合物和晶胞配位数的确定

物质结构与性质高考热点归纳配位数的确定一、各种典型配合物中配位数的判断1.配位数可以等同于中心离子(或原子)与配位原子形成的配位键键数,也可以等同于配位体的数目。
如[Ag(NH3)2]NO3、[Ag(CN)2]-、[Cu(NH3)4]SO4、[Cu(H2O)4]2+、[Zn(NH3)4]2+、[Zn(CN)4]2-、K3[Fe(SCN)6]、[Fe(CN)6]3-、[FeF6]3-等配合物或配离子中的中心离子与配位体的数目以及配位原子形成的配位键键数均相等,其中Ag+离子的配位数为2,Cu2+离子与Zn2+离子的配位数均为4,Fe3+离子的配位数为6。
一般规律:一般配合物的配位数可以按中心离子电荷数的二倍来计算。
又如Ni(CO)4、Fe(CO)5、Cr(CO)6等羰基化合物中Ni、Fe、Cr原子的配位数分别为4、5、6。
[Co(NH3)4(H2O)2]Cl2、[CrCl(H2O)5]Cl2中Co2+离子与Cr3+离子的配位数均为6。
说明:羰基化合物中的中心原子呈电中性,此类配合物的配位数由化学式直接判断。
Co2+离子与Cr3+离子的电荷数分别为2、3,但配位数都是6。
所以,配合物的配位数不一定按中心离子(或原子)的电荷数判断。
2.当中心离子(或原子)与多基配体配合时,配位数可以等同于配位原子的数目,但不是配位体的数目。
如[Cu(EN)2]中的EN是乙二胺(NH2CH2CH2NH2)的简写,属于双基配体,每个乙二胺分子有2个N原子与Cu2+离子配位,故Cu2+离子的配位数是4而不是2。
3.当中心离子(或原子)同时以共价键与配位键结合时,配位数不等于配位键的键数。
如[BF4]-、[B(OH)4]-、[AlCl4]-、[Al(OH)4]-等配离子中,B、Al原子均缺电子,它们形成的化学键,既有共价键,又有配位键,配位数与配位键的键数不相等,配位数均为4。
又如Al2Cl6(如下左图所示)中Al原子的配位数为4。
晶体结构,配合物结构知识点与习题1-1
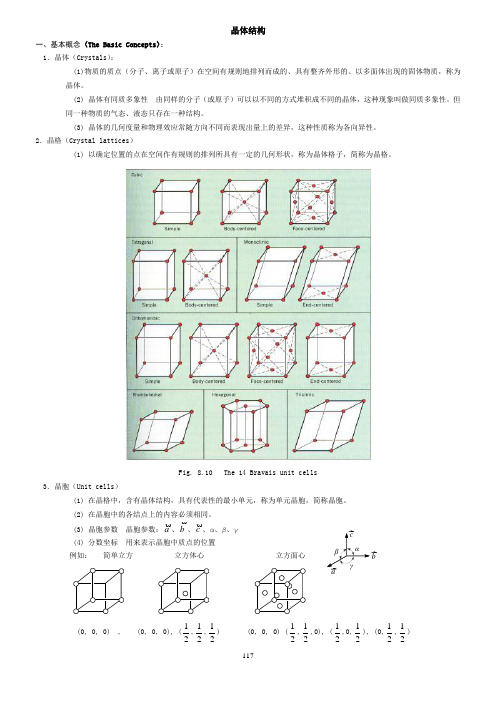
117晶体结构一、基本概念(The Basic Concepts ): 1.晶体(Crystals ):(1)物质的质点(分子、离子或原子)在空间有规则地排列而成的、具有整齐外形的、以多面体出现的固体物质,称为晶体。
(2) 晶体有同质多象性 由同样的分子(或原子)可以以不同的方式堆积成不同的晶体,这种现象叫做同质多象性。
但同一种物质的气态、液态只存在一种结构。
(3) 晶体的几何度量和物理效应常随方向不同而表现出量上的差异,这种性质称为各向异性。
2.晶格(Crystal lattices )(1) 以确定位置的点在空间作有规则的排列所具有一定的几何形状,称为晶体格子,简称为晶格。
Fig. 8.10 The 14 Bravais unit cells3.晶胞(Unit cells )(1) 在晶格中,含有晶体结构,具有代表性的最小单元,称为单元晶胞,简称晶胞。
(2) 在晶胞中的各结点上的内容必须相同。
(3) 晶胞参数 晶胞参数:a、b、c、α、β、γ (4) 分数坐标 用来表示晶胞中质点的位置例如: 简单立方 立方体心 立方面心(0, 0, 0) , (0, 0, 0), (21,21,21) (0, 0, 0) (21,21,0), (21,0,21), (0,21,21) αβγbc a118在分数坐标中,绝对不能出现1,因为1即0。
这说明晶胞是可以前后、左右、上下平移的。
等价点只需要一个坐标来表示即可,上述三个晶胞中所含的质点分别为1、2、4,所以分数坐标分别为1组、2组和4组。
(5) 晶面指数 晶面在三维空间坐标上的截距的倒数(h 、k 、l )来表示晶体中的晶面,称为晶面指数,如立方晶系中(100),(110),(111)面分别为(100) (110)(111)lFig. 8.12 Selected planes and their Miller indices for cubic system用X-ray 的衍射可以测量晶体中的面间距,2d ·sin θ = n ·λ。
晶体结构配合物结构知识点与习题

配合物结构一、配位化合物的定义由提供孤电子对(NH3、H2O、X「)或n电子(H2C= CH2、| 、)的物种与提供适当空轨道的物种(金属原子或金属离子)组成的化合物称为配位化合物,简称为配合物。
二、配位化合物的组成1 .配合物由内界(inner)和外界(outer)组成。
外界为简单离子,配合物可以无外界,但不可以无内界。
例如:Fe(CO)5 Pt(NH3)2Cl22 .内界由中心体(center)和配位体(ligand)组成。
(1) 中心体:提供适当的空轨道的原子或离子,绝大部分是d区或ds区元素。
用M表示。
(2) 配位体(L)(简称配体):提供孤对电子对或n电子的离子,离子团或中性分子。
三、配位化合物的分类 (Classification )1. Classical complexes :配体提供孤电子对,占有中心体的空轨道而形成的配合物。
例如:Ag(NH 3)2 , Cu(CN) 42. n -complexes :配体提供n电子,占有中心体的空轨道而形成的配合物。
例如:Fe(C5H5)2, K[PtCl 3(C2H4)](第一个n配合物,Zeise's salt)出匚CH2 IMM配体提供:2个n电子4个n电子6个n电子四、配位体(L) Ligand1.根据配体中配位原子的不同,配体可分类成:(1) 单基(齿)配体(unidentate ligand ):配体中只含有一个配位原子;例如:NH3、H2。
、X「、(py)N(2) 多基(齿)配体(multidentate ligand ):配体中含有两个或两个以上的配位原子。
由单齿配体组成的配合物,称为简单配合物;由多齿配体组成的配合物,称为螯合物(chelate)。
2 .一些常见的配体:(1) 单基配体:X : F (fluoro)、Cl (chloro)、Br (bromo)、I (iodo)、H2O (aquo)、CO (carbonyl)、NO (nitrosyl)、C5H5N (py)、OH (hydroxo)(2) 双基配体:en (乙二胺)H2NCH2CH2NH2 (ethylenediamine)(oxalate ion^N Ci giy C (氨基乙酸根)O(2,2 -d ipyridyl )(3) 多基配体:EDTA (乙二胺四乙酸)(六齿) (H4Y)HOOCH2C CH2COOHNCH 2CH2N、(ethyle nediami netetracetato)HOOCH2C CH2COOH五、配位数(Coordination Number1.中心原子(或离子)所接受的配位原子的数目,称为配位数2 .若单基配体,则配位数=配体数;若多基配体,则配位数=配体数配位原子数/每个配体3 .确定配位数的经验规则一EAN规则(Effective atomic number rule )或十八电子(九轨道)规则(1) 含义:a. EAN规则:中心体的电子数加上配体提供给中心体的电子数等于某一稀有气体的电子构型( 36, 54,86)+配体提供的电子数=18, (n 1)d10nEnp6b.十八电子规则:中心体的价电子数c .九轨道规则:五个 (n 1)d 轨道(或者五个nd 轨道),1个ns 轨道和3个np 轨道(9个价轨道)都充满电子。
配合物结构-晶体分子

14000
13600
[MoCl6]319200
● 配位体的影响:光谱化学序列 (ectrochemical series)
o /cm-1
[CoF6]313000
[Co(H2O)6]3+ [Co(NH3)6]3+ [Co(CN)6]3-
18600
22900
34000
各种配பைடு நூலகம்对同一M产生的晶体场分裂能的值由小到大的顺序:
Et2=1.78Dq,
Ee=-2.67Dq
E = 12.28 Dq
d x 2 y2
d E = 6 Dq
能
E = 1.78 Dq
量
d
E = 0 Dq
= 4.45 Dq
= 10 Dq
d
E = -2.67 Dq
E = -4 Dq
四面体场
d
八面体场
E = 2.28 Dq d xy s = 17.42Dq
dx2-y2 极大值指向面心
dxy
c
极大值指向棱的中点
x y
d 轨道在四面体场中的能级分裂
能级计算:
Es
1.78Dq 2.67Dq
t2 (dxy, dyz, dxz)
t=
4
9
10Dq
e(dx2-y2, dz2)
自由离子 球形场 四面体场
配体相同,中心离子与配体距离相同时,分裂 能Δt=4/9Δo
μ 0
4d
Ag
4d
[Ag(NH 3 ) 2 ]
5s
5p
sp 5p
[
]
NH3 NH3
四 配
1s Be 2
位 的
1s [BeX 4 ]2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d电子在不同场强度的排布
八面体场d轨道中电子的排布
Δ <P(弱场)时,按高自旋排布; Δ >P(强场)时,按低自旋排布。
d电子 数目 弱场(Δo<P) t2g eg
↑
↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑↓ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑
强场(Δo>P) t2g eg
↑
↑ ↑ ↑ ↑ ↑ ↑
4. 配合物的化学键理论
配合物的化学键理论
• 目标:解释性质,如配位数、几何结构、 磁学性质、光谱、热力学稳定性、动力学 反应性等。 • • • • 三种理论: ①价键理论 ②晶体场理论 ③分子轨道理论
4.2.1 价键理论 (valence bond theory) 同一原子内,轨道的杂化和不同原子间轨道的重叠构成了
d轨道能级分裂(单电子能级的分裂) 由于d轨道空间取向不同,与配体所形 成的非球形对称静电场的作用则不相同, 引起d轨道能级发生分裂。 分裂样式与配体所形成的非球形对称 静电场有关。
正八面体场中d轨道的分裂
d轨道与电 场的作用
x
z
y
x
y
y
z
x
z
x
y
正八面体场中d轨道的分裂
能级计算:
6Dq 4Dq Es eg(dx2_y2 , d z2)
CFSE - 4 Dq - 8 Dq - 12 Dq - 6 Dq - 20 Dq - 24 Dq - 18 Dq - 12 Dq - 6 Dq 0 Dq
• 值得注意的是,分裂能仅占配合物总结合 能的5~10% ,但它却是晶体场理论的核心。
• Ti(H2O)63+的水合热 △hH=4184KJ/mol, • 而 △o = 251.04KJ/mol
共价键理论的核心论点之一.这里把第二章的s-p杂化轨道扩大
到d轨道上,形成s-p-d杂化轨道.
(1) 价键理论的要点 ● 形成体(M)有空轨道,配位体(L)有孤对电子,形成配位键 ML ● 形成体(中心离子)采用杂化轨道成键 ● 杂化方式与空间构型有关
二配位的配合物
[Ag(NH3 ) 2 ]
Ag
● 中心M离子:电荷Z增大, o增大;主量子数n增大, o增大 [Cr (H2O)6]3+ [Cr (H2O)6]2+ [CrCl6]3[MoCl6]3-
o /cm-1
17600
14000
13600
19200
● 配位体的影响:光谱化学序列 (ectrochemical series)
o /cm-1
d 轨道在八面体场中的能级分裂
正四面体场中d轨道能级的分裂
d轨道与电场的作用 z
b a y
b a y d c z
z b a y d c
x
y c
d
极大值指向面心
dx2-y2
dxy 极大值指向棱的中点
x y
d 轨道在四面体场中的能级分裂
能级计算:
t2 (dxy, d yz, dxz)
1.78 Dq 2.67Dq t
4.2 晶体场理论(Crystal field theory)
由Bethe和Van Vleck提出 • 要点: ① 把配体视为点电荷或偶极子(不考虑其结 构); ② 配体与中心离子间的作用是纯静电相互作 用,不形成任何共价键。
贝蒂(Hans Albrecht Bethe,美国物理学家,曾 获1967诺贝尔物理学奖) 约翰· 哈斯布鲁克· 范弗累克,著名的美国理论物理学家,1977年 诺贝尔物理学奖的获得者
FG24_024.JPG
色环
[Ti(H2O)6]3+的吸收光谱图
例
由[Ti(H2O)6]3+的吸收光谱图分析 计算配合物的晶体场稳定化能.
配合物为八面体,由图可知 o 等于
20300cm-1,Ti3+为d1 组态离子,唯一的
20301d 电子添入三条 t2g 轨道之一, 因而,CFSE = 1x(-0.4 o)= - 8120 cm-1
o = 10 Dq
t2g(dxy,dyz,dxz)
自由离子 d轨道
球形场
八面体场
分裂能Δo=Eeg-Et2g =10Dq (1) 根据能量重心原理: 2Eeg+3Et2g=5Es Eeg=6Dq 若取Es为能量零点,则 2Eeg+3Et2g=0 (2) Et2g=-4Dq 解得
(2) 配体对中心离子的影响(d轨道的分裂)
轨道ns,np,nd进行杂化生成能量相同,数目相等的杂化轨道与配
体结合
[Fe(CN)6]3- 外轨配合物 内轨配合物 配位原子的电负性较小,如氰基(CN-,以C配 位),氮(-NO2,以N配位),较易给出孤电子对,对中心离子的影响较大,使电 子层结构发生变化,(n-1)d 轨道上的成单电子被强行配对,腾出内层能 量较低的 d 轨道接受配位体的孤电子对,形成配合物.
● 影响CFSE的因素
▲ d 电子数目
▲ 配位体的强弱
▲ 晶体场的类型
八面体场的 CFSE
dn 构型 d1 d2 d3 d4 d5 d6 d7 d8 d9 d 10
1 t 2g 2 t 2g 3 t 2g 3 1 t 2g eg 3 2 t 2g eg 4 2 t 2g eg 5 2 t 2g eg 6 2 t 2g eg 6 3 t 2g eg 6 4 t 3g eg
弱
场
强
场
CFSE - 4 Dq - 8 Dq - 12 Dq - 6 Dq 0 Dq - 4 Dq - 8 Dq - 12 Dq - 6 Dq 0 Dq
构型
1 t 2g 2 t 2g 3 t 2g 4 t 2g 5 t 2g 6 t 2g 6 1 t 2g eg 6 2 t 2g eg 6 3 t 2g eg 6 4 t 2g eg
直线形
μ 0
4d 4d [
5s sp ]
NH3 NH3
5p 5p
[Ag(NH3 ) 2 ]
四 配 位 的 配 合 物
1s
2s 2s
2p 2p
Be 2
[BeX4 ]
2
1s
F(H 2 O)
F-
F-
F-
(H 2 O) (H 2 O) (H 2 O)
3d
sp3杂化 4s 4s
5p 4p
Ni 2
乘以换算因子1 kJmol-1/83.6 cm-1
得 CFSE = -97.1 kJ mol-1
配合物颜色与晶体场
图中连接圆圈的棕色曲线示出下述反
应水合焓的变化趋势. 试用晶体场稳定化 能解释水合焓的这种变化趋势.
M 2 (g ) 6H 2 O MH 2 O 6 (aq)
d E = 6 Dq E = 0 Dq = 10 Dq E = 2.28 Dq d xy
s = 17.42Dq
E = -4..28 Dq d 2
z
E = -4 Dq
d
四面体场
八面体场
E = -5.14 Dq
d xz d yz
正方形场
不同晶体场中的相对大小示意图
(3) 影响的因素(中心离子, 配位体, 晶体场)
弱
场
强
场
CFSE - 4 Dq - 8 Dq - 12 Dq - 6 Dq 0 Dq - 4 Dq - 8 Dq - 12 Dq - 6 Dq 0 Dq
= 4 9
10Dq
Es
e(dx2-y2, dz2)
自由离子 球形场
四面体场
配体相同,中心离子与配体距离相同时,分裂 能Δt=4/9Δo
Et2=1.78Dq, Ee=-2.67Dq
E = 12.28 Dq
d
x y2
2
能 量
E = 1.78 Dq d
= 4.45 Dq d E = -2.67 Dq
-
内轨配合物比外轨配合物稳定
(2) 配合物的磁性
配合物磁性的测定是判断配合物结构的一个重要手段. 磁 矩: µ =[n(n+2)]1/2 (B.M.)玻尔磁子.
外轨型配合物
3d 4s 4p 4d
sp3d2
内轨型配合物
3d 4s 4p
d2sp3
价键理论的成功与不足
1)成功 ① 杂化轨道 配位数、构型 ② 内、外轨型配合物 磁性 ③ 继承了传统的价键概念(配位共价键),简明易 于理解。 2)不足 ① 定量程度差,无法解释配合物的吸收光谱 ② 无法说明Cu2+平面正方形内轨型配合物的稳定 性
(6) 晶体场理论的应用
晶体场理论和前面讲的价键理论同样可以依据配合物中电子的自旋状 态解释配合物的磁性. 同时也能从配合物的空间结构解释其稳定性. 下面举例说明晶体场理论是如何解释配合物的颜色和离子水合热变化 规律. ● 配合物离子的颜色
▲ 所吸收光子的频率与分裂能大小有关 ▲ 颜色的深浅与跃迁电子数目有关 ▲ 此类跃迁为自旋禁阻跃迁, 因此配离 子颜色均较浅
成对能:P
当电子在分裂后的d轨道排列时,与简并的d轨道 排列方式存在差异。 差异影响配合物的性质。
eg
(2) d4、 d5、d6、d7有两种不同的排法,自旋态不一样
eg
Weak field P> △
小 大 t 2g field P <△ Strong t
high-spin,paramagnetism low-spin , inverse magnetism 2g or weak give the maximum number of magnetism, give minimum number of unpaired electron 八面体配合物的中心离子的 unpaired electron
