幂的运算复习导学案
幂的有关运算复习导学稿

数学学科导学案课题 幂的有关运算 课型 复习课 备课组 七年级数学备课组 主备人 备课时间 2011.6 总课时 1课时 复习目标1、巩固同底数幂乘除法及幂的乘方、积的乘方的运算性质的同时,回顾运算性质的文字叙述。
2、正确灵活的运用以上运算性质的推广与逆用。
3、能够利用所学知识解决实际问题。
复习重点:幂的有关运算的运算性质及其语言叙述 复习难点:各个运算性质的灵活运用一、 复习导学,解下列各题,并从解题过程的每一个步骤中去体会其中运用了哪些知识点。
例: 9824)(a a a aa =⋅=⋅ 幂的乘方1、 =⋅44x x2、=⋅⋅x x x 343、=+3443)()(a a4、=3)2(ab5、=÷734x x )( 6、=+202-3--21)()(π同底数幂的乘法三、误区警示,判断下列计算是否正确,并说明理由:1、532m m m m =⋅⋅2、3322x x -=-)( 3、532a a a =+ 4、623)(xy xy =5、2224)(c b bc bc -=-÷-)(6、126324316)(2x x x x =÷÷-)(四、典例精析1、(2009,丽水中考)23a a ⋅=( )A 5aB 6aC 8aD 9a 2、(2010,四川省成都市)3x 表示( )A 3xB x x x ++C x x x ⋅⋅D 3x + 3、在下列各式中的括号内填入3a 的是( )A 212) (=aB 312) (=aC 412) (=aD 612) (=a4、(2009,临沂中考)下列各式计算正确的是( )A 34x x x +=B 2510x x x ⋅=C 428()x x =D 632)-(x x = 5、(2010,甘肃省天水市)下列计算正确的是( )A 3-2-10=B 224()mn mn =C 623)-3(x x =D 1064m m m ÷= 6、(2011,辽宁朝阳)计算=-233)(3ab b a )( 7、已知23x =,求32x +的值。
华东师大版八年级数学上册12.1幂的运算(复习)导学案(无答案)

南城中学八年级数学导学案班级:编制:八年级数学备课组课题: 12.幂的运算(复习)课时:第课时学习目标:1.理解同底数幂的乘法,幂的乘方,积的乘方,幂的除法,并能够正确的运用.2.学生在已有的知识基础上,自主探索,获得幂的运算的各种感性认识,进而在理性上获得运算法则.3.培养良好的数学构建思想和辨析能力和一定的思维批判性.重点: 理解4个运算法则.难点: 正确使用4个幂的运算法则.预习案一、复习回顾⑴叙述幂的运算法则?(4个)⑵谈谈这4个幂运算的联系与区别?二、回顾教材P18~ P24⑴下列计算是否有错,错在那里?请改正.①(xy)2=xy2②(3xy)2=12x4y4③(-7x3)3=49x6④(-72x)3=-3432x3⑤x5·x4=x20⑥(x3)2=x5⑵计算:(x3y2)2·(x3y2)3⑶计算:-x2·(-x)2·(-x2)3-2x10(请填充运算依据)解:原式=-x2·x2·(-x6)-2x10()=x2+2+6-2x10()=x10-2x10()=-x10()我的疑惑:探究案一、展示预习案二、课堂探究⑴计算:①x3·x n+3;②(-45x2y)3;③ (-ab3c2)2n;④(-3x2)2-[(2x)2]3; ⑤(-a)5÷a⑵下列各式中错误的是()A.-x2·x=x3B.(-x3)2=x6C.m5·m5=m10D.(-p)2 ·p=p3⑶(-12x2y)3的计算结果是()姓名:A .-12x 6y 3B . -16x 6y 3C . -18x 6y 3D . 18x 6y 3⑷若x m -1·x m +1=x 8,则m 的值为( )A .4B .2C .8D .10B 组⒈计算:⑴a ·a 2·a 3·a 4 ⑵(-x )6·(-x )5·(-x )2 ⑶-[(-a )2]3⑷[(-3xy 2)2]3 ⑸-14[-x 2·(-x 3)] ⑹(2x +1)3·(2x +1)4⑺x 10÷(x 2)4 ⑻(x -y )3÷(y -x )2 ⑼a 4-a 4·(-a 2)3÷a 6⒉一个正方形的边长增加了3厘米,它的面积就增加39平方厘米,求这个正方形的边长?⒊阅读题:已知:2m =5 求:23m 和23+m 的值.解:23m =(2m )3=53=12523+m =___________仿照上面,已知:3n =7 求:34n ,34+n 和3n -3的值.4.找简便方法计算:⑴2100×(0.5)101 ⑵22×3×52 ⑶24×32×545.⑴已知:a m =2,b n =3,求:a 2m +b 3n 的值;⑵已知:a 2m =2,a 3n =3,求:a 6m -9n 的值;6.观察下列计算过程,并完成以下问题:∵23÷25=2325=2323×22=122,a 2÷a 7=a 2a 7 =a 2a 2·a 5 =1a 5(a ≠0), 而依照幂的运算:23÷25=23-5=2-2;a 2÷a 7=a 2-7=a -5∴2-2=122,a -5=1a 5(a ≠0).由此可归纳出的规律是: a -p =_______(a ≠0,p 为正整数).运用上述规律计算:⑴3-3=_____;⑵1×10-2=________;⑶把0.000 032写成a ×10n 形式_________; ⑷计算:x 2·x 4÷x 7(x ≠0)。
幂的运算复习教案

幂的运算复习教案一、教学目标1.知识目标:复习幂的概念和运算方法,包括幂的乘法、幂的除法、幂的乘方和幂的负指数。
2.能力目标:能够灵活运用幂的运算法则进行计算,并能解决与幂相关的实际问题。
3.情感目标:培养学生对数学的兴趣和好奇心,促进学生的思维发展和逻辑思维能力。
二、教学重点1.幂的乘法运算和除法运算。
2.幂的乘方运算。
三、教学难点1.幂的负指数,并结合实际问题进行思考和解答。
2.将实际问题转化为幂的运算。
四、教学过程1.复习幂的概念和符号表示。
通过问答和示范板书复习幂的概念和符号表示,引导学生回顾相关知识点。
2.幂的乘法运算和除法运算2.1幂的乘法运算通过例题展示幂的乘法运算法则,引导学生进行讨论和总结,确保学生理解该法则。
例题1:计算并化简:2²×2³。
例题2:计算并化简:(3×10⁴)×(4×10²)。
2.2幂的除法运算通过例题展示幂的除法运算法则,引导学生进行讨论和总结,确保学生理解该法则。
例题3:计算并化简:16⁴÷16²。
例题4:计算并化简:(2²×3³)÷(2³×3²)。
3.幂的乘方运算3.1幂的乘方法则通过例题展示幂的乘方运算法则,引导学生进行讨论和总结,确保学生理解该法则。
例题5:计算并化简:(5⁴)²。
例题6:计算并化简:(10⁵)⁴。
3.2幂的乘方与乘法的关系通过例题展示幂的乘方与乘法的关系,引导学生进行讨论,确保学生理解该关系。
例题7:计算并化简:3⁴×3⁵。
例题8:计算并化简:5⁸÷5³。
4.幂的负指数通过例题展示幂的负指数运算法则,引导学生进行讨论和总结,确保学生理解该法则。
例题9:计算并化简:2⁻³。
例题10:计算并化简:(5⁻²)²。
5.综合练习通过一些综合性的练习题,引导学生运用所学知识解决实际问题。
14幂的运算导学案

14.1.1同底数幂的乘法学习目标:正确计算同底数幂的乘法。
学习过程:一、复习引入23表示 结果是: 32 表示 结果是: 5a 表示 m a 表示在m a 中,a 叫做 m 叫做 m a 叫做二、自主学习1.请同学们通过计算探索规律(1)32×42=(2×2×2)×(2×2×2×2)=2×2×2×2×2×2×2=()2(2)35⨯45)(5= (3)7)3(-⨯6)3(-())(3-= (4)3a ⨯4a =()a 2.观察:(1)这几道题目有什么共同特点? (2)请同学们看一看自己的计算结果,想一想这个结果有什么规律 3. 推算一下m a ⨯na =4.由以上计算过程得出同底数幂的乘法法则:同底数幂相乘,底数 ,指数三、自学检测1.填空 ①310⨯410= ②3a a ⋅= ③53a a a ⋅⋅= ④57x x ⋅=⑤532333⋅⋅= ⑥ y y y y ⋅⋅⋅425 = ⑦11010+⋅m n = 2.判断正误(1)5552b b b =⨯ ( ) (2)655b b b =+ ( )(3)2555b b b =⨯ ( ) (4)65b b b =∙ ( )(5)5552a a a =∙ ( ) (6)523m n m =∙ ( )3.计算① 4444⨯- ②x x x x ⋅+⋅22 ③()3922-⨯ ④12222+⨯n n ⑤()()43y x y x ++ ⑥()()()3645p p p p ⋅-+-⋅- ⑦()()()x y y x y x ---234.已知9x x xn m n m =⋅-+求m 的值.14.1.2幂的乘方学习目标:正确计算幂的乘方学习过程:一、复习引入同底数幂的乘法法则:=⨯32a a =⨯n m 1010 =⋅⋅32a a a二、自主学习1. 请同学们通过计算探索规律①=23)3((把33看做整体)3333⨯=②=34)2( × × =③=3)(m a × × =2.由以上计算过程可以得出=n m a )( 幂的乘方的计算法则:幂的乘方,底数 指数 三、自学检测1.计算())(2223= ())(x x =54 ())(223100=()3510 ()3n x ()77x - 2.判断①()633x x=( ) ②2446a a a =⋅( ) 3.计算:①()47p ;②()732x x ⋅ ;③()()4334a a - ④ n 10101057⋅⋅ ;⑤()[]32b a - ⑥()[]622-4.已知168123=⎪⎭⎫ ⎝⎛n 则n = 5.已知:a m =3 ;b n =3 ,用a ,b 表示n m +3和n m 323+14.1.3积的乘方学习目标:正确计算积的乘方学习过程一、复习引入m a ⨯n a = =n m a )(二、自主学习1.观察下面计算过程,探索计算规律①22222)()()()()(b a b a b b a a ab ab ab =∙=∙∙∙=∙=2.按照上面的计算过程,完成下面各题②)()()(2222ab ab ab ∙== =③=3)(xyz ④ =43)2(a3.由以上计算过程可以得出 =n ab )(积的乘方法则:积的乘方,等于把积的每一个因式分别 ,再把所得的幂三、自学检测1.计算①()32b ②()232a ③()43x - ④332)5(c b a - ⑤33221⎪⎭⎫ ⎝⎛y x ⑥()33n - ⑦()a a a 234-+-2.计算 ①20082008)20091()2009(⨯ ②555)31()32()9(⨯-⨯- ③()()20092008425.0-⨯-3. ①已知 m a =5, n a =3. 求 n m a 32+ 的值。
幂的运算巩固练习导学案

幂的运算巩固练习导学案时间: 班级: 教师: 指导: 教学目标:知识与技能目标:使学生对同底数幂的乘法、幂的乘方、积的乘方有一个正确的理解,注意它们的区别。
过程与分析目标:经历自主、合作探索、获得幂的运算的各种感性的认识,百而在理性上获得运算法则。
情感与态度目标:培养学生主动建构、辩析是非的能力,同时形成一定的思维批判性。
教学重点:教学中应把这三个运算法则探索过程作为重点。
教学难点:正确使用这三个幂的运算法则。
教学关键:对三个幂的运算法则的理解和区分。
教学过程:一、回顾1、 口述幂的三个运算法则:2、 这三个幂的运算法则有什么联系和区别?二、参与其中,主动探究例1:计算-2x ·()2x -·()32x --210x例2:下列计算错在哪里?并加以改正:(1)()2xy =x 2y (2) ()43xy =1244y x(3) ()237x-=-492x (4) 327⎪⎭⎫ ⎝⎛-x =-2243-3x(5) 45x x ∙=20x (6) ()523x x =例3 计算()()323223y x y x ∙ 解法一:()()323223y x y x ∙ 解法二:()()323223y x y x ∙=6946y x y x ∙ =()3223+y x=6496++y x =()532y x=1015y x =1015y x三、随堂练习计算:1、33+∙n x x2、n 32·133+n3、()n ma 2- 4、()[]32a -5、3245⎪⎭⎫ ⎝⎛-y x6、()n c ab 232-7、()[]()[]()n n n y x y x y x 532-+-∙-四 、全课小结正确理解和掌握幂的运算法则,熟练掌握计算方法,注意观察算式的特征。
五、作业布置:课时作业优化设计。
六、课后反思:1. 。
2. 。
第八章:幂的运算全章复习教案 2020—2021学年苏科版数学七年级下册

一对一辅导教案
学生姓名 性别 年级 学科 授课教师
上课时间 年 月 日
第( )次课 共( )次课
课时: 课时
教学课题
幂的运算复习
教学目标 1. 幂的运算性质的正确应用
2. 逆用法则进行计算 3. 混合运算
教学重点与难点
重点:
教学过程: 【知识梳理】
1、同底数幂的乘法法则 n m n m a a a +=⨯(m 、n 是正整数)
2、幂的乘方法则
()m n
n
m a a =(m 、n 是正整数)
3、积的乘方法则
()n n n
b a ab =(n 是正整数)
4、同底数幂的除法法则 n
m n m a a a -= (m 、n 是正整数,m >n )
5、推广
()np mp p
n m
b a b a
= (m 、n 、p 是正整数)
6、零指数和负指数法则=0a 1
()0≠a
=
-n a n
a 1
(0≠a ,n 是正整数)
7、科学记数法 n
a N 10⨯=(1≤a <10,n 为整数) 数零法
3
5
a a = C. 的是( )3
a C. (-()
2
x -,结果正确的是( B. 6
x C. 、下列各式中,正确的个数有:(8x ②x 12
a
()4
42a a +()2
2a - ()()
3
2
2a a a --
1001
1000
35⎛⎫⨯- ⎪⎝⎭
70
110
127⎛⎫⨯ ⎪⎝⎭
9y
的值; 8y
的值。
幂函数复习导学案(珍藏版)
2.3幂函数复习导学案(珍藏版)一.学习目标:(1)了解幂函数概念。
(2)会画常见幂函数的图象。
(3)结合图象了解幂函数图象的变化情况和简单性质。
(4)会用幂函数的单调性比较两个底数不同而指数相同的幂的大小。
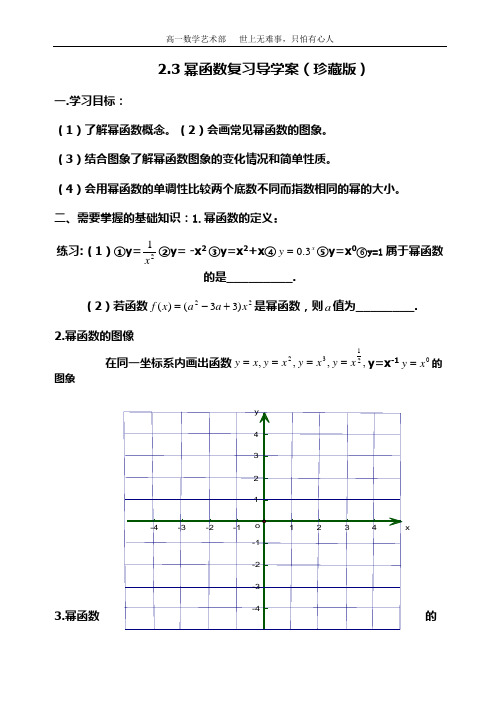
二、需要掌握的基础知识:1.幂函数的定义: 练习:(1)①y=21x②y= -x 2 ③y=x 2+x ④xy 3.0=⑤y=x 0⑥y=1属于幂函数的是_________.(2)若函数22)33()(x a a x f +-=是幂函数,则a 值为________. 2.幂函数的图像在同一坐标系内画出函数,,,,2132x y x y x y x y ====y=x -10x y =的图象3.幂函数的x性质:①所有幂函数在_________都有定义,并且图像都过点________; ②0a >时,幂函数的图像通过_________,并且在区间[)0,+∞上是_________,特别的,当1a >时,幂函数的图像________,当01a <<时,幂函数的图像________。
③0a <时,幂函数的图像在区间()0,+∞上是_________,在第一象限内,当x 从右边趋向原点时,图像在y 轴右方无限地逼近y 轴正半轴,当x 趋向+∞时,图像在x 轴上方无限地逼近x 轴正半轴。
(4)幂函数y x α=的图象,在第一象限内,直线1x =的右侧,图象由下至上,指数 . y 轴和直线1x =之间,图象由上至下,指数α函数,,,,2132x y x y x y x y ====x y =-1的性质4.性质的应用.),0[)(1上是增函数在、证明幂函数+∞=x x f2.比较下列各组中值的大小,并说明理由:(1)1.10.5,1.40.5 (2) (-π)-1, (-3.14)-1 (3)1.40.5,1.433、下列函数中不是幂函数的是 ( )A. B. C. y=2x D.y=x -14、幂函数的如图所示,曲线是幂函数αx y =在第一象限内的图象,已知α分别取2,21,1,1-四个值,则相应图象依次为:________________ 5、幂图像过点,则它的单调递增区间是( )A[)1,-+∞B[)0,+∞C(),-∞+∞D(),0-∞6.若幂函数y=f(x)的图像经过点()9,3,则f(25)=______________7.比较下列各组数的大小:(1)0.7521_____0.7621 (2)(-3.14)2_____2π (3)4.06.03.0___2.0(4)3232)6_____()32(----π8. 幂函数y=(m 2-m-1)x m 在区间()+∞,0上是减函数,则 m 的值为________。
七年级数学下册6.2.2幂的运算导学案新版北京课改版word版本

6.2.2幂的运算预习案一、学习目标1、掌握幂的乘方的运算法则.2、通过“幂的乘方的运算法则”的推导和应用,•使学生初步理解特殊到般再到特殊的认知规律.3、能灵活运用幂的乘方的运算法则解决一些实际问题.二、预习内容范围:自学课本P68-P69,完成练习.三、预习检测计算:(1) (103)5;(2) (a4)4;(3) (a m)2; (4) -(x4)3.解:探究案一、合作探究(10分钟)探究要点幂的乘方的运算法则.实践:计算:(103)2=______________.(52)4=________________.(a2)3=______________.猜想:(a m)n=_______.实际上,根据幂的意义和同底数幂乘法的运算性质,有这就是说,幂的乘方,底数_______,指数_______. 幂的乘方的运算性质:(a m)n =a mn(m,n都是正整数).(此公式可以逆用)典例:例、计算:(1)(105)2;(2)(x5)6;(3)(x2)10;(4)(y2)3·y.跟踪训练:计算:(1) (104)3; (2) (b4)5;(3) (a2)n; (4) -(y3)3.归纳:二、小组展示(10分钟)每小组口头或利用投影仪展示一道题, 一个小组展示时,其他组要积极思考,勇于挑错,谁挑出错误或提出有价值的疑问,给谁的小组加分(或奖星)三、归纳总结本节的知识点:1、幂的乘方的运算法则.2、灵活运用幂的乘方的运算法则解决一些实际问题.四、课堂达标检测1、下列各式对吗?请说出你的观点和理由:(1) (a4)3=a7 ( ) (2) a4 a3=a12 ( )(3)(a2)3+(a3)2=(a6)2 ( ) (4) (-x3)2=(-x2)3 ( )2、若x5·(x m)3=x11,则m=____.3、已知64×83=2x,则x=____.4、已知3x=9y+1,27y=3x-1,则x-y的值为____.5、已知a2n=3.求:a4n-9;解:6、已知2x+5y-3=0,求4x·32y的值.解:五、学习反馈通过本节课的学习你收获了什么?参考答案预习检测解:(1) (103)5 =103×5=1015;(2) (a4)4 =a4×4=a16;(3) (a m)2 =a m×2=a2m;(4) -(x4)3 =-x4×3=-x12.课堂达标检测1、(1)× (2)× (3)× (4)×2、23、154、35、解:a2n=3,∴a4n-9=(a2n)2-9=9-9=0.6、解:4x·32y=22x·25y=22x+5y=23=8.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
龙文教育学科导学案教师: 学生: 年级 七年级 日期: 星期: 时段: 学情分析课 题幂的运算复习课 学习目标与考点分析 学习目标 1. 能说出同底数幂的乘(除)法、幂的乘方、积的乘方运算性质;2.了解零指数幂和负整数指数幂的意义,并能用科学记数法表示绝对值小于1的数;3.会运用幂的运算性质熟练进行计算;4.通过具体的例子体会本章学习中体现的从具体到抽象、从特殊到一般的思考问题的方法,渗透转化、化归等思想方法,发展合情推理能力和演绎推理能力.考点分析:主要考查幂的运算性质的应用学习重点 运用幂的运算性质进行计算.学习方法转化、化归、合情推理、演绎推理 学习内容与过程一. 梳理知识:①同底数幂的乘法 文字叙述: ;字母表示: . ②幂的乘方法则 文字叙述: ;字母表示: . ③积的乘方 文字叙述: ;字母表示: . ④同底数幂的除法 文字叙述: ;字母表示: . ⑤零指数幂的规定 字母表示: .⑥负整指数幂的规定 字母表示: .二.误区警示,排忧解难.例1.下面的计算,对不对,如不对,错在哪里?(1) 2)(a -=-a 2; (2)(x-y)3=(y-x)3;(3)(a-b)2=-(b-a)2; (4) (0.5-21)0=1; (5)(-2x)3=2x 3;例2.已知m 10=4,n 10=5,求n m 2310+的值例3若x =2m +1,y =3+4m,则用x 的代数式表示y 为______.例4、试比较355,444,533的大小.例5 1993+9319的个位数字是( )A .2B .4C .6D .8四、探究性学习:在一次水灾中,大约有2.5×105个人无家可归,假如你负责这些灾民,而你的首要工作就是要将他们安置好。
(1) 假如一顶帐篷占地100m 2,可以安置40个床位,为了安置所有无家可归的人,需要多少顶帐篷?(2) 请计算一下这些帐篷大约要占多少地方?(3) 估计一下,你学校操场可以安置多少人?要安置这些人,大约需要多少个这样的操场?五.方法指引,融会贯通.1.你知道下列各式错在哪里吗?在横线填上正确的答案:(1)a 3+a 3=a 6;________ (2)a 3·a 2=a 6;_________ (3)(x 4)4=x 8;________(4)(2a 2)3=6a 6;_________ (5)(3x 2y 3)2=9x 4y 5;________(6)(-x 2)3=x 6;_________(7)(-a 6) (-a 2)2=a 8;___ _ (8)(32a )2=92a 2;_________ (9)-2-2=4;_________ 1.知识练习:★基础题 计算: (1)x 3·x ·x 2 (2)(a m -1)3 (3)[(x +y )4]5 (4)(-12a 5b 2)3(5)(-2x )6÷(-2x )3 (6)(-3a 3)2÷a 2 (7)(-12) 2 ÷(-2) 3 ÷(-2) -2 ÷(π-2005) 0★提高题 计算:(1)(-x )3·x ·(-x )2 (2)(-x )8÷x 5+(-2x )·(-x )2(3) y 2y n -1+y 3y n -2-2y 5y n -4(4)计算:(-22)3+22×24+(1125)0+||-5-(17)-1★ 拓展题 计算:(1)(m -n )9· (n -m )8÷(m -n )2 (2)(x +y -z )3n ·(z -x -y )2n ·(x -z +y )5n2.逆向思维训练:(1)计算: A (-2)2010+ (-2) 2009 B (-0.25)2010×42009(2)已知:4m = a , 8n = b 求: ① 22m+3n 的值; ② 24m -6n 的值.课内练习与训练一.填空:1.―y 2· y 5= ; (-2 a ) 3 ÷a -2= ; 2×2m +1÷2m = .2. a 12=( )2=( )3=( )4 ; 若x 2n =2,则x 6n = .3. 若a =355,b =444,c =533,请用“<”连接a 、b 、c .4. 把-2360000用科学计数法表示 ;1纳米 = 0.000000001 m ,则2.5纳米用科学记数法表示为 m .二.选择:1. 若a m =3,a n =2,则a m +n 的值等于 ( )A .5B .6C .8D .92. -x n 与(-x )n 的正确关系是 ( )A .相等B .当n 为奇数时它们互为相反数,当n 为偶数时相等C .互为相反数D .当n 为奇数时相等,当n 为偶数时互为相反数3.如果a =(-99)0,b =(-0.1)-1,c =(-53)-2, 那么a 、b 、c 三数的大小为 ( ) A . a >b >c B . c >a >b C . a >c >b D . c >b >a三.计算:(1)(-a 3)2 · (-a 2)3 (2) -t 3·(-t )4·(-t )5 (3) (p -q )4÷(q -p )3 · (p -q )2(4)(-3a )3-(-a ) · (-3a )2 (5)4-(-2)-2-32÷(3.14—π)0四.解答:1.已知a x =3,a y =2,分别求①a 2x +3y 的值 ②a 3x -2y 的值2.已知 3×9m ×27m =316,求m 的值.3.已知 x 3=m ,x 5=n 用含有m 、n 的代数式表示x 14.思维体操:已知P =999999,Q =119990,试说明P =Q课外练习:一.填空题1.计算:(1)()=-42x (2)()=32y x (3)()()=-∙342a a (4)()()=-÷-a a 4 2.填上适当的指数: (1)()54a aa =∙ (2)()45a a a =÷ (3)()()84aa = (4)()()()333b a ab ab =÷ 3.填上适当的代数式: (1)()843x x x =∙∙ (2)()612a a =÷ (3) ()()()345-=-∙-y x y x4. 计算:(1) ()=÷44ab ab . (2) =÷+22x x n(3) 83a a a a m =∙∙,则m= (4)(7104⨯)()5102⨯÷= 5.用小数表示=⨯-41014.36.一种细菌的半径是00003.0厘米,用科学计数法表示为 厘米二.选择题1.下列各式中,正确的是( )A .844m m m = B.25552m m m =C.933m m m =D.66y y 122y = 2. 下列各式中错误的是( )A.()[]()623y x y x -=-B.(22a -)4=816aC.363227131n m n m -=⎪⎭⎫ ⎝⎛-D.()=-33ab -b a 363.下列各式(1) 523743x x x =∙; (2) 933632x x x =∙ (3) (5x )72x = (4) (3xy)3=933y x ,其中计算正确的有 ( )A.0个B.1个C.2个D.3个4.下列各式(1)55b b ∙52b = (2) (-2a 2)2=4-4a (3) (1-n a )3=13-n a (4) 963321256454y x y x =⎪⎭⎫ ⎝⎛, 其中计算错误的有 ( )A.1个B.2个C.3个D.4个5.下列4个算式(1)()()-=-÷-24c c 2c (2) ()y -()246y y -=-÷ (3)303z z z =÷ (4)44a a a m m =÷ 其中,计算错误的有 ( )A.4个B.3个C.2个D.1个6.()21--k x 等于 ( ) A.12--k x B.22--k x C.22-k x D.12-k x7.已知n 是大于1的自然数,则()c -1-n ()1+-∙n c 等于 ( ) A. ()12--n c B.nc 2- C.c-n 2 D.n c 2 8.计算()734x x ∙的结果是 ( )A. 12xB. 14xC. x 19D.84x 9.下列等式正确的是 ( )A.()532x x -=-B. 248x x x =÷C.3332x x x =+D.(xy )33xy =11.计算()+-03221-⎪⎭⎫ ⎝⎛-÷2-的结果是 ( ) A.1 B.-1 C.3 D.89 12.下列运算中与44a a ∙结果相同的是 ( )A.82a a ∙B.()2a 4C.()44aD.()()242a a ∙413.下列计算正确的是 ( )A.523a a a =∙B.aa a =÷33 C.()a a =325 D.(a 3)333a = 14.下列计算正确的是 ( )A.5322x x x =+B.632x x x =∙C.)(3x -62x -=D.x x x =÷36315.下列计算正确的是 ( )A .143341-=⨯÷- B.()121050=÷- C.52⨯2210= D.81912=⎪⎭⎫ ⎝⎛-- 三.解答题1.计算(1) (b a 2)()3ab ∙2 (2) ()m m x x x 232÷∙(3)323221⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛-z xy (4) ()()y x x y --2+3)(y x -+()x y y x -∙-2)(22.计算 (1()()2302559131-÷-+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-- (2)()10-053102)(-⨯⨯-2101012⨯⨯⎪⎭⎫ ⎝⎛-(3)()1132)(--∙÷∙n m n m x x x x (4)()a b - ()3a b -()5b a -3.计算(1)()m m a b b a 25)(--()m a b 7-÷ (m 为偶数,b a ≠)(2)()[]3m n -p ()[]5)(p n m n m --∙4.用简便方法计算(1)()5.1)32(2000⨯1999()19991-⨯ (2) )1(1699711111-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛11学生收获你这次课一定有不少收获吧,请写下来: 教学反思本次课后作业学生对于本次课的评价:○ 特别满意 ○ 满意 ○ 一般 ○ 差学生签字:教师评定:1、 学生上次作业评价: ○ 非常好 ○好 ○ 一般 ○ 需要优化2、 学生本次上课情况评价:○非常 好 ○好 ○ 一般 ○ 需要优化 教师签字:学科组长签字:。
