山东建筑大学机械控制课件第二章
合集下载
机械电气控制(第二章)ppt课件

精选PPT课件
10
精选PPT课件
11
三. 电器设备接线图
它是根据原理图,配合安装要求来绘制的, 用来表示各电器元件之间实际接线情况。
电器设备接线图为各电器元件的配线、检 修和施工提供了方便,实际工作时一般要与电 器控制原理图配合使用。
精选PPT课件
12
绘制电器设备接线图的主要规定:
⑴同一电器元件的各个部件应画在一起; ⑵不在同一控制柜或配电屏上的电器元件的电气连
精选PPT课件
6
2.控制线路的全部触点都要按“平常” (即未通电或未受外力作用时)状态绘出。
3. 同一电器元件的各部分分别绘在它
们完成作用的地方,但需用同一文字符号标
出。若有多个同一种类的电器元件,可在文 字符号的后面加上数字序号的下标,如KM1 、 KM2等。
精选PPT课件
7
4.对具有循环运动的机构,应给出工 作循环图,如行程开关等应绘出动作程序 和动作位置。
QF KM
M 3~
精选PPT课件
18
2. 过电流保护
对于直流电动机和绕线 式异步电动机的限流起动, 过流保护元件是过流继电器 KA,串联于主电路的隔离开 关QS与接触器KM的主触点之 间。KA的动作值一般定为1.2 倍的电动机起动电流。
精选PPT课件
19
3. 过载保护
当电动机长期超载运行时, 其绕组的温升将超 过允许值而损坏,所以应设过载保护环节,此保护 元件多采用热继电器。
热继电器具有反时限特性,但因热惯性的关系,热继 电器不会受短路电流的冲击而瞬时动作。例如当有8-10 倍的额定电流通过热继电器时,需经1-3秒的时间才能动 作,这样在热继电器动作前,就可能使热继电器的发热元 件先烧坏。所以在使用热继电器作过载保护时,还必须 将熔断器与热继电器配合使用。
机械控制工程(董玉红 第二版)—第二章 系统的数学模型

*
模型类型(与物理性能、分析、设计方法有关) 系统允许的误差条件(在允许的条件下尽可能取简单的模型形式)
Ui(S)
U0(S)
1/R
R1
CS
R2
I1(S)
I2(S)
I(S)
+
-
U0(S)
+
一、机械系统的 微分方程
1、机械平动系统 平动即直线运动,其主要元件为质量、弹簧、阻尼器。
(一)机械系统 机械系统分为平动系统和旋转系统,其数学模型的建立主要应用牛顿定理来列写。
数学模型:描述系统输入、输出变量以及内部各变 量之间关系的数学表达式。 数学模型的主要形式 :
引言
数学模型
微分方程
传递函数
频率特性
结构框图
信号流图
复域
时域
※
L
L-1
频域
*
主要解决的问题: 为什么要建立系统的数学模型 什么是数学模型 对系统数学模型的基本要求
*
为什么要建立控制系统的数学模型?
预备知识
电容两端电压为:
解:设电路中电流为 i(t)
整理得:
例2.3 无源电器网如图2-3所示, 为输入电压, 为输出电压,列写其关于输入输出微分方程模型。
图2-3
uo(t)
Ui(t)
C
L
R
机械系统(a)和电系统(b)具有相同的数学 模型,故这些物理系统为相似系统。(即电系 统为机械系统的等效网络) 物理本质不同的系统可有相似的数学模型,同 一数学模型可以描述不同的系统。 我们可以利用简单易实现的系统(如电的系统) 去模拟其它难于实现的系统(机械系统)......
机械控制工程基础
第二章 系统的数学模型
模型类型(与物理性能、分析、设计方法有关) 系统允许的误差条件(在允许的条件下尽可能取简单的模型形式)
Ui(S)
U0(S)
1/R
R1
CS
R2
I1(S)
I2(S)
I(S)
+
-
U0(S)
+
一、机械系统的 微分方程
1、机械平动系统 平动即直线运动,其主要元件为质量、弹簧、阻尼器。
(一)机械系统 机械系统分为平动系统和旋转系统,其数学模型的建立主要应用牛顿定理来列写。
数学模型:描述系统输入、输出变量以及内部各变 量之间关系的数学表达式。 数学模型的主要形式 :
引言
数学模型
微分方程
传递函数
频率特性
结构框图
信号流图
复域
时域
※
L
L-1
频域
*
主要解决的问题: 为什么要建立系统的数学模型 什么是数学模型 对系统数学模型的基本要求
*
为什么要建立控制系统的数学模型?
预备知识
电容两端电压为:
解:设电路中电流为 i(t)
整理得:
例2.3 无源电器网如图2-3所示, 为输入电压, 为输出电压,列写其关于输入输出微分方程模型。
图2-3
uo(t)
Ui(t)
C
L
R
机械系统(a)和电系统(b)具有相同的数学 模型,故这些物理系统为相似系统。(即电系 统为机械系统的等效网络) 物理本质不同的系统可有相似的数学模型,同 一数学模型可以描述不同的系统。 我们可以利用简单易实现的系统(如电的系统) 去模拟其它难于实现的系统(机械系统)......
机械控制工程基础
第二章 系统的数学模型
机械控制.pptx

H. Hazen
机械控制理论
第一章 绪 论
(5) 英国A. M. Turine提出图灵计算机的设想(1937) (6) 在贝尔实验室Bode领导的火炮控制系统研究小组工作的C. Shannon 提出继电器逻辑自动化理论(1938),随后,发表专著《通信的数字理论》 (The Mathematical Theory of Communication),奠定了信息论的基础
西汉漏壶
第一章 绪 论
(2) 亚历山大的希罗发明开闭庙门和分发圣水等自动装置(100年)
(3) 中国张衡发明水运浑象,研制出自动测量地震的候风地动仪(132年)
机械控制理论
机械控制理论
第一章 绪 论
(4) 中国马钧研制出用齿轮传动的自动指示方向的指南车(235年)
(5) 中国明代宋应星所著《天工开物》 记载有程序控制思想(CNC)的提花织 机结构图(1637年)
Lan J. Chu
(8) 美国W. Evans提出根轨迹法(Root Locus Method) (1948),以单 输入线性系统为对象的经典控制研究工作完成。
V. Bush
机械控制理论
第一章 绪 论
(4) 美国H.S. Black提出放大器性能的负反馈方法(Negative Feedback Amplifier) (1927)
H. S. Black
第一章 绪 论
(5) 自动控制的基础为闭环控制。控制论的奠基人N.Wiener 给出的定义为:
“Feedback is a method of controlling a system by inserting into it the result of its past performance”
机械控制理论
第一章 绪 论
(5) 英国A. M. Turine提出图灵计算机的设想(1937) (6) 在贝尔实验室Bode领导的火炮控制系统研究小组工作的C. Shannon 提出继电器逻辑自动化理论(1938),随后,发表专著《通信的数字理论》 (The Mathematical Theory of Communication),奠定了信息论的基础
西汉漏壶
第一章 绪 论
(2) 亚历山大的希罗发明开闭庙门和分发圣水等自动装置(100年)
(3) 中国张衡发明水运浑象,研制出自动测量地震的候风地动仪(132年)
机械控制理论
机械控制理论
第一章 绪 论
(4) 中国马钧研制出用齿轮传动的自动指示方向的指南车(235年)
(5) 中国明代宋应星所著《天工开物》 记载有程序控制思想(CNC)的提花织 机结构图(1637年)
Lan J. Chu
(8) 美国W. Evans提出根轨迹法(Root Locus Method) (1948),以单 输入线性系统为对象的经典控制研究工作完成。
V. Bush
机械控制理论
第一章 绪 论
(4) 美国H.S. Black提出放大器性能的负反馈方法(Negative Feedback Amplifier) (1927)
H. S. Black
第一章 绪 论
(5) 自动控制的基础为闭环控制。控制论的奠基人N.Wiener 给出的定义为:
“Feedback is a method of controlling a system by inserting into it the result of its past performance”
机械工程控制基础课件(第2章宋文强)

实部
虚部
复变函数的一般表示形式
若有复变函数
K ( s z1 )(s z 2 ) ( s z m ) G( s) ( s p1 )(s p2 ) ( s pn )
当s=z1,z2,……,zm时,G(s)=0,则称z1,z2,……,zm 为G(s)的零点
当s=p1,p2,……,pn时,G(s)=∞,则称p1,p2,……,pn 为G(s)的极点
L[e
at
的拉氏变换
sin t ]
( s a) 2 2
同理可求得
sa ( s a) 2 2 n! at n L[e t ] ( s a) n 1 L[e at cost ]
4. 微分定理
若时间函数f(t)的拉氏变换为F(s),且其一阶导数 f’(t)存在,则
f (t ) Me
at
式中,M,a均为实常数,这一个条件使拉氏变换的被 积函数的绝对值收敛
由于
f (t )e
所以
st
f (t ) e
st
f (t ) e
t
f (t )e st Me at e t Me ( a ) t
只要在复平面上对于Re(s)>a的所有复数s,都能 使前式的积分绝对收敛,则Re(s)>a为拉氏变换的 定义域,a称为收敛坐标
2. 实数域的位移定理(滞后定理)
若f(t)的拉氏变换为F(s),则对任意正实数a,有
L[ f (t a)] e
as
F ( s)
f(t-a)是函数f(t)在时间上滞后了a秒的延时函数。 当t<a时,f(t-a)=0 证明(令 t-a = τ )
L[ f (t a )] f (t a )e st dt
《机械控制技术》PPT课件

停止: 按下停止按钮SB21 KM因线圈断电而释放
KM动合辅助触点断开 KM主触点断开 电动机M停转
编辑ppt
17
连续控制电路的保护功能:
欠压保护 接触器本身自带欠压保护功能,当电动机运行 时,电源电压下降到工作电压的85%以下时,接触器的磁通 变弱,电磁铁吸力不足,衔铁在反力弹簧的作用下释放,自 锁触点断开,失去自锁,同时主触点断开,电机停转。
电气接线图的绘制原则是:
1)各电气元件 均按实际安装位置 绘出,元件所占图 面按实际尺寸以统 一比例绘制。
2)一个元件中所 有的带电部件均画 在一起,并用点划 线框起来,即采用 集中表示法。
编辑ppt
8
3)各电气元件的图形符号和文字符号必须与电气 原理图一致,并符合国家标准。
4)各电气元件上凡是需接线的部件端子都应绘出, 并予以编号,各接线端子的编号必须与电气原理图上 的导线编号相一致。
2.电气控制线路分为主电路和控制电路。 主电路用粗线画出,控制电路用细线画出。 一般主电路画在左侧,控制电路画在右侧
3.同一电气的各导电部件用同一文字表示 4.电气控制线路中的全部触点都按“常态”绘出。
编辑ppt
3
5.原理图的绘制要层次分明,各电器元件及 触头的安排要合理,既要做到所用元件、触头 最少,耗能最少,又要保证电路运行可靠,节 省连接导线以及安装、维修方便。
一、三相异步电动机单向旋转控制线路
(一) 点动控制
点动控制是指按下按钮,电动机就得电运行;松开 按钮,电动机就失电停转。
编辑ppt
11
点动控制原理图
起动:按下按钮SB 接触器线圈KM得电 主触点KM闭合 电动机M起动运转
停止:松开按钮SB 接触器线圈KM失电 主触点KM分断
机械控制工程基础(第二章)ppt课件

dt
a0x0t
bm
dmxi t
dtm
bm1
dm1xi t
d tm1
b1
d xi t
dt
b0xi
t
在初始条件为零时,对上式进行拉氏变换
ansnan 1sn 1 a 1sa0X 0s b m smb m 1sm 1 b 1sb 0X i s
故得系统(或环节)的传递函数为
G sX X 0 is sb a m n s sm n a b n m 精 1 1 选s sn Pm P 1 T1 课 件 a b 1 1 s s a b 0 0
x0(t)Txi(t)
精选PPT课件
16
例 下图是简化了的直流发电机组。激磁电压 v恒i 定,磁通不变。
此时电枢电压 与转v速0 成正比•。若 为输入,输出是电压 ,
试v求0此系统的传递函数。
R
•
解:v 0 T
vi i
LM
式中 T——常数
v0 VsT s s 0
GsV 0ssTs
即直流发电机作为测速发电机时,可认为是微分环节。
2
x0
0
精选PPT课件
xi
3
x• 0
0
精选PPT课件
xi
4பைடு நூலகம்
F
0
x?
F
0
x?
精选PPT课件
5
线性化方法:
利用台劳公式 f(x)k n 1 0f(k k )!(a)(xa)kR n(x)
f(a)k n 1 1f(k k )!(a)(x a)kR n(x)
f( x ) f( x 0 ) f( x 0 )x ( x 0 )
物理系统的数学模型
及传递函数
a0x0t
bm
dmxi t
dtm
bm1
dm1xi t
d tm1
b1
d xi t
dt
b0xi
t
在初始条件为零时,对上式进行拉氏变换
ansnan 1sn 1 a 1sa0X 0s b m smb m 1sm 1 b 1sb 0X i s
故得系统(或环节)的传递函数为
G sX X 0 is sb a m n s sm n a b n m 精 1 1 选s sn Pm P 1 T1 课 件 a b 1 1 s s a b 0 0
x0(t)Txi(t)
精选PPT课件
16
例 下图是简化了的直流发电机组。激磁电压 v恒i 定,磁通不变。
此时电枢电压 与转v速0 成正比•。若 为输入,输出是电压 ,
试v求0此系统的传递函数。
R
•
解:v 0 T
vi i
LM
式中 T——常数
v0 VsT s s 0
GsV 0ssTs
即直流发电机作为测速发电机时,可认为是微分环节。
2
x0
0
精选PPT课件
xi
3
x• 0
0
精选PPT课件
xi
4பைடு நூலகம்
F
0
x?
F
0
x?
精选PPT课件
5
线性化方法:
利用台劳公式 f(x)k n 1 0f(k k )!(a)(xa)kR n(x)
f(a)k n 1 1f(k k )!(a)(x a)kR n(x)
f( x ) f( x 0 ) f( x 0 )x ( x 0 )
物理系统的数学模型
及传递函数
机械工程控制基础(第二章)杨叔子 第五版

Kx,
其中: K
df (x) dx
x
x0
上式即为非线性系统的线性化模型,称为增量
方程。y0 = f (x0)称为系统的静态方程;
23
增量方程的数学含义就是将参考坐标的原点移到系统 或元件的平衡工作点上,对于实际系统就是以正常工 作状态为研究系统运动的起始点,这时,系统所有的 初始条件均为零。
对多变量系统,如:y = f (x1, x2),同样可采用泰勒级 数展开获得线性化的增量方程。
estdt
0
称为拉普拉氏积分;
F(s)称为函数f(t)的拉普拉氏变换或象函数, 它是一个复变函数;f(t)称为F(s)的原函数;
L为拉氏变换的符号。
2、拉氏反变换
f (t) L1
F (s)
1
2j
j j
F
(s)e
st
ds
,
t 0
L-1为拉氏反变换的符号。
33
3、几种典型函数的拉氏变换
单位阶跃函数1(t) f(t)
1
3、数学模型的形式
➢ 时间域:微分方程(一阶微分方程组)、差 分方程、状态方程
➢ 复数域:传递函数、结构图
➢ 频率域:频率特性 二、系统的微分方程
1、定义:时域中描述系统动态特性的数学模型。
2、 建立数学模型的一般步骤
➢ 分析系统工作原理和信号传递变换的过程,
确定系统和各元件的输入、输出量;
2
➢ 从输入端开始,按照信号传递变换过程,依据 各变量遵循的物理学定律,依次列写出各元件、 部件的动态微分方程;
R
dt
即:
RC
duo (t) dt
ui
(t)
14
例:列写下图所示机械系统的微分方程
机械设计基础课件第2章
F=3n-2pL-pH=3×4-2×6-0=0
第2章 平面机构的运动简图及自由度 图2-16 机车车轮联动机构中的虚约束
第2章 平面机构的运动简图及自由度
按照上述计算结果,一般而论,这类机构是不能运动的。 但在某些特定的几何条件下,出现了虚约束,机构就能够产生 运动。
为了便于分析,将构件4及回转副E、F拆除,得图(c)所 示机构运动图。又由题中给定的构件长度关系可知,ABCD为 一平行四边形,BC始终平行于AD,所以连杆BC作平动,其上 任一点的轨迹形状相同,连杆上E点的轨迹是以F为中心,EF为 半径的圆弧。显然,无论构件4及回转副E、F是否存在对整个 机构的运动都不发生影响。也可以说,构件4和回转副E、F引 入的一个约束不起限制作用,是虚约束。
各构件之间的联接方式如下:5和6, 7和8之间构成高副; 1和4,8和4之间构成移动副;7和4, 2和1, 2和3, 3和4之间均 为相对转动, 构成回转副。
第2章 平面机构的运动简图及自由度 图2-9 内燃机及其机构运动简图
第2章 平面机构的运动简图及自由度
2.3 平面机构的自由度
2.3.1 平面运动的自由构件具有三个自由度。当两个构件组成运
第2章 平面机构的运动简图及自由度
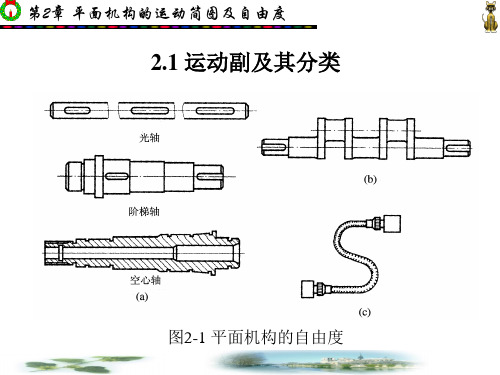
2.1 运动副及其分类
图2-1 平面机构的自由度
第2章 平面机构的运动简图及自由度
2.1.1
1.
若组成运动副的两个构件只能在一个平面内作相对转动, 这种运动副称为回转副,或称铰链。如图2-2(a)所示的轴承1与轴 2组成的回转副,它有一个构件是固定的,故称为固定铰链。图 2-2(b)所示构件1与构件2也组成了回转副,它的两个构件都未固 定,故称为活动铰链。例如图1-1中曲轴与气缸体所组成的回转 副是固定铰链,活塞与连杆、连杆与曲轴所组成的回转副是活动 铰链。
第2章 平面机构的运动简图及自由度 图2-16 机车车轮联动机构中的虚约束
第2章 平面机构的运动简图及自由度
按照上述计算结果,一般而论,这类机构是不能运动的。 但在某些特定的几何条件下,出现了虚约束,机构就能够产生 运动。
为了便于分析,将构件4及回转副E、F拆除,得图(c)所 示机构运动图。又由题中给定的构件长度关系可知,ABCD为 一平行四边形,BC始终平行于AD,所以连杆BC作平动,其上 任一点的轨迹形状相同,连杆上E点的轨迹是以F为中心,EF为 半径的圆弧。显然,无论构件4及回转副E、F是否存在对整个 机构的运动都不发生影响。也可以说,构件4和回转副E、F引 入的一个约束不起限制作用,是虚约束。
各构件之间的联接方式如下:5和6, 7和8之间构成高副; 1和4,8和4之间构成移动副;7和4, 2和1, 2和3, 3和4之间均 为相对转动, 构成回转副。
第2章 平面机构的运动简图及自由度 图2-9 内燃机及其机构运动简图
第2章 平面机构的运动简图及自由度
2.3 平面机构的自由度
2.3.1 平面运动的自由构件具有三个自由度。当两个构件组成运
第2章 平面机构的运动简图及自由度
2.1 运动副及其分类
图2-1 平面机构的自由度
第2章 平面机构的运动简图及自由度
2.1.1
1.
若组成运动副的两个构件只能在一个平面内作相对转动, 这种运动副称为回转副,或称铰链。如图2-2(a)所示的轴承1与轴 2组成的回转副,它有一个构件是固定的,故称为固定铰链。图 2-2(b)所示构件1与构件2也组成了回转副,它的两个构件都未固 定,故称为活动铰链。例如图1-1中曲轴与气缸体所组成的回转 副是固定铰链,活塞与连杆、连杆与曲轴所组成的回转副是活动 铰链。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
拉氏变换的定义
第 二 节 拉 氏 变 换
1
阶跃函数
单位阶 跃函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
阶跃函数
阶跃响应 函数实例
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
2
单位脉冲函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
初值定理
应用
计算 初值
终值定理
应用
计算 终值
卷积定理
第二章 机械工程控制论的数学基础
拉氏逆变换的定义
第 三 拉 氏 逆 变 换
拉氏逆变换的定义
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
拉 氏 逆 变 换 的 数 学 方 法
有理函数法
根据拉氏逆变换公式 求解。 拉氏变换表查出相应 的原函。 通过代数运算将一个复 杂的象函数化为数个简 单的部分分式之和。
本 章 小 结
数学基础
复数和复变函数
拉氏变换
拉氏逆变换
复数; 复数运算规则; 复变函数; 复变函数零点和极点。
拉氏变换定义; 典型环节的拉氏变换; 拉氏逆变换定义; 拉氏逆变换的工程应用 拉氏变换定理; 拉氏变换表; 拉氏变换的工程应用。
第二章 机械工程控制论的数学基础
本 章 小 结
拉氏变换是分将微分方程代数化的数学工具,通过拉氏变换将 1 复杂的微积分运算变换为简单的代数运算,是分析机电控制系 统的基本数学方法之一。
第 三 拉 氏 逆 变 换
1
只包含不相同极点的情况
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
不同极点
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
f (t ) L1[ F ( s)] (4 3j)e ( 1 j) t (4 3j)e ( 1 j) t 5e2 t 3e 4 t e t [4(e( jt ) e( jt ) ) 3j(e jt e jt )] 5e2 t 3e4 t e t (8 cos t 6 sin t ) 5e 2 t 3e 4 t
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
拉氏逆变换的数学方法
通过拉氏变换将常微分方程化 第一步 为象函数的代数方程;
第二步 解出象函数;
由拉氏逆变换求得常微分方程 第三步 的解。
第二章 机械工程控制论的数学基础
1
虚数单位
注意! j 是正体
2
虚数
3
复数
第二章 机械工程控制论的数学基础
复数
第 一 节 复 数 和 复 变 函 数
4
一个复数为零
5
共轭复数 复数有多种表示形式
6
第二章 机械工程控制论的数学基础
复数的运算规则
第 一 节 复 数 和 复 变 函 数
1
两个复数相加(或相减)
2
两个复数相乘
3
两个复数相除
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
组合机床 动力滑台 示意图
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
组合机床动 力滑台动力 学模型
质量-弹簧阻尼系统
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
微分定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
积分定理
多重积分的拉氏变换
当所有初始值均为零时
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
查表法
部分分式法
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
拉氏逆变换的求解
1
只包含不相同极点的情况
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
1
只包含不相同极点的情况
不同极点
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
5
正弦函数和余弦函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
6
幂函数
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
线性定理
1
卷积定理
9
2 相似定理
终值定理 8
拉氏变换 主要运算定理
3 时域位移定理
初值定理 7
6 5
4
复域位移定理
2 3
复变函数的零、极点表示 复变函数的零点
4
复变函数的极点
第二章 机械工程控制论的数学基础
复变函数的零点和极点
第 一 节 复 数 和 复 变 函 数
拉 氏 变 换 的 定 义
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
1 拉氏变换的定义
第二章 机械工程控制论的数学基础
第二章 机械工程控制论的数学基础
复数和复变函数
拉氏变换
拉氏逆变换
拉氏变换在控制工程中的应用
第二章 机械工程控制论的数学基础
典型环节的Bode图
第 一 节 复 数 和 复 变 函 数
复数
1
复数和 复变函数 复变函数零 3 点和极点
2 复数运
算规则
第二章 机械工程控制论的数学基础
复数
第 一 节 复 数 和 复 变 函 数
解: (1)列写时域内方程
时域内表达式
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
(2)推导复域内方程
复域内表达式
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
(3)求时域内解
时域内解
第二章 机械工程控制论的数学基础
典型的时间函数的拉氏变换、拉氏变换的主要运算定理有助于 2 分析和研究其他复杂系统函数的拉氏变换,简化运算。
3 拉氏逆变换是拉氏变换的逆变换。
拉式变换是分析研究线性动态系统的有力数学工具。通过拉式 4 变换将时域的微分方程变换为复数域的代数方程进行求解,通 过拉氏逆变换获得系统的时域解。
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
2
包含多重极点的情况
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
2
包含多重极点的情况
相同极点
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
1 拉氏变换的定义
f(t) 分段函数
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
2
拉氏变换的定义域
拉氏变换 定义域
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
3
象函数
4
原函数
第二章 机械工程控制论的数学基础
第 二 节 拉 氏 变 换
单位脉冲函数
单位脉冲 函数
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
3
单位斜坡函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
4
指数函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
s1 r11 r1 (1 2 ) s2 r2 2 r2
极坐标运 算形式
第二章 机械工程控制论的数学基础
复变函数的零点和极点
第 一 节 复 数 和 复 变 函 数
拉 氏 变 换 的 定 义
1
复变函数 复变函数 =
G(s) u jv
实部
+
G ( s)
j虚部
K ( s z1 )(s z2 ) s( s p1 )(s p2 )
注意! 代数运 算形式
第二章 机械工程控制论的数学基础
复数的运算规则
第 一 节 复 数 和 复 变 函 数
1
用矢量表示复数
s1 (r11 )
s2 (r2 2 )
2
两个复数相乘
s1 s2 (r11 )(r22 ) r1r2(1 2 )
注意! 3 两个复数相除
积分定理
微分定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
线性定理
相似定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
时域位移定理
复域位移定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
第 二 节 拉 氏 变 换
1
阶跃函数
单位阶 跃函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
阶跃函数
阶跃响应 函数实例
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
2
单位脉冲函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
初值定理
应用
计算 初值
终值定理
应用
计算 终值
卷积定理
第二章 机械工程控制论的数学基础
拉氏逆变换的定义
第 三 拉 氏 逆 变 换
拉氏逆变换的定义
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
拉 氏 逆 变 换 的 数 学 方 法
有理函数法
根据拉氏逆变换公式 求解。 拉氏变换表查出相应 的原函。 通过代数运算将一个复 杂的象函数化为数个简 单的部分分式之和。
本 章 小 结
数学基础
复数和复变函数
拉氏变换
拉氏逆变换
复数; 复数运算规则; 复变函数; 复变函数零点和极点。
拉氏变换定义; 典型环节的拉氏变换; 拉氏逆变换定义; 拉氏逆变换的工程应用 拉氏变换定理; 拉氏变换表; 拉氏变换的工程应用。
第二章 机械工程控制论的数学基础
本 章 小 结
拉氏变换是分将微分方程代数化的数学工具,通过拉氏变换将 1 复杂的微积分运算变换为简单的代数运算,是分析机电控制系 统的基本数学方法之一。
第 三 拉 氏 逆 变 换
1
只包含不相同极点的情况
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
不同极点
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
f (t ) L1[ F ( s)] (4 3j)e ( 1 j) t (4 3j)e ( 1 j) t 5e2 t 3e 4 t e t [4(e( jt ) e( jt ) ) 3j(e jt e jt )] 5e2 t 3e4 t e t (8 cos t 6 sin t ) 5e 2 t 3e 4 t
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
拉氏逆变换的数学方法
通过拉氏变换将常微分方程化 第一步 为象函数的代数方程;
第二步 解出象函数;
由拉氏逆变换求得常微分方程 第三步 的解。
第二章 机械工程控制论的数学基础
1
虚数单位
注意! j 是正体
2
虚数
3
复数
第二章 机械工程控制论的数学基础
复数
第 一 节 复 数 和 复 变 函 数
4
一个复数为零
5
共轭复数 复数有多种表示形式
6
第二章 机械工程控制论的数学基础
复数的运算规则
第 一 节 复 数 和 复 变 函 数
1
两个复数相加(或相减)
2
两个复数相乘
3
两个复数相除
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
组合机床 动力滑台 示意图
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
组合机床动 力滑台动力 学模型
质量-弹簧阻尼系统
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
微分定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
积分定理
多重积分的拉氏变换
当所有初始值均为零时
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
查表法
部分分式法
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
拉氏逆变换的求解
1
只包含不相同极点的情况
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
1
只包含不相同极点的情况
不同极点
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
5
正弦函数和余弦函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
6
幂函数
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
线性定理
1
卷积定理
9
2 相似定理
终值定理 8
拉氏变换 主要运算定理
3 时域位移定理
初值定理 7
6 5
4
复域位移定理
2 3
复变函数的零、极点表示 复变函数的零点
4
复变函数的极点
第二章 机械工程控制论的数学基础
复变函数的零点和极点
第 一 节 复 数 和 复 变 函 数
拉 氏 变 换 的 定 义
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
1 拉氏变换的定义
第二章 机械工程控制论的数学基础
第二章 机械工程控制论的数学基础
复数和复变函数
拉氏变换
拉氏逆变换
拉氏变换在控制工程中的应用
第二章 机械工程控制论的数学基础
典型环节的Bode图
第 一 节 复 数 和 复 变 函 数
复数
1
复数和 复变函数 复变函数零 3 点和极点
2 复数运
算规则
第二章 机械工程控制论的数学基础
复数
第 一 节 复 数 和 复 变 函 数
解: (1)列写时域内方程
时域内表达式
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
(2)推导复域内方程
复域内表达式
第二章 机械工程控制论的数学基础
第 四 拉 氏 变 换 在 控 制 工 程 中 的 应 用
(3)求时域内解
时域内解
第二章 机械工程控制论的数学基础
典型的时间函数的拉氏变换、拉氏变换的主要运算定理有助于 2 分析和研究其他复杂系统函数的拉氏变换,简化运算。
3 拉氏逆变换是拉氏变换的逆变换。
拉式变换是分析研究线性动态系统的有力数学工具。通过拉式 4 变换将时域的微分方程变换为复数域的代数方程进行求解,通 过拉氏逆变换获得系统的时域解。
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
2
包含多重极点的情况
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
2
包含多重极点的情况
相同极点
第二章 机械工程控制论的数学基础
拉氏逆变换的数学方法
第 三 拉 氏 逆 变 换
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
1 拉氏变换的定义
f(t) 分段函数
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
2
拉氏变换的定义域
拉氏变换 定义域
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
3
象函数
4
原函数
第二章 机械工程控制论的数学基础
第 二 节 拉 氏 变 换
单位脉冲函数
单位脉冲 函数
第二章 机械工程控制论的数学基础
拉氏变换的定义
第 二 节 拉 氏 变 换
3
单位斜坡函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
4
指数函数
第二章 机械工程控制论的数学基础
典型时间函数的拉氏变换
第 二 节 拉 氏 变 换
s1 r11 r1 (1 2 ) s2 r2 2 r2
极坐标运 算形式
第二章 机械工程控制论的数学基础
复变函数的零点和极点
第 一 节 复 数 和 复 变 函 数
拉 氏 变 换 的 定 义
1
复变函数 复变函数 =
G(s) u jv
实部
+
G ( s)
j虚部
K ( s z1 )(s z2 ) s( s p1 )(s p2 )
注意! 代数运 算形式
第二章 机械工程控制论的数学基础
复数的运算规则
第 一 节 复 数 和 复 变 函 数
1
用矢量表示复数
s1 (r11 )
s2 (r2 2 )
2
两个复数相乘
s1 s2 (r11 )(r22 ) r1r2(1 2 )
注意! 3 两个复数相除
积分定理
微分定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
线性定理
相似定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
时域位移定理
复域位移定理
第二章 机械工程控制论的数学基础
拉氏变换的主要运算定理
第 二 节 拉 氏 变 换
