钢结构4
钢结构设计原理 第四章-轴心受力构件

因此,失稳时杆件的整个截面都处于加载的过 程中,应力-应变关系假定遵循同一个切线模量 Et,此时轴心受压杆件的屈曲临界力为:
N cr ,t
2 Et I
2 二、实际的轴心受压构件的受力性能
在钢结构中,实际的轴压杆与理想的直杆受力性能之间差别很大,实 际上,轴心受压杆的屈曲性能受许多因素影响,主要的影响因素有:
一、理想轴压构件的受力性能 理想轴压构件是指满足下列4个条件: o杆件本身绝对直杆; o材料均质且各向同性; o无荷载偏心且在荷载作用之前无初始应力; o杆端为两端铰接。 在轴心压力作用下,理想的压杆可能发生三种形式的屈曲: 弯曲屈曲、扭转屈曲、弯扭屈曲——见教科书P97图4–6 轴心受压构件具体以何种形式失稳,主要取决于截面的形式 和尺寸、杆的长度以及杆端的支撑条件。
l N 2 EI 对一无残余应力仅存在初弯曲的轴压杆,杆件中点截面边缘开始 式中 N l2 NE 屈服的条件为:
0
1
经过简化为:
N N vm v0 v0 fy v m v0 v 1 1 N NE A W N N v0 N E fy A W NE N
An—构件的净截面面积_
N fy r f R An
P94式4-2
(1)当轴力构件采用普通螺栓连接时 螺栓为并列布置:
n1 n2 n3
按最危险的截面Ⅰ-Ⅰ 计算,3个截面净截面面积 相同,但 Ⅰ-Ⅰ截面受力最大。
N n
Ⅰ-Ⅰ:N Ⅱ-Ⅱ:N-Nn1/n Ⅲ-Ⅲ:N-N(n1+n2)/n
Ⅰ Ⅱ Ⅲ
2 2
从上面两式我们可以看出,绕不同轴屈曲时,不仅临界力不同,且残余 应力对临界应力的影响程度也不同。因为k1,所以残余应力对弱轴的 影响比对强轴的影响严重的多。
钢结构讲义4

一. 弯曲屈曲
静力法:据曲线平衡状态求解微分 求临界力的方法 方程。属于精确法。 z 能量法:属于近似法。 P 列平衡方程 Py M 静力法: P M 即: EIy Py 0 V y 注意:对实心截面,可以不考虑剪力 y 影响,薄壁截面不能忽略。 能量法稳定准则:杆件从直杆平衡状态转变为无限 临近的曲杆平衡状态时,外荷势能的变化和杆件中应变 能的变化总量不变。 即: V U 0 应变能的变化 外荷势能的变化
曲杆平衡
N
cr
受压构件的承载力常决定于稳定
2
EI
2
因而为了提高临界力,应采用较为开展的截面型式 即提高回转半径 i 。 通常采用实腹式截面和格构式截面。 实腹式:沿构件全长都是连续分布的。 格构式:由柱肢和缀材组成截面,缀材沿构件全长 是间隔分布的。
(d)格构式构件截面 1
l
I i A
2
§4.3 轴心受压构件的临界力 理想轴心受压构件丧失稳定,或者称屈曲,有三种 情况: 弯曲屈曲:杆件纵轴线发生弯曲变形 扭转屈曲:杆件各截面绕纵轴线扭转变形 弯扭屈曲:既有各截面绕纵轴线的扭转,又有纵 轴线的弯曲变形 需算出三种屈曲情况的屈曲临界力,然后取小值, 作为轴压构件的临界力。 确定轴心受压构件的临界力时,采用下列假设: ① 杆件为两端铰接的理想直杆; ② 轴心压力作用于杆件两端,且为保向力(即弯 曲时,轴心压力方向不变)。 ③ 屈曲时变形很小,忽略杆长的变化。 ④ 屈曲时轴线挠曲成正弦半波曲线,截面仍保持 平面。
V M 应变能为:U dz dz 2 EI 2 l l
2
N y2 Vg 1 y
式中:M N cr y
2 cr
N N 故: U y dz 2 y dz 2 EI
钢结构基础第四章课后习题答案
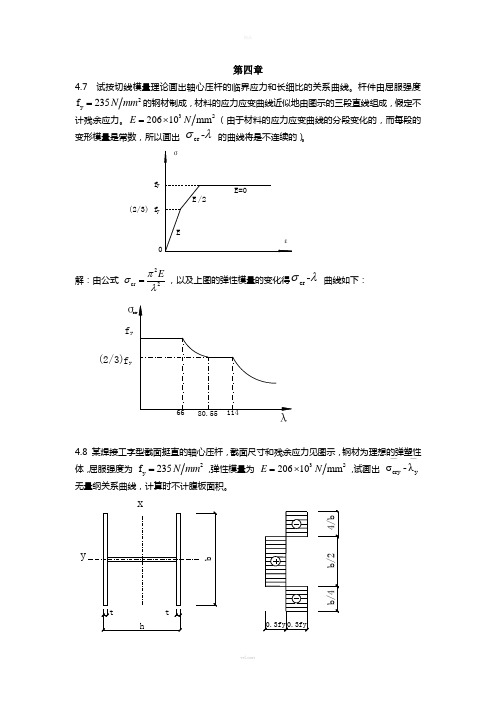
第四章4.7 试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度2y f 235N mm =的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定不计残余应力。
320610mm E N =⨯2(由于材料的应力应变曲线的分段变化的,而每段的变形模量是常数,所以画出 cr -σλ 的曲线将是不连续的)。
解:由公式 2cr 2Eπσλ=,以及上图的弹性模量的变化得cr -σλ 曲线如下:4.8 某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑性体,屈服强度为 2y f 235N mm =,弹性模量为 320610mm E N =⨯2,试画出 cry y σ-λ——无量纲关系曲线,计算时不计腹板面积。
f yyf (2/3)f y(2/3)f yx解:当 cr 0.30.7y y y f f f σ≤-=, 构件在弹性状态屈曲;当 cr 0.30.7y y y f f f σ>-=时,构件在弹塑性状态屈曲。
因此,屈曲时的截面应力分布如图全截面对y 轴的惯性矩 3212y I tb =,弹性区面积的惯性矩 ()3212ey I t kb =()322232232212212ey cryy y y yI t kb E E E k I tb πππσλλλ=⨯=⨯= 截面的平均应力 2220.50.6(10.3)2y ycr y btf kbt kf k f btσ-⨯⨯==-二者合并得cry y σ-λ——的关系式cry cry342cry σ(0.0273)σ3σ10y λ+-+-= 画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为0.6f yfyλσ0.20.40.60.81.0cryN=1500KN 。
解:已知 N=1500KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ,对弱轴的计算长度 oy =400cm l 。
钢结构原理-第4章轴心受力构件

存在,且都是变量,再 加上材料的弹塑性,轴 压构件属于极值点失稳, 其极限承载力Nu很难用 解析法计算,只能借助 计算机采用数值法求解。
《钢结构原理》 第4章 轴心受力构件
缺陷通常只考虑影响最大的残余应力和初弯曲(l/1000)。 采用数值法可以计算出轴压构件在某个方向(绕 x 或 y 轴)的 柱子曲线,如下图,纵坐标为截面平均应力与屈服强度的比值, 横坐标为正则化长细比。
《钢结构原理》 第4章 轴心受力构件
4.1 概述
4.1.1 定义:构件只承受轴心力的作用。 承受轴心压力时称为轴心受压构件。 承受轴心拉力时称为轴心受拉构件。
N
N
N
N
《钢结构原理》 第4章 轴心受力构件
4.1.2 轴心受力构件的应用 平面及空间桁架(钢屋架、管桁架、塔桅、网架等); 工业及民用建筑结构中的一些柱; 支撑系统;等等。
(a) N
(b) N
Hale Waihona Puke (c) NNN
N
《钢结构原理》 第4章 轴心受力构件
4.4.3 理想轴心受压构件的弯曲屈曲 4.4.3.1 弹性弯曲屈曲
取隔离体,建立平衡微分方程
EyIN y0
用数学方法解得:N 的最 小值即分岔屈曲荷载 Ncr,又称 为欧拉荷载 NE 。
Ncr2EI/l2
对应的临界应力为:
《钢结构原理》 第4章 轴心受力构件
4.4 轴心受压构件的整体稳定
概念:在压力作用下,构件的外力必须和内力相平衡。 平衡有稳定、不稳定之分。当为不稳定平衡时,轻微的扰 动就会使构件产生很大的变形而最后丧失承载能力,这种 现象称为丧失稳定性,简称失稳,也称屈曲。 特点:与强度破坏不同,构件整体失稳时会导致完全 丧失承载能力,甚至整体结构倒塌。失稳属于承载能力极 限状态。与混凝土构件相比,钢构件截面尺寸小、构件细 长,稳定问题非常突出。只有受压才有稳定问题。
水工钢结构 第4章

M In
y1
σ和σc均以拉应力为正值,压应力为负值; In——梁净截面惯性矩; y1——所计算点至梁中和轴的距离; β1——计算折算应力的强度设计值增大系数;当σ与σc异号时 ,取β1=1.2;当σ与σc同号或σc=0 时,取β1=1.1。
4.2.2
梁的刚度
w ≤ [w]
— 梁的刚度用荷载标准值作用下的挠度大小来度量。应 按下式验算梁的挠度:
·梁的挠度可按力学的方法计算,也可由结构静力计算手册
取用。受多个集中荷载的梁 (如吊车梁、楼盖主梁等),其挠 度的精确计算较为复杂,但与最大弯矩相同的均布荷载作用 下的挠度接近。于是,可采用下列近似公式验算梁的挠度:
对等截面简支梁:
w l 5 qk l
3
5 qk l l
2
M kl 10 EI x
• 整体失稳的原因:
– 梁的EIy和GJ较小,梁截面中受压翼缘绕y轴失稳(产 生侧向微弯曲),而受拉翼缘阻碍侧向弯曲,导致整个 截面侧向弯曲与扭转.
• 提高整体稳定性的措施:
– 加大压缘宽度b,以增大EIy和GJ; – 设置压缘的侧向支撑,即减小压缘绕y轴失稳的自由 长度l1; – 将铺板与压缘相连接,使压缘不会发生侧向位移.
·规范规定:当梁受压翼缘的自由外伸宽度b与其厚度t之比
大于 而不超过 时,应取γx=1.0。直接承受动 力荷载且需要计算疲劳的梁,宜取γx=γy=1.0,即按弹性 工作阶段进行计算。
13 fy 235
15
235 fy
4.2.1.2 梁的抗剪强度 – 一般情况下,梁既承受弯矩,同时又承受剪力。工
字形和槽形截面梁腹板上的剪应力分布如图4.8所示。
图4.7
钢结构第4章例题
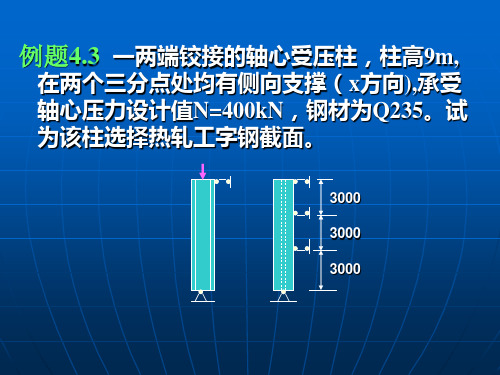
1 l1 i1 0.7 max
max max 0 x, y
缀板柱的分肢长细比:
1 l01 i1 40且0.5max
max max 0 x, y
当max 50时, 取max 50
例题4.5 试设计一两端铰接的轴心受压格构式柱。
d、柱单肢的稳定性验算
lo1=2a=2×30.98=61.96cm,
λmax=λox=41.2<50, 取λmax=50 λ1=lo1/i1=61.96/2.11=29
<0.7λmax=0.7×50=35, 单肢稳定性满足要求。
e、缀条与柱肢的连接焊缝计算 采用两边侧面角焊缝连接,取hf=4mm.
1、按对实轴的整体稳定确定柱的截面(分肢截面);
2、按等稳定条件确定两分肢间距a,即 λ0x=λy; 双肢缀条柱:
0x
2 x
27
A A1
y
即: x
双肢缀板柱:
2 y
27
A A1
(4 61)
0 x 2x 12 y
即: x 2y 12
b、按柱对虚轴x的稳定性确定两个单肢间距
设缀条布置为单斜式。
试选用最小角钢 45×4作为柱的斜缀条, 查角钢表知:A1x/2 =3.49cm2。
λx=√λy2-27A/A1x =√38.22-27×57.68/(3.49×2)=35.2
ix =lox/λx=600/35.2=17.1cm
由回转半径与截面宽度的近似关系,得
梁
填板
Ⅰ
Ⅱ
柱
柱顶板 垫板 加劲肋
15-20mm
(三)、柱头的计算
钢结构基本原理第4章

第4.1节 概述
本节目录
1. 轴心受力构件的应用 2. 轴心受力构件类型 3. 轴心受力构件的截面形式 4. 轴心受力构件的计算内容
基本要求
了解轴心受力构件的类型、应用及计算内容
4.1.1 轴心受力构件的应用
轴心受力构件是指承受通过截面形心轴线的轴向力 作用的构件。
图4.1.1 桁架
图4.1.2 网架
由于组合截面制作费时费工,其总的成本并 不一定很低,目前只在荷载较大或构件较高时使 用。
4.1.4 轴心受力构件的计算内容
件轴 心 受 力 构
强度 (承载能力极限状态) 轴心受拉构件 刚度 (正常使用极限状态)
强度 (承载能力极限状态) 轴心受压构件 稳定
刚度 (正常使用极限状态)
第4.2节 轴心受力构件的强度和刚度
②理想轴心压杆的弹塑性弯曲屈曲临界力和临界应力
对于长细比λ<λp的轴心压杆发生弯曲屈曲时,构件截 面应力已超过材料的比例极限,并很快进入弹塑性状态, 由于截面应力与应变的非线性关系,这时构件的临界力和 临界应力公式采用切线模量理论计算。
N cr
2Et I
l2
cr
2Et 2
Et ---切线摸量
A
N f
A
N ——轴心压力设计值;
A ——构件毛截面积;
f ——钢材抗压强度设计值;
——
cr
/
f
,称为轴心受压构件整体稳定系数,
y
根据截面分类和构件长细比,由柱子曲线或查表确定。
轴心受压构件的柱子曲线
压杆失稳时临界应力σcr与长细比λ之间的关系曲线 称为柱子曲线。
规范在制定轴心受压构件的柱子曲线时,根据不同 截面形状和尺寸、不同加工条件和相应的残余应力分布 和大小、不同的弯曲屈曲方向以及l/1000的最大初弯曲, 按照最大强度准则,对多种实腹式轴心受压构件弯曲失 稳算出了近200条柱子曲线。
(完整版)钢结构基础第四章课后习题答案
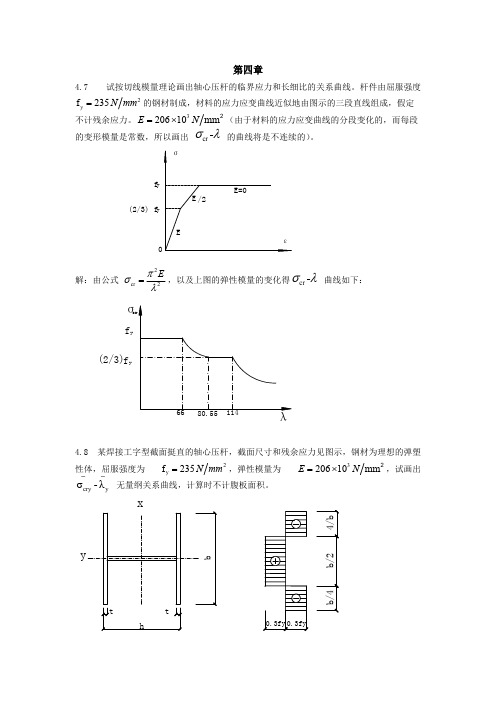
第四章4.7试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定2y f 235N mm =不计残余应力。
(由于材料的应力应变曲线的分段变化的,而每段320610mm E N =⨯2的变形模量是常数,所以画出 的曲线将是不连续的)。
cr -σλ(2/3)解:由公式 ,以及上图的弹性模量的变化得 曲线如下:2cr 2Eπσλ=cr -σλ(2/3)4.8 某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑性体,屈服强度为,弹性模量为,试画出2y f 235N mm =320610mm E N =⨯2 无量纲关系曲线,计算时不计腹板面积。
cry y σ-λ——解:当 , 构件在弹性状态屈曲;当 时,cr 0.30.7y y y f f f σ≤-=cr 0.30.7y y y f f f σ>-=构件在弹塑性状态屈曲。
全截面对y 轴的惯性矩 ,弹性区面积的惯性矩 3212y I tb =()3212ey I t kb =()322232232212212ey cryy y y yI t kb E E E k I tb πππσλλλ=⨯=⨯=截面的平均应力2220.50.6(10.3)2y ycr ybtf kbt kf k f btσ-⨯⨯==-二者合并得的关系式cryy σ-λ——cry cry342cry σ(0.0273)σ3σ10y λ+-+-=画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为钢,翼缘为火焰切割Q235边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为。
N=1500KNt h i nhe i rg解:已知 ,由支撑体系知对截面强轴弯曲的计算长度 ,对弱N=1500KN ox =1200cm l 轴的计算长度 。
抗压强度设计值 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高强度蝶拴连接摩擦面应保持干燥、整洁,不应有飞边、毛刺 5 、焊接飞溅物,焊疤、氧化铁皮、污垢等,除设计要求外摩擦 面不应涂漆 6 高强度螺栓应自由穿人螺栓孔。高强度螺拴孔不应采用气割扩 孔,扩孔数量应征得设计同意,扩孔后的孔径不应超过1.2d 监理 施 工 单 位 检 查 结 果 (建 设) 专业监理工程师: 专业施工员: 项目专业质检员: 年 月 日 单位 (建设单位项目专业技术负责人) 验收 结论 年 月 日
施工班组长:
DBJ04-226-2003
高强度螺栓连接工程检验批质量验收记录表 施工单位名称 施工工艺标准名称及编号 分部及部位 项目经理 钢结构工程施工质量验收规范 GB50205-2001 施工单位检查记录
010902 020402
0 0 2
施工质量验收规范的规定 钢结构连接用高强度大六角头螺栓连接副、扭剪型高强度螺拴 1 连接副、钢网架用高强度螺栓.其品种、规格、性能等应符合 现行国家产品标准和设计要求 高强度大六角头螺栓连接副按本规范附录B检验扭矩系数,扭 2 剪型高强度螺栓连接副按本规范附录B规定检验预拉力,检验 主 结果应符合本规范附录B的规定 控 钢结构制作和安装单位应按本规范附录B的规定分别进行高强 度螺栓连接摩擦面的抗滑移系数试验和复验,现场处理的构件 3 项 摩擦面应单独进行摩擦面抗滑移系数试验,其结果应符合设计 要求 目 高强度大六角头螺拴连接副终拧完成1h后、48h内应进行终拧 扭矩检查,检查结果应符合本规范附录B规定。扭剪型高强度 螺栓连接副终拧后,除因构造原因无法使用专用扳手终拧掉梅 4 花头者外,未在终拧中拧掉梅花头的螺栓数不应大于该节点螺 栓数的5%。对所有梅花头未拧掉的扭剪型高强度螺栓连接副应 采用扭矩法或专角法进行终拧并作标记,且按前面方法做扭矩 检查 高强度螺栓连接副,应按包箱配套供货,包装箱上应标明批号 1 、规格、数量及生产日期。螺栓、螺母、垫圈外对表面应涂油 保护,不应出现生锈和沾染赃物.螺纹不应损伤 对建筑结构安全等级为一级,跨度40m及以上的螺拴球节点钢 网架结构,其连接高强度螺栓应进行表面硬度试验。对8.8级的 2 高强度螺栓其强度应为HRC21~29;10.9级高强度螺栓其硬度 一 应为HRC32~36,且不得有裂纹或损伤 般 3 高强度螺栓连接副的施拧顺序和初拧、复拧扭矩应符合设计要 求和行标JCJ82规定 项 目 4 高强度螺栓连接副终拧后,螺栓丝扣外露应为2~3扣,其中允 许有10%的螺栓丝扣外露1扣或4扣
