第20章《平行四边形的判定》测试题
(完整word版)平行四边形的判定练习题

(一) 平行四边形的判定一、教学目的:1.在探索平行四边形的判别条件中,理解并掌握用边、对角线来判定平行四边形的方法.2.会综合运用平行四边形的判定方法和性质来解决问题.3.培养用类比、逆向联想及运动的思维方法来研究问题.二、重点、难点1.重点:平行四边形的判定方法及应用.2.难点:平行四边形的判定定理与性质定理的灵活应用.平行四边形的判定方法平行四边形判定方法1(与边相关) 两组对边分别相等的四边形是平行四边形。
平行四边形判定方法2 (与边相关) 两组对边分别平行的四边形是平行四边形平行四边形判定方法3 (与边相关) 一组对边平行且相等的四边形是平行四边形平行四边形判定方法4 (与角相关) 两组对角分别相等的四边形是平行四边形平行四边形判定方法5 (与对角线相关)对角线互相平分的四边形是平行四边形。
三、练习题1.如图,在四边形ABCD中,AC、BD相交于点O,(1)若AD=8cm,AB=4cm,那么当BC=___ _cm,CD=___ _cm时,四边形ABCD为平行四边形;(2)若AC=10cm,BD=8cm,那么当AO=__ _cm,DO=__ _cm时,四边形ABCD为平行四边形.(3).(选择)下列条件中能判断四边形是平行四边形的是( ).(A)对角线互相垂直 (B)对角线相等(C)对角线互相垂直且相等(D)对角线互相平分2.判断题:(1)相邻的两个角都互补的四边形是平行四边形;()(2)两组对角分别相等的四边形是平行四边形; ( )(3)一组对边平行,另一组对边相等的四边形是平行四边形; ( )(4)一组对边平行且相等的四边形是平行四边形; ( )(5)对角线相等的四边形是平行四边形; ( )(6)对角线互相平分的四边形是平行四边形.()3.(选择)在下列给出的条件中,能判定四边形ABCD为平行四边形的是().(A)AB∥CD,AD=BC (B)∠A=∠B,∠C=∠D(C)AB=CD,AD=BC (D)AB=AD,CB=CD4.已知:如图,AC∥ED,点B在AC上,且AB=ED=BC,找出图中的平行四边形,并说明理由.5.已知:如图,ABCD中,点E、F分别在CD、AB上,DF∥BE,EF交BD于点O.求证:EO=OF.6.已知:如图,△ABC,BD平分∠ABC,DE∥BC,EF∥AC,求证:BE=CF7。
平行四边形的判定测试题
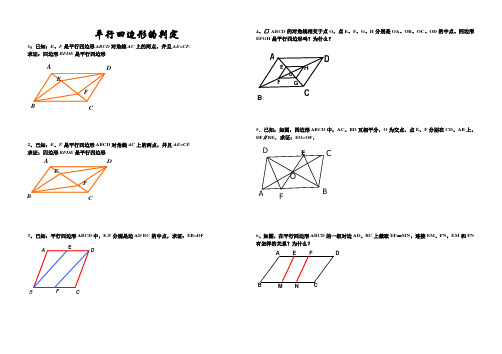
平行四边形的判定1:已知:E 、F 是平行四边形ABCD 对角线AC 上的两点,并且AE =CF . 求证:四边形BFDE 是平行四边形2、已知:E 、F 是平行四边形ABCD 对角线AC 上的两点,并且AE=CF . 求证:四边形BFDE 是平行四边形3、已知:平行四边形ABCD 中,E.F 分别是边AD BC 的中点,求证:EB=DF4、□ ABCD 的对角线相交于点O ,点E 、F 、G 、H 分别是OA 、OB 、OC 、OD 的中点。
四边形EFGH 是平行四边形吗?为什么?5.已知:如图,四边形ABCD 中,AC 、BD 互相平分,O 为交点,点E 、F 分别在CD 、AB 上,DF ∥BE .求证:EO=OF .6、如图,在平行四边形ABCD 的一组对边AD 、BC 上截取EF =MN ,连接EM 、FN ,EM 和FN 有怎样的关系?为什么?CDFBABCDEFOA BCDE F M NDA B C E F D A B C E F G E F D O H C B A巨型的性质7:□ABCD 的对角线AC 与BD 相交于点O ,(1)若AC=BD ,则□ABCD 是 形; (2)若∠ABC 是直角,则□ABCD 是形; 8:9.已知△ABC 是Rt △,∠ABC=900, BD 是斜边AC 上的中线(1)若BD=3㎝ 求AC(2) 若∠C=30°,AB =5㎝,求AC 与BD10.已知菱形的周长是12cm ,那么它的边长是______. 菱形ABCD 中∠BAD =60度,则∠ABD =_______.11、如图,将矩形ABCD 沿AE折叠,使点D 落在BC 边上的F 点处。
(1)若∠BAF =60°,求∠EAF 的度数;(2)若AB =6cm ,AD =10cm ,求线段CE 的长12、将长方形ABCD 的纸片,沿EF 折成如图所示;已知∠EFG=55º,求∠FGE13、练习3如图,矩形ABCD 沿BE 折叠,使点C 落在AD 边上的F 点处,如果∠ABF=60º,求∠CBEC BACCDA。
第20章 平行四边形的判定

第20章平行四边形的判定(1)平行四边形是中心对称图形,具有两组对边分别平行且相等、对角相等及邻角互补、两条对角线互相平分等特征.(2)平行四边形的判定方法有:有5种方法①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③一组对边平行且相等的四边形是平行四边形;④两组对角分别相等的四边形是平行四边形;⑤对角线互相平分的四边形是平行四边形.(3)矩形、菱形、正方形都是特殊的平行四边形,它们除了具有平行四边形的所有特征外,还具有以下性质:矩形:四个角都是直角、对角线互相平分且相等.菱形:四条边都相等、对角线互相垂直平分且每一条对角线平分一组对角.正方形:四条边都相等、四个角都是直角、对角线互相垂直平分且相等,每一条对角线平分一组对角(具有矩形、菱形的所有特征).(4)矩形、菱形、正方形既是轴对称图形,又是中心对称图形;矩形、菱形都有两条对称轴,而正方形有四条对称轴,它们的对称中心都是对角线的交点.(5)矩形、菱形、正方形的判定方法有:分别有3 3 2 种方法①有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;③两条对角线相等的平行四边形是矩形;④有一组邻边相等的平行四边形是菱形;⑤有四条边相等的四边形是菱形;⑥两条对角线垂直的平行四边形是菱形;⑦有一组邻边相等的矩形是正方形;⑧有一个角是直角的菱形是正方形.(6)有且只有一组对边平行的四边形叫做梯形,这组平行的边叫做梯形的上底与下底,不平行的两边叫做梯形的腰,两腰相等的梯形叫做等腰梯形,有一个角是直角的梯形叫做直角梯形.(7)等腰梯形是轴对称图形,它的对称轴是过两底中点的直线,它有以下性质:①等腰梯形同一底上的两个内角相等;②等腰梯形的两条对角线相等.(8)等腰梯形的判定方法有:①两腰相等的梯形是等腰梯形②同一底上的两个角相等的梯形是等腰梯形;③两条对角线相等的梯形是等腰梯形..例1(补充)已知:如图,ABCD中,E、F分别是AD、BC的中点,求证:BE=DF.分析:证明BE=DF,可以证明两个三角形全等,也可以证明四边形BEDF是平行四边形,比较方法,可以看出第二种方法简单.例2(教材P96例3)已知:如图ABCD的对角线AC、BD交于点O,E、F是AC 上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.分析:欲证四边形BFDE是平行四边形可以根据判定方法2来证明.(证明过程参看教材)问;你还有其它的证明方法吗?比较一下,哪种证明方法简单.例3(补充)已知:如图,A′B′∥BA,B′C′∥CB,C′A′∥AC.求证:(1) ∠ABC=∠B′,∠CAB=∠A′,∠BCA=∠C′;(2) △ABC的顶点分别是△B′C′A′各边的中点.六、随堂练习1.已知:ABCD中,点E、F分别在CD、AB上,DF∥BE,EF交BD于点O.求证:EO=OF.1.(选择)下列条件中能判断四边形是平行四边形的是().(A)对角线互相垂直(B)对角线相等(C)对角线互相垂直且相等(D)对角线互相平分2.已知:如图,△ABC,BD平分∠ABC,DE∥BC,EF∥BC,求证:BE=CF五、例习题分析例1(补充)已知:如图,ABCD中,E、F分别是AD、BC的中点,求证:BE=DF.分析:证明BE=DF,可以证明两个三角形全等,也可以证明四边形BEDF是平行四边形,比较方法,可以看出第二种方法简单.证明:∵例2(补充)已知:如图,ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.求证:四边形BEDF是平行四边形.分析:因为BE⊥AC于E,DF⊥AC于F,所以BE∥DF.需再证明BE=DF,这需要证明△ABE与△CDF全等,由角角边即可.证明:、.1.(选择)在下列给出的条件中,能判定四边形ABCD为平行四边形的是().(A)AB∥CD,AD=BC (B)∠A=∠B,∠C=∠D(C)AB=CD,AD=BC (D)AB=AD,CB=CD2.已知:如图,AC∥ED,点B在AC上,且AB=ED=BC,找出图中的平行四边形,并说明理由.3.已知:如图,在ABCD中,AE、CF分别是∠DAB、∠BCD的平分线.求证:四边形AFCE是平行四边形.七、课后练习1.判断题:(1)相邻的两个角都互补的四边形是平行四边形;()(2)两组对角分别相等的四边形是平行四边形;()(3)一组对边平行,另一组对边相等的四边形是平行四边形;()(4)一组对边平行且相等的四边形是平行四边形;()(5)对角线相等的四边形是平行四边形;()(6)对角线互相平分的四边形是平行四边形.()2.延长△ABC的中线AD至E,使DE=AD.求证:四边形ABEC是平行四边形.3.在四边形ABCD中,(1)AB∥CD;(2)AD∥BC;(3)AD=BC;(4)AO=OC;(5)DO=BO;(6)AB=CD.选择两个条件,能判定四边形ABCD是平行四边形的共有_______2.已知:三角形的各边分别为8cm 、10cm和12cm ,求连结各边中点所成三角形的周长.3.如图,△ABC中,D、E、F分别是AB、AC、BC的中点,(1)若EF=5cm,则AB= cm;若BC=9cm,则DE= cm;(2)中线AF与DE中位线有什么特殊的关系?证明你的猜想.七、课后练习1.(填空)一个三角形的周长是135cm,过三角形各顶点作对边的平行线,则这三条平行线所组成的三角形的周长是cm.2.(填空)已知:△ABC中,点D、E、F分别是△ABC三边的中点,如果△DEF的周长是12cm,那么△ABC的周长是cm.3.已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.。
八年级数学下册《平行四边形的判定》练习题及答案

八年级数学下册《平行四边形的判定》练习题及答案一 单选题1.如图 在△ABC 中 AB =10 BC =6 点D 为AB 上一点 BC =BD BE ⊥CD 于点E 点F 为AC 的中点 连接EF 则EF 的长为( )A .1B .2C .3D .42.如图的ABC ∆中 AB AC BC >>且D 为BC 上一点.今打算在AB 上找一点P 在AC 上找一点Q 使得APQ ∆与PDQ ∆全等 以下是甲 乙两人的作法:(甲)连接AD 作AD 的中垂线分别交AB AC 于P 点 Q 点 则P Q 两点即为所求(乙)过D 作与AC 平行的直线交AB 于P 点 过D 作与AB 平行的直线交AC 于Q 点 则P Q 两点即为所求对于甲 乙两人的作法 下列判断何者正确?( )A .两人皆正确B .两人皆错误C .甲正确 乙错误D .甲错误 乙正确3.为了测量水池的宽AB 在水池外找一点P 点C D 分别为PA PB 的中点 测得8=CD m 则水池的宽AB 为( )A .16mB .14mC .12mD .10m4.如图 在▱ABCD 中 已知AD =8cm AB =6cm DE 平分∠ADC 交BC 边于点E 则BE 等于( )A .2cmB .4cmC .6cmD .8cm5.如图 △ABC 的周长为8cm 以它的三边中点为顶点组成一个新的三角形 这个新三角形的周长是( )A .6B .5C .4D .26.如图 四边形ABCD 的对角线AC BD 交于点O 则添加下列条件 一定可使四边形ABCD 成为平行四边形的是( )A .AC =BDB .AB ∥CD AD =BCC .AC 平分BD D .AD ∥BC OA =OC7.下列给出的条件中 不能判定四边形ABCD 是平行四边形的是( )A .AB=CD,AD=BCB .AD∥BC ∠A=∠BC .AD∥BC ∠A=∠CD .AD∥BC AB∥CD8.已知四边形ABCD 是平行四边形 对角线AC BD 交于点O E 是BC 的中点 以下说法错误的是( )A .2OE DC =B . OA OC = C .BOE OBA ∠=∠D .OBE OCE ∠=∠9.如图 在Rt ABC △中90C ∠=︒ 3AC = 4BC = D E 分别是边AC BC 的中点 则DE 的长为( )A .1.5B .2C .2.5D .510.下列能判定一个四边形是平行四边形的是( )A .对角线相等 且一组对角相等的四边形是平行四边形B .一对邻角的和为180°的四边形是平行四边形C .两条对角线相互垂直的四边形是平行四边形D .一组对边平行且相等的四边形是平行四边形11.如图 四边形ABCD 的对角线AC 和BD 相交于点O 下列不能判定四边形ABCD 为平行四边形的条件是( )A .OA OC OB OD ==, B .OA OC AB DC =,∥C .ABD ADB BAO DCO ∠=∠∠=∠, D .AB DC AD BC ==,12.一个三角形的周长是36cm 以这个三角形各边中点为顶点的三角形的周长是( )A .18cmB .15cmC .12cmD .8cm二 填空题13.平行四边形的判定方法有:从边的条件有:①两组对边_________的四边形是平行四边形;②两组对边_________的四边形是平行四边形;③一组对边_________的四边形是平行四边形从对角线的条件有:④两条对角线_________的四边形是平行四边形.从角的条件有:⑤两组对角_________的四边形是平行四边形.注意:一组对边平行另一组对边相等的四边形_________是平行四边形(填“一定”或“不一定”).14.如图 A B 、两点被一座山隔开 M N 、分别是AC BC 、中点 测量MN 的长度为30米 那么AB 的长度为_______米.15.等腰三角形的两条中位线分别为3和5 则等腰三角形的周长为_____.16.如图 剪两张对边平行的纸条 随意交叉叠放在一起 重合部分构成了一个四边形ABCD 当线段AD =3时 线段BC 的长为__________.17.为了更好开展劳动教育 实现五育并举 某校开设了劳动实践课程:该校的某劳动实践小组协助公园园区工人测量人工湖湖辟A B 两点之间的距离 如图 是该实践小组所画的示意图 先在湖边地面上确定点O 再用卷尺分别确定OA OB 的中点C D 最后用卷尺量出10CD =m 则AB 之间的距离是______m .18.如图 点E F 在ABCD 的对角线AC 上 连接BE DE DF BF 请添加一个条件使四边形BEDF 是平行四边形 那么需要添加的条件是______.(只填一个即可)19.如图四边形ABCD中AD∥BC添加一个条件使得△ADB≌△CBD添加的条件是_____.20.如图△ABC的周长为26 点D E都在边BC上∠ABC的平分线垂直于AE垂足为Q∠ACB的平分线垂直于AD垂足为P.若BC=10 则PQ的长是_________.三解答题21.如图在线段AD上有两点E F且AE=DF过点E F分别作AD的垂线BE和CF连接AB CD BF CE且AB//CD.求证:四边形BECF是平行四边形.22.如图在四边形ABCD中点P是对角线BD的中点点E F分别是AB CD的中点AD BC=30∠=︒°求PFEPEF∠的度数.23.如图在△ABC中已知∠BDC=∠EFD∠AED=∠ACB.(1)试判断∠DEF与∠B的大小关系并说明理由;(2)若D E F分别是AB AC CD边上的中点S△DEF=4 S△ABC=24.判断命题“一组对边平行另一组对边相等的四边形是平行四边形”真假 若是真命题 请给出证明;若是假命题 请修改其中一个条件使其变成真命题(一个即可)并请写出证明过程.(要求:画出图形 写出已知 求证和证明过程)25.在平行四边形ABCD 中 对角线AC BD 相交于点O CA AB ⊥ BE DF 分别平分∠ABC 和∠ADC 交对角线AC 于点E F .(1)若28EBC ∠=︒ 求∠CAD 的度数;(2)求证:EO FO =.参考答案1.【答案】B2.【答案】A3.【答案】A4.【答案】A5.【答案】C6.【答案】D7.【答案】B8.【答案】D9.【答案】C10.【答案】D11.【答案】C12.【答案】A13.【答案】分别平行 分别相等平行且相等 互相平分 分别相等不一定 14.【答案】6015.【答案】22或26.16.【答案】317.【答案】2018.【答案】AF CE =(答案不唯一)19.【答案】AD=BC(符合要求的其它条件均可以)20.【答案】321.【答案】四边形BECF 是平行四边形.22.【答案】30︒23.【答案】(1)∠DEF=∠B (2)3224.【答案】假命题 详见解析25.【答案】(1)34 (2)EO =FO 。
第20章《平行四边形的判定》测试题3

第20章《平行四边形的判定》测试题3一、填空题1、顺次连接一个任意四边形四边的中点,得到一个四边形。
2.命题“平行四边形的对角线互相平分”的逆命题是 .3.矩形的对角线相交成的角中,有一个角是60°,这个角所对的边长为20cm ,则其对角线长为_______,矩形的面积为________.4.一个菱形的两条对角线长分别为6cm ,8cm ,这个菱形的边长为_______,•面积S=______.5.如图,□ABCD 中,AE 、CF 分别是∠BAD 和∠BCD 的角平分线,根据现有的图形,请添加一个条件,使四边形AECF 为菱形,则添加的一个条件可以是 (只需写出一个即可,图中不能再添加别的“点”和“线”).6、如图,在平行四边形ABCD 中,E 、F 是对角线BD 上的两点,要使△ADF ≌△CBE ,还需添加一个什么条件? 。
(只需添加一个条件)三、证明题1、在平行四边形ABCD 中,E 、F 为对角线BD 上的三等分点。
求证:四边形AFCE 是平行四边形。
2、在如图菱形ABCD 中,对角线AC 、BD 相交于O ,E 、F 分别是AB 、BC 的中点。
求证:OE=OF 。
A B C DE F (第15题)B D A CF E3、已知:如图,已知:D 是△ABC 的边AB 上一点,CN ∥AB ,DN 交AC 于, 若MA=MC ,求证:四边形ADCN 是平行四边形4.已知:如图,D 是△ABC 的BC 边上的中点,DE ⊥AC ,DF ⊥AB ,垂足分别是E 、F ,且BF=CE.求证:(1)△ABC 是等腰三角形;(2)当∠A=90°时,试判断四边形AFDE 是怎样的四边形,证明你的结论.4、已知:如图7,在梯形ABCD 中A D ∥BC ,AB=DC 。
点E 、F 、G 分别在边AB 、BC 、CD 上,AE=GF=GC 。
(1) 求证:四边形AEFG 是平行四边形;(2) 当∠FGC=2∠EFB 时,求证:四边形AEFG 是矩形。
第20章《平行四边形的判定》测试题2

第20章《平行四边形的判定》测试题2(一)选择题:1.顺次连结等腰梯形各边中点所得的四边形一定是().(A)菱形(B)矩形(C)梯形(D)两条对角线相等的四边形2.已知下列四个命题:(1)对角线互相垂直平分的四边形是正方形;(2)对角线垂直相等的四边形是菱形;(3)对角线相等且互相平分的四边形是矩形;(4)四边都相等的四边形是正方形.其中真命题的个数是().(A)1 (B)2 (C)3 (D)0 3.下列命题中的真命题是().(A)一组对边平行,另一组对边相等的四边形是平行四边形(B)有一组对边和一组对角分别相等的四边形是平行四边形(C)两组对角分别相等的四边形是平行四边形(D)两条对角线互相垂直且相等的四边形是正方形4.矩形的边长为10 cm和15 cm,其中一内角平分线分长边为两部分,分别长().(A)6 cm和9 cm (B)5 cm和10 cm(C)4 cm和11 cm (D)7 cm和8 cm 5.如图,在等腰梯形ABCD中,AD∥BC,AC、BD相交于点O,则图中全等三角形共有().(A)1对(B)3对(C)2对(D)4对6.菱形周长为20 cm,它的一条对角线长6 cm,则其面积为().(A)6 (B)12 (C)18 (D)24(二)证明题:7.已知:如图,矩形ABCD中,E、F是AB上的两点,且AF=BE.求证:∠ADE=∠BCF.8.已知:如图,AD∥BC,ED∥BF,且AF=CE.求证:四边形ABCD是平行四边形.(三)附加题9.已知:如图,在梯形ABCD中,AD∥BC,AB=DC,P是AD中点.求证:BP=PC.10.证明等腰梯形判定定理:在同一底上的两个角相等的梯形是等腰梯形.(四)课后思考题(每小题10分,共30分)11.如图,在正方形ABCD中,点E、F分别在BC、CD上移动,但A到EF的距离AH 始终保持与AB长相等,问在E、F移动过程中:(1)∠EAF的大小是否有变化?请说明理由.(2)△ECF的周长是否有变化?请说明理由.。
中考数学模拟题汇总《平行四边形的判定与证明》专项练习(附答案解析)

中考数学模拟题汇总《平行四边形的判定与证明》专项练习(附答案解析)一、综合题1.如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F在AC的延长线上,∠FEC=∠B.(1)求证:DE=CF;(2)若AC=6cm,AB=10cm,求四边形DCFE的面积.2.已知△ABC内接于⊙O,AB是⊙O的直径,OD∥AC,AD=OC.(1)求证:四边形OCAD是平行四边形;(2)若AD与⊙O相切,求∠B.3.已知:如图,点D在ΔABC的边AB上,CF//AB,DF交AC于E,EA=EC.(1)如图1,求证:CD=AF;(2)如图2,若AD=BD,请直接写出和ΔBDC面积相等的三角形.4.如图,在四边形ABCD中,点E和点F是对角线AC上的两点,AE=CF,DF=BE,且DF//BE,过点C作CG⊥AB交AB的延长线于点G.(1)求证:四边形ABCD是平行四边形;(2)若tan∠CAB=25,∠CBG=45°,BC=4√2,则▱ABCD的面积是.5.已知,如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.(1)求证:△AFD≌△CEB;(2)四边形ABCD是平行四边形吗?请说明理由.6.如图,▱ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.(1)求证:BE=DF;(2)设ACBD=k,当k为何值时,四边形DEBF是矩形?请说明理由.7.如图,在ΔABC中,点D、E、F分别在AB、AC、BC上,DE // BC,EF // AB.(1)求证:ΔADE∽ΔEFC;(2)如果AB=6,AD=4,求SΔADESΔEFC的值.8.如图,已知平行四边形ABCD,过A点作AM⊥BC于M,交BD于E,过C点作CN⊥AD于N,交BD于F,连接AF、CE.(1)求证:四边形AECF为平行四边形;(2)当AECF为菱形,M点为BC的中点时,求AB:AE的值.BC,9.如图,等边△ABC的边长是4,D、E分别为AB、AC的中点,延长BC至点F,使CF=12连接CD和EF .(1)求证:DE=CF;(2)求EF的长.10.如图,在四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD交于点H.(1)求证:四边形DEBC是平行四边形;(2)若BD=9,求DH的长.11.已知锐角△ABC内接于⊙O,AD⊥BC于点D,连接AO.(1)如图1,求证:∠BAO=∠CAD;(2)如图2,CE⊥AB于点E,交AD于点F,过点O作OH⊥BC于点H,求证:AF=2OH;,BC=2√15,求AC的长.(3)如图3,在(2)的条件下,若AF=AO,tan∠BAO=1312.如图,抛物线y=x2+bx+c与x轴交于点A(−1,0),B(5,0),与y轴交于点C.(1)求抛物线的解析式和顶点D的坐标.(2)连结AD,点E是对称轴与x轴的交点,过E作EF∥AD交抛物线于点F(F在E的右侧),过点F作FG∥x轴交ED于点H,交AD于点G,求HF的长.13.如图,CD是⊙O的直径,点A是⊙O外一点,AD与⊙O相切于点D,点B是⊙O上一点(点B不与点C,D重合),连接AO,AB,BC .(1)当BC与AO满足什么位置关系时,AB是⊙O的切线?请说明理由;(2)在(1)的条件下,当∠DAO=度时,四边形AOCB是平行四边形.(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足14.如图,已知函数y= kx为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点EOD,求a、b的值;(1)若AC= 32(2)若BC∥AE,求BC的长.15.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.16.如图.在一次数学研究性学习中,小华将两个全等的直角三角形纸片Rt△ABC和Rt△DEF拼在一起,使点A与点F重合,点C与点D重合(如图),其中∠ACB=∠DFE=90°,发现四边形ABDE是平行四边形.如图,小华继续将图中的纸片Rt△DEF沿AC方向平移,连结AE,BD,当点F与点C重合时停止平移.(1)请问:四边形ABDE是平行四边形吗?说明理由.cm时,请判断四边形ABDE的形(2)如图,若BC=EF=6cm,AC=DF=8cm,当AF=92状,并说明理由.参考答案与解析1.【答案】(1)证明:在△CDE 和△ECF 中,∵∠ACB=∠ECF=90°,点D 、E 是分别是AB 、BC 的中点.∴CD=BD=AD ,∴∠B=∠DCE ,∠CED=∠ECF=90°, 又∵∠FEC=∠B ..∠FEC=∠DCE ,又∵CE=EC .∴△CDE ≌△ECF (ASA ),∴DE=CF ;(2)解:在Rt △ABC 中,∵∠ACB=90°,∴BC=√AB 2−AC 2=√102−62=8cm , ∵点D 、E 分别是AB 、BC 的中点,∴DE ∥CF ,又DE=CF , ∴四边形DCFE 是平行四边形,∴DE=12AC=12×6=3cm ,CE=12BC=12×8=4cm , ∴S 四边形DCFE =DE ×CE=3×4=12cm . 2.【答案】(1)证明:∵OA =OC =AD , ∴∠OCA =∠OAC ,∠AOD =∠ADO , ∵OD ∥AC , ∴∠OAC =∠AOD ,∴180°﹣∠OCA ﹣∠OAC =180°﹣∠AOD ﹣∠ADO , 即∠AOC =∠OAD , ∴OC ∥AD , ∵OD ∥AC ,∴四边形OCAD 是平行四边形;(2)解:∵AD 与⊙O 相切,OA 是半径, ∴∠OAD =90°, ∵OA =OC =AD , ∴∠AOD =∠ADO =45°,∵OD∥AC,∴∠OAC=∠AOD=45°,∵AB是⊙O的直径,∴∠ACB=90°,∴∠B=45°.3.【答案】(1)证明:∵CF//AB∴∠DFC=∠ADF,∠DAC=∠ACF又∵EA=EC∴ΔADE≌ΔCFE(AAS)∴CF=AD又∵CF//AD∴四边形ADCF为平行四边形∴DC=AF(有一组对边平行且相等的四边形为平行四边形)(2)解:ΔADC,ΔADF,ΔCFD,ΔCFA∵AD=BD,∴SΔADC=SΔBDC (等底等高面积相等)∵四边形ADCF是平行四边形,∴SΔADC=SΔCDF=SΔADF=SΔACFF (等底等高面积相等) .故与ΔBDC面积相等的三角形为:ΔADC,ΔADF,ΔCFD,ΔCFA.4.【答案】(1)证明:∵AE=CF,∴AE+EF=CF+EF,即AF=CE,∵DF//BE,∴∠DFA=∠BEC,∵DF=BE,∴ΔADF≅ΔCBE(SAS),∴AD=CB,∠DAF=∠BCE,∴AD//CB,四边形ABCD是平行四边形(2)245.【答案】(1)证明:∵DF∥BE,∴∠DFA=∠BEC,在△ADF和△CBE中{DF=BE∠DFA=∠BECAF=CE,∴△AFD≌△CEB(SAS).(2)解:四边形ABCD是平行四边形,理由如下:∵△AFD≌△CEB,∴AD=CB,∠DAF=∠BCE,∴AD∥BC,∴四边形ABCD是平行四边形.6.【答案】(1)证明:如图,连接DE,BF,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵E,F分别是OA,OC的中点,∴OE=12OA=12OC=OF,∴四边形DEBF是平行四边形,∴BE=DF .(2)解:由(1)已证:四边形DEBF是平行四边形,要使平行四边形DEBF是矩形,则BD=EF,∵OE=12OA=12OC=OF,∴EF=OE+OF=12OA+12OC=OA=12AC,即AC=2EF,∴k=ACBD =2EFEF=2,故当k=2时,四边形DEBF是矩形. 7.【答案】(1)证明:∵DE//BC,EF//AB,∴∠A=∠CEF,∠AED=∠C,∴△ADE∽△EFC.(2)解:∵AB=6,AD=4,∴DB=6-4=2,∵DE//BC,EF//AB,∴四边形DBFE是平行四边形,∴EF=DB=2,∵△ADE∽△EFC,SΔADE SΔEFC =(ADEF)2=(42)2=4.8.【答案】(1)证明∵四边形ABCD是平行四边形(已知),∴BC∥AD(平行四边形的对边相互平行)。
八年级数学下册平行四边形的判定练习题

BDCAO图1FEDCBA图2F E D CBA HG FEOAB C DOM ABCD图1FE DCB A4321图3F ED CBA H G 图2F E DCB A八年级数学下册平行四边形的判定练习题识记知识1)定义:两组对边分别平行的四边形是平行四边形.∵ , ∴四边形ABCD 是平行四边形.2)定理:两组对边分别相等的四边形是平行四边形.∵∴四边形ABCD 是平行四边形.3)定理:一组对边平行且相等的四边形是平行四边形.∵∴四边形ABCD 是平行四边形.4)定理:对角线互相平分的四边形是平行四边形.∵∴四边形ABCD 是平行四边形.5)定理:两组对角分别相等的四边形是平行四边形∵∴四边形ABCD 是平行四边形. 二、平行四边形性质与判定的综合应用例1: 如图, 已知:E 、F 是平行四边形ABCD 对角线AC 上的两点,并且AE=CF 。
求证:四边形BFDE 是平行四边形变式一:在□ABCD 中,E ,F 为AC 上两点,BE//DF .求证:四边形BEDF 为平行四边形.变式二:在□ABCD 中,E,F 分别是AC 上两点,BE ⊥AC 于E ,DF ⊥AC 于F.求证:四边形BEDF 为平行四边形想一想:在□ABCD 中, E ,F 为AC 上两点, BE =DF .那么可以证明四边形 BEDF 是平行四边形吗?例2:如图,平行四边形ABCD 中,AF =CH ,DE =BG 。
求证:EG 和HF 互相平分。
练习1、如图所示,在四边形ABCD 中,M 是BC 中点,AM 、BD 互相平分于点O ,那么请说明AM=DC 且AM ∥DC:1、以不在同一直线上的三点为顶点作平行四边形,最多能作( )A 、4个B 、3个C 、2个D 、1个 2、如图,在□ABCD 中,已知两条对角线相交于点O ,E 、F 、G 、H 分别是AO 、BO 、CO 、DO 的中点,以图中的点为顶点,尽可能多地画出平行四边形在四边形ABCD 中,AD ∥BC ,且AD >BC ,BC = 6cm ,P ,Q 分别从A ,C 同时出发,P 以1厘米/秒的速度由A 向D 运动,Q 以2厘米/秒的速度由C 向B 运动,几秒后四边形ABQP 成为平行四边形?1、下列条件中,能判定四边形是平行四边形的是( )A 、一组对边相等,另一组对边平行;C 、一组对角相等,一组邻角互补;B 、一组对边平行,一组对角互补;D 、一组对角互补,另一组对角相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第20章《平行四边形的判定》测试题
一、选择题
1.能判定四边形ABCD为平行四边形的题设是().
(A)AB∥CD,AD=BC; (B)∠A=∠B,∠C=∠D; (C)AB=CD,AD=BC; (D)AB=AD,CB=CD 2.在给定的条件中,能画出平行四边形的是().
(A)以60cm为一条对角线,20cm、34cm为两条邻边;
(B)以6cm、10cm为对角线,8cm为一边;
(C)以20cm、36cm为对角线,22cm为一边;
(D)以6cm为一条对角线,3cm、10cm为两条邻边
3.正方形具有而菱形不一定具有的性质是()
(A)对角线互相平分; (B)对角线相等;
(C)对角线平分一组对角; (D)对角线互相垂直4.在下列说法中不正确的是()
(A)两条对角线互相垂直的矩形是正方形;
(B)两条对角线相等的菱形是正方形;
(C)两条对角线垂直且相等的平行四边形是正方形;
(D)两条对角线垂直且相等的四边形是正方形5.下列说法不正确的是()
(A)对角线相等且互相平分的四边形是矩形;
(B)对角线互相垂直平分的四边形是菱形;
(C)一组对边平行且不等的四边形是梯形;
(D)一边上的两角相等的梯形是等腰梯形
6.不能判定四边形ABCD为平行四边形的题设是()
(A)AB=CD,AD=BC (B)AB // CD
(C)AB=CD,AD∥BC (D)AB∥CD,AD∥BC
7.四边形ABCD的对角线AC,BD相交于点O,能判定它为正方形的题设是()
(A)AO=CO,BO=DO; (B)AO=CO=BO=DO;
(C)AO=CO,BO=DO,AC⊥BD; (D)AO=BO=CO=DO,AC⊥BD 8.下列说法不正确的是()
(A)只有一组对边平行的四边形是梯形;
(B)只有一组对边相等的梯形是等腰梯形;
(C)等腰梯形的对角线相等且互相平分;
(D)在直角梯形中有且只有两个角是直角
9.如图1,在□ABCD中,MN分别是AB、CD的中点,BD分别交AN、CM于点P、Q,在结论:
①DP=PQ=QB ②AP=CQ ③CQ=2MQ ④S△ADP=1
4S ABCD
中,正确的个数为().
(A)1 (B)2 (C)3 (D)4
(1) (2) (3)
10.如图2,在梯形ABCD中,AD∥CB,AD=2,BC=8,AC=6,BD=8,则梯形ABCD的面积为().
(A)24 (B)20 (C)16 (D)12
二、填空题
11.在□ABCD中,AC与BD交于O,则其中共有_____对全等的三角形.
12.矩形的对角线相交成的角中,有一个角是60°,这个角所对的边长为20cm,则其对角线长为_______,矩形的面积为________.
13.一个菱形的两条对角线长分别为6cm,8cm,这个菱形的边长为_______,•面积S=______.
14.如果一个四边形的四个角的比是3:5:5:7,则这个四边形是_____形.
15.如图3,等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AB=6,AD=5,则△CDE的周长是________.
16.如图4,在正方形ABCD的外侧,作等边△ADE,则∠AEB=_______.
(4) (5) (6)
17.在长为1.6m,宽为1.2m的矩形铅板上,剪切如图5所示的直角梯形零件(•尺寸单位为mm),则这块铅板最多能剪出______个这样的零件.
18.如图6,ABCD中,过对角线交点O,引一直线交BC于E,交AD于F,若AB=2.4cm,BC=4cm,OE=1.1cm,则四边形CDFE周长为________.
19.已知等腰梯形的一个锐角等于60•°,•它两底分别为15cm,•49cm,•则腰长为_______.
20.已知等腰梯形ABCD中AD∥BC,BD平分∠ABC,BD•⊥DC,•且梯形ABCD•的周长为30cm,则AD=_____.
三、计算题
21.如图,已知等腰梯形ABCD中,AD∥BC,对角线AC⊥BD,AD=3cm,BC=7cm,•DE•⊥BC于E,试求DE的长.
四、证明题
22.如图,已知四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA边上的中点,求证:四边形EFGH是菱形.
23.已知如图,梯形ABCD中,AD∥BC,AM=MB,DN=NC.求证:
MN∥BC,MN=1
2(BC+AD).
答案:
1.(C)2.(C)3.(B)4.(D)5.(D)6.(C)7.(D)8.(C)9.(C)10.(A)
11.4 12.40cm
40013.5cm 24cm2 14.直角梯形
15.15 16.15°•17.12 18.8.6cm 19.34cm 20.如图,作AE⊥BC于E,DF⊥BC于F,
∴AD=EF,设BE=x.
则AB=2x,DC=2x,FC=x,
∴BD平分∠ABC,∴∠
DBC=30°.
∴DC=1
2BC,∴BC=4x.
∴EF=2x=AD.
又∵AB+BC+CD+AD=30,
∴4x+6x=30,x=3,∴AD=6(cm).
21.过D点作DF∥AC,交BC的延长线于点F,则四边形ACFD为平行四边形,•
所以AC=DF,AD=CF.
因为四边形ABCD为等腰梯形,所以AC=BD,所以BD=DF,又已知AC⊥BD,DF∥AC,•
所以BD⊥DF,则△BDF为等腰直角三角形.又因为DF⊥BC,所以
DE=1
2BF=
1
2(BC+CF)=
1
2(BC+AD)=
1
2(7+3)=5(cm).
22.证明:∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴EF=1
2AC,HG=
1
2AC,
FG=1
2BD,EH=
1
2BD.
∴EF=HG=
1
2AC,
FG=EH=1
2BD.
又∵AC=BD,∴EF=HG=FG=EH.
∴四边形EFGH是菱形.
23.证明:如图,连接AN并延长,交BC的延长线于点E.∵DN=NC,∠1=∠2,∠D=∠3,
∴△ADN≌△ECN,
∴AN=EN,AD=EC.
又AM=MB,∴MN是△ABE的中位线.
∴MN∥BC,MN=1
2BE(三角形中位线定理)
∵BE=BC+CE=BC+AD,
∴MN=1
2(BC+AD).。
