苏教版八年级下附参考答案

合集下载

苏科苏教八年级苏科苏教初二下学期物理期末试卷及答案全

苏科苏教八年级苏科苏教初二下学期物理期末试卷及答案全一、选择题1．如图所示，在水槽中有体积相等的甲、乙两个小球。

甲球漂浮在水面，乙球悬浮在水中。

它们受到的浮力分别为F甲和F乙；它们的密度分别为ρ甲和ρ乙。

下列关于甲、乙受到的浮力和它们的密度的说法，正确的是（）A．F甲>F乙，ρ甲>ρ乙B．F甲<F乙，ρ甲<ρ乙C．F甲>F乙，ρ甲=ρ乙D．F甲<F乙，ρ甲>ρ乙2．毛皮摩擦过的橡胶棒，能使毛皮和橡胶棒都带上电荷．下列说法正确的是（）A．毛皮中的原子核带负电B．橡胶棒中电子与原子核之间有斥力C．橡胶棒带正电D．毛皮与橡胶棒相互吸引3．在室温下，吹鼓一个气球，把它放进真空罩中，抽走真空罩中的气体，发现气球变大了。

下列说法正确的是（）A．气球变大因为气球内的气压变大B．抽气后，真空罩内气压大于气球内的气压C．气球内气体质量变大，体积变大，密度不变D．气球内气体质量不变，体积变大，密度变小4．如图所示的实例中，为了增大压强的是A．载重汽车安装了很多车轮B．铁轨铺在枕木上C．吸管的一端剪成斜口D．图钉帽的面积做得较大5．2017年底，“悟空”号卫星上的计算机被太空中带正电的某些粒子击中，导致“死机”。

在遥控指令下，计算机重新启动，卫星恢复正常，带正电的粒子可能是（）A．原子核质子B．原子核中子C．中子质子D．电子中子6．如图所示四个实例中，属于增大摩擦的是A．轴承之间装滚珠B．写字时用力C．门轴加润滑油D．滑冰穿冰鞋滑行7．下列关于弹簧测力计使用的说法，错误的是（）A．每个弹簧测力计都有一个测量范围，被测力应小于这个范围B．使用前必须先对弹簧测力计校零C．弹簧测力计只能竖直放置，测竖直方向的力D．弹簧测力计可以测不同方向的力8．下列实例中，通过增大压力的方法来增大摩擦的是A．运动员手上涂镁粉B．捏紧自行车的刹车装置C．给车轮转轴添加润滑油D．鞋底有凹凸不平的花纹9．我国完成了速度超过400km/h的高铁交会试验，两列高速运行的列车交会过程中，产生“强吸力”的原因是两车之间的空气（）A．流速大，压强大于列车外侧压强B．流速小，压强小于列车外侧压强C．流速大，压强小于列车外侧压强D．流速小，压强大于列车外侧压强10．将重为8牛质量分布均匀的物块（不吸水）轻放入装满水的足够大的烧杯中，溢出重为5牛的水。

苏教版八年级下附参考答案解析

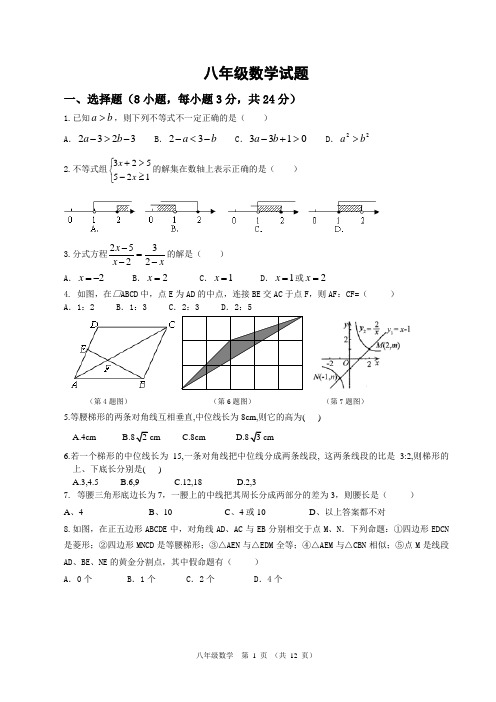
八年级数学试题一、选择题（8小题，每小题3分，共24分）1.已知b a >，则下列不等式不一定正确的是（）A ．3232->-b aB ．b a -<-32C ．0133>+-b aD ．22b a > 2.不等式组⎩⎨⎧≥->+125523x x 的解集在数轴上表示正确的是（）3.分式方程xx x -=--23252的解是（） A ．2-=x B ．2=x C ．1=x D ．1=x 或2=x4. 如图，在□ABCD 中，点E 为AD 的中点，连接BE 交AC 于点F ，则AF ：CF=（） A ．1：2 B ．1：3 C ．2：3 D ．2：5（第4题图）（第6题图）（第7题图）5.等腰梯形的两条对角线互相垂直,中位线长为8cm,则它的高为( )A.4cm C.8cm 6.若一个梯形的中位线长为15,一条对角线把中位线分成两条线段, 这两条线段的比是3:2,则梯形的上、下底长分别是( )A.3,4.5B.6,9C.12,18D.2,37. 等腰三角形底边长为7，一腰上的中线把其周长分成两部分的差为3，则腰长是（） A 、4 B 、10 C 、4或10 D 、以上答案都不对8.如图，在正五边形ABCDE 中，对角线AD 、AC 与EB 分别相交于点M 、N ．下列命题：①四边形EDCN 是菱形；②四边形MNCD 是等腰梯形；③△AEN 与△EDM 全等；④△AEM 与△CBN 相似；⑤点M 是线段AD 、BE 、NE 的黄金分割点，其中假命题有（） A ．0个 B ．1个 C ．2个 D ．4个NMDCBAN M E D CBA（第8题图）（第13题图）（第17题图）二、填空题（10小题，每小题3分，共30分）9．等腰三角形的底角为15º，腰长为10㎝，则它的面积是。

10. 如图，在等腰梯形ABCD 中，AB ∥C D ，对角线AC 平分∠BAD ，∠B =60°， CD=2㎝。

苏教版八年级下册数学(含答案)

苏教版八年级下册数学题号一二三总分得分一、选择题(本大题共20小题，共60.0分)1.要使二次根式√2x −4在实数范围内有意义，则x 的取值范围是（）A.x ＞2B.x ≥2C.x ＜2D.x =22.把√452√20化成最简二次根式的结果是（） A.32 B.34 C.√52D.2√5 3.下列二次根式中，与√a 是同类二次根式的是（）A.√3aB.√2a 2C.√a 3D.√a 44.下列各式计算正确的是（）A.√5+√2=√7B.5√6-3√3=2√3C.（√8+√50）÷2=√4+√25=7D.3√3+√27=6√35.如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，则小巷的宽度为（）A.0.7米B.1.5米C.2.2米D.2.4米6.“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a ，较短直角边长为b ，若（a +b ）2=21，大正方形的面积为13，则小正方形的面积为（）A.3B.4C.5D.67.如图，一艘海轮位于灯塔P 的南偏东45°方向，距离灯塔60nmile 的A 处，它沿正北方向航行一段时间后，到达位于灯塔P 的北偏东30°方向上的B 处，这时，B 处与灯塔P 的距离为（）A.60√3nmileB.60√2nmileC.30√3nmileD.30√2nmile8.如图，等边△OAB 的边长为2，则点B 的坐标为（）A.（1，1）B.（√3，1）C.（√3，√3）D.（1，√3）9.下列几组数中，为勾股数的是（） A.3、4、6 B.13、14、15C.7、24、25 D.0.9、1.2、1.610.若直角三角形的三边长为偶数，则这三边的边长可能是（）A.3，4，5B.6，8，10C.7，24，29D.8，12，2011.满足下列条件的三角形中，不是直角三角形的是（）A.三内角的度数之比为1：2：3B.三内角的度数之比为3：4：5C.三边长之比为3：4：5D.三边长的平方之比为1：2：312.在平行四边形ABCD 中，∠A 的平分线把BC 边分成长度是3和4的两部分，则平行四边形ABCD 周长是（）A.22B.20C.22或20D.1813.在探索“尺规三等分角”这个数学名题的过程中，曾利用了如图．该图中，四边形ABCD是矩形，E 是BA 延长线上一点，F 是CE 上一点，∠ACF=∠AFC ，∠FAE=∠FEA ．若∠ACB=21°，则∠ECD 的度数是（）A.7°B.21°C.23°D.24°14.已知平行四边形ABCD，AC、BD是它的两条对角线，那么下列条件中，能判断这个平行四边形为矩形的是（）A.∠BAC=∠DCAB.∠BAC=∠DACC.∠BAC=∠ABDD.∠BAC=∠ADB15.如图，在菱形ABCD中，AC=8，BD=6，则△ABC的周长是（）A.14B.16C.18D.2016.均匀地向一个容器注水，最后把容器注满，在注水过程中，水面高度h随时间t的变化规律如图所示（图中OABC为折线），这个容器的形状可以是（）A. B. C. D.17.已知点A（-1，1），B（1，1），C（2，4）在同一个函数图象上，这个函数图象可能是（）A. B. C. D.18.下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差：甲乙丙丁平均数（环）9.149.159.149.15方差 6.6 6.8 6.7 6.6根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（）A.甲B.乙C.丙D.丁19.“莲城读书月”活动结束后，对八年级（三）班45人所阅读书籍数量情况的统计结果如下表所示：阅读数量1本2本3本3本以上人数（人）1018134根据统计结果，阅读2本书籍的人数最多，这个数据2是（）A.平均数B.中位数C.众数D.方差20.关于2、6、1、10、6的这组数据，下列说法正确的是（）A.这组数据的众数是6B.这组数据的中位数是1C.这组数据的平均数是6D.这组数据的方差是10二、填空题(本大题共11小题，共33.0分)21.把m√−1m根号外的因式移到根号内，结果为______ ．22.能使得√(3−a)(a+1)=√3−a•√a+1成立的所有整数a的和是______ ．23.在△ABC中BC=2，AB=2√3，AC=b，且关于x的方程x2-4x+b=0有两个相等的实数根，则AC边上的中线长为______ ．24.如图，已知△ABC三条边AC=20cm，BC=15cm，AB=25cm，CD⊥AB，则CD=______ cm．25.如图，在矩形ABCD中，AB=√2，E是BC的中点，AE⊥BD于点F，则CF的长是______ ．26.如图，在正方形ABCD中，AD=2√3，把边BC绕点B逆时针旋转30°得到线段BP，连接AP并延长交CD于点E，连接PC，则三角形PCE的面积为______ ．27.在平行四边形ABCD中，对角线AC与BD相交于点O，要使四边形ABCD是正方形，还需添加一组条件．下面给出了四组条件：①AB⊥AD，且AB=AD；②AB=BD，且AB⊥BD；③OB=OC，且OB⊥OC；④AB=AD，且AC=BD．其中正确的序号是______ ．28.等腰三角形的周长为16cm，底边长为xcm，腰长为ycm，则x与y之间的关系式为______ ．29.已知函数y=2x2a+b+a+2b是正比例函数，则a= ______ ．30.记实数x1，x2中的最小值为min{x1，x2}，例如min{0，-1}=-1，当x取任意实数时，则min{-x2+4，3x}的最大值为______ ．31.当k= ______ 时，函数y=（k+3）x k2−8-5是关于x的一次函数．三、解答题(本大题共9小题，共72.0分)32.计算：-12017-丨1-√33tan60°丨+√(−2)2×（12）-2+（2017-π）0．33.已知：x2+y2-10x+2y+26=0，求（√x+y）（√x-y）的值．34.在R t△ABC中，a为直角边，c为斜边，且满足√c−5+2√10−2c=a-4，求这个三角形的周长和面积．35.已知△ABC的三边为a、b、c，且a+b=7，ab=12，c=5，试判定△ABC的形状．36.如图，在平行四边形ABCD中，边AB的垂直平分线交AD于点E，交CB的延长线于点F，连接AF，BE．（1）求证：△AGE≌△BGF；（2）试判断四边形AFBE的形状，并说明理由．37.矩形ABCD中，E、F分别是AD、BC的中点，CE、AF分别交BD于G、H 两点．求证：（1）四边形AFCE是平行四边形；（2）EG=FH．38.如图，矩形ABCD中，∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F．（1）求证：四边形BEDF是平行四边形；（2）当∠ABE为多少度时，四边形BEDF是菱形？请说明理由．39.如图，在四边形ABCD中，BD为一条对角线，AD∥BC，AD=2BC，∠ABD=90°，E为AD的中点，连接BE．（1）求证：四边形BCDE为菱形；（2）连接AC，若AC平分∠BAD，BC=1，求AC的长．40.如图，矩形ABCD中，AD=6，DC=8，菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上，AH=2．（1）若DG=6，求AE的长；（2）若DG=2，求证：四边形EFGH是正方形．苏教版八年级下册数学答案和解析【答案】1.B2.B3.C4.D5.C6.C7.B8.D9.C 10.B 11.B 12.C 13.C 14.C 15.C 16.D17.B 18.D 19.C 20.A21.-√−m 22.5 23.2 24.12 25.√2 26.6√3-10 27.①③④ 28.y =8-12x （0＜x ＜8） 29.23 30.3 31.332.解：原式=-1-|1-√33×√3|+2×4+1 =-1-0+8+1 =8．33.解：∵x 2+y 2-10x +2y +26=0，∴（x -5）2+（y +1）2=0，∴x =5，y =-1，∴（√x +y ）（√x -y ）=x -y 2=5-（-1）2．=4．34.解：∵√c −5+2√10−2c =a -4，∴c -5=0，解得c =5，∴a -4=0，解得a =4，∵在R t △ABC 中，a 为直角边，c 为斜边，∴b =√c 2−a 2=3，∴这个三角形的周长是5+4+3=12，面积是4×3÷2=6．35.解：a 2+b 2=（a +b ）2-2ab =25，c 2=25，∴a 2+b 2=c 2，∴△ABC 是直角三角形．36.（1）证明：∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠AEG=∠BFG ，∵EF 垂直平分AB ，∴AG=BG ，在△AGEH 和△BGF 中，{∠AEG =∠BFG ∠AGE =∠BGF AG =BG，∴△AGE ≌△BGF （AAS ）；（2）解：四边形AFBE 是菱形，理由如下：∵△AGE ≌△BGF ，∴AE=BF ，∵AD ∥BC ，∴四边形AFBE 是平行四边形，又∵EF ⊥AB ，∴四边形AFBE 是菱形．37.解：（1）证明：∵四边形ABCD 是矩形，∴AD ∥BC ，AD=BC ，∵E 、F 分别是AD 、BC 的中点，∴AE=12AD ，CF=12BC ，∴AE=CF ，∴四边形AFCE 是平行四边形；（2）∵四边形AFCE 是平行四边形，∴CE ∥AF ，∴∠DGE=∠AHD=∠BHF ，∵AB ∥CD ，∴∠EDG=∠FBH ，在△DEG 和△BFH 中 {∠DGE =∠BHF∠EDG =∠FBH DE =BF，∴△DEG ≌△BFH （AAS ），∴EG=FH ．38.证明：（1）∵四边形ABCD 是矩形，∴AB ∥DC 、AD ∥BC ，∴∠ABD=∠CDB ，∵BE 平分∠ABD 、DF 平分∠BDC ，∴∠EBD=12∠ABD ，∠FDB=12∠BDC ，∴∠EBD=∠FDB ，∴BE ∥DF ，又∵AD ∥BC ，∴四边形BEDF 是平行四边形；（2）当∠ABE=30°时，四边形BEDF 是菱形，∵BE 平分∠ABD ，∴∠ABD=2∠ABE=60°，∠EBD=∠ABE=30°，∵四边形ABCD 是矩形，∴∠A=90°，∴∠EDB=90°-∠ABD=30°，∴∠EDB=∠EBD=30°，∴EB=ED ，又∵四边形BEDF 是平行四边形，∴四边形BEDF 是菱形．39.（1）证明：∵AD=2BC ，E 为AD 的中点，∴DE=BC ，∵AD ∥BC ，∴四边形BCDE是平行四边形，∵∠ABD=90°，AE=DE，∴BE=DE，∴四边形BCDE是菱形．（2）解：连接AC．∵AD∥BC，AC平分∠BAD，∴∠BAC=∠DAC=∠BCA，∴AB=BC=1，∵AD=2BC=2，，∴sin∠ADB=12∴∠ADB=30°，∴∠DAC=30°，∠ADC=60°，在R t△ACD中，∵AD=2，∴CD=1，AC=√3．40.（1）解：∵AD=6，AH=2∴DH=AD-AH=4∵四边形ABCD是矩形∴∠A=∠D=90°∴在R t△DHG中，HG2=DH2+DG2在R t△AEH中，HE2=AH2+AE2∵四边形EFGH是菱形∴HG=HE∴DH2+DG2=AH2+AE2即42+62=22+AE2∴AE=√48=4√3；（2）证明：∵AH=2，DG=2，∴AH=DG，∵四边形EFGH是菱形，∴HG=HE，HG=EH在R t△DHG和R t△AEH中，{，DG=AH∴R t△DHG≌R t△AEH（HL），∴∠DHG=∠AEH，∵∠AEH+∠AHE=90°，∴∠DHG+∠AHE=90°，∴∠GHE=90°，∵四边形EFGH是菱形，∴四边形EFGH是正方形．【解析】1. 解：∵二次根式√2x−4在实数范围内有意义，∴2x-4≥0，解得：x≥2，则实数x的取值范围是：x≥2．故选：B．直接利用二次根式的概念．形如√a（a≥0）的式子叫做二次根式，进而得出答案．此题主要考查了二次根式有意义的条件，正确把握二次根式的定义是解题关键．2. 解：原式=12×√4520=12×√94=34，故选：B ．根据同底数幂的除法，可得答案．本题考查了最简二次根式，利用二次根式的除法、二次根式的性质是解题关键．3. 解：A 、√3a 与√a 不是同类二次根式；B 、√2a 2=√2a 与√a 不是同类二次根式；C 、√a 3=a √a 与√a 是同类二次根式；D 、√a 4=a 2与√a 不是同类二次根式；故选：C ．根据二次根式的性质把各个二次根式化简，根据同类二次根式的概念判断即可．本题考查的是同类二次根式的概念，判断两个二次根式是否是同类二次根式，首先要把它们化为最简二次根式，然后再看被开方数是否相同．4. 解：A 、√5+√2无法计算，故此选项错误；B 、5√6-3√3无法计算，故此选项错误；C 、（√8+√50）÷2=7√22，故此选项错误；D 、3√3+√27=6√3，正确．故选：D ．直接利用二次根式的加减运算法则化简求出答案．此题主要考查了二次根式的加减运算，正确化简二次根式是解题关键．5. 解：在R t △ACB 中，∵∠ACB=90°，BC=0.7米，AC=2.4米，∴AB 2=0.72+2.42=6.25．在R t △A ′BD 中，∵∠A ′DB=90°，A ′D=2米，BD 2+A ′D 2=A ′B ′2，∴BD 2+22=6.25，∴BD 2=2.25，∵BD ＞0，∴BD=1.5米，∴CD=BC+BD=0.7+1.5=2.2米．故选C ．先根据勾股定理求出AB 的长，同理可得出BD 的长，进而可得出结论．本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．6. 解：∵如图所示：∵（a +b ）2=21，∴a 2+2ab +b 2=21，∵大正方形的面积为13，2ab =21-13=8，∴小正方形的面积为13-8=5．故选：C ．观察图形可知，小正方形的面积=大正方形的面积-4个直角三角形的面积，利用已知（a +b ）2=21，大正方形的面积为13，可以得出直角三角形的面积，进而求出答案．此题主要考查了勾股定理的应用，熟练应用勾股定理是解题关键．7. 解：如图作PE ⊥AB 于E ．在R t △PAE 中，∵∠PAE=45°，PA=60nmile ，∴PE=AE=√22×60=30√2nmile ，在R t △PBE 中，∵∠B=30°，∴PB=2PE=60√2nmile ，故选B如图作PE ⊥AB 于E ．在RT △PAE 中，求出PE ，在R t △PBE 中，根据PB=2PE 即可解决问题．本题考查方向角、直角三角形、锐角三角函数的有关知识．解一般三角形的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．8. 解：如图所示，过B 作BC ⊥AO 于C ，则∵△AOB 是等边三角形，∴OC=12AO=1，∴R t △BOC 中，BC=√OB 2−OC 2=√3，∴B （1，√3），故选：D ．先过B 作BC ⊥AO 于C ，则根据等边三角形的性质，即可得到OC 以及BC 的长，进而得出点B 的坐标．本题主要考查了等边三角形的性质以及勾股定理的运用，解题的关键是作辅助线构造直角三角形．9. 解：A 、32+42≠62，不是勾股数；B 、（13）2+（14）2≠（15）2，不是勾股数；C 、72+242=252，是勾股数；D 、0.92+1.22≠1.62，不是勾股数．故选：C根据勾股数的定义：满足a 2+b 2=c 2 的三个正整数，称为勾股数解答即可．本题考查了勾股数的定义，比较简单．10. 解：A 、3，4，5都是奇数，选项错误；B 、∵62+82=102，∴三角形是直角三角形；C 、7，24，29中7和29是奇数，故选项错误；D 、∵82+122=208，202=400，∴82+122≠202，∴三角形不是直角三角形．故选B ．判断是否为勾股数，必须根据勾股数是正整数，同时还需验证两小边的平方和是否等于最长边的平方．本题考查了勾股定理的逆定理，解答此题要用到勾股数的定义，及勾股定理的逆定理：已知△ABC 的三边满足a 2+b 2=c 2，则△ABC 是直角三角形．11. 解：A 、因为根据三角形内角和定理可求出三个角分别为30度，60度，90度，所以是直角三角形；B 、根据三角形内角和定理可求出三个角分别为45度，60度，75度，所以不是直角三角形；C 、因为32+42=52，符合勾股定理的逆定理，所以是直角三角形；D 、因为1+2=3，所以是直角三角形．故选B ．根据三角形的内角和定理及勾股定理的逆定理进行分析，从而得到答案．本题考查了直角三角形的判定，关键是掌握勾股定理的逆定理：如果三角形的三边长a ，b ，c 满足a 2+b 2=c 2，那么这个三角形就是直角三角形．有一个角是直角的三角形是直角三角形．12. 解：在平行四边形ABCD 中，AD ∥BC ，则∠DAE=∠AEB ．∵AE 平分∠BAD ，∴∠BAE=∠DAE ，∴∠BAE=∠BEA ，∴AB=BE，BC=BE+EC，①当BE=3，EC=4时，平行四边形ABCD的周长为：2（AB+AD）=2（3+3+4）=20．②当BE=4，EC=3时，平行四边形ABCD的周长为：2（AB+AD）=2（4+4+3）=22．故选：C．根据AE平分∠BAD及AD∥BC可得出AB=BE，BC=BE+EC，从而根据AB、AD的长可求出平行四边形的周长．本题考查平行四边形的性质、等腰三角形的判定；根据题意判断出AB=BE是解答本题的关键．13. 解：∵四边形ABCD是矩形，∴∠D=90°，AB∥CD，AD∥BC，∴∠FEA=∠ECD，∠DAC=∠ACB=21°，∵∠ACF=∠AFC，∠FAE=∠FEA，∴∠ACF=2∠FEA，设∠ECD=x，则∠ACF=2x，∴∠ACD=3x，在R t△ACD中，3x+21°=90°，解得：x=23°；故选：C．由矩形的性质得出∠D=90°，AB∥CD，AD∥BC，证出∠FEA=∠ECD，∠DAC=∠ACB=21°，由三角形的外角性质得出∠ACF=2∠FEA，设∠ECD=x，则∠ACF=2x，∠ACD=3x，在R t△ACD中，由互余两角关系得出方程，解方程即可．本题考查了矩形的性质、平行线的性质、直角三角形的性质、三角形的外角性质；熟练掌握矩形的性质和平行线的性质是解决问题的关键．14. 解：A、∠BAC=∠DCA，不能判断四边形ABCD是矩形；B、∠BAC=∠DAC，能判定四边形ABCD是菱形；不能判断四边形ABCD是矩形；C、∠BAC=∠ABD，能得出对角线相等，能判断四边形ABCD是矩形；D、∠BAC=∠ADB，不能判断四边形ABCD是矩形；故选：C．由矩形和菱形的判定方法即可得出答案．本题考查了矩形的判定、平行四边形的性质、菱形的判定；熟练掌握矩形的判定是解决问题的关键．15. 解：∵在菱形ABCD中，AC=8，BD=6，∴AB=BC，∠AOB=90°，AO=4，BO=3，∴BC=AB=√42+32=5，∴△ABC的周长=AB+BC+AC=5+5+8=18．故选：C．利用菱形的性质结合勾股定理得出AB的长，进而得出答案．此题主要考查了菱形的性质、勾股定理，正确把握菱形的性质，由勾股定理求出AB是解题关键．16. 解：注水量一定，函数图象的走势是稍陡，平，陡；那么速度就相应的变化，跟所给容器的粗细有关．则相应的排列顺序就为D．故选：D．根据每一段函数图象的倾斜程度，反映了水面上升速度的快慢，再观察容器的粗细，作出判断．此题考查函数图象的应用，需注意容器粗细和水面高度变化的关联．17. 解：∵A（-1，1），B（1，1），∴A与B关于y轴对称，故C，D错误；∵B（1，1），C（2，4）∴当x＞0时，y随x的增大而增大，故D正确，A错误．∴这个函数图象可能是B，故选B．初中数学试卷第11页，共15页由点点 A （-1，1），B （1，1），C （2，4）在同一个函数图象上，可得A 与B 关于y 轴对称，当x ＞0时，y 随x 的增大而增大，继而求得答案．此题考查了函数的图象．注意掌握排除法在选择题中的应用是解此题的关键．18. 解：丁的平均数最大，方差最小，成绩最稳当，所以选丁运动员参加比赛．故选D ．利用平均数和方差的意义进行判断．本题考查了方差：一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差．方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．19. 解：由题意2出现的次数最多，故2是众数．故选C一组数据中出现次数最多的数据叫做众数，由此即可判定2是众数本题考查众数、平均数、中位数、方差等知识、解题的关键是熟练掌握这些基本概念，一组数据中出现次数最多的数据叫做众数，属于中考常考题型．20. 解：数据由小到大排列为1，2，6，6，10，它的平均数为15（1+2+6+6+10）=5，数据的中位数为6，众数为6，数据的方差=15[（1-5）2+（2-5）2+（6-5）2+（6-5）2+（10-5）2]=10.4．故选A ．先把数据由小到大排列，然后根据算术平均数、中位数和众数的定义得到数据的算术平均数，中位数和众数，再根据方差公式计算数据的方差，然后利用计算结果对各选项进行判断．本题考查了方差：一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差，关键是根据平均数，中位数和众数的定义解答．21. 解：∵-1m ≥0，∴m ＜0，∴m √−1m =-（-m ）•√−1m =-√(−m)2•√−1m =-√m 2⋅(−1m )=-√−m ．故答案为-√−m ．根据二次根式有意义的条件易得m ＜0，再根据二次根式的性质有m √−1m =-（-m ）•√−1m =-√(−m)2•√−1m ，然后根据二次根式的乘法法则进行计算即可．本题考查了二次根式的性质与化简：a =√a 2（a ≥0）．也考查了二次根式的乘法法则．22. 解：由题意可知：{(3−a)(a +1)≥0(3−a)≥0a +1≥0解得：-1≤a ≤3∵a 是整数，∴a =-1，0，1，2，3∴所有整数a 的和为：5，故答案为：5由二次根式有意义的条件即可求出a 的值．本题考查二次根式的乘除法，解题的关键是正理解二次根式的性质，本题属于基础题型．23. 解：∵关于x 的方程x 2-4x +b =0有两个相等的实数根，∴△=16-4b =0，∴AC=b =4，∵BC=2，AB=2√3，∴BC 2+AB 2=AC 2，∴△ABC 是直角三角形，AC 是斜边，初中数学试卷第12页，共15页 ∴AC 边上的中线长=12AC=2；故答案为：2．由根的判别式求出AC=b =4，由勾股定理的逆定理证出△ABC 是直角三角形，再由直角三角形斜边上的中线性质即可得出结论．本题考查了根的判别式，勾股定理的逆定理，直角三角形斜边上的中线性质；证明△ABC 是直角三角形是解决问题的关键．24. 解：∵202+152=252，∵AC 2+BC 2=AB 2，∴△ACB 是直角三角形，∵S △ACB =12⋅AC •BC=12AB •CD ，∴AC •BC=AB •CD ，20×15=25•CD ，CD=12．故答案为：12．首先利用勾股定理逆定理证明△ACB 是直角三角形，再利用三角形的面积公式可得AC •BC=AB •CD ，再代入相应数据进行计算即可．此题主要考查了勾股定理逆定理，以及直角三角形的面积，关键是掌握如果三角形的三边长a ，b ，c 满足a 2+b 2=c 2，那么这个三角形就是直角三角形．25. 解：∵四边形ABCD 是矩形，∴∠ABE=∠BAD=90°，∵AE ⊥BD ，∴∠AFB=90°，∴∠BAF+∠ABD=∠ABD+∠ADB=90°，∴∠BAE=∠ADB ，∴△ABE ∽△ADB ，∴AD AB =AB BE ，∵E 是BC 的中点，∴AD=2BE ，∴2BE 2=AB 2=2，∴BE=1，∴BC=2，∴AE=√AB 2+BE 2=√3，BD=√BC 2+CD 2=√6，∴BF=AB⋅BEAE =√63，过F 作FG ⊥BC 于G ，∴FG ∥CD ，∴△BFG ∽△BDC ，∴FG CD =BF BD =BGBC ，∴FG=√23，BG=23， ∴CG=43，∴CF=√FG 2+CG 2=√2．故答案为：√2．根据四边形ABCD 是矩形，得到∠ABE=∠BAD=90°，根据余角的性质得到∠BAE=∠ADB ，根据相似三初中数学试卷第13页，共15页角形的性质得到BE=1，求得BC=2，根据勾股定理得到AE=√AB 2+BE 2=√3，BD=√BC 2+CD 2=√6，根据三角形的面积公式得到BF=AB⋅BE AE =√63，过F 作FG ⊥BC 于G ，根据相似三角形的性质得到CG=43，根据勾股定理即可得到结论．本题考查了矩形的性质，相似三角形的判定和性质，勾股定理，熟练掌握相似三角形的判定和性质是解题的关键．26. 解：∵四边形ABCD 是正方形，∴∠ABC=90°，∵把边BC 绕点B 逆时针旋转30°得到线段BP ，∴PB=BC=AB ，∠PBC=30°，∴∠ABP=60°，∴△ABP 是等边三角形，∴∠BAP=60°，AP=AB=2√3，∵AD=2√3，∴AE=4，DE=2，∴CE=2√3-2，PE=4-2√3，过P 作PF ⊥CD 于F ，∴PF=√32PE=2√3-3， ∴三角形PCE 的面积=12CE •PF=12×（2√3-2）×（4-2√3）=6√3-10，故答案为：6√3-10．根据旋转的想知道的PB=BC=AB ，∠PBC=30°，推出△ABP 是等边三角形，得到∠BAP=60°，AP=AB=2√3，解直角三角形得到CE=2√3-2，PE=4-2√3，过P 作PF ⊥CD 于F ，于是得到结论．本题考查了旋转的性质，正方形的性质，等边三角形的判定和性质，解直角三角形，正确的作出辅助线是解题的关键．27. 解：∵四边形ABCD 是平行四边形，AB=AD ，∴四边形ABCD 是菱形，又∵AB ⊥AD ，∴四边形ABCD 是正方形，①正确；∵四边形ABCD 是平行四边形，AB=BD ，AB ⊥BD ，∴平行四边形ABCD 不可能是正方形，②错误；∵四边形ABCD 是平行四边形，OB=OC ，∴AC=BD ，∴四边形ABCD 是矩形，又OB ⊥OC ，即对角线互相垂直，∴平行四边形ABCD 是正方形，③正确；∵四边形ABCD 是平行四边形，AB=AD ，∴四边形ABCD 是菱形，又∵AC=BD ，∴四边形ABCD 是矩形，∴平行四边形ABCD 是正方形，④正确；故答案为：①③④．由矩形、菱形、正方形的判定方法对各个选项进行判断即可．本题考查了矩形、菱形、正方形的判定；熟记判定是解决问题的关键．28. 解：∵等腰三角形的周长为16cm ，底边长为xcm ，腰长为ycm ．∴x +2y =16，∴y =8-12x （0＜x ＜8）．故答案为：y =8-12x （0＜x ＜8）．根据三角形周长公式可写出y与x的函数关系式，注意用三角形三边关系表示出x的取值范围．此题主要考查等腰三角形的性质及三角形三边关系的综合运用．29. 解：∵函数y=2x2a+b+a+2b是正比例函数，∴2a+b=1，a+2b=0，解得a=2，3．故答案为23根据正比例函数的定义进行选择即可．本题考查了正比例函数的定义，掌握正比例函数的一般式y=kx是解题的关键．30. 解：画出函数y=-x2+4和y=3x的图象如图：由图可知：当x=1时，函数有最大值，最大值为3，所以min{-x2+4，3x}的最大值为3．故答案为3．在同一坐标系中画出两个函数的图象，观察最大值的位置，通过求函数值，求出最大值．本题考查了二次函数的性质和正比例函数的性质，画出函数的图象，数形结合容易求解．31. 解：∵函数y=（k+3）x k2−8-5是关于x的一次函数，∴k2-8=1，且k+3≠0．解得k=3．故答案是：3．根据一次函数的定义得到k2-8=1，且k+3≠0．本题考查了一次函数的定义．注意，一次函数的自变量x的系数不为零．32.直接利用绝对值的性质以及负指数幂的性质以及零指数幂的性质分别化简求出答案．此题主要考查了二次根式的混合运算以及绝对值的性质、负指数幂的性质、零指数幂的性质等知识，正确化简各数是解题关键．33.先配方，根据非负数的性质得出x，y的值，再代入计算即可．本题考查了二次根式的化简求值，掌握非负数的性质以及配方法是解题的关键．34.根据二次根式的性质可得c的值，进一步得到a的值，根据勾股定理可求b的值，再根据三角形的周长和面积公式计算即可求解．考查了二次根式的应用，勾股定理，三角形的周长和面积，关键是根据二次根式的性质可得a、c的值．35.根据题意求出a2+b2的值，与c2进行比较，根据勾股定理的逆定理判断即可．本题考查勾股定理的逆定理的应用，判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．36.初中数学试卷第14页，共15页（1）由平行四边形的性质得出AD∥BC，得出∠AEG=∠BFG，由AAS证明△AGE≌△BGF即可；（2）由全等三角形的性质得出AE=BF，由AD∥BC，证出四边形AFBE是平行四边形，再根据EF⊥AB，即可得出结论．本题考查了平行四边形的性质、菱形的判定方法、全等三角形的判定与性质、线段垂直平分线的性质；熟练掌握平行四边形的性质，证明三角形全等是解决问题的关键．37.（1）根据一组对边平行且相等的四边形是平行四边形证明即可；（2）可证明EG和FH所在的△DEG、△BFH全等即可．本题考查了矩形的性质、平行四边形的判断和性质以及全等三角形的判断和性质，熟记矩形的各种性质是解题的关键．38.（1）由矩形可得∠ABD=∠CDB，结合BE平分∠ABD、DF平分∠BDC得∠EBD=∠FDB，即可知BE∥DF，根据AD∥BC即可得证；（2）当∠ABE=30°时，四边形BEDF是菱形，由角平分线知∠ABD=2∠ABE=60°、∠EBD=∠ABE=30°，结合∠A=90°可得∠EDB=∠EBD=30°，即EB=ED，即可得证．本题主要考查矩形的性质、平行四边形、菱形，熟练掌握矩形的性质、平行四边形的判定与菱形的判定是解题的关键．39.（1）由DE=BC，DE∥BC，推出四边形BCDE是平行四边形，再证明BE=DE即可解决问题；（2）在R t△只要证明∠ADC=60°，AD=2即可解决问题；本题考查菱形的判定和性质、直角三角形斜边中线的性质、锐角三角函数等知识，解题的关键是熟练掌握菱形的判定方法，属于中考常考题型．40.（1）先根据矩形的性质，利用勾股定理列出表达式：HG2=DH2+DG2，HE2=AH2+AE2，再根据菱形的性质，得到等式DH2+DG2=AH2+AE2，最后计算AE的长；（2）先根据已知条件，用HL判定R t△DHG≌R t△AEH，得到∠DHG=∠AEH，因为∠AEH+∠AHE=90°，∠DHG+∠AHE=90°，可得菱形的一个角为90°，进而判定该菱形为正方形．本题主要考查了矩形、菱形的性质以及正方形的判定，解决问题的关键是掌握：矩形的四个角都是直角，菱形的四条边都线段，有一个角为直角的菱形是正方形．在解题时注意，求直角三角形的边长时，一般都需要考虑运用勾股定理进行求解．初中数学试卷第15页，共15页。

新苏教版八年级下册语文练习册答案初二课堂同步练习题参考答案

新苏教版八年级下册语文练习册答案初二课堂同步练习题参考答案新苏教版八年级下册语文练习册答案初二课堂同步练习题参考答案苏教版八下语文同步练习参考答案第一课海燕第一单元积累与运用1．高尔基春天的旋律暴风雨的预言者《童年》《在人间》《我的大学》 2．散文诗歌 3．shēn y ín cuàn qiè fěi háolüèwān yánhǒu 4．A 5．（1）压冲（2）碰箭（3）抱甩摔 6．（1）比喻拟人（2）排比（3）反复（4）比喻 7．（1）“高傲”：运用拟人的手法，表现海燕藐视狂风乌云，充满自信，压倒一切邪恶势力的气概。

（2）“飞窜”，四处逃窜，写出海鸥的惶惶不可终日，与海燕的矫健勇猛形成对比。

理解与鉴赏1.通过声音（呻吟）、动作（躲藏）、外形（肥胖）、心理（恐惧）等方面，作者将海上群鸟害怕暴风雨的各种丑态揭露无遗。

反衬出了海燕的英雄形象。

2．连用“抱”“甩”“摔”等几个动词，赋予狂风人的性格和行为，表现了风的猖狂气焰。

3．拟人。

“歌唱”“冲向”“迎接”等词语，赋予波浪以人的行为动作，突出了它积极主动的战斗热情和乐观勇敢的革命精神。

4．说明光明必将战胜黑暗，革命必将战胜反动，这是不以人的意志为转移的客观规律。

5．海燕象征英勇善战的无产阶级革命先驱者；暴风雨象征席卷一切反动腐朽势力的革命浪潮；雷电象征沙皇反动统治；大海象征革命高潮时广大人民群众力量；海鸥、海鸭、企鹅象征那些害怕革命会破坏他们安乐窝的形形色色的假革命者和不革命者。

6．（1）B（2）A （3）E拓展与提高1．略提示：举生活中遭受困难挫折的事例，紧扣勇敢顽强、乐观进取的生活态度回答。

第二课白杨礼赞积累与运用1．《见闻杂记》茅盾沈德鸿雁冰《子夜》《林家铺子》 2．抒情白杨树是“不平凡”的北方的农民，尤其象征了今天我们民族解放斗争中不可缺的朴质、坚强、力求上进的精神崇敬而赞美黄土高原非常平坦磨刀石 3．zǎi娑虬jiànɡ综颀qiàoyùn 怠nánqiánnáo恹恹逸 4．（1）扑入（2）翻起（3）涌起5．你应该联想到，在敌后的广大土地上，到处有坚强不屈，就像这白杨树一样傲然挺立的守卫他们家乡的哨兵。

苏科版八年级苏科初二下学期数学期末试卷及答案全

苏科版八年级苏科初二下学期数学期末试卷及答案全一、解答题1．自2009年以来，“中国•兴化千垛菜花旅游节”享誉全国．“河有万湾多碧水，田无一垛不黄花”所描绘的就是我市发达的油菜种植业．为了解某品种油菜籽的发芽情况，农业部门从该品种油菜籽中抽取了6批，在相同条件下进行发芽试验，有关数据如表：（1）分别求a和b的值；（2）请根据以上数据，直接写出该品种油菜籽发芽概率的估计值（精确到0.1）；（3）农业部门抽取的第7批油菜籽共有6000粒．请你根据问题（2）的结果，通过计算来估计第7批油菜籽在相同条件下进行发芽试验时的发芽粒数．2．某文化用品商店用120元从某厂家购进一批套尺，很快销售一空；第二次购买时，该厂家回馈老客户，给予8折优惠，商店用100元购进第二批该款套尺，所购到的数量比第一批还多1套．（1）求第一批套尺购进时的单价；（2）若商店以每套5.5元的价格将第二批套尺全部售出，可以盈利多少元？3．某校计划组织学生参加“书法”、“摄影”、“航模”、“围棋”四个课外兴趣小组，要求每人必须参加，并且只能选择其中一个小组．学校从全体学生中随机抽取部分学生进行问卷调查，并把调查结果制成如图所示的条形统计图和扇形统计图（部分信息未给出）．请你根据给出的信息解答下列问题：（1）求参加这次问卷调查的学生人数；（2）补全条形统计图；（3）若该校共有1200名学生，请你过计算估计选择“围棋”课外兴趣小组的学生有多少人．4．如图，在Rt △ABC 中，∠BAC ＝90°，D 是BC 的中点，E 是AD 的中点，过点A 作AF ∥BC 交BE 的延长线于点F ．（1）求证：四边形ADCF 是菱形；（3）若AC ＝6，AB ＝8，求菱形ADCF 的面积．5．如图，四边形ABCD 是正方形，点E 是BC 边上的动点（不与点B 、C 重合），将射线AE 绕点A 按逆时针方向旋转45°后交CD 边于点F ，AE 、AF 分别交BD 于G 、H 两点．（1）当∠BEA ＝55°时，求∠HAD 的度数；（2）设∠BEA ＝α，试用含α的代数式表示∠DFA 的大小；（3）点E 运动的过程中，试探究∠BEA 与∠FEA 有怎样的数量关系，并说明理由．6．如图，在正方形ABCD 内有一点P 满足AP AB =，PB PC =.连接AC 、PD .（1）求证：APB DPC ∆∆≌；（2）求PAC ∠的度数.7．已知23x =23y =求22x xy y ++的值。

苏教版八年级下册语文补充习题答案

八、（１）相同的生存环境— — —都生存在恶劣２九、略上的相似。问题探究一、１．不好。递减的排列能突出白杨树给人的震撼；连“一株” 白杨树都足以使
产党所领导的北方抗日军民的热爱。的环境中；深化了内容的表达。境，衬托出它傲然挺立的形象。
第一单元
一海燕随文练习一、犮犺 ì 犮狌 à 狀犺 á 狅狕犺 ē 二、怯呻吟崖翡蜒藏三、略四、１．“对
暴风雨的”表现了海燕渴望战斗的特点，“ 愤怒的 ” 表现了 “ 力量 ” 的不可战胜，“ 热情的”表现了“火焰”的旺盛，“胜利的”表现了“信心” 的来源，三个修饰语写出了海燕的勇敢和乌云的胆怯。惧的战斗精神和勇敢。
人改变“恹恹欲睡的情绪”，充分表现了白杨树的不平凡意义，递减的排列实质上愈益
２．写黄土高原，写种种感受，展现了白杨树不寻常的生长环二、１．白杨树与北方的农民；都具有顽强的生命力，适应恶劣环境，不怕磨折压迫。 “尤其” 在这里突出了坚持抗战的中国共产党及其所领导下的根据地抗日军民。日战争时期，需要大声疾呼，鼓动全民抗战。实际上，由于这篇文章发表于国民党统治区，限于当时的环境，有些话已经说得比较隐蔽，如没有明确提出讴歌中国共产党及其所领导的根据地军民，而是称作“北方的农民”等。此题可以有不同看法。
问题探究一、１．一方是凶狠、强大的乌云、狂风、雷声和闪电，一方是顽强、无畏、自信的海
燕和大海。最后的结果，必然是海燕和大海取得胜利。从 “ 它在大笑，它又在号

苏教版八年级下册英语配套练习册答案

苏教版八年级下册英语配套练习册答案导读：本文苏教版八年级下册英语配套练习册答案，仅供参考，如果觉得很不错，欢迎点评和分享。

Unit 2 How do you study for a test?Section B Part 21—5 CBABB 6—10 ACCCD Part 41—5 BDABC Reading Part 21—5 BCACA 6—10 Part 31. English.2. say3. about. “5.ed, don’t play5.is used6.has changed7.to ride8.riding9.bought 10.will buy B 1.are not interesting in ed to 3.is afraid of 4.playing the piano C 1—5 CCBBC 6—10 BABCC Section B Part 21—5 BDBAC 6—10 DCBAB Part 41—5 ABABC Reading Part 21—5 CDBAD 6—10 ABCDB Part 31. felling frightened when you’rearound other people 2. More than 80% of them3. Because of their life experiences（山东教育版）Unit 1 Have you ever been to anamusement park?Section A Part 3A 1.have,been,have been to2.has gone to3.has been in4.Have,been to5.has,been B 1.Have,cleaned,have done, did 3.has Finished6.gave C 1—8 BCBACBAC Section B Part 21—8 Part 41—6 DDDADC 1—5 —10 Part 32.那个人把帽子和大衣拉的越紧。

新苏科苏教版八年级苏科苏教初二下学期物理期末试卷及答案全

新苏科苏教版八年级苏科苏教初二下学期物理期末试卷及答案全一、选择题1．行驶的车辆突然刹车时人向前倾的原因是（）A．人具有惯性B．车辆具有惯性C．人受到向前推的力D．车辆对人施加一个向前的力2．有A、B两个实心球，A球的质量是B球的两倍，A球的体积是B球的四倍，那么A球的密度是B球的（）A．两倍B．一倍C．二分之一D．四分之一3．流体的压强与流速有关，下列现象与这一物理知识无关的是（）A．如图中，同学向前吹气，纸条向上运动B．如图中，在气球的左侧吹气，气球向左侧运动C．如图中，同学用吸管吸饮料，饮料进入口中D．如图中，在硬币上方吹气，可以将硬币吹入碗中4．甲、乙两相同的容器中装有体积相等的两种液体，静止放置在水平桌面上．将同种材料制作的实心物体A、B分别放入两容器中，静止时液面等高，如图所示．则A．A的重力等于B的重力B．甲杯中液体的密度小于乙杯中液体的密度C．甲杯对桌面的压力大于乙杯对桌面的压力D．两容器底部所受液体压强相等5．我们经常看到这样的现象：在无风的天气，汽车在马路上快速驶过以后，马路两边的树叶会随风飘动，如图所示，汽车向左行驶，马路两边的树叶会沿着A、B、C哪一个方向飘动（）A．向A方向飘动B．向B方向飘动C．向C方向飘动D．条件不足，无法判断6．把体积相等的甲乙两个实心小球同时放入装有适量水的杯中，两球均沉在杯底（如图），向水杯中加入适量盐水后。

甲球上浮，乙球仍沉在杯底，则下列分析中正确的是（）A．甲球的密度大于乙球的密度B．加入盐水前，甲乙两球对杯底的压力相等C．加入盐水后，甲球所受浮力变大，乙球所受浮力不变D．加入盐水后，乙球对杯底的压力变小7．以下物体中质量最接近200g的是（）A．苏科版物理八年级（下）课本的质量B．一个鸡蛋C．一张课桌D．一只母鸡8．下列关于惯性的说法正确的是（）A．行驶的车突然刹车，乘客前倾，说明车有惯性B．足球在草地上越滚越慢，它的惯性越来越小C．跳绳时加大摇绳的速度，可以增加绳的惯性提高成绩D．骑电动车戴头盔，可减小摔倒时惯性带来的伤害9．公交车配备逃生锤，遇到紧急情况时，乘客可以用逃生锤打破车窗玻璃逃生，为了更容易打破玻璃，逃生锤外形应选择图中的A．B．C．D．10．水平桌面上放有甲、乙两个装有不同液体的相同容器，现把两个完全相同的实心小球分别缓慢放入两容器中，两小球静止时液面恰好相平，如图所示，下列5个说法中正确的有（）①两小球受到的浮力相等②甲容器中液体的密度较小③甲容器中液体的质量较小④甲容器底部受到液体压强大⑤甲容器对水平桌面的压力小A．1 个B．2 个C．3 个D．4 个11．下列说法符合科学事实的是（）A．如图：马德堡半球实验第一次测出了标准大气压的大小B．如图：牛顿受小球从斜面滚下的实验及其他研究启发得出了惯性定律C．如图：阿基米德原理揭示了物体浸入液体的深度越深，受到的浮力也越大D．如图：太阳光的色散主要是由于光的反射12．成语“孤掌难鸣”说明的力学道理是（）A．一个巴掌的力太小B．一个物体也能产生力的作用C．力是物体对物体的作用D．两个不接触的物体之间能产生力的作用二、填空题13．如图a所示，盛有水的烧杯随小车一起水平向右做______运动，当烧杯中的水面出现如图b所示的状态时，则小车此时正在做______（加速/减速/匀速）运动，做出上述判断的根据是______具有惯性。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

10. 如图，在等腰梯形ABCD 中，AB ∥C D ，对角线AC 平分∠BAD ，∠B =60°， CD=2㎝。

则梯形ABCD 的面积是 . 11．矩形的两条对角线相交于点O ，若∠AOD=120°，AC+AB=18cm ，则矩形的对角线长是 cm.12．已知如下图：菱形ABCD 中，对角线AC = 16 cm ，BD = 12 cm ，BE ⊥BC 于点E ，则BE 的长.为。

13. 如图，以点O 为位似中心，将五边形ABCDE 放大后得到五边形E D C B A '''''，已知OA=10cm ，A O '=20cm ，则五边形ABCDE 的周长与五边形E D C B A '''''的周长的比值是______. 14.若关于x 的分式方程8128-++=-x m x x 有增根，则m = ． 15. 从1、2、3、4这四个数中一次随机地取两个数，则其中一个数是另一个数两倍的概率是 . 16在平面直角坐标系中，过坐标原点的一条直线与函数xy 2=的图像交于P 、Q 两点，则线段PQ 长的最小值是 . 17. 如图，DE 是△ABC 的中位线，M 、N 分别是BD 、CE 的中点，则△ADE 与四边形BCNM 的面积之比等于 .三、解答题（10小题，共96分）19.（8分）解不等式组 ⎩⎨⎧≥+->+.33)1(2,03x x x ，并判断23=x 是否该不等式组的解．20. （8分）化简，求值： 111(11222+---÷-+-m m m m m m ），其中m =3．21.如图，△ABC 中，BD 、CE 是△ABC 的两条高，点F 、M 分别是DE 、BC 的中点。

求证：FM ⊥DE 。

C22.已知:如图所示,BD 是△ABC 的角平分线,EF 是BD 的垂直平分线,且交AB 于E,交BC 于点F. 求证:四边形BFDE 是菱形.23．如图，等腰梯形ABCD 中，AD ∥BC ，∠DBC=45º。

翻折梯形ABCD ，使点B 重合于点D ，折痕分别交边AB 、BC 于点F 、E 。

若AD=2，BC=8，求：（1）BE 的长。

（2）CD ：DE 的值。

E BFA D DB AEF24．正方形ABCD的边长为４，BE∥AC交DC的延长线于E。

（１）如图１，连结AE，求△AED的面积。

（２）如图２，设P为BE上（异于B、E两点）的一动点，连结AP、CP，请判断四边形APCD 的面积与正方形ABCD的面积有怎样的大小关系？并说明理由。

23. （10分）某市在道路改造过程中，需要铺设一条长为1000米的管道，决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米，且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.（1）甲、乙工程队每天各能铺设多少米？（2）如果要求完成该项工程的工期不超过10天，那么为两工程队分配工程量（以百米为单位，取整数）的方案有几种？请你帮助设计出来.24.（10分）近年来，我国煤矿安全事故频频发生，其中危害最大的是瓦斯，其主要成分是CO.在一次矿难事件的调查中发现：从零时起，井内空气中CO的浓度达到4 mg/L，此后浓度呈直线型增加，在第7小时达到最高值46 mg/L，发生爆炸；爆炸后，空气中的CO浓度成反比例下降.如图，根据题中相关信息回答下列问题：（1）求爆炸前后．．空气中CO浓度y与时间x的函数关系式，并写出相应的自变量取值范围；（2）当空气中的CO浓度达到34 mg/L时，井下3 km的矿工接到自动报警信号，这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生？（3）矿工只有在空气中的CO浓度降到4 mg/L及以下时，才能回到矿井开展生产自救，求矿工至少在爆炸后多少小时才能下井?（第24题图）25.（10分）如图，正比例函数12y x=的图象与反比例函数kyx=(0)k≠在第一象限的图象交于A点，过A点作x轴的垂线，垂足为M，已知OAM∆的面积为1.（1）求反比例函数的解析式；（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x 轴上求一点P，使PA PB+最小.（第25题图）26.（10分）数学课上，李老师出示了这样一道题目：如图1，正方形ABCD的边长为12，P为边BC延长线上的一点，E为DP的中点，DP的垂直平分线交边DC于M，交边AB的延长线于N.当6CP=时，EM与EN的比值是多少？经过思考，小明展示了一种正确的解题思路：过E作直线平行于BC交DC，AB分别于F，G，如图2，则可得：DF DEFC EP=，因为DE EP=，所以DF FC=.可求出EF和EG的值，进而可求得EM与EN的比值.(1) 请按照小明的思路写出求解过程.(2) 小东又对此题作了进一步探究，得出了DP MN=的结论.你认为小东的这个结论正确吗？如果正确，请给予证明；如果不正确，请说明理由.（第26题图）27．(12分)（1）探究新知：如图1，已知△ABC与△ABD的面积相等，试判断AB与CD的位置关系，并说明理由．HG FE（第27题图）（2）结论应用：如图2，点M ，N 在反比例函数xky =（k ＞0）的图象上，过点M 作ME ⊥y 轴，过点N 作NF ⊥x 轴，垂足分别为E ，F ．试证明：MN ∥EF ．（3）变式探究：如图3，点M ，N 在反比例函数xky =（k ＞0）的图象上，过点M 作ME ⊥y 轴，过点N 作NF ⊥x 轴，过点M 作MG ⊥x 轴，过点N 作NH ⊥y 轴，垂足分别为E 、F 、G 、H ．试证明：EF ∥GH ．28.（12分）如图，凸四边形ABCD 中，点E 在边CD 上，连接AE 、BE ．给出下列五个关系式:①AD ∥BC ；②DE=EC ； ③∠1=∠2； ④∠3＝∠4； ⑤AD+BC=AB .将其中的三个关系式作为已知条件、另外两个关系式作为结论，可以构成一些命题（下面各小题的命题须符合此要求）． (1)共计能够成个命题； (2)写出三个真命题：①如果、、，那么、； ②如果、、，那么、； ③如果、、，那么、 . 请选择上述三个命题中的一个写出它是真命题的理由：证明：我选择证明命题（填序号），理由如下：4321ED CBA（第28题图）(3)请写出一个假命题（不必说明理由）：如果、、，那么、 .2010-2011学年度第二学期期末考试八年级数学试题参考答案一、选择题（每小题3分，共24分）二、填空题（每小题3分，共30分）9.答案不唯一，比如：012>+x ； 10.①②④；11. 对角线互相平分的四边形是平行四边形； 12.30000 13. 1︰2； 14. 7； 15.31； 16.4； 17. 4:7； 18.4. 三、解答题（ 10小题，共96分）19.不等式租的解集是13≤<-x （6分），23=x 是该不等式组的解（2分）． 20.解：原式=1)1()1)(1(11222+--+-÷-+-m m m m m m m=111)1)(1()1(22+--+∙+--m m m m m m=m m m m m -+∙+-2111 =m m m --21 =)1(1--m m m =m1．（ 6分）∴当m =3时，原式=3331=．（ 8分） 21.如右图（8分）。

22. （1）乙盒中蓝球的个数为3个（4分）；（2）从甲、乙两盒中分别任意摸取一球，这两球均为蓝球的概率为81.（8分） 23.（1）解：设甲工程队每天能铺设x 米，则乙工程队每天能铺设（20x -）米. 根据题意得：35025020x x =-. 解得70x =.检验: 70x =是原分式方程的解.答：甲、乙工程队每天分别能铺设70米和50米. （5分）（2）解：设分配给甲工程队y 米，则分配给乙工程队（1000y -）米.由题意，得10,70100010.50yy ⎧≤⎪⎪⎨-⎪≤⎪⎩解得500700y ≤≤．所以分配方案有3种．方案一：分配给甲工程队500米，分配给乙工程队500米；方案二：分配给甲工程队600米，分配给乙工程队400米；方案三：分配给甲工程队700米，分配给乙工程队300米．（10分） 24.解：（1）因为爆炸前浓度呈直线型增加，所以可设y 与x 的函数关系式为1y k x b =+ 由图象知1y k x b =+过点（0，4）与（7，46） ∴14746b k b =⎧⎨+=⎩. 解得164k b =⎧⎨=⎩,∴64y x =+,此时自变量x 的取值范围是0≤x ≤7. (不取x =0不扣分，x =7可放在第二段函数中) 因为爆炸后浓度成反比例下降，所以可设y 与x 的函数关系式为2k y x=. 由图象知2k y x=过点（7,46）， ∴2467k =. ∴3222k =, ∴322y x=，此时自变量x 的取值范围是x ＞7. （2）当y =34时，由64y x =+得,6x +4=34，x =5 . ∴撤离的最长时间为7-5=2(小时). ∴撤离的最小速度为3÷2=1.5(km/h)(3)当y =4时，由322y x=得, x =80.5，80.5-7=73.5(小时). ∴矿工至少在爆炸后73.5小时能才下井25.解：（1）设A 点的坐标为（a ，b ），则k b a =.∴ab k =.∵112ab =,∴112k =.∴2k =. ∴反比例函数的解析式为2y x=.（4分） (2) 由212y xy x ⎧=⎪⎪⎨⎪=⎪⎩ 得2,1.x y =⎧⎨=⎩ ∴A 为（2，1）. 设A 点关于x 轴的对称点为C ，则C 点的坐标为（2，1-）. 令直线BC 的解析式为y mx n =+.∵B 为（1，2）∴2,12.m n m n =+⎧⎨-=+⎩∴3,5.m n =-⎧⎨=⎩∴BC 的解析式为35y x =-+. 当0y =时，53x =.∴P 点为（53，0）. （用几何方法——相似三角形来计算，亦可）（10分） 26.（1）解：过E 作直线平行于BC 交DC ，AB 分别于点F ，G ，则DF DE FC EP =，EM EF EN EG=，12GF BC ==. ∵DE EP =，∴DF FC =.∴116322EF CP ==⨯=，12315EG GF EF =+=+=.∴31155EM EF EN EG ===. （5分）（2）正确，理由如下：作M H ∥BC 交AB 于点H ，则MH CB CD ==，90MHN ∠=︒. ∵1809090DCP ∠=︒-︒=︒， ∴DCP MHN ∠=∠.∵90MNH CMN DME CDP ∠=∠=∠=︒-∠，90DPC CDP ∠=︒-∠， ∴DPC MNH ∠=∠.∴DPC MNH ∆≅∆. ∴DP MN =.（10分）27．（1）证明：分别过点C ，D ，作CG ⊥AB ，DH ⊥AB ，垂足为G ，H ，则∠CGA ＝∠DHB ＝90°． ∴ CG ∥DH ．∵ △ABC 与△ABD 的面积相等， ∴ CG ＝DH ． ∴ 四边形CGHD 为平行四边形． ∴ AB ∥CD ．（4分）（2）①证明：连结MF ，NE ．设点M 的坐标为（x 1，y 1），点N 的坐标为（x 2，y 2）． ∵ 点M ，N 在反比例函数xky =（k ＞0）的图象上， ∴ k y x =11，k y x =22．∵ ME ⊥y 轴，NF ⊥x 轴， ∴ OE ＝y 1，OF ＝x 2． ∴ S △EFM ＝k y x 212111=⋅， S △EFN ＝k y x 212122=⋅． ∴S △EFM ＝S △EFN ．由（1）中的结论可知：MN ∥EF ．（8分）（3）法一：连接FM 、EN 、MN ，同（2）可证MN ∥EF ，同法可证GH ∥MN ，故EF ∥GH ．法二：直接利用OE ·OG=OF ·OH 证△OEF ∽△OHG(具体过程略)（12分）根据表格容易知道本题答案应为：(1)10（3分）;（2）表中9个真命题任选其3（5分），理由略（8分）；（3）假命题是：“如果DE=EC 、∠1=∠2、∠3＝∠4，那么AD ∥BC 、AD+BC=AB.”（12分）（时间紧促，水平有限，以上答案仅供参考，敬请批评指正！欢迎交流：江苏省兴化市板桥初级中学顾厚春，QQ ：646002269，谢谢！2011年6月）。