第二十三章《旋转》复习课
第23章旋转复习课
[解析] B根据轴对称图形和中心对称图形的定义可知A是轴对称图形,但不是中心对称图形;B是中心对称图形,但不是轴对称图形;是轴对称图形,但不是中心对称图形;D中心对称图形又是轴对称图形.考点二与旋转变换有关的作图问题例2 如图23-2所示,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-点C的坐标为(-3,3).(1)将Rt△ABC沿x轴正方向平移5Rt△A1B1C1,试在图上画出Rt△A1B1C1出点A1的坐标;(2)将原来的Rt△ABC绕点B顺时针旋转得到Rt△A2B2C2,试在图上画出Rt[解析] 本题是一道平移和旋转作图题,平移的特征,可以先确定点A,B,对应点A1,B1,C1.然后顺次连接A1B1C1A1,即得平移后的三角形;根据旋转的特征,确定点A1,B1,C1旋转后的对应点C2,然后顺次连接三个点即得Rt△解:(1)A(-1,1),如下图;(2)如下图.考点三图案设计问题例3 用四块如图23-4(1)所示的正方形卡片解:解法不唯一,如图23-5:考点四旋转中的计算问题例4 如图23-6所示,将△OAB绕点O按逆时针方向旋转至△OA′B′,使点B恰好落在边′B′上.已知AB=4 cm,BB′=1 cm,则的长是___3_____cm.解析] 由旋转可知,△OAB≌△OA′B′,所以′B′=AB=4 cm,所以A′B=A′B′-B′=3(cm).例5 如图23-7①,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C 连接AF和BE.(1) 线段AF和BE有怎样的大小关系?证明你的结论;(2) 将图23-7①中的△CEF绕点C旋转一定的中的结论还成立吗?绕点C旋转一定的(1)中的结论是否还根据以上的活动,归纳你的发现.解析] 解答本题时应着眼于图形的旋转不变FC=EC,∠BCF=∠FCE+∠CEF有公共顶点,不论两个三角形旋转至怎样的位置,总有通过这节课的复习,你对旋转这一章有什么样题,83页第题页,做练习册第二十三章旋转复习。
人教版九年级数学上册课件:第二十三章 旋转 单元复习课(共19张PPT)

6
变式训练
2. 如图1-23-36-4, ABCD的两条对角线AC,BD相交
于点O. 以O为坐标原点,建立平面直角坐标系,点A的
坐标为(-3,2),点B的坐标为(2,2).
(1)写出点D,C的坐标;
(2)求S
.
7
变式训练
解:(1)点D的坐标为(-2,-2),点C的坐标为(3,
பைடு நூலகம்
-2).
(2)如答图23-36-1所示,过点B作BE⊥CD于点E.
3
典型例题
知识点2:中心对称与中心对称图形
【例2】如图1-23-36-3,△ABC绕点O旋转180°后得
到△A1B1C1,下列说法: ①∠BAC=∠B1A1C1;②AC=A1C1;③OA=OA1; ④△ABC与△A1B1C1的面积相等,其中正确的有 ( D)
A. 1个
B. 2个
C. 3个
D. 4个
∵点A的坐标为(-3,2),点B的坐标为(2,2),
∴AB=2+3=5.
∵点C的坐标为(3,-2),
∴BE=2+2=4.
∴S
=AB·BE=5×4=20.
8
变式训练
3. △ABC在平面直角坐标系中的位置如图1-23-36-6所 示,其中每个小正方形的边长为1个单位长度.
9
变式训练
(1)画出△ABC关于原点O的中心对称图形△A1B1C1; (2)△A1B1C1中顶点A1的坐标为__(__1_,_-_2_)__,若P (a,b)为△ABC边上一点,则按照(1)中作图,点 P对应的点P1的坐标为__(_-_a_,__-b_)__.
12
巩固训练
7. 如图1-23-36-8,已知∠BAC=40°,把△ABC绕着 点A顺时针旋转,使得点B与CA的延长线上的点D重合. (1)△ABC旋转了多少度? (2)连接CE,试判断△AEC的形状; (3)求∠AEC的度数.
人教版数学九年级上册第二十三章《旋转复习课》课件

B. -1
C. 1
B )
D. -7
13. 如图,正方形 OABC 的边长为2,将正方形 OABC 绕原点 O 逆时针旋转45°,则点
B 的对应点 B1的坐标为(
D )
A. (0,2)
B. (-2,0)
C. (0, 2 )
D. (-2 2 ,0)
14. [2023·濮阳统考二模]如图,点 A 的坐标为(-4,4),点 C 的坐标为(-2,
(-1,-1) .
第6题图
类型之四
旋转的性质与中心对称的性质应用
7. 如图,在Rt△ ABC 中,∠ B =32°,∠ C =90°,将其绕点 A 按顺时针方向旋转到
△ AB1 C1的位置,使得 C , A , B1在同一条直线上,那么旋转角的度数为(
A. 32°
B. 90°
第7题图
C. 122°
度的正方形).
(1)若△ ABC 和△ A1 B1 C1关于原点 O 成中心对称,画出△ A1 B1 C1;
(2)将△ ABC 绕着点 A 顺时针旋转90°,画出旋转后得到的△ AB2 C2;
解:(1)(2)如答图所示,△ A1 B1 C1和△ AB2 C2即为所作.
答图
(3)在 x 轴上存在一点 P ,满足点 P 到点 B1与点 C1距离之和最小,请直接写出 PB1+
(2)将△ ADE 绕点 A 逆时针旋α,如图2所示,直线 BD , CE 相交于点 F ,连接 AF .
求证:∠ BFC =∠ AFB =∠ AFE ;
(2)证明:如答图1,分别过点 A 作 AN ⊥ BD 于点 N ,
AM ⊥ EC 于点 M . ∵△ ABC 和△ ADE 是两个等边三角形,
第23章 旋转复习课-九年级数学上册教学课件(人教版)

考点3:中心对称
典 1.中心对称:把一个图形绕着某一个点旋转_1_8_0_º_,如果它能与 例 另一个图形重合,那么就说这两个图形成中心对称,这个点叫
原 做对称中心,这两个图形中的对应点叫做关于中心的对称点. 理 2.中心对称的特征:中心对称的特征:在成中心对称的两个图
精 形中,对应点所连线段都经过 对称中心 ,并且被对称中心_平__分_ 炼 3.中心对称图形:把一个图形绕某个点旋转180º,如果旋转后
典 4.如图,从前一个农民有一块平行四边形的土地,地里有一 例 个圆形池塘.财主立下遗嘱:要把这块土地平分给他的两个儿
子,中间池塘也平分.财主的两个儿子不知怎么做,你能想个 原 理 办法吗?
解析 先找到平行四边形对角线的交点A 精 ,过点A、B两点作一条直线可以了.
炼
AB
提 升
03
OPTION
目录
原 解:(1)如图所示;
理 (2)如图所示,点A2的坐标为(-3,-2),B2的
坐标为(-1,-3).
精 炼
易错提示:作旋转图形不要搞错方向.
y A1 B
B1 O
A x
A2
提 升
B2
考点2:旋转变换
典 3.如图,有一张不规则纸片,若连接EB,则纸片被分为矩形FABE 例 和菱形EBCD,请你用无刻度的直尺画一条直线把这张纸片分成
升 中心.
图2 M N
旋转的特征
典 1.旋转过程中,图形上_每__一__点__都__绕__旋__转__中__心__,按_同__一__旋__转__方__向_ 例 旋转_同_ 样大小的角度.
原 2.任意一对对应点与旋转中心的连线所成的角都是_旋__转__角___, 理 对应点到旋转中心的距离都__相__等__.
人教版数学九年级上册第二十三章《旋转第一课时》复习课件

.
思路分析:首先根据关于原点对称的点的坐标特征可得 b=3,2a-1=3,计
算出 a,b 的值,再根据关于 y 轴对称的点的坐标特点:横坐标互为相反数,
纵坐标不变可得答案.
解析:由题意,得 b=3,2a-1=3,
解得 b=3,a=2,
则 P(2,3),
点 P(2,3)关于 y 轴的对称点 P′的坐标为(-2,3).
OD=OB=4;③由△BOD 为等边三角形得到∠BDO=60°,再利用旋转的性质得
CD=AO=3, 然 后 根 据 勾 股 定 理 的 逆 定 理 可 证 明 △ OCD 为 直 角 三 角 形 ,
∠ODC=90°,所以∠BDC=∠BDO+∠ODC=150°.(2)根据旋转的性质得∠OBD=
∠ABC=90°,BO=BD,CD=AO,则可判断△OBD 为等腰直角三角形,则 OD= 2OB,
将△BAO 绕点 B 顺时针旋转后得到△BCD,连接 OD.当 OA,OB,OC 满足什么
条件时,∠ODC=90°?请给出证明.
思路分析:(1)①根据等边三角形的性质得 BA=BC,∠ABC=60°,再根据旋转
的性质得∠OBD=∠ABC=60°,于是可确定旋转角的度数为 60°;②由旋转
的性质得 BO=BD,加上∠OBD=60°,则可判断△OBD 为等边三角形,所以
质并准确识图是解题的关键.
1.如图,将△ABC 绕点 A 按顺时针方向旋转 115°后能与△
AB1C1 重合,若∠C=90°,且点 C,A,B1 在同一条直线上,
则∠BAC1 等于( C
A.30°
)
B.40°
C.50°
D.60°
知识点二:轴对称图形和中中心对称图形的是(
第23章旋转复习课课件
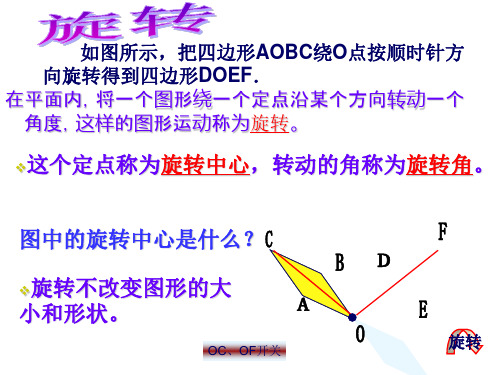
B C
对应点到旋转中心的距离相等; 对应点与旋转中心连线段的夹角等于旋转角.
用“旋转”来分析图案的形成过程.
如图:1.是由
为基本图案,
2.绕
旋转
次得到.
3.旋转角分别是:
。
4.这个图案至少绕中心点旋转 才能与原图案重合。
度,
试一试
(2)如图,香港特别行政区区旗中央的紫荆花图案由 5 个相同的花瓣组成,它是由其中一个花瓣经过 几次旋转得到的? 其中旋转角多少度?
3.写出函数y=- 3
x
与y=
3 x
具有的一个共同
性质________(用对称的观点写).
☆归纳
两个点关于原点对称时,它们的坐标符号相反, 即点P(x,y)关于原点O的对称点P/(-x,-y).
☆练一练
1.下列函数中,图象一定关于原点对称的图象是( )
A.y= 1
x
B.y=2x+1
C.y=-2x+1
D.以上三种都不可能
2.如果点P(-3,1),那么点P(-3,1)关于原点 的对称点P/的坐标是P/_______.
3
旋转后与另一图形重合
有一条对称轴—线
图形沿轴对折180
°
°
翻折后与另一图形重合
名称
线 段
角
图形
等腰三角 形
平行四边 形
中心对称 轴对称图 对称中心,对称轴
图形Hale Waihona Puke 形线段中点是
是 线段的中垂线和
线段本身所在的
直线
不是 是
角平分线所在 的直线
不是
是 底边的中垂线
是 不是 对角线交点
名称
矩形
菱形 正方形 圆
人教版数学九年级上册 第二十三章 旋转(章末总结)(复习课件)

B.
C.
D.
的
07
题型七(设计图案)
14 在下列四种图形变换中,如图图案包含的变换是( )
A.平移、旋转和轴对称 B.轴对称和平移
C.平移和旋转
D.旋转和轴对称
15 五一节前,市园林部门准备在文化广场特设直径均为4米的八个圆形花坛,在内放置面
积相同的两种颜色的盆栽草花,要求各个花坛内两种草花的摆设不能相同,如图中的①、
故选:B.
)
04
题型四(中心对称的性质)
7 如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是(
A.O1
B.O2
C.O3
D.O4
8.(2020·甘肃张掖市九年级期末)如图,四边形ABCD是
菱形,O是两条对角线的交点,过O点的三条直线将菱形分成
阴影和空白部分.当菱形的两条对角线的长分别为6和8时,
形重合,那么就说这两个图形关于这个点对称或中心对称。
1)这个点叫做对称中心。
2)这两个图形中的对应点叫做关于中心的对称点。
中心对称的性质: 1)中心对称的两个图形,对称点所连线段经过对称中心,而且被对
称中心所平分。
2)中心对称的两个图形是全等形。
基础巩固(平移、轴对称、旋转的区别与联系)
04
平移
相同点
120°
旋转角度是_________.
O
120°
P′
02
基础巩固(旋转的性质)
1)旋转前、后的图形全等。
2)对应点到旋转中心的距离相等。
3)对应点与旋转中心所连线段的夹角等于旋转角。
03
基础巩固(理解中心对称的概念和性质)
中心对称的概念: 像这样,把一个图形绕某一个点旋转180º,如果它能够与另一个图
23章 旋转复习课

教学过程一、导入新课1.同学们可以回想一下,旋转的知识中学会了那些知识?我们一起本章的知识结构图。
结构图图形的旋转1.旋转的定义:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形变换称为旋转,这个定点称为旋转中心,转动的角称为旋转角.注意:在旋转过程中保持不动的点是旋转中心.2.旋转的三个要素:旋转中心、旋转的角度和方向.3.旋转的性质:(1)对应点到旋转中心的距离相等;(2)对应点与旋转中心所连线段的夹角等于旋转角;(3)旋转前后的图形全等.4.简单图形的旋转作图:(1)确定旋转中心;(2)确定图形中的关键点;(3)将关键点沿指定的方向旋转指定的角度;(4)连结各点,得到原图形旋转后的图形.5.对称中心的确定:将其中的两个关键点和它们的对称点的连线作出来,两条连线的交点就是对称中心.6.关于中心对称的作图:(1)确定对称中心;(2)确定关键点;(3)作关键点的关于对称中心的对称点;(4)连结各点,得到所需图形.7、关于原点对称的点的坐标:(a,b)关于原点的对称点是(-a,-b)二、例题讲解例1.把△AOB绕点O逆时针方向旋转90°,画出旋转后的图形.解:按逆时针方向把OA旋转到OA′,使∠AOA′=90°,把OB旋转到OB′,使∠BOB′=90°,如图.例2.如图,Rt△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C的位置,使B在斜边A′B′上,A′C与AB相交于D,试确定∠BDC的度数.解:∵△A′B′C是由△ABC旋转所得,∴∠B′=∠ABC=60°,B′C=BC,∴△B′BC是等边三角形∴∠BCB′=60°.∵∠BCD=90°-60°=30°,∴∠BDC=180°- (60°+30°)=180°-90°=90°.例3.已知E、F分别在正方形ABCD边AB和BC上,AB=1,∠EDF=45°.求△BEF的周长.解:∵ABCD是正方形,∴∠ADC=90°,AD=DC=AB=BC=1.三,小结师:今天我们一起度过了开心快乐的一节课,相信大家一定会有所收获你有哪些收获?学生发言,教师点评四.板书设计第23章旋转复习课1.结构图2.例题作业设计必做选做教学反思。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第23章《旋转》系统复习课学案
学习目标:1.了解旋转定义;2.理解旋转的性质;3.了解中心对称的性质;4.了解各种中
心对称图形;5.探索图形的变换。
学习过程:
一. 基本知识梳理
1.如图,请同学们在正方形网格中画出将△ABC 绕着点A 顺时针旋转90°的图形 △ AB 1C 1 。
2.再如上图,请同学们在正方形网格中画出将△ABC 绕着点A 顺时针旋转180°的图形 △ AB 2C 2 。
3.如图,若以点A 为坐标原点以AB 所在的直线为x 轴建立直角坐标系,则点C 的坐标为__________ 。
C 2呢?
练一练
1.在下列现象中:①时针转动,②电风扇叶片的转动,③转呼啦圈, ④传送带上的电视机,其中是旋转的有( )
A .①②
B .②③ C. ①④ D .③④ 2.如图,如果把钟表的指针看做三角形OAB ,它绕O 点 按顺时针方向旋转得到△OEF , 在这个旋转过程中:
(1)旋转中心是____旋转角是___
(2)经过旋转,点A 、B 对应点分别为______.
3.下列图形中,是中心对称图形,但不是轴对称图形的是( ) A .正方形 B .矩形
C .菱形
D .平行四边形
4.点A (﹣3,m )和点B (3,2)关于原点对称,则m= .
二.例题精讲
例 如图△ABC 和△CEF 是两个大小不等的等边三角形,且有一个公共顶点C ,连接AF 和BE.
(1)将图①中的△CEF 绕点C 旋转一定的角度,得到图②,线段AF 和BE 有怎样的大小关系?作出判断并说明理由;
(2) 将图①中的△CEF 逆时针绕点C 旋转一定的角度(A ,C ,F 三点不共线时),画出变换后的图形,(1)中的结论是否还成立?
三.习题精练
如图1,点O 是正方形ABCD 两对角线的交点,分别延长OD 到点G ,OC 到点E ,使OG =2OD ,
OE =2OC ,然后以OG 、OE 为邻边作正方形OEFG ,连接AG ,DE . (1)求证:DE ⊥AG ;
(2)正方形ABCD 固定,将正方形OEFG 绕点O 逆时针旋转α角(0°<α<360°)得到正方形OE ′F ′G ′,如图2.①在旋转过程中,当∠OAG ′是直角时,求α的度数; ②若正方形ABCD 的边长为1,在旋转过程中,求AF ′长的最大值和此时α的度数,直接写出结果不必说明理由.
A B C A B C
四.训练题
1.如图,在△ABC 中,∠CAB =65°,将△ABC 在平面内绕点A 旋转 到△AB ′C ′的位置,使CC ′∥AB ,则旋转角的度数为( ) A .35° B .40° C .50° D .65°
2.将一副三角尺(在Rt △ABC 中,∠ACB=90°,∠B=60°,在Rt △DEF 中,∠EDF=90°,∠E=45°)如图摆放,点D 为AB 的中点,DE 交AC 于点P ,DF 经过点C .将△DEF 绕点D 顺时针方向旋转角α(0°<α<60°),DE ′交AC 于点M ,DF ′交BC 于点N ,则
的值为( )
A
. B . C . D .
3.已知在△ABC 中,AB =AC =8,∠BAC =30°.将△ABC 绕点A 旋转,使点B 落在原△ABC 的点C 处,此时点C 落在点D 处.延长线段AD ,交原△ABC 的边BC 的延长线于点E ,那么线段DE 的长等于___________.
4.如图(a ),两个不全等的等腰直角△OAB 和△OCD 叠放在一起,并且有公共的直角顶点O . (1).将图(a )中△OAB 的绕点O 顺时针旋转90°角,在图(b )中作出旋转后的图形 (保留作图痕迹,不写作法,不证明).
(2).在图(a )中,你发现线段AC,BD 的数量关系是 ,
(3).将图(a )中△OAB 的绕点顺时针旋转一个锐角,得到图(c ),这时(b )中的结论是否依然成立?作出判断并说明理由.
5.如图,已知,在△ABC 中,CA =CB ,∠ACB =90°,E ,F 分别是CA ,CB 边的三等分点,将△ECF 绕点C 逆时针旋转α角(0°<α<90°),得到△MCN ,连接AM ,BN .
(1)求证:AM =BN ;
(2)当MA ∥CN 时,试求旋转角α的余弦值.
6.如图,点P 是正方形ABCD 内一点,点P 到点A ,B 和D 的距离分别为1,,.△ADP 沿点A 旋转至△ABP ’,连结PP ’,并延长AP 与BC 相交于点Q . (1)求证:△APP ’是等腰直角三角形;
(2)求∠BPQ 的大小; (3)求CQ 的长.
图(a )
图(b )
图(c )。
