八年级数学特殊平行四边形
人教版八年级数学下册18.2 特殊的 平行四边形第二课时 矩形的性质课件

(1)证明:∵AO=OC, BO=OD, ∴四边形ABCD是平行四边形. 又∵∠AOB=2∠OAD,∠AOB=∠OAD+∠ADO, ∴∠OAD=∠ADO,∴AO=OD. ∵AC=AO+OC=2AO,BD=BO+OD=2OD, ∴AC=BD,∴四边形ABCD是矩形.
(2)解:设∠AOB=4x,∠ODC=3x, 则∠OCD=∠ODC=3x. ∵∠DOC+∠OCD+∠CDO=180°, ∴4x+3x+3x=180°,解得x=18°, ∴∠ODC=3×18°=54°, ∴∠ADO=90°-∠ODC=90°-54°=36°.
(1)证明:方法一 ∵四边形ABCD是平行四边形, ∴AD∥BC,AD=BC,AB=DC. ∵CE=BC,∴AD=CE. 又∵AD∥CE,∴四边形ACED是平 行四边形. ∵AB=AE,∴DC=AE, ∴四边形ACED是矩形.
证明:方法二 ∵四边形ABCD是平行四边形, ∴AD∥BC,AD=BC,AB=DC. ∵CE=BC,∴AD=CE. 又∵AD∥CE, ∴四边形ACED是平行四边形. ∵AB=AE,BC=CE, ∴AC⊥BE,∴∠ACE=90°, ∴四边形ACED是矩形.
几何语言
∵四边形ABCD是平行四边形 且AC=BD ∴四边形ABCD是矩形
A
D
O
B
C
小试牛刀
1.如图,下列条件不能判定四边形ABCD是矩形的是( C )
A.∠DAB=∠ABC=∠BCD=90° B.AB∥CD,AB=CD,AB⊥AD C.AO=BO,CO=DO D.AO=BO=CO=DO
2.如图 ABCD 中, ∠1= ∠2中.此时四边形ABCD是矩
解:∵四边形ABCD是平行四边形,
∴OA=OC=
1 2
AC,OB=OD= 1
初中数学八年级下册第十八章《平行四边形》简介

初中数学八年级下册第十八章《平行四边形》简介平行四边形是特殊的四边形。
本章我们在平行线、三角形和四边形的基础上进一步研究平行四边形;并通过平行四边形角、边的特殊化,研究矩形、菱形和正方形等特殊的平行四边形,认识这些概念之间的联系与区别,明确它们的内涵与外延;探索并证明平行四边形、矩形、菱形、正方形的有关性质定理和判定定理,进一步明确命题及其逆命题的关系,不断发展学生的合情推理和演绎推理能力。
本章教学时间约需14课时,具体分配如下(仅供参考):18.1 平行四边形6课时18.2 特殊的平行四边形6课时数学活动小结2课时一、教科书内容和本章学习目标(一)本章知识结构框图(二)教科书内容平行四边形是常见的几何图形,既有丰富的性质,又在现实生活中具有广泛的应用,尤其是矩形、菱形、正方形等特殊平行四边形的性质更加丰富、应用更加广泛。
学生在第一学段已经学习过平行四边形,本学段七年级下册“三角形”一章中研究了多边形及其内角和等内容,包括四边形及其内角和;八年级上册“全等三角形”一章又研究了三角形全等的判定及全等三角形的性质。
这些内容是学习本章的重要基础。
本章引言直接进入特殊的四边形——平行四边形:两组对边分别平行的四边形的学习,在平行四边形的基础上,学习矩形、菱形、正方形这些特殊平行四边形。
“18.1 平行四边形”主要研究平行四边形的概念、性质定理和判定定理;在平行四边形概念和性质的基础上,介绍两条平行线间距离的概念;作为性质定理和判定定理的一个应用,探究并证明三角形中位线定理。
“18.2 特殊的平行四边形”首先研究特殊的平行四边形:矩形和菱形,它们分别是有一个角是直角,或有一组邻边相等的特殊的平行四边形。
18.2.1和18.2.2分别研究矩形和菱形的概念、性质定理和判定定理,在矩形和菱形的基础上,再研究它们的特殊情况:同时具有两个特殊条件的平行四边形:正方形,它是有一个角是直角的特殊菱形,或者是有一组邻边相等的特殊矩形。
人教版八年级数学下册知识点第十八章《平行四边形》

第十八章平行四边形【思维导图】【平行四边形】(1)平行四边形的定义与表示定义:两组对边分别平行的四边形叫做平行四边形。
表示:平行四边形用“□”表示。
2)符号“□”必须与表示顶点的字母同时使用,不能单独使用。
的顺序依次排列。
点拨:1)在用“□”表示平行四边形时, 应把表示顶点的字母按顺时针或逆时针边形。
平行四边形ABCD 记作“□ABCD”,读作“平行四边形ABCD”。
如图,在四边形ABCD 中,AB ∥DC ,AD ∥BC ,那么四边形ABCD 是平行四(2)平行四边形的基本元素如图,在□ABCD 中,邻边:AD 和AB ,AD 和DC ,DC 和BC ,BC 和AB对边:AB 和DC ,AD 和BC邻角:∠BAD 和∠ADC ,∠ADC 和∠DCB ,∠DCB 和∠ABC ,∠ABC 和∠BAD 对角:∠BAD 和∠BCD ,∠ABC 和∠ADC对角线:AC 和BD【平行四边形的性质】性质1:平行四边形的对边相等几何语言:如图1,∵四边形ABCD 是平行四边形,∴AB=CD ,AD=BC性质2:平行四边形的对角相等几何语言:如图1,∵四边形ABCD 是平行四边形,∴∠A=∠C ,∠B=∠D下面证明性质1和2证明:如图2,连接AC。
∵AD∥BC,AB∥CD∴∠1=∠2,∠3=∠4.又∵AC=CA,∴△ABC≌△CDA∴AD=BC,AB=CD,∠B=∠D∴∠1=∠2,∠3=∠4,∴∠1+∠4=∠2+∠3,即∠BAD=∠BCD性质3:平行四边形的对角线互相平分几何语言:如图3,∵四边形ABCD是平行四边形,∴OA=0C=1/2AC,OB=OD=1/2BD【典例】(中考)在□ABCD中,下列结论一定正确的是()A.AC⊥BDB.∠A+∠B=1800C.AB=ADD.∠A≠∠C解析:平行四边形的对角线互相平分但不一定垂直,所以选项A错误;@简单初中生平行四边形的邻角互补,所以选项B正确;平行四边形的对边相等但邻边不一定相等,所以选项C错误;平行四边形的对角相等,所以∠A=∠C,所以选项D错误。
初中数学《特殊平行四边形》单元教学设计以及思维导图精选全文完整版

可编辑修改精选全文完整版特殊平行四边形主题单元教学设计主题单元学习目标知识与技能:理解平行四边形是中心对称图形,矩形、菱形、正方形都具有这样的特征矩形、菱形、正方形作为特殊的平行四边形,不仅具有平行四边形的特征,还分别具有各自的特征,而且它们都是轴对称图形.掌握特殊平行四边形的性质和判定,并能运用有关知识进行推理证明和计算边、角、对角线及面积;通过知识的综合应用的说理,初步培养学生的逻辑思维能力.过程与方法:通过探索、归纳几类特殊四边形的特征和识别,了解它们之间的包含关系;让学生在探索知识之间的相互联系及应用的过程中,体验推理的方法和技巧,获取推理的经验;通过探索,进行观察、猜想、分析、归纳、推理,培养学生发散思维能力;同时提高学生分析问题,解决问题的能力;情感态度与价值观:通过基础题和探究题体验数学活动的逻辑性和趣味性,同时增强解题的自信心;对应课标1.理解平行四边形、矩形、菱形、正方形的概念,以及他们之间的关系2.探索并证明矩形、菱形、正方形的性质定理:矩形的四个角都是直角,对角线相等;菱形的四条边相等,对角线互相垂直;以及它们的判定定理:三个角是直角的四边形是矩形;对角线相等的平行四边形是矩形。
四边相等的四边形是菱形;对角线互相垂直的平行四边形是菱形。
正方形具有矩形和菱形的一切性质主题单元问题设计1.矩形、菱形、正方形的定义2.矩形的边、角、对角线有怎样的特征?矩形有怎样的性质?3.菱形的边、角、对角线有怎样的特征?菱形有怎样的性质?怎样的性质?5. 如何判断一个平行四边形是矩形?6. 如何判断一个四边形是矩形?7. 矩形的判定?所需教学材料和资源信息化资源PPT , 几何画板课件常规资源作图工具(直尺、三角板、圆规等)教学支撑环境多媒体教室,几何画板软件其他纸笔等学习活动设计第一课时矩形的性质活动一:说说生活中的矩形【活动步骤】1.结合图,回顾矩形定义2.举出几个生活中矩形的例子.活动二:探索矩形的一般性质(即平行四边形所有性质)【技术应用】在PPT中动态演示菱形活动4:认识菱形【活动步骤】教师点拨:1.菱形是中心对称图形么?是轴对称图形么?【技术应用】几何画板演示菱形的中心对称和轴对称性活动5:探究菱形性质1.菱形的边有什么特性?菱形的角有什么特性?菱形的对角线有什么特性?活动三:推导菱形判定定理【活动步骤】1.写出命题2.思考:证明命题的步骤3.推理得出菱形的判定定理【技术应用】使用专门制作的几何画板课件探究、演示.第三课时(课外)折叠菱形活动一:折一折剪一剪1.如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?2.组内交流活动二:展示成果1.作品展示交流.2.说明下面这问同学剪法的依据。
(word版)浙教版数学八年级下《第章特殊平行四边形》精品教案

第6章特殊平行四边形与梯形教案一、矩形1、有一角是直角的平行四边形是矩形2、矩形的四个角都是直角;3、矩形的对角线相等。
4、矩形判定定理1:有三个角是直角的四边形是矩形5、矩形判定定理2:对角线相等的平行四边形是矩形6、直角三角形斜边上的中线等于斜边的一半二、菱形1、把一组邻边相等的平行四边形叫做菱形.2、定理1:菱形的四条边都相等3、菱形的对角线互相垂直,并且每条对角线平分一组对角.4、菱形的面积等于菱形的对角线相乘除以25、菱形判定定理1:四边都相等的四边形是菱形6、菱形判定定理2:对角线互相垂直的平行四边形是菱形。
三、正方形1、有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形2、性质:(1)四个角都是直角,四条边相等(2)对角线相等,并且互相垂直平分,每条对角线平分一组对角3、判定:(1)一组邻边相等的矩形是正方形(2)有一个角是直角的菱形是正方形四、梯形1、一组对边平行而另一组对边不平行的四边形叫做梯形。
2、等腰梯形:两腰相等的梯形叫做等腰梯形。
3、直角梯形:一腰和底垂直的梯形叫做直角梯形。
4、①等腰梯形是轴对称图形,对称轴是连接两底中点的直线。
②等腰梯形同一底上的两个内角相等,两条对角线相等。
5、在同一底上的两个角相等的梯形是等腰梯形。
6、作出下列梯形常用的辅助线五、综合1、下列判定正确的是()A、对角线互相垂直的四边形是菱形B、两角相等的四边形是等腰梯形C、四边相等且有一个角是直角的四边形是正方形D、对角线相等且互相垂直的四边形是正方形2、平行四边形的各个内角平分线若能围成一个四边形,则这个四边形一定是()A、正方形B、矩形C、菱形D、平行四边形顺次连接矩形各边中点所得的四边形是_______________;顺次连接对角线互相垂直的四边形各边中点所得的四边形是____________________.下列图形不符合“既是中心对称图形,又是轴对称图形”的是()A、线段B、半圆C、矩形D、菱形3、下列说法中错误..的是()A、四个角相等的四边形是矩形B、四条边相等的四边形是正方形C、对角线相等的菱形是正方形D、对角线互相垂直的矩形是正方形下列性质,矩形没有而菱形有的是()A、对角线互相垂直B、对角线互相平分C、对角线相等D、以上都不对4、下列判断错误的是()A、对角线相等的平行四边形是矩形B、对角线互相垂直平分且相等的四边形是菱形C、对角线垂直且相等的四边形是正方形D、对角线平分一个内角的平行四边形是菱形1、在线段、角、等边三角形、平行四边形、矩形、菱形、正方形中,是轴对称图形的是。
八年级数学特殊的平行四边形——正方形人教实验版知识精讲
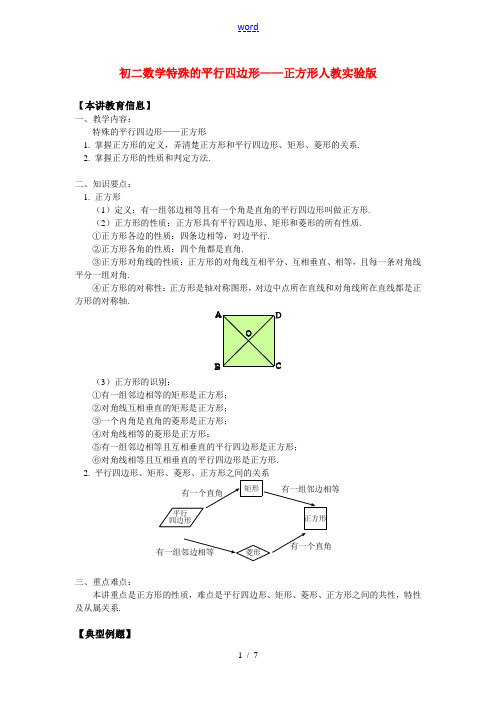
初二数学特殊的平行四边形——正方形人教实验版【本讲教育信息】一、教学内容:特殊的平行四边形——正方形1. 掌握正方形的定义,弄清楚正方形和平行四边形、矩形、菱形的关系.2. 掌握正方形的性质和判定方法.二、知识要点: 1. 正方形(1)定义:有一组邻边相等且有一个角是直角的平行四边形叫做正方形. (2)正方形的性质:正方形具有平行四边形、矩形和菱形的所有性质. ①正方形各边的性质:四条边相等,对边平行. ②正方形各角的性质:四个角都是直角.③正方形对角线的性质:正方形的对角线互相平分、互相垂直、相等,且每一条对角线平分一组对角.④正方形的对称性:正方形是轴对称图形,对边中点所在直线和对角线所在直线都是正方形的对称轴.B(3)正方形的识别:①有一组邻边相等的矩形是正方形; ②对角线互相垂直的矩形是正方形; ③一个内角是直角的菱形是正方形; ④对角线相等的菱形是正方形;⑤有一组邻边相等且互相垂直的平行四边形是正方形; ⑥对角线相等且互相垂直的平行四边形是正方形. 2. 平行四边形、矩形、菱形、正方形之间的关系平行四边形三、重点难点:本讲重点是正方形的性质,难点是平行四边形、矩形、菱形、正方形之间的共性,特性及从属关系.【典型例题】例1. 如图所示,已知正方形ABCD ,点E 是AB 延长线上一点,连结EC ,作AG ⊥EC 于G ,AG 交BC 于F ,求证:AF =CE.ABC DEFG分析:AF 、CE 分别在R t △ABF 与R t △CBE 中,可考虑证明它们全等,而四边形ABCD 为正方形,有相等的直角和相等的边,为证全等提供了条件.证明:因为四边形ABCD 是正方形, 所以AB =BC ,∠ABC =∠CBE =90°. 因为AG ⊥CE ,所以∠CGF =90°,所以∠BCE +∠CFG =90°,∠BCE +∠E =90°, 所以∠CFG =∠E ,又因为∠CFG =∠AFB , 所以∠E =∠AFB.所以△ABF ≌△CBE (SAS ). 所以AF =CE.例2. 把一X 矩形纸片像图中那样折一下,再沿CD 剪下,则纸片ABCD 是什么样的四边形?说明理由.分析:根据矩形的性质和图形折叠前后的变化规律判断四边形ABCD 的形状. 解:正方形. 理由如下:因为这是一X 矩形纸片,所以∠BAD =∠B =90°. △ADC 是△ABC 折叠得到的,即△ABC ≌△ADC. 所以∠ADC =∠B =90°, 所以四边形ABCD 是矩形. 又AB =AD ,所以纸片ABCD 是正方形.例3. 如图所示,E 是正方形ABCD 的对角线BD 上一点,EF ⊥BC ,EG ⊥CD ,垂足分别是F 、G. 试说明AE =FG .A BC DEFG分析:由EF ⊥BC ,EG ⊥CD 可得矩形EFCG ,则FG =EC ,再证△ABE ≌△CBE ,得AE =EC ,即可得到AE =FG .解:连结EC ,因为四边形ABCD 是正方形, EF ⊥BC ,EG ⊥CD ,所以四边形EFCG 为矩形. 所以FG =CE.因为BD 是正方形ABCD 的对角线. 所以∠ABE =∠CBE. 又BE =BE ,AB =CB , 所以△ABE ≌△CBE. 所以AE =EC , 所以AE =FG .评析:用CE 沟通AE 和FG 之间的联系.例4. (1)下列命题中正确的是( )A. 两条对角线互相平分的四边形是平行四边形B. 两条对角线相等的四边形是矩形C. 两条对角线互相垂直的四边形是菱形D. 两条对角线互相垂直且平分的四边形是正方形(2)如图所示,菱形ABCD 中,对角线AC 、BD 相交于点O ,若再补充一个条件能使菱形ABCD 成为正方形,则这个条件是__________(只填一个条件即可).A DC BO第(2)题 (3)如图所示,在四边形ABCD 中,AD ∥BC ,∠D =90°,若再添加一个条件,就能推出四边形ABCD 是矩形,你所添加的条件是__________. (写出一种情况即可)AB CD分析:(1)这个问题可以这样考虑:对角线互相平分的四边形是平行四边形;对角线互相平分且相等的四边形是矩形;对角线互相垂直平分的四边形是菱形;对角线互相垂直平分且相等的四边形是正方形. 故选A. (2)这个问题实际上是问什么样的菱形是正方形?有一个角是直角的菱形是正方形,对角线相等的菱形是正方形,考虑角可补充的条件是∠BAD =90°或AD ⊥AB ;考虑对角线补充:AC =BD. (3)本题应考虑和角相关的矩形的识别方法,有一个角是直角的平行四边形是矩形;有三个角是直角的四边形是矩形. 可添加的条件是∠A =90°或∠B =90°,AD =BC ,AB ∥CD 等.解:(1)A (2)∠BAD =90°(或AD ⊥AB ,AC =BD 等)(3)∠A =90°或AD =BC 或AB ∥CD例5. 如图所示,正方形ABCD ,对角线AC 、BD 相交于点O ,菱形AEFC ,EH ⊥AC ,垂足为H ,求证:EH =12FC.ABC E FHDO分析:要证EH =12FC ,EH 在矩形OBEH 中,得EH =OB =12BD ,而FC 是菱形AEFC的边,CF =AC =BD ,所以EH =12FC ,问题的关键是要证四边形OBEH 是矩形.证明:由正方形ABCD 得AC =BD ,AC ⊥BD ,∠BOC =90°. 又因为EH ⊥AC ,所以EH ∥OB.又因为四边形AEFC 是菱形,得AC =CF ,AC ∥EF ,所以OH ∥BE. 因此四边形OBEH 是矩形,因此EH =OB =12BD =12AC =12FC.评析:综合考查了正方形、菱形的性质和矩形的判定方法.【方法总结】正方形是特殊的平行四边形,是特殊的矩形,是特殊的菱形. 它具有平行四边形、矩形、菱形的所有性质. 分清楚这几种图形的从属关系,从关系图中确定它们性质的相同点和不同点.平行四边形矩形菱形正方形【模拟试题】(答题时间:60分钟)一. 选择题1. 下列选项中,正方形具有而矩形不一定具有的性质是( )A. 四边都相等B. 四角都相等C. 对角线相等D. 对角线互相平分 2. 正方形的对角线长为a ,则它的对角线的交点到各边的距离是( )A. 22aB. 24aC. a 2D. 22a3. 正方形是轴对称图形,那么它的对称轴的条数为( )A. 2B. 3C. 4D. 54. 在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的条件是( ) A. AC =BD ,AB ∥CD B. AD ∥BC ,∠A =∠CC. AO =BO =CO =DO ,AC ⊥BDD. AO =CO ,BO =DO ,AB =BC 5. 下列命题中,真命题是( ) A. 两条对角线相等的四边形是矩形 B. 两条对角线互相垂直的四边形是菱形C. 两条对角线互相垂直且相等的四边形是正方形D. 两条对角线互相平分的四边形是平行四边形6. 已知四边形ABCD 中,∠A =∠B =∠C =90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )A. ∠D =90°B. AB =CDC. AD =BCD. BC =CD*7. 如图1所示,将长为20cm ,宽为2cm 的长方形白纸条,折成图2所示的图形并在其一面着色,则着色部分的面积为( )A. 34cm 2B. 36cm 2C. 38cm 2D. 40cm 2图1二. 填空题1. 具有平行四边形、矩形和菱形性质的四边形是__________.2. 已知正方形ABCD 的对角线AC 、BD 相交于点O ,且AC =12cm ,•则BO =__________cm ,•∠OAB =__________度.3. 任意一个平行四边形,当它的一个锐角增大到_______度时,就变成了矩形;•当它的一组邻边变到_______时,就变成了菱形;当它的两条对角线变到______时,就变成了正方形.4. 矩形、菱形、正方形都是特殊的四边形,它们具有很多共性,如:__________(填一条即可).5. 正方形的面积为49,则它的边长为__________,对角线长为__________.*6. 如图所示,在正方形ABCD 中,E 是BD 上一点,过E 作EF ⊥BC 于F ,EG ⊥CD 于G ,若正方形ABCD 的周长是a ,则四边形EFCG 的周长为__________.ABCDEF G**7. 如图所示,正方形ABCD 的边长为4,E 为BC 上的一点,BE =1,F 为AB 上的一点,AF =2,P 为AC 上的一动点,则当PF +PE 为最小值时,PF +PE =__________.ABC DPEF三. 解答题 1. 如图,正方形ABCD 的对角线AC 、BD 相交于点O ,OE =OF ,求证:•∠OCF =∠OBE.ABCDE FO2. 如图所示,在△ABC 中,∠C =90°,CD 平分∠ACB ,DE ⊥BC ,DF ⊥AC ,垂足分别为点E 、F. 求证:四边形CFDE 是正方形.ABC DEF*3. 如图所示,点E 、F 分别为正方形ABCD 边AB 、BC 的中点,DF 、CE 交于点M ,CE 的延长线交DA 的延长线于G ,试探索:(1)DF 与CE 的位置关系; (2)MA 与DG 的大小关系.ABCDE F MG**4. 如图,四边形ABCD 是正方形,G 是BC 上任意一点(点G 与B 、C 不重合),AE ⊥DG 于E ,CF ∥AE 交DG 于F.(1)在图中找出一对全等三角形,并加以证明; (2)求证:AE =FC+EF.ABCDE FG【试题答案】一. 选择题1. A2. B3. C4. C5. D6. D7. B二. 填空题1. 正方形2. 6,453. 90,相等,垂直且相等4. 对边平行、对角线互相平分、对角相等等 5. 7,7 2 6. 12a 7. 17三. 解答题1. 提示:证明△OCF ≌△OBE 可得2. 先证四边形DECF 是矩形,又∵DE =DF ,∴四边形CFDE 是正方形3. (1)DF ⊥CE 提示:先证△EBC ≌△FCD ,得∠ECB =∠FDC ,根据互余的关系,•求出∠CMF =90°即可. (2)由△GAE ≌△CBE 得GA =CB ,再根据直角三角形斜边上中线的性质,得MA =12DG .4. (1)ΔAED ≌ΔDFC. 因为四边形ABCD 是正方形,所以 AD =DC ,∠ADC =90°. 又因为 AE ⊥DG ,CF ∥AE ,所以 ∠AED =∠DFC =90°,所以 ∠EAD +∠ADE =∠FDC +∠ADE =90°,所以 ∠EAD =∠FDC. 所以 ΔAED ≌ΔDFC (AAS ).(2)因为 ΔAED ≌ΔDFC ,所以 AE =DF ,ED =FC. 因为 DF =DE +EF ,所以 AE =FC +EF.。
2020-2021学年八年级数学下学期期末复习:1.4 特殊平行四边形【知识梳理+真题演练】(人教

专题1.4 特殊平行四边形知识归纳 知识点1:菱形1. 定义:一组邻边相等的平行四边形叫做菱形.2. 性质:菱形的四条边相等,两条对角线互垂直平分,且每一条对角线平分一组对角.3. 判定方法:①一组邻边相等的平行四边形是菱形;①对角线互相垂直的平行四边形是菱形;①四条边都相等的四边形是菱形.4. 设菱形对角线长分别为l 1,l 2,则S 菱形=21l 1l 2.1.(2020•荆门)如图,菱形ABCD 中,E ,F 分别是AD ,BD 的中点,若EF =5,则菱形ABCD 的周长为( )A .20B .30C .40D .502.(2020•黄冈)若菱形的周长为16,高为2,则菱形两邻角的度数之比为( )A .4:1B .5:1C .6:1D .7:13.(2020•牡丹江)如图,在平面直角坐标系中,O 是菱形ABCD 对角线BD 的中点,AD ①x 轴且AD =4,①A =60°,将菱形ABCD 绕点O 旋转,使点D 落在x 轴上,则旋转后点C 的对应点的坐标是( )A.(0,2√3)B.(2,﹣4)C.(2√3,0)D.(0,2√3)或(0,﹣2√3)4.(2020•盐城)如图,在菱形ABCD中,对角线AC、BD相交于点O,H为BC中点,AC=6,BD=8.则线段OH的长为()A.125B.52C.3D.55.(2020•辽阳)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8.BD=6,点E是CD 上一点,连接OE,若OE=CE,则OE的长是()A.2B.52C.3D.46.(2020•黑龙江)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH①AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为()A.4B.8C.√13D.67.(2020•黑龙江)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH①AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为()A.72B.24C.48D.968.(2020•贵阳)菱形的两条对角线长分别是6和8,则此菱形的周长是()A.5B.20C.24D.329.(2020•福建)如图,点E,F分别在菱形ABCD的边BC,CD上,且BE=DF.求证:①BAE=①DAF.10.(2020•滨州)如图,过①ABCD对角线AC与BD的交点E作两条互相垂直的直线,分别交边AB、BC、CD、DA于点P、M、Q、N.(1)求证:①PBE①①QDE;(2)顺次连接点P、M、Q、N,求证:四边形PMQN是菱形.11.(2020•郴州)如图,在菱形ABCD中,将对角线AC分别向两端延长到点E和F,使得AE=CF.连接DE,DF,BE,BF.求证:四边形BEDF是菱形.12.(2020•连云港)如图,在四边形ABCD中,AD①BC,对角线BD的垂直平分线与边AD、BC分别相交于点M、N.(1)求证:四边形BNDM是菱形;(2)若BD=24,MN=10,求菱形BNDM的周长.知识点2:矩形1.定义:有一个内角是直角的平行四边形叫做矩形.2.性质:矩形的对角线互相平分且相等,四个角都是直角.3.判定方法:①有三个角是直角的四边形是矩形;①对角线相等的平行四边形是矩形;①有一个角是直角的平行四边形是矩形.4. 设矩形的长和宽分别为a,b,则S矩形=ab.1.(2020秋•西安期末)如图,矩形ABCD的对角线AC、BD相交于点O,①ABO=60°,若矩形的对角线长为6.则线段AD的长是()A.3B.4C.2D.32.(2020春•漳州期末)如图,将矩形纸片右侧部分的四边形ABCD沿线段AD翻折至四边形AB′C′D的位置.若①DAB=56°,则①1的度数是()A.34°B.56°C.58°D.68°3.(2020春•复兴区期末)如图,在矩形ABCD中,AC、BD相交于点O,AE平分①BAD交BC于点E,若①CAE=15°,则①BOE的度数为()A.60°B.75°C.72°D.90°4.(2019秋•崂山区期末)如图,在矩形ABCD中,对角线AC与BD相交于点O,AE①BD,垂足为点E,AE=5,且EO=2BE,则OA的长为()A.B.C.3D.5.(2020春•新乐市期末)如图,在①ABC中,点D在BC上,DE①AC,DF①AB,下列四个判断中不正确的是()A.四边形AEDF是平行四边形B.若①BAC=90°,则四边形AEDF是矩形C.若AD①BC且AB=AC,则四边形AEDF是菱形D.若AD平分①BAC,则四边形AEDF是矩形6.(2020秋•太原期末)如图所示,在平行四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定平行四边形ABCD为矩形的是()A.①ABC=90°B.AC=BD C.AD=AB D.①BAD=①ADC7.(2020秋•紫金县期末)四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是()A.AB=CD B.AC=BD C.AB=BC D.AD=BC8.(2020春•南宁期末)如图,在△ABC中,∠ACB=90°,D是AB的中点,且DC=AC,则∠B的度数是()A.25°B.30°C.45°D.60°9.(2020•聊城)如图,在①ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,求证:四边形ABFC是矩形.10.(2020•遂宁)如图,在①ABC中,AB=AC,点D、E分别是线段BC、AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.(1)求证:①BDE①①F AE;(2)求证:四边形ADCF为矩形.11.(2020•北京)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF①AB,OG①EF.(1)求证:四边形OEFG是矩形;(2)若AD=10,EF=4,求OE和BG的长.知识点3:正方形1. 正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形.2. 正方形的性质(1)正方形既有矩形的性质,又有菱形的性质.(2)正方形的四个角都是直角,四条边相等.(3)正方形的对角线相等且互相垂直平分.3. 正方形的判定方法(1)有一组邻边相等的矩形是正方形.(2)对角线互相垂直的矩形是正方形.(3)有一个角是直角的菱形是正方形.(4)对角线相等的菱形是正方形.4. 平行四边形、矩形、菱形与正方形之间的联系1.(2020秋•大东区期末)如图,正方形ABCD中,点E是对角线AC上的一点,且AE=AB,连接BE,DE,则①CDE的度数为()A.20°B.22.5°C.25°D.30°2.(2020春•十堰期末)如图,在正方形OABC中,点B的坐标是(6,6),点E、F分别在边BC、BA 上,OE=3.若①EOF=45°,则F点的纵坐标是()A.2B.C.D.13.(2020春•漳州期末)如图,在正方形ABCD中,BF①CE于点F,交AC于点G,则下列结论错误的是()A.①BCG①①CDE B.AG=BE C.①OBG=①OCE D.①ABG=①AGB 4.(2020•湘西州)如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.(1)求证:①BAE①①CDE;(2)求①AEB的度数.5.(2020•自贡)如图,在正方形ABCD中,点E在BC边的延长线上,点F在CD边的延长线上,且CE =DF,连接AE和BF相交于点M.求证:AE=BF.。
初中数学8年级下册《特殊的平行四边形》导学案

课题 19.2 特殊的平行四边形课时:五课时第一课时 19.2.1 矩形的性质【学习目标】1.掌握矩形的性质定理及推论。
2.能熟练应用矩形的性质进行有关证明和计算。
【重点难点】重点:掌握矩形的性质定理。
难点:利用矩形的性质进行证明和计算。
【导学指导】阅读教材P94-P96相关内容,思考、讨论、合作交流后完成下列问题:1.什么是矩形?2.矩形是特殊的平行四边形,平行四边形具有的性质它有没有?平行四边形的边有什么性质?角呢?对角线呢?那么它特殊在什么地方?所以它有什么性质?如何记住它呢?3.矩形的一条对角线把它分成了两个什么三角形?由矩形的性质,你可以得到这个三角形的什么性质?【课堂练习】1.教材P95练习第1,2,3题。
2.Rt△ABC中,两条直角边分别为6和8,则斜边上的中线长为。
【要点归纳】今天你有什么收获?与同伴交流一下。
【拓展训练】1. 将矩形纸片ABCD 沿对角线BD 对折,再折叠使AD 与对角线BD 重合,得折痕DG ,若AB=8,BC=6,求AG 的长。
2. 在四边形ABCD 中,∠ABC=∠ADC=90°,E 是AC 的中点,EF 平分∠BED 交BD 于点F 。
(1) 猜想:EF 与BD 具有怎样的关系?(2) 试证明你的猜想。
ABD第二课时矩形的判定【学习目标】1.理解并掌握矩形的判定方法。
2.能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养分析能力。
【重点难点】重点:矩形的判定定理及推论。
难点:定理的证明方法及运用。
【导学指导】复习旧知:1.什么是平行四边形?什么是矩形?2.矩形有哪些性质?你能猜想如何判定矩形吗?学习新知:阅读教材P95-P96相关内容,思考、讨论、合作交流后完成下列问题:1.利用矩形的定义可以判定一个平行四边形是矩形,由此你发现什么?2.还有哪些方法可以证明一个四边形是矩形?如何证明?试一试。
【课堂练习】1.教材P96练习第1,2题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
O
B C
边
(1) AB=CD (2) AD=BC (3) AB=BC (4) AB∥CD (5) AD ∥BC
角
对角 线
(9) OA=OC (10) OB=OD (11) AC⊥BD (12) AC=BD
(6) ∠BAD=∠BCD (7) ∠ABC=∠ADC (8) ∠BAD=90。
A 你能在四边形的基础上,从下列条件 中选四个,得到正方形吗?
D
O
B C
边
(1) AB=CD (2) AD=BC (3) AB=BC (4) AB∥CD (5) AD ∥BC
角
对角 线
(9) OA=OC (10) OB=OD (11) AC⊥BD (12) AC=BD
(6) ∠BAD=∠BCD (7) ∠ABC=∠ADC (8) ∠BAD=90。
1. 平行四边形的一个角是另一个角的5倍,这个平行 150º 四边形较大的角是—— 2. 已知平行四边形的周长是30cm,两邻边之比为1:5, 2.5cm 那么较小边的边长为—— 3. 已知:如图(1)在菱形ABCD中,E、F分别是BC、CD 100º 上的点,且AE=EF=AF=AB,则∠ C=—— 4.已知菱形的一边和等腰直角三角形的直角边相等,若菱形的一角 3 :1 为60º ,则菱形和三角形的面积比是—— 5. 如图(2),在正方形ABCD中,延长BC至E,使CE=AC,AE交 112.5º CD于F,那么∠ AFC=—— A A D
本节目标:
1. 进一步熟练掌握特殊平行四边形的性质和判定。 2. 通过本节学习提高综合应用能力,和推理证明能力。 3. 进一步体会证明的必要性和证明在解决问题中的作用。
一组邻边 相等 两组对边分别平行
有一个内角 是直角
有一个内 角是直角
一组邻边 相等
A
O B C
D
如果四边形ABCD是平行四边形,AC、 BD相交于点O,你能得到那些结论?
上海自动化仪表厂系统工程公司、“销售公司”、“上海自动化仪表厂系统工程公司系统工程公司”、“DCS分公司”、“进出口部”、“国内 备品备件部”、共有18个工厂、21家合资企业。上海自动化仪表厂系统工程公司 上海自动化仪表厂系统工程公司 duh61exc 主要产品有工业生产过程控制系统装置和仪表分析仪器、汽车电子、计算机、楼宇控制系统、商业和金融自动化系统、可编程序控制 器(PLC)、家用电器及仪表控制柜、各种仪表元件和气动元件等。在工业生产过程控制方面的产品有20个大类、150个系列、3000多种品种, 拥有作为现代工业过程控制的分散控制系统(DCS)及各类控制、调节、温度、测量、显示、记录仪以及执行机构和调节阀。 日飞升,真是神仙哪!”下人涕泗横流的报告。老太太回来后听说,登时就怒了,对着明远:“请了活神仙来家,怎么不赶紧叫我去 见?”“„„”明远一脸委屈的想,“要不是这家伙临走前来了这一手,谁认他是真神仙?还不当他是江湖把式吗?请您搁下要事回府、屈尊 去见他,怎开得了这个口!”正是临走前使的一招,才使得张神仙的“活儿”有了质的飞跃,成为上上下下里里外外诸色人等口中津津乐道的 话题。而韩毓笙“芙蓉花主”的名头,听说的人更多了。第三十四章 凭尽栏杆说元夜(1)宝音的身体好得很快。老太太原是不想留个病人在 屋里的,见她病势来得急去得快,刘大夫也说不过是饮食不当、热毒急了攻破喉头,其实无事,也便放宽了心,留她在屋中再看看。这日但见 宝音对着一本书,一边还比着手势,便动问道:“怎么了?不好好养身子,这还比划捣药呢?”宝音忙阖起书,屈膝道:“这本书„„写着捣 茶。”她从明秀那儿,没借佛经,倒借了本茶经,还是挺古早的簿子,里头说吃茶,要捣、要煎、要放盐放油放香料,甚或有把茶叶都吃下去 的!可是作怪。丫头们都纳闷:“好茶叶一捣,不就坏了么,还怎么泡?”老太太倒触动心上痒处,笑道:“你们不知道。拿来我看看。”丫 头捧起书,且喜书上字体不小,她眯着眼看了会儿,道:“果然如此,这倒说的是古法儿的吃茶法呢!——你们单知道‘喝茶’,土话儿也叫 ‘吃茶’,哪知道老早时候,兴的就是吃茶?茶叶先经蒸制,压成饼,好的茶饼,只取芽尖一缕,光明莹洁,状若银线,压得密,手掌薄、半 个手掌大这么一小团,拿起来沉甸甸的,就快半斤了!叫密云团。用时切一小片,磨细下来,已够煮三五碗茶汤——三碗为佳,最多煮五碗, 这才是会吃茶的人。我的爷爷,每次只吃三碗,他就有那种密云团,茶汤浓得呀,再没其他相仿佛的好比拟,那种着实劲儿,用‘喝’就太轻 浮了,所以叫‘吃’。我小时候,从京城以降,已经都兴起炒青泡茶法儿了,他还恋着团茶,我亲手伺候他,煮完了最后一片密云团,再就没 了。市面上再没人能做那种茶啦!”老太太的爷爷,其实是晚年获罪,被抄赃,一吓而亡。老太太很少讲她爷爷的事,无非一次兴起,跟宝音 提过她十来岁时跟爷爷学得一手好煮茶手艺,也不过那么几句话,点到即止。现在她也打算“即止”了,但小丫头们没有宝音识相,簇拥过来 还想听她讲团茶,宝音在当中只凑趣插了几句嘴,老太太忽然发现自己已经兴致勃勃谈起来了。跟她的爷爷无关,只是团茶。话头被引导得那 么好,纯粹说古制,给小孩子们开开眼。她不觉间讲解了螃蟹眼、鹧鸪斑、三沸三辨、十二先生、兔豪鱼目、冷粥栗纹。这些术语、掌故,久 储在她心里,而今渐渐活了过来。老人
角:对角相等 平行四边形 的性质 边:对边平行且相等 对角线:互相平分
A
O B
D
C
如果四边形ABCD是矩形,AC、BD相交 于点O,你能得到那些结论?
角:四个角都相等 矩形的性质
边:对边平行且相等
对角线:互相平分且相等
A
O B
D
C
如果四边形ABCD是菱形,AC、BD相交 于点O,你能得到那些结论?
D
E A
C
2.在矩形ABCD中,两条对角线AC、 BD相交于点O, ∠AOB= 60。, AB=3cm。请判定△AOB的形状, 并求出对角线的长。
有一块形状为平行四边形的
铁 片,AB 表 示 其 比 较 长 的 一 边, AD 表 示 较 短 的 一 边,且 AD:AB=1:2 。现 在 想 用 这 块 铁 片 截 一 个 直 角 三 角 形,并 且 希 望 以 AB 为 斜 边,直 角 顶 点 在 CD 上, 问:这 件 事 能 否 办 成 ?如 果 能 的 话,请 说 明 应 该 怎 样 截;如 果 不 能 的 话,请 说 明 理 由。
角:对角相等 菱形的性质
边:对边平行,四条边都相等
对角线:互相垂直平分
A
D
O B C
如果四边形ABCD是正方形,AC、BD相 交于点O,你能得到那些结论?
角:四个角都相等 正方形的 性质
边:对边平行,四条边都相等
对角线:互相垂直平分且相等
A 你能在四边形的基础上,从下列条 件中选三个,得到矩形吗? B
3. 下列图形中不是轴对称图形的是( B),不是中心对称图形的 是( A )
A. 等腰三角形 B. 平行四边形
C. 菱形
D.正方形
小明用两根同样长的竹棒做对角线, 制作四边形的风筝,则该风筝的形 状一定是( ) A C 矩形 等腰梯形 B D 正方形 无法确定
A 1. 已知菱形ABCD中,AE⊥BC于 E,AF⊥CD于F,你能判断AE与AF的关 系吗?证明你的判断。 B F D O B A 3.四边形ABCD和BEFG都是 正方形,则AG=CE吗?证明你 的判断。 F G B E C C D
B E
C F (1)
D B
(2)
F C E
1. 正方形具有而菱形不具有的性质是( C)
A. 对角线互相平分
C. 对角线相等
B. 每条对角线平分一组对角
D.对角线பைடு நூலகம்相垂直
2. 将一个菱形绕两条对角线的交点旋转90。,所得图形与原来 的图形重合,此时的菱形是( C)
A. 矩形 C. 正方形 B.菱形 D.平行四边形
D
O
C
边
(1) AB=CD (2) AD=BC (3) AB=BC (4) AB∥CD (5) AD ∥BC
角
对角 线
(9) OA=OC (10) OB=OD (11) AC⊥BD (12) AC=BD
(6) ∠BAD=∠BCD (7) ∠ABC=∠ADC (8) ∠BAD=90。
A 你能在四边形的基础上,从下 列条件中选三个,得到菱形吗?
