中考数学第33讲
如何做中考探索(规律)题第33讲

第33讲:如何做中考探索(规律)题随着课程改革的不断深入,规律探索型试题自近几年出现以来,正受到越来越多的省市所青睐.因此,这就需要我们在平时的学习及复习时注重进行观察能力、分析能力、探索研究能力、归纳能力和创新能力的训练与培养.规律探索型题包括探索数字规律型、探索运算规律型、探索等式的规律型、探索几何图形排列规律型等等试题,因为涉及的知识点较多,并且能够综合考查学生的探索、归纳、概括、类比等等能力,因此是中考的热点题型.解决这类问题的一般思路是:首先认真阅读所给出的条件,从中发现其变化规律,大胆猜想,由特殊的情况总结出一般性的结论,最后再进行验证以确保所归纳结论的正确性.题型一探索数字规律探索数字规律的题目在中考中经常出现,做这类试题,要认真分析所给出的数字之间的关系以及每个数字与所处的数位的关系,找出规律性,推测出所要求填写的项或者通项公式。
例1、(2007辽宁沈阳)有一组数:1,2,5,10,17,26,……,请观察这组数的构成规律,用你发现的规律确定第8个数为.解析:仔细分析数字的特征,1=02+1,2=12+1,5=22+1,10=32+1,17=42+1,26=52+1…,容易推测出第8个数为72+1=50。
例2、(2007重庆)将正整数按如图所示的规律排列下去。
若用有序实数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示实数9,则(7,2)表示的实数是。
解析:到第6排最后共有1+2+3+4+5+6=21个数,则第7排第2个数为23。
题型二探索运算规律根据已经提供的数字之间的运算规律,探究出一般性的结论或者推测出某些算式,是解决探究运算规律试题的基本解法。
例3、(2007山东烟台)观察下列各式:===请你将发现的规律用含自然数n(n≥1)的等式表示出来.(n+例4、(2007浙江临安)已知:, ……,若符合前面式子的规律,则a + b = ___ ____.解析:首先可以猜测出a=102-1=99,b=10,所以a+b=109。
2015届安徽中考数学总复习课件:第33讲 锐角三角函数和解直角三角形

要点梳理 5.直角三角形的边角关系在现实生活中有着广泛的 应用,它经常涉及测量、工程、航海、航空等,其中 包括了一些概念,一定要根据题意明白其中的含义才 能正确解题. (1)铅垂线:重力线方向的直线;
要点梳理
(2)水平线:与铅垂线垂直的直线 ,一般情况下 ,地平面 上的两点确定的直线我们认为是水平线;
(3)仰角:向上看时,视线与水平线的夹角;
(4)俯角:向下看时,视线与水平线的夹角;
(5)坡角:坡面与水平面的夹角;
要点梳理
(6)坡度:坡面的铅直高度与水平宽度的比叫做坡度 (或坡 比),一般情况下,我们用 h 表示坡的铅直高度,用 l 表 h 示坡的水平宽度,用 i 表示坡度,即 i= l =tanα,显然, 坡度越大,坡角就越大,坡面也就越陡;
3. (2014· 毕节)如图是以△ABC 的边 AB 为直径的半圆 O, 点 C 恰好在半圆上, 过 C 作 CD⊥AB 交 AB 于 D.已知 cos 3 ∠ACD=5,BC=4,则 AC 的长为( D ) A.1 20 B. 3 C.3 16 D. 3
4.(2014· 丽水 )如图 ,河坝横断面迎水坡 AB 的坡比是 1∶ 3(坡比是坡面的铅直高度 BC 与水平宽度 AC 之比),
sin(90°-?)=__cosα__; cos(90°-?)=__sinα__.
函数的增减性:(0°<?<90°)
(1)sinα,tanα的值都随 ?__增大而增大__;
(2)cosα随 ?__增大而减小__.
要点梳理
4.解直角三角形的概念、方法及应用: 解直角三角形:由直角三角形中除直角外的已知元素 ,求出所有未
三角函数值)转化为旧知识(求直角三角形的边长),因
此不可避免地用到勾股定理.若原题没有图形,可以
初中数学中考复习考点知识与题型专题讲解33 相似形(解析版)

初中数学中考复习考点知识与题型专题讲解专题33相似形【知识要点】考点知识一相似图形及比例线段相似图形:在数学上,我们把形状相同的图形称为相似图形.相似多边形:若两个边数相同的多边形,它们的对应角相等、对应边成比例,则这两个多边形叫做相似多边形。
特征:对应角相等,对应边成比例。
比例线段:对于四条线段a、b、c、d,如果其中两条线段的比与另两条线段的比相等,如a:b=c:d,我们就说这四条线段是成比例线段,简称比例线段。
考点知识二相似三角形相似图形的概念:形状相同的图形叫做相似图形。
相似图形的概念:对应角相等、对应边成比例的两个三角形叫做相似三角形。
相似用符号“∽”,读作“相似于”。
相似比的概念:相似三角形对应边的比叫做相似比相似三角形的判定:判定方法(一):平行于三角形一边的直线和其他两边相交,所构成的三角形和原三角形相似.判定方法(二):如果两个三角形的三组对应边的比相等,那么这两个三角形相似.判定方法(三):如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.判定方法(四):如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.判定方法(五):斜边和任意一条直角边成比例的两个直角三角形相似。
相似三角形的性质:1.相似三角形的对应角相等,对应边的比相等;2.相似三角形中的重要线段的比等于相似比;相似三角形对应高,对应中线,对应角平分线的比都等于相似比.3.相似三角形的面积比等于相似比的平方.相似三角形与实际应用:关键:巧妙利用相似三角形性质,构建相似三角形求解。
考点知识三位似位似图形定义:如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.注意:1.位似图形是相似图形的一种特殊形式。
2.位似图形的对应顶点的连线所在直线相交与一点,位似图形的对应边互相平行或者共线。
位似中心的位置:形内、形外、形上。
第33讲 视图与投影
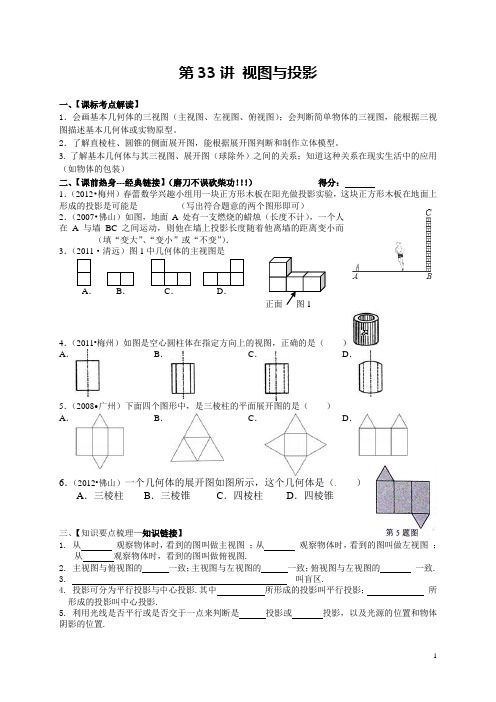
第33讲 视图与投影一、【课标考点解读】1.会画基本几何体的三视图(主视图、左视图、俯视图);会判断简单物体的三视图,能根据三视图描述基本几何体或实物原型。
2.了解直棱柱、圆锥的侧面展开图,能根据展开图判断和制作立体模型。
3. 了解基本几何体与其三视图、展开图(球除外)之间的关系;知道这种关系在现实生活中的应用(如物体的包装)二、【课前热身---经典链接】(磨刀不误砍柴功!!!) 得分:1.(2012•梅州)春蕾数学兴趣小组用一块正方形木板在阳光做投影实验,这块正方形木板在地面上形成的投影是可能是________ (写出符合题意的两个图形即可)2.(2007•佛山)如图,地面A 处有一支燃烧的蜡烛(长度不计),一个人在A 与墙BC 之间运动,则他在墙上投影长度随着他离墙的距离变小而________(填“变大”、“变小”或“不变”).3.(2011·清远)图1中几何体的主视图是. ... (2012•佛山)A .三棱柱B .三棱锥C .四棱柱D .四棱锥三、【知识要点梳理—知识链接】1. 从 观察物体时,看到的图叫做主视图 ;从 观察物体时,看到的图叫做左视图 ;从 观察物体时,看到的图叫做俯视图.2. 主视图与俯视图的 一致;主视图与左视图的 一致;俯视图与左视图的 一致.3. 叫盲区.4. 投影可分为平行投影与中心投影.其中 所形成的投影叫平行投影; 所形成的投影叫中心投影.5. 利用光线是否平行或是否交于一点来判断是 投影或 投影,以及光源的位置和物体阴影的位置.B . A .C .D .四、【中考名题---考点链接】考点 简单几何体的三视图例1. (2012•南平)如图所示,水平放置的长方体底面是长为4和宽为2的矩形,它的主视图的面积为12,则长方体的体积等于( )A .16B .24C .32D .48【点评】本题考查了简单几何体的三视图.关键是明确主视图是由长和高组成的.答案选B .考点 投影例2. (2012•绵阳)把一个正五菱柱如图摆放,当投射线由正前方射到后方时,它的正投影是( )【点评】本题考查正投影的定义及正投影形状的确定,解题时要有一定的空间想象能力.答案选B .五、【中考链接一湛江真题】快乐一练! 得分___________1.(2012•湛江)如图所示的物体由两个紧靠在一起的圆柱组成,小明准备画出它的三视图.那么他所画的三视图中的俯视图应该是( )A .两个外切的圆B .两个内切的圆C .两个相交的圆D .两个外离的圆2、(2011•湛江)下面四个几何体中,主视图是四边形的几何体共有( )A .1个B .2个C .3个D .4个3.(2010•湛江)下列几何体的主视图、左视图和俯视图都是..矩形的是( )A B C D4.(2009•湛江)在右图的几何体中,它的左视图是( )5.(2007•湛江)图2是由6个相同的小立方块搭成的几何体,那么这个几何体的主视图是 ( )B . C. D . A .第1题 A . B . C . D . 第4题 A B C D 图2六、【中考演练二----2010-2012年中考题】 得分___________1.(2012•玉林)下列基本几何体中,三视图都相同图形的是( )2.(2012•岳阳)如图,是由6个棱长为1个单位的正方体摆放而成的,将正方体A 向右平移2个单位,向后平移1个单位后,所得几何体的视图( )A .主视图改变,俯视图改变B .主视图不变,俯视图不变C .主视图不变,俯视图改变D .主视图改变,俯视图不变3.(2012•肇庆)如图是某几何体的三视图,则该几何体是( )A .圆锥B .圆柱C .三棱柱D .三棱锥4.(2012•益阳)下列命题是假命题的是( )A .中心投影下,物高与影长成正比B .平移不改变图形的形状和大小C .三角形的中位线平行于第三边D .圆的切线垂直于过切点的半径5.(2010•淄博)图中的八边形是一个正八棱柱的俯视图,如果要想恰好看到这个正八棱柱的三个侧面,在图中标注的4个区域中,应该选择站在( )A .①B .②C .③D .④6.(2010•达州)已知,如图,AB 和DE 是直立在地面上的两根立柱,AB=5m ,某一时刻AB 在阳光下的投影BC=3m .(1)请你在图中画出此时DE 在阳光下的投影;(2)在测量AB 的投影时,同时测量出DE 在阳光下的投影长为6m ,请你计算DE 的长.A . 圆柱B . 三棱柱C . 球D . 长方体七、【中考演练三---备考核心演练】 得分___________1. 如图所示的物体是一个几何体,其主视图是( )2.3. 在一个晴朗的上午,小丽拿着一块矩形木板在阳光下做投影实验,矩形木板在地面上形成的投影不可能是( )4. 如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面, 与“迎”相对的面上的汉字是( )A.文B.明C.奥D.运5. 右图是某一几何体的三视图,则这个几何体是( )A .圆柱体B .圆锥体C .正方体D .球体6.下图的几何体是由三个同样大小的立方体搭成的,其左视图为( )7. 当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小.(填 “相同”、 “不一定相同”、“不相同”之一).8.如图,水平放置的长方体 的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于 .9.将一个三角板放在太阳光下,它所形成的投影是________,也可能是_______.10.(2010•茂名)如图,小华、小军、小丽同时站在路灯下,其中小军和小丽的影子分别是AB ,CD .(1)请你在图中画出路灯灯泡所在的位置(用点P 表示);(2)画出小华此时在路灯下的影子(用线段EF 表示)讲 文 明 迎 奥 运A. B. C. D. A.B.C.D. 4 2 B .。
全国181套中考数学试题分类汇编33网格问题

全国181套中考数学试题分类汇编33⽹格问题33⽹格问题⼀、选择题1.(浙江⾈⼭、嘉兴3分)如图,点A、B、C、D、O都在⽅格纸的格点上,若△COD是由△AOB 绕点O按逆时针⽅向旋转⽽得,则旋转的⾓度为(A)30°(B)45°(C)90°(D)135°【答案】C。
【考点】旋转的性质,勾股定理的逆定理。
【分析】△COD是由△AOB绕点O按逆时针⽅向旋转⽽得,由图可知,∠AOC为旋转⾓,可利⽤△AOC的三边关系解答:设⼩⽅格的边长为1,从图知,=AC=4。
从⽽OA,OC,AC满⾜OC2+OA2=AC2,∴△A OC是直⾓三⾓形,∴∠AOC=90°。
故选C。
2.(浙江⾦华、丽⽔3分)如图,在平⾯直⾓坐标系中,过格点A,B,C作⼀圆弧,点B与下列格点的连线中,能够与该圆弧相切的是A、点(0,3)B、点(2,3)C、点(5,1)D、点(6,1)【答案】 C。
【考点】切线的性质;坐标与图形性质;勾股定理;垂径定理。
【分析】如图,根据垂径定理的性质得出圆⼼所在位置O(2,0),再根据切线的性质得出∠OBD+∠EBF=90°时,BF与圆相切,∴当△BOD≌△FBE时,∴EF=BD=2,F点的坐标为:(5,1)。
故选C。
3.(⼴西贺州3分)如图,在⽅格纸中的△ABC经过变换得到△DEF,正确的变换是A.把△ABC向右平移6格,B.把△ABC向右平移4格,再向上平移1格C.把△ABC绕着点A顺时针⽅向90o旋转,再右平移6格D.把△ABC绕着点A逆时针⽅向90o旋转,再右平移6格【答案】D。
【考点】平移和旋转变换。
【分析】根据平移和旋转变换的特点,直接得出结果。
故选D。
4.(⼴西南宁3分)在边长为1的⼩正⽅形组成的⽹格中,有如图所⽰的A 、B 两点,在格点中任意放置点C ,恰好能使△A BC 的⾯积为1的概率为A .3 25 B .4 25 C . 1 5 D . 625【答案】D 。
2013届上海市中考复习方案课件(第8单元统计与概率)

第33讲┃ 考点聚焦
将一组数据按照由小到大(或由大到小)的 顺序排列,如果数据的个数是奇数,则处 于________________就是这组数据的中位 中间位置的数 数,如果数据的个数是偶数,则中间 ________________就是这组数据的中位数 两个数据的平均数 确定中位数时,一定要注意先把整组数据 按照大小顺序排列,再确定 一组数据中出现次数________的数据叫做 最多 这组数据的众数 (1)一组数据中众数不一定只有一个;(2)当 一组数据中出现异常值时,其平均数往往 不能正确反映这组数据的集中趋势,就应 考虑用中位数或众数来考查
第32讲 数据的收集与整理 第33讲 数据的分析与决策 第34讲 概率
第32讲┃ 数据的收集与整理
第32讲┃ 考点聚焦
考点聚焦
考点1 统计方法
为一特定目的而对________考察对象做的调查, 所有 叫全面调查,也叫普查 为一特定目的而对________考察对象做的调查, 部分 抽样调查 叫抽样调查 不宜采用普查的条件:①受客观条件限制,无法 拓展 对所有个体进行普查;②调查具有破坏性;③调 查对象的个体数目庞大,个体之间差异不大 全面调查
第33讲┃ 考点聚焦 考点3 用样本估计总体
统计的基 利用样本特征去估计总体的特征是统计的基本思 本思想 想.注意样本的选取要有足够的代表性 利用数据进行决策时,要全面、多角度地去分析已 利用数据 有数据,比较它们的代表性和波动大小,发现它们 进行决策 的变化规律和发展趋势,从而作出正确决策
第33讲┃ 皖考探究
第33讲┃ 归类示例
例 1 [2012· 黄冈] 为了全面了解学生的学习、生活及家庭 的基本情况,加强学校、家庭的联系,梅灿中学积极组织全体 教师开展“课外访万家活动”, 王老师对所在班级的全体学生 进行实地家访,了解到每名学生家庭的相关信息,现从中随机 抽取 15 名学生家庭的年收入情况,数据如下表: 年收入 2 2.5 3 4 5 9 13 (单位:万元) 家庭个数 1 3 5 2 2 1 1 (1)求这 15 名学生家庭年收入的平均数、中位数、众数; (2)你认为用(1)中的哪个数据来代表这 15 名学生家庭年收 入的一般水平较为合适?请简要说明理由.
【中考备战策略】2014中考数学总复习 第33讲 数据的收集、整理与描述课件 新人教版

解析:∵方差越大波动越大,越不稳定,且 17.5> 15,∴(2)班比(1)班成绩稳定.故选 B.
8.(2013· 河池)2013 年河池市初中毕业升学考试的 考生人数约为 3.2 万名,从中抽取 300 名考生的数学成 绩进行分析,在本次调查中,样本指的是( A A.300 名考生的数学成绩 B.300 C.3.2 万名考生的数学成绩 D.300 名考生 )
6. (2013· 潍坊)在某校“我的中国梦”演讲比赛中, 有 9 名学生参加决赛,他们决赛的最终成绩各不相 同.其中的一名学生要想知道自己能否进入前 5 名,不 仅要了解自己的成绩,还要了解这 9 名学生成绩的 ( D ) B.方差 D.中位数 A.众数 C.平均数
解析:9 名选手的得分各不相同,则这组得分的中 就可判断能否进入前 5 名.故选 D.
9. (2013· 自贡 )某班七个合作学习小组人数如下: 4,5,5,x,6,7,8,已知这组数据的平均数是 6,则这组数 据的中位数是( C A.5 C.6 ) B.5.5 D.7
1 解析: 根据题意,可得 × (4+ 5+ 5+ x+ 6+ 7+ 8) 7 =6,∴x=7.将这组数据从小到大排列为 4,5,5,6,7,7,8, 排在最中间的数是 6,即中位数是 6.故选 C.
10. (2013· 聊城)某校七年级共 320 名学生参加数学 测试,随机抽取 50 名学生的成绩进行统计,其中 15 名 学生的成绩达到优秀. 估计该校七年级学生在这次数学 测试中达到优秀的人数大约有________人.( D A.50 C.90 B.64 D.96 )
5.某灯具厂从 1 万件同批次产品中随机抽取了 100 件进行质检, 发现其中有 2 件不合格,估计该厂这 1 万件产品中不合格品约为 200 件.
2015届九年级数学中考复习课件:第七章33讲

要点梳理 各象限内和坐标轴上的点的坐标规律
第一象限:(+,+);
第二象限:(-,+);
第三象限:(-,-);
第四象限:(+,-);
x轴正方向:(+,0);x轴负方向:(-,0);
y轴正方向:(0,+);y轴负方向:(0,-);
x轴上的点的纵坐标为0;y轴上的点的横坐标为0;
原点坐标为(0,0).
要点梳理
一个思想 本讲中比较广泛地应用数形结合的思想来研究问题.
数形结合,直观形象,为分析问题和解决问题创造了有
利条件,如用点的位置解答相关问题是典型的数形结合
思想的应用.
四种定位方法
(1)方位角定位法;(2)方向角距离定位法;(3)数轴法;
(4)直角坐标系法.
1.(2014·南通)点P(2,-5)关于x轴对称的点的坐
②g(m,n)=(-m,-n),如g(2,1)=(-2,-1)
按照以上变换有:f[g(3,4)]=f(-3,-4)=(-3,4), (3, 2)
那么g[f(-3,2)]=
.
Байду номын сангаас (2)在平面直角坐标系中,设点 P 到原点 O 的距离为 ?,
OP 与 x 轴正方向的夹角为 ?,则用[?,α]表示点 P 的 极坐标,显然,点 P 的极坐标与它的坐标存在一一对应
(2)(2014· 邵阳)如图,在平面直角坐标系 xOy 中,已知点 A(3,
4),将 OA 绕坐标原点 O 逆时针旋转 90°至 OA? 的 ,则点 A?
坐标是__(-4,3)__.
【点评】
(1)本题考查了坐标与图形变化——平移,熟记
标为( B )
A.(-2,5)
C.(-2,-5)
B.(2,5)
