(完整版)一次函数与不等式应用题(含答案)-
(常考题)人教版高中数学必修第一册第二单元《一元一次函数,方程和不等式》测试卷(含答案解析)(1)
一、选择题1．已知a >0，b >0，a +b =1，则下列等式可能成立的是（ ） A ．221a b += B ．1ab = C ．212a b +=D ．2212a b -=2．已知0a >，0b >，且1a b +=，则14a b+的最小值为（ ） A ．9B ．8C ．7D ．63．设1a b +=，0b >，则2244||ab b a a b++的最小值为（ ）A ．14B ．34C ．54D ．744．已知函数()24x x af x x++=，若对于任意[)1,x ∈+∞，()0f x >恒成立，则实数a的取值范围为（ ）A ．[)5,+∞B ．()5,-+∞C ．()5,5-D ．[]5,5-5．甲、乙、丙、丁四人参加数学竞赛，四人在成绩公布前作出如下预测： 甲预测说：获奖者在乙、丙、丁三人中； 乙预测说：我不会获奖，丙获奖 丙预测说：甲和丁中有一人获奖； 丁预测说：乙的猜测是对的成绩公布后表明，四人的猜测中有两人的预测与结果相符.另外两人的预测与结果不相符，已知有两人获奖，则获奖的是（） A ．甲和丁 B ．乙和丁 C ．乙和丙 D ．甲和丙6．若不等式210x ax -+≥对一切[2,)x ∈+∞恒成立，则实数a 的最大值为（ ） A ．0B ．2C ．52D ．37．下列命题中是真命题的是（ ）A ．y =的最小值为2；B ．当a ＞0，b ＞0时，114a b++； C ．若a 2+b 2=2，则a +b 的最大值为2；D ．若正数a ，b 满足2,a b +=则11+4+22a b +的最小值为12.8．已知A 、B 、C 为ABC 的三内角，且角A 为锐角，若tan 2tan B A =，则11tan tan B C+的最小值为（ ） A ．13B ．12C ．23D ．19．已知AB AC ⊥，1AB t=，AC t =，若P 点是ABC 所在平面内一点，且4AB AC AP ABAC=+，则·PB PC 的最大值等于（ ）. A ．13B ．15C ．19D ．2110．如图，平行四边形ABCD 的对角线相交于点O ，过点O 的直线与AB ，AD 所在直线分别交于点M ，N ，若AB ＝m AM ，AN ＝n AD （m ＞0，n ＞0），则mn的最大值为（ ）A ．22B ．1C ．2D ．211．已知1x >，则41x x +-的最小值为 A ．3B ．4C ．5D ．612．若直线20(,1)ax by a b +-=>始终把圆222220x y x y +---=的周长分为1:2．则11a b+的最大值为（ ） A ．423-B ．22-C 21D 2二、填空题13．设0b >，21a b -=，则242a a b+的最小值为_________.14．已知向量()2,1a y =-，(),3b x =，且a b ⊥，若x ，y 均为正数，则32x y+的最小值是______．15．设A .B 分别为双曲线22221x y a b-=（a >0，b >0）的左.右顶点，P 是双曲线上不同于A .B的一点，直线AP .BP 的斜率分别为m .n ，则当3b a 取最小值时，双曲线的离心率为__________.16．已知0x >，0y >，满足2126x y x y+++=，存在实数m ，对于任意x ，y ，使得2m x y ≤+恒成立，则m 的最大值为____________.17．ABC 中，点M ，N 在线段AB 上，且满足AM BM =，2BN AN =，若6C π=，||4CA CB ⋅=∣∣，则CM NC ⋅的最大值为________.18．已知关于x 的不等式()()22454130m m x m x +---+>对一切实数x 恒成立，则实数m 的取值范围为_____________. 19．已知0a >，0b >，若不等式212ma b a b+≥+恒成立，则m 的最大值为______． 20．若正数a ，b 满足2ab =，则11112M a b=+++的最小值为________. 三、解答题21．已知函数2()21f x kx kx =+-.（1）若不等式()0f x <的解集为3,12⎛⎫- ⎪⎝⎭，求实数k 的值；（2）若方程()0f x =在[]12，有解，求实数k 的取值范围. 22．2020年11月23日，贵州宣布最后9个深度贫困县退出贫困县序列，这不仅标志着贵州省66个贫困县实现整体脱贫，这也标志着国务院扶贫办确定的全国832个贫困县全部脱贫摘帽，全国脱贫攻坚目标任务已经完成.在脱贫攻坚过程中，某地县乡村三级干部在帮扶走访中得知某贫困户的实际情况后，为他家量身定制了脱贫计划，政府无息贷款10万元给该农户种养羊，每万元可创造利润0.15万元.若进行技术指导，养羊的投资减少了x ()0x >万元，且每万元创造的利润变为原来的()10.25x +倍.现将养羊少投资的x 万元全部投资网店，进行农产品销售，则每万元创造的利润为()0.150.875a x -万元，其中0a >. （1）若进行技术指导后养羊的利润不低于原来养羊的利润，求x 的取值范围； （2）若网店销售的利润始终不高于技术指导后养羊的利润，求a 的最大值. 23．已知2,()23a f x ax x ∈=+-R ．（Ⅰ）关于x 的方程()0f x =有且只有正根，求实数a 的取值范围； （Ⅱ）若()30f x a -≥对[1,0]a ∈-恒成立，求实数x 的取值范围．24．已知关于x 的不等式()22600kx x k k -+<≠.（1）若不等式的解集是{3x x <-或}2x >-，求k 的值；（2）若不等式的解集是R ，求k 的取值范围； （3）若不等式的解集为∅，求k 的取值范围．25．已知函数()|21||2|f x x x =---，M 为不等式()1f x <-的解集. （1）求M ；（2）当,a b M ∈且1a b +=时，4a b tab +≥恒成立，求t 的最大值.26．设2()(1)1f x m x mx m =+-+-.（1）当1m =时，解关于x 的不等式()0f x >；（2）若关于x 的不等式()0f x m ->的解集为()1,2，求m 的值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】根据已知条件由2()2a b ab +≤可求出2212a b +≥，又由完全平方公式可得221a b +<，即可判断A 、B ；由已知条件可知01b <<，则2b b >，因此22212a b a b +>+≥，可判断C ；由平方差公式可得12a b -=，与1a b +=联立可求出满足条件的a 、b ，故D 可能成立. 【详解】001a b a b >>+=，，2222211()21212()12()222a b a b a b ab ab +∴+=+-=-≥-⋅=-⨯=， 当且仅当12a b ==时等号成立， 又0ab >，222()2121b a b a ab a b +=+-=-<∴，22112a b ≤+<∴，则221a b +=不可能成立； 2211()()224a b ab ≤==+，当且仅当12a b ==时等号成立，故1ab =不可能成立；001a b a b >>+=，，，01b ∴<<，2b b ∴>，22212b a b a +>+≥∴（由A 可知），则212a b +=不可能成立； ()()2212a b a b a b a b -=+-=-=，联立112a b a b +=⎧⎪⎨-=⎪⎩，解得31,44a b ==，满足条件，D 成立. 故选：D2．A解析：A 【分析】利用“1”的代换，转化()1414a b a b a b ⎛⎫+=++ ⎪⎝⎭，结合基本不等式即可得解. 【详解】1a b +=，0a >，0b > ()1414455549b a a b a b a b a b ⎛⎫+++=++≥+=+= ⎪⎝⎭∴=， 当且仅当4b a a b =，即13a =，23b =时，等号成立. 14a b ∴+的最小值为9 故选：A. 【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件： （1）“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.3．B解析：B 【分析】利用1a b +=，0b >，10b a =->，1a ∴>且0a ≠； 对a 进行分类讨论，分为10a >>和0a >，进行讨论，然后，求解即可得到2244||ab b a a b++的最小值【详解】1a b +=，0b >，10b a =->，1a ∴>且0a ≠；当10a >>，22224414||444ab b a ab b a b a a b ab a b ++++==++1544≥+=；当且仅当4b aa b =，又1b a =-，解得1a =-或13a =，又由10a >>，得13a =时，此时，23b =，2244||ab b a a b ++的最小值54；当0a >，222244134||4444ab b a ab b a b a a b ab a b ++++⎛⎫⎛⎫==-+-+-≥ ⎪ ⎪-⎝⎭⎝⎭，当且仅当4b aa b -=-时，解得1a =-或13a =，又由0a >，得1a =-，此时，2b =，2244||ab b a a b ++的最小值34；综上，2244||ab b a a b ++的最小值34；故选：B 【点睛】关键点睛：解题的关键在于利用1a b +=，0b >，10b a =->，可得1a >且0a ≠，对a 进行分类讨论，难点在于利用基本不等式进行求最值，本题属于中档题4．B解析：B 【分析】根据条件将问题转化为“24a x x >--在[)1,+∞上恒成立”，再根据()2max4a x x>--求解出a 的范围. 【详解】因为对于任意[)1,x ∈+∞，()0f x >恒成立，所以240x x a ++>对[)1,x ∈+∞恒成立， 所以()2max4a x x>--，[)1,x ∈+∞，又因为24y x x =--的对称轴为2x =-，所以24y x x =--在[)1,+∞上单调递减， 所以()()2max4145x x --=--=-，所以5a >-，故选：B. 【点睛】方法点睛：一元二次不等式在指定区间上恒成立求解参数范围问题的处理方法： （1）分类讨论法：根据参数的临界值作分类讨论；（2）分离参数法：将自变量和参数分离开来，自变量部分构造新函数，分析新函数的最值与参数的大小关系.5．B解析：B 【分析】从四人的描述语句中可以看出，乙、丁的表述要么同时与结果相符，要么同时与结果不符，再进行判断 【详解】若乙、丁的预测成立，则甲、丙的预测不成立，推出矛盾．故乙、丙预测不成立时，推出获奖的是乙和丁 答案选B 【点睛】真假语句的判断需要结合实际情况，作出合理假设，才可进行有效论证6．C解析：C 【分析】采用参变分离法对不等式变形，然后求解变形后的函数的值域，根据参数与新函数的关系求解参数最值. 【详解】因为不等式210x ax -+≥对一切[)2,x ∈+∞恒成立，所以对一切[)2,x ∈+∞，21ax x ≤+，即21x a x+≤恒成立．令()[)()2112,x g x x x x x+==+∈+∞．易知()1g x x x=+在[)2,+∞内为增函数． 所以当2x =时，()min 52g x =，所以a 的最大值是52．故选C ． 【点睛】常见的求解参数范围的方法：（1）分类讨论法（从临界值、特殊值出发）； （2）参变分离法（考虑新函数与参数的关系）.7．B解析：BCD 【分析】利用基本不等式分别判断A 、B 、D 选项，C 选项可设,a b αα==，利用三角函数的值域求范围. 【详解】A 选项，222x +≥0>，∴2y=≥==，即221x+=±时成立，又222x≥+，故A错；B选项，当a＞0，b＞0时，1124a b+++≥⨯=，当且仅当1a b=⎧=，即1a b==时等号成立，B正确；C选项，设,a bαα==，则2sin24a bπααα⎛⎫+==+≤⎪⎝⎭，C正确；D选项，2a b+=，()212192a b⎡⎤⎛⎫∴+++=⎪⎢⎥⎝⎭⎣⎦，则()121252229291111++4+22442+2242a b a baba ba b⎛⎫+⎪⎡⎤+⎛⎫⎛⎫+++=⨯++⎪⎪ ⎪⎢⎥++⎝⎭⎝=+⎣+⎭⎦ ⎪⎝⎭251942⎛≥⨯+=⎝⎭，当且仅当122422aba b++=++且2a b+=时等号成立，解得1a b==，故D正确.故选：BCD【点睛】本题考查基本不等式的应用、利用三角函数的值域求范围，注意取等号的条件，属于中档题.8．C解析：C【分析】将11tan tanB C+化为关于tan A的式子，然后利用基本不等式可以求出最小值.【详解】在ABC中，()tan tanC A B=-+，111111tan tantan tan tan tan tan tan tanA BB C B A B B A B，tan 2tan B A =， 211tan tan 112tan 12tan tan tan tan 2tan 3tan 6tan 3A B AAB A B A AA ,角A 为锐角,tan 0A ∴>，12tan 12tan 226tan 36tan 33A AA A ， 当且仅当12tan 6tan 3A A ，即1tan 2A =时，等号成立，∴11tan tan B C +的最小值为23. 故选：C. 【点睛】本题考查三角形中角的互化，和的正切公式的应用，以及利用基本不等式求最值，属于中档题.9．A解析：A 【详解】以A 为坐标原点，建立平面直角坐标系，如图所示，则1(,0)B t，(0,)C t ，1AP =（，0)+4(0,1)=(1,4)，即1P（，4)，所以114)PB t=--（，，14)PC t =--（，，因此PB PC ⋅11416t t =--+117(4)t t =-+，因为114244t t t t+≥⋅=，所以PB PC ⋅的最大值等于13，当14t t =，即12t =时取等号．考点：1、平面向量数量积；2、基本不等式．10．B解析：B 【分析】根据向量共线的推论，结合向量的线性运算求得12m n+=，再用基本不等式即可求得结果. 【详解】 因为1122AO AB AD =+，又AB ＝m AM ，AN ＝n AD ， 故可得 122m AO AM AN n=+，又,,O M N 三点共线， 故可得1122m n +=，即12m n+=. 故211114m m m n n n ⎛⎫=⨯≤+= ⎪⎝⎭，当且仅当1m n ==时取得最大值. 故选：B . 【点睛】本题考查平面向量共线定理的推论以及基本不等式的应用，属综合中档题.11．C解析：C 【分析】由1x >，得10x ->，则441111x x x x +=-++--，利用基本不等式，即可求解． 【详解】由题意，因为1x >，则10x ->，所以44111511x x x x +=-++≥=--， 当且仅当411x x -=-时，即3x =时取等号，所以41x x +-的最小值为5，故选C ． 【点睛】本题主要考查了基本不等式的应用，其中解答中熟记基本不等式的使用条件，合理构造是解答的关键，着重考查了推理与运算能力，属于基础题．12．B解析：B 【分析】由圆的方程得圆心和半径，根据圆的周长被分为1:2，可推出圆心到直线的距离为1，即1=，化简整理后，再结合基本不等式的性质可得ab 的最小值，再求出11a b+的最大值． 【详解】把圆222220x y x y +---=化成标准形式为22(1)(1)4x y -+-=，其中圆心为(1,1)，半径为2．设直线与圆交于A 、B 两点，圆心为C ， 因为直线把圆的周长分为1:2，所以13601203ACB ∠=⨯︒=︒， 所以圆心(1,1)C 到直线20ax by +-=的距离为12221a b a b+-=+，因为a ，1b >，所以202()a ab b -++=，由基本不等式的性质可知，22()4ab a b ab +=+， 当且仅当a b =时，等号成立，此时有2(22)ab +，所以21(2)1111122222(22)ab a b a b ab ab ab+++===++=+． 所以11a b +的最大值为22- 故选：B ． 【点评】本题主要考查直线与圆的综合问题，除圆的标准方程、点到直线的距离公式等基础知识外，还涉及利用基本不等式的性质求最值，考查学生的逻辑推理能力和运算能力，属于中档题．二、填空题13．4【分析】两次应用基本不等式验证等号能同时成立即得【详解】由题意当且仅当即时上述不等式中等号同时成立故答案为：4【点睛】本题考查了基本不等式求最值考查了运算求解能力逻辑推理能力在连续运用基本不等式求解析：4 【分析】两次应用基本不等式，242a a b +≥12b b +≥，验证等号能同时成立即得． 【详解】由题意211a b =+≥，2442a a b +≥===≥， 当且仅当2142b baa b⎧=⎪⎪⎨⎪=⎪⎩，即21a b =⎧⎨=⎩时上述不等式中等号同时成立． 故答案为：4． 【点睛】本题考查了基本不等式求最值，考查了运算求解能力，逻辑推理能力，在连续运用基本不等式求最值时，要注意等号能否同时成立．14．8【分析】由题意利用两个向量垂直的性质基本不等式求得的最大值可得要求式子的最小值【详解】解：向量且若均为正数则当且仅当时取等号则故答案为：8【点睛】本题主要考查两个向量垂直的性质基本不等式的应用属于解析：8 【分析】由题意利用两个向量垂直的性质，基本不等式，求得xy 的最大值，可得要求式子的最小值． 【详解】 解：向量(2,1)a y =-，(,3)b x =，且a b ⊥，∴23(1)0a b x y =+-=．若x ，y 均为正数，则23326x y xy +=，38xy ∴，当且仅当3232x y ==时，取等号． 则32233838y xx y xy++==， 故答案为：8． 【点睛】本题主要考查两个向量垂直的性质，基本不等式的应用，属于中档题．15．【分析】先根据点的关系确定mn 再根据基本不等式确定最小值最后根据最小值取法确定双曲线的离心率【详解】设则因此当且仅当时取等号所以离心率是故答案为：【点睛】本题考查双曲线离心率和基本不等式求最值的简单 【分析】先根据点的关系确定mn ，再根据基本不等式确定最小值，最后根据最小值取法确定双曲线的离心率. 【详解】设11(,)P x y ，则 22111222111y y y b mn x a x a x a a =⋅==+--，因此3b a+3b a a b =+≥= 当且仅当3a b 时取等号,所以离心率是c e a ===.【点睛】本题考查双曲线离心率和基本不等式求最值的简单综合问题，属于基础题型，一般求双曲线离心率的方法是1.直接法：直接求出,a c ，然后利用公式ce a=求解；2.公式法：c e a ===3.构造法：根据条件，可构造出,a c 的齐次方程，通过等式两边同时除以2a ，进而得到关于e 的方程.16．2【分析】首先根据题意得到从而得到即再根据恒成立即可得到的最大值【详解】因为所以所以即解得因为恒成立所以即所以的最大值为故答案为：【点睛】本题主要考查基本不等式同时考查了不等式的恒成立问题属于中档题解析：2 【分析】首先根据题意得到()228x y xy +≤，从而得到()8622x y y x≤+++，即224x y ≤+≤，再根据2m x y ≤+恒成立，即可得到m 的最大值.【详解】因为0x >，0y >，所以()()22221122248x y x y xy x y ++=⋅≤⨯=， 所以()()()22122862222228y x y x x y x y x y x y x y xy y x x y ++=+++=++≥++=++++. 即()8622x y y x≥+++， ()()226280x y x y +-++≤，解得224x y ≤+≤.因为2m x y ≤+恒成立，所以()min 2m x y ≤+，即2m ≤. 所以m 的最大值为2. 故答案为：2 【点睛】本题主要考查基本不等式，同时考查了不等式的恒成立问题，属于中档题.17．；【分析】由平面向量数量积的运算可知再根据平面向量的线性运算可分别得到故由基本不等式的性质可知将所得结论均代入的表达式即可得解【详解】解：根据题意作出如下图形由基本不等式的性质可知的最大值为故答案为解析：4233--； 【分析】由平面向量数量积的运算可知23CA CB =，再根据平面向量的线性运算可分别得到1()2CM CA CB =+，1(2)3NC CA CB =-+，故221(23)6CM NC CA CB CA CB =-++，由基本不等式的性质可知，22222||||CA CB CA CB +，将所得结论均代入CM NC 的表达式即可得解． 【详解】解：根据题意，作出如下图形，6C π=，||||4CA CB =，∴4cos236CA CB π=⨯=AM BM =，∴1()2CM CA CB =+，2BN AN =，∴111()(2)333NC AC AN AC AB CA CB CA CA CB =-=-=---=-+，∴22111()[(2)](23)236CM NC CA CB CA CB CA CB CA CB =+-+=-++，由基本不等式的性质可知，222222||||22||||82CA CB CA CB CA CB +=+=，∴142(82323)36CM NC -⨯⨯=∴CM NC 的最大值为423-故答案为：423- 【点睛】本题考查平面向量的线性运算和数量积运算、基本不等式的性质，熟练掌握平面向量的加法、减法、数乘和数量积的运算法则是解题的关键，考查学生的逻辑推理能力和运算能力，属于中档题．18．【分析】分和两种情况讨论结合题可得出关于实数的不等式组由此可解得实数的取值范围【详解】当时可得或①当时可得合乎题意；②当时可得解得不合乎题意；当时由题意可得解得综上所述实数的取值范围是故答案为：【点 解析：1,19【分析】分2450m m +-=和2450m m +-≠两种情况讨论，结合题可得出关于实数m 的不等式组，由此可解得实数m 的取值范围. 【详解】当2450m m +-=时，可得1m =或5m =-. ①当1m =时，可得30>，合乎题意；②当5m =-时，可得2430x +>，解得18x >-，不合乎题意；当2450m m +-≠时，由题意可得()()22245016112450m m m m m ⎧+->⎪⎨∆=--+-<⎪⎩，解得119m <<.综上所述，实数m 的取值范围是1,19. 故答案为：1,19. 【点睛】本题考查利用一元二次不等式在实数集上恒成立求参数，考查计算能力，属于中等题.19．9【分析】将题目所给不等式分离常数利用基本不等式求得的最大值【详解】由得恒成立而故所以的最大值为【点睛】本小题主要考查不等式恒成立问题求解策略考查利用基本不等式求最值考查化归与转化的数学思想方法属于解析：9. 【分析】将题目所给不等式分离常数m ，利用基本不等式求得m 的最大值. 【详解】 由212m a b a b +≥+得()212m a b a b ⎛⎫≤++ ⎪⎝⎭恒成立，而()212225a b a b a b b a ⎛⎫++=++ ⎪⎝⎭5549≥+=+=，故9m ≤，所以m 的最大值为9. 【点睛】本小题主要考查不等式恒成立问题求解策略，考查利用基本不等式求最值，考查化归与转化的数学思想方法，属于中档题.20．【分析】求出设（当且仅当时成立）求出的最小值即可【详解】解：设（当且仅当时成立）的最小值为故答案为：【点睛】本题考查了基本不等式的性质考查转化思想属于中档题解析：23【分析】求出23154a M a a =-++，设254445259a a N a a a a a++==+++=（当且仅当2a =时“=”成立），求出M 的最小值即可． 【详解】 解：2ab =，0a >，0b >，2b a∴=， 21111114311411211414541a a M a b a a a a a a a a∴=+=+=+=+-=-++++++++++，设254445259a a N a a a a a++==+++=（当且仅当2a =时“=”成立）， 1109N ∴<，1303N--<，23113N -<， 11112M a b ∴=+++的最小值为23， 故答案为：23． 【点睛】本题考查了基本不等式的性质，考查转化思想，属于中档题．三、解答题21．（1）13；（2）11,103⎡⎤⎢⎥⎣⎦. 【分析】 （1）由题意可得32-、1是方程2210kx kx +-=的两个根，利用两根之积列方程即可求解；（2）方程()0f x =在[]12，有解，可得212k x x=+在[]12，有解，利用二次函数的性质求出22y x x =+的范围，即可求解. 【详解】（1）因为2210kx kx +-<的解集是3,12⎛⎫- ⎪⎝⎭， 所以32-、1是方程2210kx kx +-=的两个根， 由根与系数的关系可得：31122k -⨯=-，解得：13k =， （2）因为方程()0f x =在[]12，有解， 所以2210kx kx +-=在[]12，有解， 212k x x=+在[]12，有解， 因为22y x x =+对称轴为14x =-，在[]12，上单调递增， 所以[]223,10y x x =+∈，可得2111,2103k x x ⎡⎤=∈⎢⎥+⎣⎦，所以实数k 的取值范围11,103⎡⎤⎢⎥⎣⎦. 【点睛】方法点睛：已知函数有零点(方程有根)求参数值(取值范围)常用的方法： （1）直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围； （2）分离参数法：先将参数分离，转化成求函数的值域问题加以解决；（3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解22．（1）x 的取值范围为06x <≤；（2）a 的最大值为6.5． 【分析】（1）由题意得()()0.1510.25100.1510x x +-≥⨯，解不等式可得结果；（2）由题意得()()()0.150.8750.1510.2510a x x x x -≤+-恒成立，分离出参数a 得510 1.58x a x ≤++恒成立，只要利用基本不等式求出5108x x +的最小值即可 【详解】 解：（1）由题意，得()()0.1510.25100.1510x x +-≥⨯， 整理得260x x -≤，解得06x ≤≤，又0x >，故06x <≤． （2）由题意知网店销售的利润为()0.150.875a x x -万元， 技术指导后，养羊的利润为()()0.1510.2510x x +-万元， 则()()()0.150.8750.1510.2510a x x x x -≤+-恒成立，又010x <<，∴5101.58x a x≤++恒成立， 又51058x x+≥，当且仅当4x =时等号成立， ∴0 6.5a <≤，即a 的最大值为6.5．答：（1）x 的取值范围为06x <≤；（2）a 的最大值为6.5．【点睛】关键点点睛：此题考查利用数学知识解决实际问题，考查不等式的解法，第2问解题的关键是由()()()0.150.8750.1510.2510a x x x x -≤+-恒成立，转化为5101.58x a x≤++恒成立，然后利用基本不等式求5108x x+的最小值即可，属于中档题 23．无 24．无 25．无 26．无。
(完整版)一元一次不等式与一次函数习题(含答案)
一元一次不等式与一次函数1．如图，函数y=2x和y=ax+4的图象相交于点A〔m，3〕，那么不等式2x＜ax+4的解集为〔〕(5)A．x＜B．x＜3C．x＞D．x＞32．一次函数y=ax+b的图象过第一、二、四象限，且与x轴交于点〔2，0〕，那么关于x的不等式a〔x﹣1〕﹣b＞0的解集为〔〕A．x＜﹣1B．x＞﹣1C．x＞1D．x＜13．如图，直线y1=k1x+a与y2=k2x+b的交点坐标为〔1，2〕，那么使y1＜y2的x的取值范围为〔〕A．x＞1B．x＞2C．x＜1D．x＜24．直线l1：y=k1x+b与直线l2：y=k2x+c在同一平面直角坐标系中的图象如下图，那么关于x的不等式k1x+b＜k2x+c的解集为〔〕A．x＞1B．x＜1C．x＞﹣2D．x＜﹣25．如图，一次函数y=kx+b的图象经过A、B两点，那么kx+b＞0解集是〔〕A．x＞0B．x＞﹣3C．x＞2D．﹣3＜x＜26．如图，函数y=kx和y=﹣x+3的图象相交于〔a，2〕，那么不等式kx＜﹣x+3的解集为〔〕A．B．x＞C．x＞2D．x＜2 x＜7．〔如图，直线l是函数y= x+3的图象．假设点P〔x，y〕满足x＜5，且y＞，那么P点的坐标可能是〔〕(6)(8)1A．〔4，7〕B．〔3，﹣5〕C．〔3，4〕D．〔﹣2，1〕8．如图，一次函数y=kx+b的图象经过点A〔5，0〕与B〔0，﹣4〕，那么关于x的不等式kx+b＜0的解集是〔〕A．x＜5B．x＞5C．x＜﹣4D．x＞﹣49．如图，一次函数y=kx+b的图象经过点〔2，0〕与〔0，3〕，那么关于x的不等式k x+b＞0的解集是〔〕(10)(11)A．x＜2B．x＞2C．x＜3D．x＞310．如图，直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2，根据图象有以下3个结论：①a＞0；②b＞0；③x＞﹣2是不等式3x+b＞ax﹣2的解集．其中正确的个数是〔〕A．0B．1C．2D．3二．填空题〔共8小题〕11．如图，经过点B〔﹣2，0〕的直线y=kx+b与直线y=4x+2相交于点A〔﹣1，﹣2〕，那么不等式4x+2＜kx+b＜0的解集为_________．12．如图，l1反映了某公司的销售收入与销量的关系，l2反映了该公司产品的销售本钱与销量的关系，当该公司赢利〔收入＞本钱〕时，销售量必须_________．(13)(14)(15)13．如图，函数y=2x和y=ax+5的图象相交于A〔m，3〕，那么不等式2x＜ax+5的解集为_________．14．如图，直线y1=x+m与y2=kx﹣1相交于点P〔﹣1，1〕，那么关于x的不等式x+m＞kx﹣1的解集为_________．15．如图，直线y1=kx+b与直线y2=mx交于点P〔1，m〕，那么不等式mx＞kx+b的解集是_________．216．如图，函数y=x+b和y=ax+3的图象相交于点P，那么关于x的不等式x+b＜ax+3的解集为_________．(17)(18)17．如图，直线y=kx+b经过点A〔﹣1，1〕和点B〔﹣4，0〕，那么不等式0＜kx+b＜﹣x的解集为_________．18．如图，直线y=kx+b交坐标轴于A〔﹣3，0〕、B〔0，5〕两点，那么不等式﹣kx﹣b＜0的解集是_________．三．解答题19．在平面直角坐标系中，直线y=kx﹣15经过点〔4，﹣3〕，求不等式kx﹣15≥0的解．20．如图，直线l1与l2相交于点 P，点P横坐标为﹣1，l1的解析表达式为y= x+3，且l1与y轴交于点A，l2与y轴交于点B，点A与点B恰好关于x轴对称．1〕求点B的坐标；2〕求直线l2的解析表达式；3〕假设点M为直线l2上一动点，直接写出使△MAB的面积是△PAB的面积的的点M的坐标；〔4〕当x为何值时，l1，l2表示的两个函数的函数值都大于0？3（21．：直线l1的解析式为y1=x+1，直线l2的解析式为y2=ax+b〔a≠0〕；两条直线如下图，这两个图象的交点（在y轴上，直线l2与x轴的交点B的坐标为〔2，0〕〔1〕求a，b的值；（〔2〕求使得y1、y2的值都大于0的取值范围；（〔3〕求这两条直线与x轴所围成的△ABC的面积是多少？（〔4〕在直线AC上是否存在异于点C的另一点P，使得△ABC与△ABP的面积相等？请直接写出点P的坐标．（（（（（（（（（（（（（（（（（（（（（（22．如图，直线y=kx+b经过点A〔0，5〕，B〔1，4〕．（1〕求直线AB的解析式；（2〕假设直线y=2x﹣4与直线AB相交于点C，求点C的坐标；3〕根据图象，写出关于x的不等式2x﹣4≥kx+b的解集．4AACBBAAAAD﹣2＜x＜﹣1．大于4．x＜．x＞﹣1．x＞1．x＜1．﹣4＜x＜﹣1．x＞﹣19 x≥5．20.解：〔1〕当x=0时，x+3=0+3=3，∴点A的坐标是〔0，3〕，∵点A与点B恰好关于x轴对称，∴B点坐标为〔0，﹣3〕；2〕∵点P横坐标为﹣1，∴〔﹣1〕+3=，∴点P的坐标是〔﹣1，〕，设直线l2的解析式为y=kx+b，那么，解得，∴直线l2的解析式为y=﹣x﹣3；〔3〕∵点P横坐标是﹣1，△MAB的面积是△PAB的面积的，∴点M的横坐标的长度是，①当横坐标是﹣时，y=〔﹣〕×〔﹣〕﹣3=﹣3=﹣，②当横坐标是时，y=〔﹣〕×﹣3=﹣﹣3=﹣，∴M点的坐标是〔﹣，﹣〕或〔，﹣〕；〔4〕l1：y=x+3，当y=0时，x+3=0，解得x=﹣6，l：y=﹣x﹣3，当y=0时，﹣x﹣3=0，2解得x=﹣，∴当﹣6＜x＜﹣时，l12、l表示的两个函数的函数值都大于0．解：〔1〕由直线l1的解析式为y1=x+1，可求得C〔0，1〕；那么依题意可得：，5解得：．〔2〕由〔1〕知，直线l2：y=﹣x+1；y1=x+1＞0，∴x＞﹣1；∵；∴﹣1＜x＜2．〔3〕由题意知A〔﹣1，0〕，那么AB=3，且OC=1；∴S△ABC= AB?OC=．〔4〕由于△ABC、△ABP同底，假设面积相等，那么P点纵坐标为﹣1，代入直线l1可求得：P的坐标为〔﹣2，﹣1〕．解：〔1〕∵直线y=﹣kx+b经过点A〔5，0〕、B〔1，4〕，∴，解方程组得，∴直线AB的解析式为y=﹣x+5；〔2〕∵直线y=2x﹣4与直线AB相交于点C，∴解方程组，解得，∴点C的坐标为〔3，2〕；〔3〕由图可知，x≥3时，2x﹣4≥kx+b．6。
一元一次不等式与一次函数的应用(含答案)
一元一次不等式与一次函数1、某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同，设汽车每月行驶x千米，个体车主收费y1元，国营出租车公司收费为y2元，观察下列图象可知，当x取值范围为什么时，选用个体车较合算.2、甲有存款600元，乙有存款2000元，从本月开始，他们进行零存整取储蓄，甲每月存款500元，乙每月存款200元.(1)列出甲、乙的存款额y1、y2(元)与存款月数x(月)之间的函数关系式，画出函数图象.(2)请问到第几个月，甲的存款额超过乙的存款额？3、某商场计划投入一笔资金采购一批紧俏商品，经市场调研发现，如果本月初出售，可获利10%，然后将本利再投资其他商品，到下月初又可获利10%；如果下月初出售可获利25%，但要支付仓储费8000元.请你根据商场的资金情况，向商场提出合理化建议，说明何时出售获利较多．4、某市为鼓励居民节约用水，对每户用水按如下标准收费：若每户每月用水不超过8 m3，则每m3按1元收费；若每户每月用水超过8m3，则超过部分每m3按2元收费.某用户7月份用水比8m3多xm3，交纳水费y 元.(1)求y关于x的函数解析式，并写出x的取值范围.(2)此用户要想每月水费控制在20元以内，那么每月的用水量最多不超过多少m3?5、某商场用36万元购进A、B两种商品，销售完后共获利6万元，其进价和售价如下表：(1) 该商场购进A、B两种商品各多少件?(2) 商场第二次以原进价购进A、B两种商品．购进B种商品的件数不变，而购进A种商品的件数是第一次的2倍，A种商品按原价出售，而B种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于81600元，B种商品最低售价为每件多少元?6、为了加快教学手段的现代化，某校计划购置一批电脑，已知甲公司的报价是每台5800元，优惠条件是购买10台以上，则从第11台开始按报价的70%计算；乙公司的报价也是每台5800元，优惠条件是每台均按报价的85%计算.假如你是学校有关方面负责人，在电脑品牌、质量、售后服务等完全相同的前提下，你如何选择？请说明理由？7、苏州地处太湖之滨，有丰富的水产养殖资源，水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖，他了解到如下信息：①每亩水面的年租金为500元，水面需按整数亩出租；②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗；③每公斤蟹苗的价格为75元，其饲养费用为525元，当年可获1400元收益；④每公斤虾苗的价格为15元，其饲养费用为85元，当年可获160元收益；（1）若租用水面n亩，则年租金共需__________元；（2）水产养殖的成本包括水面年租金、苗种费用和饲养费用，求每亩水面蟹虾混合养殖的年利润（利润=收益－成本）；（3）李大爷现在资金25000元，他准备再向银行贷不超过25000元的款，用于蟹虾混合养殖.已知银行贷款的年利率为8%，试问李大爷应该租多少亩水面，并向银行贷款多少元，可使年利润超过35000元？8、某汽车租赁公司要购买轿车和面包车共10辆，其中轿车至少要购买3辆，轿车每辆7万元，面包车每辆4万元，公司可投入的购车款不超过55万元；（1）符合公司要求的购买方案有几种？请说明理由；（2）如果每辆轿车的日租金为200元，每辆面包车的日租金为110元，假设新购买的这10辆车每日都可租出，要使这10辆车的日租金不低于1500元，那么应选择以上那种购买方案？9、哈尔滨市移动通讯公司开设了两种通讯业务：“全球通”使用者先缴50元月基础费，然后每通话1分钟，再付0.4元；“神州行”不缴月基础费，每通话1分钟，付话费0.6元（这里均指市内通话）.若一个内通话时间为x分钟，两种通讯方式的费用分别为y1元和y2元.（1）写出y1，y2与x的关系式；（2）一个月通话为多少分钟时，两种通讯方式的费用相同？参考答案1、＞15002、(1)y 1=600+500x y 2=2000+200x(2)x ＞432，到第5个月甲的存款额超过乙的存款额. 3、设商场投入资金x 元，如果本月初出售，到下月初可获利y 1元，则y 1＝10%x ＋(1＋10%)x ·10%＝0.1x ＋0.11x ＝0.21x ；如果下月初出售，可获利y 2元，则y 2＝25%x －8000＝0.25x －8000当y 1＝y 2即0.21x ＝0.25x －8000时，x ＝200000当y 1＞y 2即0.21x ＞0.25x －8000时，x ＜200000当y 1＜y 2即0.21x ＜0.25x －8000时，x ＞200000∴ 若商场投入资金20万元，两种销售方式获利相同；若商场投入资金少于20万元，本月初出售获利较多，若投入资金多于20万元，下月初出售获利较多．4、(1)y=2x+8(x ≥0) (2)145、（1）该商场分别购进A 、B 两种商品200件、120件.（2）B 种商品最低售价为每件1080元.6、解：如果购买电脑不超过11台，很明显乙公司有优惠，而甲公司没优惠，因此选择乙公司.如果购买电脑多于10台.则：设学校需购置电脑x 台，则到甲公司购买需付[10×5800＋5800（x －10）×70%]元，到乙公司购买需付5800×85% x 元.根据题意得：1）若甲公司优惠：则10×5800＋5800（x －10）×70%＜5800×85% x解得： x ＞302）若乙公司优惠：则10×5800＋5800（x －10）×70%＞5800×85% x解得： x ＜303）若两公司一样优惠：则10×5800＋5800（x －10）×70%＝5800×85% x解得： x ＝30答：购置电脑少于30台时选乙公司较优惠，购置电脑正好30台时两公司随便选哪家，购置电脑多于30台时选甲公司较优惠，7、（1）他继续在A 窗口排队所花的时间为42844a a -⨯-=（分） （2）由题意，得42625246a a -⨯-⨯+⨯>,解得 a ＞20. 8、解：（1）500n（2）每亩年利润＝（1400×4＋160×20）－（500＋75×4＋525×4＋15×20＋85×20）＝3900（元）（3）n 亩水田总收益＝3900n需要贷款数＝（500＋75×4＋525×4＋15×20＋85×20）n －25000＝4900n －25000贷款利息＝8％×(4900n －25000)＝392n －2000根据题意得：35000)2000392(3900≥--n n 解得：n ≥9.41∴ n ＝10需要贷款数：4900n －25000＝24000(元)答：李大爷应该租10亩水面，并向银行贷款24000元，可使年利润超过35000元9、解：（1）设轿车要购买x 辆，那么面包车要购买（10－x ）辆，由题意得：7x ＋4（10－x ）≤55解得：x ≤5又∵x ≥3，则 x ＝3，4，5∴购机方案有三种：方案一：轿车3辆，面包车7辆；方案二：轿车4辆，面包车6辆；方案三：轿车5辆，面包车5辆；（2）方案一的日租金为：3×200＋7×110＝1370（元）方案二的日租金为：4×200＋6×110＝1460（元）方案三的日租金为：5×200＋5×110＝1550（元）为保证日租金不低于1500元，应选择方案三.10、（1）y 1＝50＋0.4x ，y 2＝0.6x ；（2）当y 1＝y 2，即50＋0.4x ＝0.6x 时，x ＝250（分钟），即当通话时间为250分钟时，两种通讯方式的费用相同；（3）由y 1＜y 2即50＋0.4x ＜0.6x ，知x ＞250，即通话时间超过250分钟时用“全球通”的通讯方式便宜.。
一元一次不等式与一次函数习题精选(含答案)
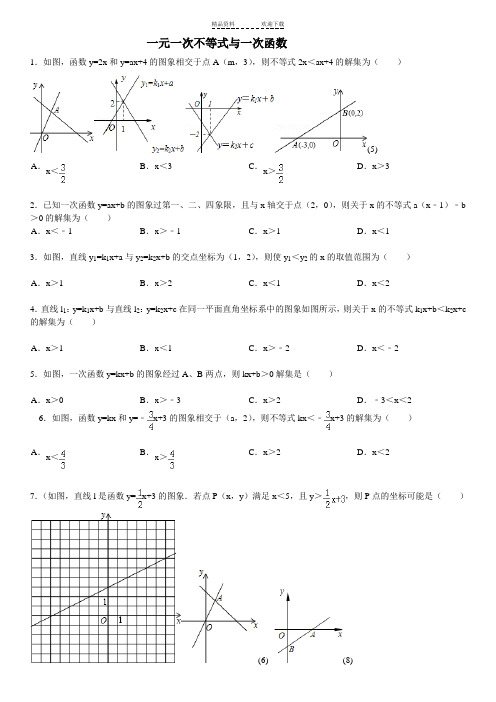
一元一次不等式与一次函数1．如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x＜ax+4的解集为（）(5)2．已知一次函数y=ax+b的图象过第一、二、四象限，且与x轴交于点（2，0），则关于x的不等式a（x﹣1）﹣b3．如图，直线y1=k1x+a与y2=k2x+b的交点坐标为（1，2），则使y1＜y2的x的取值范围为（）4．直线l1：y=k1x+b与直线l2：y=k2x+c在同一平面直角坐标系中的图象如图所示，则关于x的不等式k1x+b＜k2x+c 的解集为（）5．如图，一次函数y=kx+b的图象经过A、B两点，则kx+b＞0解集是（）6．如图，函数y=kx和y=﹣x+3的图象相交于（a，2），则不等式kx＜﹣x+3的解集为（）＞7．（如图，直线l是函数y=x+3的图象．若点P（x，y）满足x＜5，且y＞，则P点的坐标可能是（）8．如图，已知一次函数y=kx+b的图象经过点A（5，0）与B（0，﹣4），那么关于x的不等式kx+b＜0的解集是（）9．如图，一次函数y=kx+b的图象经过点（2，0）与（0，3），则关于x的不等式kx+b＞0的解集是（）10．如图，已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2，根据图象有下列3个结论：①a＞0；②b＞0；③x ＞﹣2是不等式3x+b＞ax﹣2的解集．其中正确的个数是（）二．填空题（共8小题）11．如图，经过点B（﹣2，0）的直线y=kx+b与直线y=4x+2相交于点A（﹣1，﹣2），则不等式4x+2＜kx+b＜0的解集为_________．12．如图，l1反映了某公司的销售收入与销量的关系，l2反映了该公司产品的销售成本与销量的关系，当该公司赢利（收入＞成本）时，销售量必须_________．(13) (14) (15)13．如图，函数y=2x和y=ax+5的图象相交于A（m，3），则不等式2x＜ax+5的解集为_________．14．如图，已知直线y1=x+m与y2=kx﹣1相交于点P（﹣1，1），则关于x的不等式x+m＞kx﹣1的解集为_________．15．如图，直线y1=kx+b与直线y2=mx交于点P（1，m），则不等式mx＞kx+b的解集是_________．16．如图，已知函数y=x+b和y=ax+3的图象相交于点P，则关于x的不等式x+b＜ax+3的解集为_________．(17) (18)17．如图，直线y=kx+b经过点A（﹣1，1）和点B（﹣4，0），则不等式0＜kx+b＜﹣x的解集为_________．18．如图，直线y=kx+b交坐标轴于A（﹣3，0）、B（0，5）两点，则不等式﹣kx﹣b＜0的解集是_________．三．解答题19．在平面直角坐标系中，直线y=kx﹣15经过点（4，﹣3），求不等式kx﹣15≥0的解．20．如图，直线l1与l2相交于点P，点P横坐标为﹣1，l1的解析表达式为y=x+3，且l1与y轴交于点A，l2与y轴交于点B，点A与点B恰好关于x轴对称．（1）求点B的坐标；（2）求直线l2的解析表达式；（3）若点M为直线l2上一动点，直接写出使△MAB的面积是△PAB的面积的的点M的坐标；（4）当x为何值时，l1，l2表示的两个函数的函数值都大于0？21．已知：直线l1的解析式为y1=x+1，直线l2的解析式为y2=ax+b（a≠0）；两条直线如图所示，这两个图象的交点在y轴上，直线l2与x轴的交点B的坐标为（2，0）（1）求a，b的值；（2）求使得y1、y2的值都大于0的取值范围；（3）求这两条直线与x轴所围成的△ABC的面积是多少？（4）在直线AC上是否存在异于点C的另一点P，使得△ABC与△ABP的面积相等？请直接写出点P的坐标．22．如图，直线y=kx+b经过点A（0，5），B（1，4）．（1）求直线AB的解析式；（2）若直线y=2x﹣4与直线AB相交于点C，求点C的坐标；（3）根据图象，写出关于x的不等式2x﹣4≥kx+b的解集．AACBBAAAAD﹣2＜x＜﹣1．大于4．x＜．x＞﹣1．x＞1．x＜1．﹣4＜x＜﹣1．x＞﹣时，+3=）的面积的，的横坐标的长度是，时，）（﹣﹣，时，（﹣×﹣﹣点的坐标是（﹣，﹣）或（，﹣）x+3时，x时，﹣﹣时，﹣；=OC=解方程组得∴解方程组，。
(常考题)人教版高中数学必修第一册第二单元《一元一次函数,方程和不等式》测试卷(含答案解析)(3)
一、选择题1．若对(0,)t ∀∈+∞，都有22(1)3x t x t+<+成立，则x 的取值范围是（ ） A ．()2,6-B ．(,3)(2,6)-∞--C ．(,3)(2,)-∞-⋃-+∞D ．(,3)(2,)-∞-⋃-+∞ 2．已知关于x 的不等式210mx mx ++>恒成立，则m 的取值范围为（ ）．A ．()0,4B ．[)0,4C ．[]0,4D ．(](),04,-∞⋃+∞3．已知0a >，0b >，且1a b +=，则14a b+的最小值为（ ） A ．9B ．8C ．7D ．64．已知0,0,23x y x y >>+=，则1421x y++的最小值是（ ） A ．3B ．94 C ．4615D ．95．对于任意实数x ，不等式210ax ax -+>恒成立，则实数a 的取值范围是（ ）A ．(]0,4B ．[)0,4C ．(][),04,-∞+∞ D ．()(),04,-∞+∞6．若集合{}2|10A x ax ax =-+<=∅,则实数a 的取值范围是 ( ) A ．{}|04a a << B ．{|04}a a ≤< C ．{|04}a a <≤D ．{|04}a a ≤≤7．如图，在ABC 中，23BD BC =，E 为线段AD 上的动点，且CE xCA yCB =+，则13x y+的最小值为（ ）A ．16B ．15C ．12D ．108．已知AB AC ⊥，1AB t=，AC t =，若P 点是ABC 所在平面内一点，且4AB AC AP ABAC=+，则·PB PC 的最大值等于（ ）. A ．13B ．15C ．19D ．219．若,b R,,a a b ∈≠且则下列式子：（1）22a 32b ab +>，（2）553223a b b a a b +>+，（3）2252(2)a b a b ++≥-，（4）2b aa b+>.其中恒成立的个数是 A ．1个 B ．2个C ．3个D ．4个10．若过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(),P x y ，则PA PB ⋅的最大值是（ ）A ．4B ．5C ．6D ．811．若两个正实数,x y 满足112x y+=，且不等式2x y m m +<-有解，则实数m 的取值范围是（ ） A ．()1,2- B ．()4,1- C ．()(),12,-∞-+∞D ．()(),14,-∞-+∞12．若,,a b c 为实数，则下列命题错误的是( ) A ．若22ac bc >，则a b > B ．若0a b <<，则22a b < C ．若0a b >>，则11a b< D ．若0a b <<,0c d >>，则ac bd <二、填空题13．已知a 、b 都是正数，且0a b ab +-=，则1911b a b +--的最小值是__________．14．≤对任意0,0x y >>恒成立，则a 的最小值是_______．15．已知0x >，0y >，22x y +=，则223524x y x yxy+++的最小值为______.16．已知正实数m ，n 满足119222m n m n +++=，则2m n +的最小值是_______． 17．某企业开发一种产品，生产这种产品的年固定成本为3600万元，每生产x 千件，需投入成本c （x ）万元，c （x ）＝x 2+10x ．若该产品每千件定价a 万元，为保证生产该产品不亏损，则a 的最小值为_____．18．已知函数121()22x x f x +-+=+，如果对任意t ∈R ，f （3t 2+2t ）+f （k 2﹣2t 2）＜0恒成立，则满足条件的k 的取值范围是_____．19．已知方程210(0)x kx k ++=>有实根，则1k k+的最小值是______． 20．已知正实数x ，y 满足x +y =1，则1412x y +++的最小值为________ ．三、解答题21．已知函数()()223f x x bx b R =-+∈.（1）若()f x 在区间[22]-，上单调递减，求实数b 的取值范围； （2）若()f x 在区间[22]-，上的最大值为9，求实数b 的值.22．已知命题:p 实数x 满足28200x x --≤，命题:q 实数x 满足222(1)0(0)x x m m -+-≤>，若p ⌝是q ⌝的必要不充分条件，求实数m 的取值范围.23．已知集合{}2430A x x x =-+≤，B =______.若“x A ∈”是“x B ∈”的必要不充分条件，给出如下三个条件：①{}1x a x a -≤≤，②{}2x a x a ≤≤+，③{}3x ≤≤.请从中任选一个补充到横线上.若问题中的a 存在，求出a 的取值范围.24．已知函数2(),(,)f x x ax b a b R =-+∈． （Ⅰ）不等式()0f x ≤的解集为[1,2]-，求a ，b 的值； （Ⅱ）令函数()()2xg x f =，对于任意的实数12,[1,2]x x∈，不等式()()125g x g x -≤恒成立，求a 的取值范围．25．已知正数,,a b c 满足3a b c ++=. （Ⅰ）若221a b +=，求c 的取值范围； （Ⅱ）求证：3bc ac aba b c++≥.26．已知0a b c d >>>>，ad bc =． （Ⅰ）证明：a d b c +>+； （Ⅱ）证明：a b c b c a a b c a b c >．【参考答案】***试卷处理标记，请不要删除一、选择题 1．B解析：B 【分析】首先利用基本不等式得到2(1)4t t +≥，再根据题意得到243x x <+，解不等式即可.【详解】令()2(1)t t t f +=，()0,t ∈+∞，()2)2(11t t f t t t==+++，因为()0,t ∈+∞，所以()1224f t t t=++≥=， 当1t t=即1t =时取等号，又因为(0,)t ∀∈+∞，都有22(1)3x t x t +<+，所以243x x <+即可.由243x x <+得()243033x x x x +-<++，即241203x x x --<+， ()()241230xx x --+<，所以()()()6230x x x -++<，解得3x <-或26x -<<. 故选：B. 【点睛】易错点点睛：利用基本不等式求最值时，要注意其必须满足的三个条件： （1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.2．B解析：B 【分析】分0m =和0m ≠两种情况讨论，结合已知条件可得出关于实数m 的不等式组，由此可解得实数m 的取值范围. 【详解】因为关于x 的不等式210mx mx ++>恒成立，分以下两种情况讨论： （1）当0m =时，可得10>，合乎题意； （2）当0m ≠时，则有240m m m >⎧⎨∆=-<⎩，解得04m <<.综上所述，实数m 的取值范围是[)0,4. 故选：B. 【点睛】结论点睛：利用二次不等式在实数集上恒成立，可以利用以下结论来求解： 设()()20f x ax bx c a =++≠①()0f x >在R 上恒成立，则00a >⎧⎨∆<⎩；②()0f x <在R 上恒成立，则00a <⎧⎨∆<⎩；③()0f x ≥在R 上恒成立，则00a >⎧⎨∆≤⎩； ④()0f x ≤在R 上恒成立，则00a <⎧⎨∆≤⎩.3．A解析：A 【分析】利用“1”的代换，转化()1414a b a b a b ⎛⎫+=++ ⎪⎝⎭，结合基本不等式即可得解. 【详解】1a b +=，0a >，0b >()1414455549b a a b a b a b a b ⎛⎫+++=++≥+=+= ⎪⎝⎭∴=， 当且仅当4b a a b =，即13a =，23b =时，等号成立. 14a b ∴+的最小值为9 故选：A. 【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件： （1）“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.4．B解析：B 【分析】由已知条件代入后凑出积为定值，再由基本不等式得最小值． 【详解】∵0,0,23x y x y >>+=，所以(2x+1)+y=4则()()421141141549=2152142142144x yx y x y x y x y ++++++=⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭++=+++ 当且仅当()42121x y x y +=+且214x y ++=即18,63x y ==时取等号， 则1421x y ++的最小值是94. 故选：B ． 【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件： （1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方5．B解析：B 【分析】讨论0a =和0a ≠情况，再根据一元二次不等式与二次函数的关系，解不等式得解. 【详解】 关于x 的不等式210ax ax -+>恒成立，当0a =时，10>恒成立，满足题意当0a ≠时，即函数()21f x ax ax =-+恒在x 轴上方即可，所以00a >⎧⎨∆<⎩，即2040a a a >⎧⎨-<⎩，解得04a <<，所以实数a 的取值范围是[0,4).故选：B 【点睛】本题考查了一元二次不等式恒成立求参数的取值范围，考查了一元二次不等式的解法，属于基础题.6．D解析：D 【分析】本题需要考虑两种情况，00a a =≠，，通过二次函数性质以及即集合性质来确定实数a 的取值范围．【详解】设()21f x ax ax =-+当0a =时，()10f x =>，满足题意 当0a ≠时，()f x 时二次函数 因为{}2|10A x ax ax =-+<=∅ 所以()21f x ax ax =-+恒大于0，即0≤所以240a a -≤，解得04a ≤≤． 【点睛】本题考察的是集合和带有未知数的函数的综合题，需要对未知数进行分类讨论．7．A解析：A 【分析】由已知可得A ，D ，E 三点共线，结合平面向量基本定理可得31x y +=，0x >，0y >，再利用基本不等式即可求解. 【详解】 解：∵23BD BC =， ∴3CB CD =，3CE xCA yCB xCA yCD =+=+，因为A ，D ，E 共线，所以31x y +=，则()3313333101016x y x y y x x y x y x y +++=+=++≥+. 当且仅当33y x x y =且31x y +=即14x y ==时取等号， 故选：A. 【点睛】本题主要考查三点共线的向量表示，考查基本不等式求最值，意在考查学生对这些知识的理解掌握水平.8．A解析：A 【详解】以A 为坐标原点，建立平面直角坐标系，如图所示，则1(,0)B t，(0,)C t ，1AP =（，0)+4(0,1)=(1,4)，即1P（，4)，所以114)PB t=--（，，14)PC t =--（，，因此PB PC ⋅11416t t =--+117(4)t t =-+，因为114244t t t t+≥⋅=，所以PB PC ⋅的最大值等于13，当14t t =，即12t =时取等号．考点：1、平面向量数量积；2、基本不等式．9．A解析：A 【解析】分析：将不等式两侧的式子做差和0比即可，或者将不等式两侧的式子移到一侧，再配方即可. 详解：(1) 22a 32b ab +-=22322b a b ⎛⎫+- ⎪⎝⎭,当a=1,b=-2.时不等式不成立；(2)553223 a b b a a b +>+=()()()222a b a b a ab b -+++当a=1,b=-1时，不等式不成立；(3)()22522a b a b ++--()()22=a 210b -++≥恒成立.选项正确. (4) b aab +,2][2,)∈-∞-⋃+∞（,故不正确. 故答案为A.点睛：这个题目考查了基本不等式的应用条件，两式比较大小的方法；两个式子比较大小的常用方法有：做差和0比，作商和1比，或者直接利用不等式的性质得到大小关系，有时可以代入一些特殊的数据得到具体值，进而得到大小关系.10．B解析：B 【分析】先计算出两条动直线经过的定点，即A 和B ，注意到两条动直线相互垂直的特点，则有PA PB ⊥；再利用基本不等式放缩即可得出||||PA PB 的最大值．【详解】解：由题意可知，动直线0x my +=经过定点(0,0)A ，动直线30mx y m --+=即(1)30m x y --+=，经过点定点()1,3B ，注意到动直线0x my +=和动直线30mx y m --+=始终垂直，P 又是两条直线的交点，则有PA PB ⊥，222||||||10PA PB AB ∴+==．故22||||||||52PA PB PA PB +=（当且仅当||||PA PB ==时取“=” ) 故选：B ． 【点睛】本题是直线和不等式的综合考查，特别是“两条直线相互垂直”这一特征是本题解答的突破口，从而有22||||PA PB +是个定值，再由基本不等式求解得出．直线位置关系和不等式相结合，不容易想到，是个灵活的好题．11．C解析：C 【解析】 正实数x ,y 满足112x y+=， 则()111112222224y x x y x y x y x y ⎛⎫+=++=+++=⎪⎝⎭， 当且仅当1,y x x y ==+取得最小值2. 由2x y m m +<-有解,可得22m m ->， 解得m >2或m <−1. 本题选择C 选项.点睛：在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误．12．B解析：B 【分析】由题意利用不等式的性质逐一考查所给的四个选项中的结论是否正确即可.其中正确的命题可以用不等式的性质进行证明，错误的命题给出反例即可. 【详解】对于A ，若22ac bc >，则0c ≠，2222ac bc c c>，即a b >，故正确；对于B ，根据不等式的性质，若0a b <<，不妨取2,1a b =-=-，则22a b >，故题中结论错误；对于C ，若0a b >>，则a b ab ab>，即11a b <，故正确；对于D ，若0a b <<,0c d >>，则0a b ->->，故ac bd ->-，ac bd <，故正确. 故选B. 【点睛】本题主要考查不等式的性质及其应用，属于中等题.二、填空题13．【分析】由可得出根据已知条件得出将代入所求代数式可得出利用基本不等式可求得的最小值【详解】所以由解得则所以当且仅当时等号成立因此的最小值为故答案为：【点睛】易错点睛：利用基本不等式求最值时要注意其必 解析：15【分析】由0a b ab +-=可得出1b a b =-，根据已知条件得出1b >，将1b a b =-代入所求代数式可得出()19919111b b a b b +=-++---，利用基本不等式可求得1911ba b +--的最小值. 【详解】0a b ab +-=，所以，()1a b b -=-，1b a b ∴=-， 由010b a b b ⎧=>⎪-⎨⎪>⎩，解得1b >，则10b ->， 所以，()()919191919915111111b b b b a b b b b -++=+=-++≥=------， 当且仅当4b =时，等号成立， 因此，1911ba b +--的最小值为15. 故答案为：15. 【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件： （1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.14．【分析】不等式变形为然后利用基本不等式求得的最大值可得的最小值【详解】原不等式可化为因为所以即时等号成立又所以时等号成立所以的最大值是即的最小值是故答案为：【点睛】易错点睛：利用基本不等式求最值时要【分析】不等式变形为a ≥的最大值，可得a 的最小值．【详解】原不等式可化为a ≥，因为222m n mn +≥，所以222222()2()m n m mn n m n +≥++=+，即m n +≤，m n =时等号成立．又0,0x y >>≤=x y =时等号成立．a ≥a【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：（1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方．15．16【分析】由条件可知则原式变形为展开后利用基本不等式求最小值【详解】原式；当且仅当即时取等所以的最小值为16故答案为：16【点睛】关键点点睛：本题的关键是结合1的妙用利用基本不等式求最值解析：16【分析】 由条件可知()1212x y +=，则原式变形为()1243522x y x y y x y x ⎛⎫=++++ ⎪⎝⎭，展开后，利用基本不等式求最小值.【详解】原式()124493524162x y x y x y y x y x y x⎛⎫=++++=++≥ ⎪⎝⎭； 当且仅当23x y =即67x =，47y =时取等. 所以223524x y x y xy+++的最小值为16. 故答案为：16【点睛】关键点点睛：本题的关键是结合 “1”的妙用，利用基本不等式求最值.16．【分析】利用基本不等式可求得再结合可得从而可求出的取值范围即可得到的最小值【详解】由题意当且仅当时等号成立又所以令则解得所以即的最小值是故答案为：【点睛】关键点点睛：本题考查求代数式的最值解题关键是 解析：32【分析】()1112222n m m n m n m n ⎛⎫++=+++ ⎪⎝⎭，利用基本不等式，可求得()119222m n m n ⎛⎫++≥ ⎪⎝⎭，再结合()119222m n m n +=-+，可得()()992222m n m n ⎡⎤+-+≥⎢⎥⎣⎦，从而可求出2m n +的取值范围，即可得到2m n +的最小值.【详解】由题意，()11155922222222n m m n m n m n ⎛⎫++=+++≥+=+= ⎪⎝⎭，当且仅当n m m n=时，等号成立， 又()119222m n m n +=-+，所以()()()1199222222m n m n m n m n ⎛⎫⎡⎤++=+-+≥ ⎪⎢⎥⎝⎭⎣⎦， 令2m n t +=，则9922t t ⎛⎫-≥⎪⎝⎭，解得332t ≤≤， 所以32,32m n ⎡⎤+∈⎢⎥⎣⎦，即2m n +的最小值是32. 故答案为：32. 【点睛】关键点点睛：本题考查求代数式的最值，解题关键是利用基本不等式求出()119222m n m n ⎛⎫++≥ ⎪⎝⎭，再根据()119222m n m n ⎛⎫+++= ⎪⎝⎭，可得到只包含2m n +的关系式()()992222m n m n ⎡⎤+-+≥⎢⎥⎣⎦，从而可求出2m n +的范围.考查学生的逻辑推理能力，计算求解能力，属于中档题.17．130【分析】本题先根据题意建立函数与不等式关系再运用参变分离化简最后运用基本不等式求最值即可【详解】解：有题意建立利润函数关系：（）整理得：为保证生产该产品不亏损则（）即当且仅当即取最小值130此 解析：130【分析】本题先根据题意建立函数与不等式关系，再运用参变分离化简，最后运用基本不等式求最值即可.【详解】解：有题意建立利润函数关系：2()(103600)f x ax x x =-++，（0x >） 整理得：2()(10)3600f x x a x =-+--，为保证生产该产品不亏损，则2()(10)36000f x x a x =-+--≥，（0x >）即36001010130a x x ≥++≥=， 当且仅当3600x x=即60x =，a 取最小值130，此时产品不亏损 故答案为：130.【点睛】 本题考查函数与不等式关系、参变分离法，基本不等式解决实际问题中的最值问题，是基础题.18．k<-1或k>1【分析】利用定义先求出函数为单调减函数与奇函数然后化简得到然后利用不等式得恒成立条件求出答案【详解】对于函数定义域为且所以为奇函数且对求导可得则在时为减函数可得利用为奇函数化简得利用 解析：k <-1或k >1.【分析】利用定义，先求出函数()f x 为单调减函数与奇函数，然后化简()()2223220f t t f k t ++-<得到222t t k --<，然后利用不等式得恒成立条件求出答案【详解】对于函数()f x ，定义域为R ，且()12122x x f x ---+-=+1122222xx x x+-+=+()12122x x f x +-==-+，所以，()f x 为奇函数，且对()f x 求导可得()'0f x <，则()f x 在x ∈R 时为减函数， ()()2223220f t t f k t ++-<，可得()()222322f t t f k t +<--，利用()f x 为奇函数 化简得()()222322f t t f t k +-<，利用()f x 在x ∈R 时为减函数，得222322t t t k +->，化简得222t t k --<恒成立，令()22g t t t =--，则有()2max g t k <，而()()max 11g t g =-=，所以21k <，得到1k >或1k <-答案：1k >或1k <-【点睛】本题考查函数的单调性、奇偶性以及不等式的恒成立问题，属于中档题19．【分析】先根据一元二次方程有解得再根据函数的单调性求解即可【详解】解：方程有实根解得又在上单调递增 的最小值是故答案为：【点睛】本题主要考查了利用基本不等式求最值的问题根据条件求出k 的范围利用对勾函 解析：52【分析】先根据一元二次方程有解得2k ≥，再根据函数1y k k=+的单调性求解即可. 【详解】 解：方程210(0)x kx k ++=>有实根， 240k ∴-≥，解得2k ≥， 又1y k k=+在[)2+∞，上单调递增， ∴ 1k k +的最小值是15222+=， 故答案为：52． 【点睛】 本题主要考查了利用基本不等式求最值的问题，根据条件求出k 的范围，利用对勾函数在区间内的最值即可求出结果．20．【分析】由可得且则利用基本不等式可求出的最小值【详解】由可得且则（当且仅当即时取=）故的最小值为故答案为：【点睛】利本题考查基本不等式求最值注意用基本不等式求最值必须具备三个条件：①各项都是正数；② 解析：94【分析】由1x y +=，可得(1)(2)4x y +++=且10,20x y +>+>，则()()()112411411412412214142y x x y x y x y x y ⎛⎫⎛⎫+=+=+++⎡⎤ ⎪+ +⎪⎣⎦++++++⎝+⎭⎝+⎭+，利用基本不等式可求出1412x y +++的最小值. 【详解】由1x y +=，可得()()124x y +++=且10,20x y +>+>， 则()()114114124122x y x y y x ⎛⎫+=+⎡⎤ ⎪⎣⎦++++⎝+⎭++ ()11914541244412x y y x =+⎛⎛⎫ +++≥+= ⎪ ++⎝⎭⎝+，（当且仅当()24121x y x y =++++即12,33x y ==时取“=”）. 故1412x y +++的最小值为94. 故答案为：94. 【点睛】利本题考查基本不等式求最值，注意用基本不等式求最值必须具备三个条件：①各项都是正数；②和（或积）为定值；③等号取得的条件，属于中档题. 三、解答题21．无22．无23．无24．无25．无26．无。
八年级下册数学 一次函数与不等式练习题
八年级下册数学一次函数与不等式练习题1.一次函数与一元一次方程、一元一次不等式1.1 一次函数与一元一次方程1) 一次函数与一元一次方程的关系：① (从数值上看) 方程 $ax+b=(a\neq0)$ 的解$\Leftrightarrow$ 函数 $y=kx+b(a\neq0)$ 中，$y$ 等于时，$x$ 的值。
② (从形式上看) 方程 $ax+b=(a\neq0)$ 的解$\Leftrightarrow$ 函数 $y=kx+b(a\neq0)$ 的图像与 $x$ 轴交点的横坐标。
2) 利用一次函数的图像解一元一次方程的步骤：转化→画图像→ 找交点。
1.2 一次函数与一元一次不等式1) 一次函数与一元一次不等式的关系：① (从数值上看) $ax+b>0$ 的解集 $\Leftrightarrow$ 函数$y=kx+b$ 中 $y>0$ 时 $x$ 的取值范围；$ax+b<0$ 的解集$\Leftrightarrow$ 函数$y=kx+b$ 中$y<0$ 时$x$ 的取值范围。
② (从形式上看) $ax+b>0$ 的解集 $\Leftrightarrow$ 直线位于 $x$ 轴上方的部分对应的 $x$ 的取值范围；$ax+b<0$ 的解集 $\Leftrightarrow$ 直线位于 $x$ 轴下方的部分对应的$x$ 的取值范围。
2) 应用：在同一直角坐标系中，比较两直线上函数值大小的方法：当自变量取同一个值时，对应图像上的点在上方的函数值就大。
例1：已知方程 $x+b=-2$ 的解是 $x=-2$，下列可能为直线 $y=x+b$ 的图象是（）。
例2：直线 $y=kx+3$ 经过点 $A(2,1)$，则不等式$kx+3\geq0$ 的解集是（）。
针对训练1、一次函数 $y=kx+b$ 的图象如图所示，则方程$kx+b=0$ 的解为（）。
2、如图，一次函数 $y=kx+b$ 的图象经过 $A$、$B$ 两点，则不等式 $kx+b<0$ 的解集是（）。
一次函数与方程不等式专项练习60题(有答案)15页
1．一次函数y=kx+b A x=2＜＞ A x＜﹣1x＜﹣2 A．=与﹣，11．如图，已知直线y=ax+b，则方程．已知直线与kx+b＜0．_________ ．18．一元一次方程0.5x+1=020．一次函数y1=kx+b22．一次函数y=ax+b24．一次函数y=ax+b的图象如图所示，则一元一次方程30．当自变量x的取值满足什么条件时，函数x=≤＞≥﹣＞＜①a＞0；②b＞0； A037．如图，直线y=kx+b．ax+b＜cx+d＜2的解集为 42．如图，直线y=kx+b）两点，则不等式x）两点，则不等式x 54．画出函数y=3x+12的图象，并回答下列问题：的解集是 的解集是 的解集是 57．在平面直角坐标系x0y）根据图象可知：方程组的解为 m=，的坐标是（，＜；故选=＜，．联立两函数的解析式，得：，解得；﹣，﹣．﹣．由直线与=×a=，可化为：x由此可画出的图形为：．函数与x轴的交点A坐标为（∴，解得：﹣，﹣，﹣，解得：＞．故选＞．故选∴，解得，y=x+2．故答案为：x＞﹣3，x＜﹣3）两点，可得：，解得；则不等式组x可化为x46． ∵一次函数把（2，0）代入解析式，=＜，48．由图象可知x＞﹣．∵一次函数y=kx+b52． 列表：描点，过（﹣，（1）由图象看出当﹣时，﹣是方程（2）不等式2x+1≥0≥﹣是不等式）由勾股定理得它们之间的距离为﹣，﹣，54. 当x=0时，y=12；当y=3x+12的图象，从图象得出函数值随﹣6≤y≤6时，相应的）根据题意得：解得：56．由题意知：由图象知不等式组的解集的解集为：由题知：由图象知不等式组的解集为：由题意知：根据函数图象知不等式组的解集是空集；故答案为：空集∴，解得：，不等式kx+b≤0的解集为：在x轴的上方，故．（2）解：由图象可知：方程组的解为，故答案为：．（3）解：根据题意得：（1）由图象知：随着x（3）由图象知：与x轴的交点坐标是（（4）由图象知：这个函数中，随着（5）由图象知：当x=1。
(完整版)一元一次不等式与一次函数习题精选(含答案)
一元一次不等式与一次函数1．如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x＜ax+4的解集为（）(5)A．x＜B．x＜3 C．x＞D．x＞32．已知一次函数y=ax+b的图象过第一、二、四象限，且与x轴交于点（2，0），则关于x的不等式a（x﹣1）﹣b ＞0的解集为（）A．x＜﹣1 B．x＞﹣1 C．x＞1 D．x＜13．如图，直线y1=k1x+a与y2=k2x+b的交点坐标为（1，2），则使y1＜y2的x的取值范围为（）A．x＞1 B．x＞2 C．x＜1 D．x＜24．直线l1：y=k1x+b与直线l2：y=k2x+c在同一平面直角坐标系中的图象如图所示，则关于x的不等式k1x+b＜k2x+c 的解集为（）A．x＞1 B．x＜1 C．x＞﹣2 D．x＜﹣25．如图，一次函数y=kx+b的图象经过A、B两点，则kx+b＞0解集是（）A．x＞0 B．x＞﹣3 C．x＞2 D．﹣3＜x＜26．如图，函数y=kx和y=﹣x+3的图象相交于（a，2），则不等式kx＜﹣x+3的解集为（）A．x＜B．x＞C．x＞2 D．x＜27．（如图，直线l是函数y=x+3的图象．若点P（x，y）满足x＜5，且y＞，则P点的坐标可能是（）A．（4，7）B．（3，﹣5）C．（3，4）D．（﹣2，1）8．如图，已知一次函数y=kx+b的图象经过点A（5，0）与B（0，﹣4），那么关于x的不等式kx+b＜0的解集是（）A．x＜5 B．x＞5 C．x＜﹣4 D．x＞﹣49．如图，一次函数y=kx+b的图象经过点（2，0）与（0，3），则关于x的不等式kx+b＞0的解集是（）(10) (11)A．x＜2 B．x＞2 C．x＜3 D．x＞310．如图，已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2，根据图象有下列3个结论：①a＞0；②b＞0；③x ＞﹣2是不等式3x+b＞ax﹣2的解集．其中正确的个数是（）A．0B．1C．2D．3二．填空题（共8小题）11．如图，经过点B（﹣2，0）的直线y=kx+b与直线y=4x+2相交于点A（﹣1，﹣2），则不等式4x+2＜kx+b＜0的解集为_________．12．如图，l1反映了某公司的销售收入与销量的关系，l2反映了该公司产品的销售成本与销量的关系，当该公司赢利（收入＞成本）时，销售量必须_________．(13) (14) (15)13．如图，函数y=2x和y=ax+5的图象相交于A（m，3），则不等式2x＜ax+5的解集为_________．14．如图，已知直线y1=x+m与y2=kx﹣1相交于点P（﹣1，1），则关于x的不等式x+m＞kx﹣1的解集为_________．15．如图，直线y1=kx+b与直线y2=mx交于点P（1，m），则不等式mx＞kx+b的解集是_________．16．如图，已知函数y=x+b和y=ax+3的图象相交于点P，则关于x的不等式x+b＜ax+3的解集为_________．(17) (18)17．如图，直线y=kx+b经过点A（﹣1，1）和点B（﹣4，0），则不等式0＜kx+b＜﹣x的解集为_________．18．如图，直线y=kx+b交坐标轴于A（﹣3，0）、B（0，5）两点，则不等式﹣kx﹣b＜0的解集是_________．三．解答题19．在平面直角坐标系中，直线y=kx﹣15经过点（4，﹣3），求不等式kx﹣15≥0的解．20．如图，直线l1与l2相交于点P，点P横坐标为﹣1，l1的解析表达式为y=x+3，且l1与y轴交于点A，l2与y轴交于点B，点A与点B恰好关于x轴对称．（1）求点B的坐标；（2）求直线l2的解析表达式；（3）若点M为直线l2上一动点，直接写出使△MAB的面积是△PAB的面积的的点M的坐标；（4）当x为何值时，l1，l2表示的两个函数的函数值都大于0？21．已知：直线l1的解析式为y1=x+1，直线l2的解析式为y2=ax+b（a≠0）；两条直线如图所示，这两个图象的交点在y轴上，直线l2与x轴的交点B的坐标为（2，0）（1）求a，b的值；（2）求使得y1、y2的值都大于0的取值范围；（3）求这两条直线与x轴所围成的△ABC的面积是多少？（4）在直线AC上是否存在异于点C的另一点P，使得△ABC与△ABP的面积相等？请直接写出点P的坐标．22．如图，直线y=kx+b经过点A（0，5），B（1，4）．（1）求直线AB的解析式；（2）若直线y=2x﹣4与直线AB相交于点C，求点C的坐标；（3）根据图象，写出关于x的不等式2x﹣4≥kx+b的解集．AACBBAAAAD﹣2＜x＜﹣1．大于4．x＜．x＞﹣1．x＞1．x＜1．﹣4＜x＜﹣1．x＞﹣19 x≥5．20.解：（1）当x=0时，x+3=0+3=3，∴点A的坐标是（0，3），∵点A与点B恰好关于x轴对称，∴B点坐标为（0，﹣3）；（2）∵点P横坐标为﹣1，∴（﹣1）+3=，∴点P的坐标是（﹣1，），设直线l2的解析式为y=kx+b，则，解得，∴直线l2的解析式为y=﹣x﹣3；（3）∵点P横坐标是﹣1，△MAB的面积是△PAB的面积的，∴点M的横坐标的长度是，①当横坐标是﹣时，y=（﹣）×（﹣）﹣3=﹣3=﹣，②当横坐标是时，y=（﹣）×﹣3=﹣﹣3=﹣，∴M点的坐标是（﹣，﹣）或（，﹣）；（4）l1：y=x+3，当y=0时，x+3=0，解得x=﹣6，l2：y=﹣x﹣3，当y=0时，﹣x﹣3=0，解得x=﹣，∴当﹣6＜x＜﹣时，l1、l2表示的两个函数的函数值都大于0．21 解：（1）由直线l1的解析式为y1=x+1，可求得C（0，1）；解得：．（2）由（1）知，直线l2：y=﹣x+1；∵y1=x+1＞0，∴x＞﹣1；∵；∴﹣1＜x＜2．（3）由题意知A（﹣1，0），则AB=3，且OC=1；∴S△ABC=AB•OC=．（4）由于△ABC、△ABP同底，若面积相等，则P点纵坐标为﹣1，代入直线l1可求得：P的坐标为（﹣2，﹣1）．22. 解：（1）∵直线y=﹣kx+b经过点A（5，0）、B（1，4），∴，解方程组得，∴直线AB的解析式为y=﹣x+5；（2）∵直线y=2x﹣4与直线AB相交于点C，∴解方程组，解得，∴点C的坐标为（3，2）；（3）由图可知，x≥3时，2x﹣4≥kx+b．。
一次函数应用题含答案
一次函数应用题含答案一次函数应用题含答案一、方案优化问题我市某乡A、B两村盛产柑桔，A村有柑桔200吨，B村有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库，已知C仓库可储存240吨，D仓库可储存260吨；从A村运往C、D两处的费用分别为每吨20元和25元，从B村运往C、D两处的费用分别为每吨15元和18元.设从A村运往C仓库的柑桔重量为x吨，A、B两村运往两仓库的柑桔运输费用分别为yA元和yB元.（1）请填写下表，并求出yA，yB与x之间的函数关系式；（2）试讨论A、B两村中，哪个村花的运费较少；（3）考虑到B村的经济承受能力，B村的柑桔运费不得超过4830元.在这种情况下，请问该怎样调运才能使两村运费之和最小？求出这个最小值.解：（1）yA=-5x+5000（0≤x≤200），yB=3x+4680（0≤x≤200）.（2）当yA=yB时，-5x+5000=3x+4680，x=40；当yA>yB时，-5x+5000>3x+4680，x<40；当yA<yb时，-5x+5000<3x+4680，x style="padding: 0px; margin: 0px; font-family: Arial, 宋体; font-size: 14px; white-space: normal; background-color: rgb(255, 255, 255);">40.当x=40时，yA=yB即两村运费相等；当0≤x<40时，ya>yB即B村运费较少；当40<x≤200时，ya<yb即a村费用较少.（3）由yB≤4830得3x+4680≤4830∴x≤50设两村的运费之和为y，∴y=yA+yB.即：y=-2x+9680.又∵0≤x≤50时，y随x增大而减小，∴当x=50时，y有最小值，y最小值=9580（元）.答：当由A村调往C仓库的柑桔重量为50吨、调往D仓库为150吨，由B村调往C仓库为190吨、调往D仓库110吨的时候，两村的运费之和最小，最小费用为9580元.要点提示：解答方案比较问题，求函数式时，对有图象的，多用待定系数法求；对没有给出图象的，直接依题意列式子；方案比较问题通常与不等式、方程相联系；比较方案，即比较同一自变量所对应的函数值，要将函数问题转化为方程、不等式问题；解答方案比较问题尤其要注意：不同的区间，对应的大小关系也多不同.二、利润最大化问题某个体小服装店主准备在夏季来临前，购进甲、乙两种T恤.两种T恤的相关信息如下表：根据上述信息，该店决定用不少于6195元，但不超过6299元的资金购进这两种T恤共100件.请解答下列问题：（1）该店有哪几种进货方案？（2）该店按哪种方案进货所获利润最大，最大利润是多少？（3）两种T恤在夏季很快销售一空，该店决定再拿出385元全部用于购进这两种T恤，在进价和售价不变的情况下，全部售出.请直接写出该店按哪种方案进货才能使所获利润最大.解：（1）设购进甲种T恤x件，则购进乙种T恤（100-x）件.可得，6195≤35x+70（100-x）≤6299.解得，20■≤x≤23.∵x为解集内的正整数，∴x=21，22，23.∴有三种进货方案：方案一：购进甲种T恤21件，购进乙种T恤79件；方案二：购进甲种T恤22件，购进乙种T恤78件；方案三：购进甲种T恤23件，购进乙种T恤77件.（2）设所获得利润为W元.W=30x+40（100-x）=-10x+4000.∵k=-10<0，∴W随x的增大而减小.∴当x=21时，W=3790.该店购进甲种T恤21件，购进乙种T恤79件时获利最大，最大利润为3790元.（3）购进甲种T恤9件、乙种T恤1件.要点提示：在一次函数y=kx+b中，x、y均可取一切实数.如果缩小x的取值范围，则其函数值就会出现最大值或最小值.求一次函数的最大值、最小值，一般都是采用“极端值法”，即用自变量的端点值，根据函数的增减性，对应求出函数的端点值（最值）.三、行程问题从甲地到乙地，先是一段平路，然后是一段上坡路.小明骑车从甲地出发，到达乙地后立即原路返回甲地，途中休息了一段时间.假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km，下坡的速度比在平路上的速度每小时多5km.设小明出发x h后，到达离甲地y km的地方，图1中的折线OABCDE表示x与y之间的函数关系.（1）小明骑车在平路上的速度为 km/h；他途中休息了 h；（2）求线段AB、BC所表示的y与x之间的函数关系式；（3）如果小明两次经过途中某一地点的时间间隔为0.15h，那么该地点离甲地多远？解：（1）小明骑车在平路上的速度为：4.5÷0.3=15，∴小明骑车在上坡路的速度为：15-5=10，小明骑车在下坡路的速度为：15+5=20.∴小明返回的时间为：（6.5-4.5）÷20+0.3=0.4小时，∴小明骑车到达乙地的时间为：0.3+2÷10=0.5.∴小明途中休息的时间为：1-0.5-0.4=0.1小时.故答案为：15，0.1（2）小明骑车到达乙地的时间为0.5小时，∴B（0.5，6.5）.小明下坡行驶的时间为：2÷20=0.1，∴C（0.6，4.5）.设直线AB的解析式为y=k1x+b1，由题意得4.5=0.3k1+b16.5=0.5k1+b1，解得：k1=10b1=1.5，∴y=10x+1.5（0.3≤x≤0.5）；设直线BC的解析式为y=k2x+b2，由题意得6.5=0.5k2+b24.5=0.6k2+b2，解得：k2=-20b2=16.5，∴y=-20x+16.5（0.5<x≤0.6）（3）小明两次经过途中某一地点的时间间隔为0.15h，由题意可以得出这个地点只能在坡路上.设小明第一次经过该地点的时间为t，则第二次经过该地点的时间为（t+0.15）h，由题意得10t+1.5=-20（t+0.15）+16.5，解得：t= 0.4，∴y=10×0.4+1.5=5.5，∴该地点离甲地5.5km.要点提示：行程类一次函数试题以图象、点坐标相组合的形式呈现，灵活性强，对学生分析问题、解决问题的能力要求较高，重在考查学生的识图能力和创新意识.解决图象中的行程问题除了要掌握好路程、速度和时间三者之间的基本关系外，最重要的'是要学会从图象中获取信息，理清各变量之间的关系，然后根据题意选择适当的解题方法.四、分段计费问题已知某市2013年企业用水量x（吨）与该月应交的水费y（元）之间的函数关系.（1）当x≥50时，求y关于x的函数关系式；（2）若某企业2013年10月份的水费为620元，求该企业2013年10月份的用水量；（3）为实施省委“五水共治”发展战略，鼓励企业节约用水，该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费，规定若企业的月用水量x超过80吨，则除按2013年收费标准收取水费外，超过80吨部分每吨另加收■元.若某企业2014年3月份的水费和污水处理费共600元，求这个企业该月的用水量.解：（1）设y关于x的函数关系式y=kx+b，∵直线y=kx+b经过点（50，200），（60，260）∴50k+b=20060k+b=260解得k=6b=-100∴y关于x的函数关系式是y=6x-100（x≥50）；（2）由可知，当y=620时，x>50∴6x-100=620，解得x=120.答：该企业2013年10月份的用水量为120吨.（3）由题意得6x-100+■（x-80）=600，化简得x2+40x-14000=0解得：x1=100，x2=-140（不合题意，舍去）.答：这家企业2014年3月份的用水量是100吨.要点提示：分段函数的特征是不同的自变量区间所对应的函数式不同，其函数图象是一个折线.解决分段计费问题，关键是要与所在的区间相对应.分段函数中“折点”既是两段函数的分界点，同时又分别在两段函数上，在求解析式时要用好“折点”坐标，同时在分析图象时还要注意“折点”所表示的实际意义，“折点”的纵坐标通常是不同区间的最值.2015年第3期《锐角三角函数》参考答案1.D；2.A；3.B；4.■；5.9■；6.2■；7.120；8. 解：（1）■-3tan30°+（π-4）0-（■）-1=2■-3×■+1-2=■-1（2）■（2cos45°-sin60°）+■=■（2×■-■）+■=2-■+■=29. 解：过点A作直线BC的垂线，垂足为D.则∠CDA=90°，∠CAD=60°，∠BAD=30°，CD=240米，在Rt△ACD中，tan∠CAD=■，∴AD=■=■=80■，在Rt△ABD中，tan∠BAD=■，∴BD=ADtan30°=80■×■=80，∴BC=CD-BD=240-80=160. 答：这栋大楼的高为160米. 10.解：在Rt△CDB中，∠C=90°，BC=■=■=4，∴tan∠CBD=■.在Rt△ABC中，∠C=90°，AB=■=4■，∴sinA=■.。
一次函数与一元一次方程和不等式同步辅导(含答案)--绝对经典
11.3.1 -11.3.2 一次函数与一元一次方程和不等式重点知识讲解1．一元一次方程ax+b=0（a≠0）与一次函数y=ax+b（a≠0）的关系（1）一元一次方程ax+b=0（a≠0）是一次函数y=ax+b（a≠0）的函数值为0时的特殊情形．（2）直线y=ax+b与x轴交点的横坐标就是一元一次方程ax+b=0的解x=-ba。
2．一元一次不等式与一次函数的关系（1）一元一次不等式ax+b>0或ax+b<0（a≠0）是一次函数y=ax+b（a≠0）•的函数值不等于0的情形．（2）直线y=ax+b上使函数值y>0（x轴上方的图像）的x的取值范围是ax+b>0的解集；使函数值y<0（x 轴下方的图像）的x的取值范围是ax+b<0的解集．经验与方法技巧1．利用一次函数求一元一次方程的解题步骤（1）将一元一次方程化成ax+b=0的形式．（2）画出y=ax+b的图像，确定其与x轴交点的横坐标．2．利用一次函数求一元一次不等式的解集的技巧根据不等式的特点，灵活采用求解方法：（1）利用一个一次函数；（2）•利用两个一次函数．典型例题例1画出y=-3x+5的图象，利用图像求方程-3x+5=0的解．解析取点（0，5），（53，0），图像如图所示．∵直线y=-3x+5与x轴交点的横坐标为53，∴方程-3x+5=0的解为x=53。
评注画函数图像时要准确，求出直线y=-3x+5与x•轴交点的横坐标即为方程的解．例2画出函数y=-3x+12的图像，利用图像求：（1）不等式-3x+12>0的解集．（2）不等式-3x+12≤0的解集．（3）如果y的值在-6≤y≤6的范围内，那么相应的x的值在什么范围内？解析取点（0，12），（4，0），作出函数图像，如图所示，由图像可以看出：（1）当y>0时，x的取值范围为x<4，∴不等式-3x+12>0的解集为x<4．（2）当y≤0时，x的取值范围为x≥4．∴不等式-3x+12≤0的解集为x≥4．（3）当-6≤y≤6时，x的取值范围为2≤x≤6．评注借助图像求不等式的解集，关键是要清楚以下几点：①y>0时，x•的取值范围就是x轴上方的图像所对应的x的取值范围．②y<0时，x的取值范围就是x•轴下方的图像所对应的x的取值范围．③y=0时，x的值就是图像与x轴交点的横坐标．④当y>a或y<a（a≠0）时，应先确定当y=a时对应的x值，然后再进一步确定x的取值范围．例3若y1=-x+3，y2=3x-4，当x取何值时，y1<y2？解析∵y1<y2，∴-x+3<3x-4，解得x>74，∴当x>74时，y1<y2．评注此题是两个一次函数之间的关系，可以直接借助一元一次不等式求出x的取值范围．教材例题习题的变形题例（P41例2）用画图像的方法解下列各题：- 1 -（1）解不等式：5x+4>2x+10．（2）解方程：5x+4=2x+10．解析（1）如图，原不等式可化为3x-6>0，画出直线y=3x-6，由图像可以看出，当x>2时，这条直线上的点在x轴的上方，即这时y=3x-6>0，所以不等式的解集为x>2．（2）原方程可化为3x-6=0．由图像可以看出，y=3x-6与x轴交点的横坐标为2，所以原方程的解为x=2．评注①从函数的角度看问题，能发现一次函数与一元一次不等式、•一元一次方程之间的联系，体现了数形结合的思想．②本题求不等式的解集时，还可将不等式的两边分别看作两个一次函数，画出两条直线，比较直线上点的位置的高度，也可求得不等式的解集．学科内综合题例1甲、乙两辆摩托车分别从相距20km的A，B两地出发，相向而行，图中的L1，L2分别表示甲、乙两辆摩托车离开A地的距离s（km）与行驶时间t（h）•之间的函数关系．（1）哪辆摩托车的速度较快？（2）经过多长时间，甲摩托车行驶到A，B两地的中点？解析（1）由图像可以看出，甲摩托用了0．6h行驶了20km，而乙摩托车用了0．•5h行驶了20km，所以乙摩托车的速度较快．（2）设L1的关系式为y=kx，把x=0．6，y=20代入，得20=0．6k，解得k=1003，∴y=1003x.当y=10时，10=1003x．所以经过0．3h，甲摩托车行驶到A，B两地的中点．评注本题第（1）题是比较速度的大小，这一点可以通过图像提供的数量直接分析出来．第（2）题的关键是要分析出甲摩托车行驶到中点时所行驶的路程为10km．例2已知y=12x-2．（1）x取何值时，y>0？（2）x取何值时，y<0？（3）当x>4时，求y的取值范围．解析作出y=12x-2的图像，如图所示．（1）当x>4时，y>0．（2）当x<4时，y<0．（3）当x>4时，y的取值范围是y>0．评注本题可以通过图像直观地得出结论．综合应用题例1某单位计划在新年期间组织员工到某地旅游，参加旅游的人数估计为10～20人，甲、乙两家旅行社的服务质量相同，且报价都是每人200元．经过协商，•甲旅行社表示可给予每位游客七五折优惠；乙旅行社表示可先免去一位游客的旅游费用，再给其余游客八折优惠．该单位选择哪一家旅行社支付的旅游费用较少？解析设该单位参加这次旅游的人数是x人，选择甲旅行社时所需的费用为y1元，选择乙旅行社时所需的费用为y2元，则y1=200×0．75x，即y1=150x；y2=200×0．8（x-1），即y2=160x-160．由y1=y2，得150x=160x-160，解得x=16；- 2 -由y1>y2，得150x>160x-160，解得x<16；由y1<y2，得150x<160x-160，解得x>16．因为参加旅游的人数估计为10～20人，所以，当x=16时，甲、•乙两家旅行社的收费相同；当17≤x≤20时，选择甲旅行社费用较少；当10≤x≤15时，选择乙旅行社费用较少．评注已知前提条件，设计方案是解决实际问题的一种常见形式．明确每一种收费方式占优势时对应的自变量的取值范围是解决此类问题的关键，•借助不等式就可确定自变量的取值范围．例2兄弟俩赛距，哥哥先让弟弟跑9m，然后自己才开始跑．已知弟弟每秒跑3m，•哥哥每秒跑4m．列出函数关系式，作出函数图像，观察图像回答下列问题：（1）何时弟弟跑在哥哥前面？（2）何时哥哥跑在弟弟前面？（3）谁先跑过20m？谁先跑过100m？解析设哥哥跑了ts，则哥哥所跑的路程与时间的关系式为s1=4t；弟弟所跑的路程与时间的关系为s2=3t+9．图像如图所示．当s1=s2时，4t=3t+9，t=9．（1）当0≤t<9时，弟弟跑在哥哥的前面．（2）当t>9时，哥哥跑在弟弟的前面．（3）∵20<36，∴弟弟先跑过20m．∵100>36，∴哥哥先跑过100m．评注本题可以从时间或路程两个角度进行分析．在同一时间内，谁跑的路程远，谁就在前面，谁就先跑过20m，100m．也可比较他们各自所用的时间，谁用的时间短，•谁就先跑过．本题既可以通过计算来进行比较，也可通过图像直观地进行判断．创新题例（探究题）我边防局接到情报，在离海岸5海里处有一可疑船只A•正向公海方向行驶，边防局迅速派出快艇B追赶．图中L1，L2分别表示两船相对于海岸的距离s（海里）与追赶时间t（min）之间的关系．（1）A，B哪一个的速度快？（2）至少要用多长时间才能追上可疑船只A？解析由图像可确定L表示快艇B的图像，L表示可疑船只A的图像．（1）快艇10min行驶了5海里，所以其速度为5÷10=0．5（海里/min）．可疑船只10min行驶了7-5=2（海里），所以其速度为2÷10=0．2（海里/min）．所以快艇B的速度快．（2）设L1的关系式为y1=kx，把（10，5）代入，得5=10k，解得k=0．5，∴y1=0．5x．设L2的关系式为y2=kx+5，把（10，7）代入，得7=10k+5，解得k=0．2，∴y2=0．2x+5．当y1≥y2，即0．5x≥0．2x+5时，0．3x≥5，x≥503.所以至少需要503min，快艇才能追上可疑船只．中考题例（2004年苏州卷）如图，平面直角坐标系中画出了函数y=kx+b的图像．（1）根据图像，求k和b的值．（2）在图中画出函数y=-2x+2的图像．（3）求x的取值范围，使函数y=kx+b的函数值大于函数y=-2x+2的函数值．解析（1）∵直线y=kx+b经过点（-2，0），（0，2）．- 3 -- 4 -∴02,20,k b b =-+⎧⎨=+⎩ 解得1,2,k b =⎧⎨=⎩ ∴y=x+2．（2）y=-2x+2经过（0，2），（1，0），图像如图所示．（3）当y=kx+b 的函数值大于y=-2x+2的函数值时，也就是x+2>-2x+2，解得x>0，•即x 的取值范围为x>0．11.3.1 一次函数与一元一次方程同步练习［要点再现］1.由于任何一元一次方程都可以转化为 的形式，所以解一元一次方程可以转化为：当 时，求 的值。
一次函数的应用专项练习30题有答案
一次函数的应用专项练习30题（有答案）1．向一个空水池注水，水池蓄水量y（米3）与注水时间x（小时）之间的函数图象如图所示．（1）第20小时时蓄水量为_________ 米3；（2）水池最大蓄水量是_________ 米3；（3）求y与x之间的函数关系式．2．小王的父母经营一家饲料店，拟投入a元购入甲种饲料，现有两种方案：①如果月初出售这批甲种饲料可获利8%，并用本金和利润再购入乙种饲料，到月底售完又获利10%；②如果月底出售这批甲种饲料，可获利20%，但要付仓储费600元．（1）分别写出方案①、②获利金额的表达式；（2）请你根据小王父母投入资金的多少，定出可多获利的方案．3．某工厂现在年产值是15万元，计划以后每年增加2万元，设x年后的年产值为y（万元）．（1）写出y与x之间的关系式；（2）用表格表示当x从0变化到5（每次增加1）y的对应值；（3）求10年后的年产值？4．我们知道海拔一定高度的山区气温随着海拔高度的增加而下降．小明暑假到去旅游，沿途他利用随身所带的测量仪器，测得以下数据：1400 1500 1600 1700 …海拔高度x（m）气温y（°C）32.00 31.40 30.80 30.20 …（1）现以海拔高度为x轴，气温为y轴建立平面直角坐标系，根据提供的数据描出各点；（2）已知y与x的关系是一次函数关系，求出这个关系式；（3）若小明到达天都峰时测得当时的气温是29.24°C．求天都峰的海拔高度．5．如图，l1，l2分别表示一种白炽灯和一种节能灯的费用y与照明时间x（h）的函数图象，假设两种灯的使用寿命都是2000h，照明效果一样．（费用=灯的售价+电费，单位：元）（1）根据图象分别求出l1，l2的函数关系式．（2）当照明时间为多少时，两种灯的费用相等？6．某物流公司的快递车和货车每天沿同一公路往返于A、B两地，快递车比货车多往返一趟．图表示快递车与货车距离A地的路程y（单位：千米）与所用时间x（单位：时）的函数图象．已知货车比快递车早1小时出发，到达B 地后用2小时装卸货物，然后按原路、原速返回，结果比快递车最后一次返回A地晚1小时．（1）两车在途中相遇的次数为_________ 次；（直接填入答案）（2）求两车最后一次相遇时，距离A地的路程和货车从A地出发了几小时．7．某农户有一水池，容量为10立方米，中午12时打开进水管向水池注水，注满水后关闭水管同时打开出水管灌溉农作物，当水池中的水量减少到1立方米时，再次打开进水管向水池注水（此时出水管继续放水），直到再次注满水池后停止注水，并继续放水灌溉，直到水池中无水，水池中的水量y（单位：立方米）随时间x（从中午12时开始计时，单位：分钟）变化的图象如图所示，其中线段CD所在直线的表达式为y=﹣0.25x+33，线段OA所在直线的表达式为y=0.5x，假设进水管和出水管每分钟的进水量和出水量都是固定的．（1）求进水管每分钟的进水量；（2）求出水管每分钟的出水量；（3）求线段AB所在直线的表达式．8．为发展电信事业，方便用户，电信公司对移动采取不同的收费方式，其中“如意卡”无月租，每通话一分钟收费0.25元，“便民卡”收费信息如图（1）分别求出两种卡在某市围每月（30天）的通话时间x（分钟）与通话费y（元）之间的函数关系式．（2）请你帮助用户计算一下，在一个月使用哪种卡便宜．9．如图是甲、乙两人去某地的路程S（km）与时间t（h）之间的函数图象，请你解答下列问题：（1）甲去某地的平均速度是多少？（2）甲出发多长时间，甲、乙在途中相遇？10．如图，在甲、乙两同学进行400米跑步比赛中，路程s（米）与时间t（秒）之间的函数关系的图象分别为折线OAB和线段OC，请根据图上信息回答下列问题：（1）_________ 先到达终点；（2）第_________ 秒时，_________ 追上_________ ；（3）比赛全程中，_________ 的速度始终保持不变；（4）写出优胜者在比赛过程中所跑的路程s（米）与时间t（秒）之间的函数关系式：_________ ．11．甲、乙两组工人同时加工某种零件，乙组工作中有一次停产更换设备，更换设备后，乙组的工作效率是原来的2倍．两组各自加工零件的数量y（件）与时间x（时）的函数图象如图所示．（1）求甲组加工零件的数量y与时间x之间的函数关系式．（2）当x=2.8时，甲、乙两组共加工零件_________ 件；乙组加工零件总量a的值为_________ ．（3）加工的零件数达到230件装一箱，零件装箱的时间忽略不计，若甲、乙两组加工出的零件合在一起装箱，当甲组工作多长时间恰好装满第2箱？12．甲、乙两个工程队分别同时开挖两段河渠，所挖河渠的长度y（m）与挖掘时间x（h）之间的关系如图所示，请根据图象提供的信息解答下列问题：（1）甲队在0≤x≤6的时间段，挖掘速度为每小时_________ 米；乙队在2≤x≤6的时间段，挖掘速度为每小时_________ 米；请根据乙队在2≤x≤6的时间段开挖的情况填表：时间（h） 2 3 4 5 630 50乙队开挖河渠（m）（2）①请直接写出甲队在0≤x≤6的时间段，y甲与x之间的关系式；②根据（1）中的表中规律写出乙队在2≤x≤6的时间段，y乙与x之间的关系式；（3）在（1）的基础上，如果甲队施工速度不变，乙队在开挖6小时后，施工速度增加到每小时12米，结果两队同时完成了任务．问甲队从开挖到完工所挖河渠的长度为多少米？13．百舟竞渡，激悄飞扬，端午节期间，龙舟比赛在九龙江举行．甲、乙两支龙舟队在比赛时的路程y（米）与时间x（分钟）的函数关系的图象如图所示，根据图象解答下列问题：（1）出发后1.5分钟，_________ 支龙舟队处于领先位置（填“甲”或“乙“）；（2）_________ 支龙舟队先到达终点（填“甲“或“乙”），提前_________ 分钟到达；（3）求乙队加逨后，路程y（米）与时问分钟）之间的函数关系式，并写出自变x的取值围．14．在人才招聘会上，某公司承诺：录用后第一年的月工资为2000元，以后每年的月工资比上一年的月工资增加300元，一年按12个月计算．（1）如果某人在该公司连续工作x年，他在第x年后的月工资是y元，写出y与x的关系式．（2）如果这个人期望第五年的工资收入超过4万元，那么他是否应该在该公司应聘？15．褚向同学乘车从学校出发回家，他离家的路程y（km）与所用时间x（时）之间的关系如图所示．（1）求y与x之间的关系式；（2）求学校和褚向同学家的距离．16．某软件公司开发出一种图书管理软件，前期投入的各种费用总共50000元，之后每售出一套软件，软件公司还需支付安装调试费用200元，设销售套数x（套）．（1）试写出总费用y（元）与销售套数x（套）之间的函数关系式．（2）该公司计划以400元每套的价格进行销售，并且公司仍要负责安装调试，试问：软件公司售出多少套软件时，收入超出总费用？17．甲和乙上山游玩，甲乘坐缆车，乙步行，两人相约在山顶的缆车终点会合．已知乙行走到缆车终点的路程是缆车到山顶的线路长的2倍，甲在乙出发后50min才乘上缆车，缆车的平均速度为180m/min．设乙出发xmin后行走的路程为ym．图中的折线表示乙在整个行走过程中y与x的函数关系．（1）乙行走的总路程是_________ m，他途中休息了_________ min．（2）①当50≤x≤80时，求y与x的函数关系式；②当甲到达缆车终点时，乙离缆车终点的路程是多少？18．经理到家果园里一次性采购一种水果，他俩商定：经理的采购价y（元/吨）与采购量x（吨）之间函数关系的图象如图中的折线段ABC所示（不包含端点A，但包含端点C）．（1）如果采购量x满足20≤x≤40，求y与x之间的函数关系式；（2）已知家种植水果的成本是2 800元/吨，经理的采购量x满足20≤x≤40，那么当采购量为多少时，家在这次买卖中所获的利润w最大？最大利润是多少？19．某移动通讯公司开设了“全球通”和“神舟行”两种通讯业务，收费标准见下表：通讯业务月租费（元）通话费（元/分钟）全球通50 0.4神舟行0 0.6某用户一个月通话x分钟，“全球通”和“神舟行”的收费分别为y1元和y2元．（1）写出y1、y2与x之间的函数关系式；（2）在通话时间相同的情况下，你认为该用户应选择哪种通讯业务更为合算？20．某长途汽车客运站规定，乘客可以免费携带一定质量的行，但超过该质量则需交纳行费，已知行费y（元）是行质量x（千克）的一次函数．现在黄明带了60千克的行，交了行费5元，王华带了78千克的行，交了8元．（1）写出y与x之间的函数关系式；（2）旅客最多可以免费携带多少千克的行？21．某长途汽车客运站规定，乘客可免费携带一定质量的行，但超过该质量则需要购买行票，且行费y（元）是行质量x（千克）的一次函数，如图所示．（1）求y与x之间的函数关系式．（2）最多可免费携带多少质量的行？22．小明从A地出发向B地行走，同时小聪从B地出发向A地行走．如图所示，线段l1、l2分别表示小明、小聪离B地的距离y（km）与已用时间x（h）之间的关系．观察图象，回答以下问题：（1）出发_________ （h）后，小明与小聪相遇，此时两人距离B地_________ （km）；（2）求小聪走1.2（h）时与B地的距离．23．某公司生产一种新产品，前期投资300万元，每生产1吨新产品还需其他投资0.3万元，如果生产这一产品的产量为x吨，每吨售价为0.5万元．（1）设生产新产品的总投资y1万元，试写出y1与x之间的函数关系式和定义域；（2）如果生产这一产品能盈利，且盈利为y2万元，求y2与x之间的函数关系式，并写出定义域；（3）请问当这一产品的产量为1800吨时，该公司的盈利为几万元？24．根据市场调查，某厂家决定生产一批产品投放市场，安排750名工人计划10天完成a件的生产量．（1）按计划，该厂平均每天应生产产品多少件？（用含a的式子表示）（2）该厂按计划生产几天后，该厂家又抽调了若干名工人支援生产，同时，通过技术革新等手段使每位工人的工作效率比原计划每位工人的工作效率提高25%，结果提前完成任务，图中折线表示实际工作情况．求厂家又抽调了多少名工人支援生产？25．某公司库存挖掘机16台，现在运往甲、乙两地支援建设，每运一台到甲、乙两地的费用分别是500元和300元．设运往甲地x台挖掘机，运这批挖掘机的总费用为y元．（1）写出y与x之间的函数关系式；（2）如果公司决定将这16台挖掘机平均分配给甲、乙两地，求此次运输的总费用；（3）如果公司决定按运输费用平均分配这16台挖掘机，求此时运输的总费用又是多少．26．A市和B市各有机床12台和6台，现运往C市10台，D市8台．若从A市运1台到C市、D市各需要4万元和8万元，从B市运1台到C市、D市各需要3万元和5万元．（1）设B市运往C市x台，求总费用y关于x的函数关系式；（2）若总费用不超过90万元，问共有多少种调运方法？（3）求总费用最低的调运方法，最低费用是多少万元？27．某房地产开发公司计划建A、B两种户型的住房共80套，该公司所筹资金不少于2060万元，但不超过2096万元，且所筹资金全部用于建房，两种户型的建房成本和售价如下表：A B成本（万元/套）25 28售价（万元/套）30 34（1）该公司如何建房获得利润最大？（2）根据市场调查，每套B型住房的售价不会改变，每套A型住房的售价将会提高a万元（a＞0），且所建的两种住房可全部售出，该公司又将如何建房获得利润最大？（注：利润=售价﹣成本）28．某工厂研制一种新产品并投放市场，根据市场调查的信息得出这种新产品的日销售量y（万件）与销售的天数x（天）的关系如图所示．根据图象按下列要求作出分析：（1）求开始时，不断上升的日销售量y（万件）与销售天数x（天）的函数关系式；（2）已知销售一件产品获利0.9元，求在该产品日销售量不变期间的利润有多少万元．29．两种移动计费方式如下：全球通神州行月租费15元/月0本地通话费0.10元/分0.20元/分（1）一个月某用户在本地通话时间是x分钟，请你用含有x的式子分别写出两种计费方式下该用户应该支付的费用．（2）若某用户一个月本地通话时间是5个小时，你认为采用哪种方式较为合算？（3）小王想了解一下一个月本地通话时间为多少时，两种计费方式的收费一样多．请你帮助他解决一下．30．为了学生的健康，学校课桌、课凳的高度都是按一定的关系科学设计的，小明对学校所添置的一批课桌、课凳进行观察研究，发现他们可以根据人的身长调节高度，于是，他测量了一套课桌、课凳上相对的四档高度，得到如下数据：档次/高度第一档第二档第三档第四档凳高x/cm 37.0 40.0 42.0 45.0桌高y/cm 70.0 74.8 78.0 82.8（1）小明经过数据研究发现，桌高y是凳高x的一次函数，请你求出这个一次函数的解析式（不要求写出x的取值围）．（2）小明回家后，量了家里的写字台和凳子，凳子的高度是41厘米，写字台的高度是75厘米，请你判断它们是否配套．一次函数的应用30题参考答案：1．（1）由图形可知，当x=20时，y=1000，∴第20小时时蓄水量为1000米3．（2）由图形可知，当x=230时，y=4000，∴水池最大储水量为4000米3．（3）由图形可知，x=20为图象的拐点，①当0＜x＜20时：为正比例函数，设y1=kx1，过点（20，1000），∴k=50，∴y1=50x1，（0＜x＜20）．②当20≤x ≤30时，设y2=k1x2+b，过点（20，1000）和（30，4000），∴代入方程式中，求解为k1=300，b=﹣5000，∴y2=300x2﹣5000，（20≤x≤30）2．（1）方案①获利a（1+8%）•（1+10%）﹣a=0.188a 方案②a•20%﹣600=0.2a﹣600（2）当0.188a=0.2a﹣600时，解得：a=50000．当a=50000元时，获利一样多；当a高于50000元时，第二种方案获利多一些；当a低于50000元时，第一种方案获利多一些3．（1）依题意，得y=15+2x；（2）列表如下：x 0 1 2 3 4 5y 15 17 19 21 23 25（3）当x=10时，y=15+2×10=35，即10年后的年产值为35万元4．（1）描点：（2）设解析式为y=kx+b，把点（1400，32），（1500，31.4）分别代入可得：，解得：，所以此一次函数关系式为：y=﹣x+40.4；（3）当y=29.24时，有：x+40.4=29.24，解得：x=，即山巅的海拔为：米5．（1）设l1、l2的解析式分别为y1=k1x+b1，y2=k2x+b2，由图象，得，，解得：，．故l1的解析式为：y1=x+2，l2的解析式为：y2=x+20（2）由题意，得x+2=x+20，解得x=1000．故当照明1000小时时两种灯的费用相等6．（1）由图象得：两车在途中相遇的次数为4次．故答案为：4；（2）由题意得：快递车的速度为：400÷4=100，货车的速度为：400÷8=50，∴200÷50=4，600÷100=6∴E（6，200），C（7，200）．如图，设直线EF的解析式为y=k1x+b1，∵图象过（10，0），（6，200），∴，∴k1=﹣50，b1=500，∴y=﹣50x+500①．设直线CD的解析式为y=k2x+b2，∵图象过（7，200），（9，0），∴，∴k1=﹣100，b 1=900，∴y=﹣100x+900②．解由①，②组成的方程组得：，解得：，∴最后一次相遇时距离A地的路程为100km，货车从A 地出发了8小时．7．（1）∵线段OA所在直线的表达式为y=0.5x，∴x=1时，y=0.5，则求出进水管每分钟的进水量为0.5立方米．（2）∵线段CD所在直线的表达式为y=﹣0.25x+33，∴10=﹣0.25x+33，解得：x=92，0=﹣0.25x+33，解得：x=132，∵132﹣92=40（分钟），∴10÷40=0.25，则求出出水管每分钟的出水量为0.25立方米．（3）对于C来说，纵坐标为10，代入y=﹣0.25x+33中得：10=﹣0.25x+33，解得：x=92，点A的纵坐标为10，代入y=0.5x中得到x=20，故A（20，10），设从B到C经过了a分钟，则：（0.5﹣0.25）a=10﹣1=9，解得：a=36，∴B的横坐标为92﹣36=56，故B（56，1）．设AB 解析式为y=kx+b（k≠0），将A，B坐标代入得：，解得：，即直线AB 解析式为8．（1）设便民卡每月的通话时间与费用之间的关系为y2=kx+b，根据图象得：，解得：，故使用如意卡每月的费用与时间之间的关系式为：y1=0.25x；“便民卡”y与x之间的函数关系式为：y2=0.2x+12．（2）当y1＞y2时，0.25x＞0.2x+12，解得：x＞240；当y1=y2时，0.25x=0.2x+12，解得：x=240当y1＜y2时，0.25x＜0.2x+12，解得x＜240．故当x＜240时使用如意卡划算些，当x=240时，两种收费一样划算，当x＞240时．使用便民卡划算些9．（1）利用图表得出甲所行驶的总路程为：30千米，行驶时间为：3小时，故甲去某地的平均速度是：30÷3=10千米/时；（2）由图象得出：直线CD经过点（3，30），（1，0）代入s=kt+b，得：，解得：，故直线CD解析式为：s=15t﹣15，由图象得出s=15千米时两人相遇，则15=15t﹣15，解得：t=2．故甲出发2小时，甲、乙在途中相遇10．依题意，得（1）乙先到达终点；（2）第40秒时，乙追上甲；（3）比赛全程中，乙的速度始终保持不变；（4）乙的速度为：400÷50=8，∴S=8t（0≤t≤50）．故答案为：（1）乙；（2）40，乙，甲；（3）乙；（4）S=8t （0≤t≤50）11．（1）∵图象经过原点及（6，360），∴设解析式为：y=kx，∴6k=360，解得：k=60，∴y=60x（0＜x≤6）；（2）∵乙2小时加工100件，∴乙的加工速度是：每小时50件，∴2.8小时时两人共加工60×2.8+50×2=268（件），∴乙组在工作中有一次停产更换设备，更换设备后，乙组的工作效率是原来的2倍．∴更换设备后，乙组的工作速度是：每小时加工50×2=100件，a=100+100×（4.8﹣2.8）=300；（3）乙组加工的零件的个数y与时间x的函数关系式为y=50x（0≤x≤2）y=100（2＜x≤2.8）y=100x﹣（2.8＜x≤4.8）∵当2.8＜x≤4.8时，60x+100x﹣=230×2，得x=4，∴再经过4小时恰好装满第2箱12．（1）甲：60÷6=10；乙：（50﹣30）÷（6﹣2）=20÷4=5；30+5（3﹣2）=35，30+5（4﹣2）=40，30+5（5﹣2）=45，∴表格容依次填35、40、45；（3分）（2）①∵甲图象经过点（0，0）（6，60），∴设y甲与x之间的关系式是y甲=ax，则6a=60，解得a=10，∴y甲与x之间的关系式是：y甲=10x，（5分）②∵图象经过点（2，30）（6，50），∴设y乙与x之间的关系式是y乙=kx+b，则，解得，∴y乙与x之间的关系式是：y乙=30+5（x﹣2）=5x+20；（7分）（3）设甲队从开挖到完工所挖河渠的长度为z米，由题意得=（9分）解得z=110，∴甲队从开挖到完工所挖河渠的长度为110米．13．（1）当x=1.5时，甲对应的函数图象在乙的图象的上方，所以甲支龙舟队处于领先位置．故答案为甲；（2）乙比赛用时4.5分，甲用时5分，所以乙支龙舟队先到达终点，比甲提前0.5分钟到达．故答案为乙，0.5；（3）设乙队加逨后，路程y（米）与时间（分钟）之间的函数关系式为y=kx+b，把（2，300）和（4.5，1050）代入得，2k+b=300，4.5k+b=1050，解得k=300，b=﹣300，∴y=300x﹣300（2≤x≤4.5）14．（1）由题意得y=2000+300（x﹣1）=1700+300x；（2）把x=5代入y=1700+300n=3200（元），3200×12=38400（元）．∵38400元＜40 000元，∴他不可以到该公司应聘15．（1）设y与x的关系式为y=kx+b，有函数的图象可知点（3，40），（5，0），则，解得：所以y与x的关系式为y=﹣20x+100；（2）当x=0时，y=100，所以学校与褚向同学的距离为100千米．16．（1）设总费用y（元）与销售套数x（套），根据题意得到函数关系式：y=50000+200x．（2）设软件公司至少要售出x套软件才能收入超出总费用，则有：400x＞50000+200x解得：x＞250．答：软件公司至少要售出251套软件才能收入超出总费用17．（1）由图象得：乙行走的总路程是：3600米，他途中休息了20分钟．故答案为：3600，20；（2）①当50≤x≤80时，设y与x的函数关系式为y=kx+b．根据题意得：，解得：，∴y与x的函数关系式为：y=55x﹣800②缆车到山顶的路线长为3600÷2=1800（m），缆车到达终点所需时间为1800÷=10（min）．甲到达缆车终点时，乙行走的时间为10+50=60（min）．把x=60代入y=55x﹣800，得y=55×60﹣800=2500．所以，当甲到达缆车终点时，乙离缆车终点的路程是：3600﹣2500=1100（m）18．（1）当20≤x≤40时，设y与x之间的函数关系式：y=kx+b，∵当x=20时，y=8000，当x=40时，y=4000∴，，∴y=﹣200x+12000；（2）当20≤x≤40时，w=（y﹣2800）x=﹣200x2+9200x=﹣200（x﹣23）2+105800，∴当x=23时，w有最大值，是105800，当采购量为23吨时，家在这次买卖中所获的利润w最大，最大利润是105800元19．（1）利用图表直接得出：y1=0.4x+50；y2=0.6x；（2）当y1=y2，即0.4x+50=0.6x时，解得：x=250；当y1＜y2，即0.4x+50＜0.6x时，解得：x＞250；当y1＞y2，即0.4x+50＞0.6x时，解得：x＜250；答：通话时间为250分钟时，两种通讯业务一样，当通话时间为大于250分钟时，全球通业务合算，当通话时间为小于250分钟时，神舟行业务合算20．（1）设行费y（元）关于行质量x（千克）的一次函数关系式为y=kx+b，由题意得，解得k=，b=﹣5，∴该一次函数关系式为；（2）∵，解得x≤30，∴旅客最多可免费携带30千克的行．答：（1）行费y （元）关于行质量x（千克）的一次函数关系式为；（2）旅客最多可免费携带30千克的行21．（1）设一次函数y=kx+b，∵当x=60时，y=6，当x=80时，y=10，∴，解之，得，∴所求函数关系式为y=x﹣6（x≥30）；（2）当y=0时，x﹣6=0，所以x=30，故旅客最多可免费携带30kg行．22.（1）由函数图象可以得出l1、l2的交点坐标是（0.6，2.4），故出发0.6小时后，小明与小聪相遇，此时两人距B地2.4，（2）设l2的解析式为y=kx，由题意，得2.4=0.6k，k=4则l2的解析式为y=4x．当x=1.2时，y=4.8答：小聪走1.2（h）时与B地的距离是4.8（km）．故答案为：0.6，2.4．23．（1）由题意，得y1=0.3x+300，定义域为x＞0．（2）由题意，得y2=0.5x﹣0.3x﹣300，y2=0.2x﹣300；定义域为x＞1500；（3）当x=1800时，y2=0.2×1800﹣300=60．故当这一产品的产量为1800吨时，该公司的盈利为60万元24．（1）由题意，得该厂平均每天应生产产品的件数为：件，故答案为：；（2）设厂家又抽调了x名工人支援生产，由题意及图象得：×2+（1+25%）（750+x）×6=a，解得：x=50．答：厂家又抽调了50名工人支援生产25．（1）设运往甲地x台挖掘机，运这批挖掘机的总费用为y元，则：y=500x+300（16﹣x）=200x+4800；（2）当x=8时，y=200x+4800=1600+4800=6400；（3）依题意有500x=300（16﹣x），解得：x=6，当x=6时，y=200x+4800=1200+4800=6000．26．（1）设B市运往C市x台，则运往D市（6﹣x）台，A市运往C市（10﹣x）台，运往D市（x+2）台，由题意得：y=4（10﹣x）+8（x+2）+3x+5（6﹣x），y=2x+86．（2）由题意得：，解得：0≤x≤2，∵x为整数，∴x=0或1或2，∴有3种调运方案．当x=0时，从B市调往C市0台，调往D市6台．从A市调往C 市10台，调往D市2台，当x=1时，从B市调往C市1台，调往D市5台．从A市调往C 市9台，调往D市3台，当x=2时，从B市调往C市2台，调往D市4台．从A市调往C 市8台，调往D市4台，（3）∵y=2x+86．∴k=2＞0，∴y随x的增大增大，∴当x最小为0时，y最小，∴运费最小的调运方案是：从B市调往C市0台，调往D市6台，从A市调往C市10台，调往D市2台．y最小=86万元27．（1）设建A型的住房x套，B型的住房（80﹣x）套，利润为y，根据题意得：，解得：48≤x≤50．利润y=（30﹣25）x+（34﹣28）（80﹣x）=480﹣x．∵y随x的增加而减小，∴x=48时利润最大，即建A型住房48套，B型住房32套．（2）利润y=480+（a﹣1）x．当a＞1时，x=50时利润y最大，即建A型住房50套，B型住房30套．当a=1时，建A型住房48到50之间即可．当0＜a＜1时，x=48时利润最大，即建A型48套，建B型32套28．（1）设开始时，不断上升的日销售量y（万件）与销售天数x （天）的函数关系式为y=kx，由图象得：3=60k，k=，故y与x之间的函数关系式为：y=x（0≤x≤60）；（2）由图象得日销售量不变期间的销量为：3万件．则利润为：3×0.9=2.7万元29.（1）全球通：15+0.1x，神州行：0.2x；（2）5小时=300分钟，全球通：15+0.1×300=45（元），神州行：0.2×300=60（元），∴应选择全球通；（3）∵两种计费方式的收费一样多，∴0.2x=15+0.1x，解得：x=150，答：一个月本地通话时间为150分钟时，两种计费方式的收费一样多30．（1）设一次函数的解析式为：y=kx+b，将x=37，y=70；x=42，y=78代入y=kx+b，得，解得，∴y=1.8x+10.8；（2）当x=41时，y=1.8×41+10.8=84.6，∴家里的写字台和凳子不配套．。
(常考题)人教版高中数学必修第一册第二单元《一元一次函数,方程和不等式》测试题(有答案解析)
一、选择题1．已知,,(0,)x y t ∈+∞，且11tx y+=， A ．当2t =时，当且仅当2x y ==时，2x y +有最小值 B ．当8t =时，当且仅当253x y ==时，2x y +的最小值为25 C ．若2x y +的最小值为9，则t 的值为2 D ．若2x y +的最小值为25，则t 的值为62．在弹性限度内，弹簧拉伸的距离与所挂物体的质量成正比，即md k=，其中d 是距离（单位cm ），m 是质量（单位g ），k 是弹簧系数（单位g/cm ）．弹簧系数分别为1k ，2k 的两个弹簧串联时，得到的弹簧系数k 满足12111k k k =+，并联时得到的弹簧系数k 满足12k k k =+．已知物体质量为20g ，当两个弹簧串联时拉伸距离为1cm ，则并联时弹簧拉伸的最大距离为（ ） A ．1cm 4B ．1cm 2C ．1cmD ．2cm3．在区间1,23⎡⎤⎢⎥⎣⎦上，不等式2410mx x -+<有解，则m 的取值范围为（ ）A ．4m ≤B ．74m <C ．4m <D ．3m <4．若,a b 为实数，且2a b +=，且33a b +的最小值为（ ） A ．18B ．6C ．23D ．4235．若不等式210x ax -+≥对一切[2,)x ∈+∞恒成立，则实数a 的最大值为（ ） A ．0B ．2C ．52D ．36．已知A 、B 、C 为ABC 的三内角，且角A 为锐角，若tan 2tan B A =，则11tan tan B C+的最小值为（ ） A ．13B ．12C ．23D ．17．若实数,x y 满足0xy >，则的最大值为（ ） A ．22B ．22+C ．422+D ．422-8．若不等式2210ax ax ++>对任意的x ∈R 恒成立，则实数a 的取值范围是（ ）A ．[)0,1B ．[)0,+∞C ．(](),01,-∞+∞D ．()0,19．若过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(),P x y ，则PA PB ⋅的最大值是（ ）A ．4B ．5C ．6D ．810．已知1x >，则41x x +-的最小值为 A ．3B ．4C ．5D ．611．若关于x 的不等式20x px q ++<的解集为{|23}x x <<，则关于x 的不等式22028x px qx x ++>--的解集是（ ） A ．()2,3 B ．()(),24,-∞-+∞C ．()()2,23,4-D ．()()(),22,34,-∞-+∞12．已知3x >，13y x x =+-，则y 的最小值为（ ） A ．2B ．3C ．4D ．5二、填空题13．若对(,1]x ∈-∞-时，不等式21()2()12xxm m --<恒成立，则实数m 的取值范围是____________..14．已知函数2()34(0)f x ax x a =-+>，若存在32m n a<≤，使得()f x 在区间[,]m n 上的值域为[,]m n ，则a 的取值范围________． 15．已知正实数m ，n 满足119222m n m n +++=，则2m n +的最小值是_______． 16．某学习小组，调查鲜花市场价格得知，购买2支玫瑰与1支康乃馨所需费用之和大于8元，而购买4支玫瑰与5支康乃馨所需费用之和小于22元.设购买2支玫瑰花所需费用为A 元，购买3支康乃馨所需费用为B 元，则A 、B 的大小关系是______________ 17．ABC 中，点M ，N 在线段AB 上，且满足AM BM =，2BN AN =，若6C π=，||4CA CB ⋅=∣∣，则CM NC ⋅的最大值为________.18．函数()10y x x x=->的图象上一点到坐标原点的距离的平方的最小值为________． 19．已知,a b 为正实数，直线y x a =-与曲线ln()y x b =+相切，则23a b+的最小值为__________.20．已知实数x ，y ，z 满足：222336x y z x y z ++=⎧⎨++=⎩，则x y z ++的最大值为_________.三、解答题21．近年来，某西部乡村农产品加工合作社每年消耗电费24万元.为了节能环保，决定修建一个可使用16年的沼气发电池，并入该合作社的电网.修建沼气发电池的费用（单位：万元）与沼气发电池的容积x （单位：米3）成正比，比例系数为0.12.为了保证正常用电，修建后采用沼气能和电能互补的供电模式用电.设在此模式下，修建后该合作社每年消耗的电费C （单位：万元）与修建的沼气发电池的容积x （单位：米3）之间的函数关系为()50kC x x =+（0x ≥，k 为常数）.记该合作社修建此沼气发电池的费用与16年所消耗的电费之和为F （单位：万元）.（1）解释()0C 的实际意义，并写出F 关于x 的函数关系；（2）该合作社应修建多大容积的沼气发电池，可使F 最小，并求出最小值.（3）要使F 不超过140万元，求x 的取值范围.22．已知关于x 的不等式()24(4)0()kx k x k --->∈R 的解集为A . （1）写出集合A ；（2）若集合A 中恰有9个整数，求实数k 的取值范围.23．已知函数()()223f x x bx b R =-+∈.（1）若()f x 在区间[22]-，上单调递减，求实数b 的取值范围； （2）若()f x 在区间[22]-，上的最大值为9，求实数b 的值.24．已知函数2()1()f x ax ax a R =--∈.(1)若对任意实数x ，()0f x <恒成立，求实数a 的取值范围； (2)解关于x 的不等式()23f x x <-.25．设0x >，0y >，4xy x y a =++，其中a 为参数. （1）当0a =时，求x y +的最小值； （2）当5a =时，求xy 的最小值.26．（1）已知2x <，求()92f x x x =+-的最大值； （2）已知x 、y 是正实数，且9x y +=，求13x y+的最小值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】 当2t =时，121x y +=，()1222x y x y x y ⎛⎫+=++ ⎪⎝⎭展开后利用基本不等式即可判断A ；当当8t =时，181x y +=，()2812x y x y x y ⎛⎫+=++ ⎪⎝⎭展开后利用基本不等式即可判断B ；()1221212122x y x y t t t x y x t y tx y ⎛⎫+=++=+++≥++=++ ⎪⎝⎭分别令129t ++=和1225t ++=即可求出t 的值，可判断选项C 、D ，进而可得正确选项. 【详解】对于选项A ：当2t =时，121x y+=， ()122225259x x y x y x y x y y ⎛⎫+=++=++≥+= ⎪⎝⎭，当且仅当12122x y y x xy ⎧+=⎪⎪⎨⎪=⎪⎩即3x y ==时等号成立，所以3x y ==时，2x y +有最小值，故选项A 不正确；对于选项B ：当8t =时，181x y+=，()188222171725x x y x y x y x y y ⎛⎫+=++=++≥+= ⎪⎝⎭，当且仅当18128x y y x xy ⎧+=⎪⎪⎨⎪=⎪⎩即510x y =⎧⎨=⎩时等号成立，所以510x y =⎧⎨=⎩时，2x y +有最小值，故选项B 不正确；对于选项C ：()12212221x y x t y tx y t t x y x y ⎛⎫+=++=+++≥++⎪⎝⎭12t =++129t ++=即0==即2t =，当且仅当12122x y y x xy ⎧+=⎪⎪⎨⎪=⎪⎩即3x y ==时等号成立，所以2t =，故选项C 正确；对于选项D ：()12212221x y x t y tx y t t x y x y ⎛⎫+=++=+++≥++⎪⎝⎭12t =++1225t ++=即0==，即8t =，当且仅当12128x y y x xy ⎧+=⎪⎪⎨⎪=⎪⎩即510x y =⎧⎨=⎩时等号成立，所以8t =，故选项D 不正确；故选：C 【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件： （1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.2．A解析：A 【分析】先利用串联列关系()121220k k k k +=，结合基本不等式求得12k k +最小值，再利用并联关系得到12k k k '=+最小时求得弹簧拉伸的最大距离即可. 【详解】依题意设两个弹簧的弹簧系数分别为1k ，2k ，串联时弹簧系数为k ，并联时弹簧系数为k '. 两个弹簧串联时，由m d k =知，20201m k d ===，则12111k k k =+即12121211120k k k k k k +=+=， 即()()2121212204k k k k k k ++=≤，故1280k k +≥，当且仅当1240k k ==时等号成立，两个弹簧并联时，12k k k '=+，拉伸距离12m md k k k '==+'，要是d '最大，则需12k k k '=+最小，而1240k k ==时()12min 80k k +=，故此时d '最大，为284001m d k '==='cm. 故选：A. 【点睛】 思路点睛： 利用基本不等式求最值时，需注意取等号条件是否成立. （1）积定，利用x y +≥，求和的最小值；（2）和定，利用()24x y xy +≤，求积的最大值；（3）妙用“1”拼凑基本不等式求最值.3．C解析：C 【分析】令()241f x mx x =-+，对二次项系数m 分三种情况讨论，再对二次函数的对称轴分类讨论，分别求出参数的取值范围，最后取并集即可； 【详解】解：令()241f x mx x =-+当0m =时，原不等式为410x -+<，解得14x >，满足条件； 当0m <时，函数的对称轴为20x m =<，要使不等式2410mx x -+<在区间1,23⎡⎤⎢⎥⎣⎦有解，只需()20f <，即4700m m -<⎧⎨<⎩解得0m <当0m >时，函数的对称轴为20x m =>，要使不等式2410mx x -+<在区间1,23⎡⎤⎢⎥⎣⎦有解，当2103m <<，即6m >时，只需103f ⎛⎫< ⎪⎝⎭，即110936m m ⎧-<⎪⎨⎪>⎩无解；当22m >，即01m <<时，只需()20f <，即47001m m -<⎧⎨<<⎩解得01m <<；当1223m ≤≤，即16m ≤≤时，只需20f m ⎛⎫< ⎪⎝⎭，即481016m m m ⎧-+<⎪⎨⎪≤≤⎩解得14m ≤<；综上可得4m < 故选：C 【点睛】本题考查一元二次不等式的解，一元二次方程根的分布问题，解答的关键是对对称轴即二次项系数分类讨论，分别求出各种情况的参数的取值范围，最后取并集；4．B解析：B 【分析】根据基本不等式可知33a b +≥，结合条件求解出33a b +的最小值. 【详解】因为233236a ba b ++≥=⋅=，取等号时1a b ==，所以33a b +的最小值为6， 故选：B. 【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件： （1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.5．C解析：C 【分析】采用参变分离法对不等式变形，然后求解变形后的函数的值域，根据参数与新函数的关系求解参数最值. 【详解】因为不等式210x ax -+≥对一切[)2,x ∈+∞恒成立，所以对一切[)2,x ∈+∞，21ax x ≤+，即21x a x+≤恒成立．令()[)()2112,x g x x x x x+==+∈+∞．易知()1g x x x=+在[)2,+∞内为增函数． 所以当2x =时，()min 52g x =，所以a 的最大值是52．故选C ． 【点睛】常见的求解参数范围的方法：（1）分类讨论法（从临界值、特殊值出发）； （2）参变分离法（考虑新函数与参数的关系）.6．C解析：C 【分析】将11tan tan B C +化为关于tan A 的式子，然后利用基本不等式可以求出最小值. 【详解】在ABC 中，()tan tan C A B =-+，111111tan tan tan tan tan tan tan tan tan A BB C B A B B A B，tan 2tan B A =， 211tan tan 112tan 12tan tan tan tan 2tan 3tan 6tan 3A B AAB A B A AA ,角A 为锐角,tan 0A ∴>，12tan 12tan 226tan 36tan 33A AA A ， 当且仅当12tan 6tan 3A A ，即1tan 2A =时，等号成立，∴11tan tan B C +的最小值为23. 故选：C. 【点睛】本题考查三角形中角的互化，和的正切公式的应用，以及利用基本不等式求最值，属于中档题.7．D解析：D 【解析】试题分析：由实数,x y 满足0xy >，，设{2m x y n x y=+=+，解得2{x m ny n m =-=-，则222224()442x y m n n m n m x y x y m n m n --+=+=-+≤--++，当且仅当2n m m n=，及2n m =时等号成立，所以的最大值为422-，故选D.考点：基本不等式的应用.8．A解析：A 【分析】设函数()221f x ax ax =++，把不等式2210ax ax ++>在x ∈R 上恒成立，转化为()0f x >对于x R ∀∈恒成立，结合函数的性质，即可求解.【详解】解：设函数()221f x ax ax =++，则不等式2210ax ax ++>在x ∈R 上恒成立，即()0f x >对于x R ∀∈恒成立， 当0a =时，()10f x =>，显然成立； 当0a ≠时，要使()0f x >在x ∈R 上恒成立，需函数()221f x ax ax =++开口向上，且与x 轴没有交点，即20(2)410a a a >⎧⎨∆=-⨯⨯<⎩，解得01a <<， 综上知，实数a 的取值范围为[0,1).故选：A. 【点睛】本题主要考查了不等式的恒成立问题，以及二次函数的图象与性质的应用，其中解答中把不等式的恒成立问题转化为利用二次函数的性质求解是解答的关键，着重考查转化思想，以及推理与计算能力.9．B解析：B 【分析】先计算出两条动直线经过的定点，即A 和B ，注意到两条动直线相互垂直的特点，则有PA PB ⊥；再利用基本不等式放缩即可得出||||PA PB 的最大值． 【详解】解：由题意可知，动直线0x my +=经过定点(0,0)A ，动直线30mx y m --+=即(1)30m x y --+=，经过点定点()1,3B ，注意到动直线0x my +=和动直线30mx y m --+=始终垂直，P 又是两条直线的交点，则有PA PB ⊥，222||||||10PA PB AB ∴+==．故22||||||||52PA PB PA PB +=（当且仅当||||PA PB ==时取“=” ) 故选：B ． 【点睛】本题是直线和不等式的综合考查，特别是“两条直线相互垂直”这一特征是本题解答的突破口，从而有22||||PA PB +是个定值，再由基本不等式求解得出．直线位置关系和不等式相结合，不容易想到，是个灵活的好题．10．C解析：C 【分析】由1x >，得10x ->，则441111x x x x +=-++--，利用基本不等式，即可求解． 【详解】由题意，因为1x >，则10x ->，所以44111511x x x x +=-++≥=--， 当且仅当411x x -=-时，即3x =时取等号，所以41x x +-的最小值为5，故选C ． 【点睛】本题主要考查了基本不等式的应用，其中解答中熟记基本不等式的使用条件，合理构造是解答的关键，着重考查了推理与运算能力，属于基础题．11．D解析：D 【分析】根据关于x 的不等式20x px q ++<的解集为{|23}x x <<，利用韦达定理得到5,6p q =-=，则不等式22028x px q x x ++>--转化为 2256028x x x x -+>--，再利用穿根法求解.【详解】因为关于x 的不等式20x px q ++<的解集为{|23}x x <<， 所以由韦达定理得：5,6p q =-=，所以22028x px q x x ++>--，即为2256028x x x x -+>--，即为()()()()23042x x x x -->-+，即为()()()()23420x x x x ---+>用穿根法得不等式的解集为：()()(),22,34,-∞-+∞，【点睛】本题主要考查一元二次不等式的解集的应用以及穿根法求高次不等式，属于中档题. 12．D解析：D【分析】由3x >，得到30x ->，化简113333y x x x x =+=-++--，结合基本不等式，即可求解.【详解】因为3x >，所以30x ->，则11333533y x x x x =+=-++≥=--， 当且仅当133x x -=-，即4x =时取等号， 故选：D.【点睛】本题主要考查了利用基本不等式求最值问题，其中解答中熟记基本不等式的“一正、二定、三相等”的条件，合理运算是解得的关键，着重考查推理与运算能力.二、填空题13．【分析】运用换元法参变分离法来求解不等式恒成立问题【详解】不等式转化为化简为令又则即恒成立令又当时取最小值所以恒成立化简得解不等式得故答案为：【点睛】方法点晴：本题考查了不等式恒成立问题在求解过程中 解析：()2,3-【分析】运用换元法,参变分离法来求解不等式恒成立问题.【详解】不等式()21212x xm m ⎛⎫--< ⎪⎝⎭转化为2214x x m m +-<,化简为2211()22x x m m -<+， 令12xt =,又(],1x ∈-∞-,则[)2,t ∈+∞, 即22m m t t -<+恒成立，令2()f t t t =+，又[)2,t ∈+∞， 当2t =时，()f t 取最小值min ()(2)6f t f ==，所以，26m m -<恒成立,化简得260m m --<，解不等式得23m -<<.故答案为：()2,3-方法点晴：本题考查了不等式恒成立问题,在求解过程中运用了参变分离法,注意题目中变量的取值范围.14．【分析】由二次函数的性质可得化简得进而可得是方程两个不相等的实数根即可得解【详解】因为函数的图象开口朝上且对称轴为所以函数在区间上单调递减所以两式相减化简得将代入可得同理所以是方程两个不相等的实数根 解析：113164a ≤< 【分析】由二次函数的性质可得()()223434f m am m n f n an n m⎧=-+=⎪⎨=-+=⎪⎩，化简得2m n a +=，进而可得,m n 是方程22240ax x a-+-=两个不相等的实数根，即可得解. 【详解】 因为函数2()34(0)f x ax x a =-+>的图象开口朝上且对称轴为32x a =，32m n a<≤， 所以函数2()34(0)f x ax x a =-+>在区间[,]m n 上单调递减，所以()()223434f m am m n f n an n m ⎧=-+=⎪⎨=-+=⎪⎩，两式相减化简得2m n a +=， 将2m n a =-代入234an n m -+=可得22240an n a-+-=， 同理22240am m a -+-=， 所以,m n 是方程22240ax x a-+-=两个不相等的实数根， 又函数2224y ax x a =-+-的图象开口朝上，对称轴为132x a a =<， 所以24440a a ⎛⎫∆=--> ⎪⎝⎭且当32x a =时，22240ax x a-+-≥， 所以22444033224022a a a a a a ⎧⎛⎫--> ⎪⎪⎝⎭⎪⎨⎛⎫⎛⎫⎪⋅-⋅+-≥ ⎪ ⎪⎪⎝⎭⎝⎭⎩，解得113164a ≤<， 所以a 的取值范围为113164a ≤<. 故答案为：113164a ≤<.关键点点睛：解决本题的关键是利用二次函数的性质转化条件为2m n a+=，再结合一元二次方程根的分布即可得解. 15．【分析】利用基本不等式可求得再结合可得从而可求出的取值范围即可得到的最小值【详解】由题意当且仅当时等号成立又所以令则解得所以即的最小值是故答案为：【点睛】关键点点睛：本题考查求代数式的最值解题关键是 解析：32【分析】()1112222n m m n m n m n ⎛⎫++=+++ ⎪⎝⎭，利用基本不等式，可求得()119222m n m n ⎛⎫++≥⎪⎝⎭，再结合()119222m n m n +=-+，可得()()992222m n m n ⎡⎤+-+≥⎢⎥⎣⎦，从而可求出2m n +的取值范围，即可得到2m n +的最小值.【详解】由题意，()11155922222222n m m n m n m n ⎛⎫++=+++≥+=+= ⎪⎝⎭，当且仅当n m m n=时，等号成立， 又()119222m n m n +=-+，所以()()()1199222222m n m n m n m n ⎛⎫⎡⎤++=+-+≥ ⎪⎢⎥⎝⎭⎣⎦， 令2m n t +=，则9922t t ⎛⎫-≥ ⎪⎝⎭，解得332t ≤≤， 所以32,32m n ⎡⎤+∈⎢⎥⎣⎦，即2m n +的最小值是32. 故答案为：32. 【点睛】关键点点睛：本题考查求代数式的最值，解题关键是利用基本不等式求出()119222m n m n ⎛⎫++≥ ⎪⎝⎭，再根据()119222m n m n ⎛⎫+++= ⎪⎝⎭，可得到只包含2m n +的关系式()()992222m n m n ⎡⎤+-+≥⎢⎥⎣⎦，从而可求出2m n +的范围.考查学生的逻辑推理能力，计算求解能力，属于中档题.16．A>B 【分析】设每支支玫瑰x 元每支康乃馨y 元则由题意可得：代入可得：根据不等式性质联立即可得解【详解】设每支支玫瑰x 元每支康乃馨y 元则由题意可得：代入可得：根据不等式性质可得：而可得故故答案为：【点 解析：A >B【分析】设每支支玫瑰x 元，每支康乃馨y 元，则2,3x A y B ==，由题意可得：284522x y x y +>⎧⎨+<⎩，代入可得：8352223B A B A ⎧+>⎪⎪⎨⎪+<⎪⎩，根据不等式性质，联立即可得解.【详解】设每支支玫瑰x 元，每支康乃馨y 元，则2,3x A y B ==，由题意可得：284522x y x y +>⎧⎨+<⎩， 代入可得：8352223B A B A ⎧+>⎪⎪⎨⎪+<⎪⎩， 根据不等式性质可得：6B <， 而83B A >-，可得6A >, 故A B >，故答案为：A B >.【点睛】 本题考查了利用不等式解决实际问题，考查了不等式性质，同时考查了转化思想和计算能力，属于中档题.17．；【分析】由平面向量数量积的运算可知再根据平面向量的线性运算可分别得到故由基本不等式的性质可知将所得结论均代入的表达式即可得解【详解】解：根据题意作出如下图形由基本不等式的性质可知的最大值为故答案为解析：3； 【分析】 由平面向量数量积的运算可知23CA CB =1()2CM CA CB =+，1(2)3NC CA CB =-+，故221(23)6CM NC CA CB CA CB =-++，由基本不等式的性质可知，22222||||CA CBCA CB +，将所得结论均代入CM NC 的表达式即可得解．【详解】解：根据题意，作出如下图形，6C π=，||||4CA CB =，∴4cos 236CA CB π=⨯=AM BM =，∴1()2CM CA CB =+， 2BN AN =，∴111()(2)333NC AC AN AC AB CA CB CA CA CB =-=-=---=-+， ∴22111()[(2)](23)236CM NC CA CB CA CB CA CB CA CB =+-+=-++， 由基本不等式的性质可知，222222||||22||||82CA CB CA CB CA CB +=+=， ∴142(82323)36CM NC -⨯⨯= ∴CM NC 的最大值为423- 故答案为：423- 【点睛】 本题考查平面向量的线性运算和数量积运算、基本不等式的性质，熟练掌握平面向量的加法、减法、数乘和数量积的运算法则是解题的关键，考查学生的逻辑推理能力和运算能力，属于中档题．18．【分析】设曲线上任一点坐标为求出它是原点距离的平方用基本不等式求得最小值【详解】设曲线上作一点的坐标为则当且仅当即时等号成立故答案为：【点睛】本题考查用基本不等式求最值属于基础题 解析：22【分析】设曲线上任一点坐标为1,x x x ⎛⎫-⎪⎝⎭，求出它是原点距离的平方，用基本不等式求得最小值．【详解】设曲线上作一点P 的坐标为1,(0)x x x x ⎛⎫-> ⎪⎝⎭，则2222211222OP x x x x x ⎛⎫=+-=+-≥ ⎪⎝⎭，当且仅当2212x x =，即142x -=时等号成立，故答案为：2．【点睛】本题考查用基本不等式求最值，属于基础题．19．【分析】函数求导由切线方程可得再利用基本不等式求得最值【详解】的导数为由切线的方程可得切线的斜率为1可得切点的横坐标为切点为代入得为正实数则当且仅当即时取得最小值故答案为：【点睛】本题考查导数的运算解析：5+【分析】函数求导，由切线方程y x a =-可得1a b +=，再利用基本不等式求得最值.【详解】ln()y x b =+的导数为1y x b'=+， 由切线的方程y x a =-可得切线的斜率为1，可得切点的横坐标为1b -，切点为(1,0)b -，代入y x a =-，得1a b +=，,a b 为正实数，则2323233()()2355b a a a b a b a b a b b+=++=+++≥+=+当且仅当3a b =，即2,3a b ==5+.故答案为：5+【点睛】 本题考查导数的运算、导数的几何意义及基本不等式求最值，属于基础题.20．【分析】按的正负分类讨论由得至少有一个正数然后分全正一负二负然后利用基本不等式可得结论【详解】首先至少有一个正数（1）如果则由得不成立；（2）若中只有一个负数不妨设则又∴即当且仅当时等号成立；（3）解析：1+【分析】按,,x y z 的正负分类讨论，由3x y z ++=得,,x y z 至少有一个正数，然后分全正，一负，二负，然后利用基本不等式可得结论．【详解】首先,,x y z 至少有一个正数，（1）如果0,0,0x y z ≥≥≥，则由3x y z ++=得,,[0,3]x y z ∈，2222736x y z ++<<，不成立；（2）若,,x y z 中只有一个负数，不妨设0,0,0x y z ≥≥<，则3z x y -=+-，22()6()9z x y x y =+-++，又2222()36()362x y z x y +=-+≤-， ∴2()6()9x y x y +-++2()362x y +≤-，即2()4()180x y x y +-+-≤，2x y +≤2231x y z x y z x y ++=+-=+-≤+12x y ==+，1z =时等号成立；（3）若,,x y z 中有两个负数，不妨设0,0,0x y z ≥<<，则3y z x --=-，2222()362y z y z x ++=-≥， ∴22(3)362x x --≥，整理得22210x x --≤，01x ≤≤+231x y z x y z x ++=--=-≤+1x =+12y z ==-时等号成立；综上所述，x y z ++的最大值是1+故答案为：1+【点睛】 本题考查用基本不等式求最值，解题关键是根据绝对值的定义分类讨论去掉绝对值符号，然后利用基本不等式．三、解答题21．（1）()0C 的实际意义是未修建沼气发电池时，该合作社每年消耗的电费；192000.1250F x x =++，0x ≥；（2）该合作社应修建容积为350立方米的沼气发电池时，可使F 最小，且最小值为90万元；（3）3050100,3⎡⎤⎢⎥⎣⎦. 【分析】（1）根据题中函数关系式，可直接得到()0C 的实际意义；求出k ，进而可得F 关于x 的函数关系；（2）根据（1）中F 的函数关系，利用基本不等式，即可求出最小值；（3）将140F ≤，转化为关于x 的不等式，求解即可.【详解】（1）()0C 的实际意义是修建这种沼气发电池的面积为0时的用电费用，即未修建沼气发电池时，该合作社每年消耗的电费；由题意可得，()02450k C ==，则1200k =； 所以该合作社修建此沼气发电池的费用与16年所消耗的电费之和为120019200160.120.125050F x x x x =⨯+=+++，0x ≥； （2）由（1）()19200192000.120.125065050F x x x x =+=++-++690≥=， 当且仅当()192000.125050x x =++，即350x =时，等号成立, 即该合作社应修建容积为350立方米的沼气发电池时， 可使F 最小，且最小值为90万元；（3）为使F 不超过140万元，只需192000.1214050F x x =+≤+， 整理得2333503050000x x -+≤，则()()330501000x x --≤，解得30501003x ≤≤， 即x 的取值范围是3050100,3⎡⎤⎢⎥⎣⎦【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：（1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方. 22．无23．无24．无25．无26．无。
一次函数与一元一次方程和不等式同步辅导(含答案)--绝对经典
11.3.1 —11.3.2 一次函数与一元一次方程和不等式重点知识讲解1．一元一次方程ax+b=0（a≠0）与一次函数y=ax+b（a≠0）的关系（1）一元一次方程ax+b=0（a≠0）是一次函数y=ax+b（a≠0）的函数值为0时的特殊情形．(2)直线y=ax+b与x轴交点的横坐标就是一元一次方程ax+b=0的解x=—ba。
2．一元一次不等式与一次函数的关系(1）一元一次不等式ax+b〉0或ax+b〈0（a≠0)是一次函数y=ax+b（a≠0）•的函数值不等于0的情形．（2)直线y=ax+b上使函数值y>0（x轴上方的图像）的x的取值范围是ax+b〉0的解集；使函数值y<0(x轴下方的图像）的x的取值范围是ax+b〈0的解集．经验与方法技巧1．利用一次函数求一元一次方程的解题步骤（1）将一元一次方程化成ax+b=0的形式．（2）画出y=ax+b的图像，确定其与x轴交点的横坐标．2．利用一次函数求一元一次不等式的解集的技巧根据不等式的特点，灵活采用求解方法：（1）利用一个一次函数；（2）•利用两个一次函数．典型例题例1画出y=—3x+5的图象,利用图像求方程-3x+5=0的解．解析取点(0，5）,(53，0），图像如图所示．∵直线y=-3x+5与x轴交点的横坐标为53，∴方程-3x+5=0的解为x=53。
评注画函数图像时要准确，求出直线y=-3x+5与x•轴交点的横坐标即为方程的解．例2画出函数y=—3x+12的图像,利用图像求：（1）不等式-3x+12〉0的解集．(2)不等式-3x+12≤0的解集．(3)如果y的值在—6≤y≤6的范围内，那么相应的x的值在什么范围内？解析取点(0，12），(4，0)，作出函数图像，如图所示,由图像可以看出:（1)当y〉0时，x的取值范围为x〈4，∴不等式—3x+12>0的解集为x<4．（2)当y≤0时，x的取值范围为x≥4．∴不等式—3x+12≤0的解集为x≥4．（3）当—6≤y≤6时,x的取值范围为2≤x≤6．评注借助图像求不等式的解集，关键是要清楚以下几点：①y〉0时，x•的取值范围就是x轴上方的图像所对应的x的取值范围．②y〈0时,x的取值范围就是x•轴下方的图像所对应的x的取值范围．③y=0时，x的值就是图像与x轴交点的横坐标．④当y>a或y<a(a≠0)时，应先确定当y=a时对应的x值，然后再进一步确定x的取值范围．例3若y1=-x+3,y2=3x—4，当x取何值时，y1<y2？解析∵y1<y2，∴-x+3〈3x—4,解得x〉74，∴当x>74时,y1〈y2．评注此题是两个一次函数之间的关系，可以直接借助一元一次不等式求出x的取值范围．教材例题习题的变形题例（P41例2）用画图像的方法解下列各题：（1）解不等式：5x+4〉2x+10．(2）解方程:5x+4=2x+10．解析（1）如图，原不等式可化为3x—6〉0，画出直线y=3x—6，由图像可以看出，当x>2时，这条直线上的点在x轴的上方，即这时y=3x-6〉0，所以不等式的解集为x〉2．（2）原方程可化为3x-6=0．由图像可以看出，y=3x-6与x轴交点的横坐标为2，所以原方程的解为x=2．评注①从函数的角度看问题,能发现一次函数与一元一次不等式、•一元一次方程之间的联系,体现了数形结合的思想．②本题求不等式的解集时，还可将不等式的两边分别看作两个一次函数，画出两条直线，比较直线上点的位置的高度，也可求得不等式的解集．学科内综合题例1甲、乙两辆摩托车分别从相距20km的A,B两地出发，相向而行，图中的L1，L2分别表示甲、乙两辆摩托车离开A地的距离s（km)与行驶时间t（h）•之间的函数关系．（1)哪辆摩托车的速度较快?（2）经过多长时间，甲摩托车行驶到A，B两地的中点？解析（1）由图像可以看出，甲摩托用了0．6h行驶了20km，而乙摩托车用了0．•5h 行驶了20km，所以乙摩托车的速度较快．（2）设L1的关系式为y=kx，把x=0．6，y=20代入，得20=0．6k，解得k=1003,∴y=1003x。
专题十三 不等式与一次函数应用题(含答案)
专题十三 不等式与一次函数应用题1．（2007年眉山市）某县响应“建设环保节约型社会”的号召，决定资助部分付镇修建一批沼气池，使农民用到经济、环保的沼气能源．幸福村共有264户村民，政府补助村里34万元，不足部分由村民集资．修建A 型、B 型沼气池共20个．两种型号沼气池每个修建费用、可供使用户数、修建用地情况如下表： 沼气池 修建费用(万元/个) 可供使用户数(户/个) 占地面积(m 2/个)A 型3 20 48 B 型2 3 6 政府相关部门批给该村沼气池修建用地708m 2．设修建A 型沼气池x 个，修建两种型号沼气池共需费用y 万元．(1)求y 与x 之间的函数关系式；(2)不超过政府批给修建沼气池用地面积，又要使该村每户村民用上沼气的修建方案有几种； (3)若平均每户村民集资700元，能否满足所需费用最少的修建方案．2．（2007年泰州市）通过市场调查，一段时间内某地区某一种农副产品的需求数量y （千克）与市场价格x （元/千克）（030x <<）存在下列关系： x （元/千克） 5 10 15 20 y （千克） 4500 4000 3500 3000又假设该地区这种农副产品在这段时间内的生产数量z （千克）与市场价格x （元/千克）成正比例关系：400z x =（030x <<）．现不计其它因素影响，如果需求数量y 等于生产数量z ，那么此时市场处于平衡状态．（1）请通过描点画图探究y 与x 之间的函数关系，并求出函数关系式；（2）根据以上市场调查，请你分析：当市场处于平衡状态时，该地区这种农副产品的市场价格与这段时间内农民的总销售收入各是多少？（3）如果该地区农民对这种农副产品进行精加工，此时生产数量z 与市场价格x 的函数关系发生改变，而需求数量y 与市场价格x 的函数关系未发生变化，那么当市场处于平衡状态时，该地区农民的总销售收入比未精加工市场平衡时增加了17600元．请问这时该农副产品的市场价格为多少元？ （1）描点略． ······························ 1分 设y kx b =+，用任两点代入求得1005000y x =-+， ············· 3分 再用另两点代入解析式验证． ························ 4分 （2）y z = ，1005000400x x ∴-+=，10x ∴=． ································ 6分∴总销售收入10400040000=⨯=（元） ·················· 7分∴农副产品的市场价格是10元/千克，农民的总销售收入是40000元． ······················· 8分 （3）设这时该农副产品的市场价格为a 元/千克，则(1005000)4000017600a a -+=+， ··················· 10分 解之得：118a =，232a =．030a << ，18a ∴=． ························· 11分∴这时该农副产品的市场价格为18元/千克．················· 12分3．（南充）今年6月份，我市某果农收获荔枝30吨，香蕉13吨，现计划租用甲、乙两种货车共10辆将这批水果全部运往深圳，已知甲种货车可装荔枝4吨和香蕉1吨，乙种货车可装荔枝、香蕉各2吨； （1）该果农安排甲、乙两种货车时有几种方案？请你帮助设计出来； （2）若甲种货车第辆要付运输费2000元，乙种货车每辆要付运输费1300元，则该果农应选择哪种方案，使运费最少？最少运费是多少元？ 解：（1）设安排甲种货车x 辆，则安排乙种货车（10－x ）辆，依题意，得⎩⎨⎧≥-+≥-+13)10(230)10(24x x x x 解这个不等式组，得 ⎩⎨⎧≤≥75x x75≤≤∴x x 是整数，∴x 可取5、6、7，既安排甲、乙两种货车有三种方案：甲种货车5辆，乙种货车5辆；① 甲种货车6辆，乙种货车4辆；甲种货车7辆，乙种货车3辆；（2）方法一：由于甲种货车的运费高于乙种货车的运费，两种货车共10辆，所以当甲种货车的数量越少时，总运费就越少，故该果农应选择① 运费最少，最少运费是16500元； 方法二：方案①需要运费 2000×5＋1300×5＝16500（元） 方案②需要运费 2000×6＋1300×4＝17200（元） 方案③需要运费 2000×7＋1300×3＝17900（元） ∴该果农应选择① 运费最少，最少运费是16500元；5 10 15 x (元／千y (千克) 5000 450400（第28题O4．（2007山东青岛）某饮料厂开发了A 、B 两种新型饮料，主要原料均为甲和乙，每瓶饮料中甲、乙的含量如下表所示．现用甲原料和乙原料各2800克进行试生产，计划生产A 、B 两种饮料共100瓶．设生产A 种饮料x 瓶，解答下列问题：（1）有几种符合题意的生产方案？写出解答过程；（2）如果A 种饮料每瓶的成本为2.60元，B 种饮料每瓶的成本为2.80元，这两种饮料成本总额为y 元，请写出y 与x 之间的关系式，并说明x 取何值会使成本总额最低？⑴ 设生产A 种饮料x 瓶，根据题意得：解这个不等式组，得20≤x ≤40．因为其中正整数解共有21个，所以符合题意的生产方案有21种．⑵ 根据题意，得 y ＝2.6x ＋2.8(100－x)．整理，得 y ＝－0.2x ＋280．∵k ＝－0.2＜0，∴y 随x 的增大而减小．∴当x ＝40时成本总额最低． 5、（2007年长沙）某班到毕业时共结余经费1800元，班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品，其余资金用于在毕业晚会上给50位同学每人购买一件文化衫或一本相册作为纪念品．已知每件文化衫比每本相册贵9元，用200元恰好可以买到2件文化衫和5本相册． （1）求每件文化衫和每本相册的价格分别为多少元？（2）有几购买文化衫和相册的方案？哪种方案用于购买老师纪念品的资金更充足？解：(1)设每件文化衫和每本相册的价格分别为x 元和y 元，则⎩⎨⎧=+=-200529y x y x ,解得⎩⎨⎧==2635y x ， ∴每件文化衫和每本相册的价格分别为35元和26元．(2)设购买文化衫t 件，则购买相册(50-t)本，则1500≤35t+26(50-t)≤1530． 解得9200≤t ≤9230． ∵t 为正整数 ∴t=23，24，25，即有三种方案：第—种方案：购买文化衫23件、相册27本，此时余下资金293元； 第二种方案：购买文化衫24件、相册26本，此时余下资金284元； 第三种方案：购买文化衫25件、相册25本，此时余下资金275元． ∴第一种方案用于购买教师纪念品的资金更充足．6、（河南省）某商场用36万元购进A 、B 两种商品，销售完后共获利6万元，其进价和售价如下表：A B 进价(元/件)1200 1000 售价(元/件)13801200（注：获利＝售价－进价）(1) 该商场购进A 、B 两种商品各多少件?(2) 商场第二次以原进价购进A 、B 两种商品．购进B 种商品的件数不变，而购进A 种商品的件数是第一次的2倍，A 种商品按原价出售，而B 种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于81600元，B 种商品最低售价为每件多少元?（1）设购进A 种商品x 件，B 种商品y 件．根据题意，得12001000360000,(13801200)(12001000)60000.x y x y +=⎧⎨-+-=⎩化简，得651800,9103000.x y x y +=⎧⎨+=⎩解之，得200,120.x y =⎧⎨=⎩答：该商场购进A 、B 两种商品分别为200件和120件．（2）由于A 商品购进400件，获利为（1380－1200）×400 = 72000（元）．从而B 商品售完获利应不少于81600－72000 = 9600（元）． 设B 商品每件售价为x 元，则120（x －1000）≥9600．所以，B 种商品最低售价为每件1080元． 7．（2007年日照市）某水产品市场管理部门规划建造面积为2400m 2的集贸大棚，大棚内设A 种类型和B种类型的店面共80间，每间A 种类型的店面的平均面积为28m 2，月租费为400元；每间B 种类型的店面的平均面积为20m 2，月租费为360元.全部店面的建造面积不低于大棚总面积的80%，又不能超过大棚总面积的85%.(1)试确定A 种类型店面的数量；(2)该大棚管理部门通过了解业主的租赁意向得知， A 种类型店面的出租率为75%,B 种类型店面的出租率为90%.为使店面的月租费最高，应建造A 种类型的店面多少间？ 解：（1）设A 种类型店面的数量为x 间，则B 种类型店面的数量为(80-x )间，根据题意，得：⎩⎨⎧⨯≤-+⨯≥-+%.852400)80(2028%,802400)80(2028x x x x ……………………………………………………3分解之，得⎩⎨⎧≤≥.55,40x x∴A 种类型店面的数量为40≤x ≤55,且x 为整数. …………………………………5分 (2) 设应建造A 种类型的店面x 间，则店面的月租费为： W =400×75%·x +360×90%·(80-x )=-24x +25920, …………………………………………………………………………7分∵-24＜0,40≤x ≤55,∴为使店面的月租费最高，应建造A 种类型的店面40间.…………………………9分8、我市为绿化城区，计划购买甲、乙两种树苗共计500棵，甲种树苗每棵50元，乙种树苗每棵80元，调查统计得：甲、乙两种树苗的成活率分别为90%、95%．(1)如果购买两种树苗共用28000元，那么甲、乙两种树苗各买了多少棵？(2)市绿化部门研究决定，购买树苗的钱数不得超过34000元，应如何选购树苗？(3)要使这批树苗的成活率不低于92%，且使购买树苗的费用最低，应如何选购树苗？最低费用是多少？2030(100)28004020(100)2800x x x x +-+-⎧⎨⎩，．≤ ≤解：（1）设购买甲种树苗x 棵，则乙种树苗（500-x ）棵，由题意得：50x+80（500-x ）=28000 解得x=400 所以500-x=100 答：购买甲种树苗400棵，则乙种树苗100棵．（2）由题意得：50x+80（500-x ）≤34000解得x ≥200，（注意x ≤500） 答：购买甲种树苗不少于200棵，其余购买乙种树苗．（若为购买乙种树苗不多于300棵，其余购买甲种树苗也对）（3）由题意得：90%x+95%（500-x ）≥500×92%，解得x ≤300 设购买两种树苗的费用之和为y ，则y=50x+80（500-x ）=40000-30x在此函数中，y 随x 的增大而减小所以当x=300时，y 取得最小值，其最小值为40000-30×300=31000 答：购买甲种树苗300棵，乙种树苗200棵，即可满足这批树苗的成活率不低于92%，又使购买树苗的费用最低，其最低费用为31000．9、在一条笔直的公路上有A 、B 两地，它们相距150千米，甲、乙两部巡警车分别从A 、B 两地同时出发，沿公路匀速相向而行，分别驶往B 、A 两地．甲、乙两车的速度分别为70千米/ 时、80千米/ 时，设行驶时间为x 小时．(1)从出发到两车相遇之前，两车的距离是多少千米？（结果用含x 的代数式表示）（2）已知两车都配有对讲机，每部对讲机在15千米之内（含15千米）时能够互相通话，求行驶过程中两部对讲机可以保持通话的时间最长是多少小时？解：（1）(150—150x) 千米．………………………………………3分（2）相遇之后，两车的距离是（150 x —150）千米，…………………4分依题意可得不等式组： ⎩⎨⎧≤-≤-．15150150,15150150x x ……………………………………………6分解得1.19.0≤≤x ，…………………………………………8分2.09.01.1=-．答：两部对讲机可以保持通话的时间最长是0.2小时．. ……………9分10、某园林的门票每张10元，一次性使用．考虑到人们的不同需求，也为了吸引更多的游客，该园林除保留原来的售票方法外，还推出了一种“购买个人年票”的售票方法（个人年票从购买日起，可供持票者使用一年）．年票分A 、B 、C 三类，A 类年票每张120元，持票者进人园林时，无需再购买门票；B 类年票每张60元，持票者进入该园林时，需再购买门票，每次2元；C 类年票每张40元，持票者进入该园林时，需再购买门票，每次3元．（1）如果你只选择一种购买门票的方式，并且你计划在一年中用80元花在该园林的门票上，试通过计算，找出可使进入该园林的次数最多的购票方式；（2）求一年中进入该园林至少超过多少次时，购买A 类年票比较合算解：（1）根据题意，需分类讨论．因为80＜120，所以不可能选择A 类年票；若只选择购买B 类年票，则能够进入该园林 （80-60）÷2=10（次）； 若只选择购买C 类年票，则能够进入该园林（ 80-40）÷3≈13（次）； 若不购买年票，则能够进入该园林 80÷10=8（次）． 所以，计划在一年中用80元花在该园林的门票上，通过计算发现：可使进入该园林的次数最多的购票方式是选择购买C 类年票． （2）设一年中进入该园林至少超过x 次时，购买A 类年票比较合算，根据题意， 得 {60+2x ＞120① 40+3x ＞120②10x ＞120③．由①，解得x ＞30；由②，解得x ＞26 23；由③，解得x ＞12． 解得原不等式组的解集为x ＞30．答：一年中进入该园林至少超过30次时，购买A 类年票比较合算．11、某饮料厂生产一种饮料，经测算，用1吨水生产的饮料所获利润y(元)是1吨水价格x 的一次函数. (1)根据下表提供的数据，求y 与x 的函数关系式；当水价为每吨10元时，1吨水生产出的饮料所获利润是多少?(2)为节约用水，这个市场规定：该长日用水量不超过20吨时，水价每吨按4元收费，日用水量超过20吨时，超过部分按每吨40元收费，已知该厂日用水量不少于20吨，设该长日用水量为t 吨，当日获利润为w 元，求w 与t 的函数关系式；该厂加强管理，积极节水，使用水量不超过25吨，但仍不少于20吨，求该厂的日利润的取值范围.解：(1) 用1吨水生产的饮料所获利润y （元）是1吨水的价格x （元）的一次函数式为： b kx y +=，根据题意得：⎩⎨⎧+=+=b k b k 61984200 解得：⎩⎨⎧=-=2041b k∴所求一次函数式是：204+-=x y 当x =10时，y=－10+204＝194（元）（2）当1吨水的价格为40元时，所获利润是：y ＝－40＋204＝164（元）．∴W 与t 的函数关系式是：164)20(20200⨯-+⨯=x w即：720164+=t w∵20 ≤ t ≤ 25， ∴4000≤w ≤4820。
一元一次不等式与一次函数习题精选(含答案)
一元一次不等式与一次函数1．如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x＜ax+4的解集为（）(5)2．已知一次函数y=ax+b的图象过第一、二、四象限，且与x轴交于点（2，0），则关于x的不等式a（x﹣1）﹣b3．如图，直线y1=k1x+a与y2=k2x+b的交点坐标为（1，2），则使y1＜y2的x的取值范围为（）4．直线l1：y=k1x+b与直线l2：y=k2x+c在同一平面直角坐标系中的图象如图所示，则关于x的不等式k1x+b＜k2x+c 的解集为（）5．如图，一次函数y=kx+b的图象经过A、B两点，则kx+b＞0解集是（）6．如图，函数y=kx和y=﹣x+3的图象相交于（a，2），则不等式kx＜﹣x+3的解集为（）＞7．（如图，直线l是函数y=x+3的图象．若点P（x，y）满足x＜5，且y＞，则P点的坐标可能是（）(6) (8)8．如图，已知一次函数y=kx+b的图象经过点A（5，0）与B（0，﹣4），那么关于x的不等式kx+b＜0的解集是（）9．如图，一次函数y=kx+b的图象经过点（2，0）与（0，3），则关于x的不等式kx+b＞0的解集是（）10．如图，已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2，根据图象有下列3个结论：①a＞0；②b＞0；③x ＞﹣2是不等式3x+b＞ax﹣2的解集．其中正确的个数是（）二．填空题（共8小题）11．如图，经过点B（﹣2，0）的直线y=kx+b与直线y=4x+2相交于点A（﹣1，﹣2），则不等式4x+2＜kx+b＜0的解集为_________ ．12．如图，l1反映了某公司的销售收入与销量的关系，l2反映了该公司产品的销售成本与销量的关系，当该公司赢利（收入＞成本）时，销售量必须_________ ．(13) (14) (15)13．如图，函数y=2x和y=ax+5的图象相交于A（m，3），则不等式2x＜ax+5的解集为_________ ．14．如图，已知直线y1=x+m与y2=kx﹣1相交于点P（﹣1，1），则关于x的不等式x+m＞kx﹣1的解集为_________ ．15．如图，直线y1=kx+b与直线y2=mx交于点P（1，m），则不等式mx＞kx+b的解集是_________ ．16．如图，已知函数y=x+b和y=ax+3的图象相交于点P，则关于x的不等式x+b＜ax+3的解集为_________ ．(17) (18)17．如图，直线y=kx+b经过点A（﹣1，1）和点B（﹣4，0），则不等式0＜kx+b＜﹣x的解集为_________ ．18．如图，直线y=kx+b交坐标轴于A（﹣3，0）、B（0，5）两点，则不等式﹣kx﹣b＜0的解集是_________ ．三．解答题19．在平面直角坐标系中，直线y=kx﹣15经过点（4，﹣3），求不等式kx﹣15≥0的解．20．如图，直线l1与l2相交于点P，点P横坐标为﹣1，l1的解析表达式为y=x+3，且l1与y轴交于点A，l2与y轴交于点B，点A与点B恰好关于x轴对称．（1）求点B的坐标；（2）求直线l2的解析表达式；（3）若点M为直线l2上一动点，直接写出使△MAB的面积是△PAB的面积的的点M的坐标；（4）当x为何值时，l1，l2表示的两个函数的函数值都大于0？21．已知：直线l1的解析式为y1=x+1，直线l2的解析式为y2=ax+b（a≠0）；两条直线如图所示，这两个图象的交点在y轴上，直线l2与x轴的交点B的坐标为（2，0）（1）求a，b的值；（2）求使得y1、y2的值都大于0的取值范围；（3）求这两条直线与x轴所围成的△ABC的面积是多少？（4）在直线AC上是否存在异于点C的另一点P，使得△ABC与△ABP的面积相等？请直接写出点P的坐标．22．如图，直线y=kx+b经过点A（0，5），B（1，4）．（1）求直线AB的解析式；（2）若直线y=2x﹣4与直线AB相交于点C，求点C的坐标；（3）根据图象，写出关于x的不等式2x﹣4≥kx+b的解集．AACBBAAAAD﹣2＜x＜﹣1 ．大于4 ．x＜．x＞﹣1 ．x＞1 ．x＜1 ．﹣4＜x＜﹣1 ．x＞﹣时，+3=）﹣的面积的的横坐标的长度是，时，）（﹣﹣，时，（﹣×﹣﹣﹣点的坐标是（﹣，﹣）或（，﹣）x+3时，x时，﹣﹣时，，﹣；=OC=解方程组得∴解方程组，。
(完整版)一次函数与一元一次不等式练习(1)附答案
一次函数与一元一次不等式练习（1）附答案一、选择题1．如图1，直线y=kx+b与x轴交于点A（-4，0），则当y>0时，x的取值范围是（ • ） A．x>-4 B．x>0 C．x<-4 D．x<0（1）（2）2．已知一次函数y=kx+b的图像，如图2所示，当x<0时，y的取值范围是（ •）A．y>0 B．y<0 C．-2<y<0 D．y<-23．已知y1=x-5，y2=2x+1．当y1>y2时，x的取值范围是（）．A．x>5 B．x<12C．x<-6 D．x>-64．函数y=12x-3与x轴交点的横坐标为（）．A．-3 B．6 C．3 D．-65．对于函数y=-x+4，当x>-2时，y的取值范围是（）．A．y<4 B．y>4 C．y>6 D．y<6二、填空题1．对于一次函数y=2x+4，当______时，2x+4>•0；•当________•时，•2x+•4<•0；•当_______时，2x+4=0．2．已知y1=2x-5，y2=-2x+3，当_______时，y1≤y2．3．已知关系x的方程ax-5=7的解为x=1，则一次函数y=ax-12与x•轴交点的坐标为________．4．已知2x-y=0，且x-5>y，则x的取值范围是________．5．关于x的方程3x+3a=2的解是正数，则a________．三、解答题1．已知y1=-x+2，y2=3x+4．（1）当x分别取何值时，y1=y2，y1<y2，y1>y2？（2）在同一坐标系中，分别作出这两个函数的图像，请你说说（1）中的解集与函数图像之间的关系．2．某单位急需用车，但又不准备买车，他们准备和一个个体车主或一国营出租车公司签订月租车合同．设汽车每月行驶x（cm），应付给个体车主的月费用为y1元，•应付给汽车出租公司的月费用为y2元，y1，y2分别与x之间的函数关系的图像（两条射线）如图所示，观察图像回答下列问题：（1）每月行驶的路程在什么范围内，租出租公司的车合算？（2）每月行驶的路程等于多少时，租两家车的费用相同？（3）如果这个单位估计每月行驶的路程为2300km，那么这个单位租哪家车合算？3．某学校计划购买若干台电脑，•现从两家商场了解到同一型号电脑每台报价均为6000元，并且多买都有一定的优惠．甲商场的优惠条件是：第一台按原报价收费，其余每台优惠25%，那么甲商场的收费y1（元）与所买电脑台数x之间的关系式是________．乙商场的优惠条件是：每台优惠20%，那么乙商场的收费y2（元）与所买电脑台数x 之间的关系式是_________．（1）什么情况下到甲商场购买更优惠？（2）什么情况下到乙商场购买更优惠？（3）什么情况下两家商场的收费相同？探究应用拓展性训练1．（与现实生活联系的应用题）某单位要制作一批宣传材料．甲公司提出：每份材料收费20元，另收3000元设计费；乙公司提出：每份材料收费30元，不收设计费．问：让哪家公司制作这批宣传比较合算？2．（学科内综合题）下图表示学校浴室淋浴器水箱中的水量y（L）•与进水时间x（min）的函数关系．（1）求y与x之间的函数关系式．（2）进水多少分钟后，水箱中的水量超过100L？3．小明准备将平时的零用钱节约一些储存起来，他已存有50元，从现在起每个月存12元．（1）试写出小明的存款数与从现在开始的月份数之间的函数关系式．（2）小明的同学小丽以前没有存过零用钱，听到小明在存零用钱，•表示从现在起每个月存18元，争取超过小明．请你在同一平面直角坐标系中分别画出小明和小丽存款数和月份数的函数关系的图像．半年以后小丽的存款数是多少？能否超过小明？•至少几个月后小丽的存款数超过小明？4．（探究题）某企业急需一辆汽车，但无资金购买，公司经理决定租一辆汽车，•使用期限为一个月．甲汽车出租公司的出租条件为每千米的租车费为1．2元，•乙汽车出租公司的条件是每月须支付司机800元的工资，另外每千米的租车费为1元，设在这一个月中汽车行驶x（km），租用甲公司的费用为y1（元），租用乙公司的费用为y2（元）．（1）试分别写出y1，y2与x之间的函数关系式．（2）当汽车行驶路程为多少千米时，租用乙公司的汽车合算？5．（2003年郑州卷）某学校餐厅计划购买12张餐桌和一批餐椅，现从甲、•乙两商场了解到同一型号的餐桌报价均为每张200元，餐椅每把50元．甲商场称：每张餐桌送一把餐椅；乙商场规定：所有餐桌、餐椅均按报价的八五折销售．那么，什么情况下甲商场更优惠？答案:教材基础知识针对性训练一、1．A 解析：由图像可看出y>0（即x轴上方的图像）对应的x的范围为x>-4，故选A．提示：本题只能通过一次函数y=kx+b的图像确定x的取值范围．2．D 解析：由图像可以看出，当x<0时，对应的图像位于y轴的左侧，•这部分图像对应的y值的范围为y<-2，故应选D．提示：此题已知自变量x的取值范围确定y的取值范围，可以通过图像直接观察，•也可先求出一次函数的解析式，借助不等式作答．3．C 解析：∵y1>y2，∴x-5>2x+1，-x>6，x<-6，故选C．4．B 解析：当y=0时，12x-3=0，12x=3，x=6，故应选B．5．D 解析：∵y=-x+4，∴x=4-y．又∵x>-2，∴4-y>-2，-y>-6，y<6，故选D．提示：此题打破常规，将解析式进行变形，用含y的代数式表示x（可认为y•是自变量，x是因变量），然后借助不等式求出y的取值范围．此题还可画出图像，•借助图像的直观性直接确定y的取值范围．二、1．解析：∵2x+4>0，∴2x>-4，x>-2．∵2x+4<0，∴2x<-4，x<-2．∵2x+4=0，∴2x=-4，x=-2．答案：x>-2 x<-2 x=-22．解析：∵y1≤y2，∴2x-5≤-2x+3，4x≤8，x≤2，∴x≤2时，y1≤y2．答案：x≤23．解析：∵ax-5=7，∴ax-12=0．又y=ax-12与x轴的交点的横坐标就是方程ax-5=7的解，即x=1，∴y=ax-12与x轴的交点坐标为（1，0）．答案：（1，0）提示：此题还可通过先确定a的值，进而再确定y=ax-12与x轴的交点坐标．4．解析：∵2x-y=0，∴y=2x．又∵x-5>y，∴x-5>2x，x<-5．∴x的取值范围为x<-5．答案：x<-55．解析：∵3x+3a=2，∴x=23-a．∵3x+3a=2的解为正数，即x>0．∴23-a>0，-a>-23，a<23.答案：a<2 3三、1．解析：（1）当y1=y2时，-x+2=3x-4，-4x=-6，x=32.当y1>y2时，-x+2>3x-4，-4x>-6，x<32,当y1<y2时，-x+2<3x-4，-4x<-6，x>32.所以当x=32时，y1=y2；当x<32时，y1>y2；当x>32时，y1<y2.（2）y1与y2的图像如答图所示．通过图像，也能得出（1）中相同的答案．2．解析：（1）当x<1500km时，租出租公司的车合算．（2）当x=1500km时，租两家的费用相同．（3）当x>2300km时，对应的y1在y2的下方，所以租个体车主的车合算．3．解析：y1=6000+（1-25%）×6000（x-1），化简得y1=4500x+1500．y1=（1-20%）6000x，化简，得y2=4800x．（1）当y1<y2时，4500x+1500<4800x，即300x<1500，x>5，•所以当所买电脑台数大于5时，甲商场更优惠．（2）当y2<y1时，4800x<4500x+1500，即300x<1500，x<5，•所以当所买电脑台数小于5台时，乙商场更优惠．（3）当y1=y2时，4500x+1500=4800x，即300x=1500，x=5，当购买5台时，两家商场收费相同．探究应用拓展性训练1．解析：设甲公司的总费用为y1元，乙公司的总费用y2元．制作材料x份，则y1=3000+20x，y2=30x．（1）当y1<y2时，3000+20x<30x，10x>3000，x>300．当制作的材料大于300份时，•选甲公司合算．（2）当y2<y1时，30x<3000+20x，10x<3000，x<300．当制作的材料小于300份时，•选乙公司合算．（3）当y2=y1时，3000+20x=30x，10x=3000，x=300，当制作的材料等于300份时，•两家公司收费相同．2．解析：（1）设y=kx+b，由图像可看出图像经过（10，50），（50，150）两点，∴1050,50150,k bk b+=⎧⎨+=⎩解得5,225.kb⎧=⎪⎨⎪=⎩∴y=52x+25．（2）水箱中的水超过100L，即y>100，∴52x+25>100，52x>75，x>30．当进水时间多于30min后，水箱中的水量超过100L．3．解析：（1）设小明的存款为y1，从现在开始的月份数为x，则y1=12x+50．（2）设小丽的存款数为y2，则y2=18x．图像略．当x=6时，y1=12×6+50=72+50=122，y2=18×6=108．因108<122，所以半年后小丽的存款为108元，不能超过小明．当y2>y1时，18x>12x+50，x>813,∴至少9个月后小丽的存款数超过小明．4．解析：（1）y1=1．2x，y2=x+800．（2）当y2<y1时，x+800<1．2x，0．2x>800，x>4000．所以当汽车行驶路程多于4000km 时，租用乙公司的汽车合算．5．解析：设学校餐厅计划购买x把椅子，在甲商场购买的总费用为y1元，•在乙商场购买的总费用为y2元，则y1=200×12+50（x-12），即y1=50x+1800．当y1<y2时，50x+1800<852x+2040，152x<240，x<32．所以当购买的椅子把数小于32时，甲商场更优惠．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一次函数与不等式应用题【例题经典】例1 （2006年武汉市）某公司以每吨200元的价格购进某种矿石原料300吨，用于生产甲、乙两种产品，生产1吨甲产品或1 吨乙产品所需该矿石和煤原料的吨数如下表．甲乙矿石（吨）104煤（吨）48煤的价格为400元/吨，生产1吨甲产品除原料费用外，还需其他费用400元， 甲产品每吨售价4600元；生产1吨乙产品除原料费用外，还需其他费用500元， 乙产品每吨售价5500元，现将该矿石原料全部用完，设生产甲产品x 吨，乙产品m 吨，公司获得的总利润为y 元．（1）写出m 与x 之间的关系式；（2）写出y 与x 的函数表达式（不要求写自变量的范围）；（3）若用煤不超过200吨，生产甲产品多少吨时，公司获得的总利润最大？ 最大利润是多少？【点评】主要考查的是一次函数与不等式的实际应用．例2 （2006年黄冈市）我市英山县某茶厂种植“春蕊牌”绿茶，由历年来市场销售行情知道，从每年的3月25日起的180天内，绿花市场销售单价y （元） 与上市时间t （天）的关系可以近似地用如图（1）中的一条折线表示．绿茶的种植除了与气候、 种植技术有关外，某种植的成本单价z （元）与上市时间t （天）的关系可以近似地用如图（2）的抛物线表示．（1）直接写出图（1）中表示的市场销售单价y （元）与上市时间t （天）（t>0） 的函数关系式；（2）求出图（2）中表示的种植成本单价z （元）与上市时间t （天）（t>0） 的函数关系式；（3）认定市场销售单价减去种植成本单价为纯收益单价，问何时上市的绿茶纯收益单价最大？（说明：市场销售单价和种植成本单价的单位：元/500克．）【点评】主要考查同学们从两个图像中获取信息的能力．【考点精练】1．（2006年广安市）某电信公司开设了甲、乙两种市内移动通信业务． 甲种使用者每月需缴15元月租费，然后每通话1分钟，再付话费0.3元；乙种使用者不缴月租费，每通话1分钟，付话费0.6元．若一个月内通话时间为x 分钟，甲、 乙两种的费用分别为y 1和y 2元．（1）试分别写出y 1、y 2与x 之间的函数关系式； （2）在同一坐标系中画出y 1，y 2的图像；（3）根据一个月通话时间，你认为选用哪种通信业务更优惠？2．为了鼓励小强勤做家务，培养他的劳动意识，小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的． 若设小强每月的家务劳动时间为x 小时，该月可得（即下月他可获得）的总费为y 元，则y （元）和x （小时）之间的函数图像如图所示．（1）根据图像，请你写出小强每月的基本生活费为多少元； 父母是如何奖励小强家务劳动的？（2）写出当0≤x≤20时，相对应的y 与x 之间的函数关系式；（3）若小强5月份希望有250元费用，则小强4月份需做家务多少时间？3．（2006年泸州市）“五一黄金周”的某一天，小刚全家上午8时自驾小汽车从家里出发，到距离180千米的某著名旅游景点游玩，该小汽车离家的距离S （千米）与时间t （时）的关系可以用下图的折线表示，根据图像提供的有关信息，解答下列问题： （1）小刚全家在旅游景点游玩了多少小时？（2）求出返程途中S （千米）与时间t （时）的函数关系式，并求出自变量t 的取值范围．4．随着大陆惠及台胞政策措施的落实，台湾水果进入了大陆市场．一水果经销商购A 、B 两种台湾水果各10箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店） 销售．预计每种水果的盈利情况如下表：A 种水果/箱B 种水果/箱甲店 11元 17元乙店 9元 13元有两种配货方案（整箱配货）：方案一：甲、乙两店各配货10箱，其中A 种水果两店各5箱，B 种水果两店各5箱．方案二： 按照甲、 乙两店盈利相同配货， 其中A 种水果甲店______ 箱， 乙店______箱，B 种水果甲店_______，乙店_______箱．（1）如果按照方案一配货，请你计算出经销商盈利多少元； （2）请你将方案二填写完整（只填写一种情况即可），并根据你填写的方案二与方案一作比哪种方案盈利较多？（3）在甲、乙两店各配货10箱，且保证乙店盈利不小于100元的条件下，请你设计出经销商盈利最大的配货方案，并求出最大盈利为多少？5．（2006年芜湖市）某种内燃动力机车在青藏铁路试验运行前， 测得该种机械效率η和海拔高度h（0≤h≤6.5，单位km）的函数关系式如图所示．（1）请你根据图象写出机车的机械效率η和海拔高度h（km）的函数关系；（2）求在海拔3km的高度运行时，该机车的机械效率为多少？6．（2006年遂宁市）有一种笔记本原售价为每本8元，甲市场用如下办法促销， 每次购买1～8本打九折，9～16本打八五折，17～25本打八折，超过25本打七五折．乙商场用如下办法促销：购买本数（本）1~56~1011~15超过15每本价格（元）7.607.20 6.40 6.00（1）请仿照乙商场的促销列表，列出甲商场促销笔记本的购买本数与每本价格的对照表．（2）某学校有A、B两个班都需要买这种笔记本，A班需要8本，B班需要15本， 问他们到哪家商场购买花钱较少？（3）设某班需要购买这种笔记本本数为x且9≤x≤40，总花费为y元， 从最省钱的角度出发，写出y与x的函数关系式．7．某校部分住校生，放学后到学校锅炉房打水，每人接水2升，他们先同时打开两个放水笼头，后来因故障关闭一个放水笼头．假设前后两人接水间隔时间忽略不计， 且不发生泼洒，锅炉内的余水量y （升）与接水时间x （分）的函数图象如图． 请结合图像，回答下列问题：（1）根据图中信息，请你写出一个结论； （2）问前15位同学接水结束共需要几分钟？（3）小敏说：“今天我们寝室的8位同学去锅炉房连续接完水恰好用了3分钟．”你说可能吗？请说明理由．8．（2006年泉州市）为实现泉州市森林城市建设的目标， 在今年春季的绿化工作中，绿化办计划为某住宅小区购买并种植400株树苗．某树苗公司提供如下信息：信息一：可供选择的树苗有杨树，丁香树，柳树三种，并且要求购买杨树， 丁香树的数量相等．信息二：如下表：树 苗每株树亩批发价格（元）两年后每株树苗对空气的净化指数杨 树 3 0.4丁香树 2 0.1柳 树 P 0.2设购买杨树，柳树分别为x 株，y 株．（1）写出y 与x 之间的函数关系式（不要求写出自变量的取值范围）；（2）当每株柳树的批发价P 等于3元时，要使这400 株树苗两年后对该住宅小区的空气净化指数不低于90，应怎样安排这三种树苗的购买数量，才能使购买树苗的总费用最低？最低的总费用是多少元；（3）当每株柳树批发价格P （元）与购买数量y （株）之间存在关系．P=3-0.005y 时， 求购买树苗的总费用W （元）与购买杨树数量x （株）之间的函数关系式（ 不要求写出自变量的取值范围）．答案:例题经典例1：解：（1）m=300104x-（2）生产1吨甲产品获利：4600-10 ×200-4×400-400=600；生产1吨乙产品获利：5500-4×200-8×400-500=1000，∴y与x 的函数表示式为：y=600x+1000×300104x-=-1900x+75000；（3）∵4x+8×300104x-≤200，∴30≥x≥25，∴当生产甲产品25吨时，公司获得的总利润最大，y最大=-1900×25+75000=27500（元）．例2：解：（1）依题意，可建立的函数关系式为：y=2160(0120), 380(120150),220(150180). 5t ttt t⎧-+<<⎪⎪≤<⎨⎪⎪+≤≤⎩（2）由题目已知条件可设z=a（t-110）2+20，∵图像过点（60，853），∴853=a（60-110）2+20，∴a=1300，∴z=1300（t-110）2+20（t>0）．（3）设纯收益单价为W元，则W=销售单价-成本单价．故W=22221160(100)20(0120), 3300180(110)20(120150),3002120(110)20(150180). 5300t t tt tt t t⎧-+---<<⎪⎪⎪---≤<⎨⎪⎪+---≤≤⎪⎩化简得W=2221(10)100(0120),3001(110)60(120150), 3001(170)56(150180).300t tt tt t⎧--+<<⎪⎪⎪--+≤<⎨⎪⎪--+≤≤⎪⎩，①当W=-1300（t-10）2+100（0<t<120）时，有t=10时，W最大，最大值为100；②当W=-1300（t-110）2+60（120≤t<150）时， 由图象知， 有t=120时，W最大，最大值为5923；③当W=-1300（t-170）2+56（150≤t≤180）时，有t=170时，W最大，最大值为56．综上所述，在t=10时，纯收益单价有最大值，最大值为100元．考点精练：1．分析：在解决问题（3）时，因一个月通话时间没有确定， 而两种通信业务的费用都与通话时间有关，因此需要进行讨论，可观察图象得出结论，也可按①y1>y2，②y1=y2，③y1<y2进行求解．解：（1）y1=15+0.3x（x≥0），y2=0.6x（x≥0）（2）如图（3） 由图知：当一个月通话时间为50分钟时，两种业务一样优惠；当一个月通话时间少于50分钟时，乙种业务更优惠；当一个月通话时间大于50分钟时，甲种业务更优惠．2．（1）小强每月生活费为150元，当家务劳动时间每月不超过20小时/月时，每小时有2.5元的报酬，即y=2.5x+150（0≤x≤20），当家务劳动时间超过20小时/月时，超过部分每小时4元报酬，即y=4x+120（x≥20）（2）y=2.5x+150（0≤x≤20）（3）250>200， ∴y=4x+120，250=4x+120，x=32.5，即小强4月份做家务32.5小时．3．（1）游玩了4 个小时（2）S=-60t+1020（14≤t≤17）4．（1）按照方案一配货，经销商盈利：5×11+5×9+ 5×17+5×13=250（元）（2）只要求填写一种情况：第一种情况：2，8，6，4；第二种情况：5，5，4，6；第三种情况：8，2，2，8．按第一种情况盈利：（2×11+17×6）×2=248（元）；按第二种情况盈利：（5×11+4×17）×2=246（元）；按第三种情况盈利：（8×11+2×17）×2=244（元）；方案一比方案二盈利多（3）设甲店配A种水果x箱，则甲店配B 种水果（10-x ）箱，乙店配A 种水果（10-x ）箱，乙店配B 种水果10-（10-x ）=x 箱，∵9×（10- x） +13x≥100，∴x≥212．经销商盈利y=11x+17×（10-x ）+9×（10-x ）+13x=-2x+260．当x= 3时，y 值最大．方案：甲店配A 种水果3箱，B 种水果7箱．乙店配A 种水果7箱，B 种水果3箱时盈利最大，最大盈利为-2×3+260=254（元）5．解：（1）由图象可知，η与h 的函数关系为一次函数，设η=kh+b（k≠0），∵一次函数图象过（0，40%），（5，20%）两点，∴40%,20%5.b k b =⎧⎨=+⎩解得：k=-0.04，b=0.4，∴η=-0.04h+0．4（0≤h≤6.5）（2）当h=3km 时，代入η=-0.04h+0.4，解得η=0.28．∴当机车运行在海拔高度为3km 的时候，其机车的运行效率为28%． 6．（1） 甲购买本数（本）1-89-1617-25超过25本每本价格（元）7.2 6.8 6.4 6（2）A 两商场一样 B 到乙商场花钱较少（3）甲商场：y= 6.8(916),7.2(916),6.4(1725),: 6.4(1115),6(2540).6(1640).x x x x x x y x x x x x x ≤≤≤≤⎧⎧⎪⎪≤≤=≤≤⎨⎨⎪⎪<≤≤≤⎩⎩乙乙乙7．解：（1） 锅炉内原有水96升，接水2分钟后，锅炉内的余水量为80升，接水4分钟，锅炉内的余水量为72升；2分钟前的水流量为每分钟8升等．（2）当0≤x≤2时， 设函数解析式为y=k 1x+b 1，把x=0，y=96和x=2，y=80代入得：1111196,8,280,96.b k k b b ==-⎧⎧⎨⎨+==⎩⎩乙乙，∴y=-8x+96（0≤x≤2），当x>2时，设函数解析式为y=k 2x+b 2，把x=2，y=80和x=4，y=72代入得：222222802,4,724,88.k b k k b b =+=-⎧⎧⎨⎨=+=⎩⎩乙乙，∴y=-4x+88（x>2）．∵前15位同学接完水时余水量为96-15×2=66（升），∴66=-4x+88，x=5.5．答：前15 位同学接完水需5.5分钟．（3）①若小敏他们是一开始接水的，则接水时间为8×2÷8=2（分），即8位同学接完水，只需要2分钟，与接水时间恰好3分钟不符．②若小敏他们是在若干位同学接完水后开始接水的，设8位同学从t分钟开始接水，挡0<t≤2时，则8（2-t）+4[3-（2-t）]=8×2，16-8t+4+4t=16，∴t=1（分），∴（2-t）+[3-（2-t）]=3（分），符合．当t>2时，则8×2÷4=4（W发），即8位同学接完水，需7分钟，与接水时间恰好3分钟不符．所以小敏说法是可能的．即从1分钟开始8位同学连续接完水恰好用了3分钟8．（ 1）y=400-2x（2）当购买200株杨树，200株丁香树，不购买柳树苗时，能使购买费用最低，最低总费用为1000元（3）W=3x+2x+p·y，即W=-0.02x2+7x+400．。