电工基础课件——第十讲 叠加定理及应用
合集下载
叠加定理课件教学内容

4V电压源发出的功率: P431W 2
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
叠加定理课件
Chapter 2
对n个独立电源的线性电路,响应:
ft pkiusi
q
kjisj
i1
j1
其中: p + q = n
ki、kj 均为常数
叠加原理:在线性电路中,任一时刻,任一处的响应等 于各独立源单独作用时,在该处响应的叠加。
Chapter 2
使用叠加定理时应注意: 1.叠加定理只适用于线性电路。 2.叠加定理包含了“加性”和“齐性”两重含义。
4Ω
1Ω 2A
4Ω
4Ω
图b
图c
6A单独作用(如图b):
I 4 68 44/4 /21 3
2A单独作用(如图c):
I 1 22 14/4 /42 9
叠加: IIII282 2.2 2 339
Chapter 2
例 用叠加原理求4V电压源发出的功率 。
解:用叠加原理求电流 I 。
3V电源单独作用:
Ix 2Ω
I 2Ω
4V
I x I y
I′
3V
2IxБайду номын сангаас
2Ω 2Ω
I x 3 A Iy2Ix 3A
3V
2 I x
2
22
I Ix Iy 3 A
Chapter 2
4V电源单独作用:
Ix 4 2A 2
Iy2Ix44A 2
I x I y
I″
2Ω 2Ω
4V 2 I x
I Ix Iy 6 A
叠加: I I I 3 6 3 A
Chapter 2
叠加原理PPT课件

14
-
小试牛刀
1、叠加原理只适用于_线_性_电路,而且叠加原理只能来 计算电路中的_电_压_和_电_流__,不能直接用于计算_电_功__率_。
2、如图所示电路中,已知E1 单独作用时,R1、R2、R3的
电流分别是-4A、2A、-2A, E2 单独作用时,R1、R2、R3的
电流分别是3A、2A、5A,则
1、叠加原理只适用于线性电路。
2、计算某一独立电源单独作用时,应将电路中其他 独立恒压 源视为短路,独立恒流源视为开路,所有独立电源的内阻保 持不变。
3、进行叠加时,注意各分量参考方向与总量的参考方向是否一 致,一致则叠加时取正,否则取负。
4、线性电路中,功率P不能用叠加原理计算,因为P=I2R、 P=U2/R不是线性关系
叠加原理
科目:电工基础 作课人:毛东建 部系:电气工程事业部
1
-
部分电路欧姆定律
(一)部分电路欧姆定律定律:
导体中的电流与导体两端的电压成正比,与 导体的电阻成反比。
即ΣI=0
2
-
(二)回路电压定律:
在任一回路中,各段电路电压降的代数和恒 等于零。
即ΣE= ΣIR或ΣE- ΣIR=0
3
-
戴维南定理
各支路电流I1=__-1_A,I2=__4_A
I3=__5_A.
15
-
归纳总结与作业
通过本课题学习,重点掌握以下内容: 1、叠加定理解题的一般步骤。 2、相关注意事项
作业:练习册第二题(包括1、2两道计算题)
16
-
17
-
注:独立源单独作用是指当某一独立源起作用 时,其他独立源都不起作用,即独立恒压源用 短路代替,独立恒流源用开路代替。
叠加定理PPT课件

用叠加定理求电流I;
求电阻R 4 上消耗的功率。10-2(a)所示:R 34 =R 3 ∥R 4 =10∥10=5Ω,I′= 3 + 4 ·
1
2 + 34 + 1
1
5
· =2×5+5+5×3=0.5A。
当 单独作用时,如图2-10-2(b)所示:R 12 =R 1 +R 2 =10Ω,R=R 12 ∥R 4 =10∥10=5Ω,
在使用叠加定理分析计算电路应注意以下几点:
叠加定理只能用于计算线性电路(即电路中的元件均为线性元件)的支路电流或电压(不能
直接进行功率的叠加计算);
电压源不作用时应视为短路,电流源不作用时应视为开路;
叠加时要注意电流或电压的参考方向,正确选取各分量的正负号。
知识点精讲
如图2-10-1所示电路, =30V, =3A,R 1 =R 2 =5Ω,R 3 =R 4 =10Ω。
直流电路
考纲解读
一、最新考纲要求
1.理解叠加定理的内容;
2.掌握叠加定理的应用。
二、考点解读
必考点:叠加定理的内容及应用。
重难点:叠加定理的内容、应用与计算。
知识清单
叠加定理表述为:
当线性电路中有几个电源共同作用时,各支路的电流(或电压)等于各个电源分别单独作用
时在该支路产生的电流(或电压)的代数和(叠加)。
如图2-10-5所示电路, 1 =10V, 2 =15V,当开关S置于位置1时,毫安表的读数I 1 =40mA;当
开关S置于位置2时,毫安表的读数I 2 =-60mA。若把开关S置于位置3,则毫安表的读数为多少?
【答案】应用叠加定理。
开关置于位置1时,相当于 单独作用,I 1 =40mA,如图2-10-6所示。
求电阻R 4 上消耗的功率。10-2(a)所示:R 34 =R 3 ∥R 4 =10∥10=5Ω,I′= 3 + 4 ·
1
2 + 34 + 1
1
5
· =2×5+5+5×3=0.5A。
当 单独作用时,如图2-10-2(b)所示:R 12 =R 1 +R 2 =10Ω,R=R 12 ∥R 4 =10∥10=5Ω,
在使用叠加定理分析计算电路应注意以下几点:
叠加定理只能用于计算线性电路(即电路中的元件均为线性元件)的支路电流或电压(不能
直接进行功率的叠加计算);
电压源不作用时应视为短路,电流源不作用时应视为开路;
叠加时要注意电流或电压的参考方向,正确选取各分量的正负号。
知识点精讲
如图2-10-1所示电路, =30V, =3A,R 1 =R 2 =5Ω,R 3 =R 4 =10Ω。
直流电路
考纲解读
一、最新考纲要求
1.理解叠加定理的内容;
2.掌握叠加定理的应用。
二、考点解读
必考点:叠加定理的内容及应用。
重难点:叠加定理的内容、应用与计算。
知识清单
叠加定理表述为:
当线性电路中有几个电源共同作用时,各支路的电流(或电压)等于各个电源分别单独作用
时在该支路产生的电流(或电压)的代数和(叠加)。
如图2-10-5所示电路, 1 =10V, 2 =15V,当开关S置于位置1时,毫安表的读数I 1 =40mA;当
开关S置于位置2时,毫安表的读数I 2 =-60mA。若把开关S置于位置3,则毫安表的读数为多少?
【答案】应用叠加定理。
开关置于位置1时,相当于 单独作用,I 1 =40mA,如图2-10-6所示。
叠加原理.ppt

+
++
I2'
U–S
E –
R1
R3 US'
–
R2
I2
+
R1
R3 IS U–S
(a)
(b) E单独作用
(c) IS单独作用
解:由图(c)
I
2
U
S
R3
RI22
R3
R2
5 IS 5 5
0.5 5
1 0.5A
2.5V
I2
I
2
I
2
1
0.5
0.5A
US
U
S
U
S
5
2.5
7.5V
B
根据叠加原理,I2 = I2´ + I2
解: I2´= I2"=
?1A ?–1A
I2 = I2´ + I2 =
0A
【例题讲解】 I= ? 用叠加原理求:
10 4A
10
10
-
I
20V
+
“恒流源失效” 即令其开路。
解:
10
原电路=
10 10
I´
+
10 10
I"
4A
I'=2A
I"= -1A
I = I'+ I"= 1A
【 重点与难点 】
叠加定理中对不工作电源的处理: 电流源不工作,相当于开路 电压源不工作,相当于短路
例1:电路如图,已知 E =10V、IS=1A ,R1=10 R2= R3= 5 ,试用叠加原理求流过 R2的电流 I2 和理想电流源 IS 两端的电压 US。
叠加定理课件

方法(四) 可直接抓住触电者干燥而不贴身的衣服拖离带电
体,但要注意此时不能碰到金属物体和触电者裸露的身躯。
对体弱者和儿童吹气时用力 应稍轻,以免肺泡破裂。 如触电者牙关紧闭,无 法撬开,可采取口对鼻 吹气的方法。
将触电者头部尽量后仰,鼻孔 朝天,颈部伸直。救护人一只 先使触电者仰卧,解开衣领、围巾、 手捏紧触电者的鼻孔,另一只 紧身衣服等,除去口腔中的粘液、 手掰开触电者的嘴巴。救护人 血液、食物、假牙等杂物。 深吸气后,紧贴着触电者的嘴 巴大口吹气,使其胸部膨胀; 之后救护人换气,放松触电者 的嘴鼻,使其自动呼气。如此 反复进行,吹气2秒,放松3秒, 大约5秒钟一个循环。
吹气时要捏紧鼻孔,紧贴嘴巴,不使 漏气,放松时应 能使触电者自动呼 气。其操作示意如图a∽图d所示。
帮助触电者恢复心跳的有效方法。操作要领如图a∽图d所示。
电气设备外壳有保护接地 时通过人体的电流:
Ib Ie
R0 Rb与Ro并联,地装置的分流
作用来减少通过人体 的电流。
所以通过人体的电流可减小到安 全值以内。
保护接零(用于 380V / 220V 三相四线制系统)
当电气设备绝缘损坏造成 一相碰壳,该相电源短路,其 短路电流使保护设备动作,将 故障设备从电源切除,防止人 身触电。
把电源碰壳,变成单相短路,使保护设备能迅速可靠 地动作,切断电源。
方法(一) 如果开关或插头在附近,应立即拉闸刀开关或拨去电 源插头,不能直接拉触电者。
方法(二) 可用竹竿、木棒等绝缘物挑开电线,也可戴上绝 缘手套或用干燥的衣物包在手上,再使触电者脱离带电体。
方法(三) 可站在绝缘垫或干燥的木板上,使触电者脱离带电 体(此时尽量用一只手进行操作。
XXX
叠加定理PPT
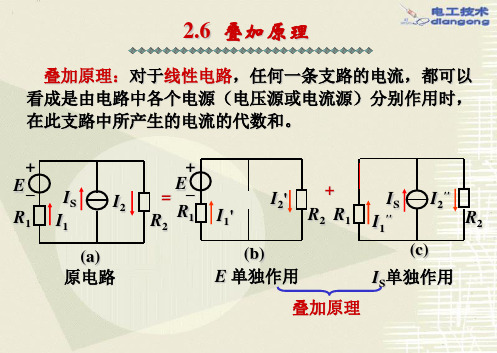
列方程:
I1 IS I2
E I1R1 I2 R2
解方程得:
I1
R1
E R2
R2 R1 R2
IS
I1'
I1''
E I2 R1 R2
R1 R1 R2
IS
I2'
I2''
注意事项:
① 叠加原理只适用于线性电路。
② 线性电路的电流或电压均可用叠加原理计算,
但功率P不能用叠加原理计算。例:
P1
I2 1
R1
(
I
1
I
1
)2
R1
I12 R1
I
1
R2 1
③ 不作用电源的处理:
E = 0,即将E 短路; Is=0,即将 Is 开路 。
④ 解题时要标明各支路电流、电压的参考方向。 若分电流、分电压与原电路中电流、电压的参考方 向相反时,叠加时相应项前要带负号。
⑤ 应用叠加原理时可把电源分组求解 ,即每个分电路 中的电源个数可以多于一个。
(c) IS单独作用
将 IS 断开
将 E 短接
解:由图( b)
I2
E R2 R3
10 A 1A 55
US I2 R2 1 5V 5V
例1:电路如图,已知 E =10V、IS=1A ,R1=10 R2= R3= 5 ,试用叠加原理求流过 R2的电流 I2 和理想电流源 IS 两端的电压 US。
叠加原理
R1 I1
+ E1
R2 I2
+ E2
R3
I3
E1和E2共同作用时,求得电流及方向如图所示
R1 I1
R2 I2 + E2
电工技术叠加定理解题步骤 ppt课件

I144641.6A
U1 446649.6V
一、叠加定理的应用
(3)求代数和
Us= Us' +Us"= -6+25.6=19.6V
电工技术叠加定理解题步骤
内容:在线性电路中,当所有激励都增大或缩小k倍(k为实常数)时,其 响应(支路电流或电压)也将同样增大或缩小k倍。
意义: 反映线性电路的齐次性(比例性) 注意: 1)激励是指独立电源;
I 故,各支路电流也增加到原来的3.63倍,即:
1
I2
k
I
' 1
k
I
' 2
4 .7 6 A 7 .6 2 A
I3
k
I
' 3
3 .9 9
A
I4
k
I
' 4
3 .6 3 A
I1 6 +10 I1–
例2:(1)画如出分图电电路图路,求10V电+– 压Us4。
+ Us 4A
–
解: 10V电压源单独作用:
4A电流源单独作用:
一、叠加定理的应用
(2)对各分电路进行求解
U'S1I01U'
I1
10 64
1A
Us'= -10 I1'+U1’= -10 I1'+4I1'
= -101+41= -6V
递推法
二、齐次定理
•设I递4' 1推A 法
UB' D22V
I3' 1.1A
若给定电压为120V,这相
当于电压增加到原来的
3.63倍 (k 120 3.63) 33.02
电路原理-叠加定理

THANKS FOR WATCHING
感谢您的观看
对数运算的叠加定理
总结词
对数运算的叠加定理是指当多个同底数的对 数相加或相减时,其结果等于将这些对数分 别代入公式后相加或相减的结果。
详细描述
对数运算的叠加定理是电路原理中非常重要 的概念,它描述了多个电压或电流源作用于 电路时,其效果等于这些源分别作用于电路 所产生的效果的叠加。这个定理在分析复杂 电路时非常有用,因为它可以将多个源的效 应分解为单个源的效应,从而简化分析过程。
对时间的叠加定理
总结词
对时间的叠加定理是指当多个信号同时作用于电路时 ,其输出信号的时间响应等于这些信号分别作用于电 路所产生的输出信号的时间响应的叠加。
详细描述
在电路原理中,对时间的叠加定理描述了多个信号同 时作用于电路时,其输出信号的时间响应如何计算。 这个定理指出,如果多个信号同时作用于电路,那么 其总的时间响应可以通过将每个信号单独作用于电路 所产生的响应叠加起来得到。这个定理在分析时域电 路行为时非常有用,因为它可以帮助我们理解多个信 号如何共同影响电路的输出。
04
叠加定理的证明
数学推导
线性电路元件的电压和电流关系可以用线性方程表示,即 $i_1 = a_1v + b_1i$ 和 $i_2 = a_2v + b_2i$。
根据线性电路的性质,当有两个独立电源同时作用于线性电路时,线性电路元件的 电压和电流等于每个电源单独作用于该元件时的电压和电流之和。
通过数学推导,可以证明叠加定理在电路分析中的正确性。
理解电路的基本原理
通过叠加定理,可以深入理解电路中各个元件的工作原理以及它们之间的相互 作用关系,对于理解电路的基本原理和设计复杂的电路系统具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
= [8cos(ω t) + 3sin( 2ω t)]V
例2 用叠加定理求图 (a)电路中电压u。
解 : 画 出 独 立 电 压 源 uS 和 独 立 电 流 源 iS 单 独 作 用 的 电 路 , 如 图 ( b) 和 ( c) 所 示 。 由 此 分 别 求 得 u’ 和 u”, 然 后 根 据 叠 加定理将u’和u”相加得到电压u
第一项i1 和u2是该电路在独立电流源开路(iS=0)时,由
独立电压源单独作用所产生的i1和u2。
第二项i1和u2是该电路在独立电压源短路(uS=0)时,
由独立电流源单独作用所产生的i1和u2。
以上叙述表明,由几个独立电源共同产生的各支路电 流或电压响应,等于每个独立电源单独作用所产生各支路 电流或电压响应之和。线性电路的这种叠加性称为叠加定 理。
一、叠加定理
3.4 叠加定理及应用
叠加定理是线性网络的基本定 理。现以图(a)所示两个独立电 源共同作用的线性电路为例加 以说明。
列出图(a)电路的网孔方程:
(R + R )i + R i = u
12123源自Si =i3
S
(R + R )i + R i = u
1
21
23
S
i3 = iS
求解上式可得到电阻R1的电流i1和电阻R2上电压u2
例1 电路如图所示。若已知:
(1) uS1 = 5V, uS2 = 10V (2) uS1 = 10V, uS2 = 5V
(3) uS1 = 20 cos tV, uS2 = 15sin 2 t V
试用叠加定理计算电压u 。
解:①画出uS1和uS2单独作用的电路,如图(b)和(c)所示,分别求出:
u'
=
R4 R2 + R4
uS
u"
=
R2 R4 R2 + R4
iS
u
= u'
+u"
=
R4 R2 + R4
(uS
+ R2iS )
二、叠加定理的应用
应用叠加定理时注意的问题: 1、叠加定理只适用于线性电路,不适用于非线性电
路。 2、叠加时,电路的联接方式以及电路中的有电阻和
受控源都不能变动。电压源不作用以短路代替;电 流源不作用以开路代替。 3、叠加时要注意电流和电压的参考方向,即各个电 源单独作用时产生的分电流或分电压的参考方向, 与电路中全部电源共同作用时对应的电流或电压的 参考方向相同时取正号,反之取负号。 4、叠加定理不能用于计算功率。
u = u ' + u" = 0.4uS1 + 0.2uS2
③代入uS1和uS2数据,分别得到:
(1) u = 0.4 5V + 0.210V = 4V (2) u = 0.410V + 0.2 5V = 5V (3) u = [0.4 20 cos(ω t) + 0.215sin( 2ω t)]V
i1
=
R1
1 +
R2
uS
+
- R2 R1 + R2
iS
=
i1'
+ i1"
其中:
i1'
= i1
iS =0
=
R1
1 + R2
uS
i1"
= i1 uS =0
=
- R2 R1 + R2
iS
电流i1的叠加
i1
=
R1
1 + R2
uS
+
- R2 R1 + R2
iS
= i1' + i1"
i1'
=
i1
iS =0
=
R1
2
u'
==
3 1+ 2
u S1
=
0.4u S1
3
u"
==
0.5 2 + 0.5 u S 2
= 0.2u S 2
(1) uS1 = 5V, uS2 = 10V (2) uS1 = 10V, uS2 = 5V
(3) uS1 = 20 cos( t)V, uS2 = 15sin( 2 t) V
②根据叠加定理:
1 + R2
uS
+ i1"
= i1 uS =0
=
- R2 R1 + R2
iS
电压u2的叠加
u2
=
R2 R1 + R2
uS
+
R1R2 R1 + R2
iS
= u2' + u2"
+ u2'
=
u2
iS =0
=
R2 R1 + R2
uS
u2"
=
u2
uS =0
=
R1R2 R1 + R2
iS
从上可见:电流i1和电压u2均由两项相加而成。
例2 用叠加定理求图 (a)电路中电压u。
解 : 画 出 独 立 电 压 源 uS 和 独 立 电 流 源 iS 单 独 作 用 的 电 路 , 如 图 ( b) 和 ( c) 所 示 。 由 此 分 别 求 得 u’ 和 u”, 然 后 根 据 叠 加定理将u’和u”相加得到电压u
第一项i1 和u2是该电路在独立电流源开路(iS=0)时,由
独立电压源单独作用所产生的i1和u2。
第二项i1和u2是该电路在独立电压源短路(uS=0)时,
由独立电流源单独作用所产生的i1和u2。
以上叙述表明,由几个独立电源共同产生的各支路电 流或电压响应,等于每个独立电源单独作用所产生各支路 电流或电压响应之和。线性电路的这种叠加性称为叠加定 理。
一、叠加定理
3.4 叠加定理及应用
叠加定理是线性网络的基本定 理。现以图(a)所示两个独立电 源共同作用的线性电路为例加 以说明。
列出图(a)电路的网孔方程:
(R + R )i + R i = u
12123源自Si =i3
S
(R + R )i + R i = u
1
21
23
S
i3 = iS
求解上式可得到电阻R1的电流i1和电阻R2上电压u2
例1 电路如图所示。若已知:
(1) uS1 = 5V, uS2 = 10V (2) uS1 = 10V, uS2 = 5V
(3) uS1 = 20 cos tV, uS2 = 15sin 2 t V
试用叠加定理计算电压u 。
解:①画出uS1和uS2单独作用的电路,如图(b)和(c)所示,分别求出:
u'
=
R4 R2 + R4
uS
u"
=
R2 R4 R2 + R4
iS
u
= u'
+u"
=
R4 R2 + R4
(uS
+ R2iS )
二、叠加定理的应用
应用叠加定理时注意的问题: 1、叠加定理只适用于线性电路,不适用于非线性电
路。 2、叠加时,电路的联接方式以及电路中的有电阻和
受控源都不能变动。电压源不作用以短路代替;电 流源不作用以开路代替。 3、叠加时要注意电流和电压的参考方向,即各个电 源单独作用时产生的分电流或分电压的参考方向, 与电路中全部电源共同作用时对应的电流或电压的 参考方向相同时取正号,反之取负号。 4、叠加定理不能用于计算功率。
u = u ' + u" = 0.4uS1 + 0.2uS2
③代入uS1和uS2数据,分别得到:
(1) u = 0.4 5V + 0.210V = 4V (2) u = 0.410V + 0.2 5V = 5V (3) u = [0.4 20 cos(ω t) + 0.215sin( 2ω t)]V
i1
=
R1
1 +
R2
uS
+
- R2 R1 + R2
iS
=
i1'
+ i1"
其中:
i1'
= i1
iS =0
=
R1
1 + R2
uS
i1"
= i1 uS =0
=
- R2 R1 + R2
iS
电流i1的叠加
i1
=
R1
1 + R2
uS
+
- R2 R1 + R2
iS
= i1' + i1"
i1'
=
i1
iS =0
=
R1
2
u'
==
3 1+ 2
u S1
=
0.4u S1
3
u"
==
0.5 2 + 0.5 u S 2
= 0.2u S 2
(1) uS1 = 5V, uS2 = 10V (2) uS1 = 10V, uS2 = 5V
(3) uS1 = 20 cos( t)V, uS2 = 15sin( 2 t) V
②根据叠加定理:
1 + R2
uS
+ i1"
= i1 uS =0
=
- R2 R1 + R2
iS
电压u2的叠加
u2
=
R2 R1 + R2
uS
+
R1R2 R1 + R2
iS
= u2' + u2"
+ u2'
=
u2
iS =0
=
R2 R1 + R2
uS
u2"
=
u2
uS =0
=
R1R2 R1 + R2
iS
从上可见:电流i1和电压u2均由两项相加而成。
