第一章计数原理小结
计数原理知识点

计数原理知识点1. 什么是计数原理?计数原理是指在数字系统中,通过一组逻辑电路和时钟信号来完成对输入信号的计数功能。
计数原理在数字电路、计算机科学和通信工程等领域中被广泛应用。
2. 二进制计数在计数原理中,最基本的计数方式是二进制计数。
二进制计数是一种以2为基数的计数系统,只包含两个数字0和1。
它是现代计算机系统中最基本的计数方式,因为计算机内部的数字电路使用的是二进制编码。
在二进制计数中,每一位的权值为2的幂。
例如,一个3位的二进制数可以表示的最大值是7,是因为:2^0 * 1 + 2^1 * 1 + 2^2 * 1 = 1 + 2 + 4 = 73. 计数器计数器是实现计数功能的重要组件。
它是一种时序电路,可以根据时钟信号来逐步改变输出状态,以实现计数的目的。
计数器有多种类型,其中最简单的是二进制计数器,它可以按照二进制方式计数。
除此之外,还有BCD计数器、同步计数器、触发器计数器等等。
4. 硬件计数器硬件计数器是一种专门的数字电路,用于实现计数功能。
它由触发器和逻辑门构成,可以根据时钟信号和输入信号来进行计数操作。
硬件计数器通常由多个触发器级联而成,每个触发器代表一位的计数。
例如,一个4位的硬件计数器可以用4个触发器来表示。
硬件计数器可以实现正向计数和逆向计数,而且可以自由设置起始值和终止值。
它可以应用于时序控制、频率分析、数据采样等领域。
5. 软件计数器软件计数器是在程序中实现的计数器。
与硬件计数器不同,软件计数器是通过编程来实现的。
在编程语言中,通常使用循环语句来实现计数功能。
例如,在C语言中,可以使用for循环来进行计数操作。
软件计数器可以灵活地控制计数的步长、起始值和终止条件。
它可以方便地应用于各种算法和数据处理任务。
6. 计数原理的应用计数原理的应用非常广泛,不仅仅局限于数字电路和计算机科学中。
在通信工程中,计数原理可以用于数据传输的控制和同步。
例如,可以使用计数器来实现数据包的计数和时钟同步。
计数原理知识点

计数原理知识点
计数原理是组合数学中的基本概念之一,用于计算某个事件发生的可能性。
其核心思想是将复杂的问题拆解为若干个简单的子问题,然后通过对这些子问题进行计数来得到最终的答案。
计数原理包括三个基本概念:乘法原理、加法原理和排列组合。
1. 乘法原理:当一个事件可以分成多个独立的步骤时,可以通过将每个步骤的可能性相乘得到最终结果的总可能性。
例如,在一次实验中,如果第一个步骤有m种可能性,第二个步骤
有n种可能性,那么整个实验的可能性就是m乘以n。
这个原理也可以推广到更多步骤的情况。
2. 加法原理:当一个事件可以通过多种不同的方式实现时,可以通过将每种方式的可能性相加得到最终结果的总可能性。
例如,在一个实验中,如果第一个步骤有m种可能性,第二个
步骤有n种可能性,而这两个步骤不能同时发生,那么整个实验的可能性就是m加上n。
3. 排列组合:当从一个集合中选择元素进行排列或组合时,可以使用排列和组合的方法进行计数。
- 排列是指在选择元素时考虑元素的顺序。
当从n个元素中选
择r个元素进行排列时,可以使用排列数P(n,r) = n! / (n-r)!来
计算不同排列的总数,其中n!表示n的阶乘。
- 组合是指在选择元素时不考虑元素的顺序。
当从n个元素中
选择r个元素进行组合时,可以使用组合数C(n,r) = n! / (r!(n-
r)!)来计算不同组合的总数。
通过灵活应用乘法原理、加法原理和排列组合,可以解决各种不同的计数问题,例如生日问题、抽签问题、排队问题等。
计数原理不仅在组合数学中有广泛的应用,也被应用于统计学、概率论等领域。
计数原理心得(优秀5篇)

计数原理心得(优秀5篇)计数原理心得篇1计数原理心得1.计数原理的重要性计数原理是概率论和数理统计的基础,是解决计数问题的基本工具。
掌握计数原理的重要性不言而喻。
2.计数原理的简介计数原理是指:在计数时,要把所有的对象放在一起,按一定的标准分类,然后分别计算每一类别的数量,所有类别的数量之和就是总数量。
3.计数原理的应用计数原理可以应用于各个领域,例如:在心理学中,计数可以帮助我们了解多少人参加了实验;在商业中,计数可以让我们知道有多少产品可用;在医学中,计数可以让我们知道有多少病人需要治疗。
4.计数原理的优点计数原理具有简单、易懂、实用的优点,可以帮助我们更好地理解计数问题,并且可以快速地解决计数问题。
5.计数原理的缺点计数原理也有缺点,例如:有些计数问题可能无法用计数原理来解决,需要其他更复杂的方法。
此外,计数原理只适用于计数问题,对于其他问题,例如:概率问题,可能需要其他的方法来解决。
6.计数原理的总结计数原理是解决计数问题的基本工具,可以应用于各个领域。
计数原理具有简单、易懂、实用的优点,可以快速地解决计数问题。
但是,有些计数问题可能无法用计数原理来解决,需要其他更复杂的方法。
计数原理心得篇2____计数原理心得____计数原理是数学的基础,它为解决各种问题提供了有效的手段。
以下是我对计数原理的一些心得和总结。
____理解计数原理的重要性____:计数原理是数学的基础,它为解决各种问题提供了有效的手段。
计数原理是数学中最基本的原理之一,它在概率论、组合数学、统计学等领域都有广泛应用。
因此,理解计数原理并熟练掌握其应用对于数学学习和问题解决至关重要。
____理解分类计数原理____:分类计数原理是计数原理中最重要的一种。
它是指,在解决某一问题时,可以将问题分成若干个步骤,每一步骤都有不同的选择。
每一步都有若干种可能的结果,问题解决的步骤数等于所有可能的结果数。
例如,在解决一个包含三个步骤的问题时,每一步都有两种可能的结果,那么问题就有2x2x2=8种可能的结果。
(完整版)计数原理知识点、题型小结doc

第一章、计数原理知识点小结一、分类加法计数原理与分步乘法计数原理1.分类计数原理-加法原理:如果完成一件事有 不同的方案,由第1类方案中有1m 种方法,在第2类方案中有2m 种不同的方法,种方法类方案中有第n m n 那么,完成这件工作共有 种不同的方法.2.分步计数原理-乘法原理:完成一件事需要 步骤,完成第1步有1m 种不同的方法,完成第2步有2m 种不同的方法,,种方法步中有第n m n 那么,完成这件工作共有 种不同方法。
3.两种方法的区别与联系:4.用两个计数原理解决计数问题时,需要注意的问题有哪些?最重要的是在开始计算之前进行仔细分析,弄清楚是一件什么事,正确选择是先分类还是先分步.分类要做到“不重不漏”,分类后再分别对每一类进行计数,最后用加法原理求和;分步要做到“步骤完整”,完成所有步骤,恰好完成任务. 分步后要计算每一步的方法数,把每一步的方法数相乘,得到总数。
5.常用的方法有:填空法,使用时注意:6.常见的题型:(1)有关数字排列问题例1:由数字4,5,6,7组成的所有的不重复的三位数的个数为?(可以重复的三位数字又有多少个呢?)变式1:由0,1,2,3,4,5,6,这七个数字可以组成多少个无重复数字的四位偶数?小结:(2)形如n m m n 和的问题。
例2:5名学生从3项体育项目中选择参赛,若每一名学生只能参加一项,则有多少种不同的参赛方法?变式1:若5名学生争夺3项比赛冠军(每一名学生参赛项目不限),则冠军获得者有几种不同的情况(没有并列冠军)小结:(3)涂色问题 4块(ABCD )涂色要求共边两块颜色互异,求有多少种不同的涂色方案?变式:将红、黄、绿、黑四种不同的颜色涂入图中的五个区域内,要求相邻的两个区域的颜色都不同,则有多少种不同的涂色方法?小结:1.排列的定义:一般地,从n 个 元素中取出m ( )个元素,按照一定的 排成一排,叫做从 个不同元素中取出 个元素的一个排列.2.排列问题有何特点?什么条件下是排列问题?3.排列数的定义:从 个 元素中取出 (n m ≤)个元素的 的个数,叫做从n个不同元素取出m 元素的排列数,用符合 表示.4.排列数公式:从n 个不同元素中取出m (n m ≤)个元素的排列数=m n A5.全排列:从n 个不同元素中 取出的一个排列,叫做n 个元素的一个全排列,用公式表示为=n n A6.n 的阶乘定义: 用 表示。
计数原理知识点

计数原理知识点
计数原理是概率论中的一种基本原理,也是计数学中的一个重要方法。
它用于解决计数问题,即通过一些简单的问题和已知的条件,推导出所需的计数结果。
计数原理包括了乘法原理和加法原理两个部分。
乘法原理是指,如果一个实验的过程可以划分为两个步骤,第一步有m种可能的选择,第二步有n种可能的选择,那么整
个实验的结果就有m*n种可能的情况。
举个例子,如果一串密码由4个数字组成,每个数字的取值范围都是1到9,那么根据乘法原理,总共可能的密码数量就是
9*9*9*9=6561种。
加法原理是指,如果一个实验的结果可以分为两种互斥的情况,第一种情况有m种可能,第二种情况有n种可能,那么整个
实验的结果就有m+n种可能的情况。
举个例子,如果一部电影院提供两个不同的电影放映时间,第一个电影共有4个时间选择,第二个电影共有3个时间选择,那么根据加法原理,总共的放映时间选择有4+3=7种可能。
在实际问题中,可以通过乘法和加法原理来解决复杂的计数问题,其中有些问题可能还需要用到排列组合等进一步的数学方法。
计数原理是处理计数问题时的基本思路和方法,它在概率、组合数学、统计学等领域中具有广泛的应用。
高中数学知识点总结 计数原理
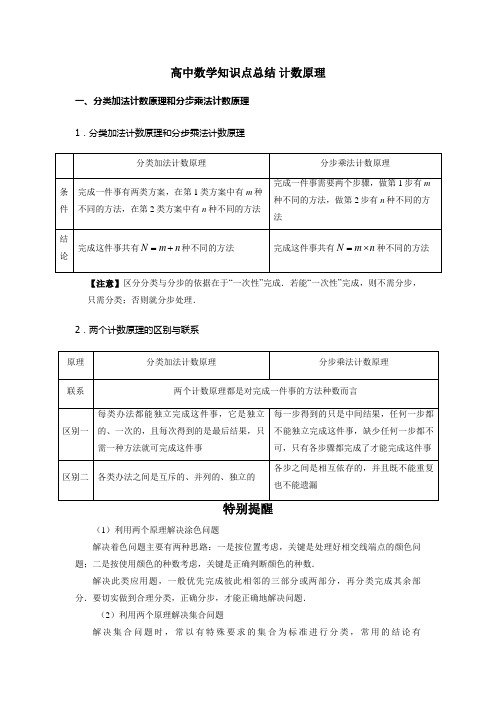
高中数学知识点总结计数原理一、分类加法计数原理和分步乘法计数原理1.分类加法计数原理和分步乘法计数原理【注意】区分分类与分步的依据在于“一次性”完成.若能“一次性”完成,则不需分步,只需分类;否则就分步处理.2.两个计数原理的区别与联系123,,,,{}n a a a a 的子集有2n 个,真子集有21n -个.二、排列1.排列的定义一般地,从n 个不同元素中取出()m m n ≤个元素,按照一定的顺序排成一列,叫做从n 个不同元素中取出m 个元素的一个排列. 特别提醒确定一个具体问题是否为排列问题的方法:(1)首先要保证元素的无重复性,即是从n 个不同元素中取出m (m ≤n )个不同的元素,否则不是排列问题.(2)其次要保证元素的有序性,即安排这m 个元素时是有顺序的,有序的就是排列,无序的不是排列.而检验它是否有顺序的依据是变换元素的位置,看结果是否发生变化,有变化就是有顺序,无变化就是无顺序.2.解决排列应用问题的步骤:(1)分清问题是否与元素的顺序有关,若与顺序有关则是排列问题.(2)注意对元素或位置有无特殊要求.(3)借助排列数公式计算. 特别提醒当问题的正面分类较多或计算较复杂,而问题的反面分类较少或计算更简便时往往使用“间接法”.含“至多”、“至少”类词语的排列(组合)问题,是需要分类问题,常用间接法(即排除法)解答.这时可以先不考虑特殊元素(位置),而列出所有元素的全排列数,从中再减去不满足特殊元素(位置)要求的排列数,即排除法.3.排列数、排列数公式从n 个不同元素中取出()m m n ≤个元素的所有不同排列的个数叫做从n 个不同元素中取出m 个元素的排列数,用符号A mn 表示.特别提醒排列与排列数是两个不同的概念,一个排列是指“按照一定的顺序排成一列”,它是具体的一件事,排列数是指“从n 个不同元素中取出()m m n ≤个元素的所有不同排列的个数”,它是一个数.三、组合1.组合的定义一般地,从n 个不同元素中取出()m m n ≤个元素合成一组,叫做从n 个不同元素中取出m 个元素的一个组合.特别提醒解答排列、组合综合问题的一般思路和注意点:(1)一般思路:“先选后排”,也就是把符合题意的元素都选出来,再对元素或位置进行排列.(2)注意点:①元素是否有序是区分排列与组合的基本方法,元素无序是组合问题,元素有序是排列问题.②对于有多个限制条件的复杂问题,应认真分析每个限制条件,然后再考虑是分类还是分步,这是处理排列、组合的综合问题的一般方法.3.组合数的性质性质1:C C m n m n n-=. 性质1表明从n 个不同元素中取出m 个元素的组合,与剩下的n m -个元素的组合是一一对应关系.性质2:11C C C m m m n n n-+=+. 性质2表明从1n +个不同元素中任取m 个元素的组合,可以分为两类:第1类,取出的m 个元素中不含某个元素a 的组合,只需在除去元素a 的其余n 个元素中任取m 个即可,有C mn 个组合;第2类,取出的m 个元素中含有某个元素a 的组合,只需在除去a 的其余n 个元素中任取1m -个后再取出元素a 即可,有1C m n-个组合.四、二项式定理1.二项式定理 011()C C C C ()n n n k n k k n n n n n na b a a b a b b n --*+=+++++∈L L N ,这个公式叫做二项式定理,等号右边的多项式叫做()n a b +的二项展开式,共有n +1项,其中各项的系数C ({0,1,2,,})kn k n ∈L 叫做二项式系数.二项展开式中的C k n k k n a b -叫做二项展开式的通项,用1k T +表示,即通项为展开式的第1k +项:1C k n k k k nT a b -+=. 2.二项式系数的性质(4)奇数项的二项式系数之和等于偶数项的二项式系数之和,即2131C C C C 2n n n n n -++=++=L L . 特别提醒求二项展开式的特定项问题,实质是考查通项的特点,一般需要建立方程求k,再将k 的值代回通项求解,注意k的取值范围(0,1,2,,L).k n(1)第m项::此时k+1=m,直接代入通项.(2)常数项:即这项中不含“变元”,令通项中“变元”的幂指数为0建立方程.(3)有理项:令通项中“变元”的幂指数为整数建立方程.。
高中数学选修计数原理概率知识点总结

选修2-3定理概念及公式总结第一章基数原理1.分类计数原理:做一件事情,完成它可以有n 类办法,在第一类办法中有1m 种不同的方法,在第二类办法中有2m 种不同的方法,……,在第n 类办法中有n m 种不同的方法 N=m 1+m 2+……+m n 种不同的方法2.分步计数原理:做一件事情,完成它需要分成n 个步骤,做第一步有m 1种不同的方法,做第二步有m 2种不同的方法,……,做第n 步有m n 种不同的方法,那么完成这件事有N=m 1×m 2×……m n 种不同的方法 分类要做到“不重不漏”,分步要做到“步骤完整”3.两个计数原理的区别:如果完成一件事,有n 类办法,不论哪一类办法中的哪一种方法,都能独立完成这件事,用分类计数原理,如果完成一件事需要分成几个步骤,各步骤都不可缺少,需要完成所有步骤才能完成这件事,是分步问题,用分步计数原理.!4.排列:从n 个不同的元素中取出m 个(m ≤n)元素并按一定的顺序排成一列,叫做从n 个不同元素中取出m 个元素的一个排列.(1)排列数: 从n 个不同的元素中取出m 个(m ≤n)元素的所有排列的个数.用符号m n A 表示 (2)排列数公式:)1()2)(1(+-⋅⋅⋅--=m n n n n A mn用于计算, 或m nA )!(!m n n -=()n m N m n ≤∈*,, 用于证明。
nnA =!n =()1231⨯⨯⨯⨯- n n =n(n-1)! 规定0!=1 5.组合:一般地,从n 个不同元素中取出m ()m n ≤个元素并成一组,叫做从n 个不同元素中取出m 个元素的一个组合(1)组合数: 从n 个不同元素中取出m ()m n ≤个元素的所有组合的个数,用mn C 表示[(2)组合数公式: (1)(2)(1)!m m n nm m A n n n n m C A m ---+== 用于计算,或)!(!!m n m n C m n -=),,(n m N m n ≤∈*且 用于证明。
高中数学选修课件第一章计数原理章末优化总结

1 2
二项式展开式的应用
利用二项式展开式求解一些特定数列的和问题。
二项式系数的性质
利用二项式系数的性质求解组合数的问题。
3
二项式定理在概率论中的应用
利用二项式定理求解一些概率问题,如抛硬币、 抽奖等。
概率与统计中的高级计数技巧
分步计数原理与分类计数原理的综合运用
根据问题的实际情况,灵活选择分步或分类计数原理进行求解。
计数原理在概率论、 统计学、计算机科学 等领域具有广泛应用 。
它提供了系统的方法 来确定在特定条件下 不同事件的组合数或 排列数。
计数原理的基本思想
分类计数原理
当完成一件事情有多种方法时,根据方法的种类将事件分为不相交的类别,然 后分别计算每类方法下的可能情况数,最后将各类情况数相加得到总的可能情 况数。
THANKS
感谢观看
题目1
将4个相同的小球放进3个不同的盒子中,每个盒子至少 放一个,有多少种不同的放法?
题目2
用0,1,2,3,4这5个数字可以组成多少个无重复数字 的三位数?
答案解析
将4个小球分为3组,一组1个,另两组都是1个,然后将3 组小球放入3个不同的盒子中,即C(3,1)=3,所以共有3 种不同的放法。
答案解析
高中数学选修课件第一章计数原理 章末优化总结
汇报人:XX 20XX-01-29
目录
• 计数原理概述 • 计数原理基础知识回顾 • 计数原理在解题中的应用技巧 • 计数原理的拓展与提高 • 计数原理的章末总结与反思 • 练习题精选及解析
01计数Leabharlann 理概述计数原理的定义与重要性
计数原理是数学中的 一个基本概念,用于 解决各种计数问题。
包括加法原理、乘法原理、排列的性 质(如排列的有序性、排列与元素顺 序有关等)、组合的性质(如组合的 无序性、组合与元素顺序无关等)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章计数原理
1.1 分类加法计数原理与分步乘法计数原理
分类加法计数原理:
完成一件事有n类不同方案,
在第1类方案中有m1种不同的方法,
在第2类方案中有m2种不同的方法,…,
在第n类方案中有m n种不同的方法,
那么完成这件事共有
N=m1+m2+…+m n 种不同的方法
分类加法计数原理的特点:
1、每一类的任何一种方法都能独立完成整个事情
2、任何一种方法都只能属于某一类
3、分类时:不能重复
不能遗漏
分步乘法计数原理:
完成一件事需要分成n个步骤,
做第1步有m1种不同的方法,
做第2步有m2种不同的方法,…,
做第n步有m n种不同的方法,
那么完成这件事共有
N=m1×m2×…×m n 种不同的方法
分步乘法计数原理的特点:
任何一步的任何一种方法都只能完成整个事情的一部分,它可以和上下步的任何一种方法联结成为一种方案。
所有的步骤都执行完才能恰好完成整个事情。
小结:分类计数与分步计数原理的区别和联系
计算完成一件事的方法数的步骤:
1、确认事件是什么?
2、如何完成这件事:分类还是分步
3、检查:类:不重不漏
步:各步任务清晰,完整 小结
1.分类加法计数原理和分步乘法计数原理,都是解决完成一件事的方法数的计数问题,其不同之处在于,前者是针对“分类”问题的计数方法,后者是针对“分步”问题的计数方法.
2.在“分类”问题中,各类方案中的每一种方法相互独立,选取任何一种方法都能完成这件事;在“分步”问题中,各步骤中的方法相互依存,只有各步骤各选一种方法才能完成这件事.
3.在应用分类加法计数原理时,分类方法不惟一,但分类不能重复,也不能遗漏. 在应用分步乘法计数原理时,分步方法不惟一,但分步不能重叠,也不能缺少.
1.2 排列与组合
1.2.1排列
一般地,从n 个不同的元素中取出m(m ≤n)个元素,按照一定的顺序排成一列,叫做从n 个不同元素中取出m 个元素的一个排列。
说明:1、元素不重复。
n 个中不能重复,m 个中也不能重复。
2、“按一定顺序”就是与位置有关,这是判断一个问题是否是排列问题的关键。
3、两个排列相同,当且仅当这两个排列中的元素完全相同,而且元素的排列顺序也完全相同。
4、m <n 时的排列叫选排列,m =n 时的排列叫全排列。
5、为了使写出的所有排列情况既不重复也不遗漏,最好采用“树形图”。
从n 个不同的元素中取出m(m ≤n)个元素的所有排列的个数,叫做从n 个不同的元素中取出m 个元素的排列数。
用符号 表示。
排列数公式
这里m 、n ∈N *
且m <n ,
特点:(1)共有m 个因数.
(2)第一个因数是n ,后面每一个因数比它前面一个因数少1. (3)最后一个因数是n -m +1. 当m=n 时 正整数1到n 的连乘积,叫做n 的阶乘,用n! 表示。
= 排列数公式: (1) =
(2) = 为了使当m =n 时上面的公式也成立,规定: =
说明:1、排列数公式的第一个常用来计算,第二个常用来证明。
2、对于m n 的条件要留意,往往是解方程时的隐含条件。
全排列的定义:n 个不同元素全部取出的一个排列,叫做 n 个不同元素的一个全排列. 一般地对于有限制条件的排列应用题,可以有两种不同的计算方法: (l )直接计算法 :
排列问题的限制条件一般表现为:某些元素不能在某个(或某些)位置、某个(或某些)位置只能放某些元素,因此进行算法设计时,常优先处理这些特殊要求.便有了:先处理特殊
m
n A =n(n-1)(n-2)(n-m+1)∙∙ n n
A =n(n-1)(n-2)321=!n n
A n )
*,,)(1()2)(1(n m N n m m n n n n A m n ≤∈+---= )!
(!m n n A m n -=1!0=
元素或先处理特殊位置的方法.这些统称为“特殊元素(位置)优先考虑法”.
(2)间接计算法:先不考虑限制条件,把所有的排列种数算出,再从中减去全部不符合条件的排列数,间接得出符合条件的排列种数.这种方法也称为“去杂法”.在去杂时,特别注意要不重复,不遗漏(去尽). 小结: 1、 相邻问题:捆绑法 2、 不相邻问题:插空法 3、 顺序一定:只排其它元素
方法总结
1.对有约束条件的排列问题,应注意如下类型:
⑴某些元素不能在或必须排列在某一位置;⑵某些元素要求连排(即必须相邻);⑶某些元素要求分离(即不能相邻); 2.基本的解题方法:
(1)有特殊元素或特殊位置的排列问题,通常是先排特殊元素或特殊位置,称为优先处理特殊元素(位置)法(优先法);特殊元素,特殊位置优先安排策略
(2)某些元素要求必须相邻时,可以先将这些元素看作一个元素,与其他元素排列后,再考虑相邻元素的内部排列,这种方法称为“捆绑法”;相邻问题捆绑处理的策略
(3)某些元素不相邻排列时,可以先排其他元素,再将这些不相邻元素插入空挡,这种方法称为“插空法”;不相邻问题插空处理的策略
1.2.2组合 1、组合:一般地,从n
个不同元素中取出
m
(m 小于n )个元素合成一组,叫做从
n
个不同元素中取出m
个元素的一个组合。
2.组合数:从n
个不同元素中取出
m
(m 小于n )个元素的所有不同组合的个数,
叫做从
n
个不同元素中取出
m
个元素的组合数...
.用符号m
n C
表示.
3、组合的特点: (1).一个组合就是一种取法; (2).n 个元素的不重复性;
(3).取出元素的任意性及无序性; (4).相同组合:元素相同。
4、排列与组合的区别:
共同点: 都要“从n 个不同元素中任取m 个元素” 不同点: 排列与元素的顺序有关, 而组合则与元素的顺序无关. 5、排列与组合的联系:
排列可以看成由两步来完成的事情:
第一步:从n 个不同元素中任取m 个元素(组合);
第二步:把所取的m 个元素排成一列(m 个元素的全排列 6.组合数公式: )
,,(n m N m n ≤∈*
且
∈
= = =
小结:组合只取元素,排列既取元素又排顺序;排列问题可看成先取元素,后排顺序. 组合数的性质1: --
=
说明:1、规定:
10=n
C ;
2、公式特征:等式两边下标相同,上标之和等于下标;
3、当
2n m >时,将 转为计算 组合数的性质2: = = 说明:
1、公式特征:下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与大的相同的一个组合数;
2、此性质的作用:恒等变形,简化运算。
课堂小结
1、若抽出的组合中的元素有差异性,则应将所有的元素按照这种差异性分类,各类中分别抽取;
2、若部分元素具有双重性,则应按取出的组合中的某类元素的来源进行分类;
3、注意两个原理的使用:按元素的性质进行分类、按事件发生的连续过程分步,是处理组合应用题的基本思想方法
分配问题: 均匀分配问题
不均匀分配问题;先分组再分配 课堂小结:
1.按元素的性质进行分类、按事件发生的连续过程分步,是处理组合应用题的基本思想方法;
2.对于有限制条件的问题,要优先安排特殊元素、特殊位置; 3.对于含“至多”、“至少”的问题,宜用排除法或分类解决;
4.需要注意的是,均匀分组(不计组的顺序)问题不是简单的组合问题。
一般地,将
m n
⋅个不同元素均匀分成
n
组,有
(1)m m
m mn
n m
m
m m
C C
C
A
- 种分
法;
5.按指定的一种顺序排列的问题,实质是组合问题。
(1)(2)(1)!m m n
n m m A n n n n m C A m ---+== )!
(!!
m n m n C m
n
-=
m
n n
m n C C -=m n C m n n
C -11-++=m n m n m
n C C C。
