2018届初三质量检测数学试卷
2018至2018学年九年级质量检测数学试卷及答案
剑川县2018至2018学年上学期九年级质量检测数学试卷一、选择题（本大题共9小题，每小题3分，满分27分）1、下列计算中正确的是（）A、2+3=5B、x2+x3=x5C、（－2）2 =－4D、6x3y2÷2xy2=3x22、我剑川县双河水坝工程是我县防洪效益最为显著的水利工程,它有效地控制洪水，增强抗洪能力。
据相关报道双河水库的防洪库容为22 150 0 m3，用科学记数法可记作（）A、221.5×103 m3B、22.15×104 m3C、2.215×105 m3D、2215×102 m33、下图是空心圆柱体在指定方向上的视图，正确的是（）4、学校开展为贫困地区捐书活动，以下是八名学生捐书的册数：2，3，2，6，5，6，2，7，则这组数据的众数和中位数分别是（）A、2 和2.5B、2和4C、6和4D、6和2.55、一辆客车从剑川出发开往下关，设客车出发t小时后与下关的距离．．．．．．为s千米，下列图象能大致反映s与t之间的函数关系的是（）A、B、C、D、ODCB A)6、下列各组图形，可由一个图形平移得到另一个图形的是（ ）7、大理啤酒厂搞有奖促销活动，在一箱啤酒（共24瓶）中有4瓶的瓶盖内印有“中奖”字样，小明的爸爸买了一箱这种品牌的啤酒，但是连续打开4瓶均末中奖，小明这时在剩下的啤酒中任意拿出了一瓶，那么他拿出的这瓶中奖的概率是（ ）A 、201B 、51C 、61D 、 218、下列命题中，逆命题是真命题的是（ ）A 、对顶角相等B 、如果两个实数相等，那么它们的平方数相等C 、等腰三角形两底角相等D 、两个全等三角形的对应角相等9、已知正比例函数y kx =（0k ≠）的函数值y 随x 的增大而减小，则一次函数y kx k =+的图象大致是（ ）二、填空题（本大题共6小题，每小题3分，满分18分）10、一元二次方程x 2＋2x ＝3的根是 。
(完整)2018年泉州市初三质检数学试题及答案,推荐文档
2018年泉州市初三质检数学试题一、选择题(本题共10小题，每小题4分，共40分) (1)化简|-3|的结果是（ ）． (A)3 (B)-3 (C)±3 (D)31(2)如图是由八个相同小正方体组合而成的几何体，则其主视图是（ ）．(3)从泉州市电子商务中心获悉，近年来电子商务产业蓬勃发展截止到2018年3月，我市电商从业人员已达873 000人，数字873 000可用科学记数法表示为（ ）． (A)8.73×103 (B)87.3×104 (C)8.73×105 (D)0.873×106 (4)下列各式的计算结果为a 5的是（ ） (A)a 7-a 2 (B)a 10÷a 2 (C)(a 2)3 (D)( -a )2·a 3 (5)不等式组⎩⎨⎧≥+->-06301x x 的解集在数轴上表示为（ ）．(6)下列图形中，是中心对称图形，但不是轴对称图形的是（ ）．(7)去年某市7月1日到7日的每一天最高气温变化如折线图所示， 则关于这组数据的描述正确的是（ ）． (A)最低温度是32℃ (B)众数是35℃ (C)中位数是34℃ (D)平均数是33℃(8)在《九章算术》中有“盈不足术”的问题，原文如下：今有共买物，人出八，盈三；人出七，不足四．问人数几何?大意为：现有一些人共同买一个物品，每人出8元，还盈余3元；每人出7元，则还差4元．问人数是多少?若设人数为x ，则下列关于x 的方程符合题意的是（ ）． (A)8x -3=7x +4 (B)8(x -3)=7(x +4) (C)8x +4=7x -3 (D)81371=-x x +4 (9)如图，在3×3的网格中，A ，B 均为格点，以点A 为圆心，以AB 的长为半径作弧，图中的点C 是该弧与格线的交点，则sin ∠BAC 的值是（ ）．(A)21 (B) 32(C) 35 (D) 552(10)如图，反比例函数y=xk的图象经过正方形ABCD 的顶点A 和中心E ，若点D 的坐标为(-1，0)，则k 的值为（ ）． (A)2 (B) 2- (C)1 (D) 1- A B C D(A) (B) (C) (D) A BC D EO xy(A) (B) (C) (D)二、填空题(本题共6小题，每小题4分，共24分) (11)已知a =(21)°，b=2-1，则a _______b (填“>”，“<”或“=”) ． (12)正八边形的每一个内角的度数为________．(13)一个暗箱中放有除颜色外其他完全相同的m 个红球，6个黄球，3个白球现将球搅匀后，任意摸出1个球记下颜色，再放回暗箱，通过大量重复试验后发现，摸到黄球的频率稳定在30%附近，由此可以估算m 的值是________．(14)如图，将△ABC 绕点A 顺时针旋转120°，得到 △ADE ．这时点D 、E 、B 恰好在同一直线上，则 ∠ABC 的度数为________．(15)已知关于x 的一元二次方程(m -1)x 2- (2m -2)x -1=0 有两个相等实数根，则m 的值为________．(16)在平行四边形ABCD 中，AB=2，AD=3，点E 为BC 中点，连结AE ，将△ABE 沿AE 折叠到△AB'E 的位置，若∠BAE=45°，则点B'到直线BC 的距离为________． 三、解答题：(本题共9小题，共86分) (17)( 8分)解方程：23-x 312+-x =1．(18) (8分)先化简，再求值：3223393a aa a a a +÷⎪⎪⎭⎫ ⎝⎛---，其中a =22．(19)(8分)如图，在锐角△ABC 中，AB=2cm ，AC=3cm ． (1)尺规作图：作BC 边的垂直平分线分别交AC ，BC 于点D 、E(保留作图痕迹，不要求写作法)； (2)在(1)的条件下，连结BD ，求△ABD 的周长．(20)(8分)为进一步弘扬中华优秀传统文化，某校决定开展以下四项活动：A 经典古诗文朗诵；B 书画作品鉴赏；C 民族乐器表演；D 围棋赛。
完整2018年福州初三质检学试题及答案推荐文档
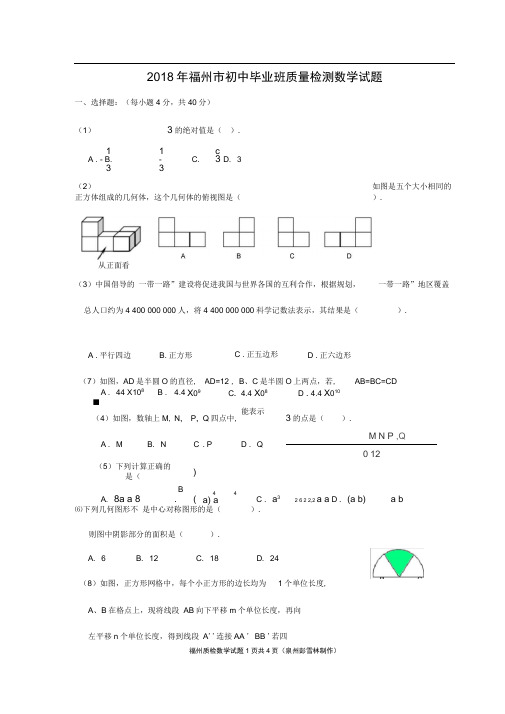
2018年福州市初中毕业班质量检测数学试题一、选择题：（每小题4分，共40分）（1）3的绝对值是（）.1 1 cA . - B. - C. 3 D. 33 3（2）如图是五个大小相同的正方体组成的几何体，这个几何体的俯视图是（）.从正面看（3）中国倡导的一带一路”建设将促进我国与世界各国的互利合作，根据规划，一带一路”地区覆盖总人口约为4 400 000 000人，将4 400 000 000科学记数法表示，其结果是（）.A . 44 X108B .■4.4X09C. 4.4 X08 D . 4.4 X010（4）如图，数轴上M, N,P,Q四点中,能表示、3的点是（）.A . M B. N C .P D . QM N P ,Q0 12（5）下列计算正确的是（)A. 8a a 8B.( 4 4a) a C . a3 2 6 2 2,2 a a D . (a b) a b⑹下列几何图形不是中心对称图形的是（）.则图中阴影部分的面积是（）.（8）如图，正方形网格中，每个小正方形的边长均为1个单位长度,A、B在格点上，现将线段AB向下平移m个单位长度，再向左平移n个单位长度，得到线段A''连接AA ' BB '若四福州质检数学试题1页共4页（泉州彭雪林制作）A .平行四边B.正方形 C .正五边形 D .正六边形（7）如图，AD是半圆O的直径, AD=12 , B、C是半圆O上两点，若, AB=BC=CDA. 6B. 12C. 18D. 24边形AA 'B'B是正方形，则m+n的值是( ).A . 3 B. 4 C. 5 D. 6(9)若数据X仁X2,…，x n的众数为a,方差为b，则数据X1+2 , X2+2,…，X n+2的众数，方差分别是( ).A . a、b B. a、b +2 C. a+2、b D. a+2、b+2(10)在平面直角坐标系xOy 中，A(0,2)，B(m，m-2)，贝U AB+OB 的最小值是().A . 2 . 5 B. 4 C. 2 3二、填空题：(每小题4分，共24分)1(11) 2 = ________ .(12) _____________________________ 若(13) 不等式2x+1》3勺解集是 ________ .(14) 一个不透明的袋子中有3个白球和2个黑球，这些球除颜色外完全相同从袋子中随机摸出1个球，这个球是白球的概率是 ____________ .(15) 如图，矩形ABCD中，E是BC上一点，将△ ABE沿AE折叠，得到△ AFE中点，贝U巴的值是__________ .AB4 k(16) 如图，直线y1= x与双曲线y2= 交于A、B两点，点C在x轴上，连3 x接AC、BC .若/ ACB=90 , △ ABC的面积为10,则k的值是_______________ .、解答题：(共86 分)(17)( 8分)先化简，再求值(1X22x 1x 1，其中x= 2 +1(18)( 8分)C, E在一条直线上, AB // DE, AC // DF，且AC=DF 若F恰好是CD的.y求证：AB=DE .（19）（8 分）如图，在Rt△KBC 中，/C=90°,/B=54°, AD 是△ABC 的角平分线.求作AB的垂直平分线MN交AD于点E,连接BE;并证明DE=DB .（要求：尺规作图，保留作图痕迹，不写作法）（20）（ 8分）我国古代数学著作《九章算术》的“方程” 一章里，一次方程是由算筹布置而成的. 如图1 ,图中各行从左到右列出的算筹数分别表示未知数x、y的系数与应的常数项，把图1所示的算筹x 4y 10图用我们现在所熟悉的方程组的形式表述出来，就是' ，请你根据图2所示的算6x 11y 34筹图，列出方程组，并求解.I 1111 -TH^III图1（21）（ 8分）如图，AB是O O的直径，点C在O O上，过点C若/ COB=2 / PCB，求证：PC是O O的切线.(22) ( 10分)已知y是x的函数，自变量x的取值范围是-3.5 < X手下表是y与x的几组对应值:x-3.5-3-2-101234y4210.670.5 2.03 3.13 3.784请你根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行探究.(1) 如图，在平面直角坐标系xOy中，描出了上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；(2) 根据画出的函数图象特征，仿照示例，完成下列表格中的函数变化规律：序号函数图象特征函数变化规律示例1在y轴右侧，函数图象呈上升状态当0<x W 4, y随x的增大而增大示例2函数图象经过点(-2 , 1)当时x=-2时，y=1(i)函数图象的最低点是(0, 0.5)(ii)在y轴左侧，函数图象呈下降状态⑶当a<xW4时，y的取值范围为0.5 < y齐a的取值范围为 _______________(23) ( 10分)李先生从家到公司上班，可以乘坐20路或66路公交车.他在乘坐这两路车时，对所需时间分别做了20次统计，并绘制如下统计图:请根据以上信息，解答下列问题: (1)完成右表中(i)、( ii )的数据： (2)李先生从家到公司，除乘车时间外 另需10分钟(含等车、步行等)•该 公司规定每天 8点上班，16点下班.(i)某日李先生7点20分从家里出发，乘坐哪路车合适？并说明理由. (ii)公司出于人文关怀，充许每个员工每个月迟到两次，若李先生每天同一时刻从家里出发，则每天最迟几点出发合适？并说明理由.(每月的上班天数按 22天计)(24) ( 12分)已知菱形 ABCD , E 是BC 边上一点，连接 AE 交BD 于点F .(1)如图1,当E 是BC 中点时，求证： AF=2EF ;⑵如图2,连接CF ，若AB=5 , BD=8，当△ CEF 为直角三角形时，求 BE 的长；⑶如图3,当/ ABC=90°时，过点 C 作CG 丄AE 交AE 的延长线于点 G ,连接DG ,若BE=BF , 求tan / BDG 的值.bx(a 0, b 0)交x 轴于0、A 两点，顶点为B .(1)直接写出A , B 两点的坐标(用含ab 的代数式表示);公交线路线20路 66路 乘车时间统计量平均数 34(i ) 中位数(ii)302(25)( 14分)如图，抛物线 y axD E图1D E图2DC⑵直线y=kx+m（k>0）过点B ,且与抛物线交于另一点D（点DCE2018年福州市初中毕业班质屍枪测数学试题答案及评分标准•汪分性明iK 礙歸左黯出了 •冲曲几IHR 注從书冒.卿封J 驚注勾義薛着不PC 证VUK 風盟芸主莽 尊点內牌迂吧呻曲爷岳峠甕和应宙澤知泊则・2.刃于计IT ■+自审里的解聲在慕一步H 迟it 剜・师果感堆工为的燃誓梅吏嗣前向客 ««.«.可規彩4的血徒定£醴摊舟的绘养，电苹紳用垃该魅务正■斡并宜抽弧玫4 不;E 果姑遇湍舟制转芒乳竝严匱的汕侥・戟叫再拾血一九 耶許tr 卡断扎井& 瀧貞纠.正故 W.寸 —1耿一1钩辻 4 §显整裁滞- imig 空£」"中拘叽KSJKi 毎小S4#.需分腑井.D <2； D □ m *4) C 小H⑹C 5 AW A (?> C5〕A二.M 空池：是小联」井，@曹上」分一cu t 4W Hi 皿 门讥的< M>i 157 車r!■&)一乐iii 町1)・牌耳带手度盹审酹的微 気，乂・如* * 1!|> ¥ '殊.去埔罟孙卓趙g 小d 無劝弘・酋应号岀：fc 字盘闲 迢期爼罐时如曲律fE WI it ■氏亠［兴|珀”僅十i ....... .......................... …"1 fh二岸”i J 厂1— I <x-iy——* “ ―i —I —-—■ ■ ■p>A Si"h2(X lY分彷 甘t f 7 8I-注士孚=工窪- f■ y生A 迥/和二DET* ff ft* -JC5 …£>AT -AC 网「mcsaF ■. AAS i, 上朋上屮.tenth A 仞做总阳求ft 更苗》B 拙的豪直年专用虹 AritjtHfne^SiAi 红胃时F 號他冲嘗戊遥列覺幷. ...................「■…■ ii ・x - " - ui ^rj-疋明’在凶「・*曲申* /r- .-mi - 5J\AZCJA^^r 1- /CtfA - W-wV.w A.4flt 射苣迟分i 命r \^a.u>\^\ -■ ■ *- fa - —tll,JJ丄由令丫戊息直冶乳』卜丘号仃罐L ・:z “■-+*-£Jf ； 「血曙卅 r・「加* WE 旧 扔叫 ZDAF zTiKr/砂 3d*.，"・/ - ■.-、W .......... ■'f ■ ■ ■ ■ 7 汕 »*r J-Xfl' - ..... .............. ■ ■ --• .. .............. .. ....... .. ■ . ..... * 号zi:样阳A 分.5>・连豪砒书1 W 矗总不叠雨 齐#fr#〕・3帕3宜■祠• “廿”儿殳 ..................,T - II.幡令fQr 殍F ? X I 关 忙卫代人曲.萍“讨 M -1L 埔溝小方腔.褂k 人 杷.代人;u ・Uy <心迪片力色m 的解* J*> >吐 方柑留对LhffH 》.卓4<1坤对一吞律】鞘.119)•KCWu ------ " ------ -- ---------- ------ ------------------ ----- --- 3 ftV ^WliilZPCB ・:.'t："P ”■' ' 'IF-\"JJ-w XA r「ocjZG< M -■ 'PfRr" ■'■…4 4im圮讯訂奁ih:* 上QCJ *■疋<7TB-W・丄二&冷-亠XUFtz ucP~yo1^ ,11-' .............. .. 1 J I I-^' '■j'飞曲；-tx/丄L屮. ■^ ■ ■■ ,T,7 *:or« ®门的平目.-\Ft* 足/VO：intU就- ■■»■■ it "ji 3进二* 0^-07) LBf7 ? fJ・F F^ODC W・ .................................................... I S 二DCD + 丄T^DfD1—90" ■- ■ I - ■・・占・ ,f =V Oil kItM ^i>ZLWt;f zrafl- izrwx i 今-V-cfCOTr ZJVJJ. …£ 紡；..：V .'I . Cl jRrjmp* 艸r ….…........... ....... ........ 。
2018-2019学年度福州市九年级质量检测数学试题与答案
A． B． C．3D．2
9．已知Rt△ABC，∠ACB 90°，AC 3，BC 4，AD平分∠BAC，则点B到射线AD的距离是
A．2B ． C． D．3
10．一套数学题集共有100道题，甲、乙和丙三人分别作答，每道题至少有一人解对，且每人都解对了其中的60道．如果将其中只有1人解对的题称作难题，2人解对的题称作中档题，3人都解对的题称作容易题，那么下列判断一定正确的是
三、解答题：本题共9小题，共86分．解答应写出文字说明、证明过程或演算步骤．
17．（本小题满分8分）
计算： ( )0．
18．（本小题满分8分）
如图，已知∠1 ∠2，∠B ∠D，求证：CB CD．
19．（本小题满分8分）
先化简，再求值：( ) ，其中 ．
20．（本小题满分8分）
如图，在Rt△ABC中，∠ACB 90°，BD平分∠ABC．
22．（本小题满分10分）
为了解某校九年级学生体能训练情况，该年级在3月份进行了一次体育测试，决定对本次测试的成绩进行抽样分析．已知九年级共有学生480人．请按要求回答下列问题：
（1）把全年级同学的测试成绩分别写在没有明显差别的小纸片上，揉成小球，放到一个不透明的袋子中，充分搅拌后，随意抽取30个，展开小球，记录这30张纸片中所写的成绩，得到一个样本．你觉得上面的抽取过程是简单随机抽样吗？
2018—2019学年度福州市九年级质量检测
小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．下列天气预报的图标中既是轴对称图形又是中心对称图形的是
2018年龙岩初中质检数学-答案-排2018.5.4
2018年龙岩市九年级学业（升学）质量检查数学试题参考答案11．2x ≥ 12．63.3610⨯ 13．= 14．3π15． 16．9 三、解答题（本大题共9题，共86分）17．（8分）解：原式23(1)1(1)(1)3x x x x x -+=⋅-+-- ………………2分1111x x x x +-=--- ………………4分 21x =- ………………6分当1x =时，原式=== ………………8分 18．（8分）证明：∵四边形ABCD 是平行四边形∴,//CD AB CD AB = ………………2分 又∵//CD AB∴DCF BAE ∠=∠ ………………4分 又∵AE CF =∴DCF ∆≌()BAE SAS ∆ ………………6分 ∴DF BE = ………………8分19. （8分）解：（Ⅰ）取线段AC 的中点为格点D ，则有DC AD =连BD ，则BD AC ⊥………………2分 理由：由图可知5BC =，连AB ，则5AB = ∴BC AB =………………3分 又CD AD =∴BD AC ⊥………………4分 （Ⅱ）由图易得5,BC = ………………5分AC == ………………6分5BC = ………………7分∴ABC ∆的周长=5510++=+8分20．（8分）解：（Ⅰ）样本容量16万………………1分2017年前三季度居民人均消费可支配收入平均数17735115%20395.2520395=⨯=≈（元）所以2017年前三季度居民人均消费可支配收入平均数为20395元. …………3分 （Ⅱ）8.3%36029.8830⨯︒=︒≈︒所以用于医疗保健所占圆心角度数为30︒. ………………5分（Ⅲ）18.3% 2.6%29.2% 6.8% 6.2%13.6%11.2%0.221-------= …………7分∴0.22111423⨯2524≈（元）所以用于居住的金额为2524元. …………8分21．（8分）解：设甲、乙两种笔各买了,x y 支，依题意得……………………1分73782x y y x +=⎧⎨=⎩……………………4分 解得612x y =⎧⎨=⎩……………………7分答：甲、乙两种笔各买了6支、12支. ……………………8分 22．（10分）解：（Ⅰ）1 …………2分（Ⅱ）（i ）过A 作AD BC ⊥，垂足为点D设,BD x CD a x ==-，则由勾股定理得2222AB BD AC CD -=- …………4分∴2222()c x b a x -=--∴2222b a c ax =+-在Rt ABD ∆中，cos xB c=即cos x c B = ∴2222cos b a c ac B =+- …………7分（ii）当3,2a b c ==时，22232232cos B =+-⨯⨯…………8分∴1cos 2B =…………9分 ∴60B ∠=︒…………10分23．（10分）解：（Ⅰ）证明：∵,90AB AC BAC =∠=︒∴45C ∠=︒ …………1分 又∵,AD BC AB AC ⊥=∴1145,,902BAC BD CD ADC ∠=∠=︒=∠=︒…………2分 又∵90,BAC BD CD ∠=︒=∴AD CD =…………3分 又∵90EAF ∠=︒ ∴,E F 是O 直径 ∴90EDF ∠=︒…………4分∴2490∠+∠=︒又∵3490∠+∠=︒ ∴23∠=∠ 又∵1C ∠=∠…………5分∴ADE ∆≌()CDF ASA ∆. …………6分（Ⅱ）当BC 与O 相切时，AD 是直径…………7分在Rt ADC ∆中，45,C AC ∠=︒8分 ∴sin ADC AC∠=∴1AD =…………9分 ∴O 的半径为12∴O 的面积为24π…………10分30ABE ∴∠=︒ …………1分（Ⅰ）分三种情况：①当点T 在AB 的上方，︒=∠90ATB ， 显然此时点T 和点P 重合，即13.AT AP AB === …………2分6分（Ⅱ）25．（14分）解：（Ⅰ）由已知得212404bc b ⎧-=⎪⎪⎨-⎪=⎪⎩ ∴21b c =-⎧⎨=⎩ ………2分 ∴抛物线的解析式为221y x x =-+ ………3分 （Ⅱ）当2b =时，22y x x c =++对称轴直线212x =-=-………………4分由图取抛物线上点Q ，使Q 与N 关于对称轴1x =-对称，由2(2,)N y 得2(4,)Q y -………………6分 又∵1(,)M m y 在抛物线图象上的点，且12y y >，由函数增减性得4m <-或2m >………………8分 （Ⅲ）三种情况：①当2b-＜-1，即b ＞2时，函数值y 随x 的增大而增大，依题意有 ⎩⎨⎧==⇒⎩⎨⎧+=++=+-334111c b b c b c b …………………………………………………10分 ②当121≤-≤-b ，即22≤≤-b 时，2bx -=时，函数值y 取最小值，（ⅰ）若012b≤-≤，即20b -≤≤时，依题意有221141421114b b b c c b c b ⎧⎧=--+=⎪⎪⇒⎨⎨=-⎪⎪⎩-+=+⎩或22411b c ⎧=+⎪⎨=+⎪⎩ （ⅱ）若102b-≤-≤，即02b ≤≤时，依题意有22142314b b c b c b c b ⎧⎧-+==±⎪⎪⇒⎨⎨=⎪⎩⎪++=+⎩（舍去）……………………………………12分 ③当2b-＞1，即b ＜-2时，函数值y 随x 的增大而减小，141111b c b b b c c -+=+=-⎧⎧⇒⎨⎨++==⎩⎩（舍去） 综上所述，⎩⎨⎧==33c b或411b c ⎧=-⎪⎨=-⎪⎩……………………………………14分。
2018年厦门初三质检数学试卷+答案
………………1 分
又因为 b－c＝4，可得 b＝1，c＝－3.
………………3 分
（2）（本小题满分 4 分）
解：由 b＋c＝－2，得 c＝－2－b.
对于 y＝x2＋bx＋c，
当 x＝0 时，y＝c＝－2－b.
抛物线的对称轴为直线 x＝－b2.
所以 B（0，－2－b），C（－b2，0）. 因为 b＞0，
由平移前的抛物线 y＝x2＋bx＋c，可得
y＝（x＋b2）2－b42＋c，即 y＝（x＋b2）2－b42－2－b.
因为平移后 A（1，－1）的对应点为 A1（1－m，2b－1） 可知，抛物线向左平移 m 个单位长度，向上平移 2b 个单位长度.
则平移后的抛物线解析式为 y＝（x＋b2＋m）2－b42－2－b＋2b.
解：如图 4，把 C（a，a＋2）代入 y＝2x＋1，可得 a＝1. ……………… 6 分
则点 C 的坐标为（1，3）.
x C
∵ AC＝CD＝CE，
yD
又∵ 点 D 在直线 AC 上，
y
∴ 点 E 在以线段 AD 为直径的圆上.
B
∴ ∠DEA＝90°.
……………… 8 分
过点 C 作 CF⊥x 轴于点 F，
（1）（本小题满分 5 分） 解：如图 5，∵ AB 是半圆 O 的直径，
M N
∴ ∠M＝90°．
………………1 分
在 Rt△AMB 中，AB＝ MA2＋MB2 ………………2 分
∴ AB＝10.
∴ OB＝5．
………………3 分
A
O
B
图5
∵ OB＝ON，
又∵ ∠NOB＝60°，
∴ △NOB 是等边三角形．
………………9 分
2018年福建省龙岩市初三质检数学试题及答案
2018年龙岩市九年级学业（升学）质量检查数 学 试 题（满分：150分 考试时间：120分钟）注意：请把所有答案填涂或书写到答题卡上！请不要错位、越界答题！ 在本试题上答题无效．一、选择题（本大题共10小题，每小题4分，共40分．每小题的四个选项中，只有一项符合题目要求） 1．计算11--的结果等于 A ．-2B ．0C ．1D ．22．下列计算正确的是 A ．4=2± B ．22(31)61x x x -=-C ．235+=a a aD ．235=a a a ⋅3．掷两枚质地相同的硬币，正面都朝上的概率是 A ．1B ．21 C ．41 D ．04．右图是一个由4个相同的正方体组成的立体图形，它的俯视图是A B C D5．我国古代数学著作《孙子算经》中有“多人共车”问题：今有三人共车，二车空；二人共车，九人步．问人与车各几何？其大意是：每车坐3人，两车空出来；每车坐2人，多出9人无车坐. 问人数和车数各多少？设车x 辆，根据题意，可列出的方程是 A ．3229x x -=+ B ．3(2)29x x -=+ C ．2932x x +=- D ．3(2)2(9)x x -=+6．如图，下列四个条件中，能判断DE //AC 的是从正面看EF D1BA 3 4 2 CA ．43∠=∠B ．21∠=∠C ．EFC EDC ∠=∠D ．AFE ACD ∠=∠7．实数,a b 在数轴上的对应点位置如图所示，把,0a b --，按照从小到大的顺序排列，正确的是A ．0a b -<<-B ．0a b <-<-C ．0b a -<<-D ．0b a <-<-8．在同一直角坐标系中，函数ky =和1+=kx y 的大致图象可能是9．已知1234-+=x x k ，则满足k 为整数的所有整数x 的和是 A ．-1B ．0C ．1D ．210．如图，︒=∠90ACB ,BC AC =,︒=∠45DCE ，如果4,3==BE AD ，则BC 的长是 A ．5B ．25C ．26D ．7二、填空题（本大题共6小题，每小题4分，共24分） 11．使代数式2-x 有意义的x 的取值范围是__________.12．2018年春节假期，某市接待游客超3360000人次，用科学记数法表示3360000，其结果是________________________.13．若甲组数据1,2,3,4,5的方差是2甲s ，乙组数据6,7,8,9,10的方差是2乙s ，则2甲s _____2乙s .（填“>”、“<”或“=”） 14．如图，在ABC ∆中，90,30ACB A ∠=︒∠=︒，2AB =，将ABC ∆绕着点C 逆时针旋转到DEC ∆位置时，点B 恰好落在DE 边上，则在旋转过程中，点B 运动到点E 的路径长为____________.15．如图，四边形ABCD 和CEFG 都是菱形，连接AG ，,GE AE ，若60,4F EF ∠=︒=，则AEG ∆的面积为________.16．非负数,,a b c 满足39=-=+a c b a ，，设c b a y ++=的最大值为m ，最小值为n ，则（第7题图）（第10题图）BACDEA B C D（第14题图）CDBA（第15题图）GFEDCBAm n -=________.三、解答题（本大题共9小题，共86分. 解答应写出文字说明、证明过程或演算步骤.） 17．（本小题满分8分）先化简，后求值：22321113x x x x x -++⋅---，其中21x =+.18．（本小题满分8分）如图，在ABCD 中，,E F 是对角线上的两点，且AE CF =，求证：DF BE =.19．（本小题满分8分）如图，在每个小正方形的边长为1的网格中，,,A B C 均为格点．（Ⅰ）仅用不带刻度的直尺作AC BD ⊥，垂足为D ，并简要说明道理；（Ⅱ）连接AB ，求ABC ∆的周长．20．（本小题满分8分）“不忘初心，牢记使命．”全面建设小康社会到了攻坚克难阶段. 为了解2017年全国居民收支数据，国家统计局组织实施了住户收支与生活状况调查，按季度发布．调查采用分层、多阶段、与人口规模大小成比例的概率抽样方法，在全国31个省（区、市）的1650个县（市、区）随机抽选16万个居民家庭作为调查户．已知2017年前三季度居民人均消费可支配收入平均数是2016年前三季度居民人均消费可支配收入平均数的00115，人均消费支出为11423元，根据下列两个统计图回答问题：（以下计算最终结果均保留整数）（第19题图）（第18题图）BACD E F 图1 2016年和2017年前三季度居民人均可支配收入平均数 图2 2017年前三季度居民人均消费支出及构成（Ⅰ）求年度调查的样本容量及2017年前三季度居民人均消费可支配收入平均数（元）； （Ⅱ）求在2017年前三季度居民人均消费支出中用于医疗保健所占圆心角度数； （Ⅲ）求在2017年前三季度居民人均消费支出中用于居住的金额．21．（本小题满分8分）甲、乙两种笔的单价分别为7元、3元，某学校用78元钱买这两种笔作为数学竞赛一、二等奖奖品，钱恰好用完.若买下的乙种笔是甲种笔的两倍，请问两种笔各买了几支?22．（本小题满分10分）（Ⅰ）知识延伸：如图1，在ABC ∆中，=90C ∠︒，,,AB c BC a AC b ===，根据三角函数的定义得：22sin cos A A += ；（Ⅱ）拓展运用：如图2，在锐角三角形ABC 中，,,AB c BC a AC b ===.（i ）求证：2222cos b a c ac B =+-⋅； （ii）已知：3,2a b c ===，求B ∠的度数.23．（本小题满分10分）如图，在ABC ∆中，90,BAC ∠=︒AB AC ==AD BC ⊥，垂足为D ，过,A D 的O 分别与,AB AC 交 于点,E F ，连接,,EF DE DF ．（Ⅰ）求证：ADE ∆≌CDF ∆； （Ⅱ）当BC 与O 相切时，求O 的面积．图1图2（第22题图）AC BABC（第23题图）BPFED C ABPF ED CA（图①） （图②） 25．（本题满分14分）已知抛物线c bx x y ++=2.（Ⅰ）当顶点坐标为），（01时，求抛物线的解析式； （Ⅱ）当2=b 时，),(1y m M ，),2(2y N 是抛物线图象上的两点，且21y y >，求实数m 的取值范围；（Ⅲ）若抛物线上的点(,)P s t ，满足11≤≤-s 时，b t +≤≤41．求,b c 的值.2018年龙岩市九年级学业（升学）质量检查数学试题参考答案11．2x ≥ 12．63.3610⨯ 13．= 14．3π15． 16．9 三、解答题（本大题共9题，共86分）17．（8分）解：原式23(1)1(1)(1)3x x x x x -+=⋅-+-- ………………2分 1111x x x x +-=--- ………………4分 21x =- ………………6分当1x =时，原式=== ………………8分 18．（8分）证明：∵四边形ABCD 是平行四边形∴,//CD AB CD AB = ………………2分 又∵//CD AB∴DCF BAE ∠=∠ ………………4分 又∵AE CF =∴DCF ∆≌()BAE SAS ∆ ………………6分 ∴DF BE = ………………8分19. （8分）解：（Ⅰ）取线段AC 的中点为格点D ，则有DC AD =连BD ，则BD AC ⊥………………2分 理由：由图可知5BC =，连AB ，则5AB = ∴BC AB =………………3分 又CD AD =∴BD AC ⊥………………4分 （Ⅱ）由图易得5,BC = ………………5分22242025AC =+== ………………6分22345BC =+= ………………7分∴ABC ∆的周长=55251025++=+………………8分20．（8分）解：（Ⅰ）样本容量16万………………1分2017年前三季度居民人均消费可支配收入平均数17735115%20395.2520395=⨯=≈（元）所以2017年前三季度居民人均消费可支配收入平均数为20395元. …………3分 （Ⅱ）8.3%36029.8830⨯︒=︒≈︒所以用于医疗保健所占圆心角度数为30︒. ………………5分（Ⅲ）18.3% 2.6%29.2% 6.8% 6.2%13.6%11.2%0.221-------= …………7分∴0.22111423⨯2524≈（元）所以用于居住的金额为2524元. …………8分21．（8分）解：设甲、乙两种笔各买了,x y 支，依题意得……………………1分73782x y y x+=⎧⎨=⎩……………………4分 解得612x y =⎧⎨=⎩……………………7分答：甲、乙两种笔各买了6支、12支. ……………………8分 22．（10分）解：（Ⅰ）1 …………2分（Ⅱ）（i ）过A 作AD BC ⊥，垂足为点D设,BD x CD a x ==-，则由勾股定理得2222AB BD AC CD -=- …………4分∴2222()c x b a x -=--∴2222b a c ax =+- 在Rt ABD ∆中，cos xB c=即cos x c B = ∴2222cos b a c ac B =+- …………7分（ii ）当3,7,2a b c ===时，222(7)32232cos B =+-⨯⨯…………8分∴1cos 2B =…………9分∴60B ∠=︒…………10分23．（10分）解：（Ⅰ）证明：∵,90AB AC BAC =∠=︒∴45C ∠=︒ …………1分 又∵,AD BC AB AC ⊥=∴1145,,902BAC BD CD ADC ∠=∠=︒=∠=︒…………2分 又∵90,BAC BD CD ∠=︒=∴AD CD =…………3分 又∵90EAF ∠=︒ ∴,E F 是O 直径∴90EDF ∠=︒…………4分 ∴2490∠+∠=︒又∵3490∠+∠=︒ ∴23∠=∠ 又∵1C ∠=∠…………5分∴ADE ∆≌()CDF ASA ∆. …………6分（Ⅱ）当BC 与O 相切时，AD 是直径…………7分在Rt ADC ∆中，45,2C AC ∠=︒=…………8分∴sin ADC AC∠=∴1AD =…………9分∴O 的半径为12∴O 的面积为24π…………10分24．（12分）解：在正方形ABCD 中，可得︒=∠90DAB .在BAE Rt ∆中，233tan 63AE ABE AB ∠===， 30ABE ∴∠=︒ …………1分（Ⅰ）分三种情况：①当点T 在AB 的上方，︒=∠90ATB ， 显然此时点T 和点P 重合，即13.2AT AP AB === …………2分 法1：②当点T 在AB 的下方，︒=∠90ATB ，如图24－①所示.在APB Rt ∆中，由BF AF =，可得：3===PF BF AF ，30BPF FBP ∴∠=∠=︒,︒=∠∴60BFT . 在ATB Rt ∆中，3===AF BF TF ，FTB ∆∴是等边三角形，3=∴TB ,3322=-=BT AB AT . …………4分 法2：当点T 在AB 的下方，︒=∠90ATB ，如图24－①所示.在APB Rt ∆中，由BF AF =，可得：3===PF BF AF ，以F 为圆心AB 长为直径作圆，交射线PF 于点T ，可知︒=∠90ATB ∵,AB PT 是直径， 90PAT APB ATB ∴∠=∠=∠=︒∴四边形APBT 是矩形 AT BP ∴=在APB Rt ∆中，,30︒=∠ABE 3323630cos =⨯=︒⋅=AB BP ， 33=∴AT .③当︒=∠90ABT 时，如图24－②所示.在FBT Rt ∆中，︒=∠60BFT ,3=BF ，tan 6033BT BF =⋅︒= 在ABT Rt ∆中：7322=+=BT AB AT .综上所述：当ABT ∆为直角三角形时，AT 的长为3或33或73. …………6分 （Ⅱ）法1：如图24－③所示，在正方形ABCD 中，可得︒=∠==90//,DAB BC AD BC AD AB ，43∠=∠∴ …………7分在EAB Rt ∆中，BE AP ⊥，易知︒=∠+∠︒=∠+∠9023,902131∠=∠∴，431∠=∠=∠∴AP PB =∠1tan ，AEAB=∠3tan 在Rt APB ∆和Rt EAB ∆中可得， AE AB AP PB =∴，BC AB AF AE ==, …………9分 AF BC AP PB =∴ 14∠=∠PBC ∴∆∽PAF ∆ …………11分 65∠=∠∴︒=∠+∠18076 ，︒=∠︒=∠+∠∴90,18075CPF 即 CP FP ∴⊥. …………12分法2：如图24－④所示，过点P 作PC BH BC PK ⊥⊥,，交于点O ，连接CO 并延长交AB 于点M . 可知BP CM ⊥，BE AP ⊥ ，MC AP //∴.在正方形ABCD 中，可得︒=∠=∠=90,DAB ABC CB AB ,AB PK //∴∴四边形PAMO 是平行四边形，AM PO =∴.易知︒=∠+∠︒=∠+∠9023,9021,31∠=∠∴BAE ∴∆≌CBM ∆BM AE =∴，AF AE = ,BM AF =∴，BF AM =∴ BF PO =∴，∴四边形PFBO 是平行四边形，BH PF // PC BH ⊥ ，CP FP ∴⊥25．（14分）解：（Ⅰ）由已知得212404bc b ⎧-=⎪⎪⎨-⎪=⎪⎩ ∴21b c =-⎧⎨=⎩ ………2分 ∴抛物线的解析式为221y x x =-+ ………3分（Ⅱ）当2b =时，22y x x c =++对称轴直线212x =-=-………………4分 由图取抛物线上点Q ，使Q 与N 关于对称轴1x =-对称， 由2(2,)N y 得2(4,)Q y -………………6分又∵1(,)M m y 在抛物线图象上的点，且12y y >，由函数增减性得4m <-或2m >………………8分 （Ⅲ）三种情况：①当2b-＜-1，即b ＞2时，函数值y 随x 的增大而增大，依题意有 ⎩⎨⎧==⇒⎩⎨⎧+=++=+-334111c b b c b c b …………………………………………………10分 ②当121≤-≤-b ，即22≤≤-b 时，2bx -=时，函数值y 取最小值，（ⅰ）若012b≤-≤，即20b -≤≤时，依题意有2211426142112614b b b c c b c b ⎧⎧=--+=⎪⎪⇒⎨⎨=-⎪⎪⎩-+=+⎩或22461126b c ⎧=+⎪⎨=+⎪⎩九年级数学试题 第11页 （共11页） （ⅱ）若102b -≤-≤，即02b ≤≤时，依题意有22142314b b c b c b c b ⎧⎧-+==±⎪⎪⇒⎨⎨=⎪⎩⎪++=+⎩（舍去）……………………………………12分 ③当2b -＞1，即b ＜-2时，函数值y 随x 的增大而减小， 141111bc b b b c c -+=+=-⎧⎧⇒⎨⎨++==⎩⎩（舍去） 综上所述，⎩⎨⎧==33c b或411b c ⎧=-⎪⎨=-⎪⎩.…………………。
(完整)2018年泉州市初三质检数学试题及答案,推荐文档
⎩1A B C D2018 年泉州市初三质检数学试题一、选择题(本题共 10 小题，每小题 4 分，共 40 分) (1)化简|-3|的结果是（ ）．1(A)3(B)-3(C)±3(D)3(2) 如图是由八个相同小正方体组合而成的几何体，则其主视图是（）．(3) 从泉州市电子商务中心获悉，近年来电子商务产业蓬勃发展截止到 2018 年 3 月，我市电商从业人员已达 873 000 人，数字 873 000 可用科学记数法表示为（ ）．(A)8.73×103 (B)87.3×104 (C)8.73×105 (D)0.873×106 (4) 下列各式的计算结果为 a 5 的是（ ） (A)a 7-a 2 (B)a 10÷a 2 (C)(a 2)3(D)( -a )2·a 3 ⎧x - 1 > 0 (5) 不等式组⎨- 3x + 6 ≥ 0 的解集在数轴上表示为（）．(A) (B) (C) (D)(6) 下列图形中，是中心对称图形，但不是轴对称图形的是（ ）．(A)(B)(C)(D)(7) 去年某市 7 月 1 日到 7 日的每一天最高气温变化如折线图所示， 则关于这组数据的描述正确的是（ ）． (A) 最低温度是 32℃ (B)众数是 35℃(C)中位数是 34℃ (D)平均数是 33℃(8) 在《九章算术》中有“盈不足术”的问题，原文如下：今有共买物，人出八，盈三；人出七，不足四．问人数几何?大意为：现有一些人共同买一个物品，每人出 8 元，还盈余 3 元；每人出 7 元，则还差 4 元．问人数是多少?若设人数为 x ，则下列关于 x 的方程符合题意的是（ ）． (A)8x -3=7x +4 (B)8(x -3)=7(x +4) 1 (C)8x +4=7x -3(D) 7x - 3 =1 x +48(9) 如图，在 3×3 的网格中，A ，B 均为格点，以点 A 为圆心，以 AB 的长为半径作弧，图中的点 C 是该弧与格线的交点，则 sin ∠BAC 的值是（ ）．1 (A)22 (B)3(C)3 k(D)5(10) 如图，反比例函数 y= 的图象经过正方形 ABCD 的顶点 A 和中心 E ，x若点 D 的坐标为(-1，0)，则 k 的值为（ ）．(A)2(B) - 2(C) (D) - 12252 5 BA yC D O xE⎝ ⎭二、填空题(本题共 6 小题，每小题 4 分，共 24 分)1(11) 已知 a =()°，b=2-1，则 ab (填“>”，“<”或“=”) ．2(12) 正八边形的每一个内角的度数为 ．(13) 一个暗箱中放有除颜色外其他完全相同的 m 个红球，6 个黄球，3 个白球现将球搅匀后，任意摸出 1个球记下颜色，再放回暗箱，通过大量重复试验后发现，摸到黄球的频率稳定在 30%附近，由此可以估算 m 的值是 ．(14) 如图，将△ABC 绕点 A 顺时针旋转 120°，得到△ADE ．这时点 D 、E 、B 恰好在同一直线上，则 ∠ABC 的度数为 ．(15) 已知关于 x 的一元二次方程(m -1)x 2- (2m -2)x -1=0 有两个相等实数根，则 m 的值为 ．A CD E B(16) 在平行四边形 ABCD 中，AB=2，AD=3，点 E 为 BC 中点，连结 AE ，将△ABE 沿 AE 折叠到△AB'E的位置，若∠BAE=45°，则点 B'到直线 BC 的距离为 ． 三、解答题：(本题共 9 小题，共 86 分) (17)( 8 分)解方程：x - 3 - 2x + 1=1． 2 3(18) (8 分)先化简，再求值： ⎛ a 2 - 9 ⎫ ÷ a 2 + 3a ，其中 a = 2 ．a - 3 a - 3 ⎪ a 3 2A(19)(8 分)如图，在锐角△ABC 中，AB=2cm ，AC=3cm ．(1) 尺规作图：作 BC 边的垂直平分线分别交 AC ，BC 于点 D 、E(保留作图痕迹，不要求写作法)； (2)在(1)的条件下，连结 BD ，求△ABD 的周长．BC(20)(8 分)为进一步弘扬中华优秀传统文化，某校决定开展以下四项活动：A 经典古诗文朗诵；B 书画作品鉴赏；C 民族乐器表演；D 围棋赛。
【数学答案】2018福州5月初三质检考试
E A
N
如图，MN 就是所求作的线段 AB 的垂直平分线，点 E 就是所求作的点，线段 BE 就 是所要连接的线段． ·········································································· 4 分 证明：在 Rt△ABC 中，∠C = 90°，∠CBA = 54°， ∴∠CAB = 90° − ∠CBA = 36°． ···················································· 5 分 ∵AD 是△ABC 的角平分线， ∴∠BAD = 1 ∠CAB = 18°． ······················································· 6 分 2 ∵点 E 在 AB 的垂直平分线上， ∴EA = EB， ∴∠EBA = ∠EAB = 18°， ∴∠DEB = ∠EBA + ∠EAB = 36°，∠DBE = ∠CBA − ∠EBA = 36°， ∴∠DEB = ∠DBE， ································································· 7 分 ∴DE = DB． ··········································································· 8 分 注：作图 3 分，垂直平分线画对得 2 分，连接 BE 得 1 分；结论 1 分（结论不全面 不给分） ．
注：方程写对一个得 2 分，未知数解对一个得 2 分．
数学试题答案及评分参考 第 2 页（共 7 页）
（21）证法一：连接 AC． ··········································································· 1 分 = CB ， ∵ CB ∴∠COB = 2∠CAB． ····························································· 2 分 ∵∠COB = 2∠PCB， ∴∠CAB = ∠PCB． ······························································· 3 分 ∵OA = OC， C ∴∠OAC = ∠OCA， ∴∠OCA = ∠PCB． ································ 4 分 A B P O ∵AB 是⊙O 的直径， ∴∠ACB = 90°， ····································· 5 分 ∴∠OCA + ∠OCB = 90°， ∴∠PCB + ∠OCB = 90°， 即∠OCP = 90°， ··································································· 6 分 ∴OC⊥CP． ········································································ 7 分 ∵OC 是⊙O 的半径， ∴PC 是⊙O 的切线． ···························································· 8 分 证法二：过点 O 作 OD⊥BC 于 D，则∠ODC = 90°， ································ 1 分 ∴∠OCD + ∠COD = 90°． ······················································ 2 分 ∵OB = OC， C ∴OD 平分∠COB， D ∴∠COB = 2∠COD． ······························ 3 分 A B P O ∵∠COB = 2∠PCB， ∴∠COD = ∠PCB， ································ 4 分 ∴∠PCB + ∠OCD = 90°， 即∠OCP = 90°， ··································································· 6 分 ∴OC⊥CP． ········································································ 7 分 ∵OC 是⊙O 的半径， ∴PC 是⊙O 的切线． ···························································· 8 分 证法三：设∠PCB = x°， ····································································· 1 分 则∠COB = 2x°． ··································································· 2 分 ∵OB = OC， C ∴∠OCB = 180° − 2 x° = 90° − x°，··············· 4 分 2 A B P O ∴∠OCP = ∠OCB + ∠PCB = 90° − x° + x° = 90°， ··················· 6 分 ∴OC⊥PC． ·········································· 7 分 ∵OC 是⊙O 的半径， ∴PC 是⊙O 的切线． ···························································· 8 分
2018年福建省莆田市初中初三市质检数学试卷及答案
2018年福建省莆田市初中初三市质检数学试卷及答案2018年莆田市初中毕业班质量检查数学试卷(满分:150分；考试时间:120分钟)注意：本试卷分为“试题”和“答题卡”两部分，答题时请按答题卡中的“注意事项”要求认真作答，答案写在答题卡上的相应位置。
一、选择题(每小题4分，共40分)(1)2018的相反数为（）(A)2018(B)12018(C) 2018-(D) 12018-(2)下列式子运算结果为2a的是（）(A)2a a⋅(B) a+2(C) aa+(D) aa÷3(3)若一个几何体的主视图、左视图、俯视图都是半径相等的圆，则这个几何体是（）(A)圆柱(B)球(C) 正方体(D)圆锥(4)下列说法中，正确的是（）(A)一组对边平行，另一组对边相等的四边形是平行四边形(B)对角线相等的四边形是矩形(C)对角线互相垂直的四边形是菱形(D)有一组邻边相等的矩形是正方形(5)若x=1是关于x的方程x2-2x+c=0的一个根，则c的值为（ ） (A)1(B)0 (C) 1 (D)2(6)如图，AB 是⊙O 的切线，A 为切点，连接OB 交⊙O 于点C ．若OA=3，tan ∠AOB=34，则BC 的长为（ ）(A)2 (B)３ (C)４ (D)５ (7)一组数据：2，3，3，4，若添加一个数据3，则发生变化的统计量是（ ） (A)平均数 (B)中位数 (C)众数(D)方差(8)已知一次函数y=kx +1的图象经过点A ，且函数值y 随x 的增大而减小，则点A 的坐标可能是（ ） (A)(2，4) (B)(-1，2) (C )(-1，-4)(D)(5，1)(9)如图，在四边形ABCD 中，∠A=120°，∠C=80°将△BMN 沿养MN 翻折，得到△FMN ．若MF ∥AD ，FN ∥DC ，则∠F 的度数为（ ） (A) 70° (B) 80° (C) 90° (D) 100°C DNFA BOxy(10)如图，点A 、B 分别在反比例函数y=x 1(x >0)，y=xa(x <0)的图象上．若OA ⊥OB ，2=OA OB ， 则a 的值为（ ） (A)4- (B)4 (C) 2- (D)2二、填空題(每小题4分，共24分）(11)计算：38=________．(12)我国五年来(2013年~2018年)经济实力跃上新台阶，国内生产总值增加到827000亿元．数据827000亿元用科学记数法表示为________亿元． (13)如图，四个全等的直角三角形围成一个大正方形ABCD ，中间阴影部分是一个小正方形EFGH ，这样就组成一个“赵爽弦图”，若AB=5，AE=4，则正方形EFCH 的面积为________．AB CDEF GHBF CD E(14)如图，△ABC 中，AB=35，AC=45．点F 在AC上，AE 平分∠BAC ，AE ⊥BF 于点E ．若点D 为 BC 中点，则DE 的长为________．(15)小峰抛掷一枚质地均匀的硬币两次，则事件“至少出现一次正面朝上”的概率为________．(16)2010年8月19日第26届国际数学家大会在印度的海德拉巴市举行，并首次颁出陈省身奖，该奖项是首个以中国人名字命名的国际主要科学奖．根据蔡勒公式可以得出2010年8月19日是星期________．(注：蔡勒(德国数学家)公式：W=110)1(26424-+⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡++-⎥⎦⎤⎢⎣⎡d m y y c c其中：W ——所求的日期的星期数(如大于7，就需减去7的整数倍)，c ——所求年份的前两位，y 所求年份的后两位，m —月份数(若是1月或2月，应视为上一年的13月或14月，即3≤m ≤14)，d ——日期数，[a ]—表示取数a 的整数部分．) 三、解答题(86分) (17)先化筒，再求值：⎪⎭⎫ ⎝⎛+-÷++111122a a a a ，其中a =3．(18)( 8分)如图，等边△ABC．(1)求作一点D，连接AD、CD，使得四边形ABCD为菱形；(要求：尺规作图，保留作图痕迹，不写作法) (2)连接BD交AC于点O，若OA=1，求菱形ABCD 的面积．(19)( 8分)保险公司车保险种的基本保费为a(单位：元)，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下表：上年度出险次数0 1 2 3 4 ≥5保费0.85a a 1.25a1.5a1.75a2a该公司随机调查了该险种的300名续保人在一年内的出险情况，得到如下统计图：(1)样本中，保费高于基本保费的人数为________名；(2)已知该险种的基本保费a 为6000元，估计一名 续保人本年度的平均保费．(20)( 8分)如图，在△ABC 中，AB=BC ，∠ABC=90°．分别以AB 、AC 为边在AB 同侧作等边△ABD 和等边△ACE ，连接DE ．(1)判断△ADE 的形状，并加以证明；(2)过图中两点画一条直线，使其垂直平分图中的某条线段，并说明理由．(21)( 8分)水果店在销售某种水果，该种水果的进价为10元/kg 根据以往的销售经验可知：日销量y(单位：kg)随售价x (单位：元/kg)的变化规律符合某种函数关系．该水果店以往的销售记录如下表：(售价不低于进价) 售价x (单10 15 20 23AD位：元/kg) 5 0 日销量y(单位：kg)30 20 15 12 1若y 与x 之间的函数关系是一次函数，二次函数，反比例函数中的某一种．(1)判断y 与x 之间的函数关系，并写出其解析式； (2)水果店销售该种水果的日利润能否达到200元?说明理由．(22)( 10分)如图，CD 是⊙O 的直径，AB 是⊙O 的弦，AB ⊥CD ，垂足为N ，连接AC ． (1)若ON=1，BN=3，求BC 长； (2)若点E 在AB 上，且AC 2=AE ·AB ，求证：∠CEB=2∠CAB ．AB D O NE(23)( 10分)规定：在平面直角坐标系内，某直线l 1与绕原点O 顺时针旋转90°，得到的直线l 2称为l 1的“旋转垂线．(1)求出直线2+-=x y 的“旋转垂线”的解析式； (2)若直线)0(111≠+=kx k y 的“旋转垂线”为直线bx k y +=2，求证：k 1·k 2=1-．(24)( 12分)如图，AD 平分∠BAC ，BD ⊥AD ，垂足为点D ．点P 是AD 上一点，PQ ⊥AC 于点Q ，连接BP 、DQ ．(1) 求证：AP AQ =ABAD； (2)求证：∠DBP=∠DQP ； (3)若BD=1，点P 在线段AD 上运动(不与A 、D 重合)，设DP=t ，QABCDP点P 到AB 的距离为d 1，点P 到DQ 的距离为d 2．记S=21d d ，求S 与t 之间的函数关系式．(25)( 14分)已知二次函数y=ax 2+bx +c (a ≠0)的图象与x轴交于A 、B 两点，顶点为C ，且△ABC 为等腰 直角三角形．(1)当A(1-，0)，B(3，0)时，求a 的值； (2)当a b 2-=，0<a 时，(i)求该二次函数的解析式(用只含a 的式子表示)； (ii)在1-≤x ≤3范围内任取三个自变量x 1、x 2、x 3，所对应的的三个函数值分别为y1、y2、y3，若以y1、y2、y3为长度的三条线段能围成三角形，求a的取值范围．参考答案与评分标准(1) C(2) C(3) B(4) D(5) C(6) A(7) D (8) B(9) B(10) A(11) 2 (12) 8.27⨯105 (13) 1 (14) 25(15) 43 (16) 四 三、解答题(17) (本小题满分8分) 解：原式=111)1(2+-+÷+a a a a┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄2分 =aa a a 1)1(2+⨯+┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分 =11+a ┄ ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分 ∵a ＝13-.∴原式=33311131==+-.┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分 (18) (本小题满分8分) (I)┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄3分如图所示，点D就是所求作的点.┄┄┄┄┄┄┄┄┄┄4分(II) 在菱形ABCD 中，∠BAC =60°，OB ⊥OA ， ┄┄┄5分∴在Rt △OAB 中，tan ∠OAB =tan60°=OA OB . ∵OA=1 ∴3=BO ，BD =32. ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄7分 又∵AC =2OA =2 ∴菱形ABCD的面积3221=⋅=AC BD S .┄┄┄┄┄┄┄┄┄┄┄┄┄8分 (19) (本小题满分8分) (I)120┄┄┄┄┄┄┄┄ ┄┄┄┄┄┄┄┄┄┄4分 (II) 解：平均保费为300)21075.1305.14025.14018085.0100(6000⨯+⨯+⨯+⨯+⨯+⨯⨯ =6950(元)┄┄┄┄┄┄┄┄ ┄┄┄┄┄┄┄┄┄┄8分(20) (本小题满分8分) (I)△ADE是等腰直角三角形.┄┄┄┄┄┄┄┄┄┄┄┄┄┄1分 理由：在等边△ABD 和等边△ACE 中，∵BA=DA，CA=EA，∠BAD=∠CAE=60°.∴∠BAD -∠CAD=∠CAE -∠CAD.即∠BAC=∠EAD.∴△ABC≌△ADE.┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄3分∴AB=AD，BC=DE，∠ABC=∠ADE∵AB=BC，∠ABC=90°∴AD=DE，∠ADE=90°即△ADE是等腰直角三角形.┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄4分(II) 连接CD，则直线CD垂直平分线段AE.(或连接BE，则直线BE垂直平分线段AC)┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分理由：由(I)得DA=DE.又∵CA=CE.∴直线CD垂直平分线段AE.┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分(21) (本小题满分8分)(I) 解：观察可知，售价x与日销量y的乘积为定值300.y与x之间的关系为反比例函数. ┄┄┄┄┄┄┄┄┄┄┄┄2分设函数解析式为)0( ≠=k x k y . 当30,10==y x 时，300=k .┄┄┄┄┄┄┄┄┄┄┄┄┄3分∴函数解析式为 300x y =. ┄┄ ┄┄┄┄┄┄┄┄┄┄4分(II)解： 能达到200元. 理由：依题意：200300)10(=⋅-x x . 解得：30=x .┄┄┄┄┄┄┄┄┄┄┄┄6分 经检验，30=x 是原方程的解，并且符合题意.┄┄┄┄┄┄┄7分答：当售价30元/kg 时，水果店销售该种水果的日利润为200元. ┄┄┄┄8分 (22) (本小题满分10分)(I)解：∵AB ⊥CD ，垂足为N ∴∠BNO =90°在Rt △ABC 中，∵ON =1，BN =3 ∴222=+=ON BN BO ，3tan ==∠ONBNBON ┄┄┄3分 ∴∠BON =60°┄┄┄┄┄┄┄┄┄┄4分21NEABDOC∴. ┄┄┄┄┄┄┄┄5分(II)证明：如图，连接BC∵CD 是⊙O 的直径，AB ⊥CD ， ∴. ┄┄┄┄┄┄┄┄┄┄┄┄6分∴∠1=∠CAB∵ABAE AC ⋅=2，且∠A =∠A∴△ACE∽△ABC┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分∴∠1=∠2 ∴∠CAB =∠2 ∴∠CEB =∠CAB +∠2=2∠CAB .┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄10分 (23) (本小题满分10分)(I)解：直线2+-=x y 经过点（2，0）与（0，2）， 则这两点绕原点O 顺时针旋转90°的对应点为（0，-2）与（2，0）┄┄┄2分 设直线2+-=x y 的“旋转垂线”的解析式为)0( ≠+=k m kx y┄┄3分把（0，-2）与（2，0）代入 m kx y +=得：⎩⎨⎧=+-=022m k b .解得⎩⎨⎧-==21m k .即直线2+-=x y 的“旋转垂线”为2-=x y ；┄┄┄┄┄┄┄┄┄┄┄┄┄5分(II) 证明：直线)0( 111≠+=kx k y 经过点（11k -，0）与（0，1）， ┄┄┄┄6分则这两点绕原点O 顺时针旋转90°的对应点为（0，11k ）与（1，0）， ┄┄8分把（0，11k ）与（1，0）代入b x k y +=2，得⎪⎩⎪⎨⎧=+=0121b k k b ∴0112=+k k ，∴121-=⋅k k .┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄10分 (24) (本小题满分12分)(I)证明∵AD 平分∠BAC ， ∴∠PAQ =∠BAD ∵PQ ⊥AC ，BD ⊥AD ∴∠PQA =∠BDA =90° ∴△PQA ∽△BDA┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄2分∴ABADAP AQ =┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄3分(II)证法一：由(I)得ABADAP AQ =又∵∠PAB =∠QAD ∴△PAB ∽△QAD┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄5分∴∠APB =∠AQD ∵∠APB =∠PDB +∠DBP ∠AQD =∠AQP +∠DQP ∴∠PDB =∠AQP =90° ∴∠DBP =∠DQP┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄7分证法二：如图，延长AC ，交BD 的延长线于点E ，连接PE ，取PE 的中点O ，连接OD,OQ. ∵∠PDE =∠PQE =90° 在Rt △PDE 与Rt △PQE 中， ∵O 是PE 的中点，∴PE DO 21=，PE QO 21= 即PO EO QO DO ===∴P 、D 、E 、Q 四点都在以O 为圆心，OP 为半径的1OQ DBC P⊙O 上，┄┄┄┄┄┄┄┄5分 ∴∠1=∠DQP ∵AD 垂直平分BE ∴PB =PE ∴∠1=∠DBP ∴∠DBP =∠DQP┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄7分(III)解：过点P 分别作PG ⊥AB 于点G ，PH ⊥DQ 于点H . 则PG =d 1，PH =d 2.∵AD 平分∠BAC ，PQ ⊥AC.∴d 1=PG =PQ . ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分∴PHPQ dd S ==21.由(II)得∠DBP =∠DQP ， ∵∠BDP =∠QHP =90°. ∴△DBP∽△HQP；┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄10分∴PDPBPH PQ =. 在Rt △BDP 中，BD =1，DP =t. ∴12+=t PB .∴tt S 12+=.H GQ DBAP┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分 25．(本小题满分14分)(I) 解：∵A (-1，0)，B (3，0)，∴该二次函数图象的对称轴为1=x ，且AB =4.过点C 作CH ⊥AB 于点H.∵△ABC 为等腰直角三角形，∴CH =21AB =2. ┄┄1分∴C (1，-2)或C (1，2)①如图1，当C (1，-2)时，可设2)1(2--=x a y .把点B (3，0)代入可得：21=a . ┄┄┄┄3分 ②如图2，当C (1，2)时，可设2)1(2+-=x a y .把点B (3，0)代入可得：21-=a .综上所述，21=a 或21-. ┄┄┄┄┄┄┄4分 (II)解：(i ) 当ab 2-=时，cax ax y +-=22=ac x a -+-2)1(.┄┄┄┄┄┄┄┄5分∴C (1，c -a ) ∴B (1+c -a，0).┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分 ∴0)(2=-+-a c a c a .O yxHB A C图1Oy xH CBA图2∴0)1)((2=+--a ac a c .∵0≠-a c ，∴aa c 1-=. ∴()ax a y 112--=.┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄8分(ii ) 法一：∵31≤≤-x ，a <0，∴当x =-1或3时，y 取得最小值aa 14-，┄┄┄┄┄┄┄┄┄┄┄┄10分当x =1时，y取得最大值a1-.┄┄┄┄┄┄┄┄┄┄┄┄11分若以321, , y y y 为长度的三条线段能围成三角形.则aa a 1)14(2->-.┄┄┄┄┄┄┄┄┄┄┄┄13分整理得：0182<-a .∴042<<-a .┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄14分法二：依题意得：ax a y1)1(211--=，ax a y1)1(222--=，ax a y 1)1(233--=.┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄9分以321, , y y y 为长度的三条线段能围成三角形.不妨设321y y y≤≤. 则321y yy >+在31≤≤-x 范围内恒成立.∴ax a a x a a x a 1)1(1)1(1)1(232221-->--+--整理得：22322211)1()1()1(a x x x <---+-.┄┄┄┄┄┄┄┄┄┄┄10分等价于232221)1()1()1(---+-x x x 最大值小于21a .当121-==x x 时，2221)1()1(-+-x x 取最大值为8；当13=x 时，23)1(-x取最小值为0.此时232221)1()1()1(---+-x x x 取最大值为8.∴218a <.┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄13分整理得：0182<-a .∵0<a . ∴042<<-a .┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄14分。
2018年九年级质量检测数学试题
2018年九年级质量检测数学试卷※ 时间：120分钟 满分：150分一、选择题（下列各题的备选答案中，只有一个答案是正确的，请将正确答案的序号填入下列表格内．每小题３分，共24分）1．实数在数轴上表示如图所示，则下列结论错误的是Ａ．0a b +< Ｂ．0ab < Ｃ．b a -> Ｄ．0a b -< 2．某商场的老板销售一种商品，他要以不低于进价20%价格才能出售，但为了获得更多利润，他以高出进价80%的价格标价．若你想买下标价为360元的这种商品，最多降价多少时商店老板才能出售A ．80元B ．100元C ．120元D ．160元 3．如图是小刚一天中的作息时间分配的扇形统计图.如果小刚希望把自己每天的阅读时间调整为2时， 那么他的阅读时间需增加A ．15分B ．48分C ．60分D ．105分 4．下列计算正确的是A ．3＋3＝ 6B ．3－3＝0C ．3·3＝9D ．(－3)2＝－35．一把遮阳伞撑开时母线的长是2米，底面半径为1米，则做这把遮阳伞需用布料的面积是 A ．4π平方米 B ．2π平方米C ．π平方米D ．1π2平方米 6．AB 是O ⊙的直径，弦CD AB ⊥于点E ，连结OC ，若5OC =，8CD =，则tan COE ∠等于 A ．35 B ．45 C ．34 D ．43第3题图第5题图B第6题图7．如图，在平面直角坐标系中，菱形OACB 的顶 点O 在原点，点C 的坐标为(40)，，点B 的纵坐 标是1-，则顶点A 的坐标是A ．(21)-，B ．(12)-，C ．(12)，D ．(21)， 8．如图，在平面直角坐标系中有两点(62)A ，，(60)B ，，以原点为位似中心，相似比为1∶3．把线段AB 缩 小，则过A 点对应点的反比例函数的解析式为A ．4y x =B ．43y x =C ．43y x =-D ．18y x=二、填空题(每题3分，共24分)9．2018年某市工业总产值突破千亿大关，提前两年完成“十一五”规划预期目标．用科学记数法表示数 1 千亿，正确的是 ． 10．三角形的两边长分别为3和6，第三边的长是方程2680x x -+=的一个根，则这个三角形的周长是 ．11．一个三角形的三边长分别为cm 8，cm 12，cm 18则它的周长是 cm ． 12．有一个不透明的布袋中，红色、黑色、白色的玻璃球共有40个，除颜色外其它完全相同．小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%，则口袋中白色球的个数很可能是 ．13．如图，等腰梯形ABCD 中，AD ∥BC ，以A 为圆心，AD 为半径的圆与BC 切于点M ，与AB 交于点E ，若AD ＝2，BC ＝6， 则⌒DE 的长为 ．14．若不等式组⎩⎨⎧>->-022x b a x 的解集是11x -<<，则2010()a b += ．15．某商店经营一种水产品，成本为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克；销售价每涨1元，月销售量就减少10千克，针对这种水产品的销售情况，销售单价定为 元时，获得的利润最多.第13题图y第7题图ME D C B A16．在平面直角坐标系中，已知点O (0，0)、A (1，n )、B (2，0)，其中n ＞0，△OAB 是等边三角形．点P 是线段OB 的中点，将△OAB 绕点O 逆时针旋转30º，记点P 的对应点为点Q ，则n ＝ ，点Q 的坐标是 ．三、（17题、18题各8分，共16分）17．如果1-是一元二次方程230x bx +-=的一个根，求它的另一根．18．在右面的网格图中按要求画出图形. （1）画出△ABC 关于x 轴对称的△A 1B 1C 1； （2）画出△ABC 关于y 轴对称的△A 2B 2C 2；；（3）画出以点O 为位似中心，与△ABC 位似且位似比为0.5的△A 3B 3C 3. （说明：必须用铅笔画图）四、（19题、20题各10分，共20分）19．我市某中学为调查本校学生使用零花钱的情况，随机调查了50名同学，下图是根据调查所得数据绘制的统计图的一部分． 请根据以上信息，解答下列问题： （1）将统计图补充完整； （2）若该校共有1000名学生，根据以上调查结果估计，该校全体学生平均每天用去多少元零花钱？（3）如果将全校1000名学生一周（7天）的零花钱节省下来，全部捐给灾区学校购买课桌椅，每套课桌椅150元，共可以为灾区学校购买多少套这样的课桌椅？20．现有边长为a 的正方形花布，问怎样剪裁，才能得到一个面积最大的正八边形花布来做一个形状为正八边形的风筝？第20题图人数/名/元第19题图21．如图，要在木里县某林场东西方向的两地之间修一条公路MN ，已知C 点周围200米范围内为原始森林保护区，在MN 上的点A 处测得C 在A 的北偏东45°方向上，从A 向东走600米到达B 处，测得C 在点B 的北偏西60°方向上． （1）MN 1.732）（2）若修路工程顺利进行，要使修路工程比原计划提前5天完成，需将原定的工作效率提高25%，则原计划完成这项工程需要多少天？22．如图，甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形．小夏和小秋利用它们来做决定获胜与否的游戏．规定小夏转甲盘一次、小秋转乙盘一次为一次游戏（当指针指在边界线上时视为无效，重转）．（1）小夏说：“如果两个指针所指区域内的数之和为6或7，则我获胜；否则你获胜” ．按小夏设计的规则，请你写出两人获胜的可能性分别是多少?（2）请你对小夏和小秋玩的这种游戏设计一种公平的游戏规则，并用一种合适的方法(例如：树状图，列表)说明其公平性．C BN M A 第21题图 第22题图）23．如图，⊙O 的直径AB 是4，过B 点的直线MN 是⊙O 的切线，D 、C 是⊙O 上的两点，连接AD 、BD 、CD 和BC ． (1)求证：CDB CBN ∠=∠；(2)若DC 是ADB ∠的平分线，且︒=∠15DAB ，求DC24．已知某种水果的批发单价与批发量的函数关系如图（1）所示． （1（2）写出批发该种水果的资金金额w （元）与批发量m （kg ）之间的函数关系式；在下图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．（3）经调查，某经销商销售该种水果的日最高销量与零售价之间的函数关系如图（2）所示，该经销商拟每日售出60kg 以上该种水果，且当日零售价不变，请你帮助该经销商设计进货和销售的方案，使得当日获得的利润最大．）N M BA 第23题图第24题图（1 第24题图（2）七、（12分）25．等腰△ABC，AB=AC，∠BAC=120°，P为BC上的中点，小慧拿着含 30°角的透明三角板，使30°角的顶点落在点P.（1）当三角板的一条直角边经过点A时，斜边交AC边于点F如图（1），△BPA与△PFA 是否相似？说明理由；（2）当三角板绕P 旋转到图（2）情形时，三角板的两边分别交BA的延长线与点E、交边AC于点F,连结EF，△BPE与△PFE是否相似？请说明理由.(1)(2)八、（14分）26．如图，抛物线n mx x y ++=221与x 轴交于A 、B 两点，与y 轴交于C 点，四边形OBHC 为矩形，CH 的延长线交抛物线于点D （5，2），连结BC 、AD .（1）求C 点的坐标及抛物线的解析式；（2）将△BCH 绕点B 按顺时针旋转90°后 再沿x 轴对折得到△BEF （点C 与点E 对应），判断点E 是否落在抛物线上，并说明理由；（3）设过点E 的直线交AB 边于点P ，交CD 边于点Q . 问是否存在点P ，使直线PQ 分梯形ABCD 的面积为1∶3两部分？若存在，求出P 点坐标；若不存在，请说明理由.。
2018年厦门九年级数学质检试题及答案
2018年厦门市初中总复习教学质量检测数 学（试卷满分：150分 考试时间：120分钟）准考证号 姓名 座位号注意事项：1．全卷三大题，25小题，试卷共4页，另有答题卡． 2．答案必须写在答题卡上，否则不能得分． 3．可以直接使用2B 铅笔作图．一、选择题（本大题有10小题，每小题4分，共40分.每小题都有四个选项，其中有且只有一个选项正确）1.计算－1＋2，结果正确的是A . 1B . －1C . －2D . －3 2.抛物线y ＝ax 2＋2x ＋c 的对称轴是A . x ＝－1aB . x ＝－2aC . x ＝1aD . x ＝2a3.如图1，已知四边形ABCD ，延长BC 到点E ，则∠DCE 的同位角是A . ∠AB . ∠BC . ∠DCBD .∠D4.某初中校学生会为了解2017年本校学生人均课外阅读量，计划开展抽样调查.下列抽样调查方案中最合适的是A .到学校图书馆调查学生借阅量B .对全校学生暑假课外阅读量进行调查C .对初三年学生的课外阅读量进行调查D .在三个年级的学生中分别随机抽取一半学生进行课外阅读量的调查 、 5.若967×85＝p ，则967×84的值可表示为A . p －1B . p －85C . p －967D .8584p 6. 如图2，在Rt△ACB 中，∠C ＝90°，∠A ＝37°，AC ＝4，则BC 的长约为（sin37°≈0.60，cos37°≈0.80，tan37°≈0.75） A . 2.4 B . 3.0 C . 3.2 D . 5.07. 在同一条直线上依次有A ，B ，C ，D 四个点，若CD －BC ＝AB ，则下列结论正确的是 A . B 是线段AC 的中点 B . B 是线段AD 的中点 C . C 是线段BD 的中点 D . C 是线段AD 的中点8. 把一些书分给几名同学，若 ；若每人分11本则不够. 依题意，设有x 名同学， 可列不等式9x ＋7＜11x ，则横线上的信息可以是 A ．每人分7本，则可多分9个人 B. 每人分7本，则剩余9本图1E DC B A图2 ABCC ．每人分9本，则剩余7本D. 其中一个人分7本，则其他同学每人可分9本9. 已知a ，b ，c 都是实数，则关于三个不等式：a ＞b ，a ＞b ＋c ，c ＜0的逻辑关系的表述，下列正确的是A . 因为a ＞b ＋c ，所以a ＞b ，c ＜0B . 因为a ＞b ＋c ，c ＜0，所以a ＞bC . 因为a ＞b ，a ＞b ＋c ，所以c ＜0D . 因为a ＞b ，c ＜0，所以a ＞b ＋c 10. 据资料，我国古代数学家刘徽发展了测量不可到达的物体的高度的“重差术”，如：通过下列步骤可测量山的高度PQ （如图3）：（1）测量者在水平线上的A 处竖立一根竹竿，沿射线QA 方向走到M 处，测得山顶P 、竹竿顶点B 及M 在一条直线上；（2）将该竹竿竖立在射线QA 上的C 处，沿原方向继续走到N 处，测得山顶P ，竹竿顶点D 及N 在一条直线上；（3）设竹竿与AM ，CN 的长分别为l ，a 1，a 2，可得公式： PQ ＝d ·la 2－a 1＋l .则上述公式中，d 表示的是A .QA 的长B . AC 的长 C .MN 的长D .QC 的长 二、填空题（本大题有6小题，每小题4分，共24分）11.分解因式： m 2－2m ＝ .12.投掷一枚质地均匀的正六面体骰子，向上一面的点数为奇数的 概率是 .13.如图4，已知AB 是⊙O 的直径，C ，D 是圆上两点，∠CDB ＝45°，AC ＝1，则AB 的长为 .14. A ，B 两种机器人都被用来搬运化工原料，A 型机器人比B 型机器人每小时多搬运30kg ，A 型机器人搬运900kg 所用时间与B 型机器人搬运600kg 所用时间相等.设B 型机器人每小时 搬运x kg 化工原料，根据题意，可列方程__________________________. 15.已知a ＋1＝20002＋20012，计算：2a ＋1＝ .16.在△ABC 中，AB ＝AC .将△ABC 沿∠B 的平分线折叠，使点A 落在BC 边上的点D 处， 设折痕交AC 边于点E ，继续沿直线DE 折叠，若折叠后，BE 与线段DC 相交，且交点不 与点C 重合，则∠BAC 的度数应满足的条件是 .三、解答题（本大题有9小题，共86分）17.（本题满分8分）解方程：2（x －1）＋1＝x .18.（本题满分8分）如图5，直线EF 分别与AB ，CD 交于点A ，C ，若AB ∥CD ，CB 平分∠ACD ，∠EAB ＝72°，求∠ABC 的度数.FE ABC D图4B图3如图6，平面直角坐标系中，直线l经过第一、二、四象限，点A（0，m）在l上.（1）在图中标出点A；（2）若m＝2，且l过点（－3，4），求直线l的表达式.20.（本题满分8分）如图7，在□ABCD中，E是BC延长线上的一点，且DE＝AB，连接AE，BD，证明AE＝BD.21.（本题满分8分）某市的居民交通消费可分为交通工具、交通工具使用燃料、交通工具维修、市内公共交通、城市间交通等五项.该市统计局根据当年各项的权重及各项价格的涨幅计算当年居民交通消费价格的平均涨幅. 2017年该市的有关数据如下表所示.（1）求p的值；（2）若2017年该市的居民交通消费相对上一年价格的平均涨幅为1.25%，求m的值.22.（本题满分10分）如图8，在矩形ABCD中，对角线AC，BD交于点O，（1）AB＝2，AO＝5，求BC的长；（2）∠DBC＝30°，CE＝CD，∠DCE＜90°，若OE＝22BD，求∠DCE的度数.l图6图7E AB CD图8OAB CDE已知点A ，B 在反比例函数y ＝6x （x ＞0）的图象上，且横坐标分别为m ，n ，过点A ，B 分别向y 轴、x 轴作垂线段，两条垂线段交于点C ，过点A ，B 分别作AD ⊥x 轴于D ，作BE ⊥y 轴于E.（1）若m ＝6，n ＝1，求点C 的坐标；（2）若3)2(=-n m ，当点C 在直线DE 上时，求n 的值．24.（本题满分11分）已知AB ＝8，直线l 与AB 平行，且距离为4，P 是l 上的动点，过点P 作PC ⊥AB 交线段AB 于点C ，点C 不与A ，B 重合，过A ，C ，P 三点的圆与直线PB 交于点D . （1）如图9，当D 为PB 的中点时，求AP 的长；（2）如图10，圆的一条直径垂直AB 于点E ，且与AD 交于点M .当ME 的长度最大时，判断直线PB 是否与该圆相切？并说明理由.25.（本题满分14分）已知二次函数y ＝ax 2＋bx ＋t －1，t ＜0， （1）当t ＝－2时，① 若函数图象经过点（1，－4），（－1，0），求a ，b 的值；② 若2a －b ＝1，对于任意不为零的实数a ，是否存在一条直线y ＝kx ＋p （k ≠0），始终与函数图象交于不同的两点？若存在，求出该直线的表达式；若不存在，请说明理由.（2）若点A （－1，t ），B （m ，t －n ）（m ＞0，n ＞0）是函数图象上的两点，且S △AOB ＝12n －2 t ，当－1≤x ≤m 时，点A 是该函数图象的最高点，求a 的取值范围.图9 A l C B DP 图10 l A M E C B D P2018年厦门市九科教学质量检测数学参考答案说明：解答只列出试题的一种或几种解法．如果考生的解法与所列解法不同，可参照评分量表的要求相应评分.一、选择题（本大题共10小题，每小题4分，共40分）11. m （m －2）. 12. 12. 13. 2. 14. 900x ＋30＝600x .15. 4001. 16.100°＜∠BAC ＜180°. 三、解答题（本大题有9小题，共86分）17.（本题满分8分）解：2x －2＋1＝x .…………………………4分 2x －x ＝2－1.…………………………6分 x ＝1.…………………………8分18.（本题满分8分）解法一:如图1∵ AB ∥CD ，∴ ∠ACD ＝∠EAB ＝72°.…………………………3分 ∵ CB 平分∠ACD ， ∴ ∠BCD ＝12∠ACD ＝36°. …………………………5分∵ AB ∥CD ，∴ ∠ABC ＝∠BCD ＝36°. …………………………8分 解法二:如图1∵ AB ∥CD ，∴ ∠ABC ＝∠BCD . …………………………3分 ∵ CB 平分∠ACD ，∴ ∠ACB ＝∠BCD . …………………………5分 ∴ ∠ABC ＝∠ACB .∵ ∠ABC ＋∠ACB ＝∠EAB ， ∴ ∠ABC ＝12∠EAB ＝36°. …………………………8分图1FE ABC D19.（本题满分8分）（1）（本小题满分3分）如图2；…………………………3分（2）（本小题满分5分）解：设直线l 的表达式为y ＝kx ＋b （k ≠0），…………………………4分 由m ＝2得点A （0，2）， 把（0，2），（－3，4）分别代入表达式，得⎩⎨⎧b ＝2，－3k ＋b ＝4.可得⎩⎪⎨⎪⎧b ＝2，k ＝－23 ．…………………………7分所以直线l 的表达式为y ＝－23x ＋2． …………………………8分20.（本题满分8分）证明：如图3∵ 四边形ABCD 是平行四边形，∴ AB ∥DC ，AB ＝DC ．………………………… 2分 ∵ DE ＝AB ， ∴ DE ＝DC ．∴ ∠DCE ＝∠DEC ．…………………………4分 ∵ AB ∥DC ，∴ ∠ABC ＝∠DCE ． …………………………5分∴ ∠ABC ＝∠DEC ． …………………………6分 又∵ AB ＝DE ，BE ＝EB ，∴ △ABE ≌△DEB ． …………………………7分 ∴ AE ＝BD ． …………………………8分21.（本题满分8分）（1）（本小题满分3分）解：p ＝1－（22%＋13%＋5%＋26%）…………………………2分＝34%． …………………………3分 （2）（本小题满分5分） 解：由题意得图3EA B C D22%×1.5%＋13%×m %＋5%×2%＋34%×0.5%＋26%×1%22%＋13%＋5%＋34%＋26%＝1.25%． …………………7分解得m ＝3． …………………………8分22.（本题满分10分）（1）（本小题满分4分）解：如图4∵四边形ABCD 是矩形，∴ ∠ABC ＝90°，AC ＝2AO ＝25．………………………2分 ∵ 在Rt △ACB 中，∴ BC ＝AC 2－AB 2 ………………………3分＝4．………………………4分 （2）（本小题满分6分）解：如图4∵ 四边形ABCD 是矩形，∴ ∠DCB ＝90°，BD ＝2OD ，AC ＝2OC ，AC ＝BD ． ∴ OD ＝OC ＝12BD ．∵ ∠DBC ＝30°，∴ 在Rt △BCD 中，∠BDC ＝90°－30°＝60°， CD ＝12BD ．∵ CE ＝CD ，∴ CE ＝12BD ．………………………6分∵ OE ＝22BD ， ∴ 在△OCE 中，OE 2＝12BD 2．又∵ OC 2＋CE 2＝14BD 2＋14BD 2＝12BD 2，∴ OC 2＋CE 2＝OE 2．∴ ∠OCE ＝90°．…………………8分 ∵ OD ＝OC ，图4OABCDE∴ ∠OCD ＝∠∴ ∠DCE ＝∠23.（本题满分11分）（1）（本小题满分解：因为当m ＝6又因为n ＝1， 所以C （1，1）（2）（本小题满分解：如图5所以A （m ，6m ），B 所以D （m ，0），E 设直线DE 把D （m ，0），E （．………………………7分因为点C 在直线所以把C （n ，6m ）代入把m ＝2n 代入m （n －2）＝3，得2n （n －2）＝3．，………………………9分 解得n ＝2±102．………………………10分因为n ＞0，所以n ＝2＋102．………………………11分24.（本题满分11分）（1）（本小题满分5分）解法一：如图6，∵ PC ⊥AB ， ∴ ∠ACP ＝90°．∴ AP 是直径．…………………2分∴ ∠ADP ＝90°． …………………3分即AD ⊥PB ．又∵ D 为PB 的中点，∴ AP ＝AB ＝8．…………………5分解法二：如图7，设圆心为O ，PC 与AD 交于点N ，连接OC ，OD ．图6A lC BD PB C A DE图5lP∵ ︵CD ＝︵CD ，∴ ∠CAD ＝12∠COD ，∠CPD ＝12∠COD ．∴ ∠CAD ＝∠CPD ．…………………1分∵ ∠ANC ＝∠PND ，又∵ 在△ANC 和△PND 中，∠NCA ＝180°－∠CAN －∠ANC ， ∠NDP ＝180°－∠CPN －∠PND ，∴ ∠NCA ＝∠NDP ． …………………2分 ∵ PC ⊥AB ，∴ ∠NCA ＝90°．∴ ∠NDP ＝90°． …………………3分 即AD ⊥PB ．又∵ D 为PB 的中点，∴ AP ＝AB ＝8．…………………5分（2）（本小题满分6分）解法一：当ME 的长度最大时，直线PB 与该圆相切． 理由如下：如图8，设圆心为O ，连接OC ，OD ． ∵ ︵CD ＝︵CD ，∴ ∠CAD ＝12∠COD ，∠CPD ＝12∠COD ．∴ ∠CAD ＝∠CPD ．又∵ PC ⊥AB ，OE ⊥AB ， ∴ ∠PCB ＝∠MEA ＝90°．∴ △MEA ∽△BCP ． …………………7分 ∴ ME BC ＝AE PC．∵ OE ⊥AB ， 又∵ OA ＝OC ， ∴ AE ＝EC ．设AE ＝x ，则BC ＝8－2x ．图8l AM EC BD PO ·由ME BC ＝AE PC ，可得ME ＝－12（x －2）2＋2．…………………8分 ∵ x ＞0，8－2x ＞0， ∴ 0＜x ＜4． 又∵ －12＜0，∴ 当x ＝2时，ME 的长度最大为2．…………………9分 连接AP ，∵ ∠PCA ＝90°， ∴ AP 为直径．∵ AO ＝OP ，AE ＝EC ， ∴ OE 为△ACP 的中位线． ∴ OE ＝12PC ．∵ l ∥AB ，PC ⊥AB ， ∴ PC ＝4． ∴ OE ＝2．∴ 当ME ＝2时，点M 与圆心O 重合．…………………10分 即AD 为直径．也即点D 与点P 重合．也即此时圆与直线PB 有唯一交点．所以此时直线PB 与该圆相切．…………………11分解法二：当ME 的长度最大时，直线PB 与该圆相切． 理由如下：如图8，设圆心为O ，连接OC ，OD ． ∵ OE ⊥AB ， 又∵ OA ＝OC ， ∴ AE ＝EC ．设AE ＝x ，则CB ＝8－2x ． ∵ ︵CD ＝︵CD ，∴ ∠CAD ＝12∠COD ，∠CPD ＝12∠COD ．∴ ∠CAD ＝∠CPD ．又∵ PC ⊥AB ，OE ⊥AB ，图8l AMEC BD PO ·∴ ∠PCB ＝∠MEA ＝90°．∴ △MEA ∽△BCP ． …………………7分∴ ME BC ＝AE PC． 可得ME ＝－12（x －2）2＋2．…………………8分 ∵ x ＞0，8－2x ＞0，∴ 0＜x ＜4．又∵ －12＜0， ∴ 当x ＝2时，ME 的长度最大为2．…………………9分连接AP ，∵ AE ＝x ＝2，∴ AC ＝BC ＝PC ＝4．∵ PC ⊥AB ，∴ ∠PCA ＝90°，∴ 在Rt △ACP 中，∠P AC ＝∠APC ＝45°．同理可得∠CPB ＝45°．∴ ∠APB ＝90°．即AP ⊥PB ． …………………10分又∵ ∠PCA ＝90°，∴ AP 为直径．∴ 直线PB 与该圆相切．…………………11分25.（本题满分14分）（1）（本小题满分7分）①（本小题满分3分）解：当t ＝－2时，二次函数为y ＝ax 2＋bx －3．把（1，－4），（－1，0）分别代入y ＝ax 2＋bx －3，得⎩⎨⎧a ＋b －3＝－4，a －b －3＝0．…………………………1分 解得⎩⎨⎧a ＝1，b ＝－2．所以a ＝1，b ＝－2．…………………………3分②（本小题满分4分）解法一：因为2a －b ＝1，所以二次函数为y ＝ax 2＋（2a －1）x －3．所以，当x ＝－2时，y ＝－1；当x ＝0时，y ＝－3．所以二次函数图象一定经过（－2，－1），（0，－3）．…………………………6分设经过这两点的直线的表达式为y ＝kx ＋p （k ≠0），把（－2，－1），（0，－3）分别代入，可求得该直线表达式为y ＝－x －3．…………7分 即直线y ＝－x －3始终与二次函数图象交于（－2，－1），（0，－3）两点．解法二：当直线与二次函数图象相交时，有kx ＋p ＝ax 2＋（2a －1）x －3．整理可得ax 2＋（2a －k －1）x －3－p ＝0．可得△＝（2a －k －1）2＋4a （3＋p ）．…………4分若直线与二次函数图象始终有两个不同的交点，则△＞0．化简可得4a 2－4a （k －p －2）＋（1＋k ）2＞0．因为无论a 取任意不为零的实数，总有4a 2＞0，（1＋k ）2≥0所以当k －p －2＝0时，总有△＞0．………………………6分可取p ＝1，k ＝3．对于任意不为零的实数a ，存在直线y ＝3x ＋1始终与函数图象交于不同的两点．…………7分（2）（本小题满分7分）解：把A （－1，t ）代入y ＝ax 2＋bx ＋t －1，可得b ＝a －1．………………………8分 因为A （－1，t ），B （m ，t －n ）（m ＞0，n ＞0），又因为S △AOB ＝12n －2t ， 所以12[（－t ）＋（n －t ）]（m ＋1）－12×1×（－t ）－12×（n －t ）m ＝12n －2t ． 解得m ＝3．………………………10分所以A （－1，t ），B （3，t －n ）．因为n ＞0，所以t ＞t －n ．当a ＞0时，【二次函数图象的顶点为最低点，当－1≤x ≤3时，若点A 为该函数图象最高点，则y A ≥y B 】，分别把A （－1，t ），B （3，t －n ）代入y ＝ax 2＋bx ＋t －1，得t ＝a －b ＋t －1，t －n ＝9a ＋3b ＋t －1．因为t ＞t －n ，所以a －b ＋t －1＞9a ＋3b ＋t －1．可得2a ＋b ＜0．即2a ＋（a －1）＜0．解得a ＜13． 所以0＜a ＜13． 当a ＜0时，由t ＞t －n ，可知：【若A ，B 在对称轴的异侧，当－1≤x ≤3时，图象的最高点是抛物线的顶点而不是点A ；若A ，B 在对称轴的左侧，因为当x ≤－b 2a时，y 随x 的增大而增大，所以当－1≤x ≤3时，点A 为该函数图象最低点；若A ，B 在对称轴的右侧，因为当x ≥－b 2a时，y 随x 的增大而减小，所以当－1≤x ≤3时，若点A 为该函数图象最高点，则】－b 2a≤－1． 即－a －12a≤－1． 解得a ≥－1．所以－1≤a ＜0．………………………13分综上，0＜a ＜13或－1≤a ＜0．………………………14分。
2018年5月厦门九年级数学质检试题及答案
2018年厦门市初中总复习教学质量检测数 学（试卷满分:150分 考试时间：120分钟）准考证号 姓名 座位号注意事项:1．全卷三大题，25小题,试卷共4页，另有答题卡． 2．答案必须写在答题卡上，否则不能得分． 3．可以直接使用2B 铅笔作图．一、选择题（本大题有10小题，每小题4分，共40分。
每小题都有四个选项，其中有且只有一个选项正确） 1.计算－1＋2，结果正确的是A 。
1B . －1C . －2D . －3 2。
抛物线y ＝ax 2＋2x ＋c 的对称轴是A 。
x ＝－错误!B . x ＝－错误!C 。
x ＝错误!D 。
x ＝错误!3.如图1，已知四边形ABCD ，延长BC 到点E ，则∠DCE 的同位角是A . ∠AB . ∠BC . ∠DCBD .∠D 4.某初中校学生会为了解2017年本校学生人均课外阅读量，计划开展抽样调查.下列抽样调查方案中最合适的是A 。
到学校图书馆调查学生借阅量B 。
对全校学生暑假课外阅读量进行调查C .对初三年学生的课外阅读量进行调查D .在三个年级的学生中分别随机抽取一半学生进行课外阅读量的调查 5。
若967×85＝p ,则967×84的值可表示为A . p －1B 。
p －85C . p －967D 。
8584p 6. 如图2，在Rt△ACB 中,∠C ＝90°，∠A ＝37°，AC ＝4，则BC 的长约为(sin37°≈0.60，cos37°≈0.80,tan37°≈0。
75) A 。
2.4 B 。
3.0 C . 3。
2 D 。
5。
07. 在同一条直线上依次有A ,B ，C ，D 四个点，若CD －BC ＝AB ，则下列结论正确的是 A . B 是线段AC 的中点 B 。
B 是线段AD 的中点 C 。
C 是线段BD 的中点 D 。
C 是线段AD 的中点8. 把一些书分给几名同学，若 ；若每人分11本则不够。
2018年九年级数学教学质量检测试卷及答案（浙教版）
2018年九年级数学教学质量检测试卷及答案（浙教版）九年级数学教学质量检测 2018、11．本试卷分试题卷和答题卷两部分。
满分120分，考试时间90分钟。
2．所有答案都必须做在答题卷指定位置上，请务必注意试题序号和答题序号相对应。
一、单项选择题（本大题共10个小题，每小题3分，满分30分） 1、37000用科学记数法表示为（）A 、37×103B 、3.7×104C 、3.7×105D 、0.37×1052.不等式组24010x x -<??+?≥的正整数解的个数是（）．A ．1个B ．2个C ．3个D ．4个 3. 下列各图中有可能是函数y=ax 2+c,(0,0)ay a c x=≠>的图象是（）4. 下列说法错误的有几个（）（1）不相交的两直线一定是平行线；（2）点到直线的垂线段就是点到直线的距离；（3）两点之间直线最短；（4）过一点有且只有一条直线与已知直线垂直 A.1个 B.2个 C.3个 D.4个5.下列各式从左到右的变形正确的是（）A ．(4x+1+4x2 )÷(4x 2－1)=2x －1 B.(4x 2－9)÷(3+2x)=2x －3C ． D.6、用若干个大小相同，棱长为1的小正方体搭成一个几何体模型，其三视图如图所示，则搭成这个几何体模型所用的小正方体的个数是（）个 A 、4 B 、5C 、6D 、77、某县教育部门对该县参加奥运知识竞赛的7500名初中学生的初试成绩（为整数）进行一次抽样调查，所得数据如上表，抽取样本的容量为（）A 、7500B 、7500名初中学生的初试成绩C 、500D 、500名初中学生的初试成绩8、如图，在Rt △ABC 中，AB=AC ，D 、E 是斜边BC 上两点，且∠DAE=45°，将△ADC 绕点A 顺时针旋转90 后，得到△AFB ，连接EF ，下列结论：①∠EAF=450；②△ADE ≌△AFE ；③EF=ED ；④BE 2＋DC 2=DE 2其中正确的个数是（） A 、1个 B 、2个 C 、3个 D 、4个9、如图：在△ABC 中，AB =10，AC =8，BC =6，经过点C 且与边AB 相切的动圆与CB 、CA 分别相交于点E 、F ，则线段EF 长度的最小值是（） A 、24B 、4.75C 、5D 、4.810.下列图中阴影部分的面积与算式2115()224--++- 的结果相同的是（）二、填空题（每小题4分，共24分）11、请你根据H 市快餐公司个数统计图和各快餐公司盒饭年销售量的平均数统计图所提供的信息，计算这三年中该地区每年平均销售盒饭多少万盒？12、在△ABC 中，若│tanA-1│+-cosB 2)=0，则∠C=_______ 13、|x+1|+|x-2|+|x-3|的最小值为。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2018-2019学年度初三质量检测数学试卷
一、选择题（本大题共6小题，每小题3分，共18分，每小题只有一个正确答案）
1. 设x是有理数，那么下列各式中一定表示正数的是（）
A. 2017x
B. x+2017
C. |2017x|
D. |x|+2017
2. 下列计算正确的是（）
A. x4·x4=x16
B. （a+b）2=a2+b2
C. =±4
D. （a6）2÷（a4）3=1
3. 已知点M将线段AB黄金分割（AM＞BM），则下列各式中不正确的是（）
A. AM：BM=AB：AM
B. BM=AB
C. AM=AB
D. AM≈0.618AB
4. 为调查某校1500名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机抽取部分学生进行调查，并结合调查数据作出如图所示的扇形统计图．根据统计图提供的信息，可估算出该校喜爱体育节目的学生共有（）
A. 1200名
B. 450名
C. 400名
D. 300名
5. 在直角坐标中，将△ABC的三个顶点的纵坐标分别乘以-1，横坐标不变，则所得图形与原图的关系是（）
A. 关于x轴对称
B. 关于y轴对称
C. 关于原点对称
D. 将原图向下平移1个单位
6. 如图所示为某几何体的示意图，则该几何体的左视图应为（）
A. （A）
B. （B）
C. （C）
D. （D）
二、填空题（本大题共6小题，每小题3分，共18分）
7. 若a与b互为相反数，则a+b=____.
8. 在直角坐标系中，O为原点，点A（a，3）在第一象限，OA与X轴所夹的锐角为α，tanα=1.5，则b=_______.
9. 底面直径和高都是1的圆柱侧面积为____.
10. 分式方程的解是_____.
11. 如图，∠ABC=∠ACD=90°，∠BAC=∠CAD，AB=4，BC=2，则△ACD的面积=_______.
12. 已知抛物线y=ax2与线段AB无公共点，且A（-2，-1），B（-1，-2），则a的取值范围是___.
三、（本大题共5小题，每小题6分，共30分）
13. （1）先化简，再求值:（a-2）2+a（a+4），其中a=；
（2）在△ABC中，D，E分别是AB,AC上的一点，且DE∥BC，，BC=12，求DE的长.
14. 关于x的不等式组：，
（1）当a=3时，解这个不等式组；
（2）若不等式组的解集是x＜1，求a的值.
15. 某校在校运会之前想了解九年级女生一分钟仰卧起坐得分情况（满分为7分），在九年级500名女生中随机抽出60名女生进行一次抽样摸底测试所得数据如下表：
（1）从表中看出所抽的学生所得的分数数据的众数是______．
A.40%
B.7
C.6.5
D.5%
（2）请将下面统计图补充完整．
（3）根据上述抽查，请估计该校考试分数不低于6分的人数会有多少人？
16. 如图，AE为菱形ABCD的高，请仅用无刻度的直尺按要求画图.（不写画法，保留画图痕迹）.
（1）在图1中，过点C画出AB边上的高；
（2）在图2中，过点C画出AD边上的高.
17. 如图，AB是半圆O的直径，点P是（不与点A，B重合）为半圆上一点.将图形沿BP折叠，分别得到点A’，O’.设∠ABP=α.
（1）当α=10°时，∠ABA’= ____度；
（2）当点O’落在弧上时，求出α的度数.
18. 从背面相同的同一副扑克牌中取出红桃9张、黑桃10张、方块11张，现将这些牌洗匀背面朝上放在桌面上.
（1）求从中抽出一张牌是红桃的概率；
（2）现从桌面上先抽掉若干张黑桃，再放入与抽掉的黑桃张数相同的红桃，并洗匀且背面都朝上排开后，随机抽一张是红桃的概率不小于，问至少抽掉了多少张黑桃？
（3）若先从桌面上抽掉9张红桃和m（m＞6）张黑桃后，再在桌面抽出一张牌.。