高一数学人教A版必修二 课件 第二章 点、直线、平面之间的位置关系 2.3.2
合集下载
高一数学人教A版必修2232平面与平面垂直的判定.ppt

第二章 2.3 2.3.2
[知识拓展](1)二面角的平面角的大小是由二面角的两个面 的位置唯一确定的,与选择棱上的点的位置无关.
(2)平面角的两边分别在二面角的两个面内,且两边都与 二面角的棱垂直,这个角所确定的平面与棱垂直.
第二章 2.3 2.3.2
在长方体ABCD-A1B1C1D1中,二面角A-BC-A1的平面 角是( )
第二章 2.3 2.3.2
已知Rt△ABC中,AB=AC=1,AD是斜边BC上的高,以 AD为折痕将△ABD折起,使∠BDC成直角.
求证:(1)平面ABD⊥平面BDC,平面ACD⊥平面BDC; (2)∠BAC=60°.
第二章 2.3 2.3.2
[证明] (1)如图(1),∵AD⊥BC,
第二章 2.3 2.3.2
∴BC= 2BD= 2× 22=1. ∴AB=AC=BC.∴∠BAC=60°.
第二章 2.3 2.3.2
建模应用之路
第二章 2.3 2.3.2
命题方向 二面角的实际应用 [例3] 如图:一山坡的坡面与水平面成30°的二面角, 坡面上有一直道AB,它和坡脚的水平线成30°的角,沿这山 路行走20m后升高了多少米?
[答案] D
第二章 2.3 2.3.2
7.如图,△ADB和△ADC都是以D为直角顶点的直角三 角形,且AD=BD=CD,∠BAC=60°,则直线AD⊥平面 BDC ;直线BD⊥平面ADC;直线CD⊥平面ABD .
[答案] BDC ADC ABD
第二章 2.3 2.3.2
新课引入
第二章 2.3 2.3.2
命题方向 面面垂直的判定 [例2] 如图所示,已知△ABC中,∠ABC=90°,P为△ ABC所在平面外一点,PA=PB=PC.求证平面PAC⊥平面 ABC.
[知识拓展](1)二面角的平面角的大小是由二面角的两个面 的位置唯一确定的,与选择棱上的点的位置无关.
(2)平面角的两边分别在二面角的两个面内,且两边都与 二面角的棱垂直,这个角所确定的平面与棱垂直.
第二章 2.3 2.3.2
在长方体ABCD-A1B1C1D1中,二面角A-BC-A1的平面 角是( )
第二章 2.3 2.3.2
已知Rt△ABC中,AB=AC=1,AD是斜边BC上的高,以 AD为折痕将△ABD折起,使∠BDC成直角.
求证:(1)平面ABD⊥平面BDC,平面ACD⊥平面BDC; (2)∠BAC=60°.
第二章 2.3 2.3.2
[证明] (1)如图(1),∵AD⊥BC,
第二章 2.3 2.3.2
∴BC= 2BD= 2× 22=1. ∴AB=AC=BC.∴∠BAC=60°.
第二章 2.3 2.3.2
建模应用之路
第二章 2.3 2.3.2
命题方向 二面角的实际应用 [例3] 如图:一山坡的坡面与水平面成30°的二面角, 坡面上有一直道AB,它和坡脚的水平线成30°的角,沿这山 路行走20m后升高了多少米?
[答案] D
第二章 2.3 2.3.2
7.如图,△ADB和△ADC都是以D为直角顶点的直角三 角形,且AD=BD=CD,∠BAC=60°,则直线AD⊥平面 BDC ;直线BD⊥平面ADC;直线CD⊥平面ABD .
[答案] BDC ADC ABD
第二章 2.3 2.3.2
新课引入
第二章 2.3 2.3.2
命题方向 面面垂直的判定 [例2] 如图所示,已知△ABC中,∠ABC=90°,P为△ ABC所在平面外一点,PA=PB=PC.求证平面PAC⊥平面 ABC.
高一数学人教A版必修2课件:2.3.1直线与平面垂直的判定 教学课件

[ 思路分析]
(1) 求线面角的关键是找出直线在平面内的射影,为此须找出
过直线上一点的平面的垂线. (2) 中过 A1 作平面 BDD1B1 的垂线,该垂线必与 B1D1、BB1垂直,由正方体的特性知,直线A1C1满足要求.
[ 解析]
(1)∵直线 A1A⊥平面 ABCD, ∴∠A1CA 为直线 A1C 与平面 ABCD 所
∵∠ABC=90°,∴AB⊥BC.
又AB∩PA=A,∴BC⊥平面PAB. (2)∵BC⊥平面PAB,AE⊂平面PAB,∴BC⊥AE.
∵PB⊥AE,BC∩PB=B,∴AE⊥平面PBC.
(3)∵AE⊥平面PBC,PC⊂平面PBC, ∴AE⊥PC.∵AF⊥PC,AE∩AF=A,∴PC⊥平面AEF.
返回导航
返回导航
第二章 点、直线、平面之间的位置关系
命题方向2 ⇨直线与平面所成的角
在正方体 ABCD-A1B1C1D1 中, 导学号 09024474
(1)求直线 A1C 与平面 ABCD 所成的角的正切值; (2)求直线 A1B 与平面 BDD1B1 所成的角.
返回导航
第二章 点、直线、平面之间的位置关系
又 BB1∥AA1,∴CD⊥BB1, 又 AA1⊂平面 ABB1A1,BB1⊂平面 ABB1A1, ∴CD⊥平面 ABB1A1.
返回导航
第二章 点、直线、平面之间的位置关系
[ 错因分析]
错解中 AA1 和BB1 是平面 ABB1A1 内的两条平行直线,不是相交
直线,故不满足直线与平面垂直的判定定理的条件.
第二章 点、
线面垂直的判定方法:
(1)证明线面垂直的方法
①线面垂直的定义.
②线面垂直的判定定理. ③如果两条平行直线的一条直线垂直于一个平面,那么另一条直线也垂直 于这个平面. ④如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一 个平面.
高中数学第二章点直线平面之间的位置关系2.3.1直线与平面垂直的判定课件新人教A版必修2

错解:因为F,G分别为棱B1B,C1C的中点,所以BC∥FG. 因为BC⊥AB,BC⊥B1B,且B1B∩AB=B, 所以BC⊥平面A1ABB1. 又因为B1E⊂平面A1ABB1, 所以BC⊥B1E, 即FG⊥B1E. 同理A1D1⊥B1E,所以B1E⊥平面A1FGD1. 纠错:本题的错误在于只证明了直线和平面内的两条平行直线垂直,不符
(2)求直线A1B和平面BB1C1C所成的角的正弦值.
(2)解:作 A1F⊥DE,垂足为 F,连接 BF. 因为 A1E⊥平面 ABC,所以 BC⊥A1E. 因为 BC⊥AE,所以 BC⊥平面 AA1DE.所以 BC⊥A1F,所以 A1F⊥平面 BB1C1C. 所以∠A1BF 为直线 A1B 和平面 BB1C1C 所成的角.
(1)证明:A1D⊥平面A1BC;
(1)证明:设E为BC的中点,连接A1E,AE.由题意得A1E⊥平面ABC,所以 A1E⊥AE. 因为AB=AC,所以AE⊥BC. 故AE⊥平面A1BC. 连接DE,由D,E分别为B1C1,BC的中点,得DE∥B1B且DE=B1B, 从而DE∥A1A且DE=A1A, 所以AA1DE为平行四边形. 于是A1D∥AE. 又因为AE⊥平面A1BC,所以A1D⊥平面A1BC.
和这个平面所成的角.
锐角
(2)一条直线垂直于平面,称它们所成的角是 直角 ;一条直线在平面内或 一条直线和平面平行,称它们所成的角是 0° 的角,于是,直线与平面 所成的角θ 的范围是0°≤θ ≤90°.
自我检测
1.(线面垂直的性质)已知直线a⊥平面α ,直线b∥平面α ,则a与b的关系为
(B ) (A)a∥b
在 Rt△A1NB1 中,sin∠A1B1N= A1N = 1 ,因此∠A1B1N=30°.所以,直线 A1B1 与平面 BCB1 所成的角为 A1B1 2
人教A版高中数学必修二 第二章 点、直线、平面之间的位置关系复习 课件 (共31张PPT)

所以 CC1⊥平面 ABC. 又 AD⊂平面 ABC,所以 CC1⊥AD.
又因为 AD⊥DE,CC1,DE⊂平面 BCC1B1,CC1∩DE=E,
所以 AD⊥平面 BCC1B1.
又 AD⊂平面 ADE,
所以平面 ADE⊥平面 BCC1B1.
(2)因为 A1B1=A1C1,F 为 B1C1 的中点,
所以 A1F⊥B1C1.
因为 CC1⊥平面 A1B1C1,且 A1F⊂平面 A1B1C1, 所以 CC1⊥A1F. 又因为 CC1,B1C1⊂平面 BCC1B1,CC1∩B1C1=C1,
所以 A1F⊥平面 BCC1B1.
由(1)知 AD⊥平面 BCC1B1,所以 A1F∥AD.
又 AD⊂平面 ADE,A1F⊄平面 ADE, 所以 A1F∥平面 ADE.
故CD⊥平面PAC.又AE⊂平面PAC,故CD⊥AE. (2)因为PA=AB=BC,∠ABC=60°,所以PA=AC. 又因为E是PC的中点,所以AE⊥PC. 由(1)知CD⊥AE,CD∩PC=C,从而AE⊥平面PCD, 故AE⊥PD. 因为PA⊥AB,AB⊥AD,所以AB⊥平面PAD, 所以BA⊥PD,又因为BA∩AE=A,所以PD⊥平面ABE.
g a
7部分
g
8部分
b
g
b g
b
a
b
a
例3.如图所示,四棱锥P-ABCD中,PA⊥底面ABCD,
AB⊥AD,AC⊥CD,∠ABC=60°,
PA=AB=BC,E是PC的中点.
求证:(1)CD⊥AE.
(2)PD⊥平面ABE.
证明:(1)因为PA⊥底面ABCD,所以CD⊥PA,又CD⊥AC,PA∩AC=A,
6. 面面平行的判定定理 a a , b a , a∩b, ⇒ a∥b. 由线面平行得面面平行. a∥ b , b∥ b , 7. 面面平行的性质定理 ab, g a = a, ⇒ a∥ b. g b = b, 由面面平行得线线平行.
人教A高中数学必修2课件 第二章 点、直线、平面之间的位置关系 2.3.2
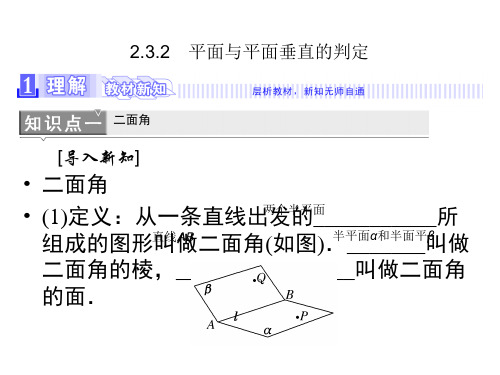
• (2)二面角的平面角:
①定义:在二面角α l β的棱l上任取一点O,如图所示,以点 O为垂足,在______________ ______分别半作平垂面直α和于半棱平l的射线 OA 和 OB , 则 射 线 OA 和 OB 构 成 的 ∠ AOB 叫 做 面__β_内____________.
二面角的平面角
(3)符号语言:AB⊥β,AB∩β=B,AB⊂α⇒α⊥β.
[化解疑难]
• 对面面垂直的判定定理的理解
• (1)该定理可简记为“线面垂直,则面面垂直 ”.
• (2)定理的关键词是“过另一面的垂线”,所 以应用的关键是在平面内寻找另一个面的垂 线.
• (3)线、面之间的垂直关系存在如下转化特征 :线线垂直⇒线面垂直⇒面面垂直.这体现 了立体几何问题求解的转化思想,应用时要 灵活把握.
连接 AD,SD,则 AD⊥BC,SD⊥BC,
∴∠ADS 为二面角 A-BC-S 的平面角.
在 Rt△BSC 中,∵SB=SC=a,
∴SD=
22a,BD=B2C=
2 2a, 在△ADS 中,∵SD2+AD2=SA2,
∴∠ADS=90°,即二面角 A-BC-S 为直二面角,
②直二面角:平面角是____直_角_____的二面角.
[化解疑难]
• 对于二面角及其平面角的理解
• (1)二面角是一个空间图形,而二面角的平面 角是平面图形,二面角的大小通过其平面角 的大小表示,体现了由空间图形向平面图形 转化的思想.
• (2)二面角的平面角的定义是两条“射线”的 夹角,不是两条直线的夹角,因此,二面角θ 的取值范围是0°≤θ≤180°.
• [类题通法]
• 证明面面垂直的方法
• (1)定义法:即说明两个半平面所成的二面角 是直二面角.
①定义:在二面角α l β的棱l上任取一点O,如图所示,以点 O为垂足,在______________ ______分别半作平垂面直α和于半棱平l的射线 OA 和 OB , 则 射 线 OA 和 OB 构 成 的 ∠ AOB 叫 做 面__β_内____________.
二面角的平面角
(3)符号语言:AB⊥β,AB∩β=B,AB⊂α⇒α⊥β.
[化解疑难]
• 对面面垂直的判定定理的理解
• (1)该定理可简记为“线面垂直,则面面垂直 ”.
• (2)定理的关键词是“过另一面的垂线”,所 以应用的关键是在平面内寻找另一个面的垂 线.
• (3)线、面之间的垂直关系存在如下转化特征 :线线垂直⇒线面垂直⇒面面垂直.这体现 了立体几何问题求解的转化思想,应用时要 灵活把握.
连接 AD,SD,则 AD⊥BC,SD⊥BC,
∴∠ADS 为二面角 A-BC-S 的平面角.
在 Rt△BSC 中,∵SB=SC=a,
∴SD=
22a,BD=B2C=
2 2a, 在△ADS 中,∵SD2+AD2=SA2,
∴∠ADS=90°,即二面角 A-BC-S 为直二面角,
②直二面角:平面角是____直_角_____的二面角.
[化解疑难]
• 对于二面角及其平面角的理解
• (1)二面角是一个空间图形,而二面角的平面 角是平面图形,二面角的大小通过其平面角 的大小表示,体现了由空间图形向平面图形 转化的思想.
• (2)二面角的平面角的定义是两条“射线”的 夹角,不是两条直线的夹角,因此,二面角θ 的取值范围是0°≤θ≤180°.
• [类题通法]
• 证明面面垂直的方法
• (1)定义法:即说明两个半平面所成的二面角 是直二面角.
人教新课标A版高中数学必修二 可编辑课件 第二章 点、直线、平面之间的位置关系 222 平面与平面平行的判定

.
2.推论:如果一个平面内有两条 相交 直线,分别平
人 教
A
行于另一个平面内的两条直线,则这两个平面平行.
版
数
用符号表示为a∥c,b∥d,a∩b=A,a⊂α,b⊂α , 学
c⊂β,d⊂β⇒α∥β
.
3.α∥β,a⊂α⇒ a∥β .
第二章 点、直线、平面之间的位置关系
人 教 A 版 数 学
第二章 点、直线、平面之间的位置关系
第二章 点、直线、平面之间的位置关系
人
2.2.2 平面与平面平行的判定
教 A 版
数
学
第二章 点、直线、平面之间的位置关系
人 教 A 版 数 学
第二章 点、直线、平面之间的位置关系
1.判定定理:如果一个平面内有两条 相交 直 线 分
别 平行 于另一个平面,那么这两个平面平行.用数学符
号表示 a∥α,b∥α,a⊂β,b⊂β,a∩b=A⇒α∥β
一、选择题
1.若两个平面内分别有一条直线,这两条直线互相平 行,则这两个平面的公共点个数
A.有限个 B.无限个
C.没有
D.没有或无限个
[答案] D
[解析] 两平面相交或平行,故选D.
(
)
人 教
A
版
数
学
第二章 点、直线、平面之间的位置关系
二、填空题
2.直线a⊂平面α,直线b⊂平面β,且α∥β,则a、b的
证明如下:在正方体ABCD-A1B1C1D1中连接PQ.
∵P,Q分别为DD1,CC1的中点,
∴PQ綊CD,CD綊AB.
人
教
∴PQ綊AB,∴四边形ABQP是平行四边形,
A 版
数
∴PA∥QB.
人教A版高中数学必修2第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系课件

C D
B A
C1 D1
B1 A1
知识小结
实例引 入平面
平面的画 法和表示
点和平面的 位置关系
平面三 个公理
空间图形
文字叙述
符号表示
2.1.2空间中两直线的位置 关系
平面有知识(复习 )
判断下列命题对错: 1、如果一条直线上有一个点在一个平面上,则这条直线上
的所有点都在这个平面内。( )
2、将书的一角接触课桌面,这时书所在平面和课桌所在平
直线。(既不相交也不平行的两条直线) 判断:
(1)
m
β
m
l
α
l
直线m和l是异面直线吗?
(2)
,则 与 是异面直线
(3)a,b不同在平面 内,则a与b异面
异面直线的画法:
通常用一个或两个平面来衬托,异面直线
不同在任何一个平面的特点
a
b
b
a
b
a
2、空间中两直线的三种位置关系
1、相交
m P
l
2、平行
m l
b′
平
a′ θ O
移
若两条异面直线所成角为90°,则称它们互相垂直。 异面直线a与b垂直也记作a⊥b 异面直线所成角θ的取值范围:
例 3 在正方体ABCD—A1B1C1D1中指出下列各对线段所
成的角:
D1
C1
1)AB与CC1; 2)A1 B1与AC; A1
B1
3)A1B与D1B1。
1)AB与CC1所成的角 = 9 0°
4、平面的基本性质
公理3 如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共直线.
符号表示为:
P l, Pl.
高一数学(人教A版)必修2课件:第二章 点、直线、平面之间的位置关系

第二章
章末归纳总结
之路 · 数学 · 人教A版 ·
点、直线、平面 之间的位置关系
必修2
判定定理:一个平面内的两条相交直线与另一个平面平行, 则这两个平面平行 平面与平面平行 性质定理:如果两个平行平面同时和第三个平面相交,那么 它们的交线平行 判定定理:一个平面过另一个平面的垂线,则这两个平面垂直 平面与平面之间的位置关系 平面与平面垂直性质定理:两个平面垂直,则一个平面内垂直于交线 的直线与另一个平面垂直 二面角的平面角 二面角 范围:[0° ,180° ]
必修2
第二章
章末归纳总结
第二章
点、直线、平面之间的位置
之路 · 数学 · 人教A版 ·
必修2
知识结构
第二章
章末归纳总结
之路 · 数学 · 人教A版 ·
点、直线、平面 之间的位置关系
必修2
平面的概念及其表示 公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内 平面 公理2:过不在一条直线上的三点,有且只有一个平面 平面的性质公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该 点的公共直线 定义:不同在任何一个平面内的两条直线 定义 直线与直线之异面直线异面直线所成的角 ,90° ] 间的位置关系 范围:0° 相交直线 平行直线 直线与平面之 间的位置关系
第二章
章末归纳总结
之路 · 数学 · 人教A版 ·
必修2
[例 1]
下面四个命题中,正确命题的个数是(
)
①如果 a,b 是两条直线,a∥b,那么 a 平行于经过 b 的 任何一个平面;②如果直线 a 和平面 α 满足 a∥α,那么 a 与 平面 α 内的任何一条直线平行;③如果直线 a,b 满足 a∥α, b∥α,则 a∥b;④如果直线 a 与平面 α 内的无数条直线平行, 那么直线 a 必平行于平面 α. A.0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通常把直立平面的竖边画成与水平平面的横边垂直,如图: 画 法
判 定 定 理
垂线 , 文字表述: 一个平面过另一个平面的 _______ 则这两个平面垂直.
a⊥β ⇒ α⊥ β 符号表示: a⊂α _______
[化解疑难 ] 作二面角的平面角的方法
方法一 (定义法 ):在二面角的棱上找一特殊点,在两个半平面内分别作垂 直于棱的射线.
解析:
证法一:利用定义证明.
∵∠ BSA=∠CSA= 60° ,SA= SB= SC, ∴△ ASB 和△ ASC 是等边三角形,则有 SA= SB= SC= AB= AC,令其值 为 a,则△ ABC 和△ SBC 为共底边 BC 的等腰三角形. 如图,取 BC 的中点 D,连接 AD, SD, 则 AD⊥ BC,SD⊥ BC, ∴∠ ADS 为二面角 A-BC-S 的平面角.
2.3.2 平面与平面垂直的判定
学案· 新知自解
1.理解二面角,面面垂直的概念. 2.掌握二面角的平面角,面面垂直的判定定理. 3.能够利用面面垂直的判定定理判断或证明有关面面垂直的问题.
二面角 1.二面角 二面角 两个半平面 所组成的图形叫作二面角. 从一条直线出发的_____________ 这条直线 叫作二面角的棱.______________ 这两个半平面 叫作二面角的面. __________ 定义
解析: 由二面角的定义可知,从一条直线出发的两个半平面所组成的图 形叫作二面角,所以①不正确;由 a,b 垂直于两个面,则 a,b 都垂直于二面 角的棱,故②正确;对于③,所作的射线不一定垂直于二面角的棱,故③不正 确;对于④,由定义可知正确.故选 B.
答案: B
3.如图,AB 是圆的直径,PA 垂直于圆所在的平面,C 是圆上一点(不同于 A,B)且 PA=AC,则二面角 P-BC-A 的大小为____________.
在 Rt△ BSC 中, ∵ SB= SC= a, 2 BC 2 ∴ SD= a,BD= = a. 2 2 2 2 在 Rt△ ABD 中, AD= a. 2 在△ ADS 中,∵ SD2+ AD2= SA2, ∴∠ ADS= 90° , 即二面角 A-BC- S 为直二面角, 故平面 ABC⊥平面 SBC.
证法二:利用判定定理. ∵ SA= AB= AC, ∴点 A 在平面 SBC 上的射影为△SBC 的外心. ∵△ BSC 为直角三角形, ∴ A 在△ BSC 上的射影 D 为斜边 BC 的中点. ∴ AD⊥平面 SBC. 又∵平面 ABC 过 AD, ∴平面 ABC⊥平面 SBC.
[归纳升华] 1.对平面与平面垂直的判定定理的认识: 平面与平面垂直的判定定理告诉我们,可以通过直线与平面垂直来证明平 面与平面垂直,通常我们将其记为“线面垂直,则面面垂直”.因此,处理面 面垂直问题转化为处理线面垂直问题,进一步转化为处理线线垂直问题.
1.长方体 ABCD-A1B1C1D1 的六个面中,与面 ABCD 垂直的面有 ( A.1 个 C.4 个 B.3 个 D.5 个
)
解析: 与面 ABCD 垂直的面有面 ABB1A1,面 BCC1B1,面 CDD1C1,面 DAA1D1,共 4 个.
答案:
C
2.下列说法: ①两个相交平面组成的图形叫作二面角; ②两条异面直线分别和一个二面角的两个半平面垂直,则这两条异面直线所 成的角与二面角的平面角相等或互补; ③二面角的平面角是从棱上一点出发, 分别在两个半平面内作射线所成的角; ④二面角的大小与其平面角的顶点在棱上的位置没有关系. 其中正确的是 ( A.①③ C.③④ ) B.②④ D.①②
如图①,∠AOB 为二面角 α-a-β 的平面角. 方法二(垂面法):过棱上一点作棱的垂直平面,该平面与二面角的两个半 平面产生交线,这两条交线所成的角,即为二面角的平面角 . 如图②,∠AOB 为二面角 α-l-β 的平面角. 方法三(垂线法):过二面角的一个面内一点作另一个平面的垂线,过垂足 作棱的垂线,利用线面垂直可找到二面角的平面角或其补角. 如图③,∠AFE 为二面角 A- BC- D 的平面角.
解析:
由条件得:PA⊥BC,AC⊥BC,
又 PA∩AC=A, ∴BC⊥平面 PAC, ∴∠PCA 为二面角 P-BC-A 的平面角. 在 Rt△PAC 中, 由 PA=AC 得∠PCA=45° .
答案:
45°
教案· 课堂探究
平面与平面垂直的判定 多维探究型 如图,已知∠BSC=90° ,∠BSA=∠CSA=60° ,又 SA=SB=SC, 求证:平面 ABC⊥平面 SBC.
2垂直,实质上是把问题转化成了求二面角 的平面角,通常情况下利用判定定理要比定义简单些,判定定理是证明面面垂 直的常用方法,即要证面面垂直,只要转证线面垂直,其关键与难点是在其中 一个平面内寻找一直线与另一平面垂直 .
1.在四面体 ABCD 中,CB=CD,AD⊥BD,且 E,F 分别是 AB,BD 的 中点. 求证:(1)直线 EF∥平面 ACD. (2)平面 EFC⊥平面 BCD.
∠AOB 叫作二面角的平面角 构成的_________
图形语言
符号语言
OB⊥l ⇒∠AOB OA⊥l ,_________ α∩β=l,O∈l,OA⊂α,OB⊂β,_________
为二面角 α-l-β 的平面角
平面与平面垂直 平面与平面垂直
直二面角 ,就说这两个平面 定 如果两个平面相交,且它们所成的二面角是 __________ α⊥ β 义 互相垂直,记作: _______
P-AB-Q或_______________ 二面角α-l-β 或二面角 二面角P-l-Q 如图, 记作: ________________ _______________
范围 0° ≤θ≤ 180°
2.二面角的平面角 在二面角 α-l-β 的棱 l 上任取一点 O,以点 O 为垂足,在半平面
垂直 于棱 l 的______ 射线 OA 和 OB, 文字语言 α 和 β 内分别作______ 则射线 OA 和 OB
判 定 定 理
垂线 , 文字表述: 一个平面过另一个平面的 _______ 则这两个平面垂直.
a⊥β ⇒ α⊥ β 符号表示: a⊂α _______
[化解疑难 ] 作二面角的平面角的方法
方法一 (定义法 ):在二面角的棱上找一特殊点,在两个半平面内分别作垂 直于棱的射线.
解析:
证法一:利用定义证明.
∵∠ BSA=∠CSA= 60° ,SA= SB= SC, ∴△ ASB 和△ ASC 是等边三角形,则有 SA= SB= SC= AB= AC,令其值 为 a,则△ ABC 和△ SBC 为共底边 BC 的等腰三角形. 如图,取 BC 的中点 D,连接 AD, SD, 则 AD⊥ BC,SD⊥ BC, ∴∠ ADS 为二面角 A-BC-S 的平面角.
2.3.2 平面与平面垂直的判定
学案· 新知自解
1.理解二面角,面面垂直的概念. 2.掌握二面角的平面角,面面垂直的判定定理. 3.能够利用面面垂直的判定定理判断或证明有关面面垂直的问题.
二面角 1.二面角 二面角 两个半平面 所组成的图形叫作二面角. 从一条直线出发的_____________ 这条直线 叫作二面角的棱.______________ 这两个半平面 叫作二面角的面. __________ 定义
解析: 由二面角的定义可知,从一条直线出发的两个半平面所组成的图 形叫作二面角,所以①不正确;由 a,b 垂直于两个面,则 a,b 都垂直于二面 角的棱,故②正确;对于③,所作的射线不一定垂直于二面角的棱,故③不正 确;对于④,由定义可知正确.故选 B.
答案: B
3.如图,AB 是圆的直径,PA 垂直于圆所在的平面,C 是圆上一点(不同于 A,B)且 PA=AC,则二面角 P-BC-A 的大小为____________.
在 Rt△ BSC 中, ∵ SB= SC= a, 2 BC 2 ∴ SD= a,BD= = a. 2 2 2 2 在 Rt△ ABD 中, AD= a. 2 在△ ADS 中,∵ SD2+ AD2= SA2, ∴∠ ADS= 90° , 即二面角 A-BC- S 为直二面角, 故平面 ABC⊥平面 SBC.
证法二:利用判定定理. ∵ SA= AB= AC, ∴点 A 在平面 SBC 上的射影为△SBC 的外心. ∵△ BSC 为直角三角形, ∴ A 在△ BSC 上的射影 D 为斜边 BC 的中点. ∴ AD⊥平面 SBC. 又∵平面 ABC 过 AD, ∴平面 ABC⊥平面 SBC.
[归纳升华] 1.对平面与平面垂直的判定定理的认识: 平面与平面垂直的判定定理告诉我们,可以通过直线与平面垂直来证明平 面与平面垂直,通常我们将其记为“线面垂直,则面面垂直”.因此,处理面 面垂直问题转化为处理线面垂直问题,进一步转化为处理线线垂直问题.
1.长方体 ABCD-A1B1C1D1 的六个面中,与面 ABCD 垂直的面有 ( A.1 个 C.4 个 B.3 个 D.5 个
)
解析: 与面 ABCD 垂直的面有面 ABB1A1,面 BCC1B1,面 CDD1C1,面 DAA1D1,共 4 个.
答案:
C
2.下列说法: ①两个相交平面组成的图形叫作二面角; ②两条异面直线分别和一个二面角的两个半平面垂直,则这两条异面直线所 成的角与二面角的平面角相等或互补; ③二面角的平面角是从棱上一点出发, 分别在两个半平面内作射线所成的角; ④二面角的大小与其平面角的顶点在棱上的位置没有关系. 其中正确的是 ( A.①③ C.③④ ) B.②④ D.①②
如图①,∠AOB 为二面角 α-a-β 的平面角. 方法二(垂面法):过棱上一点作棱的垂直平面,该平面与二面角的两个半 平面产生交线,这两条交线所成的角,即为二面角的平面角 . 如图②,∠AOB 为二面角 α-l-β 的平面角. 方法三(垂线法):过二面角的一个面内一点作另一个平面的垂线,过垂足 作棱的垂线,利用线面垂直可找到二面角的平面角或其补角. 如图③,∠AFE 为二面角 A- BC- D 的平面角.
解析:
由条件得:PA⊥BC,AC⊥BC,
又 PA∩AC=A, ∴BC⊥平面 PAC, ∴∠PCA 为二面角 P-BC-A 的平面角. 在 Rt△PAC 中, 由 PA=AC 得∠PCA=45° .
答案:
45°
教案· 课堂探究
平面与平面垂直的判定 多维探究型 如图,已知∠BSC=90° ,∠BSA=∠CSA=60° ,又 SA=SB=SC, 求证:平面 ABC⊥平面 SBC.
2垂直,实质上是把问题转化成了求二面角 的平面角,通常情况下利用判定定理要比定义简单些,判定定理是证明面面垂 直的常用方法,即要证面面垂直,只要转证线面垂直,其关键与难点是在其中 一个平面内寻找一直线与另一平面垂直 .
1.在四面体 ABCD 中,CB=CD,AD⊥BD,且 E,F 分别是 AB,BD 的 中点. 求证:(1)直线 EF∥平面 ACD. (2)平面 EFC⊥平面 BCD.
∠AOB 叫作二面角的平面角 构成的_________
图形语言
符号语言
OB⊥l ⇒∠AOB OA⊥l ,_________ α∩β=l,O∈l,OA⊂α,OB⊂β,_________
为二面角 α-l-β 的平面角
平面与平面垂直 平面与平面垂直
直二面角 ,就说这两个平面 定 如果两个平面相交,且它们所成的二面角是 __________ α⊥ β 义 互相垂直,记作: _______
P-AB-Q或_______________ 二面角α-l-β 或二面角 二面角P-l-Q 如图, 记作: ________________ _______________
范围 0° ≤θ≤ 180°
2.二面角的平面角 在二面角 α-l-β 的棱 l 上任取一点 O,以点 O 为垂足,在半平面
垂直 于棱 l 的______ 射线 OA 和 OB, 文字语言 α 和 β 内分别作______ 则射线 OA 和 OB
