4 截面图形的几何性质
北京科技大学材料力学C选择试题及答案

材料力学试题及答案一、单项选择题1. 截面上的全应力的方向( )A 、平行于截面B 、垂直于截面C 、可以与截面任意夹角D 、与截面无关 2. 脆性材料的延伸率( )A 、小于5%B 、小于等于5%C 、大于5%D 、大于等于5%3. 如图所示简支梁,已知C 点转角为θ。
在其它条件不变的情况下,若将荷载F 减小一半,则C 点的转角为( ) A 、0.125θ B 、0.5θ C 、θ D 、2θ4.危险截面是()所在的截面。
A 、最大面积B 、最小面积C 、最大应力D 、最大内力 5. 图示单元体应力状态,沿x 方向的线应变εx 可表示为( ) A 、E yσ B 、)(1y x Eμσσ- C 、)(1x y E μσσ- D 、Gτ 6. 描述构件上一截面变形前后的夹角叫(A 、线位移B 、转角C 、线应变D 、角应变7. 塑性材料的名义屈服应力使用( )A 、σS 表示B 、σb 表示C 、σp 表示 D 、σ0.2表示 8.拉(压)杆应力公式A F N=σ的应用条件是()A 、应力在比例极限内B 、应力在屈服极限内C 、外力合力作用线必须沿着杆的轴线D 、杆件必须为矩形截面杆9.下列截面中,弯曲中心与其形心重合者是()A 、Z 字形型钢B 、槽钢C 、T 字形型钢D 、等边角钢10. 如图所示简支梁,已知C 点转角为θ。
在其它条件不变的情况下,若将杆长增加一倍,则C 点的转角为( )A 、2θB 、4θC 、8θD 、16θ二、填空题1. 用主应力表示的第四强度理论的相当应力是 。
2. 已知自由落体冲击问题的动荷系数K d ,对应静载荷问题的最大位移为Δjmax ,则冲击问题的最大位移可以表示为 。
3. 图示木榫联接。
横截面为正方形,边长为a ,联接处长度为2t 。
则木榫联接处受剪切面的名义切应力等于 。
4. 主平面上的切应力等于 。
5. 功的互等定理的表达式为 。
6.自由落体冲击问题的动荷系数为jd hK ∆++=211,其中h 表示 。
4 截面图形的几何性质

C
2 πd 4 2d 2 πd 2 2d πd 2 a 8 3π 8 128 3π
将 d = 80 mm,a = 100 mm 代入后得
I x2 3 467 10 4 mm 4
从而得图a所示截面对x轴的惯性矩:
I xC
2 πd 4 2d πd 2 2d πd I x 1284.3 平行移轴公式
然后再利用平行移轴公式求半圆形对x轴的惯性矩:
I x2 I x 2d πd 2 a 3π 8
I y 1 054 10 4 mm 4
21
4.3 平行移轴公式
(3) 求 惯性积 Ixy 由
I xy xy d A 可知,只要x
A
轴或y 轴为截面的对称轴,则由于 与该轴对称的任何两个面积元素 dA的惯性积 xydA 数值相等而正负 号相反,致使整个截面的惯性积必 定等于零。图a所示截面的x 轴和y 轴都是对称轴,当然 Ixy=0。
22
4.4 惯性矩和惯性积的转轴公式
图示任意形状的截面,其面积A以及对于坐标轴x,y的 惯性矩Ix,Iy和惯性积Ixy为已知,现在来求截面对于绕原点O 旋转a 角(以逆时针为正)后的坐标轴x1y1的惯性矩 I x1, I y1和 惯性积 I x y 。
1 1
23
4.4 惯性矩和惯性积的转轴公式
由图可见,截面上任一微面积dA在x,y和x1,y1两个坐标系中坐标 的关系为
13
4.3 平行移轴公式
因截面上的任一元素dA在x,y 坐标系内的坐标为 x xC b, 于是有
2 I x y 2 d A y C a d A yC d A 2 a yC d A a 2 d A A A A A A 2
截面的几何性质

y
B
)时,y-x轴始终
A. y轴不动,x轴平移;
B. x轴不动,y轴平移; C. x轴不动,y轴任意移动;
O
x
D. y、x同时平移。
B
1、在下列关于平面图形的结论中,( A.图形的对称轴必定通过形心; B.图形两个对称轴的交点必为形心; C.图形对对称轴的静矩为零;
)是错误的。
D.使静矩为零的轴必为对称轴。
2、在平面图形的几何性质中,( 可为零。 A.静矩和惯性矩; C.惯性矩和惯性积;
D
)的值可正、可负、也
B.极惯性矩和惯性矩; D.静矩和惯性积。
证毕
A2
例3 试确定图示梯形面积的形心位置,及其对底边的静矩。
解: 图形对底边的静矩 Sx A1 y1 A2 y2
y b C1x
1 2 1 h bh h ah 2 3 2 3
h2 a 2b 6
图形对某对坐标轴惯性积为零,这对坐标轴称为该图形的主惯性轴
主惯性矩:
图形对主轴的惯性矩,称主惯性矩
形心主轴:
过形心的主轴称为形心主轴
若平面图形有两个对称轴,此二轴均为形心主轴; 若平面图形有一个对称轴,则该轴为一形心主轴, 另一形心主轴过形心, 且与 该轴垂直.
形心主矩:
图形对形心主轴的惯性矩称为形心主矩
y
120 C2 C1(0,0) C2(-35,60)
及坐标如图(a)
x
x A
i
i
A
x1 A1 x 2 A2 A1 A2
截面几何性质(材料力学)
§-4 惯性矩和惯性积的转轴公式 截面的主惯性轴和主惯性矩
1.惯性矩和惯性积的转轴公式
y
bh3 Iz 12
C z
bh3 Iz' 12
h
b
y
注意: 1. 两个座标系的原点 必须重合; 2. 两轴惯性矩之和为常量
z
O
I y1 I
z1
I y I I p z
I z1 I y1
4)解法四 y1 I z I z1
I z0 I z0 1 I z0 2 I z0 3 I z0 4
A3 y
d 4
64
2 I y 2 I z0 3 I z0 3
d4
64 Iy
2
A2 z0
d
4
128
I z I z1 I z0 3 OC
d
2
d4 Iy 128 18
1) 极惯性矩、惯性矩和惯性积均与所取的坐标系有关, 2) 惯性积可正可负 3) 单位m4 或 mm4
y dA
4. 惯性半径
Iy iy A
Iz iz A
y
(单位m 或 mm)
O
z z
例
试计算图示矩形截面对于其对称轴x和y的惯性矩。
y dy
解: 取平行于x轴的狭长条, 则 dA=b dy
h
1 2
I zc I yc
2
4 I 2c zc 321104 mm4 y
I yc 0 I min
I zc I yc 2
1 2
I zc I yc
2
4 I 2c zc 57.4 104 mm 4 y
材料力学填空与判断题解

实用文档第1 章 绪论一、是非判断题1-1 材料力学是研究构件承载能力的一门学科。
( √ ) 1-2 材料力学的任务是尽可能使构件安全地工作。
( × ) 1-3 材料力学主要研究弹性范围内的小变形情况。
( √ )1-4 因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
(×) 1-5 外力就是构件所承受的载荷。
( × )1-6 材料力学研究的内力是构件各部分间的相互作用力。
( × )1-7 用截面法求内力时,可以保留截开后构件的任一部分进行平衡计算。
( √ ) 1-8 压强是构件表面的正应力。
( × ) 1-9 应力是横截面上的平均内力。
( × )1-10 材料力学只研究因构件变形引起的位移。
( √ ) 1-11 线应变是构件中单位长度的变形量。
( × ) 1-12 构件内一点处各方向线应变均相等。
( × )1-13 切应变是变形后构件中任意两根微线段夹角的变化量。
( × ) 1-14 材料力学只限于研究等截面直杆。
( × )1-15 杆件的基本变形只是拉(压)、剪、扭和弯四种。
如果还有另一种变形,必定是这四种变形的某种组合。
( √ )第 2 章 轴向拉伸与压缩 一、是非判断题2-1 使杆件产生轴向拉压变形的外力必须是一对沿杆轴线的集中力。
(×) 2-2 拉杆伸长后,横向会缩短,这是因为杆有横向应力存在。
(×) 2-3 虎克定律适用于弹性变形范围内。
(×) 2-4 材料的延伸率与试件尺寸有关。
(√)2-5 只有超静定结构才可能有装配应力和温度应力。
(√) 二、填空题2-6 承受轴向拉压的杆件,只有在(加力端一定距离外)长度范围内变形才是均匀的。
2-7 根据强度条件][σσ≤可以进行(强度校核、设计截面、确定许可载荷)三方面的强度计算。
2-8 低碳钢材料由于冷作硬化,会使(比例极限)提高,而使(塑性)降低。
截面的几何性质面积矩惯性矩惯性积平行移轴

2
对于复杂形状,可以采用微元法或积分法计算其 惯性矩。
3
在工程实践中,常常使用软件或计算器进行惯性 矩的计算,以提高计算效率和精度。
04
CATALOGUE
惯性积
惯性积的定义
惯性积是截面的一种几何属性,用于描述截面的 形状和大小。
惯性积是一个标量,表示截面在某个方向上的投 影面积与该方向上单位长度的平方之比。
02
利用三维坐标系中的点坐标和 方向向量,通过向量的外积计 算得到截面的法向量和面积向 量,进而计算惯性积。
03
利用计算机图形学中的几何算 法,通过计算截面的顶点坐标 和法线向量,实现惯性积的精 确计算。
05
CATALOGUE
平行移轴
平行移轴的定义
一个方向上的直线,可以 是实线或虚线。
在三维空间中,与某一平 面相交的平面。
中性轴
通过截面形心并与形心轴垂直的轴线。
惯性矩的性质
01
惯性矩与截面的形状和大小有关,形状相同但尺寸不同的截面 具有不同的惯性矩。
02
惯性矩具有方向性,与中性轴的位置有关。
对于矩形、圆形、椭圆形等简单形状,其惯性矩可以通过公式
03
直接计算。
惯性矩的计算方法
1
对于简单形状,如矩形、圆形、椭圆形等,可以 直接使用公式计算其惯性矩。
截面的几何性质
目录
• 截面的定义与性质 • 面积矩 • 惯性矩 • 惯性积 • 平行移轴
01
CATALOGUE
截面的定义与性质
截面的定义
截面定义
截面是指通过一个平面与一个三维物 体相交,所形成的交线或交面。这个 平面可以是垂直的、倾斜的或与三维 物体表面平行。
截面的形状
截面的几何性质截面的几何性质

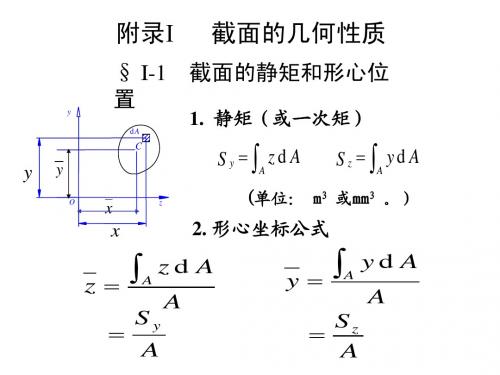
分别为图形对于z 轴和y 轴的静矩。
3
平面图形的静矩
S z = ∫A ydA
S y = ∫ A zd A
• 静矩与截面面积大小及坐标设置有关; • 静矩可正、可负、可为零; • 静矩的单位为m3或 mm3。
4
平面图形的形心Leabharlann • 平面图形的形心 — 平面图形几何形状的中心。 • 通过截面形心的坐标轴称为形心轴 。
设图形的形心C坐标为(zC , yC), 由均质等厚薄片重心坐标公式: A yC = ∫A ydA = S z
A z C = ∫ A zd A = S y Sy S yC = z , z C = A A
• 截面对形心轴的静矩必为零;反之,若截面对
某轴的静矩等于零,则该轴必为形心轴。
5
平面图形的静矩和形心
h 1 h * = b − y1 + y1 S z = A* yC 2 2 2 b 2 = ( h2 − 4 y1 ) 8
7
h 2
组合图形的静矩和形心位置 • 组合图形 — 由几个简单图形(如矩形、圆形
或三角形等规则图形)组成的图形。
zC =
8
∑ Ai zC i ∑ Ai
截面的几何性质 • 平面图形的静矩和形心 • 平面图形的惯性矩、惯性积和惯性半径 • 惯性矩和惯性积的平行移轴公式 • 惯性矩和惯性积的转轴公式 • 主惯性轴和主惯性矩
9
平面图形的极惯性矩和惯性矩 • 定义
I z = ∫A y 2dA
I y = ∫ A z 2 dA
• 组合图形对某一对正交轴的惯性积等于各组成
部分对同一对正交轴的惯性积之和。
I yz = ∑ ( I yz ) i
建筑力学第七章 截面的几何性质

第七章平面图形的几何性质研究截面几何性质的意义从上章介绍的应力和变形的计算公式中可以看出,应力和变形不仅与杆的内力有关,而且与杆件截面的横截面面积A、极惯性矩I P、抗扭截面系数W P等一些几何量密切相关。
因此要研究构件的的承载能力或应力,就必须掌握截面几何性质的计算方法。
另一方面,掌握截面的几何性质的变化规律,就能灵活机动地为各种构件选取合理的截面形状和尺寸,使构件各部分的材料能够比较充分地发挥作用,尽可能地做到“物尽其用”,合理地解决好构件的安全与经济这一对矛盾。
第一节 静矩一、静距的概念Ay S z d d =Az S y d d =⎰⎰⎰⎰====AAy y AAz z Az S S A y S S d d d d zy d A yz静距是面积与它到轴的距离之积。
平面图形的静矩是对一定的坐标而言的,同一平面图形对不同的坐标轴,其静矩显然不同。
静矩的数值可能为正,可能为负,也可能等于零。
它常用单位是m 3或mm 3。
形心d A zyy zCx Cy ⎪⎪⎭⎪⎪⎬⎫⋅∆∑=⋅∆∑=A y A y Az A z C C ⎪⎪⎭⎪⎪⎬⎫==⎰⎰A ydA y A zdA z AC A C ⎪⎪⎭⎪⎪⎬⎫==A S y A S z z C y C ⎭⎬⎫⋅=⋅=C y C z z A S y A S 平面图形对z 轴(或y 轴)的静矩,等于该图形面积A 与其形心坐标y C (或z C )的乘积。
当坐标轴通过平面图形的形心时,其静矩为零;反之,若平面图形对某轴的静矩为零,则该轴必通过平面图形的形心。
如果平面图形具有对称轴,对称轴必然是平面图形的形心轴,故平面图形对其对称轴的静矩必等于零。
⎭⎬⎫⋅=⋅=C y C z z A S y A S二、组合图形的静矩根据平面图形静矩的定义,组合图形对z 轴(或y 轴)的静矩等于各简单图形对同一轴静矩的代数和,即⎪⎪⎭⎪⎪⎬⎫=+++==+++=∑∑==ni Ci i Cn n C C y ni Ci i Cn n C C z z A z A z A z A S y A y A y A y A S 1221112211 式中 y Ci 、z Ci 及A i 分别为各简单图形的形心坐标和面积;n 为组成组合图形的简单图形的个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.惯性矩
4.惯性积
I zy zydA
A
15
5.平行移轴公式
I z I zC a 2 A 2 I y I yC b A I xy I zC yC abA
16
例 试计算图示T型截面的形心位置。
60
将截面分为I、II两个矩形,建立 如图所示坐标系。 各矩形的面积和形心坐标如下:
y
C
yC
z C zC C z
A A 20mm 60mm=1200mm2 yC 50mm yC 10mm
y 20
于是:
yC
Ay A
i
i Ci
A yC A yC A A
y
I yz yzdA
A
dA
(1)惯性积与轴有关,可正可负可 为零。
(2)若 y , z 轴有一为图形的对称轴, 则 Iyz = 0。
y
性质
O
z
z
12
平行移轴公式 1.平行移轴公式 移轴定理:图形对于 互相平行轴的惯性矩 之间的关系
I x I xC a 2 A I y I yC b2 A
空心圆形: D d
h
z
z y
d 4
64
4
z
y
bh3 Iz 12 hb3 Iy 12
y
Iz Iy Ip
Iy Iz
D 4 d 4
64
D 4
64
d
(1 4 )
32
32
Ip
D 4
dD
11
(1 4 )
4.2 惯性矩与惯性积
2.惯性积
整个截面对于z、y两坐标轴的 惯性积
13
4.3 平行移轴公式
2.组合截面的惯性矩
组合截面对某轴的惯性矩,等于它的各组成部分对同一 轴的惯性矩的代数和
d2
y2
O x y1
y b
14
d1
h
小结
1.静矩
2.形心
S z ydA , S y zdA
A A
Sy Sz yC , zC A A
I z y 2 dA, I y z 2 dA
z dz
I z y dA
2 A
同理
h 2 h 2
bh3 by 2dy 12
h
y
解:取平行于z轴的狭长条作为面积元素, 则 dA bdy
O
dy
z
I y z 2dA
A
b 2 b 2
b3 h hz 2dz 12
b
Hale Waihona Puke 104.2 惯性矩与惯性积
矩形: b
圆形: d
截面图形的几何性质
1
截面图形的几何性质
1 截面的静矩与形心
2 惯性矩与惯性积
3 平行移轴公式
2
4.1 截面的静矩与形心
1.静矩 任意平面图形 A,建立 yz 坐标系
y
平面图形的形心C(yc,zc)
C
y
dA
图形对 y 轴的静矩
S y zdA
A
yC
O
zC z
z
图形对 z 轴的静矩
S z ydA
A
静矩的单位:m3,cm3,mm3
3
4.1 截面的静矩与形心
2.形心
——图形几何形状的中心
yC
ydA
A
A
Sz zC A ,
zdA
A
A
Sy A
静矩可用面积与形心坐标的乘积表示。
4
4.1 截面的静矩与形心
静矩的性质
(1)静矩与轴有关,可正可负可为零。 (2)若yC,zC坐标轴过形心,则有
S yC 0
S zC 0
(3)组合图形静矩可分块计算求代数和
S z S z1 S z 2 A1 yC1 A2 yC 2
(4)求形心
S z A1 yC1 A2 yC 2 yC A A
A1 zC1 A2 zC 2 zC A A Sy
5
4.1 截面的静矩与形心
y
d
dA 2π d
πd 4 2 2 I P dA (2π d ) A 32 由于圆截面对任意方向的直径轴都是对称的, 故
d 2 0
O
z
I y Iz
d
所以
I P πd 4 I y Iz 2 64
9
4.2 惯性矩与惯性积
例2 试计算图示矩形截面对于其对称轴(即形心轴)z和y 的惯性矩Iz和Iy。 y
1200mm2 10mm+1200mm2 50mm 30mm 2 2 1200mm 1200mm 6
60
20
解:zC=0,只需计算yC
z
yC
C
惯性矩与惯性积
1.惯性矩
图形对 y,z 轴的 轴惯性矩
y
dA
I y z dA
2 A
y
I z y 2 dA
A
O
z
z
惯性矩的单位:m4,cm4,mm4
7
4.2 惯性矩与惯性积
图形对原点的 极惯性矩
I p 2dA ( y 2 z 2 )dA I z I y
A A
y
图形对z轴和y轴 惯性半径
dA
iz
IZ A
iy
Iy A
y
O
z
z
8
4.2 惯性矩与惯性积
例1 试计算图示圆形截面对O点的极惯性矩IP和对于其形心 轴(即直径轴)的惯性矩Iy和Iz。 解:建立如图所示坐标系,取图示微元dA,
