2章部分1答案
第2章_作业 (1)

第二章作业一、单项选择题1、通常以( C )代表时间价值率。
A、通货膨胀补偿率B、风险报酬率C、利息率D、投资利润率2、财务管理的两个基本价值观念是( A )A、时间价值和风险收益B、利润和成本C、风险和利润D、时间价值和成本3、在存本付息的情况下,若想每年都得到利息1000,利率为5%,则现在应存入的本金应为( A )元。
(永续年金的计算问题)A、20000B、50000C、500000D、2000004、一定时期内连续发生在期末的等额支付款项,被称为( B )A、先付年金B、普通年金C、永续年金D、延期年金5、下面有关资金时间价值的表述,正确的是( A )A.资金时间价值的实质是资金周转使用后的增值额B.资金时间价值是推迟消费所获得的报酬C.资金时间价值只能用绝对数来表示D.资金时间价值的量无法进行计量(选择A,严格将来,时间价值是资金周转增值额的一部分,但是因为题目中没有使用“全部”的字样,可以理解为正确;B推迟消费获得的报酬不一定能获得报酬,比如资金不周转的情形。
)6、一项借款,期限一年,年利率8%,按复利计算每半年复利一次,则借款实际利率为( D )A、0.16%B、12.49%C、18.53%D、8.16%(已知名义利率求实际利率的情形)7、永续年金具有下列特征( C )A、每期期初支付B、每期不等额支付C、没有终值D、没有现值8、资金时间价值实质是( B )。
A、资金的自然增值B、资金周转使用后的增值C、不同时间的价值量D、对暂缓消费的报酬9、为在第三年末获得本利和100元,求每年末存入多少资金,计算时应采用(B)。
A、年金现值系数B、年金终值系数C、复利现值系数D、复利终值系数(100元是终值,所以用终值系数计算)10.每年年底存款100元,求第5年末的价值,可用( D )来计算.(终值计算问题)A.PVIF i,n B.FVIF i,n C. PVIFA i,n D.FVIFA i,n11、当利率为10%,计息期为5时,后付年金现值系数为3.791;计息期为6时,后付年金现值系数为4.355,那么利率为10%。
南通大学操作系统第2章作业参考答案 (1)
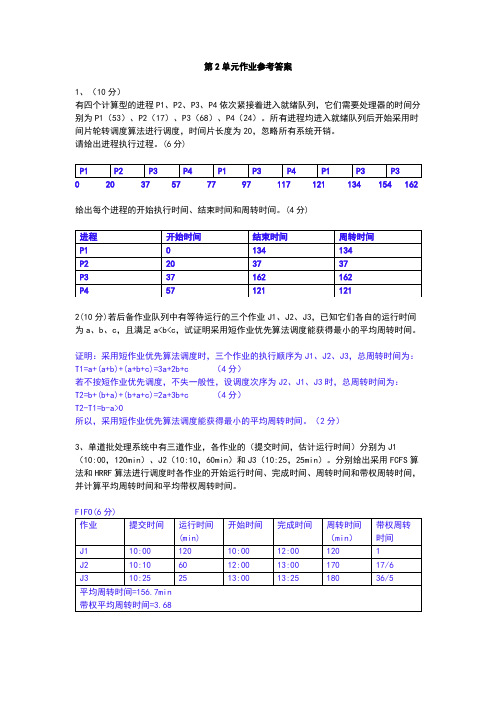
13简答题:简述处理机管理的主要功能。
进程控制和管理;⑵进程同步和互斥;⑶进程通信;⑷进程死锁;⑸线程控制和管理;⑹处理器调度。
(每条1分,总分4分)14简答题:简述中断和异常的区别中断是由与现行指令无关的中断信号触发的(异步的),且中断的发生与CPU处在用户模式或内核模式无关,在两条机器指令之间才可响应中断;异常是由处理器正在执行现行指令而引起的,一条指令执行期间允许响应异常。
(1分)⑵中断处理程序处理过程中是不能阻塞的,异常处理程序处理过程中是可以阻塞的。
(1分)⑶中断允许发生嵌套,但异常大多为一重。
(1分)异常处理过程中可能会产生中断,但中断处理过程中决不会被异常打断。
(1分)15简述进程的主要属性。
(1)动态性:有一定的生命周期⑵共享性:多个进程可执行同一程序,进程可以共享公共资源⑶独立性:是一个独立实体,有自己的虚存空间、程序计数器和内部状态,是资源分配、保护和调度的基本单位⑷制约性:存在制约关系(5)并发性:执行时间上会有所重叠16(每条1分,总分4分)16简答题:简述引起进程状态转换的具体原因。
(1)运行态→等待态:等待使用资源或某事件发生;(1分)⑵等待态→就绪态:资源得到满足或事件发生;(1分)⑶运行态→就绪态:运行时间片到;出现有更高优先权进程;(1分)⑷就绪态→运行态:CPU空闲时选择一个就绪进程。
(1分)17、简答题:进程的基本状态有哪些?请画出进程的状态转换图。
进程的基本状态包括:就绪态、运行态和等待态;(2分)⑵进程的状态转换图如下:(2分)18、简答题:简述进程映象的要素。
(1)进程控制块:标志信息、现场信息、控制信息;(1分)⑵进程核心栈:中断/异常现场、函数调用的参数和返回地址;(1分)⑶进程程序块:进程执行的程序;(1分)⑷进程数据块:私有地址空间,私有数据、用户栈。
(1分)19、简答题:简述引起进程调度的原因。
(1)进程终止⑵进程阻塞⑶进程时间片用完经,⑷进程创建⑸进程请求I/O操作完成⑹进程优先级改变⑺进程运行过程中发生中断或异常⑻进程执行系统调用(每条1分,总分4分)20、下列指令中,哪些是特权指令?⑴关中断;⑵访管指令;⑶设置系统时钟;⑷移位指令;⑸启动I/O;⑹读时钟日期;⑺控制中断屏蔽位(1)、⑶、⑸、⑺(每答对1个得1分,答错1个扣1分)。
高中人教物理选择性必修二第2章第1节法拉第电磁感应定律
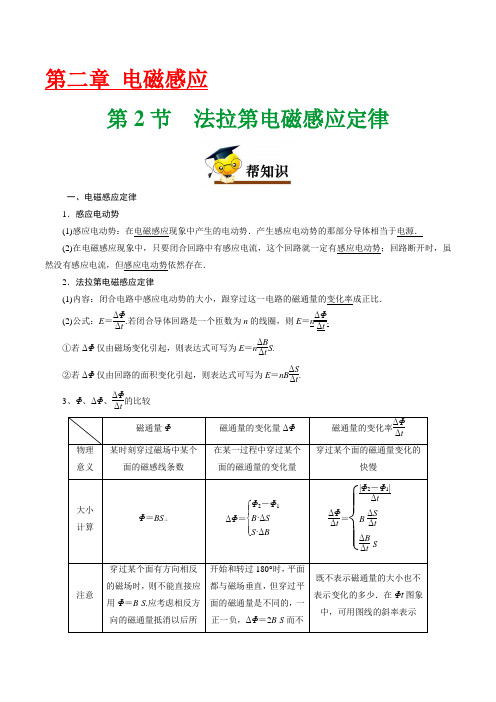
第二章 电磁感应第2节 法拉第电磁感应定律一、电磁感应定律 1.感应电动势(1)感应电动势:在电磁感应现象中产生的电动势.产生感应电动势的那部分导体相当于电源. (2)在电磁感应现象中,只要闭合回路中有感应电流,这个回路就一定有感应电动势;回路断开时,虽然没有感应电流,但感应电动势依然存在.2.法拉第电磁感应定律(1)内容:闭合电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比. (2)公式:E =ΔΦΔt .若闭合导体回路是一个匝数为n 的线圈,则E =n ΔΦΔt .①若ΔΦ仅由磁场变化引起,则表达式可写为E =n ΔBΔt S .②若ΔΦ仅由回路的面积变化引起,则表达式可写为E =nB ΔSΔt .3、Φ、ΔΦ、ΔΦΔt的比较磁通量Φ 磁通量的变化量ΔΦ 磁通量的变化率ΔΦΔt物理 意义某时刻穿过磁场中某个面的磁感线条数在某一过程中穿过某个面的磁通量的变化量穿过某个面的磁通量变化的快慢大小 计算Φ=BS ⊥ΔΦ=⎩⎪⎨⎪⎧Φ2-Φ1B ·ΔS S ·ΔBΔΦΔt =⎩⎪⎨⎪⎧|Φ2-Φ1|ΔtB ·ΔSΔtΔB Δt ·S注意穿过某个面有方向相反的磁场时,则不能直接应用Φ=B ·S .应考虑相反方向的磁通量抵消以后所开始和转过180°时,平面都与磁场垂直,但穿过平面的磁通量是不同的,一正一负,ΔΦ=2B ·S 而不既不表示磁通量的大小也不表示变化的多少.在Φt 图象中,可用图线的斜率表示剩余的磁通量 是零4、磁通量的变化率ΔΦΔt 是Φ-t 图像上某点切线的斜率大小.如图中A 点磁通量变化率大于B 点的磁通量变化率.二、导体切割磁感线时的感应电动势 1.垂直切割导体棒垂直于磁场运动,B 、l 、v 两两垂直时,如图甲,E =Bl v .2.不垂直切割导线的运动方向与导线本身垂直,但与磁感线方向夹角为 θ时,如图乙,则E =Bl v 1=Bl v sin_θ. 3、对公式E =Blv sin θ的理解(1)对 θ的理解:当B 、l 、v 三个量方向互相垂直时, θ=90°,感应电动势最大;当有任意两个量的方向互相平行时, θ=0°,感应电动势为零.(2)对l 的理解:式中的l 应理解为导线切割磁感线时的有效长度,如果导线不和磁场垂直,l 应是导线在与磁场垂直方向投影的长度;如果切割磁感线的导线是弯曲的,如图所示,则应取与B 和v 垂直的等效直线长度,即ab 的弦长.(3)对v 的理解①公式中的v 应理解为导线和磁场间的相对速度,当导线不动而磁场运动时,也有电磁感应现象产生.②公式E =Bl v 一般用于导线各部分切割磁感线速度相同的情况,若导线各部分切割磁感线的速度不同,可取其平均速度求电动势.如图所示,导体棒在磁场中绕A 点在纸面内以角速度ω匀速转动,磁感应强度为B ,平均切割速度v =12v C =ωl 2,则E =Bl v =12Bωl 2.4.公式E =Bl v sin θ与E =n ΔΦΔt的对比E =n ΔΦΔtE =Bl v sin θ区别研究对象 整个闭合回路 回路中做切割磁感线运动的那部分导体 适用范围 各种电磁感应现象 只适用于导体切割磁感线运动的情况计算结果 Δt 内的平均感应电动势某一时刻的瞬时感应电动势联系E =Bl v sin θ是由E =n ΔΦΔt 在一定条件下推导出来的,该公式可看做法拉第电磁感应定律的一个推论【例题1】 如图所示,半径为r 的金属圆环,其电阻为R ,绕通过某直径的轴OO ′以角速度ω匀速转动,匀强磁场的磁感应强度为B .从金属圆环的平面与磁场方向平行时开始计时,求金属圆环由图示位置分别转过30°角和由30°角转到330°角的过程中,金属圆环中产生的感应电动势各是多大?[思路点拨] (1)确定磁感线穿过圆环的有效面积; (2)了解磁通量正负号的含义; (3)确定不同角度转过的时间. [答案] 3Bωr 2 35Bωr 2[解析] 初始位置时穿过金属圆环的磁通量Φ1=0;由图示位置转过30°角时,金属圆环在垂直于磁场方向上的投影面积为S 2=πr 2sin 30°=12πr 2,此时穿过金属圆环的磁通量Φ2=BS 2=12B πr 2;由图示位置转过330°角时,金属圆环在垂直于磁场方向上的投影面积为S 3=πr 2sin 30°=12πr 2,此时穿过金属圆环的磁通量Φ3=-BS 3=-12B πr 2.所以金属圆环在转过30°角和由30°角转到330°角的过程中磁通量的变化量分别为 ΔΦ1=Φ2-Φ1=12B πr 2,ΔΦ2=Φ3-Φ2=-B πr 2,又Δt 1= θ1ω=π6ω=π6ω,Δt 2= θ2ω=5π3ω=5π3ω.此过程中产生的感应电动势分别为 E 1=ΔΦ1Δt 1=12B πr 2π6ω=3Bωr 2,E 2=|ΔΦ2Δt 2|=B πr 25π3ω=35Bωr 2.[例2] 如图所示,有一半径为R 的圆形匀强磁场区域,磁感应强度为B ,一条足够长的直导线以速度v 进入磁场.从直导线进入磁场至匀速离开磁场区域的过程中,求:(1)感应电动势的最大值为多少?(2)在这一过程中感应电动势随时间变化的规律如何?(3)从开始运动至经过圆心的过程中直导线中的平均感应电动势为多少? [思路点拨] (1)求瞬时感应电动势选择E =Bl v . (2)求平均感应电动势选择E =n ΔΦΔt .(3)应用E =Bl v 时找准导线的有效长度. [答案] (1)2BR v (2)2B v 2R v t -v 2t 2(3)12πBR v[解析] (1)由E =Bl v 可知,当直导线切割磁感线的有效长度l 最大时,E 最大,l 最大为2R ,所以感应电动势的最大值E =2BR v .(2)对于E 随t 变化的规律应求的是瞬时感应电动势,由几何关系可求出直导线切割磁感线的有效长度l 随时间t 变化的情况为l =2R 2-(R -v t )2,所以E =2B v 2R v t -v 2t 2.(3)从开始运动至经过圆心的过程中直导线的平均感应电动势E =ΔΦΔt =12πBR 2R v=12πBR v .1.(多选)单匝矩形线圈在匀强磁场中匀速运动,转轴垂直于磁场,若线圈所围面积里磁通量随时间变化的规律如图所示,则O ~D 过程中( )A .线圈中O 时刻感应电动势最大B .线圈中D 时刻感应电动势为零C .线圈中D 时刻感应电动势最大D .线圈中O 至D 时间内平均感应电动势为0.4 V2.如图所示,一正方形线圈的匝数为n ,边长为a ,线圈平面与匀强磁场垂直,且一半处在磁场中,在Δt 时间内,磁感应强度的方向不变,大小由B 均匀增大到2B ,在此过程中,线圈中产生的感应电动势为( )A.na 2B 2ΔtB.a 2B 2ΔtC.na 2B ΔtD.2na 2B Δt3.(多选)关于感应电动势的大小,下列说法不正确的是( ) A .穿过闭合电路的磁通量最大时,其感应电动势一定最大 B .穿过闭合电路的磁通量为零时,其感应电动势一定为零C .穿过闭合电路的磁通量由不为零变为零时,其感应电动势一定为零D .穿过闭合电路的磁通量由不为零变为零时,其感应电动势一定不为零 4.如图所示,在竖直向下的匀强磁场中,将一水平放置的金属棒ab 以水平速度v 0抛出,运动过程中棒的方向不变,不计空气阻力,那么金属棒内产生的感应电动势将( )A .越来越大B .越来越小C .保持不变D .方向不变,大小改变5、如图所示,直角三角形金属框abc 放置在匀强磁场中,磁感应强度大小为B ,方向平行于ab 边向上.当金属框绕ab 边以角速度ω逆时针转动时,a 、b 、c 三点的电势分别为U a 、U b 、U c .已知bc 边的长度为l .下列判断正确的是( )A .U a >U c ,金属框中无电流B .U b >U c ,金属框中电流方向沿a -b -c -aC .U bc =-12Bl 2ω,金属框中无电流D .U bc =12Bl 2ω,金属框中电流方向沿a -c -b -a6、如图所示,A 、B 两闭合圆形导线环用相同规格的导线制成,它们的半径之比r A ∶r B =2∶1,在两导线环包围的空间内存在一正方形边界的匀强磁场区域,磁场方向垂直于两导线环的平面向里.当磁场的磁感应强度随时间均匀增大的过程中,流过两导线环的感应电流大小之比为( )A.I AI B =1 B.I AI B =2 C.I A I B =14D.I A I B =127、如图所示,abcd 为水平放置的平行“”形光滑金属导轨,间距为l ,导轨间有垂直于导轨平面的匀强磁场,磁感应强度大小为B ,导轨电阻不计.已知金属杆MN 倾斜放置,与导轨成 θ角,单位长度的电阻为r ,保持金属杆以速度v 沿平行于cd 的方向滑动(金属杆滑动过程中与导轨接触良好).则( )A .电路中感应电动势的大小为Bl vsin θB .电路中感应电流的大小为B v sin θrC .金属杆所受安培力的大小为B 2l v sin θrD .金属杆的热功率为B 2l v 2r sin θ8.(多选)如图所示,三角形金属导轨EOF 上放有一根金属杆AB ,在外力作用下,保持金属杆AB 和OF 垂直,以速度v 匀速向右移动.设导轨和金属杆AB 都是用粗细相同的同种材料制成的,金属杆AB 与导轨接触良好,则下列判断正确的是( )A .电路中的感应电动势大小不变B .电路中的感应电流大小不变C .电路中的感应电动势大小逐渐增大D .电路中的感应电流大小逐渐增大9.一个面积为S =4×10-2 m 2、匝数为n =100匝的线圈放在匀强磁场中,磁场方向垂直于线圈平面,磁感应强度B 随时间t 变化的规律如图所示,则下列判断正确的是( )A .在开始的2 s 内穿过线圈的磁通量的变化率等于8 Wb/sB .在开始的2 s 内穿过线圈的磁通量的变化量等于零C .在开始的2 s 内线圈中产生的感应电动势的大小等于8 VD .在第3 s 末线圈中的感应电动势等于零10.(多选)如图所示,单匝线圈在匀强磁场中绕垂直于磁场的轴匀速转动,穿过线圈的磁通量Φ随时间t 的关系可用图像表示,则( )A .在t =0时刻,线圈中的磁通量最大,感应电动势也最大B .在t =1×10-2 s 时刻,感应电动势最大 C .在t =2×10-2 s 时刻,感应电动势为零D .在0~2×10-2 s 时间内,线圈中感应电动势的平均值为零11.如图所示,面积为0.2 m 2的100匝线圈处在匀强磁场中,磁场方向垂直于线圈平面.已知磁感应强度随时间变化的规律为B =(2+0.2t )T ,定值电阻R 1=6 Ω,线圈电阻R 2=4 Ω,求:(1)磁通量变化率及回路的感应电动势; (2)a 、b 两点间电压U ab .12.如图甲所示,轻质细线吊着一质量m =0.32 kg 、边长L =0.8 m 、匝数n =10的正方形线圈,总电阻为r =1 Ω,边长为L2的正方形磁场区域对称分布在线圈下边的两侧,磁场方向垂直纸面向里,大小随时间的变化关系如图乙所示,从t =0开始经t 0时间细线开始松弛,g 取10 m/s 2.求:(1)从t =0到t =t 0时间内线圈中产生的电动势; (2)从t =0到t =t 0时间内线圈的电功率; (3)t 0的值.1.【答案】:ABD【解析】:由法拉第电磁感应定律知线圈中O 至D 时间内的平均感应电动势E =ΔΦΔt =2×10-30.012 V =0.4V ,D 项正确;由感应电动势的物理意义知,感应电动势的大小与磁通量的大小Φ和磁通量的改变量ΔΦ均无必然联系,仅由磁通量的变化率ΔΦΔt 决定,而任何时刻磁通量的变化率ΔΦΔt 就是Φ-t 图像上该时刻切线的斜率,不难看出O 时刻处切线斜率最大,D 点处切线斜率最小为零,故A 、B 正确,C 错误.2.【答案】:A【解析】:正方形线圈内磁感应强度B 的变化率ΔB Δt =BΔt ,由法拉第电磁感应定律知,线圈中产生的感应电动势为E =nS ΔB Δt =n ·a 22·B Δt =na 2B2Δt,选项A 正确.3.【答案】:ABC【解析】:磁通量的大小与感应电动势的大小不存在内在的联系,故A 、B 错;当磁通量由不为零变为零时,闭合电路的磁通量发生改变,一定有感应电流产生,有感应电流就一定有感应电动势,故C 错,D 对.4.【答案】:C【解析】:由于导体棒中无感应电流,故棒只受重力作用,导体棒做平抛运动,水平速度v 0不变,即切割磁感线的速度不变,故感应电动势保持不变,C 正确.5、【答案】:C【解析】:金属框abc 平面与磁场平行,转动过程中磁通量始终为零,所以无感应电流产生,选项B 、D 错误.转动过程中bc 边和ac 边均切割磁感线,产生感应电动势,由右手定则判断U a <U c ,U b <U c ,选项A 错误.由转动切割产生感应电动势的公式得U bc =-12Bl 2ω,选项C 正确.6、【答案】:D【解析】:A 、B 两导线环的半径不同,它们所包围的面积不同,但穿过它们的磁场所在的区域面积是相等的,所以两导线环上的磁通量变化率是相等的,E =ΔΦΔt =ΔB Δt S 相同,得E A E B =1,I =E R ,R =ρlS (S 为导线的横截面积),l =2πr ,所以I A I B =r B r A ,代入数值得I A I B =r B r A =12.7、【答案】:B【解析】:由电磁感应定律可知电路中感应电动势为E =Bl v ,A 错误;感应电流的大小I =Bl v r l sin θ=B v sin θr ,B 正确;金属杆所受安培力的大小F =B B v sin θr ·l sin θ=B 2l v r ,C 错误;热功率P =(B v sin θr )2r l sin θ=B 2l v 2sin θr ,D 错误.8、【答案】:BC【解析】:设三角形金属导轨的夹角为θ,金属杆AB 由O 点经时间t 运动了v t 的距离,则E =B v t ·tan θ·v ,电路总长为l =v t +v t tan θ+v t cos θ=v t (1+tan θ+1cos θ),又因为R =ρl S ,所以I =ER =B v S sin θρ(1+sin θ+cos θ),I 与t 无关,是恒量,故选项B 正确.E 逐渐增大,故选项C 正确.9.【答案】:C【解析】:在开始的2 s 内,磁通量的变化量为ΔΦ=|-2-2|×4×10-2 Wb =0.16 Wb ,磁通量的变化率ΔΦΔt =0.08 Wb/s ,感应电动势大小为E =n ΔΦΔt=8 V ,故A 、B 错,C 对;第3 s 末虽然磁通量为零,但磁通量的变化率为0.08 Wb/s ,感应电动势不等于零,故D 错.10.【答案】:BC【解析】:由法拉第电磁感应定律知E ∝ΔΦΔt,故t =0及t =2×10-2 s 时刻,E =0,A 错,C 对.t =1×10-2s ,E 最大,B 对.0~2×10-2 s ,ΔΦ≠0,E ≠0,D 错. 11.【答案】:(1)0.04 Wb/s 4 V (2)2.4 V 【解析】:(1)由B =(2+0.2t )T 得ΔBΔt =0.2 T/s ,故ΔΦΔt =S ΔBΔt=0.04 Wb/s , E =n ΔΦΔt=4 V.(2)线圈相当于电源,U ab 是外电压,则 U ab =ER 1+R 2R 1=2.4 V .12.【答案】:(1)0.4 V (2)0.16 W (3)2 s 【解析】:(1)由法拉第电磁感应定律得 E =n ΔΦΔt =n ΔB Δt ×12×⎝⎛⎭⎫L 22=0.4 V .(2)I =Er =0.4 A ,P =I 2r =0.16 W.(3)分析线圈受力可知,当细线松驰时有 F 安=nB t 0I ·L 2=mg ,I =E r ,则B t 0=2mgrnEL =2 T.由图象知B t 0=1+0.5 t 0(T),解得t 0=2 s.。
第2章习题答案

第2章2-1 半径为a的无限薄带电圆盘上面电荷密度为ρ=r2,r为圆盘上任意点到圆心的距离,求圆盘上的总电量。
解:Q=∬ρ∙rdφdrS =∫r3∙dra∙∫dφ2π=πr42。
2-2 半径为a的球体内有均匀分布的电荷,其总电量为Q,若该球以角速度ω绕其自身的任意中轴旋转,求球体内的体电流密度。
解:J V⃗⃗⃗ =3qωrsinθ4πa3φ⃗⃗ 。
2-3 无限薄的导电面放置于z=0平面内的0<x<0.05m的区域中,流向y⃗方向的5A电流按正弦规律分布于该面内,在x=0和x=0.05m处线电流密度为0,在x=0.025m处线电流密度为最大,求J S⃗⃗ 的表达式。
解:电流分布如下图所示:x0.025 0.05J S⃗⃗ =5sin(πx0.05)a y⃗⃗⃗⃗ 。
2-4 三根长度为l、电荷均匀分布、线密度分别为ρl1,ρl2和ρl3的线电荷构成的等边三角形,设ρl1=2ρl2=2ρl3,计算三角形中心处的电场。
解:E y⃗⃗⃗⃗ =ρh4πε0∫√(h2+x2)3l2−l2=4πεh√4h2+l2,由电荷密度关系可知:2|E1|=|E2|=|E3|,|E2|=2E,|E1|=E,|E3|=2E,因此,E1⃗⃗⃗⃗ +E2⃗⃗⃗⃗ +E3⃗⃗⃗⃗ =0。
2-5 两无限长的同轴圆柱壳面,半径为a 和b ,内外导体上均匀分布电荷,密度分别为ρS1,ρS2,求r <a ,a <r <b ,r >b 时各点的电场及两导体间的电压。
解:用高斯定理求E 。
做高斯面(闭合面), ∵轴对称∴高斯面为圆柱闭合面,为左图所示 ①E1(r <a ,内导体内) 设导体为理想导体,则E 1=0;②E2(a <r <b ,内导体与外导体之间圆柱空间)∵同轴无限长,∴圆柱侧面(高斯面)上E 2处处相等,且E只有ρ方向分量d 矢量为高斯封闭面的外法线n ds n s,=E 2·d s : 上下底面:E 2·d s =0(∵E 2⊥d s,cos90°=0) 侧面:E 2·d s =E 2·ds (∵E 2∥d s,cos 0°=1)10222222επρεπρalQlE dS E dS E S d E s S=====⋅∴⎰⎰⎰⎰⎰⎰侧侧∴ρρερˆ012aE s = ③3E( r >b ,外导体壳外)E 32πl ρ=212επρπρblal s s +∴3E =ρρερρˆ021ba s s + (2)两导体内电压ab Va ba d a d E d E l d E V sb a s b aba b a ab ln 10101ερρρερρρρρ===⋅=⋅=⎰⎰⎰⎰ 当r <a 时,E⃗ =0;当a <r <b 时,E ⃗ =ρS1a+ρS2brε0r ,U =∫E ⃗ ∙dr b a =(ρS1a +ρS2b )ε0ln ab 。
电力电子技术课后答案第2章[1]
![电力电子技术课后答案第2章[1]](https://img.taocdn.com/s3/m/45e6361414791711cc7917f3.png)
30.单相桥式全控整流电路、三相桥式全控整流电路中,当负载分别为电阻负载或电感负载时,要求的晶闸管移相范围分别是多少?
答:单相桥式全控整流电路,当负载为电阻负载时,要求的晶闸管移相范围是0 ~ 180,当负载为电感负载时,要求的晶闸管移相范围是0 ~ 90。
Id=44.15(A)
ΔUd=13.25(V)
又∵ - =2XBId∕ U2
=0.4485
γ=63.35°-60°=3.35°
ud、IVT1和IVT2的波形如下:
18.单相桥式全控整流电路,其整流输出电压中含有哪些次数的谐波?其中幅值最大的是哪一次?变压器二次侧电流中含有哪些次数的谐波?其中主要的是哪几次?
ΔUd=6.7(V)
Id=44.63(A)
又∵
- =2 ∕ U2
即得出
=0.752
换流重叠角
=41.28°30°=11.28°
ud、iVT1和iVT2的波形如下:
16.三相桥式不可控整流电路,阻感负载,R=5Ω,L=∞,U2=220V,XB=0.3Ω,求Ud、Id、IVD、I2和的值并作出ud、iVD和i2的波形。
Ud=0.9U2cosα-ΔUd
ΔUd=2XBId∕π
Id=(Ud-E)∕R
解方程组得:
Ud=(πR0.9U2cosα+2XBE)∕(πR+2XB)=44.55(V)
ΔUd=0.455(V)
Id=4.55(A)
又∵
- = ∕U2
即得出
=0.4898
换流重叠角
=60.67°60°=0.67°
最后,作出整流电压Ud的波形如下:
八年级上册物理人教第2章 第1节 声音的产生和传播 同步练习及答案

第1节声音的产生和传播一、单选题(共4题;共8分)1.宇航员在太空与飞船内的对话必须借助电子通信设备才能进行,而在飞船舱内却可以直接对话其原因是()A. 太空中噪声太大B. 太空中是真空,不能传声C. 用通信设备对话更方便D. 声音只能在地面附近传播2.如图所示,在探究“声音是由物体振动产生的”实验中,将正在发声的音叉紧靠悬线下的乒乓球,发现乒乓球被多次弹开.这样做是为了()A. 使音叉的振动尽快停下来B. 延长音叉的振动时间C. 使声波被多次反射形成回声D. 把音叉的微小振动放大,便于观察3.关于声音,下列说法正确的是()A. 一切发声的物体都在振动B. 只要物体在振动,我们就能听到声音C. 声音在不同介质中的传播速度相同D. 声音在真空中的传播速度为3×108m/s4.人要区分回声和原声,两者到达人耳的时间间隔不能小于0.1 s.如果原声和回声到达人耳间隔不到0.1 s,回声就会同原声混在一起,从而加强原声.人对着障碍物大喊一声,要听清自己的回声,人到障碍物的距离最小需( )A. 340 mB. 170 mC. 34 mD. 17 m二、填空题(共6题;共11分)5.声音的传播需要________,真空不能传声.6.如图,在物理课上,同学们把正在响铃的闹钟放在玻璃罩内,逐渐抽出其中的空气,结果发现,闹钟的铃声越来越小了,这说明:声音传播需要________,真空________(选填“能”或“不能”)传声.7.如表记录了声波在五种气体中不同温度条件下的传播速度,请依据表中的相关数据回答下列问题:空气氢气氦气氮气二氧化碳0 331 1261 891 337 26910 337 1284 908 343 27320 343 1306 924 349 27930 349 1328 939 355 283①当温度为20℃时,声波在氢气中的传播速度为________米/秒.②声波的传播速度与温度的关系是:________.③根据表格中的数据,最大飞行速度一定的飞机要在空气中实现超音速飞行,在温度________的条件下更容易成功.(选填“较高”或“较低”)8.在飞机失事搜寻过程中,搜救舰船在定位和测量海深时都要用到超声测位仪(如图所示),它是利用声音可以在________中传播来工作的。
2章 基本放大电路题解1(第四版模电答案)
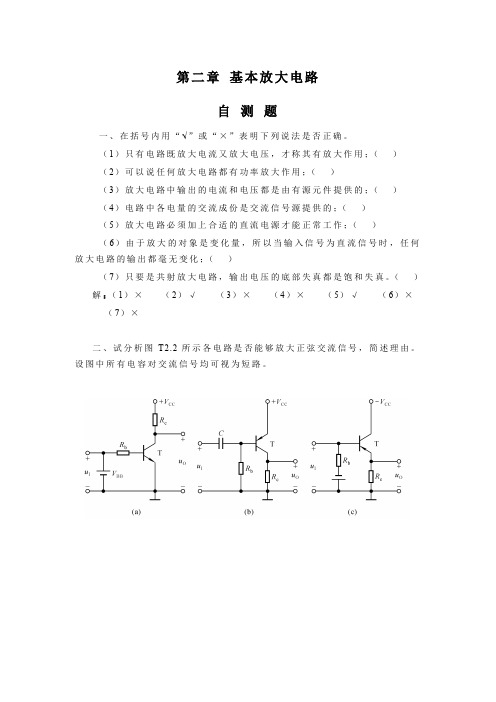
第二章基本放大电路自测题一、在括号内用“ ”或“×”表明下列说法是否正确。
(1)只有电路既放大电流又放大电压,才称其有放大作用;()(2)可以说任何放大电路都有功率放大作用;()(3)放大电路中输出的电流和电压都是由有源元件提供的;()(4)电路中各电量的交流成份是交流信号源提供的;()(5)放大电路必须加上合适的直流电源才能正常工作;()(6)由于放大的对象是变化量,所以当输入信号为直流信号时,任何放大电路的输出都毫无变化;()(7)只要是共射放大电路,输出电压的底部失真都是饱和失真。
()解:(1)×(2)√(3)×(4)×(5)√(6)×(7)×二、试分析图T2.2所示各电路是否能够放大正弦交流信号,简述理由。
设图中所有电容对交流信号均可视为短路。
图T2.2解:(a)不能。
因为输入信号被V B B短路。
(b)可能。
(c)不能。
因为输入信号作用于基极与地之间,不能驮载在静态电压之上,必然失真。
(d)不能。
晶体管将因发射结电压过大而损坏。
(e)不能。
因为输入信号被C2短路。
(f)不能。
因为输出信号被V C C短路,恒为零。
(g)可能。
(h)可能。
(i)不能。
因为T截止。
三、在图T2.3所示电路中, 已知V C C =12V ,晶体管的β=100,'b R =100k Ω。
填空:要求先填文字表达式后填得数。
(1)当iU =0V 时,测得U B E Q =0.7V ,若要基极电流I B Q =20μA , 则'b R 和R W 之和R b= ≈ k Ω;而若测得U C E Q=6V ,则R c = ≈ k Ω。
(2)若测得输入电压有效值i U =5mV 时,输出电压有效值'o U =0.6V , 则电压放大倍数 uA = ≈ 。
若负载电阻R L 值与R C 相等 ,则带上负载图T2.3 后输出电压有效值o U = = V 。
《西方经济学》习题及答案——第二章 (1)消费者选择

第二章消费者选择习题一、单选题1、人们常说“多多益善”,从经济学角度来说,这是指随着所消费的商品数量增多( )。
A 总效用递增B 边际效用递增C 总效用递减D 边际效用递减答案:A2.假设在同一时间内,罗斯消费的X商品为3单位,钱德勒消费的X商品为5个单位,根据边际效用递减规律( )。
A.罗斯的边际效用大于钱德勒的边际效用B.罗斯的边际效用等于钱德勒的边际效用C.罗斯的边际效用小于钱德勒的边际效用D.两者的边际效用的相对大小不能确定答案:B解析:在同一时间内,商品的价格是不变的。
经济学假设人是理性的,追求效用最大化的。
那么无论罗斯消费多少,钱德勒消费多少,他们一定是在有限的资金约束下,实现了身的利润最大化,那么,根据等边际原则,必然有也就是说每个人在该商品上的花费的最后一单位货币所得到的效用值必然等于货币本身的新用估加里任何一人人比如罗斯甘在该商只的消费上花费的是后3、有关消费者行为分析存在基数效用论和序数效用论之分,二者最主要的差异性在于是否假定( )。
A 需求规律B 效用取决于商品的价格C 边际效用递减D 总效用递增答案:C4、假定咖啡的价格为10元一杯,苹果汁的价格为5元一杯,当咖啡对苹果汁的MRS=3时,消费者为了达到最大的满足,会选择( )。
A 增购咖啡,减少苹果汁的购买B 增购苹果汁,减少咖啡的购买C 同时增加咖啡、苹果汁的购买D 同时减少咖啡、苹果汁的购买答案:A5.当收入没有改变时,某种普通商品价格的上升会( )。
A.使消费者对该商品的需求量增加B.减少该消费者的总效用C.改变该消费者的偏好D.对该消费者所能购买的最大化商品组合没有影响答案:B解析:普通商品价格上升使消费者对其需求量减少,A错。
预算线与无差异曲线的切点表示效用最大化的总效用,商品价格上升,预算线向内转,与新的无差异曲线相交,新的无差异曲线离原点更近,是较低水平的效用,B对,减少该消费者总效用。
商品价格和消费者偏好同为影响需求的因素,商品价格不影响消费者偏好,C错。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章 质点力学的运动定律 守恒定律一、选择题1(C),2(E),3(D),4(C),5(C),6(C),7(B),8(C),9(C),10(B),11(C),12(D),13(B) 二、填空题 (1). 12rad/s. (2). 290J (3). 3J (4). 18 N ·s(5). j t i t2323+ (SI)(6). 16 N ·s , 176 J (7). 16 N ·s ,176 J (8). M k l /0,Mknm M Ml +0(9). j i5- (10).2m v , 指向正西南或南偏西45°三、计算题1. 已知一质量为m 的质点在x 轴上运动,质点只受到指向原点的引力的作用,引力大小与质点离原点的距离x 的平方成反比,即2/x k f -=,k 是比例常数.设质点在 x =A 时的速度为零,求质点在x =A /4处的速度的大小.解:根据牛顿第二定律x m t x x m t m xk f d d d d d d d d 2v v v v =⋅==-= ∴ ⎰⎰-=-=4/202d d ,d d A A x mxkmx x k v v v v v k mAA A m k 3)14(212=-=v ∴ )/(6mA k =v2. 飞机降落时的着地速度大小v =90 km/h ,方向与地面平行,飞机与地面间的摩擦系数μ =0.10,迎面空气阻力为C x v 2,升力为C y v 2(v 是飞机在跑道上的滑行速度,C x 和C y 为某两常量).已知飞机的升阻比K =C y /C x =5,求飞机从着地到停止这段时间所滑行的距离.(设飞机刚着地时对地面无压力)解:以飞机着地点为坐标原点,飞机滑行方向为x 轴正向.设飞机质量为m ,着地后地面对飞机的支持力为N .在竖直方向上02=-+mg C N y v ∴ 2v y C mg N -= 飞机受到地面的摩擦力 )(2v y C mg N f -==μμ在水平方向上 xm t mC C mg x y d d d d )(22vv v v v ==---μ即x C C mg m y x d )(d 2-=-+v vv μμx = 0时,m/s 25km/h 900===v v .x =S (滑行距离)时,v =0⎰⎰-=-=-+020d )(d v v vv Sy x S x C C mg m μμS C C m g C C m g C C m y x y x yx -=-+-+-⎰220)(](d[21v v )v μμμμμ解得m gC C m g C C m S y x y x μμμμ20(ln 21)v -+-=∵ 飞机刚着地前瞬间,所受重力等于升力,即 20v y C mg = ∴ 2v m gC y =, 205v mg K C C y x == 代入S 表达式中并化简,然后代入数据22151ln )51(2520=-=μμg S v m3.若质量为m 1以速率v 10运动的物体A 与质量为m 2的静止物体B 发生对心完全弹性碰撞,如何选择m 2的大小,使得m 2在碰撞后具有最大的动能?又此最大动能是多少?解:在对心完全弹性碰撞中,若v 20 = 0,则有21101211012012222)(m m m m m m m m +=++-=v v v v 物体B 的动能 22110122222)2(2121m m m m m E K +==v v由 0)(2)(d d 321210211222=+-=m m m m m m E K v 得 21m m = 又 0)(432d d 121242112210212222<+-===m m m m K m m m m m m E v故 12m m = 时,m 2的动能有最大值.此最大值是 2101221v m E K =.4.一辆水平运动的装煤车,以速率v 0从煤斗下面通过,每单位时间内有质量为m 0的煤卸入煤车.如果煤车的速率保持不变,煤车与钢轨间摩擦忽略不计,试求:(1) 牵引煤车的力的大小; (2) 牵引煤车所需功率的大小;(3) 牵引煤车所提供的能量中有多少转化为煤的动能?其余部分用于何处?解:(1) 以煤车和∆t 时间内卸入车内的煤为研究对象,水平方向煤车受牵引力F 的作用,由动量定理: 000)(v v M t m M t F -+=∆∆ 求出: 00v m F =(2) 2000v v m F P ==(3) 单位时间内煤获得的动能: 20021v m E K =单位时间内牵引煤车提供的能量为 P E ===21/E E K 50%即有50%的能量转变为煤的动能,其余部分用于在拖动煤时不可避免的滑动摩擦损耗.5.一链条总长为l ,质量为m ,放在桌面上,并使其部分下垂,下垂一段的长度为a .设链条与桌面之间的滑动摩擦系数为μ.令链条由静止开始运动,则(1)到链条刚离开桌面的过程中,摩擦力对链条作了多少功?(2)链条刚离开桌面时的速率是多少?解:(1)建立如图坐标.某一时刻桌面上全链条长为y ,则摩擦力大小为 g lym f μ=摩擦力的功 ⎰⎰--==0d d al al f y gy lmy f W μ=22al y lmg-μ =2)(2a l lmg--μ(2)以链条为对象,应用质点的动能定理 ∑W =2022121v v m m - 其中 ∑W = W P +W f ,v 0 = 0W P =⎰la x P d =la l mg x x l mg la 2)(d 22-=⎰ 由上问知 la l mg W f 2)(2--=μ所以222221)(22)(v m a l l mg l a l mg =---μ 得 []21222)()(a l a l lg ---=μv6.小球A ,自地球的北极点以速度0v在质量为M 、半径为R 的地球表面水平切向向右飞出,如图所示,地心参考系中轴OO '与0v平行,小球A 的运动轨道与轴OO '相交于距O 为3R 的C 点.不考虑空气阻力,求小球A 在C 点的速度v与0v 之间的夹角θ.解:由机械能守恒:al -a-a)3/(21/21220R GMm m R GMm m -=-v v ①根据小球绕O 角动量守恒: θsin 30v v Rm Rm = ② ①、②式联立可解出. RGM /129sin 20-=v v θ7.质量为m A 的粒子A 受到另一重粒子B 的万有引力作用,B 保持在原点不动.起初,当A 离B 很远( r = ∞)时,A 具有速度0v,方向沿图中所示直线Aa ,B 与这直线的垂直距离为D .粒子A 由于粒子B 的作用而偏离原来的路线,沿着图中所示的轨道运动.已知这轨道与B 之间的最短距离为d ,求B 的质量m B .解:A 对B 所在点的角动量守恒.设粒子A 到达距B 最短距离为d 时的速度为v . d m Dm A A v v =0, d D /0v v = A 、B 系统机械能守恒(A 在很远处时, 引力势能为零)d m Gm m m B A A A /2121220-=v v解得 d Gm B /2202=-v v∴ )2/()(2022Gd d D m B v -=8.设两个粒子之间相互作用力是排斥力,其大小与粒子间距离r 的函数关系为3r k f =,k 为正值常量,试求这两个粒子相距为r 时的势能.(设相互作用力为零的地方势能为零.) 解:两个粒子的相互作用力 3r k f =已知f =0即r =∞处为势能零点, 则势能⎰⎰∞∞∞=⋅==r r P P r r kW E d d 3r f)2(2r k =四 研讨题1. 汽车发动机内气体对活塞的推力以及各种传动部件之间的作用力能使汽车前进吗?使汽车前进的力是什么力?参考解答:汽车发动机内气体对活塞的推力以及各种传动部件之间的作用力都是汽车系统的内力,内力只会改变内部各质点的运动状态,不会改变系统的总动量,所以不能使汽车前进。
使汽车前进的力只能是外力,这个外力就是地面给汽车的摩擦力。
粗略分析如下:当汽车发动机内气体对活塞的推力带动传动部件使主动轮( 一般为汽车的后轮)绕轮轴转动时,使主动轮与地面的接触部分相对地面有向后滑动的趋势,从而使地面对汽车施以向前的摩擦力,使汽车整体向前加速运动。
由于汽车前进使从动轮(汽车的前轮)相对地面有向前的运动趋势,A因此从动轮受到地面施以的方向向后的摩擦力,该摩擦力对从动轮轴的力矩使从动轮滚动起来。
所以汽车的运动最终靠的是地面施加的摩擦力。
2. 冲量的方向是否与冲力的方向相同?参考解答:冲量是力对时间的积累,由动量定理:P P P t F I t t∆=-==⎰1221d 所以,冲量的方向和动量增量P ∆的方向相同,不一定与冲力F的方向相同。
3. 一物体可否只具有机械能而无动量?一物体可否只有动量而无机械能?试举例说明。
参考解答:机械能是系统作机械运动的动能和势能的总和.动能与物体相对参考系的运动速度有关,势能则属于保守力系统,一物体具有的势能,是相对势能零点而言的。
若取保守力系统,物体相对参考系静止,那么物体的动能为零,物体的动量也为零。
该系统的机械能就是物体相对系统势能零点所具有的势能.所以,一物体可以有机械能而无动量。
例如:一质量为m 的物体(例如一气球)静止在相对于地面为h 的高处,此时对于物体和地球系统,具有的机械能为重力势能,其值为 mgh 。
由于此时物体静止,故其动量为零。
在保守力系统中,若一物体运动至某一位置时所具有的动能值,恰等于该位置相对势能零点所具有的负的势能值,则该物体的机械能为零,而因物体具有动能,因而动量不为零。
所以,一物体也可以有动量而无机械能。
例如:物体自离地面高为h 处自由下落,取物体和地球为系统,并取下落处为重力势能零点.初始时刻系统的机械能 E 0=0,下落至地面时,物体具有速度的大小为v ,动能为m v 2/2,动量的大小为 m v ,系统的机械能为 E =m v 2/2 - mgh = E 0=0.4. 在经典力学范围内,若某物体系对某一惯性系满足机械能守恒条件,则在相对于上述惯性系作匀速直线运动的其它参照系中,该物体系是否一定也满足机械能守恒条件?请举例说明.参考解答:不一定满足守恒条件.例如在水平面上以速度0v匀速直线行驶的车厢顶上悬挂一小球.以车厢为参考系,小球摆动过程中绳子张力对小球不作功,则小球+地系统机械能守恒.若以地面为参考系,小球相对于车厢的摆动速度为v,则小球对地速度v v v +='0,v '与绳张力T 不垂直,故小球摆动过程中绳张力对小球要作功,这时小球+地系统不满足机械能守恒条件.但在上述两个参考系(惯性系)中,动能定理和功能原理仍是成立的.5. 在车窗都关好的行驶的汽车内,漂浮着一个氢气球,当汽车向左转弯时,氢气球在车内将向左运动还是向右运动? 参考解答:在空气中释放一氢气球,它将受浮力的作用上升。
