现代数字信号处理Advanced Digital Signal Processing_ch2 Wiener&Kalman
数字信号处理Digital Signal Processing(DSP)

• 经过A/D变换器后,不但时间离散化了,幅度也量化 了,这种信号称为数字信号。用x(n)表示。
例子
• 如4位码,只能表示24=16种不同的信号幅度, 这些幅度称为量化电平。
• 当离散时间信号幅度与量化电平不相同时, 就要以最接近的一个量化电平来近似它。
(7)估计理论,包括功率谱估计及相关函数 估计等。
(8)信号的压缩,包括语音信号与图象信号 的压缩
(9)信号的建模,包括AR,MA,ARMA, CAPON,PRONY等各种模型。
(10)其他特殊算法(同态处理、抽取与内 插、信号重建等)
(11)数字信号处理的实现。
(12) 数字信号处理的应用。
第一节 什么是数字信号处理 第二节 数字信号处理的实现 第三节 数字信号处理的应用领域 第四节 数字信号处理器
例:直流信号:仅用一个参量可以描述。阶跃信号:可用幅 度和时间两个参量描述。正弦波信号:可用幅度、频率和 相位三个参量来描述。
• 随机信号:若信号在任意时刻的取值不能精确确定,或 说取值是随机的,即它不能用有限的参量加以描述。也无 法对它的未来值确定性地预测。它只能通过统计学的方法 来描述(概率密度函数来描述)。
• 随着信息时代、数字世界的到来,数字信号处 理已成为一门极其重要的学科和技术领域。
(四)数字信号处理系统的基本组成
• 以下所讨论的是模拟信号的数字信号处理系统.
模拟 前置预 滤波器
xa(t)
PrF
x(n)
y(n)
A/D 变换器
数字信号 处理器
D/A 变换器
ADC
DSP
DSP(Digital Signal Processor 数字信号处理器)简介

DSP(Digital Signal Processor 数字信号处理器)简介DSP是什么?DSP是数字信号处理器(Digital Signal Processor)的缩写,是一种独特的微处理器,是以数字信号来处理大量信息的器件。
其工作原理是接收模拟信号,转换为0或1的数字信号,再对数字信号进行修改、删除、强化,并在其他系统芯片中把数字数据解译回模拟数据或实际环境格式。
它与CCD一样是摄像机的核心元件,如果说CCD是摄像机的“心脏”,那么DSP就是摄像机的“大脑”。
DSP的应用很广泛,并不局限与摄像机,不过大多数人并不了解DSP,下面就来揭开DSP的神秘面纱,简单介绍下DSP。
数字信号处理DSP数字信号处理(Digital Signal Processing,简称DSP)是一门涉及许多学科而又广泛应用于许多领域的新兴学科。
20世纪60年代以来,随着计算机和信息技术的飞速发展,数字信号处理技术应运而生并得到迅速的发展。
数字信号处理是一种通过使用数学技巧执行转换或提取信息,来处理现实信号的方法,这些信号由数字序列表示。
在过去的二十多年时间里,数字信号处理已经在通信等领域得到极为广泛的应用。
德州仪器、Freescale等半导体厂商在这一领域拥有很强的实力。
而日本的SONY,SHARP以及韩国的三星,LG等厂商在摄像机上的DSP领域有着较强的实力。
DSP微处理器DSP(digital signal processor)是一种独特的微处理器,是以数字信号来处理大量信息的器件。
其工作原理是接收模拟信号,转换为0或1的数字信号,再对数字信号进行修改、删除、强化,并在其他系统芯片中把数字数据解译回模拟数据或实际环境格式。
它不仅具有可编程性,而且其实时运行速度可达每秒数以千万条复杂指令程序,远远超过通用微处理器,是数字化电子世界中日益重要的电脑芯片。
它的强大数据处理能力和高运行速度,是最值得称道的两大特色。
DSP芯片,也称数字信号处理器,是一种特别适合于进行数字信号处理运算的微处理器器,其主要应用是实时快速地实现各种数字信号处理算法。
现代数字信号处理Advanced Digital Signal Processing_ch1 fundamentals

rxx (M 1)
rxx (M 1)
rxx (0)
is an Hermite matrix.
If x(n) is real signal, then Rxx is real symmetrical and nonnegative definite matrix:
MM
airxx (i j)a*j 0
Autocovariance function (2nd-order mixed central moment, a scatter or dispersion measure)
cov(x(n1), x(n2 )) rxx (n1, n2 ) m*x (n1)mx (n2 )
E[(x(n1) mx (n1))*(x(n2 ) mx (n2 ))]
mx (n) E[x(n)] x(n) fx (x, n)dx
Mean square value (2nd-order origin moment)
E
x(n)
2
x(n) 2
fx (x, n)dx
Variance (2nd-order central moment)
• Weakly (Wide-Sense) Stationary Random Sequence
The random sequencxe(n) satisfies
Both its 1st-order and 2nd-order moments exist
For amnyx (innt)egemr xm(n, m) mx
random sequences
1.2 Stationary Random Sequence
数字信号处理中英文对照外文翻译文献

中英文对照外文翻译(文档含英文原文和中文翻译)数字信号处理一、导论数字信号处理(DSP)是由一系列的数字或符号来表示这些信号的处理的过程的。
数字信号处理与模拟信号处理属于信号处理领域。
DSP包括子域的音频和语音信号处理,雷达和声纳信号处理,传感器阵列处理,谱估计,统计信号处理,数字图像处理,通信信号处理,生物医学信号处理,地震数据处理等。
由于DSP的目标通常是对连续的真实世界的模拟信号进行测量或滤波,第一步通常是通过使用一个模拟到数字的转换器将信号从模拟信号转化到数字信号。
通常,所需的输出信号却是一个模拟输出信号,因此这就需要一个数字到模拟的转换器。
即使这个过程比模拟处理更复杂的和而且具有离散值,由于数字信号处理的错误检测和校正不易受噪声影响,它的稳定性使得它优于许多模拟信号处理的应用(虽然不是全部)。
DSP算法一直是运行在标准的计算机,被称为数字信号处理器(DSP)的专用处理器或在专用硬件如特殊应用集成电路(ASIC)。
目前有用于数字信号处理的附加技术包括更强大的通用微处理器,现场可编程门阵列(FPGA),数字信号控制器(大多为工业应用,如电机控制)和流处理器和其他相关技术。
在数字信号处理过程中,工程师通常研究数字信号的以下领域:时间域(一维信号),空间域(多维信号),频率域,域和小波域的自相关。
他们选择在哪个领域过程中的一个信号,做一个明智的猜测(或通过尝试不同的可能性)作为该域的最佳代表的信号的本质特征。
从测量装置对样品序列产生一个时间或空间域表示,而离散傅立叶变换产生的频谱的频率域信息。
自相关的定义是互相关的信号本身在不同时间间隔的时间或空间的相关情况。
二、信号采样随着计算机的应用越来越多地使用,数字信号处理的需要也增加了。
为了在计算机上使用一个模拟信号的计算机,它上面必须使用模拟到数字的转换器(ADC)使其数字化。
采样通常分两阶段进行,离散化和量化。
在离散化阶段,信号的空间被划分成等价类和量化是通过一组有限的具有代表性的信号值来代替信号近似值。
武汉大学电信学院硕士生各专业课程设(通信 测控 物理电子)
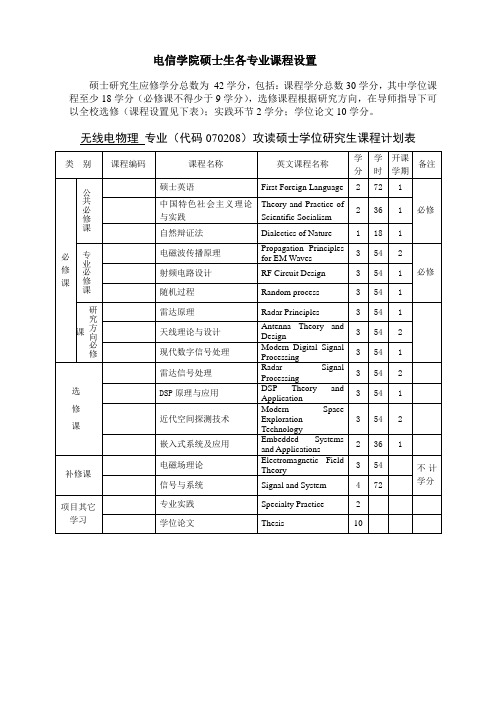
电信学院硕士生各专业课程设置硕士研究生应修学分总数为42学分,包括:课程学分总数30学分,其中学位课程至少18学分(必修课不得少于9学分),选修课程根据研究方向,在导师指导下可以全校选修(课程设置见下表);实践环节2学分;学位论文10学分。
无线电物理专业(代码070208)攻读硕士学位研究生课程计划表校选修(课程设置见下表);实践环节2学分;学位论文10学分。
电磁场微波技术专业(代码080904)攻读硕士学位研究生课程计划表校选修(课程设置见下表);实践环节2学分;学位论文10学分。
空间物理学专业(代码070802)攻读硕士学位研究生课程计划表校选修(课程设置见下表);实践环节2学分;学位论文10学分。
空间探测与信息处理技术专业(代码070820)攻读硕士学位研究生课程计划表校选修(课程设置见下表);实践环节2学分;学位论文10学分。
光学工程学科(代码0803)攻读硕士学位研究生课程计划表校选修(课程设置见下表);实践环节2学分;学位论文10学分。
物理电子学专业(代码080901)攻读硕士学位研究生课程计划表校选修(课程设置见下表);实践环节2学分;学位论文10学分。
电路与系统专业(代码080902)攻读硕士学位研究生课程计划表校选修(课程设置见下表);实践环节2学分;学位论文10学分。
通信与信息系统专业(代码081001)攻读硕士学位研究生课程计划表校选修(课程设置见下表);实践环节2学分;学位论文10学分。
信号与信息处理专业(代码081002)攻读硕士学位研究生课程计划表校选修(课程设置见下表);实践环节2学分;学位论文10学分。
检测技术与自动化装置专业(代码081102)攻读硕士学位研究生课程计划表全日制攻读电子与通信工程领域工程硕士研究生课程设置表攻读本领域工程硕士学位的研究生,应获得总学分不少于34学分。
课程学分构成:公共必修课10学分,专业必修课不少于10学分,其余为选修课学分(合计课程学分不少于28分)。
Digital Signal Processing

Digital Signal Processing Digital Signal Processing (DSP) is a crucial aspect of modern technology, playing a significant role in various fields such as telecommunications, audio processing, image processing, and many others. It involves the manipulation and analysis of digital signals to improve their quality or extract useful information from them. However, despite its numerous benefits, DSP also presents several challenges and limitations that need to be addressed. One of the primary issues in digital signal processing is the trade-off between accuracy and processing speed. As the complexity of DSP algorithms increases, the computational requirements also escalate, leading to longer processing times. This can be particularly problematic in real-time applications where immediate results are essential. Engineers and researchers are constantly striving to develop more efficient algorithms and hardware to mitigate this challenge, but it remains a significant concern in the field. Another critical problem in DSP is the issue of signal distortion and noise. Digital signals are susceptible to various forms of interference and distortion during transmission or processing, which can significantly degrade the quality of the output. Filtering and noise reduction techniques are commonly employed to address this issue, but achieving optimal results often requires a deep understanding of the specific characteristics of the signals involved. Furthermore, the implementation of DSP algorithms in hardware can be a complex and costly endeavor. Designing specialized hardware for DSP applications often involves significant research and development efforts, as well as substantial financial investment. This can be a barrier for smaller companies or research groups looking to leverage DSP for their applications. Additionally, the rapid evolution of DSP technology means that hardware designs can quickly become obsolete, necessitating frequent updates and redesigns. On the other hand, from a more positive perspective, DSP has revolutionized the way we process and manipulate signals in various applications. In the field of telecommunications,for example, DSP has enabled the development of advanced modulation and coding schemes that have greatly improved the efficiency and reliability of communication systems. In audio and image processing, DSP algorithms have facilitated the development of high-fidelity audio systems and advanced image recognitiontechniques, enhancing the overall user experience. Moreover, the ongoing advancements in DSP technology continue to open up new possibilities for innovation and improvement across a wide range of industries. The integration of DSP with other emerging technologies such as artificial intelligence and machine learning holds the potential to further enhance the capabilities of digital signal processing systems. This convergence of technologies could lead to groundbreaking developments in areas such as autonomous vehicles, healthcare diagnostics, and environmental monitoring, among others. In conclusion, while digital signal processing presents several challenges and limitations, its impact on modern technology and society cannot be overstated. The ongoing efforts to address the issues of accuracy, processing speed, signal distortion, and hardware implementation are essential for the continued advancement of DSP. Furthermore, the positive impact of DSP on various industries and its potential for future innovation highlight the importance of overcoming these challenges. As researchers and engineers continue to push the boundaries of DSP technology, we can expect to see even more remarkable developments that will shape the future of digital signal processing.。
Digital Signal Processing

Digital Signal Processing Digital Signal Processing (DSP) is a crucial aspect of modern technology, impacting various fields such as telecommunications, audio processing, image processing, and more. It involves manipulating signals in the digital domain to analyze, filter, or compress data. DSP plays a significant role in improving the quality of audio and video signals, enhancing communication systems, and enabling advancements in medical imaging and radar systems. One of the key advantages of DSP is its ability to process signals with high accuracy and precision, allowing for complex algorithms to be implemented efficiently. This is particularly beneficial in applications where real-time processing is essential, such as in speech recognition systems or in noise cancellation technology. By converting analog signals into digital form, DSP enables the implementation of sophisticated algorithms that can extract valuable information from the signal and make intelligent decisions based on the processed data. In the field of telecommunications, DSP is used extensively to improve the quality of voice and data transmission. By filtering out noise and interference, DSP algorithms can enhance the clarity of audio signals and reduce errors in data transmission. This is crucial for ensuring reliable communication in wireless networks, satellite communication systems, and internet protocols. Additionally, DSP plays a vitalrole in enabling advanced modulation techniques that increase the efficiency and capacity of communication channels. In audio processing, DSP is utilized in various applications such as equalization, compression, and reverberation. By applying digital filters and algorithms, audio signals can be modified to achieve desired effects or improve sound quality. For example, DSP is used in audioediting software to remove background noise, enhance the bass response, or create spatial effects in recordings. In the field of music production, DSP is essential for synthesizing sounds, creating digital effects, and processing recorded tracks to achieve a polished final mix. In image processing, DSP is used to enhance and analyze digital images for various applications, including medical imaging, surveillance, and remote sensing. By applying algorithms such as edge detection, image segmentation, and noise reduction, DSP can extract valuable information from images and improve their quality for human interpretation or automated analysis.In medical imaging, DSP techniques are used to enhance diagnostic images, reconstruct 3D models from scans, and detect anomalies in medical data with high accuracy. The field of DSP is constantly evolving, with new algorithms and techniques being developed to address emerging challenges and opportunities in signal processing. From machine learning algorithms for pattern recognition to deep learning techniques for image analysis, DSP continues to push the boundaries of what is possible in digital signal processing. As technology advances and computational power increases, the potential applications of DSP are expanding rapidly, paving the way for innovative solutions in diverse fields such asartificial intelligence, autonomous systems, and smart devices. In conclusion, digital signal processing is a fundamental technology that underpins many modern applications and systems. From improving communication networks to enhancing audio and video quality, DSP plays a crucial role in enabling advanced signal processing techniques that drive innovation and progress in various industries. As the demand for real-time processing and data analysis continues to grow, the importance of DSP in enabling efficient and accurate signal processing will only increase in the future. By staying at the forefront of research and development in DSP, engineers and researchers can unlock new possibilities and create groundbreaking solutions that shape the future of technology.。
现代数字信号处理英文版课程设计

现代数字信号处理英文版课程设计IntroductionModern digital signal processing (DSP) is a rapidly growing field that has become essential for a wide range of applications including audio processing, image processing, communications, and control systems. This course ms to provide students with a comprehensive understanding of modern DSP techniques, including theory, algorithms, and practical implementation.Course ObjectivesBy the end of the course, students will be able to:•Understand the fundamental concepts of digital signal processing•Design and implement common DSP algorithms for various applications•Analyze and evaluate the performance of DSP algorithms•Use MATLAB to simulate and visualize DSP algorithms Course OutlineWeek 1: Introduction to DSP•Overview of DSP•Discrete-time signals and systems•Sampling and quantizationWeek 2: Time Domn Analysis•Convolution and correlation•Discrete Fourier Transform (DFT)•Fast Fourier Transform (FFT) Week 3: Frequency Domn Analysis•Fourier series•Fourier transform•Filter designWeek 4: Digital Filters•FIR Filters•IIR Filters•Filter design and implementation Week 5: Multirate Signal Processing•Downsampling and upsampling•M-Channel filter banks•Polyphase decompositionWeek 6: Applications of DSP•Audio processing•Image processing•Communications•Control systemsGrading Policy•30% Assignments•30% Quizzes•40% Final ProjectCourse Materials•Oppenheim, A. V., & Schafer, R. W. (2010). Discrete-time signal processing. Prentice Hall.•MATLAB.Prerequisites•Linear algebra•Calculus•Basic programming skills in MATLAB or other programming languages.ConclusionDigital signal processing is a rapidly evolving field that has become essential for many applications. This course provides students with a solid foundation in modern DSP techniques, including theory, algorithms, and practical implementation. By the end of the course, students will be able to apply their knowledge to a wide range of applications in audio processing, image processing, communications, and control systems.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s(n )
e (n )
x (n )
sˆ(n)ho(0)x(n)
T h e e ( n ) c a n n o t b e r e d u c e d a n y m o r e b y a d j u s t i n g t h e h o ( n ) !
• Wiener-Hopf Equation
Advanced Digital Signal Processing
(Modern Digital Signal Processing)
Chapter 2 Discrete Wiener Filter and Discrete Kalman Filter
2.1 The Wiener Filtering Problem
Ho(ej)Pss(ejP s)s(eP jvv)(ej)
Pvv(ej) 0, Ho(ej) 1, all-passfilter; Pss(ej) 0, Ho(ej) 0; Pvv(ej) , Ho(ej)
2.3 Solutions for Wiener Filter
Causal IIR Wiener filter with a white noise
as input
Wiener-Hopf equation
w(n)
sˆ ( n )
G(z)
r w s(j) g o C IIR (m )r w w (m j), j 0 ,1 , m 0
f iltE er[e2(n)]E[s(n)sˆ(n)]2E[s(n)x(n)*h(n)]2
E s(n) x(nj)h(j)2
j
h (j) 2 E e n h e n j 2 E e n x n j 0 , j, 1 ,0 ,1 ,
Estimation error (MSE) of causal FIR Wiener filter The mean square error (MSE) for causal FIR filter is a quadratic function of the filter coefficient
• Causal FIR Wiener Filter (Solution in Time Domain)
Causal FIR filter
Wiener-Hopf equation with causal FIR filter
N 1
r x s(j)h o C F IR (i)r x x(j i), j 0 ,1 , ,N 1 i 0
The requirement for the coefficients ho(n) of Wiener filter
Ee(n)x(n j)Es(n)
ho(m)x(nm)x(n
j)
m
Es(n)x(n
j) ho(m)x(nm)x(n
rational power spectrum signal. Spectral factorization theorem
A real-valued stationary random sequence with rational power spectrum can be represented by a time series model
• Causal IIR Wiener Filter
Spectral factorization theorem
Rational power spectrum signal A random signal whose power spectrum is a
rational function ofejorcos is called a
E[sˆ(n)e(n)]E[h(j)x(n j)e(n)] j
h(j)E[e(n)x(n j)]0 j
I fth e le n g th o fh (j)is1 , th e n s ˆ ( n ) h ( 0 )x ( n ) ,a n d th e o r th o g o n a lp r in c ip le c a n b e illu s tr a te d a sf o llo w s :
P xxzw 2HzHz1
w hereHzisam inim um phasesystem .
Whitening filter
w(n)
x(n)
B(z)
x(n)
w(n)
B-1(z)
signal model (invertible)
whitening filter
B z isa m in im u m p h a s e s y s te m .
• Wiener Filter
The linear estimator of stationary random signal
with least square error (LSE, the MMSE
withouhto(pnr)iorm Pin DE F[)(s(n)x(n)*h(n))2] h(n)
If s(n) is uncorrelated with the v(n), i.e.
Pxs(ej)Pss(ej)
P x x(e j) P s s(e j) P v v(e j)
then
Ho(ej)Pss(ejP s)s(eP jvv)(ej)
• Intuitive Interpretation of the Wiener Filter
Sxs(z) Sxx(z)
= 1
2j
Sxs(z) CSxx(z)
zn1dz
If s(n) is uncorrelated with the v(n)
1
hoIIR(n)=2j
C Sss(zS )ss (zS)vv(z) zn1dz
Estimation error (MSE)
Sxs(z)Sss(z)
Sxx(z)Sss(z)Svv(z)
then
Ho(z) Sss(zS)ss(zS)vv(z)
• Wiener-Hopf Equation in Frequency-
domain
Pxs(ej) Ho(ej)Pxx(ej)
Ho
(ej
)
Pxs Pxx
(ej) (ej)
vector h and has a single minimum point C F I R E [ e 2 ( n ) ] r s s ( 0 ) R x T s R x x 1 R x s ( h R x x 1 R x s ) T R x x ( h R x x 1 R x s ) C F I R m i n r s s ( 0 ) R x T s R x x 1 R x s r s s ( 0 ) R x T s h o C F I R
For example, when N=2, i.e. h=[h(0), h(1)], the MSE function is a bowl-shaped surface with a single minimum point.
I fth e le n g th o fh ( n )in c r e a s e s ,m in C F I R w illr e d u c e g r a d u a lly
r x e (j) E e n x n j 0 , j
i.e. the filter h(n) is optimal iff the e(n) and x(n) is orthogonal.
• Understanding of the Orthogonal Principle
• State (Wave) Estimation Problem
sˆ ( n )
s(n)
x(n)
h(n)
v(n)
s(n): signal v(n): noise x(n): observation or measurement
sˆ ( n ) : estimation of s(n)
h(n): estimator or filter
m
j)
rxs(j) ho(m)rxx(m j)0, j 0,1, m
W iener-H opfEquation:thebasicequantionforW ienerfiltering
rxs(j) ho(m )rxx(mj) ho(m )rxx(jm )
( a tle a s tn o tb e la r g e rth a n th e M S E w ith s h o r te rh ( n ) ) .
• Non-causal IIR Wiener Filter
Solution
hoIIR(n) Z 1
HoIIR(z)
=
Z
1
hence,
Sss (z) Sss (z1)
Sss(z)Svv(z) 0 means ...?
IIRm in21j C SS sss(sz ()z) SS vvv(vz (z )) z1dz
I I R m i n i s t h e m i n i m u m e r r o r w h i c h a W i e n e r f i l t e r c a n r e a c h .
or
Rxs RxxhoCFIR
where hoCFIR hoCFIR(0),hoCFIR(1), ,hoCFIR(N 1) T ,
Rxs rxs(0),rxs(1), ,rxs(N 1)T ,
