4.1平行四边形的性质1
平行四边形的性质及判定

平行四边形1.平行四边形的概念定义:两组对边分别平行的四边形叫做平行四边形.2.平行四边形的性质性质:(1)平行四边形的对边平行且相等;(2)平行四边形的对角相等;(3)平行四边形的对角线互相平分.注意:平行四边形是以对角线的交点为中心的对称图形,但不一定是轴对称图形.3.平行四边形的判定判定:(1)两组对边分别相等的四边形是平行四边形;(2)对角线互相平分的四边形是平行四边形;(3)两组对角分别相等的四边形是平行四边;(4)一组对边平行且相等的四边形是平行四边形.注意:(1)平行四边形的定义既可以作为性质,又可以作为判定;(2)一组对边平行,一组对角相等的四边形是平行四边形;(3)一组对边平行,另一组对边相等的四边形不一定是平行四边形,有可能是等腰梯形. 重点记忆:(1)夹在两平行线间的平行线段相等.(2)如图31-1,四边形ABCD是平行四边形,则有4.两平行线间的距离定义:两条平行线中一条直线上任意一点到另一条直线的距离叫做两条平行线间的距离.1.平行四边形的性质一.填空题.1.如图4.1-1, D,E,F 分别在△ABC 的三边BC,AC,AB 上,且DE ∥AB, DF ∥AC, EF ∥BC,则图中共有_______________个平行四边形,分别是_______________________________________.FED CBA图4.1-12.已知平行四边形的周长是100cm, AB:BC=4 : 1,则AB 的长是________________.3.已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长是______________.4.在平行四边形ABCD 中,∠A : ∠B=3:2,则∠C=_________ 度,∠D=_____________度.5.用20米长的一铁丝围成一个平行四边形,使长边与短边的比为3:2,则它的边长为________短边长为__________.6.如图4.1-2,在平行四边形ABCD 中, BC=2AB, CA ⊥AB,则∠B=______度,∠CAD=______度.DCB A图4.1-2二.选择题.7.平行四边形ABCD 的周长32, 5AB=3BC,则对角线AC 的取值范围为( )A. 6<AC<10B. 6<AC<16C. 10<AC<16D. 4<AC<16 8. 在平行四边形ABCD 中,∠A=65°,则∠D 的度数是 ( )A. 105°B. 115°C. 125°D. 65° 9. 在平行四边形ABCD 中,∠B -∠A=20°,则∠D 的度数是 ( ) A. 80° B. 90° C. 100° D. 110°10. 由等腰三角形底边上任一点(端点除外)作两腰的平行线,则所成的平行四边形的周长等于等腰三角形的 ( ) A. 周长 B. 一腰的长 C. 周长的一半 D. 两腰的和 11. 在以下平行四边形的性质中,错误的是 ( )A. 对边平行B. 对角相等C. 对边相等D. 对角线互相垂直三. 解答题12. 平行四边形ABCD 的两条对角线AC,BD 相交于O.(1) 图4.1-3中有哪些三角形全等? 有哪些相等的线段?(2) 若平行四边形ABCD 的周长是20cm,△AOD 的周长比△ABO 的周长大6cm.求AB,AD 的长.ODCBA图4.1-313. 如图4.1-4,平行四边形ABCD 中,∠ADC 的邻补角的平分线交BC 的延长线于E,延长ED 交BA 的延长线于F,试判断△FBE 的形状.GFEDCBA图4.1-4四. 应用题14. (1) 如图4.1-5,平行四边形ABCD 中,AB=5cm, BC=3cm, ∠D 与∠C 的平分线分别交AB 于F,E, 求AE, EF, BF 的长?(2) 上题中改变BC 的长度,其他条件保持不变,能否使点E,F 重合,点E,F 重合时BC 长多少?求AE,BE 的长. (3) 由(1),(2)题,你想到了什么?请写下来与你同伴交流.F E DCBA图4.1-5五. 综合能力提高题15. 如图4.1-6,平行四边形ABCD 的四个外角的平分线分别两两交于E,F. (1) 试判断∠AED, ∠BFC 的大小.(2) 线段AE, ED, BF, FC, EC, HF 中哪些相等?H GFEDCBA图4.1-616. 如图4.1-7,BD 是平行四边形ABCD 的对角线,AE ⊥BD 于E,CF ⊥BD 于F. (1) 在图中,根据题意补全图形;(2) 试问: △ABE 与△CDF 能全等吗?请说明理由.DCB A图4.1-72. 平行四边形的判定一. 填空题1. 如图4.2-1,平行四边形ABCD 中,AE=CG, DH=BF,连结E,F,G,H,E,则四边形EFGH 是_________________.2. 如图4.2-2,平行四边形ABCD 中,E,F 是对角线AC 上的两点,且AE=CF,连结B,F,D,E,B 则四边形BEDF 是______________.HGFED CBA图4.2-1GFEDCB A图4.2-23. 一组对边平行且相等的四边形一定是_____________形.4. 有公共顶点的两个全等三角形,其中一个三角形绕公共顶点旋转180°后与另一个重合,那么不共点的四个顶点的连线构成____________形.5. 如图4.2-3,E,F 分别是平行四边形ABCD 的边AD 与BC 的三分之一点,则四边形AECF 是________________形.F EDCB A图4.2-3F E DCBA图4.2-4二. 选择题6. 如图4.2-4,平行四边形ABCD 中,E,F 分别为边AB,DC 的中点,则图中共有平行四边形的个数是 ( ) A. 3 B. 4 C. 5 D. 67. 以长为5cm, 4cm, 7cm 的三条线段中的的两条为边,另一条为对角线画平行四边形,可以画出形状不同的平行四边形的个数是 ( )A. 1B. 2C. 3D. 4 8. 能够判定一个四边形是平行四边形的条件是 ( )A. 一组对角相等B. 两条对角线互相平分C. 两条对角线互相垂直D. 一对邻角的和为180°9. 四边形ABCD 中,AD ∥BC,要判定ABCD 是平行四边形,那么还需满足 ( ) A. ∠A+∠C=180° B. ∠B+∠D=180° C. ∠A+∠B=180° D. ∠A+∠D=180° 10. 平行四边形的一组对角的平分线 ( )A. 一定相互平行B. 一点相交C. 可能平行也可能相交D. 平行或共线 三. 解答题11. 如图4.2-5,在平行四边形ABCD 中,M,N 分别是OA,OC 的中点,O 为对角线AC 与BD 的交点,试问四边形BMDN 是平行四边形吗?说说你的理由.OMNDCBA图4.2-512. 如图4.2-6,AC 是平行四边形ABCD 的一条对角线,BM ⊥AC, DN ⊥AC,垂直分别为M,N,四边形BMDN 是平行四边形吗?你有几种判别方法?NMDCBA图4.2-6 四. 应用题13. 如图4.2-7,在平行四边形ABCD 中,AC 的平行线MN 交DA 的延长线于M,交DC 的延长线于N,交AB,BC 于P,Q. (1) 请指出图中平行四边形的个数,并说明理由. (2) MP 与QN 能相等吗?NMQP DCBA图4.2-714. 已知如图4.2-8,在平行四边形ABCD 中,EF ∥DC,试说明图中平行四边形的个数.NMH G FE D CBA图4.2-8五. 综合能力提高题15. 如图4.2-9,为公园的一块草坪,其四角上各有一棵树,现园林工人想使这个草坪的面积扩大一倍,又要四棵树不动,并使扩大后的草坪为平行四边形,试问这个想法能否实现,若能请你设计出草图,否则说明理由.DCBA图4.2-916. 楠楠想出了一个测量池塘的两端A,B 引两条直线AC,BC 相交于点C,在BC 上取点E,G,使BE=CG,再分别过E,G 作EF ∥AB,交AC 于F,H.测出EF=8m, GH=3m,(如图4.2-10),她就得出了结论: 池塘的宽AB 为11m .你认为她说的对吗?图4.2-103.平行四边形性质和判定综合。
平行四边形所有判定定理

平行四边形所有判定定理1. 什么是平行四边形嘿,大家好!今天咱们要聊的就是平行四边形。
你可能在数学课上听过这个名词,但今天我想用一种轻松幽默的方式来给你讲解。
平行四边形就像个爱穿相同衣服的双胞胎,总是有一对对边平行,另一对边也绝对不会落后。
这可不是随便说说的,平行四边形在生活中到处可见,像是桌子、书本,甚至是你那张已经发黄的老照片,都是平行四边形的“忠实粉丝”。
你有没有想过,平行四边形的神奇之处在哪里呢?让我们一起深入探讨吧!2. 平行四边形的判定定理2.1 对边平行首先,咱们来聊聊平行四边形的第一个判定定理,那就是对边平行。
这就像一对好朋友,总是形影不离,绝对不让对方走丢。
只要你看到一个四边形的对边是平行的,恭喜你,这绝对是个平行四边形。
想象一下,如果你在街上看到两个兄弟穿着一模一样的T恤,他们的身高也差不多,那你肯定会觉得这俩是亲兄弟吧?这就是平行四边形的感觉!2.2 对边相等接下来,平行四边形的第二个判定定理是对边相等。
你是不是觉得这就像是一场赛跑,两个运动员在同一条跑道上,谁也不想输,最后竟然跑出了相同的成绩!在平行四边形里,两个对边的长度完全一样,像是量了一百遍的饺子皮,总是那么标准。
只要你发现了这一点,那就放心大胆地说,“这就是平行四边形!”3. 内角相等3.1 内角相等的魅力再来聊聊平行四边形的第三个定理,那就是内角相等。
这就像一场家庭聚会,每个人的性格都有点不同,但大家坐在一起的时候,总能找到共同的话题,气氛特别融洽。
在平行四边形里,两个内角是相等的,感觉就像是给你送上了一杯热腾腾的奶茶,暖心又舒适。
你只要看到其中一组对角相等,其他的角自然也就会跟着“排排坐,吃果果”了。
3.2 斜角互补当然,咱们还有个小秘密,那就是平行四边形的斜角互补。
想象一下,两个好友总是一起玩耍,互相补充,形成了一个完美的搭档关系。
在平行四边形中,一个角和其对角的和是180度,就像是两个好伙伴互相帮助,形成了和谐的“配合”。
平行四边形的面积计算知识点总结

平行四边形的面积计算知识点总结平行四边形是几何学中的一种基本图形,它具有许多有趣的性质和应用。
本文将对平行四边形的面积计算知识点进行总结,并介绍一些相关的公式和方法。
无影响阅读体验的情况下,我会适当增加字数以满足1500字的要求。
1. 平行四边形的定义平行四边形是指有两对对边分别平行的四边形。
它的特点是对边相等且对角线互相平分。
2. 平行四边形的面积计算公式平行四边形的面积可以使用以下公式进行计算:面积 = 底边长度 ×高3. 平行四边形的特殊情况当平行四边形的高度垂直于底边时,我们可以使用以下公式计算面积:面积 = 底边长度 ×高4. 平行四边形的计算方法在实际计算中,我们可以根据实际情况选择不同的方法来计算平行四边形的面积。
4.1 底边和高的已知情况当底边的长度和高度已知时,可以直接使用公式面积 = 底边长度 ×高进行计算。
4.2 边长和夹角的已知情况当平行四边形的两条边长和夹角的大小已知时,可以使用以下公式计算面积:面积 = 一条边长 ×另一条边长 × sin(夹角)4.3 对角线和夹角的已知情况当平行四边形的对角线的长度和夹角的大小已知时,可以使用以下公式计算面积:面积 = 一条对角线长度 ×另一条对角线长度 × sin(夹角)5. 平行四边形面积计算的例题解析为了更好地理解和应用上述计算方法,我们来看一个具体的例题:【例题】已知平行四边形的底边长为12 cm,高度为6 cm,求其面积。
解:根据公式面积 = 底边长度 ×高,可直接计算得到:面积 = 12 cm × 6 cm = 72 cm²6. 平行四边形的相关知识点在学习和计算平行四边形的面积过程中,还有一些相关的知识点需要了解。
6.1 平行四边形的性质平行四边形有以下几个重要的性质:- 对边相等:平行四边形的对边长度相等。
- 互补角:相邻的内角互补(和为180°)。
4.1平行四边形的性质

平行四边形的对边相等 平行四边形的对角相等
平行四边形的邻角互补
平行四边形的性质
文字叙述 边
对边平行 对边相等
A B C
D
几何语言
AB∥DC ,AD∥BC AB=DC ,AD=BC ∠A=∠C ,∠B=∠D
角
对角相等 邻角互补
∠A +∠ B =180°……
1、在 ABCD中,∠A=60°,BC=3cm, 120° 3cm 60° 则∠B=_____,∠C=_____,AD=_____.
在数学的天地里,重要的不是我 们知道什么,而是我们怎么知道 什么。
——毕达哥拉斯 大望学校 钟锋声
拼一拼
将一张纸对折,剪下
两张叠放的三角形 纸片.将它们相等的一组边重合,可以得 到一个四边形. 观察、讨论: (1)你拼出了怎样的四边形?
矩形、菱形、正方形、平行四边形 一般的四边形
A
D
做一做
1、画一个平行四边形ABCD; 2、用一张半透明的纸复制你画的平行四 边形ABCD; 3、剪下你所复制的那个平行四边形;
4、将复制后的四边形绕某个点旋转180°, 你能平移该纸片,使它与原来的四边形 ABCD重合吗?
做一做
由此你能得到什么结论? 平行四边形的对边、对角之间分别 有什么关系?
1
B
222222 22222
C
(2)这个图形中有哪些相等的角?有没有互 相平行的线段?你是怎样得到的? (3)请用简洁的语言刻画这个图形的特征, 并与同伴交流
平行四边形的定义 1、两组对边分别平行的 四边形叫做平行四边形.
如图四边形ABCD是平行四边形, 记作: ABCD
2、平行四边形不相邻的两个顶点连成的线 段叫它的对角线 3、平行四边形相对的边称为 对边 相对的角称为 对角
八年级数学上册《4.1 平行四边形的性质》学案(无答案) 北师大版

平行四边形的性质学习目标:1.了解平行四边形的相关概念;2.理解并掌握平行四边形的性质;3.会用平行四边形的性质解决相关问题.问题与题例:1.复习与回顾:(1)什么是四边形?(2)四边形的边、内角、外角、对角线的概念.2.新知探究与学习:(1)什么是平行四边形?如何记一个平行四边形?(2)平行四边形有哪些性质?(3)什么是平行线间的距离?有什么性质?3.知识应用:例1 如图:四边形ABCD是平行四边形.①求∠ADC、∠BCD度数;②边AB、BC的长度.例2 教材P100“例1”.例3 教材P101“例2”.例4 如图,□ABCD中,平行于对角线BD的直线MN分别交CD,CB的延长线于M,N,交AD 于P,交AB于Q,你能说明MQ=NP吗?说说你的理由.目标检测题:1.□ABCD 中,∠B=60°,则∠A= ,∠C= ,∠D= . 2.□ABCD 中,∠A 比∠B 大20°,则∠C= . 3.□ABCD 中,AB=3,BC=5,则AD= ,CD= .4.□ABCD 中,周长为40cm ,△ABC 周长为25,则对角线AC=____cm . 5.平行四边形ABCD 中,∠A 比∠B 大20°,则∠C 的度数为 .6.平行四边形ABCD 中,对角线AC ,BD 交于O ,则全等三角形的对数有 对. 7.在笔直的铁轨上,夹在两根铁轨之间的枕木是否一样长.答:________. 8.在□ABCD 中,∠A=48°,BC=3cm ,求∠B 、∠C 的度数与AD 的长.配餐作业题:A 组 巩固基础1.在□ABCD 中,AB=5cm ,BC=4cm ,则□ABCD 的周长为 cm . 2.在□ABCD 中,∠A =120°,则∠D =_ _°.3.如图4,□ABCD 中,对角线AC 、BD 交于点O ,请你写出其中的一对全 等三角形_________________.4.如图,在□ABCD 中,对角线AC 、BD 相交于点O ,若AC=14,BD=8, AB=10,则△OAB 的周长为________.5.在□ABCD 中,AB 、BC 、CD 三条边的长分别为(x +3)cm 、(x -4)cm 、16cm ,求这个平行四边形的周长.6.如图,E 、F 是平行四边形ABCD 对角线AC 上两点,BE ∥DF ,求证:AF=CE .B 组 强化训练1.如图,已知AC 平分BAD ∠,12∠=∠,3AB DC ==,则BC = .2.如图,在□ABCD 中,已知AD =8㎝, AB =6㎝, DE 平分∠ADC 交BC 边于点E ,则BE 等于( )A .2cmB .4cmC .6cmD .8cm图4CA B E F3.如图,□ABCD中,AC.BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为().A.3 B.6 C.12 D.244.如图,□ABCD中,E、F分别为BC、AD边上的点,要使BF=DE,需添加一个条件:.(第1题图)(第2题图)(第3题图)(第4题图)5.如图,已知:□ABCD中,∠BCD的平分线C E交边AD于E,∠ABC的平分线BG 交CE于F,交AD于G.求证:AE=DG.6.如图,在□ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AF与CE是否相等,并说明理由.7.如图,E F,是平行四边形ABCD的对角线AC上的点,CE AF.请你猜想:BE与DF有怎样的位置..关系和数量..关系?并对你的猜想加以证明.猜想:证明:C组延伸应用1.如图,在□ABCD中,已知点E在AB上,点F在CD上且AE=CF.(1)求证:DE=BF;(2)连结BD,并写出图中所有的全等三角形.(不要求证明)AB CEFG 12A BCD ABCDEAB CEDFC2.在平行四边形ABCD 中,∠B=150°,AB=10cm ,BC=8cm ,求平行四边形ABCD 的面积.3.已知:如图,在正方形ABCD 中,G 是CD 上一点,延长BC 到E ,使CE =CG ,连接BG 并延长交DE 于F .(1)求证:△BCG ≌△DCE ;(2)将△DCE 绕点D 顺时针旋转90°得到△DAH ,判断四边形HBGD 是什么特殊四边形?并说明理由.BC。
北师大版数学八年级上第四章课件

菱形的判定: 1.有一组邻边相等的平行四边形是菱形; 2.四条边都相等的四边形是菱形; 3.两条对角线互相垂直的平行四边形是 菱形; 4.两条对角线互相义:有一个内角是
4.2平行四边形的判定
• 1.定义法 • 2.两组对边分别相等的四边形是平行四边形 • 3.一组对边平行且相等的四边形是平行四边 形; • 4.两条对角线互相平分的四边形是平行四边 形
4.3菱形
• 定义:有一组邻边相等的平行四边形叫~ • 性质: 1.具有平行四边形的所有性质; 2.四条边都相等; 3.两条对角互相垂直; 4.每一条对角线平分一组对角; 5.轴对称性。
第四章 四边形性质探索
• 4.1 平行四边形的性质 • 平行四边形的定义:两组对边分别平行的 四边形叫做平行四边形。 • 平行四边形的性质: • 1.平行四边形的对边平行且相等; • 2.平行四边形的对角相等; • 3.平行四边形的两条对角线互相平分;
平行线的性质
• 从两条平行线中的任一条上任取一点做另 一条直线的垂线段,这条垂线段的长度叫 做两平行线间的距离。 • 1.平行线间的垂线段长度处处相等; • 2.在两条平行线间的平行线段相等。
平行四边形知识点
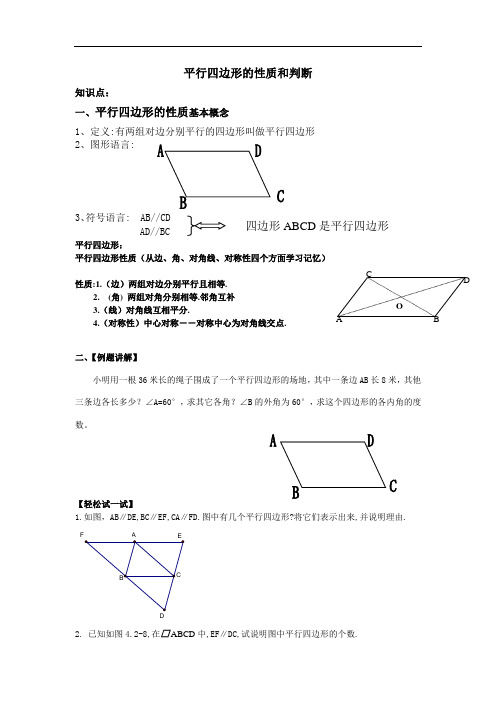
A BC DO 平行四边形的性质和判断知识点:一、平行四边形的性质基本概念1、定义:有两组对边分别平行的四边形叫做平行四边形2、图形语言:3、符号语言平行四边形:平行四边形性质(从边、角、对角线、对称性四个方面学习记忆) 性质:1.(边)两组对边分别平行且相等.2. (角) 两组对角分别相等.邻角互补3.(线)对角线互相平分.4.(对称性)中心对称--对称中心为对角线交点.二、【例题讲解】小明用一根36米长的绳子围成了一个平行四边形的场地,其中一条边AB 长8米,其他三条边各长多少?∠A=60°,求其它各角?∠B 的外角为60°,求这个四边形的各内角的度数。
【轻松试一试】1.如图,AB ∥DE,BC ∥EF,CA ∥FD.图中有几个平行四边形?将它们表示出来,并说明理由.AFD2. 已知如图4.2-8,中,EF ∥DC,试说明图中平行四边形的个数.NMH G F E D CBA图4.2-8角的计算:1、中, BC=2AB, CA ⊥AB,则∠B=______度,∠CAD=______度.DCB A2中,∠A : ∠B=3:2,则∠C=___ 度,∠D=______度.边及周长的计算1、如图,平行四边形的对角线相交于点O ,BC=7㎝,BD=10㎝,AC=6㎝。
求△AOD 的周长。
2平行四边形的周长是100cm, AB:BC=4:1,则AB 的长是_______。
3.已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长是______________.4.用20米长的一铁丝围成一个平行四边形,使长边与短边的比为3:2,则它的边长为________短边长为__________.平行四边形的判断平行四边形的四个(或五个)判定方法,这些判定的方法是: 从边看: ①两组对边分别平行的四边形是平行四边形; ②两组对边分别相等的四边形是平行四边形; ③一组对边平行且相等的四边形是平行四边形.从对角线看:对角线互相平分的四边形是平行四边形.(从角看:两组对角分别相等的四边形是平行四边形.)【例题讲解】已知:如图,ABCD 中,E 、F 分别是AD 、BC 的中点,求证:BE=DF .分析:证明BE=DF ,可以证明两个三角形全等,也可以证明四边形BEDF 是平行四边形,比较方法,可以看出第二种方法简单. 证明:∵ 四边形ABCD 是平行四边形, ∴ AD ∥CB ,AD=CD . ∵ E 、F 分别是AD 、BC 的中点, ∴ DE ∥BF ,且DE=21AD ,BF=21BC .∴ DE=BF .∴ 四边形BEDF 是平行四边形(一组对边平行且相等的四边形平行四边形). ∴ BE=DF .例2、已知:如图,ABCD 中,E 、F 分别是AC 上两点,且BE ⊥AC 于E ,DF ⊥AC 于F .求证:四边形BEDF 是平行四边形.分析:因为BE ⊥AC 于E ,DF ⊥AC 于F ,所以BE ∥DF .需再证明BE=DF ,这需要证明△ABE 与△CDF 全等,由角角边即可.证明:∵ 四边形ABCD 是平行四边形, ∴ AB=CD ,且AB ∥CD . ∴ ∠BAE=∠DCF .∵ BE ⊥AC 于E ,DF ⊥AC 于F ,∴ BE ∥DF ,且∠BEA=∠DFC=90°. ∴ △ABE ≌△CDF (AAS ). ∴ BE=DF .∴ 四边形BEDF 是平行四边形(一组对边平行且相等的四边形平行四边形)例3、 已知:如图3,E 、F 是平行四边形ABCD 对角线AC 上两点,且AE =CF 。
4.1.1 平行四边形的性质(含答案)-

4.1.1 平行四边形的性质一、填空题:1.若一凸多边形的内角和等于它的外角和,则它的边数是________.2.已知:平行四边形一边AB=12 cm,它的长是周长的61,则BC=______ cm,CD=______ cm. 3.如图1,在ABCD 中,对角线AC 、BD 相交于点O ,图中全等三角形共有________个. 4.如图1,如果该平行四边形的一条边长是8,一条对角线长为6,那么它的另一条对角线长m 的取值范围是_____.OBCADBCAD(1) (2)5. ABCD 中,若∠A ∶∠B=1∶3,那么∠A=______,∠B=_______,∠C=_______,∠D=_____. 二、选择题:1.平行四边形的两邻边分别为3、4,那么其对角线必( )A.大于1B.小于7C.大于1且小于7D.小于7或大于12.在ABCD 中,M 为CD 的中点,如DC=2AD ,则AM 、BM 夹角度数是( )A.90°B.95°C.85°D.100°3.如图2,四边形ABCD 是平行四边形,∠D=120°,∠CAD=32°.则∠ABC 、∠CAB 的度数分别为( ) A.28°,120° B.120°,28° C.32°,120° D.120°,32° 三、求解与证明:1.如图,已知ABCD 的对角线交于O ,过O 作直线交AB 、CD 的反向延长线于E 、F , OE=OF 吗?试说明理由.2.如图,四边形ABCD是平行四边形,BD⊥AD,求BC,CD及OB的长.3. 平行四边形ABCD的两条对角线AC,BD相交于O.(1) 上图中中有哪些三角形全等? 有哪些相等的线段?(2) 若平行四边形ABCD的周长是20cm,△AOD的周长比△ABO的周长大6cm.求AB,AD的长.A DOB C参考答案一、1.4 2.24 CD=12 3.4 4.10<x <22 5.45° 135° 45° 135° 二、1.C 2.A 3.B三、1.解:∵ABCD,∴OA=OC,DF ∥EB∴∠E=∠F 又∵∠EOA=∠FOC ∴△OAE ≌△OCF,∴OE=OF 2.解:∵ABCD,∴BC=AD=12CD=AB=13,OB=21BD ∵BD ⊥AD∴BD=22AD AB -=221213-=5 ∴OB=25 3、略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.平行四边形的对角相等; 平行四边形的对角相等; 平行四边形的对角相等
∵四边形ABCD是平行四边形 四边形ABCD是平行四边形 ABCD ∴∠A= C,∠B= ∴∠A=∠C,∠B=∠D
小结: 小结:平行四边形的性质是证明线段相等和 角相等的重要依据和方法。 角相等的重要依据和方法。
1.如图: ABCD中 1.如图:在 ABCD中,根据已知你能得到哪 如图 些结论?为什么? 些结论?为什么?
√
补充例题与练习: 补充例题与练习: 3、在 、 ∠D= 4、在 、 ABCD中,若∠A- ∠B=700,则∠C= 中 ABCD中, ∠A的平分线 中 的平分线
D E C
,
AE交CD于E,AB=5,BC=3, 交 于 , , , 则EC的长为 的长为 ( )
A
A、1, B、1.5, C、2, D、3 、 , 、 , 、 , 、
已知: 已知: ABCD(如图) (如图) 求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB 求证 ∠ ∠ ∠ ∠ 证明:连结 连结AC 证明 连结 ∵AB∥CD,AD∥BC(平行四边形的对边平行) ∥ , ∥ (平行四边形的对边平行) ∴∠1= ∴∠1=∠2,∠3=∠4 D A 1 在△ABC和△CDA中 和 中 4
6、在 ABCD中,AE⊥BD,CF ⊥BD垂足 、 中 ⊥ , 垂足 相等吗? 为E、F,那么 与DF相等吗?说说你的理由 、 ,那么BE与 相等吗
D E F A B C
7、如图,在 如图, ABCD中,AB=2AD,且M 中 且 的中点, 为CD 的中点,求∠AMB的度数 的度数
D M C
A
s讨
论
1.平行四边形的边具有哪些性质?说说你 平行四边形的边具有哪些性质? 平行四边形的 的理由。 的理由。 2.平行四边形的角具有哪些性质?说说你 平行四边形的角具有哪些性质? 平行四边形的 的理由。 的理由。
猜想: 猜想:
平行四边形的性质: 平行四边形的性质: 平行四边形的对边平行. 平行四边形的对边平行. 平行四边形的对边相等. 平行四边形的对边相等 平行四边形的对角相等. 平行四边形的对角相等. 平行四边形的邻角互补. 平行四边形的邻角互补.
1.平行四边形的对边平行; 平行四边形的对边平行; 平行四边形的对边平行
∵四边形ABCD是平行四边形 四边形ABCD是平行四边形 ABCD ∴AB∥CD, ∴AB∥CD,AD∥BC
2.平行四边形的对边相等; 平行四边形的对边相等; 平行四边形的对边相等
∵四边形ABCD是平行四边形 四边形ABCD是平行四边形 ABCD ∴AB=CD,AD=BC
A 30cm B
56° 56°
32cm
124° 124°
D
56° 56°
30cm
124°
2、在 、 ABCD中, 中 ∠A ∶∠ B ∶∠ C ∶∠ D的值可以是 的值可以是 A B C D 1∶2∶3∶4 ∶ ∶ ∶ 1∶2∶2∶1 ∶ ∶ ∶ 2∶2∶1∶1 ∶ ∶ ∶ 1∶2∶1∶2 ∶ ∶ ∶
∠EBH= 58° °
E
• 通过本节课的学习,你有什么收获? 通过本节课的学习,你有什么收获?
两组对边分别平行的四边形叫做平行四边形. 1.两组对边分别平行的四边形叫做平行四边形. 两组对边分别平行的四边形叫做平行四边形 平行四边形的性质: 2.平行四边形的性质:对边平行 平行四边形的性质 对边相等 对角相等 邻角互补 3.解决平行四边形的有关问题经常连结对角线转 解决平行四边形的有关问题经常连结对角线转 化为三角形。 化为三角形。
B
∠AMB=90°
8.如图,在 如图, ABCD中,∠BAD=32°,分别以 如图 中 ° 分别以BC,CD为边向 为边向 外作△ 外作△BCE和△DCF ,使BE=BC,DF=DC, ∠EBC=∠CDF.延 和 ∠ . 长AB交EC边于点 ,点H在E,C两点之间,连结AE,AF. 交 边于点H, 在 两点之间,连结 . 边于点 两点之间 (1)求证:△ABE≌△FDA. )求证: ≌ . 的度数. (2)当AE⊥AF时,求∠EBH的度数. ) ⊥ 时 的度数 F A B D C H
∠1=∠2, = , AC=CA, = , ∠3=∠4 = 2 3
B
C
ABC≌△CDA(ASA) ∴ △ABC≌△CDA(ASA) ∴AB=CD,BC=DA,∠B=∠D = , = , = ∵∠1= 又∵∠ =∠2,∠3=∠4 , = ∴∠1+ ∴∠ +∠4=∠2+∠3 = + 即∠BAD=∠DCB =
用两个全等的三角形纸片可以拼 出几种形状不同的平行四边形? 出几种形状不同的平行四边形?
从拼图可以得到什么启示? 从拼图可以得到什么启示?
小结:平行四边形可以是由两个全等的三角
形组成,因此在解决平行四边形的问题时, 形组成,因此在解决平行四边形的问题时, 通常可以连结对角线转化为两个全等的三角 形进行解题。 形进行解题。
B
超级演练
5.在平行四边形 在平行四边形ABCD中,周长为 在平行四边形 中 周长为24cm, AD-AB=4cm且 ∠A:∠B=3:1 , A - 4 且 ∠ 1)求AB的长度 的长度 的度数。 2)求∠C 的度数。
B C D
解: )∵AD+AB=12 1 + = AD-AB=4 2) - = ∵AD∥BC ∥ ∴ AB=4cm = ∴ ∠A+ ∠B = 180° ∴ ∠A= 135° (∠B = 45°) ∴ ∠C= 135°
B C
2.平行四边形不相邻的两个顶点连成的线段叫 .
对角线. 平行四边形的对角线 平行四边形的对角线. 线段AC 线段 、BD就是 就是 ABCD的两条对角线。 的两条对角线。 的两条对角线
3.平行四边形相对的边称为 对边 相对的角称为 对角 对边, 对角.
对边: 与 对边:AB与CD; BC与DA. 与 对角: 对角 ∠ABC与∠CDA; ∠BAD与∠DCB. 与 与
理解定义
两组对边分别平行的四边形叫做平行四边形 两组对边分别平行的四边形叫做平行四边形. 平行四边形. A
D 记作: 记作:
ABCD
读作:平行四边形ABCD 读作:平行四边形ABCD B ∵ AB∥CD C ∵四边形ABCD是平行四边形 四边形ABCD是平行四边形 ∴ AB∥CD AD∥BC
AD∥BC ∴四边形ABCD是平行四边形 四边形ABCD是平行四边形
平行四边形
—— 平行四边形的性质
下面的图片中,有你熟悉的哪些图形? 下面的图片中,有你熟悉的哪些图形?
平行四边形相关概念
1.两组对边分别平行的四边形叫做平行四边形. 两组对边分别平行的四边形叫做平行四边形
A D
如图:四边形 如图:四边形ABCD是平行四边形 是平行四边形 记作: 记作: ABCD
