光学设计作业答案Word版
工程光学练习题与解答

工程光学练习题与解答工程光学练习题与解答光学作为一门应用广泛的工程学科,对于工程师们来说是非常重要的一门课程。
理解光学原理和应用是工程师在设计和制造光学器件和系统时必备的技能。
为了帮助读者更好地理解和掌握工程光学知识,本文将提供一些光学练习题和详细的解答。
1. 一个平行光束垂直入射到一个半径为R的球面透镜上,透镜的焦距为f。
求出该透镜的曲率半径和球面上的光焦点位置。
解答:根据透镜公式,1/f = (n-1)(1/R1 - 1/R2),其中n为透镜的折射率,R1和R2分别为透镜两个球面的曲率半径。
由于球面透镜是对称的,所以R1 = R2 = R。
将入射光束的方向与透镜法线方向垂直,可以得到R = 2f。
由于光线垂直入射到球面透镜上,入射角为0,根据球面折射定律,折射角为0。
因此,光线通过透镜后仍然是平行光束,光焦点位置在无穷远处。
2. 一个凸透镜的焦距为20cm,物距为30cm。
求出像的位置和放大倍数。
解答:根据薄透镜公式,1/f = 1/v - 1/u,其中f为透镜焦距,v为像距,u为物距。
代入已知数据,得到1/20 = 1/v - 1/30。
解方程得到v = 60cm。
根据放大倍数公式,放大倍数为m = -v/u。
代入已知数据,得到m = -60/30 = -2。
由于负号表示像是倒立的,所以像是倒立的,并且放大倍数为2。
3. 一个凹透镜的焦距为-15cm,物距为30cm。
求出像的位置和放大倍数。
解答:由于凹透镜的焦距为负值,所以可以根据薄透镜公式得到1/f = 1/v - 1/u,其中f为焦距,v为像距,u为物距。
代入已知数据,得到1/-15 = 1/v - 1/30。
解方程得到v = -10cm。
根据放大倍数公式,放大倍数为m = -v/u。
代入已知数据,得到m = -(-10)/30 = 1/3。
由于负号表示像是倒立的,所以像是倒立的,并且放大倍数为1/3。
4. 一个平行光束垂直入射到一个半径为R的球面镜上,镜的焦距为f。
《光学教程答案》word版

第三章几何光学1.证明反射定律符合费马原理证明:设界面两边分布着两种均匀介质,折射率为山和勺(如图所示)。
光线通过笫一介质中指泄的A点后到达同一介质中指左的B点。
(1)反正法:如果反射点为位于处轴与A和3点所著称的平面之外,那么在ox轴线上找到它的垂足点C"点,.由于AC > AC ,BC >BC\故光线AC B所对应的光程总是大于光线AC B所对应的光程而非极小值,这就违背了费马原理。
故入射面和反射面在同一平面内。
(2)在图中建立坐xoy标系,则指定点A,B的坐标分别为(和yj和(w),反射点C的坐标为(圮0)所以AC3光线所对应的光程为:△=厲[JCv—xj' + y; + >](x-x2)2 + y;]根据费马原理,它应取极小值,所以有空=" 也-①利(sin_sinE = O心yjix-x^ + y- y](x-x2y+y;即:L = i22.根据费马原理可以导出在近轴光线条件下,从物点发出并会聚到像点的所有光线的光程都相等。
EF证:如图所示,有位于主光轴上的一个物点S 发出的光束经薄透镜折射后成一个 明亮的实象点S'。
设光线SC 为电光源S 发出的任意一条光线,其中球面AC 是由点光 源S 所发出光波的一个波面,而球面DB 是会聚于象点S'的球面波的一个波面,所以有关系式SC = SA, SD = SB •因为光程\CEFl)s =SC + CE + nEF + FD + DS △$ MS = SA + I1AB + BS根据费马原理,它们都应该取极值或恒定值,这些连续分布的实际光线,在近轴 条件下其光程都取极大值或极小值是不可能的,唯一的可能性是取恒定值,即它们的光程相等。
3. 睛E 和物体PQ 之间有一 块折射率为1.5的玻璃平板,平 板的厚度d 为30cmo 求物体PQ 的像P0与物体P0之间的距离妁为多少?解:根据例题3.1的结果 PP n1 PP = 30x(1 ———)=10cm1.5n =1.5题3图4.玻璃棱镜的折射棱角A为60。
光学设计简答题习题详解
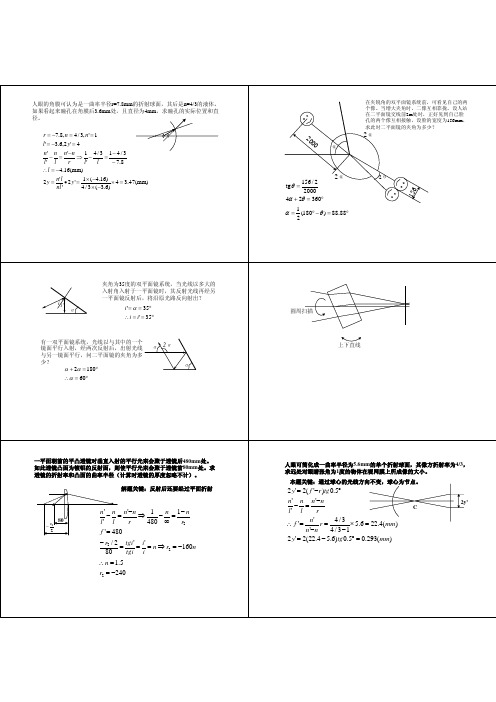
h1 h2 f1 ' = = 24.306, f 2 ' = = −54.167 u1 '−u1 u 2 '−u2
tg W =
(40 − 30) / 2 ∴ 2W = 11.42° 50
40 / 2 ∴ 2W = 43.6° tg W = 50
30
30
H1 H1’
有一焦距为50mm的放大镜,直径D=40mm,人眼瞳孔离放大镜20mm来观看位于物方 焦平面上的物体。瞳孔直径为4mm。问此系统中,何者为孔阑、何者为渐晕光阑,并 求入瞳、出瞳和渐晕光阑的像的位置和大小;并求能看到半渐晕时的视场范围。 本题在像方做较为方便。位于物方 焦面上的物成像于无穷远,由像方 无穷远轴上点判断,瞳孔为孔阑, 放大镜为渐晕光阑。 入瞳:瞳孔经放大镜所成的像
l p ' = 26.25 mm
tg W ' =
40 / 2 =1 20
2 y = 2 f ' tg W ' = 100(mm)
tg W ' = 20 ∴ 2W ' = 2 × tg −1 (20 tg 1.6°) = 58.3799° tg W
有一4倍的伽利略望远镜(目镜为负),物镜焦距160mm,直径40mm,眼瞳在 目镜后10mm,直径5mm,为出瞳。目镜直径10mm。(1)何为渐晕光阑?其在 物空间和像空间的像位置和大小?(2)无渐晕时视场角?(3)半渐晕时视场角?
一个光学系统,对100倍焦距处的物面成一缩小到1/50的像,物方孔径角为sinU≈u=0.005, 物面的照度为1000lx,反射率为ρ=0.75,系统的透过率为K=0.8,求像面的照度。
L= E' = =(
M
π
光学答案 打印

第一章 光的干涉1 波长为500nm 的绿光照射在间距为0.022cm 的双缝上,在距离180cm 处的光屏上形成干涉条纹,求两个亮条纹之间的距离。
若改用波长700nm 的红光照射此双缝,两个亮条纹之间的距离又为多少?计算这两种光第二级亮条纹位置的距离。
解:本题是杨氏双缝干涉实验, 其光路、装置如图。
由干涉花样亮条纹的分布规律:λdr j y 0= (j=0、±1、±2、…)得亮条纹间距: λdr y 0=∆ (1) 其中:λ=500nm 和700nm 、d=0.022mm 、r 0=180cm 代入公式(1)计算得到:当λ=500nm 时,两个亮条纹之间的距离:cm y 409.0=∆ 当λ=700nm 时,两个亮条纹之间的距离: cm y 573.0='∆ 第2 级亮条纹的位置:λdr jy 02= 2=j (2) 当λ=500nm 时: cm y 819.02=当λ=700nm 时: cm y 146.12=' 两种光第二级亮条纹位置间的距离: cm y y y 327.0222=-'=∆2 在杨氏实验装置中,光源的波长为640nm ,两缝间距为0.4mm ,光屏离双缝的距离为50cm ,试求:(1)光屏上第一亮条纹和中央亮条纹之间距离;(2)若P 点距离中央亮条纹0.1mm ,则两束光P 点的相位差;(3)P 点的光强度与中央亮条纹的强度之比。
解: (1) 由: λdr jy 0= (1), 已知:λ=640nm ,d=0.4mm ,r 0 = 50cm ,j=1代入公式(1)解得,第一亮纹到中央亮纹的距离:y=0.8mm(2)两束光传播到P 点的光程差为:12r y dr r =-=δ位相差为:022r dy λπδλπϕ==∆代入数据:λ=640nm 、d=0.4mm 、r 0=50cm 、y=0.1mm 得到两束光在P 点的相位差:4/πϕ=∆(3)在中央亮条纹的位置上,两光的相位差为:0=∆ϕ 光强度为:2204)cos 1(2A A I =∆+=ϕP 点的光强度为:2224.3)4/cos 1(2)cos 1(2A A A I p =+=∆+=πϕ 两条纹光强度之比为:2:7.1:0=I I p3 把折射率为1.5的玻璃片插入杨氏双缝的一束光中,光屏上原来第五级亮条纹所在的位置变为中央亮条纹,求插入的玻璃片的厚度。
光学参考答案(改)1

第十四章光学参考答案三、计算题1. 在一双缝实验中,缝间距为5.0mm ,缝离屏1.0m ,在屏上可见到两个干涉花样。
一个由480nmλ=的光产生,另一个由'600nm λ=的光产生。
问在屏上两个不同花样第三级干涉条纹间的距离是多少? 解: 对于nm 480=λ的光,第三级条纹的位置:λ3d D x =对于nm 600'=λ的光,第三级条纹的位置:'3dD 'x λ= 那么:)'(3dDx 'x x λλ∆-=-=,m 102.7x 5-⨯=∆。
2. 双缝干涉实验装置如图所示, 双缝与屏之间的距离D =120cm, 两缝之间的距离d =0.50mm, 用波长λ=5000 Å的单色光垂直照射双缝。
(1) 求原点O (零级明条纹所在处)上方的第五级明条纹的坐标。
(2) 如果用厚度e =1.0×10-2mm, 折射率n =1.58的透明薄膜覆盖在图中的s 1缝后面, 求上述第五级明条纹的坐标x '。
解: (1)光程差λδk D dxr r ==-=12 dD k x k λ=因k=5有mm x 65=(2)光程差)(12ne e r r +--=δ λk e n Ddx e n r r =--=---=)1(')1(12 有dDe n k x ])1(['-+=λ 因k =5, 有mm x 9.19'5=3. 在双缝干涉实验中,单色光源S 0到两缝S 1、S 2的距离分 别为l 1、l 2,并且123,l l λλ-=为入射光的波长,双缝之间的距离为d ,双缝到屏幕的距离为D ,如图,求: (1) 零级明纹到屏幕中央O 点的距离;(2) 相邻明条纹间的距离。
解: 两缝发出的光在相遇点的位相差:λπδϕϕϕ∆22010+-=根据给出的条件:λλπϕϕ322010⋅-=-s 1 s 2屏dDOx所以,λπδπϕ∆26+-=明条纹满足:πϕ∆k 2=,πλπδπk 226=+-,λδ)3k (+=明条纹的位置:δdD x=,λ)3k (dDx+=令0k =,得到零级明条纹的位置:λdD3x 0=,零级明条纹在O 点上方。
吴强版光学部分答案word资料19页
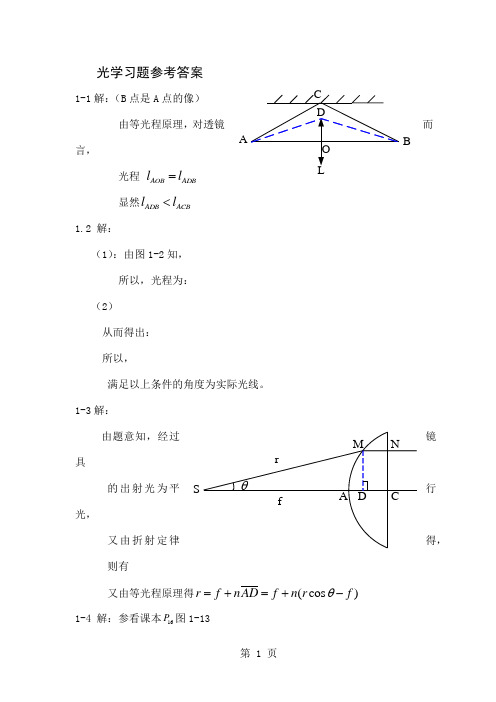
光学习题参考答案1-1解:(B 点是A 点的像) 由等光程原理,对透镜而言,光程 AOB ADB l l = 显然ADB ACB l l <1.2 解:(1):由图1-2知, 所以,光程为: (2)从而得出: 所以,满足以上条件的角度为实际光线。
1-3解:由题意知,经过镜具的出射光为平行光,又由折射定律得,则有又由等光程原理得(cos )r f nAD f n r f θ=+=+- 1-4 解:参看课本16P 图1-13ABS考虑三角形PSC ,有122211()2()cos PS x R R x R R θ⎡⎤=++-+⎣⎦,当θ很小时,2111()2x R R PS x x θ+≈+;同理有2222()2x R R SQ x x θ-≈-;此时的1x 和2x 均表示线段长度的大小,没考虑符号问题。
则根据等光程原理1212n PS n SQ n PO n OQ +=+得出2212111222112212()()22x R R x R R n x n n x n n x n x x x θθ+-++-=+;则有212121n n n n R x x -=+;考虑符号法则,凡是光线和主轴交点在顶点左方的,线段长度为负,上式变为212121n n n n R x x -=-。
物体通过透镜成像,就是由物体发出的光束在它的两个球面上相继折射的结果。
设在透镜主光轴上有一点物P ,它经过第一球面成像于1P ,1P 可看作第二球面的物,再经第二球面成像于2P ,它就是P 点经透镜所成的像。
按照上面所讲的逐次成像原理,设透镜的折射率为n ,S 为物距,'S 为像距,''S 为物点经过左半球面折射后所成的像。
对左半球面而言,取1x S =;"2112=S ;R=R ;1;x n n n ==,上式变为''111S n n R S-=- 同理,对右半球面,有'''211Sn nR S -=-,将两式相加即可得到'121111(1)()S n S R R -=-- 1-5解 (1)由等光程原理得AC nBD =minsin sin22AD nAD αδα+⇒=1.6 解:在半径相差dr 的两球面为所以,光程为 所以,当满足时,ds 最小,从而光程取最小值为由 0d d θϕ==知,光线在介质中传播不改变方向,即经过O 点和任意点A 的光线为直线。
光学设计作业答案

现代光学设计作业学号:**********姓名:***一、光学系统像质评价方法 (2)1.1 几何像差 (2)1.1.1 光学系统的色差 (3)1.1.2 轴上像点的单色像差─球差 (4)1.1.3 轴外像点的单色像差 (5)1.1.4 正弦差、像散、畸变 (7)1.2 垂直像差 (7)二、光学自动设计原理 (9)2.1 阻尼最小二乘法光学自动设计程序 (9)2.2 适应法光学自动设计程序 (11)三、ZEMAX光学设计 (13)3.1 望远镜物镜设计 (13)3.2 目镜设计 (17)四、照相物镜设计 (22)五、变焦系统设计 (26)一、光学系统像质评价方法所谓像差就是光学系统所成的实际像和理想像之间的差异。
由于一个光学系统不可能理想成像,因此就存在光学系统成像质量优劣的问题,从不同的角度出发会得出不同的像质评价指标。
(1)光学系统实际制造完成后对其进行实际测量✧星点检验✧分辨率检验(2)设计阶段的评价方法✧几何光学方法:几何像差、波像差、点列图、几何光学传递函数✧物理光学方法:点扩散函数、相对中心光强、物理光学传递函数下面就几种典型的评价方法进行说明。
1.1 几何像差几何像差的分类如图1-1所示。
图1-1 几何像差的分类1.1.1 光学系统的色差光波实际上是波长为400~760nm 的电磁波。
光学系统中的介质对不同波长光的折射率不同的。
如图1-2,薄透镜的焦距公式为()'121111n f r r ⎛⎫=-- ⎪⎝⎭(1-1) 因为折射率n 随波长的不同而改变,因此焦距也要随着波长的不同而改变,这样,当对无限远的轴上物体成像时,不同颜色光线所成像的位置也就不同。
我们把不同颜色光线理想像点位置之差称为近轴位置色差,通常用C 和F 两种波长光线的理想像平面间的距离来表示近轴位置色差,也成为近轴轴向色差。
若l ′F 和l ′c 分别表示F 与C 两种波长光线的近轴像距,则近轴轴向色差为'''FC F C l l l ∆=- (1-2)图1-2 单透镜对无限远轴上物点白光成像当焦距'f 随波长改变时,像高'y 也随之改变,不同颜色光线所成的像高也不一样。
高等光学作业附答案

3.3. 空间相干性和时间相干性指的是什么?如何量度?光源的角宽度和相干孔径角是如何定义的?证明相干长度 Lc = λ2/∆λ。
答:空间相干性是指光场中不同两点在同一时刻的相干程度。
时间相干性是指同一点在不同时刻的相干程度。
空间相干性的度量是采用相干面积进行度量。
时间相干性是采用相干时间或相干长度进行度量。
光源的角宽度定义为0a d λ=,d0是使得条纹可见的光源最大宽度。
相干孔径角定义为22c pλθ=。
证明:多色光源的干涉场分布的条纹可见度有:sin()22kl K kl ∆=∆ 当2klπ∆=条纹不可见,此时有: 2122l k λλπλλλ==∆∆∆证毕。
3.12.(1)当把一单色点光源放在一会聚透镜物空间焦点上, 观察屏与透镜空间焦面重合, 则观察到夫琅和费圆孔衍射图样。
现在将光源换为圆状准单色初级光源, 圆中心在光轴上, 圆面垂直于光轴, 要想仍获得夫琅和费圆孔衍射图样, 对光源大小。
频宽以及透镜直径应有什么限制? 答:这里可以认为光源在透镜前表面的场的相干性决定了衍射图样。
首先光源的频宽应该保证准单色有νν∆,光源宽度应保证相干面积大于透镜宽度,有L fd aλ<,dL 为透镜直径,a 为光源直径,f 是透镜焦距。
(2)在衍射计实验中, 光源不是单色点光源, 但仍引用夫琅和费圆孔衍射的结果,即取I Q I Q J u uu a ()()()()(()),sin 121222===πλφ根据(1)的结果, 试说明为什么可以如此处理?答:只要光源足够小,保证了其在屏处的相干面积大,同时圆孔本身面积远小于相干面积,加上光源准单色条件,即可认为屏幕上两孔光场依然具有足够的相干性,因此可以用夫琅和费圆孔衍射的结果。
3.1.已知太阳的表观角直径为0.5。
平均有效波长为6000A, 求阳光的相干面积。
解:由L zd aλ=,根据角直径定义,有2tan(0.25)0.00873az=≈ 因此可得相干线度为:68.7um ,相干面积4723um 2. 3.9.阻尼振子的辐射场中某点复扰动为V t A t t i t t t ()exp(/)exp()=--><⎧⎨⎩10200φπν式中t 1是自发辐射寿命。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
现代光学设计作业学号:2220110114姓名:田训卿一、光学系统像质评价方法 (2)1.1 几何像差 (2)1.1.1 光学系统的色差 (3)1.1.2 轴上像点的单色像差─球差 (4)1.1.3 轴外像点的单色像差 (5)1.1.4 正弦差、像散、畸变 (7)1.2 垂直像差 (7)二、光学自动设计原理92.1 阻尼最小二乘法光学自动设计程序 (9)2.2 适应法光学自动设计程序 (11)三、ZEMAX光学设计.133.1 望远镜物镜设计 (13)3.2 目镜设计 (17)四、照相物镜设计 (22)五、变焦系统设计 (26)一、光学系统像质评价方法所谓像差就是光学系统所成的实际像和理想像之间的差异。
由于一个光学系统不可能理想成像,因此就存在光学系统成像质量优劣的问题,从不同的角度出发会得出不同的像质评价指标。
(1)光学系统实际制造完成后对其进行实际测量✧星点检验✧分辨率检验(2)设计阶段的评价方法✧几何光学方法:几何像差、波像差、点列图、几何光学传递函数✧物理光学方法:点扩散函数、相对中心光强、物理光学传递函数下面就几种典型的评价方法进行说明。
1.1 几何像差几何像差的分类如图1-1所示。
图1-1 几何像差的分类1.1.1 光学系统的色差光波实际上是波长为400~760nm 的电磁波。
光学系统中的介质对不同波长光的折射率不同的。
如图1-2,薄透镜的焦距公式为()'121111n f r r ⎛⎫=-- ⎪⎝⎭(1-1) 因为折射率n 随波长的不同而改变,因此焦距也要随着波长的不同而改变,这样,当对无限远的轴上物体成像时,不同颜色光线所成像的位置也就不同。
我们把不同颜色光线理想像点位置之差称为近轴位置色差,通常用C 和F 两种波长光线的理想像平面间的距离来表示近轴位置色差,也成为近轴轴向色差。
若l ′F 和l ′c 分别表示F 与C 两种波长光线的近轴像距,则近轴轴向色差为'''FC F C l l l ∆=- (1-2)图1-2 单透镜对无限远轴上物点白光成像当焦距'f 随波长改变时,像高'y 也随之改变,不同颜色光线所成的像高也不一样。
这种像的大小的差异称为垂轴色差,它代表不同颜色光线的主光线和同一基准像面交点高度(即实际像高)之差。
通常这个基准像面选定为中心波长的理想像平面。
若'ZF y 和'ZC y 分别表示F 和C 两种波长光线的主光线在D 光理想像平面上的交点高度,则垂轴色差为'''FC ZF ZC y y y ∆=- (1-3)图1-3 单透镜对无线远轴外物点白光成像1.1.2 轴上像点的单色像差─球差如图1-3所示,轴上有限远同一物点发出的不同孔径的光线通过光学系统以后不再交于一点,成像不理想。
为了表示这些对称光线在光轴方向的离散程度,我们用不同孔径光线的聚交点对理想像点A’0的距离A′0A′1.0,A′0A′0.85,…表示,称为球差,用符号δL′表示,δL′的计算公式是δL′=L′−l′ (1-4)式中,L′代表一宽孔径高度光线的聚交点的像距;l′为近轴像点的像距。
球差值越大,成像质量越差。
图1-3 球差示意图1.1.3 轴外像点的单色像差轴外物点发出的通过系统的所有光线在像空间的聚交情况比轴上点复杂。
为了能够简化问题,同时又能定量地描述这些光线的弥散程度,从整个入射光束中取两个相互垂直的平面光束,用这两个平面光束的结构来近似地代表整个光束的结构。
将主光线与光轴决定的平面称为子午面,如图1-4中的平面BM+M−;将过主光线与子午面垂直的平面称为弧矢面,如图1-4中的平面 BD+D−平面。
用来描述这两个平面光束结构的几何参数分别成为子午像差和弧矢像差。
图1-4 子午面与弧矢面示意图1.1.3.1 子午像差子午光线对通过系统后的所有光线都应交在理想像平面上的同一点。
由于有像差存在,光线对的交点既不在主光线上,也不在理想像平面上。
为了表示这种差异,我们用子午光线对的交点B′T离理想像平面的轴向距离X′T表示此光线对交点偏离主光线的程度,成为“子午场曲”。
如图1-5所示。
用光线对交点B′T离开主光线的垂直距离K′T表示此光线对交点偏离主光线的程度,成为“子午彗差”。
当光线对对称地逐渐向主光线靠近,宽度趋于零时,它们的交点B′T趋近于一点B′t,B′t显然应该位于主光线上,它离开理想像平面的距离称为“细光束子午场曲”,用x′t表示。
不同宽度子午光线对的子午场曲X′T和细光束子午场曲x′t之差(X′T−x′t),代表了细光束和宽光束交点前后位置的差。
此差值成为“轴外子午球差”,用δL′T表示。
δL′T=X′T−x′t (1-5)图1-5 子午面光线像差1.1.3.2 弧矢像差如图1-6所示,阴影部分所在平面即为弧矢面。
把弧矢光线对的交点B′S到理想像平面的距离用X′S表示,称为“弧矢场曲”;B′S到主光线的距离用K′S表示,称为“弧矢彗差”。
主光线附近的弧矢细光束的交点B′S到理想像平面的距离用x′s表示,称为“细光束弧矢场曲”;X′S−x′s称为“轴外弧矢球差”,用δL′S表示。
δL′S=X′S−x′s (1-6)图1-6 弧矢面光线像差1.1.4 正弦差、像散、畸变对于某些小视场大孔径的光学系统来说,由于像高本身较小,彗差的实际数值更小,因此用彗差的绝对数值不足以说明系统的彗差特性。
一般改用彗差与像高的比值来代替系统的彗差,用符号SC′表示SC′=limY→0K′Sy′(1-7)SC′的计算公式为SC′=sinU1u′sinU′u1∙l′−l′zL′−l′z−1 (1-8)对于用小孔径光束成像的光学系统,它在理想像平面上的成像质量由细光束子午和弧矢场曲x′t,x′s决定。
二者之差反映了主光线周围的细光束偏离同心光束的程度,称为“像散”,代表了主光线周围细光束的成像质量,用符号x′ts表示x′ts=x′t−x′s (1-9)把成像光束的主光线和理想像平面交点的高度作为光束的实际像高,那么它和理想像高的差值称为“畸变”。
畸变不影响像的清晰度,只影响像的变形。
1.2 垂直像差利用不同孔径子午、弧矢光线在理想像平面上的交点和主光线在理想像平面上的交点之间的距离来表示的像差,称为垂轴几何像差。
为了表示子午光束的成像质量,在整个子午光束截面内取若干对光线,一般取±1.0h,±0.85h,±0.7071h,±0.5h,±0.3h,0h这11条不同孔径的光线,计算出它们和理想像平面交点的坐标,由于子午光线永远位于子午面内,因此在理想像平面上交点高度之差就是这些交点之间的距离。
求出前10条光线和主光线(0孔径光线)高度之差即为子午光束的垂轴像差,如图1-7所示。
δy′=y′−y′z(1-10)图1-7 子午垂轴像差为了用垂轴像差表示色差,可以将不同颜色光线的垂轴像差用同一基准像面和同一基准主光线作为基准点计算各色光线的垂轴像差。
一般情况下,我们采用平均中心波长光线的理想像平面和主光线作为基准计算各色光光线的垂轴色差。
为了了解整个像面的成像质量,同样需要计算轴上点和若干不同像高轴外点的垂轴像差。
对轴上点来说,子午和弧矢垂轴像差是完全一样的,因此弧矢垂轴像差没有必要计算0视场的垂轴像差。
二、光学自动设计原理在光学自动设计中,一般把对系统的全部要求,根据它们和结构参数的关系不同重新划分成两大类。
第一类是不随系统结构参数改变的常数。
如物距L ,孔径高H 或孔径角余弦sinU ,视场角ω或物高y ,入瞳或孔径光阑的位置以及轴外光束的渐晕系数K +,K −,等等。
在计算和校正光学系统像差的过程中这些参数永远保持不变,它们是和自变量(结构参数)无关的常量。
第二类是随结构参数改变的参数。
它们包括代表系统成像质量的各种几何像差或波像差。
同时也包括某些近轴光学特性参数,如焦距f ′,放大率,像距l ′,出瞳距l ′z ,等等。
为了简单起见,将第二类参数统称为像差,用符号F 1,…,F m 代表。
系统的结构参数用符号x 1,…,x n 代表。
两者之间的函数关系可用下列形式表示f 1(x 1,⋯,x n )=F 1(2-1) f m (x 1,⋯,x n )=F m式中,f 1,…,f m 分别代表像差F 1,…,F m 与自变量x 1,…,x n 之间的函数关系。
上式称为像差方程组。
2.1 阻尼最小二乘法光学自动设计程序当像差数大于自变量数的情形:m>n ,这时方程组是一个超定方程组,它不存在满足所有方程式的准确解,只能求它的近似解—最小二乘解。
首先定义一个函数组,他们的意义如以下公式所示:11111111n nm mm n m n f f x x F x x f f x x F x x δδϕδδδδϕδδ⎫=∆+⋅⋅⋅+∆-∆⎪⎪⎪⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⎬⎪⎪=∆+⋅⋅⋅+∆-∆⎪⎭φ1…φm 称为“像差残量”,写成矩阵形式为A X Fφ=∆-∆取各像差残量的平方和构成另一个函数()X φ∆:21()mTi i X φϕϕϕ-∆==∑()X φ∆在光学自动设计中成为“评价函数”,能够使()0X φ∆=的解(即φ1=…=φm =0),就是像差线性方程组的准确解。
当m>n 时,它实际上是不存在的。
我们改为()X φ∆的极小值解,作为方程组的近似解称为像差线性方程组的最小二乘解。
将φ代入评价函数得21min ()min min[()()]mT i i x A x F A x F φ=Φ∆==∆-∆∆-∆∑()()()[()]()()()T T T TTTT T T T T T x A x F A x F A x F A x F x A F A x F x A A x F A x x A F F FΦ∆=∆-∆∆-∆=∆-∆∆-∆=∆-∆∆-∆=∆∆-∆∆-∆∆+∆∆根据多元函数的极值理论,()X φ∆取得极小值解的必要条件是一价偏导数等于零()0x ∇Φ∆= (2-2)运用矩阵求导规则求一阶偏导数()22()0T T T T T x A A x A F A F A A x A F ∇Φ∆=∆-∆-∆=∆-∆=0T T A A x A F ∆-∆= (2-3)只要方阵A T A 为非奇异矩阵,即它的行列式值不等于零,则逆矩阵(A T A)-1存在,方程式有解,解的公式为1()T T x A A A F -∆=∆ (2-4)要使A T A 非奇异,则要求方程组的系数矩阵A 不产生列相关。
即像差线性方程组中不存在自变量相关。
在光学设计中,由于像差和结构参数之间的关系是非线性的。
