相交线与平行线证明题填空
相交线平行线命题定理证明试题

相交线平行线命题定理证明试题Company Document number:WTUT-WT88Y-W8BBGB-BWYTT-19998第二章相交线、平行线命题、定理、证明一、填空题:1.命题常写成“如果……,那么……”的形式,在这种形式中,用“”开始的部分是题设,用“”开始由部分是结论。
2.将命题“等角的余角相等”改写成“如果……,那么……”的形式为。
3.已知∠AOB为锐角,直线l1⊥OA,直线l2⊥OB,那么l1和l2的关系为。
4.如图14所示,直线l∥m,若∠α=70°,则∠β= 。
图145.如图15所示,a∥b,∠1-2∠2=60°,则∠1= ;∠2= 。
6.“同位角相等,两直线平行”这个命题中题设是。
7.“过两点有且只有一条直线”是。
8. 叫做命题,每个命题都是由;两部分组成。
图159.如果题设成立,那么结论也成立,这样的命题叫做。
10.证明一个命题的步骤是:①根据题意;②根据题设、结论、结合图形,写出;。
③经过分析,找出由推出的途径,写出。
二、选择11.下列语句中,不是命题的是。
A.两点之间,线段最短;B.对顶角不相等;C.连结A、B两点;D.不重合的两条直线有一个交点。
12.给出下列四个命题:①同角的余角相等;②相等的角是对顶角;③垂直于同一条直线的两条直线平行;④平行于同一条直线的两条直线垂直。
其中真命题有。
个;个;个;个。
13.如图16,下列推理中正确的是。
A.∵∠1=∠2,∴AB∥CDB.∵∠ABC+∠BCD=180°,∴AD∥B CC.∵AD∥BC,∴∠3=∠4D.∵∠ABC=∠ADC,∠1=∠2,∴AB∥CD14.下列命题,正确的是。
图16A.如果∠α=180°-∠β,则∠α是补角;B.如果∠α+∠β=90°则∠α是余角;°角是50°的余角;D.余角是补角的一半。
15.将命题“对顶角相等”改成“如果……,那么……”的形式正确的是。
相交线与平行线填空题

《相交线与平行线》填空习题精选1.两直线相交所成的四个角中,有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为_____________.2.两直线相交所成的四个角中,有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线,具有这种关系的两个角,互为__________.对顶角的性质:______ _________.3.两直线相交所成的四个角中,如果有一个角是直角,那么就称这两条直线相互_______.垂线的性质:⑴过一点______________一条直线与已知直线垂直.⑵连接直线外一点与直线上各点的所在线段中,_______________.4.直线外一点到这条直线的垂线段的长度,叫做________________________.5.两条直线被第三条直线所截,构成八个角,在那些没有公共顶点的角中,⑴如果两个角分别在两条直线的同一方,并且都在第三条直线的同侧,具有这种关系的一对角叫做___________ ;⑵如果两个角都在两直线之间,并且分别在第三条直线的两侧,具有这种关系的一对角叫做____________ ;⑶如果两个角都在两直线之间,但它们在第三条直线的同一旁,具有这种关系的一对角叫做_______________.6.在同一平面内,不相交的两条直线互相___________.同一平面内的两条直线的位置关系只有________与_________两种.7.平行公理:经过直线外一点,有且只有一条直线与这条直线______.推论:如果两条直线都与第三条直线平行,那么_____________________.8.平行线的判定:⑴两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:_____________________________________.⑵两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:___________________________.⑶两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:________________________________________.9.在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线_______ .10.平行线的性质:⑴两条平行直线被第三条直线所截,同位角相等.简单说成:_________________.⑵两条平行直线被第三条直线所截,内错角相等.简单说成:__________________________________.⑶两条平行直线被第三条直线所截,同旁内角互补.简单说成:____________________________________ .11.判断一件事情的语句,叫做_______.命题由________和_________两部分组成.题设是已知事项,结论是______________________.命题常可以写成“如果……那么……”的形式,这时“如果”后接的部分是_____,“那么”后接的部分是_________.如果题设成立,那么结论一定成立.像这样的命题叫做___________.如果题设成立时,不能保证结论一定成立,像这样的命题叫做___________.定理都是真命题.12.把一个图形整体沿某一方向移动,会得到一个新图形,图形的这种移动,叫做平移变换,简称_______.图形平移的方向不一定是水平的.平移的性质:⑴把一个图形整体平移得到的新图形与原图形的形状与大小完全______.⑵新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段_________________.熟悉以下各题:13. 如图,,8,6,10,BC AC CB cm AC cm AB cm ⊥===那么点A 到BC的距离是_____,点B 到AC 的距离是_______,点A 、B 两点的距离是_____,点C 到AB 的距离是________.14. 设a 、b 、c 为平面上三条不同直线,a) 若//,//a b b c ,则a 与c 的位置关系是_________;b) 若,a b b c ⊥⊥,则a 与c 的位置关系是_________;c) 若//a b ,b c ⊥,则a 与c 的位置关系是________.15.两条直线相交,有_____对对顶角,三条直线两两相交,有_____对对顶角.16.如图1,直线AB 、CD 相交于点O ,OB 平分∠DOE ,若∠DOE =60°,则∠AOC 的度数是_____.17..已知∠AOB =40°,OC 平分∠AOB ,则∠AOC 的补角等于_____.18..如图2,若l 1∥l 2,∠1=45°,则∠2=_____.图1 图2 图319.如图3,已知直线a ∥b ,c ∥d ,∠1=115°,则∠2=_____,∠3=_____.20.一个角的余角比这个角的补角小_____.21.如图4,已知直线AB 、CD 、EF 相交于点O ,∠1=95°,∠2=32°,则∠BOE =_____.图4 图522.如图5,∠1=82°,∠2=98°,∠3=80°,则∠4的度数为_____.23..如图6,AD ∥BC ,AC 与BD 相交于O ,则图中相等的角有_____对.图6 图724..如图7,已知AB ∥CD ,∠1=100°,∠2=120°,则∠α=_____.25..如图8,DAE 是一条直线,DE ∥BC ,则∠BAC =_____.26..如图9,AB∥CD,AD∥BC,则图中与∠A相等的角有_____个.图8 图9 图1027..如图10,标有角号的7个角中共有_____对内错角,_____对同位角,_____对同旁内角.28..如图11,(1)∵∠A=_____(已知),图11∴AC∥ED( )(2)∵∠2=_____(已知),∴AC∥ED( )(3)∵∠A+_____=180°(已知),∴AB∥FD( )(4)∵AB∥_____(已知),∴∠2+∠AED=180°( )(5)∵AC∥_____(已知),∴∠C=∠1( )29.a、b、c是直线,且a∥b,b⊥c,则a与c的位置关系是________.30.如图5-1,MN⊥AB,垂足为M点,MN交CD于N,过M点作MG⊥CD,垂足为G,EF过点N点,且EF∥AB,交MG于H点,其中线段GM的长度是________到________的距离,线段MN的长度是________到________的距离,又是_______的距离,点N到直线MG的距离是___.GHNMFEDCBAFEODCBA图5-1 图5-231.如图5-2,AD ∥BC ,EF ∥BC ,BD 平分∠ABC ,图中与∠ADO 相等的角有_______ 个,分别是___________.32.因为AB ∥CD ,EF ∥AB ,根据_________,所以_____________.33.命题“等角的补角相等”的题设__________,结论是__________.34.如图5-3,给出下列论断:①AD ∥BC :②AB ∥CD ;③∠A =∠C .以上其中两个作为题设,另一个作为结论,用“如果……,那么……”形式,写出一个你认为正确的命题是___________.35.如图5-4,直线AB 、CD 、EF 相交于同一点O ,而且∠B O C=23∠AOC ,∠DOF =13∠AOD ,那么∠FOC =______ 度. 36.如图5-5,直线a 、b 被c 所截,a ⊥l 于M ,b ⊥l 于N ,∠1=66°,则∠2=________.37.如图5-6,∠ACB =90°,CD ⊥AB ,则图中与∠A 互余的角有 个,它们分别是 .∠A =∠ ,根据是 .38.如图5-7,一棵小树生长时与地面所成的角为80°,它的根深入泥土,如果根和小树在同一条直线上,那么∠2等于 °.39.如图5-8,量得∠1=80°,∠2=80°,由此可以判定 ∥ ,它的根据是 .量得∠3=100°,∠4=100°,由此可以判定 ∥ ,它的根据是 .40.猜谜语:(打本章两个几何名称)剩下十分钱: ;斗牛 .41.a 、b 、c 是直线,且a ∥b , b ∥c , 则a ___c ;a 、b 、c 是直线,且a ⊥b , b ⊥c , 则a ___c ;D C B AF E O D C B A c l N M b a 21 图5-3 图5-4 图5-542. 如图5-9,直线AD 、BC 交于O 点,∠+∠=︒AOB COD 110,则∠COD 的度数为 .43. 如图5-10,直线AB 与CD 交于O 点,∠-∠=︒3180,则∠2= .44. 如图5-11,直线AB 、EF 相交于O 点,CD AB ⊥于O 点,∠=︒'EOD 12819,则∠∠BOF AOF ,的度数分别为 .45.如图,直线a 、b 相交,∠1=,则∠2= .第11题图46.如图,当剪子口∠AOB 增大15°时,∠COD 增大 .第46题图第47题图 第48题图47.如图,计划把河水引到水池A 中,先作AB ⊥CD ,垂足为B ,然后沿AB 开渠,能使所开的渠道最短,这样设计的依据是 .48.如图,直线AB ,CD ,EF 相交于点O ,且AB ⊥CD ,∠1与∠2的关系是 .49.如图,D 是AB 上一点,CE ∥BD ,CB ∥ED ,EA ⊥BA 于点A ,若∠ABC=38°,则∠AED = .第49题图 第50题图50.如图,AB ∥CD ,直线EF 分别交AB 、CD 于E 、F ,EG 平分∠BEF ,若∠1=72°,则∠2= .51.如图,直线a ∥b ,则∠ACB = .第51题图 第52题图52.如图,一个宽度相等的纸条按如图所示方法折叠一下,则∠1= .53.如图7,当剪刀口∠AOB 增大21°时,∠COD 增大 。
2023年七年级下册数学第五章相交线与平行线证明题阅读理解填理由专项训练(14道)
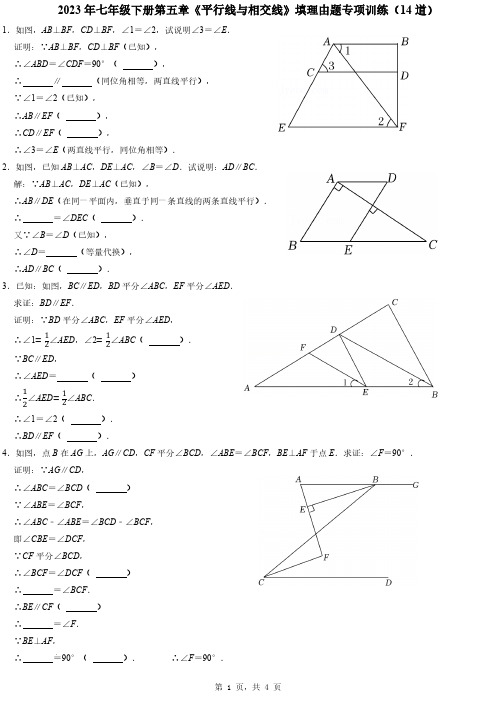
2023年七年级下册第五章《平行线与相交线》填理由题专项训练(14道)1.如图,AB⊥BF,CD⊥BF,∠1=∠2,试说明∠3=∠E.证明:∵AB⊥BF,CD⊥BF(已知),∴∠ABD=∠CDF=90°(),∴∥(同位角相等,两直线平行),∵∠1=∠2(已知),∴AB∥EF(),∴CD∥EF(),∴∠3=∠E(两直线平行,同位角相等).2.如图,已知AB⊥AC,DE⊥AC,∠B=∠D.试说明:AD∥BC.解:∵AB⊥AC,DE⊥AC(已知),∴AB∥DE(在同一平面内,垂直于同一条直线的两条直线平行).∴=∠DEC().又∵∠B=∠D(已知),∴∠D=(等量代换),∴AD∥BC().3.已知:如图,BC∥ED,BD平分∠ABC,EF平分∠AED.求证:BD∥EF.证明:∵BD平分∠ABC,EF平分∠AED,∴∠1=12∠AED,∠2=12∠ABC().∵BC∥ED,∴∠AED=()∴12∠AED=12∠ABC.∴∠1=∠2().∴BD∥EF().4.如图,点B在AG上,AG∥CD,CF平分∠BCD,∠ABE=∠BCF,BE⊥AF于点E.求证:∠F=90°.证明:∵AG∥CD,∴∠ABC=∠BCD()∵∠ABE=∠BCF,∴∠ABC﹣∠ABE=∠BCD﹣∠BCF,即∠CBE=∠DCF,∵CF平分∠BCD,∴∠BCF=∠DCF()∴=∠BCF.∴BE∥CF()∴=∠F.∵BE⊥AF,5.(2023秋•海口期末)如图,AB∥CD,∠1=∠A.(1)试说明:AC∥ED;(2)若∠2=∠3,FC与BD的位置关系如何?为什么?解:(1)∵AB∥CD,(已知)∴∠1=∠BED,()又∵∠1=∠A,(已知)∴∠BED=∠,(等量代换)∴∥.()(2)FC与BD的位置关系是:.理由如下:∵AC∥ED,(已知)∴∠2=∠.()又∵∠2=∠3,(已知)∴∠=∠.(等量代换)∴∥.()6.已知:如图,在△ABC中,FG∥CD,∠1=∠3.求证:∠B+∠BDC=180°.解:因为FG∥CD(已知),所以∠1=.又因为∠1=∠3(已知),所以∠2=(等量代换).所以BC∥(),所以∠B+∠BDE=180°().7.如图,已知∠D=108°,∠BAD=72°,AC⊥BC于C,EF⊥BC于F.求证:∠1=∠2.证明:∵∠D=108°,∠BAD=72°(已知)∴∠D+∠BAD=180°∴AB∥CD()∴∠1=()又∵AC⊥BC于C,EF⊥BC于F(已知)∴EF∥()∴∠2=()∴∠1=∠2()8.如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°.试说明:∠GDC=∠B.解:∵AD⊥BC,EF⊥BC(已知)∴∠ADB=∠EFB=90°()∴EF∥AD()∴+∠2=180°()又∵∠2+∠3=180°(已知)∴∠1=()∴∥()9.(2023秋•丹江口市期末)如图,E、F分别在AB和CD上,∠1=∠D,∠2与∠C互余,AF⊥CE于G,求证:AB∥CD.证明:∵AF⊥CE(已知),∴∠CGF=90°(垂直的定义),∵∠1=∠D(已知),∴AF∥(),∴∠4==90°(),又∵∠2+∠3+∠4=180°,∴∠2+∠3=90°,∵∠2与∠C互余(已知),∴∠2+∠C=90°,∴∠C=,∴AB∥.()10.(2023秋•青神县期末)如图,AB与EF交于点B,CD与EF交于点D,根据图形,请补全下面这道题的解答过程.(1)∵∠1=∠2(已知)∴∥CD()∴∠ABD+∠CDB=()(2)∵∠BAC=65°,∠ACD=115°,(已知)∴∠BAC+∠ACD=180°(等式性质)∴AB∥CD()(3)∵CD⊥AB于D,EF⊥AB于F,∠BAC=55°,(已知)∴∠ABD=∠CDF=90°(垂直的定义)∴∥(同位角相等,两直线平行)又∵∠BAC=55°,(已知)∴∠ACD=.()11.如图所示,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明理由.证明:∵∠1+∠2=180°()∠1=∠DFH()∴()∴EH∥AB()∴∠3=∠ADE()∵∠3=∠B∴∠B=∠ADE()∴DE∥BC∴∠AED=∠C()12.如图,已知AB∥CD,BE平分∠ABC,DB平分∠CDF,且∠ABC+∠CDF=180°.求证:BE⊥DB.证明:∵AB∥CD∴∠ABC=∠BCD()∵∠ABC+∠CDF=180°()∴∠BCD+∠CDF=180°()∴BC∥DF()于是∠DBC=∠BDF()∵BE平分∠ABC,DB平分∠CDF∴∠EBC=12∠ABC,∠BDF=()∵∠EBC+∠DBC=∠EBC+∠BDF=12(∠ABC+∠CDF)即∠EBD=∴BE⊥DB()13.如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.解:∵∠1=∠C,(已知)∴GD∥.()∴∠2=∠DAC.()∵∠2+∠3=180°,(已知)∴∠DAC+∠3=180°.(等量代换)∴AD∥EF.()∴∠ADC=∠.()∵EF⊥BC,(已知)∴∠EFC=90°.()∴∠ADC=90°.(等量代换)14.(2023秋•南关区期末)如图,已知AB∥DC,AC⊥BC,AC平分∠DAB,∠B=50°,求∠D的大小.阅读下面的解答过程,并填括号里的空白(理由或数学式).解:∵AB∥DC(),∴∠B+∠DCB=180°().∵∠B=(已知),∴∠DCB=180°﹣∠B=180°﹣50°=130°.∵AC⊥BC(已知),∴∠ACB=(垂直的定义).∴∠2=.∵AB∥DC(已知),∴∠1=().∵AC平分∠DAB(已知),∴∠DAB=2∠1=(角平分线的定义).∵AB∥DC(已知),∴+∠DAB=180°(两条直线平行,同旁内角互补).。
七年级相交线-平行线证明题(很好)
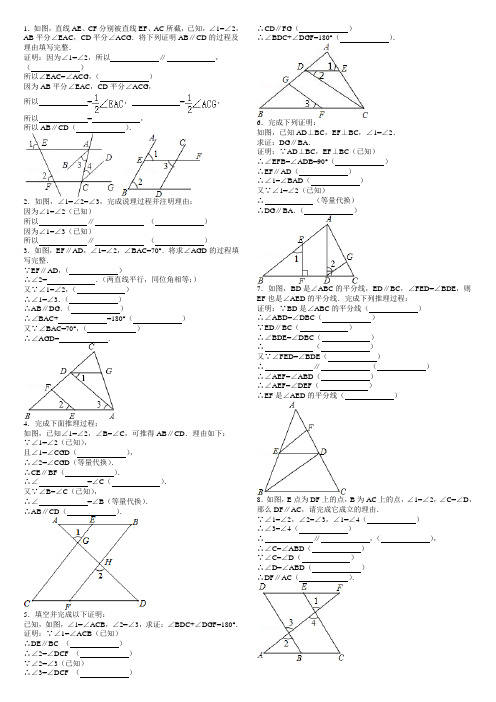
(4)∵AB∥_________(已知)
∴∠2+∠AED=180°(_________)
(5)∵AC∥_________(已知)
∴∠C=∠1(_________)
∴AE∥_________(_________)
∴∠EAC=∠_________,(_________)
而AB平分∠EAC,CD平分∠ACG(已知)
∴∠_________= ∠EAC,∠4= ∠_________(角平分线的定义)
∴∠_________=∠4(等量代换)
∴AB∥CD(_________).
∴∠AEF=∠DEF(_________)
∴EF是∠AED的平分线(_________)
8.如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由.
∵∠1=∠2,∠2=∠3,∠1=∠4(_________)
∴∠3=∠4(_________)
∴_________∥_________,(_________),
1.如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
证明:因为∠1=∠2,所以_________∥_________,(_________)
所以∠EAC=∠ACG,(_________)
因为AB平分∠EAC,CD平分∠ACG,
所以∠BAC+_________=180°(两直线平行,同旁内角互补),
因为∠BAC=70°(已知),
所以∠AGD=_________(补角的定义)
13.如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
2021届中考数学一轮复习热点题型专练 相交线与平行线【含答案】

2021届中考数学一轮复习热点题型专练相交线与平行线一、选择题1.将等腰直角三角形纸片和矩形纸片按如图方式叠放在起,若∠1=30°,则∠2的度数为( )A .10°B .15°C .20°D .30°【答案】B【解析】∠AB ∠CD , ∠∠1=∠ADC =30°,又∠等腰直角三角形ADE 中,∠ADE =45°, ∠∠1=45°﹣30°=15°, 故选:B .2.如图,直线a ∠b ,点B 在a 上,且BC AB ⊥.若︒=∠351,那么2∠等于( )A ︒45B ︒50C ︒55D ︒60【答案】C 【解析】∠a//b ∠∠1=∠BAC=35° ∠∠BCA=90°-∠BAC=55° ∠∠2=∠BCA=55°(对顶角相等)21abCA故选:C3.如图,BD∠EF,AE与BD交于点C,∠B=30°,∠A=75°,则∠E的度数为()A.135°B.125°C.115°D.105°【答案】D【解析】∠∠B=30°,∠A=75°,∠∠ACD=30°+75°=105°,∠BD∠EF,∠∠E=∠ACD=105°.故选:D.4.如图,l1∠l2,点O在直线l1上,若∠AOB=90°,∠1=35°,则∠2的度数为()A.65°B.55°C.45°D.35°【答案】B【解析】∠l1∠l2,∠1=35°,∠∠OAB=∠1=35°.∠OA∠OB,∠∠2=∠OBA=90°﹣∠OAB=55°.故选:B.5.如图,AB∠CD,∠A=50°,则∠1的度数是()A.40°B.50°C.130°D.150°【答案】C【解析】∠AB∠CD,∠∠2=∠A=50°,∠∠1=180°﹣∠2=180°﹣50°=130°,故选:C.6.已知直线m∠n,将一块含45°角的直角三角板ABC按如图方式放置,其中斜边BC与直线n交于点D.若∠1=25°,则∠2的度数为()A.60°B.65°C.70°D.75°【答案】C【解析】设AB与直线n交于点E,则∠AED=∠1+∠B=25°+45°=70°.又直线m∠n,∠∠2=∠AED=70°.故选:C.7.如图,已知//∠的大小是()a b,158∠=︒,则2A.122︒B.85︒C.58︒D.32【答案】C【解析】∠a//b∠∠1=∠2∠∠1=58°∠∠2=58°故选:C8.将一副三角板按如图所示的位置摆放在直尺上,则1∠的度数为()A.60︒B.65︒C.75︒D.85︒【答案】C【解析】如图:如图,∠∠BCA=60°,∠DCE=45°∠∠2=180°-60°-45°=75°∠HF//BC∠∠1=∠2=75°故选:C.9.如图,AB∠CD,∠B=75°,∠E=27°,则∠D的度数为()【答案】B【解析】∠AB∠CD,∠∠B=∠1,∠∠1=∠D+∠E,∠∠D=∠B﹣∠E=75°﹣27°=48°,故选:B.A.45°B.48°C.50°D.58°10.如图,//∠的度数是()AB CD,AD CD=,150∠=︒,则2A.55︒B.60︒C.65︒D.70︒【答案】C【解析】如图,∠AD=CD,∠1=50°∠∠CAD=∠ACD=65°∠AB//CD∠∠2=∠ACD=65°.故选:C.二、填空题11.一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=度.【答案】120【解析】:如图,连接BF,BF∠CD,∠CD∠AE,∠CD∠BF∠AE,∠∠1+∠BCD=180°,∠2+∠BAE=180°,∠∠BCD=150°,∠BAE=90°,∠∠1=30°,∠2=90°,∠∠ABC=∠1+∠2=120°.故答案为:120.12.如图,直线AB∠CD,直线EC分别与AB,CD相交于点A、点C,AD平分∠BAC,已知∠ACD=80°,则∠DAC的度数为.【答案】50°【解析】:∠AB∠CD,∠ACD=80°,∠∠BAC=100°,又∠AD平分∠BAC,∠∠DAC=∠BAC=50°,故答案为:50°.13.如图,直线a,b被直线c,d所截.若a∠b,∠1=130°,∠2=30°,则∠3的度数为度.【答案】100【解析】:∠a∠b,∠∠3=∠4,∠∠1=∠2+∠4=∠2+∠3,∠1=130°,∠2=30°,∠130°=30°+∠3,解得:∠3=100°.故答案为:100.14.已知直线a∠b,将一块含30°角的直角三角板ABC按如图所示方式放置(∠BAC=30°),并且顶点A,C 分别落在直线a,b上,若∠1=18°,则∠2的度数是.【答案】48°【解析】:∠a∠b,∠∠2=∠1+∠CAB=18°+30°=48°,故答案为:48°15.将一个矩形纸片折叠成如图所示的图形,若∠ABC=26°,则∠ACD=°.【答案】128°【解析】:延长DC,由题意可得:∠ABC=∠BCE=∠BCA=26°,则∠ACD=180°﹣26°﹣26°=128°.故答案为:128.16.如图,AD∠CE,∠ABC=100°,则∠2﹣∠1的度数是.【答案】80°【解析】:作BF∠AD,∠AD∠CE,∠AD∠BF∠EC,∠∠1=∠3,∠4+∠2=180°,∠3+∠4=100°,∠∠1+∠4=100°,∠2+∠4=180°,∠∠2﹣∠1=80°.故答案为:80°.17.如图,AB∥CD,∠ABD的平分线与∠BDC的平分线交于点E,则∠1+∠2=______.【答案】90°【解析】∵AB∥CD,∴∠ABD+∠CDB=180°,∵BE是∠ABD的平分线,∴∠1=∠ABD,∵BE是∠BDC的平分线,∴∠2=∠CDB,∴∠1+∠2=90°,故答案为:90°.18.如图,若AB∠CD,∠1=40度,则∠2=度.【答案】140°【解析】:∠AB∠CD,∠1=40°,∠∠3=∠1=40°,∠∠2=180°﹣∠3=180°﹣40°=140°.故答案为:140.19.把一块含有45°角的直角三角板与两条长边平行的直尺如图放置(直角顶点在直尺的一条长边上).若∠1=23°,则∠2=°.【答案】68°【解析】:∠∠ABC是含有45°角的直角三角板,∠∠A=∠C=45°,∠∠1=23°,∠∠AGB=∠C+∠1=68°,∠EF∠BD,∠∠2=∠AGB=68°;故答案为:68.20.如图//∠=︒.AB CD,//∠=︒,则DBCB DE,50【答案】130°【解析】:∠AB//CD∠∠B=∠C=50°∠BC//DE∠∠C+∠D=180°∠∠D=180°-50°=130°A 80° EB CF 图5 故答案为:130.三、计算题21.如图,直线EF ∥GH ,点A 在EF 上,AC 交GH 于点B ,若∠FAC=72°,∠ACD=58°,点D 在GH 上,求∠BDC 的度数.【解析】:∵EF ∥GH ,∴∠ABD+∠FAC=180°,∴∠ABD=180°﹣72°=108°,∵∠ABD=∠ACD+∠BDC ,∴∠BDC=∠ABD ﹣∠ACD=108°﹣58°=50°.22如图5,EF ∥BC ,AC 平分BAF ∠,80B ∠=︒.求C ∠的度数.【解析】∵EF//BC∴∠BAF=180°-∠B=100°∵AC 平分∠BAF∴∠CAF=12∠BAF=50°∵EF//BC ,∠∠C=∠CAF=50°23.如图,直线a∠b,点B在直线b上,且AB∠BC,∠1=55°,求∠2的度数.【解析】:∠AB∠BC,∠∠1+∠3=90°.∠∠1=55°,∠∠3=35°.∠a∠b,∠∠2=∠3=35°.24.如图,直线AB∠CD,BC平分∠ABD,∠1=54°,求∠2的度数.【解析】:∠直线AB∠CD,∠∠1=∠3=54°,∠BC平分∠ABD,∠∠3=∠4=54°,∠∠2的度数为:180°﹣54°﹣54°=72°.四、证明题25.如图,点A、B、C、D在一条直线上,CE与BF交于点G,∠A=∠1,CE∠DF,求证:∠E=∠F.【证明】∠CE∠DF,∠∠ACE=∠D,∠∠A=∠1,∠180°﹣∠ACE﹣∠A=180°﹣∠D﹣∠1,又∠∠E=180°﹣∠ACE﹣∠A,∠F=180°﹣∠D﹣∠1,∠∠E=∠F.26.如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°,求证:AB∠CD.【证明1】:∠∠ACD=70°,∠ACB=60°,∠∠BCD=130°.∠∠ABC=50°,∠∠BCD+∠ABC=180°.∠AB∠CD.【证明2】:∠∠ABC=50°,∠ACB=60°,∠∠CAB=180°—50°—60°=70°.∠∠ACD=70°,∠∠CAB=∠ACD.∠AB∠CD.27.如图,AE与CD交于点O,∠A=50°,OC=OE,∠C=25°,求证:AB∠C D.【证明】∵OC=OE∴∠OEC=∠OCE∵∠C=25°∴∠OEC=∠OCE=25°∴∠DOE=∠OEC+∠OCE=25°+25°=50°∵∠A=50°∴AB//CD28.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.【解析】:OA∠BC,OB∠AC.∠∠1=50°,∠2=50°,∠∠1=∠2,∠OB∠AC,∠∠2=50°,∠3=130°,∠∠2+∠3=180°,∠OA∠BC.五、作图题29.如图,D是∠ABC中BC边上一点,∠C=∠DAC.(1)尺规作图:作∠ADB的平分线,交AB于点E(保留作图痕迹,不写作法);(2)在(1)的条件下,求证:DE∠AC.【解析】(1)如图,(2)证明:∠DE平分∠ADB,∠∠ADE=∠BDE,∠∠ADB=∠C+∠DAC,而∠C=∠DAC,∠2∠BDE=2∠C,即∠BDE=∠C,∠DE∠AC.六、探究题30. 如图(13),E是直线AB、CD内部一点,AB∠CD,连接EA、ED(1)探究猜想:∠若∠A=30°,∠D=40°,则∠AED等于多少度?∠若∠A=20°,∠D=60°,则∠AED等于多少度?∠猜想图(13)中∠AED、∠EAB、∠EDC的关系并证明你的结论.(2)拓展应用:如图(14),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,∠∠∠∠分别是被射线FE隔开的4个区域(不含边界,其中区域∠∠位于直线AB上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF的关系(不要求证明).【解析】:(1)∠∠AED=70° ∠∠AED=80° ∠∠AED=∠EAB+∠EDC证明:延长AE交DC于点F∠AB∠DC∠∠EAB=∠EFD又∠∠AED是∠EFD的外角∠∠AED=∠EDF+∠EFD=∠EAB+∠EDC(2)P点在区域∠时:∠EPF=3600 -(∠PEB+∠PFC)P点在区域∠时:∠EPF=∠PEB+∠PFCP点在区域∠时:∠EPF=∠PEB-∠PFCP点在区域∠时:∠EPF=∠PFC-∠PFB。
相交线与平行线常考题目及答案(绝对经典)

相交线与平行线一.选择题(共3小题)1.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直 D.无法确定2.如图,直线AB、CD相交于O,OE⊥AB,OF⊥CD,则与∠1互为余角的有()A.3个B.2个C.1个D.0个3.如图所示,同位角共有()A.6对B.8对C.10对D.12对二.填空题(共4小题)4.一块长方体橡皮被刀切了3次,最多能被分成块.5.如图,P点坐标为(3,3),l1⊥l2,l1、l2分别交x轴和y轴于A点和B点,则四边形OAPB的面积为.6.如图,直线l1∥l2,∠1=20°,则∠2+∠3= .7.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是.三.解答题(共43小题)8.已知:直线EF分别与直线AB,CD相交于点F,E,EM平∠FED,AB∥CD,H,P分别为直线AB 和线段EF上的点.(1)如图1,HM平分∠BHP,若HP⊥EF,求∠M的度数.(2)如图2,EN平分∠HEF交AB于点N,NQ⊥EM于点Q,当H在直线AB上运动(不与点F重合)时,探究∠FHE与∠ENQ的关系,并证明你的结论.9.我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多只有三个交点,那么,四条直线相交,最多有多少个交点?一般地,n条直线最多有多少个交点?说明理由.10.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数.(2)若∠EOC:∠EOD=4:5,求∠BOD的度数.11.如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,(1)若∠AOE=40°,求∠BOD的度数;(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?112.如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.(1)若∠ADQ=130°,求∠BED的度数;(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED 的度数(用含n的代数式表示).13.如图,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=26°(1)求∠2的度数(2)若∠3=19°,试判断直线n和m的位置关系,并说明理由.14.如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.15.如图,已知AB∥PN∥CD.(1)试探索∠ABC,∠BCP和∠CPN之间的数量关系,并说明理由;(2)若∠ABC=42°,∠CPN=155°,求∠BCP的度数.16.如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°(1)求证:AE∥CD;(2)求∠B的度数.17.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由.(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?直接写出结论.18.如图1,AB∥CD,在AB、CD内有一条折线EPF.(1)求证:∠AEP+∠CFP=∠EPF.(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,试探索∠EPF与∠EQF之间的关系.(3)如图3,已知∠BEQ=∠BEP,∠DFQ=∠DFP,则∠P与∠Q有什么关系,说明理由.(4)已知∠BEQ=∠BEP,∠DFQ=∠DFP,有∠P与∠Q的关系为.(直接写结论)19.如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.试卷第2页,总6页20.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.21.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.①则∠EOF= .(用含x的代数式表示)②求∠AOC的度数.22.如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.(1)求∠EOB的度数;(2)若OF平分∠AOE,问:OA是∠COF的角平分线吗?试说明理由.23.如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.(1)求∠BOE和∠AOE的度数;(2)若射线OF与OE互相垂直,请直接写出∠DOF的度数.24.如图,直线AB,CD相交于点O,OA平分∠EOC,且∠EOC:∠EOD=2:3.(1)求∠BOD的度数;(2)如图2,点F在OC上,直线GH经过点F,FM平分∠OFG,且∠MFH﹣∠BOD=90°,求证:OE ∥GH.25.如图,直线AB.CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=70°,求∠AOF的度数;(2)若∠BOD:∠BOE=1:2,求∠AOF的度数.26.几何推理,看图填空:(1)∵∠3=∠4(已知)∴∥()(2)∵∠DBE=∠CAB(已知)∴∥()(3)∵∠ADF+=180°(已知)∴AD∥BF()27.如图,直线AB、CD相交于点O,OE平分∠BOD.(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度数.28.将一副三角板拼成如图所示的图形,∠DCE的平分线CF交DE于点F.3(1)求证:CF∥AB.(2)求∠DFC的度数.29.看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?解:因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以∥().又因为AC⊥AE(已知),所以∠EAC=90°.()所以∠EAB=∠EAC+∠1=125°.同理可得,∠FBG=∠FBD+∠2= °.所以∠EAB=∠FBG().所以∥(同位角相等,两直线平行).30.已知如图所示,∠B=∠C,点B、A、E在同一条直线上,∠EAC=∠B+∠C,且AD平分∠EAC,试说明AD∥BC的理由.31.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;(1)直接写出图中∠AOC的对顶角为,∠BOE的邻补角为;(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.32.如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN 交CD于点F(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为;(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.33.阅读下面的推理过程,在括号内填上推理的依据,如图:因为∠1+∠2=180°,∠2+∠4=180°(已知)所以∠1=∠4,()所以a∥c.()又因为∠2+∠3=180°(已知)∠3=∠6()所以∠2+∠6=180°,()所以a∥b.()所以b∥c.()试卷第4页,总6页34.已知:如图,AB∥CD,FG∥HD,∠B=100°,FE为∠CEB的平分线,求∠EDH的度数.35.已知:如图,AB∥CD,FE⊥AB于G,∠EMD=134°,求∠GEM的度数.36.如图,∠B和∠D的两边分别平行.(1)在图1 中,∠B和∠D的数量关系是,在图2中,∠B和∠D的数量关系是;(2)用一句话归纳的命题为:;并请选择图1或图2中一种情况说明理由;(3)应用:若两个角的两边分别互相平行,其中一个角是另一个角的2倍,求这两个角的度数.37.已知AD∥BC,AB∥CD,E为射线BC上一点,AE平分∠BAD.(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°.①求证:∠ABC=∠ADC;②求∠CED的度数.38.如图,已知a∥b,ABCDE是夹在直线a,b之间的一条折线,试研究∠1、∠2、∠3、∠4、∠5的大小之间有怎样的等量关系?请说明理由.39.如图,AB∥DC,增加折线条数,相应角的个数也会增多,∠B,∠E,∠F,∠G,∠D之间又会有何关系?40.已知直线AB∥CD,(1)如图1,点E在直线BD上的左侧,直接写出∠ABE,∠CDE和∠BED之间的数量关系是.(2)如图2,点E在直线BD的左侧,BF,DF分别平分∠ABE,∠CDE,直接写出∠BFD和∠BED的数量关系是.(3)如图3,点E在直线BD的右侧BF,DF仍平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.41.(1)如图,直线a,b,c两两相交,∠3=2∠1,∠2=155°,求∠4的度数.(2)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,求∠AOF 的度数.42.如图,已知CD⊥DA,DA⊥AB,∠1=∠2.试说明DF∥AE.请你完成下列填空,把解答过程补充完整.解:∵CD⊥DA,DA⊥AB,∴∠CDA=90°,∠DAB=90°.()∴∠CDA=∠DAB.(等量代换)又∠1=∠2,从而∠CDA﹣∠1=∠DAB﹣.(等式的性质)即∠3= .5∴DF∥AE.().43.如图1,AB∥CD,EOF是直线AB、CD间的一条折线.(1)说明:∠O=∠BEO+∠DFO.(2)如果将折一次改为折二次,如图2,则∠BEO、∠O、∠P、∠PFC会满足怎样的关系,证明你的结论.(3)若将折线继续折下去,折三次,折四次…折n次,又会得到怎样的结论?请写出你的结论.44.如图,已知∠1=60°,∠2=60°,∠MAE=45°,∠FEG=15°,EG平分∠AEC,∠NCE=75°.求证:(1)AB∥EF.(2)AB∥ND.45.如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.求证:DF∥AB.46.已知,直线AB∥CD,E为AB、CD间的一点,连结EA、EC.(1)如图①,若∠A=30°,∠C=40°,则∠AEC= .(2)如图②,若∠A=100°,∠C=120°,则∠AEC= .(3)如图③,请直接写出∠A,∠C与∠AEC之间关系是.47.如图,已知AB∥CD,EF⊥AB于点G,若∠1=30°,试求∠F的度数.48.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:(1)请你计算出图1中的∠ABC的度数.(2)图2中AE∥BC,请你计算出∠AFD的度数.49.如图,将一张矩形纸片ABCD沿EF对折,延长DE交BF于点G,若∠EFG=50°,求∠1,∠2的度数.50.如图所示,在长方体中.(1)图中和AB平行的线段有哪些?(2)图中和AB垂直的直线有哪些?试卷第6页,总6页本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
专题02 《相交线与平行线》解答题、证明题重点题型分类(原卷版)

专题02 《相交线与平行线》解答题、证明题重点题型分类专题简介:本份资料专攻《相交线与平行线》中“利用平行线的性质求角”、“利用平行线的判定及性质证明平行”、“利用平行线的判定及性质证明角相等”、“平行线中构造平行线”解答题、证明题重点题型;适用于老师给学生作复习培训时使用或者考前刷题时使用。
考点1:利用平行线的性质求角方法点拨:题目中出现两直线平行的条件时,应立即想到平行线的三个性质,要注意分析图形特征,明确角与角的位置关系从而明确角与角之间的数量关系是相等还是互补。
平行线还通常会和角平分线、垂线等知识结合,求角的度数时需要根据已知条件综合利用角平分线、垂线的定义以及对顶角、领补角互补等性质求解!1.如图,已知:DE//BC,CD是∠ACB的平分线,∠B=80°,∠A=50°,求:∠EDC与∠BDC的度数.2.两个直角三角板如图摆放,其中∠BAC=∠EDF=90°,∠E=45°,∠C=30°,AB与DF交于点M,BC∥EF,求∠BMD的度数.3.如图所示,AB//CD,G为AB上方一点,E、F分别为AB、CD上两点,∠AEG=4∠GEB,∠CFG=2∠GFD,∠GEB和∠GFD的角平分线交于点H,求∠G+∠H的值.4.如图所示,AB//CD,点E为两条平行线外部一点,F为两条平行线内部一点,G、H分别为AB、CD上两点,GB平分∠EGF,HF平分∠EHD,且2∠F与∠E互补,求∠EGF的大小.5.如图,CD∥AB,点O在直线AB上,OE平分∠BOD,OF⊥OE,∠D=110°,求∠DOF的度数.6.小明同学遇到这样一个问题:如图①,已知:AB∥CD,E为AB、CD之间一点,连接BE,ED,得到∠BED.求证:∠BED=∠B+∠D.小亮帮助小明给出了该问的证明.证明:过点E作EF∥AB则有∠BEF=∠B∵AB∥CD∴EF∥CD∴∠FED=∠D∴∠BED=∠BEF+∠FED=∠B+∠D请你参考小亮的思考问题的方法,解决问题:(1)直线l1∥l2,直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,猜想:如图②,若点P在线段CD上,∠PAC=15°,∠PBD=40°,求∠APB的度数.(2)拓展:如图③,若点P在直线EF上,连接PA、PB(BD<AC),直接写出∠PAC、∠APB、∠PBD之间的数量关系.考点2:利用平行线的判定及性质证明平行方法点拨:“由角定线”,也就是根据某些角的相等或互补关系来判断两直线平行,解此类题目必须要掌握好平行线的判定方法。
相交线与平行线证明题

相交线与平行线证明题励志辅导班七相交线与平行线培优题1.已知:如图⑿,CE平分∠ACD,∠1=∠B,求证:AB ∥CE 2.如图:∠1=53?,∠2=127?,∠3=53?,试说明直线AB与CD,BC与DE的位置关系。
3. 如图:已知∠A=∠D,∠B=∠FCB,能否确定ED与CF的位置关系,请说明理。
4已知:如图,,,且. 求证:EC∥DF. 5如图10,∠1∶∠2∶∠3 = 2∶3∶4,∠AFE = 60°,∠BDE =120°,写出图中平行的直线,并说明理.A 1 E F 2 3 B D 图10 ?6.如图,已知AB//CD,?B?40,CN是?BCE 的平分线,CM?CN,求?BCM的度数。
C ABNMCDE 7.如图11,直线AB、CD被EF所截,∠1 =∠2,∠CNF =∠BME。
求证:AB∥CD,MP∥NQ. E M A 1 B P N C D 2 Q F 图11 8.已知:如图:∠AHF+∠FMD=180°,GH平分∠AHM,MN平分∠DMH。
求证:GH∥MN。
9.如图,已知:∠AOE+∠BEF=180°,∠AOE+∠CDE=180°,求证:CD∥BE。
10.如图,已知:∠A=∠1,∠C=∠2。
求证:求证:AB∥CD。
11.如图,AB//CD,AE平分?BAD,CD 与AE相交于F,?CFE??E。
求证:AD//BC A1D2FBCE 12.的相反数是________,绝对值等于的数是________,∣∣=_______。
13.的算术平方根是_______,=______。
14.____的平方根等于它本身,____的立方根等于它本身,____的算术平方根等于它本身。
15.已知∣x∣的算术平方根是8,那么x的立方根是_____。
16.填入两个和为6的无理数,使等式成立:___+___=6。
17.大于,小于的整数有______个。
18.若∣a∣=6,互为相反数,则a=______,b=_____。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 相交线与平行线证明填空
1.如图①,∵∠ = ∠ ∴AD ∥BC 。
( ) (写出一个正确的就可以) 2.如图,已知直线AB 、CD 被EF 所截,且∠EOB +∠DPF =180°.求证:AB ∥CD . 解法一:∵∠EOB +∠BOP =180°(已知),
∠EOB +∠DPF =180°(已知),
∴ ∠BOP =∠DPF (等量代换)
∴ ( ).
解法二:由图知∠EOB =∠POA ,∠CPO =∠DPF (对顶角相等),
∵ ∠EOB +∠DPF =180° (已知)
∴ (等量代换)
∴ AB ∥CD (同旁内角互补,两直线平行).
3、如图5,(1)∵∠A= (已知)
∴AC ∥ED( ) (2)∵∠2= (已知)
∴AC ∥ED( ) (3)∵∠A+ =180°(已知)
∴AB ∥FD( ) (4)∵AB ∥ (已知) ∴∠2+∠AED=180°( ) (5)∵AC ∥ (已知)
∴∠C=∠1( )
4.如图,已知:AB ∥EF ,AB ∥CD ,求证:∠DCE +∠E =180°.
证明∵ AB ∥EF ,AB ∥CD (已知),
∴ EF ∥CD ( )
∴ ( ).
5.如图,AB ∥DE ,求证∠B +∠E =∠BCE .
证明:过点C 作CF ∥AB ,
则B ∠=∠____( )
又∵AB ∥DE ,AB ∥CF ,
∴____________( )
∴∠E =∠____( )
∴∠B +∠E =∠1+∠2
即∠B +∠E =∠BCE .
6.如图,已知AB ∥CD ,∠1=∠2,求证EP ∥FQ .
证明:∵AB ∥CD ,
∴∠MEB =∠MFD ( )
A B C D E F 123图5
又∵∠1=∠2,
∴∠MEB -∠1=∠MFD -∠2,
即∠MEP =∠______
∴EP ∥_____.( )
7.如图,(1)已知∠1=∠2求证:a ∥b .
⑵直线//a b ,求证:12∠=∠.
8.已知:如图∠1=∠2,∠C =∠D ,问∠A 与∠F 相等吗试说明理由.
(第8题改编).已知;如图 2-87, DF//AC ,∠C =∠D ,求证:∠AMB=∠ENF。
