(四川专用)2020届高三数学大一轮复习 4.2 同角三角函数基本关系式及诱导公式同步检测 理
【志鸿优化设计】高考数学一轮总复习 4.2 同角三角函数的基本关系式及三角函数的诱导公式精品课件

+
关闭
si n 2 α
=18.
解析
答案
-13-
考点一 同角三角函数基本关系式的应用
【例 1】 已知 tan α= ,则 cos 2α+sin2α 的值为
1 4
.
关闭
cos 2α+sin α=1-2sin α+sin α=cos α=
16 17
2
2
2
2
co s 2 α
2 si n 2 α +co s 2 α 5
=
ta n 2 α -tan ������ ta n 2 α +1
= .
解析
答案
ห้องสมุดไป่ตู้12-
5.已知 sin(3π+α)=lg 为 .
1
3
10
,则
cos(π+������) cos(������-2π) + 的值 cos������[cos(π-������)-1] cos������cos(π-������)+cos(������-2π)
150° 5������ 6 1 2 3 2 3 3
180° π
270° 3������ 2 -1 0 不存
0 1
0 -1
tan α
0
0
在
-8-
基础自测
1.已知 cos(α-π)=- ,且 α 是第四象限角,则 sin α=( ) A.12 13 5 13
B.
12 13
C.±
12 13
D.
5 12
π 2
六
π 2
-α
+α
cos α sin α
cos α -sin α
高中数学人教版一轮复习课件:4.2 同角三角函数的基本关系及诱导公式

180°
π
0 -1 0
-5-
1 2 3 4 5
1.下列结论正确的打“ ”,错误的打“×”. (1)若 α,β 为锐角,则 sin2α+ cos2β=1. ( × ) (2)若 α∈R,则 tan α= (3)诱导公式的记忆口诀中“奇变偶不变,符号看象限” ,其中的 π 奇、偶是指 的奇数倍和偶数倍,变与不变指函数名称的变化. 2 ( ) (4)六组诱导公式中的角 α 可以是任意角. ( )
)
A.1+ 3 C.-1- 3
B.1- 3 D.-1+ 3
关闭
tan 300°+sin 450°=tan(360°-60°)+sin(360°+90°) =tan(-60°)+sin 90°=-tan 60°+1=1- 3.
关闭
B
解析 答案
-8-
1 2 3 4 5
4.(2015 广州调研)已知 sin A.2 5
B.-
1 5
5π + ������ 2 1 C. 5
=
1 ,那么 5 2 D. 5
cos α= (
)
关闭
∵sin
C
5π 2
+ ������ =sin
1
π 2
+ ������ =cos α,关闭Leabharlann ∴cos α=5.故选 C.
解析
答案
-9-
1 2 3 4 5
5.(教材习题改编P22T3)已知tan θ=2,则sin θcos θ=
4 sin������ cos������
2
=
2tan ������ -3 2×2-3 4tan ������ -9 4×2-9
2024版高考数学一轮总复习第4章三角函数第2节同角三角函数的基本关系与诱导公式课件

3
3 10
=-
.
2
2
10
3 +1
本例(2)条件不变,求cos θ的值.
解:由3sin +
π
2
+sin (θ+π)=0,可得3cos θ=sin θ,可得tan θ=
3.而θ∈(-π,0),可得sin θ<0.又tan θ=3>0,所以cos θ<0,所以cos
θ=-
1
32 +12
=-
10
.
10
思路参考:解方程组ቊ
sin2 + cos2 = 1.
sin2 + cos2 = 1,
解:由ቊ
消去cos x,
3cos + 4 sin = 5,
5π
解得θ= ,
12
5π
则符合题意的θ值可以为 .
12
π
(π-θ),所以θ+ =π-θ,
6
1.诱导公式的两个应用口诀
(1)求值:负化正,大化小,化到锐角就终了.
(2)化简:统一角,统一名,同角名少目的到.
2.角的变化的通式
特殊角±已知角=所求角.
1.下列各选项中与sin 2 022°最接近的是(
-tan α
口诀
函数名不变,符号看象限
五
六
函数名改变,
符号看象限
诱导公式的记忆口诀:“奇变偶不变,符号看象限.”其含义理解
为:
π
(1)所有诱导公式均可看作k· ±α(k∈Z)和α的三角函数值之间的关
2
系,口诀中的奇、偶指的是此处的k是奇数还是偶数,变与不变是指
三角函数名称的变化.
π
(2)结果的符号与把α当成锐角时角k· ±α(k∈Z)的三角函数值的符
2020年高考数学(文)一轮复习专题4.2 同角三角函数的基本关系及诱导公式(讲)(原卷版)

专题4.2同角三角函数的基本关系及诱导公式1.理解同角三角函数的基本关系式:sin2x+cos2x=1,sin xcos x=tan x.2.能利用单位圆中的三角函数线推导出π2±α,π±α的正弦、余弦、正切的诱导公式.知识点一同角三角函数的基本关系1.同角三角函数的基本关系(1)平方关系:sin2α+cos2α=1(α∈R).(2)商数关系:tanα≠kπ+π2,k∈2.同角三角函数基本关系式的应用技巧技巧解读适合题型切弦互化主要利用公式tanθ=sinθcosθ化成正弦、余弦,或者利用公式sinθcosθ=tanθ化成正切表达式中含有sinθ,cosθ与tanθ“1”的变换1=sin2θ+cos2θ=cos2θ(1+tan2θ)=(sinθ±cosθ)2∓2sinθcosθ=tanπ4表达式中需要利用“1”转化和积转换利用关系式(sinθ±cosθ)2=1±2sinθcosθ进行变形、转化表达式中含有sinθ±cosθ或sinθcosθ知识点二三角函数的诱导公式组数一二三四五六角2kπ+α(k∈Z)π+α-απ-απ2-απ2+α正弦sinα-sin_α-sin_αsin_αcos_αcos_α余弦cosα-cos_αcos_α-cos_αsin_α-sin_α正切tanαtan_α-tan_α-tan_α考点一三角函数的诱导公式【典例1】(广东省实验中学2018-2019学年高一下学期期末)角α的终边在直线2y x =上,则()()()()sin cos sin cos αππαπαπα-+-=+--()A .13B .1C .3D .1-【方法技巧】1.诱导公式的两个应用(1)求值:负化正,大化小,化到锐角为终了.(2)化简:统一角,统一名,同角名少为终了.2.含2π整数倍的诱导公式的应用由终边相同的角的关系可知,在计算含有2π的整数倍的三角函数式中可直接将2π的整数倍去掉后再进行运算,如cos(5π-α)=cos(π-α)=-cos α.3.三角形中的三角函数关系式sin(A +B )=sin(π-C )=sin C ;cos(A +B )=cos(π-C )=-cos C ;tan(A +B )=tan(π-C )=-tan C ;sin A 2+B 2sin π2-C 2cos C 2;cos A 2+B 2=cos π2-C 2sin C 2.【变式1】(甘肃省武威第一中学2018-2019学年质量检测)已知()()sin 22sin 3cos 5πααα-=+-,则tan α()A .6-B .6C .23-D .23考点二同角三角函数的基本关系及应用【典例2】(2019·高考全国卷Ⅱ)已知α∈0,π2,2sin 2α=cos 2α+1,则sin α=()A.15 B.55 C.33 D.255【方法技巧】同角三角函数关系式的应用方法(1)利用sin 2α+cos 2α=1可实现α的正弦、余弦的互化,利用sin αcos α=tan α可以实现角α的弦切互化.(2)由一个角的任一三角函数值可求出这个角的另外两个三角函数值,因为利用“平方关系”公式,需求平方根,会出现两解,需根据角所在的象限判断符号,当角所在的象限不明确时,要进行分类讨论.(3)应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.(4)注意公式逆用及变形应用:1=sin 2α+cos 2α,sin 2α=1-cos 2α,cos 2α=1-sin 2α.【变式2】(广东省深圳市高级中学2018-2019学年高一下学期期中)α是第三象限角,且sin -2α=,则tan α=()A .BC .-3D .33考点三同角三角函数的基本式和诱导公式的综合应用【典例3】(广东省海珠区2018-2019学年期末)已知sin cos 5x x +=,则cos 2=2x π⎛⎫- ⎪⎝⎭()A .725B .725-C .45D .45-【方法技巧】同角三角函数基本关系在求值与化简时,常用方法有(1)弦切互化法:主要利用公式tan x =sin x cos x 进行切化弦或弦化切,如a sin x +b cos x c sin x +d cos x,a sin 2x +b sin x cos x +c cos 2x 等类型可进行弦化切.(2)和积转换法:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α可以知一求二.(3)巧用“1”的变换:1=sin 2θ+cos 2θ=cos 2θ(1+tan 2θ)=sin 2θtan π4=….【变式3】(江西省吉安市2019届高三教学质量检测)已知()tan 2019πθ2-+=-,则ππθsin θ64⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭()A .2-B .15+C .35+D .35。
2020版高考数学一轮复习第四章三角函数、解三角形第2讲同角三角函数的基本关系与诱导公式课件理新人教A版

触类旁通 利用诱导公式化简求值的思路
(1)给角求值问题,关键是利用诱导公式把任意角的三角函数值转化为锐 角的三角函数值求解.转化过程中注意口诀“奇变偶不变,符号看象限”的 应用.
2在对给定的式子进行化简或求值时,要注意给定的角之间存在的特定 关系,充分利用给定的关系结合诱导公式来将角进行转化.特别要注意每一个 角所在的象限,防止搞错三角函数名称及符号.
解析
2.(2019·淮北模拟)sin43π·cos56π·tan-43π的值是________. 答案 -34 3
答案
解析 原式=sinπ+3π·cosπ-6π·tan-π-π3=-sinπ3·-cos6π·-tanπ3=
第2讲
同角三角函数的基本 关系与诱导公式
基础知识整合
1.同角三角函数的基本关系式
(1)平方关系:____□_0_1_s_in_2_α_+__co_s_2_α=__1_______.
(2)商数关系:__□0_2__ta_n_α_=__csoi_ns_αα____.
2.六组诱导公式
1.同角三角函数基本关系式的常用变形 (sinα±cosα)2=1±2sinαcosα; (sinα+cosα)2+(sinα-cosα)2=2; (sinα+cosα)2-(sinα-cosα)2=4sinαcosα. 2.诱导公式可简记为:奇变偶不变,符号看象限.
)
A.-
2 4
B.
2 4
C.-2 2 D.2 2
答案 C
答案
解析 由已知得 sinα=- 1-cos2α=- csoinsαα=-2 2,选 C.
1-19=-2 32,所以 tanα=
解析
3.已知 sin(π+θ)=- 3cos(2π-θ),|θ|<π2,则 θ 等于(
2023年高考数学一轮复习讲义——同角三角函数基本关系式及诱导公式
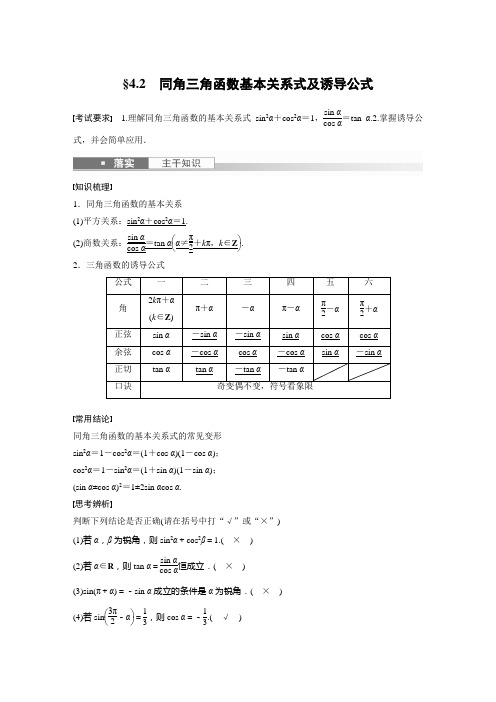
§4.2 同角三角函数基本关系式及诱导公式考试要求 1.理解同角三角函数的基本关系式sin 2α+cos 2α=1,sin αcos α=tan α.2.掌握诱导公式,并会简单应用.知识梳理1.同角三角函数的基本关系 (1)平方关系:sin 2α+cos 2α=1.(2)商数关系:sin αcos α=tan α⎝⎛⎭⎫α≠π2+k π,k ∈Z . 2.三角函数的诱导公式公式 一 二 三 四 五 六 角 2k π+α (k ∈Z ) π+α -α π-α π2-α π2+α 正弦 sin α -sin α -sin α sin α cos α cos α 余弦 cos α -cos α cos α -cos α sin α -sin α 正切 tan αtan α-tan α-tan α口诀奇变偶不变,符号看象限常用结论同角三角函数的基本关系式的常见变形 sin 2α=1-cos 2α=(1+cos α)(1-cos α); cos 2α=1-sin 2α=(1+sin α)(1-sin α); (sin α±cos α)2=1±2sin αcos α. 思考辨析判断下列结论是否正确(请在括号中打“√”或“×”) (1)若α,β为锐角,则sin 2α+cos 2β=1.( × ) (2)若α∈R ,则tan α=sin αcos α恒成立.( × )(3)sin(π+α)=-sin α成立的条件是α为锐角.( × ) (4)若sin ⎝⎛⎭⎫3π2-α=13,则cos α=-13.( √ )教材改编题1.已知α是第二象限角,sin α=55,则cos α的值为 . 答案 -255解析 ∵sin α=55,α是第二象限角, ∴cos α=-1-sin 2α=-255.2.已知sin α-2cos α3sin α+5cos α=-5,那么tan α的值为 .答案 -2316解析 由sin α-2cos α3sin α+5cos α=-5,知cos α≠0,等式左边分子、分母同时除以cos α,可得tan α-23tan α+5=-5,解得tan α=-2316.3.化简cos ⎝⎛⎭⎫α-π2sin ⎝⎛⎭⎫5π2+α·sin(α-π)·cos(2π-α)的结果为 . 答案 -sin 2α解析 原式=sin αcos α·(-sin α)·cos α=-sin 2α.题型一 同角三角函数基本关系例1 (1)已知cos α=-513,则13sin α+5tan α= .答案 0解析 ∵cos α=-513<0且cos α≠-1,∴α是第二或第三象限角. ①若α是第二象限角,则sin α=1-cos 2α=1-⎝⎛⎭⎫-5132=1213, ∴tan α=sin αcos α=1213-513=-125.此时13sin α+5tan α=13×1213+5×⎝⎛⎭⎫-125=0. ②若α是第三象限角, 则sin α=-1-cos 2α=-1-⎝⎛⎭⎫-5132 =-1213,∴tan α=sin αcos α=-1213-513=125,此时,13sin α+5tan α=13×⎝⎛⎭⎫-1213+5×125=0. 综上,13sin α+5tan α=0.(2)已知tan α=12,则sin α-3cos αsin α+cos α= ;sin 2α+sin αcos α+2= .答案 -53 135解析 已知tan α=12,所以sin α-3cos αsin α+cos α=tan α-3tan α+1=-53.sin 2α+sin αcos α+2 =sin 2α+sin αcos αsin 2α+cos 2α+2=tan 2α+tan αtan 2α+1+2=⎝⎛⎭⎫122+12⎝⎛⎭⎫122+1+2=135.(3)已知sin θ+cos θ=713,θ∈(0,π),则tan θ= .答案 -125解析 由sin θ+cos θ=713,得sin θcos θ=-60169,因为θ∈(0,π),所以sin θ>0,cos θ<0, 所以sin θ-cos θ=1-2sin θcos θ=1713, 联立⎩⎨⎧sin θ+cos θ=713,sin θ-cos θ=1713,解得⎩⎨⎧sin θ=1213,cos θ=-513,所以tan θ=-125.教师备选1.(2022·锦州联考)已知sin α+3cos α3cos α-sin α=5,则cos 2α+12sin 2α等于( )A.35 B .-35C .-3D .3答案 A解析 由sin α+3cos α3cos α-sin α=5,得tan α+33-tan α=5,可得tan α=2,则cos 2α+12sin 2α=cos 2α+sin αcos α=cos 2α+sin αcos αcos 2α+sin 2α=1+tan α1+tan 2α=35. 2.若α∈(0,π),sin(π-α)+cos α=23,则sin α-cos α的值为( ) A.23B .-23 C.43 D .-43答案 C解析 由诱导公式得sin(π-α)+cos α=sin α+cos α=23, 所以(sin α+cos α)2=1+2sin αcos α=29,则2sin αcos α=-79<0,因为α∈(0,π),所以sin α>0, 所以cos α<0,所以sin α-cos α>0, 因为(sin α-cos α)2=1-2sin αcos α=169,所以sin α-cos α=43.思维升华 (1)应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.(2)注意公式逆用及变形应用:1=sin 2α+cos 2α,sin 2α=1-cos 2α,cos 2α=1-sin 2α. 跟踪训练1 (1)(2021·新高考全国Ⅰ)若tan θ=-2,则sin θ(1+sin 2θ)sin θ+cos θ等于( )A .-65B .-25 C.25 D.65答案 C解析 方法一 因为tan θ=-2, 所以角θ的终边在第二或第四象限,所以⎩⎨⎧sin θ=25,cos θ=-15或⎩⎨⎧sin θ=-25,cos θ=15,所以sin θ(1+sin 2θ)sin θ+cos θ=sin θ(sin θ+cos θ)2sin θ+cos θ=sin θ(sin θ+cos θ) =sin 2θ+sin θcos θ =45-25=25.方法二 (弦化切法)因为tan θ=-2, 所以sin θ(1+sin 2θ)sin θ+cos θ=sin θ(sin θ+cos θ)2sin θ+cos θ=sin θ(sin θ+cos θ) =sin 2θ+sin θcos θsin 2θ+cos 2θ=tan 2θ+tan θ1+tan 2θ=4-21+4=25.(2)已知α是三角形的内角,且tan α=-13,则sin α+cos α的值为 .答案 -105解析 由tan α=-13,得sin α=-13cos α,将其代入sin 2α+cos 2α=1,得109cos 2α=1,所以cos 2α=910,易知cos α<0,所以cos α=-31010,sin α=1010,故sin α+cos α=-105. 题型二 诱导公式例2 (1)已知sin ⎝⎛⎭⎫α-π4=13,则cos ⎝⎛⎭⎫π4+α的值为( ) A.223B .-223C.13 D .-13答案 D解析 cos ⎝⎛⎭⎫π4+α=cos ⎣⎡⎦⎤π2+⎝⎛⎭⎫α-π4 =-sin ⎝⎛⎭⎫α-π4=-13.延伸探究 本例(1)改为已知θ是第二象限角,且sin ⎝⎛⎭⎫θ+π4=45,则tan ⎝⎛⎭⎫θ-π4= . 答案 34解析 ∵θ是第二象限角,且sin ⎝⎛⎭⎫θ+π4=45, ∴θ+π4为第二象限角,∴cos ⎝⎛⎭⎫θ+π4=-35, ∴tan ⎝⎛⎭⎫θ-π4=sin ⎝⎛⎭⎫θ-π4cos ⎝⎛⎭⎫θ-π4 =sin ⎣⎡⎦⎤⎝⎛⎭⎫θ+π4-π2cos ⎣⎡⎦⎤⎝⎛⎭⎫θ+π4-π2 =-cos ⎝⎛⎭⎫θ+π4sin ⎝⎛⎭⎫θ+π4=-⎝⎛⎭⎫-3545=34. (2)tan (π-α)cos (2π-α)sin ⎝⎛⎭⎫-α+3π2cos (-α-π)sin (-π-α)的值为( )A .-2B .-1C .1D .2 答案 B解析 原式=-tan α·cos α·(-cos α)cos (π+α)·[-sin (π+α)]=tan α·cos 2α-cos α·sin α =-sin αcos α·cos αsin α=-1.教师备选1.已知函数f (x )=a x -2+2(a >0且a ≠1)的图象过定点P ,且角α的始边与x 轴的正半轴重合,终边过点P ,则cos ⎝⎛⎭⎫11π2-αsin ⎝⎛⎭⎫9π2+α+sin 2αcos ⎝⎛⎭⎫π2+αsin (-π-α)等于( )A.23 B .-23C.32 D .-32答案 B解析 易知函数f (x )=a x -2+2(a >0且a ≠1)的图象过定点P (2,3), 故tan α=32,则cos ⎝⎛⎭⎫11π2-αsin ⎝⎛⎭⎫9π2+α+sin 2αcos ⎝⎛⎭⎫π2+αsin (-π-α)=cos ⎝⎛⎭⎫3π2-αsin ⎝⎛⎭⎫π2+α+sin 2αcos ⎝⎛⎭⎫π2+αsin α=-sin αcos α+2sin αcos α-sin αsin α=-cos αsin α=-1tan α=-23.2.若sin x =3sin ⎝⎛⎭⎫x -π2,则cos x ·cos ⎝⎛⎭⎫x +π2等于( ) A.310 B .-310C.34 D .-34答案 A解析 易知sin x =3sin ⎝⎛⎭⎫x -π2=-3cos x , 所以tan x =-3, 所以cos x cos ⎝⎛⎭⎫x +π2 =-sin x cos x =-sin x cos xsin 2x +cos 2xtan 2x +110思维升华 (1)诱导公式的两个应用①求值:负化正,大化小,化到锐角为终了; ②化简:统一角,统一名,同角名少为终了. (2)诱导公式的应用步骤任意负角的三角函数――――――→利用诱导公式三或一任意正角的三角函数――――――→利用诱导公式一0~2π内的角的三角函数――――――→利用诱导公式二或四或五或六锐角三角函数. 跟踪训练2 (1)已知cos(75°+α)=13,求cos(105°-α)+sin(15°-α)= .答案 0解析 因为(105°-α)+(75°+α)=180°, (15°-α)+(α+75°)=90°,所以cos(105°-α)=cos[180°-(75°+α)] =-cos(75°+α)=-13,sin(15°-α)=sin[90°-(α+75°)] =cos(75°+α)=13.所以cos(105°-α)+sin(15°-α)=-13+13=0.(2)(2022·盐城南阳中学月考)设tan(5π+α)=2,则sin (-3π+α)+cos (α-π)cos ⎝⎛⎭⎫α-112π+sin ⎝⎛⎭⎫9π2+α= .答案 3解析 由已知tan(5π+α)=tan α=2, sin (-3π+α)+cos (α-π)cos ⎝⎛⎭⎫α-112π+sin ⎝⎛⎭⎫9π2+α=sin (π+α)+cos (π-α)cos ⎝⎛⎭⎫α+π2+sin ⎝⎛⎭⎫π2+α-sin α+cos α=sin α+cos αsin α-cos α=tan α+1tan α-1=3. 题型三 同角三角函数基本关系式和诱导公式的综合应用 例3 已知f (α)=sin (α-3π)cos (2π-α)sin ⎝⎛⎭⎫-α+3π2cos (-π-α)sin (-π-α).(1)化简f (α);(2)若α=-31π3,求f (α)的值;(3)若cos ⎝⎛⎭⎫-α-π2=15,α∈⎣⎡⎦⎤π,3π2,求f (α)的值. 解 (1)f (α)=sin (α-3π)cos (2π-α)sin ⎝⎛⎭⎫-α+3π2cos (-π-α)sin (-π-α)=-sin α×cos α×(-cos α)-cos α×sin α=-cos α. (2)若α=-31π3,则f (α)=-cos ⎝⎛⎭⎫-31π3=-cos π3=-12. (3)由cos ⎝⎛⎭⎫-α-π2=15, 可得sin α=-15,因为α∈⎣⎡⎦⎤π,3π2, 所以cos α=-265,所以f (α)=-cos α=265.教师备选设f (α)=2sin (π+α)cos (π-α)-cos (π+α)1+sin 2α+cos ⎝⎛⎭⎫3π2+α-sin 2⎝⎛⎭⎫π2+α(1+2sin α≠0). (1)化简f (α);(2)若α=-23π6,求f (α)的值. 解 (1)f (α)=(-2sin α)·(-cos α)-(-cos α)1+sin 2α+sin α-cos 2α=2sin αcos α+cos α2sin 2α+sin α=cos α(2sin α+1)sin α(2sin α+1)=cos αsin α=1tan α. (2)当α=-23π6时, f (α)=f ⎝⎛⎭⎫-23π6=1tan ⎝⎛⎭⎫-23π6 =1tan ⎝⎛⎭⎫-4π+π6 =1tan π6=133= 3. 思维升华 (1)利用同角三角函数关系式和诱导公式求值或化简时,关键是寻求条件、结论间的联系,灵活使用公式进行变形.(2)注意角的范围对三角函数符号的影响.跟踪训练3 (1)(2022·聊城模拟)已知α为锐角,且2tan(π-α)-3cos ⎝⎛⎭⎫π2+β+5=0,tan(π+α)+6sin(π+β)-1=0,则sin α的值是( )A.355B.377C.31010D.13答案 C解析 由已知得⎩⎪⎨⎪⎧3sin β-2tan α+5=0,tan α-6sin β-1=0. 消去sin β,得tan α=3,∴sin α=3cos α,代入sin 2α+cos 2α=1,化简得sin 2α=910,则sin α=31010(α为锐角). (2)已知-π<x <0,sin(π+x )-cos x =-15,则sin 2x +2sin 2x 1-tan x= . 答案 -24175解析 由已知,得sin x +cos x =15, 两边平方得sin 2x +2sin x cos x +cos 2x =125, 整理得2sin x cos x =-2425. ∴(sin x -cos x )2=1-2sin x cos x =4925, 由-π<x <0知,sin x <0,又sin x cos x =-1225<0, ∴cos x >0,∴sin x -cos x <0,故sin x -cos x =-75. ∴sin 2x +2sin 2x 1-tan x =2sin x (cos x +sin x )1-sin x cos x=2sin x cos x (cos x +sin x )cos x -sin x=-2425×1575=-24175.课时精练1.cos ⎝⎛⎭⎫-19π3等于( ) A .-32 B .-12 C.12D.32 答案 C解析 cos ⎝⎛⎭⎫-19π3=cos 19π3=cos ⎝⎛⎭⎫6π+π3=cos π3=12. 2.若cos 165°=a ,则tan 195°等于( )A.1-a 2B.1-a 2aC .-1-a 2aD .-a 1-a 2 答案 C解析 若cos 165°=a ,则cos 15°=cos(180°-165°)=-cos 165°=-a ,sin 15°=1-a 2,所以tan 195°=tan(180°+15°)=tan 15°=sin 15°cos 15°=-1-a 2a. 3.若cos ⎝⎛⎭⎫α-π5=513,则sin ⎝⎛⎭⎫7π10-α等于( ) A .-513B .-1213 C.1213 D.513答案 D解析 因为7π10-α+⎝⎛⎭⎫α-π5=π2,所以7π10-α=π2-⎝⎛⎭⎫α-π5,所以sin ⎝⎛⎭⎫7π10-α=cos ⎝⎛⎭⎫α-π5=513.4.(2022·天津西青区模拟)已知sin α+cos α=-2,则tan α+1tan α等于() A .2 B.12 C .-2 D .-12答案 A解析 由已知得1+2sin αcos α=2,∴sin αcos α=12,∴tan α+1tan α=sin αcos α+cos αsin α=sin 2α+cos 2αsin αcos α=112=2.5.(多选)在△ABC 中,下列结论正确的是( )A .sin(A +B )=sin CB .sin B +C 2=cos A 2C .tan(A +B )=-tan C ⎝⎛⎭⎫C ≠π2D .cos(A +B )=cos C答案 ABC解析 在△ABC 中,有A +B +C =π,则sin(A +B )=sin(π-C )=sin C ,A 正确.sin B +C 2=sin ⎝⎛⎭⎫π2-A 2=cos A 2,B 正确.tan(A +B )=tan(π-C )=-tan C ⎝⎛⎭⎫C ≠π2,C 正确.cos(A +B )=cos(π-C )=-cos C ,D 错误.6.(多选)已知α∈(0,π),且sin α+cos α=15,则( ) A.π2<α<π B .sin αcos α=-1225C .cos α-sin α=75D .cos α-sin α=-75答案 ABD解析 ∵sin α+cos α=15, 等式两边平方得(sin α+cos α)2=1+2sin αcos α=125, 解得sin αcos α=-1225,故B 正确; ∵α∈(0,π),sin αcos α=-1225<0, ∴α∈⎝⎛⎭⎫π2,π,故A 正确;cos α-sin α<0,且(cos α-sin α)2=1-2sin αcos α=1-2×⎝⎛⎭⎫-1225=4925, 解得cos α-sin α=-75,故D 正确. 7.cos 1°+cos 2°+cos 3°+…+cos 177°+cos 178°+cos 179°= .答案 0解析 因为cos(180°-α)=-cos α,于是得cos 1°+cos 2°+cos 3°+…+cos 89°+cos 90°+cos 91°+…+cos 177°+cos 178°+cos 179° =cos 1°+cos 2°+cos 3°+…+cos 89°+cos 90°-cos 89°-…-cos 3°-cos 2°-cos 1° =cos 90°=0.8.设f (θ)=2cos 2θ+sin 2(2π-θ)+sin ⎝⎛⎭⎫π2+θ-32+2cos 2(π+θ)+cos (-θ),则f ⎝⎛⎭⎫17π3= . 答案 -512解析 ∵f (θ)=2cos 2θ+sin 2θ+cos θ-32+2cos 2θ+cos θ=cos 2θ+cos θ-22cos 2θ+cos θ+2,又cos 17π3=cos ⎝⎛⎭⎫6π-π3=cos π3=12,∴f ⎝⎛⎭⎫17π3=14+12-212+12+2=-512.9.(1)已知cos α是方程3x 2-x -2=0的根,且α是第三象限角,求sin ⎝⎛⎭⎫-α+3π2cos ⎝⎛⎭⎫3π2+αtan 2(π-α)cos ⎝⎛⎭⎫π2+αsin ⎝⎛⎭⎫π2-α的值;(2)已知sin x +cos x =-713(0<x <π),求cos x -2sin x 的值.解 (1)因为方程3x 2-x -2=0的根为x 1=1,x 2=-23,又α是第三象限角,所以cos α=-23,所以sin α=-53,tan α=52.所以原式=-cos αsin αtan 2α-sin αcos α=tan 2α=54.(2)∵sin x +cos x =-713(0<x <π),∴cos x <0,sin x >0,即sin x -cos x >0,把sin x +cos x =-713,两边平方得1+2sin x cos x =49169, 即2sin x cos x =-120169, ∴(sin x -cos x )2=1-2sin x cos x =289169, 即sin x -cos x =1713, 联立⎩⎨⎧ sin x +cos x =-713,sin x -cos x =1713,解得sin x =513,cos x =-1213, ∴cos x -2sin x =-2213. 10.(2022·衡水模拟)已知角α的终边经过点P (3m ,-6m )(m ≠0).(1)求sin (α+π)+cos (α-π)sin ⎝⎛⎭⎫α+π2+2cos ⎝⎛⎭⎫α-π2的值; (2)若α是第二象限角,求sin 2⎝⎛⎭⎫α+3π2+sin(π-α)cos α-cos ⎝⎛⎭⎫π2+α的值. 解 (1)∵m ≠0,∴cos α≠0,即sin (α+π)+cos (α-π)sin ⎝⎛⎭⎫α+π2+2cos ⎝⎛⎭⎫α-π2 =-sin α-cos αcos α+2sin α=-tan α-11+2tan α. 又∵角α的终边经过点P (3m ,-6m )(m ≠0),∴tan α=-6m 3m=-2, 故sin (α+π)+cos (α-π)sin ⎝⎛⎭⎫α+π2+2cos ⎝⎛⎭⎫α-π2=-tan α-11+2tan α =2-11+2×(-2)=-13. (2)∵α是第二象限角,∴m <0,则sin α=-6m (3m )2+(-6m )2 =-6m 35|m | =255, cos α=3m(3m )2+(-6m )2 =3m 35|m | =-55, ∴sin 2⎝⎛⎭⎫α+3π2+sin(π-α)cos α-cos ⎝⎛⎭⎫π2+α =cos 2α+sin αcos α+sin α=⎝⎛⎭⎫-552+255×⎝⎛⎭⎫-55+255=-1+255.11.(多选)已知角α满足sin α·cos α≠0,则表达式sin (α+k π)sin α+cos (α+k π)cos α(k ∈Z )的取值可能为( )A .-2B .-1或1C .2D .-2或2或0答案 AC解析 当k 为奇数时,原式=-sin αsin α+-cos αcos α=(-1)+(-1)=-2;当k 为偶数时,原式=sin αsin α+cos αcos α=1+1=2. ∴原表达式的取值可能为-2或2.12.(2022·河北六校联考)若sin α是方程5x 2-7x -6=0的根,则sin ⎝⎛⎭⎫-α-3π2sin ⎝⎛⎭⎫3π2-αtan 2(2π-α)cos ⎝⎛⎭⎫π2-αcos ⎝⎛⎭⎫π2+αsin (π+α)等于( )A.35B.53C.45D.54答案 B解析 方程5x 2-7x -6=0的两根为x 1=-35,x 2=2,则sin α=-35. 原式=cos α(-cos α)tan 2αsin α(-sin α)(-sin α)=-1sin α=53. 13.曲线y =e x +x 2-23x 在x =0处的切线的倾斜角为α,则sin ⎝⎛⎭⎫2α+π2= . 答案 45解析 由题意得y ′=f ′(x )=e x +2x -23, 所以f ′(0)=e 0-23=13, 所以tan α=13, 所以α∈⎝⎛⎭⎫0,π2, 所以cos α=310, 所以sin ⎝⎛⎭⎫2α+π2 =cos 2α=2cos 2α-1=2×910-1=45. 14.函数y =log a (x -3)+2(a >0且a ≠1)的图象过定点Q ,且角α的终边也过点Q ,则3sin 2α+2sin αcos α= .答案 75解析 由题意可知点Q (4,2),所以tan α=12, 所以3sin 2α+2sin αcos α=3sin 2α+2sin αcos αsin 2α+cos 2α =3tan 2α+2tan α1+tan 2α=3×14+2×121+14=75.15.(多选)已知f (α)=2sin αcos α-2sin α+cos α+1⎝⎛⎭⎫0≤α≤π2,则下列说法正确的是() A .f (α)的最小值为- 2B .f (α)的最小值为-1C .f (α)的最大值为2-1D .f (α)的最大值为1- 2答案 BD解析 设t =sin α+cos α=2sin ⎝⎛⎭⎫α+π4,由0≤α≤π2,得π4≤α+π4≤3π4,则1≤t ≤2,又由(sin α+cos α)2=t 2,得2sin αcos α=t 2-1,所以f (α)=g (t )=t 2-1-2t +1=t -1-2t +1,又因为函数y =t -1和y =-2t +1在[1,2]上单调递增,所以g (t )=t -1-2t +1在[1,2]上单调递增, g (t )min =g (1)=-1,g (t )max =g (2)=1- 2.16.已知关于x 的方程2x 2-(3+1)x +m =0的两根分别是sin θ和cos θ,θ∈(0,2π),求:(1)sin 2θsin θ-cos θ+cos θ1-tan θ的值; (2)m 的值;(3)方程的两根及此时θ的值.解 (1)原式=sin 2θsin θ-cos θ+cos θ1-sin θcos θ=sin 2θsin θ-cos θ+cos 2θcos θ-sin θ=sin 2θ-cos 2θsin θ-cos θ=sin θ+cos θ.由已知得sin θ+cos θ=3+12, 所以sin 2θsin θ-cos θ+cos θ1-tan θ=3+12. (2)由已知得sin θcos θ=m 2, 因为1+2sin θcos θ=(sin θ+cos θ)2,所以1+m =⎝⎛⎭⎪⎫3+122, 解得m =32. (3)联立⎩⎪⎨⎪⎧ sin θ+cos θ=3+12,sin θcos θ=34,解得⎩⎨⎧ sin θ=32,cos θ=12 或⎩⎨⎧ sin θ=12,cos θ=32.因为θ∈(0,2π),所以θ=π3或π6.。
2020版高考数学新增分大一轮新高考第四章 4.2 同角三角函数基本关系式及诱导公式 Word版含解析

§同角三角函数基本关系式及诱导公式
最新考纲.理解同角三角函数的基本关系式:+=,=..借助单位圆中的三角函数线推导出±α,π±α的正弦、余弦、正切的诱导公式.
.同角三角函数的基本关系
()平方关系:α+α=.
()商数关系:=α.
.三角函数的诱导公式
公式一二三四五六
角π+α(∈) π+α-απ-α-α+α
正弦α-α-αααα
余弦α-αα-αα-α
正切αα-α-α
口诀函数名不变,符号看象限函数名改变,符号看象限
概念方法微思考
.使用平方关系求三角函数值时,怎样确定三角函数值的符号?
提示根据角所在象限确定三角函数值的符号.
.诱导公式记忆口诀:“奇变偶不变,符号看象限”中的奇、偶是何意义?
提示所有诱导公式均可看作·±α(∈)和α的三角函数值之间的关系,口诀中的奇、偶指的是此处的是奇数还是偶数.
题组一思考辨析
.判断下列结论是否正确(请在括号中打“√”或“×”)
()若α,β为锐角,则α+β=.(×)
()若α∈,则α=恒成立.(×)
()(π+α)=-α成立的条件是α为锐角.(×)
()若(π-α)=(∈),则α=.(×)
题组二教材改编
.若α=,<α<π,则α=.
答案-
解析∵<α<π,
∴α=-=-,
∴α==-.
.已知α=,则的值为.
答案
解析原式===.。
2020版高考数学一轮复习第四章三角函数、解三角形第二节同角三角函数的基本关系与诱导公式教案理(含解析)

第二节 同角三角函数的基本关系与诱导公式1.同角三角函数的基本关系式 (1)平方关系: sin 2α+cos 2α=1; (2)商数关系: tan α=sin αcos α.2.诱导公式[小题体验]1.已知sin ⎝ ⎛⎭⎪⎫π2+α=35,α∈⎝⎛⎭⎪⎫0,π2,则sin(π+α)=______.答案:-452.若sin θcos θ=12,则tan θ+cos θsin θ的值为________.答案:21.利用诱导公式进行化简求值时,先利用公式化任意角的三角函数为锐角三角函数,其步骤:去负—脱周—化锐.特别注意函数名称和符号的确定.2.在利用同角三角函数的平方关系时,若开方,要特别注意判断符号. 3.注意求值与化简后的结果一般要尽可能有理化、整式化. [小题纠偏]1.(2019·盐城期中)已知tan(π-α)=34,α是第四象限角,则sin α=________.解析:因为tan(π-α)=34,所以tan α=-34,因为sin 2α+cos 2α=1,α是第四象限角, 所以sin α=-35.答案:-352.化简:1-π+π+=________.解析:原式=1-2sin 2cos 2=|sin 2-cos 2|,因为sin 2>0,cos 2<0,所以原式=sin 2-cos 2.答案:sin 2-cos 2考点一 三角函数的诱导公式基础送分型考点——自主练透 [题组练透]1.(2019·启东调研)sin 4π3·cos 5π6·tan ⎝ ⎛⎭⎪⎫-4π3的值是________. 解析:原式=sin ⎝ ⎛⎭⎪⎫π+π3·cos ⎝ ⎛⎭⎪⎫π-π6·tan ⎝ ⎛⎭⎪⎫-π-π3=-sin π3·⎝ ⎛⎭⎪⎫-cos π6·⎝ ⎛⎭⎪⎫-tan π3=-32×⎝ ⎛⎭⎪⎫-32×(-3)=-334.答案:-3342.(2018·镇江中学测试)求值:sin 26π3+cos ⎝⎛⎭⎪⎫-17π4=________.解析:sin 26π3+cos ⎝ ⎛⎭⎪⎫-17π4=sin ⎝ ⎛⎭⎪⎫9π-π3+cos ⎝ ⎛⎭⎪⎫4π+π4=sin ⎝ ⎛⎭⎪⎫π-π3+cos π4=sin π3+ cos π4=3+22.答案:3+223.已知tan ⎝ ⎛⎭⎪⎫π6-α=33,则tan ⎝ ⎛⎭⎪⎫5π6+α=________.解析:tan ⎝ ⎛⎭⎪⎫5π6+α=tan ⎝ ⎛⎭⎪⎫π-π6+α=tan ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫π6-α=-tan ⎝ ⎛⎭⎪⎫π6-α=-33.答案:-334.(易错题)设f (α)=π+απ-α-π+α1+sin 2α+cos ⎝ ⎛⎭⎪⎫3π2+α-sin 2⎝ ⎛⎭⎪⎫π2+α⎝ ⎛⎭⎪⎫sin α≠-12,则f ⎝ ⎛⎭⎪⎫-23π6=________.解析:因为f (α)=-2sin α-cos α+cos α1+sin 2α+sin α-cos 2α=2sin αcos α+cos α2sin 2α+sin α =cosα+2sin αsinα+2sin α=1tan α, 所以f ⎝ ⎛⎭⎪⎫-23π6=1tan ⎝ ⎛⎭⎪⎫-23π6 =1tan ⎝⎛⎭⎪⎫-4π+π6=1tan π6= 3. 答案: 3[谨记通法]1.利用诱导公式把任意角的三角函数转化为锐角三角函数的步骤也就是:“负化正,大化小,化到锐角就好了.” 2.利用诱导公式化简三角函数的要求 (1)化简过程是恒等变形;(2)结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值. 考点二 同角三角函数的基本关系重点保分型考点——师生共研 [典例引领]1.(2019·昆山一模)已知α∈⎝⎛⎭⎪⎫0,π2,tan α=3,则sin 2α+2sin αcos α=________.解析:∵α∈⎝⎛⎭⎪⎫0,π2,tan α=3,∴sin 2α+2sin αcos α=sin 2α+2sin αcos αsin 2α+cos 2α=tan 2α+2tan αtan 2α+1=9+69+1=32. 答案:322.若sin θ,cos θ是方程4x 2+2mx +m =0的两个根,则m =________. 解析:由题意得sin θ+cos θ=-m 2,sin θ·cos θ=m4,又(sin θ+cos θ)2=1+2sin θ·cos θ,所以m 24=1+m2,解得m =1±5,又Δ=4m 2-16m ≥0,解得m ≤0或m ≥4,所以m =1- 5. 答案:1- 5[由题悟法]同角三角函数基本关系式的应用技巧[即时应用]1.若sin α=-513,且α为第四象限角,则tan α=________.解析:法一:因为α为第四象限的角,故cos α=1-sin 2α= 1-⎝ ⎛⎭⎪⎫-5132=1213, 所以tan α=sin αcos α=-5131213=-512.法二:因为α是第四象限角,且sin α=-513,所以可在α的终边上取一点P (12,-5),则tan α=y x =-512.答案:-5122.(2019·苏州调研)已知sin θ+cos θ=15,θ∈(0,π),则tan θ的值为________.解析:∵sin θ+cos θ=15,①两边平方,得1+2sin θcos θ=125,∴2sin θcos θ=-2425,又θ∈(0,π),∴sin θ>0,cos θ<0, ∵(sin θ-cos θ)2=1-2sin θcos θ=4925,∴sin θ-cos θ=75,②由①②得sin θ=45,cos θ=-35.∴tan θ=-43.答案:-43考点三 同角三角函数关系与诱导公式的综合应用题点多变型考点——多角探明 [锁定考向]同角三角函数关系与诱导公式一般不单独考查,常相结合命题,主要考查三角函数值的计算.常见的命题角度有: (1)由同角关系求值;(2)由角的三角函数值求值; (3)由角的关系式求值.[题点全练]角度一:由同角关系求值1.(2018·玄武高中检测)已知sin α是方程5x 2-7x -6=0的根,α是第三象限角,则sin ⎝ ⎛⎭⎪⎫-α-3π2sin ⎝ ⎛⎭⎪⎫3π2-αtan 3αcos ⎝ ⎛⎭⎪⎫π2-αcos ⎝ ⎛⎭⎪⎫π2+α=________.解析:由已知得sin α=-35.因为α是第三象限角,所以cos α=-1-sin 2α=-45.所以原式=cos α-cos α⎝ ⎛⎭⎪⎫sin αcos α3sin α-sin α=sin αcos α=34.答案:34角度二:由角的三角函数值求值2.(2018·启东调研)如图,A ,B 是单位圆O 上的点,且B 在第二象限,C 是圆与x 轴的正半轴的交点,A 点的坐标为⎝ ⎛⎭⎪⎫513,1213,∠AOB =90°.(1)求cos ∠COA ; (2)求tan ∠COB .解:(1)因为A 点的坐标为⎝ ⎛⎭⎪⎫513,1213, 根据三角函数的定义可得cos ∠COA =513.(2)因为∠AOB =90°,sin ∠COA =1213,所以cos ∠COB =cos(∠COA +90°)=-sin ∠COA =-1213.又点B 在第二象限,所以sin ∠COB =1-cos 2∠COB =513,故tan ∠COB =sin ∠COB cos ∠COB =-512.角度三:由角的关系式求值3.(2019·滨海模拟)已知角θ的终边与单位圆x 2+y 2=1在第四象限交于点P ,且点P的坐标为⎝ ⎛⎭⎪⎫12,y .(1)求tan θ的值;(2)求cos ⎝ ⎛⎭⎪⎫π2-θ+θ-2πsin θ+π+θ的值.解:(1)由θ为第四象限角,终边与单位圆交于点P ⎝ ⎛⎭⎪⎫12,y , 得⎝ ⎛⎭⎪⎫122+y 2=1,y <0,解得y =-32.∴tan θ=-3212=- 3.(2)∵tan θ=-3,∴cos ⎝ ⎛⎭⎪⎫π2-θ+θ-2πsin θ+π+θ=sin θ+cos θsin θ-cos θ=tan θ+1tan θ-1=-3+1-3-1=2- 3. [通法在握]求值问题的一般解题步骤(1)将已知条件或所求式子利用诱导公式进行化简; (2)从已知条件中结合三角函数关系得出需要的结论; (3)代入化简后的所求式子,得出最后的结论.[演练冲关](2019·镇江中学测试)已知sin(π-α)-cos(π+α)=23,⎝ ⎛⎭⎪⎫π2<α<π.求下列各式的值:(1)sin α-cos α;(2)sin 2⎝ ⎛⎭⎪⎫π2-α-cos 2⎝ ⎛⎭⎪⎫π2+α.解:(1)由sin(π-α)-cos(π+α)=23, 得sin α+cos α=23.① 将①式两边平方,得1+2sin αcos α=29.所以2sin αcos α=-79.又π2<α<π,所以sin α>0,cos α<0,所以sin α-cos α>0, 所以(sin α-cos α)2=(sin α+cos α)2-4sin αcos α=29+149=169,所以sin α-cos α=43.(2)sin 2⎝ ⎛⎭⎪⎫π2-α-cos 2⎝ ⎛⎭⎪⎫π2+α=cos 2α-sin 2α=(cos α-sin α)(cos α+sin α)=43×23=429.一抓基础,多练小题做到眼疾手快1.若α∈⎝ ⎛⎭⎪⎫-π2,π2,sin α=-35,则cos(-α)=________.解析:因为α∈⎝ ⎛⎭⎪⎫-π2,π2,sin α=-35,所以cos α=45,即cos(-α)=45.答案:452.(2019·镇江调研)已知α是第二象限角,cos ⎝ ⎛⎭⎪⎫π2-α=45,则tan α=________.解析:∵α是第二象限角,cos ⎝ ⎛⎭⎪⎫π2-α=sin α=45, ∴cos α=-1-sin 2α=-35,则tan α=sin αcos α=-43.答案:-433.(2018·江苏百校联盟)已知倾斜角为α的直线l 与直线x +2y -3=0垂直,则cos ⎝⎛⎭⎪⎫2 019π2-2α=________. 解析:由题意可得tan α=2, 所以cos ⎝⎛⎭⎪⎫2 019π2-2α=-sin 2α=-2sin αcos αsin 2α+cos 2α=-2tan αtan 2α+1=-45.答案:-454.(2018·扬州期末)若点P (3cos θ,sin θ)在直线l :x +y =0上,则tan θ=________.解析:∵点P (3cos θ,sin θ)在直线l :x +y =0上, 即3cos θ+sin θ=0, ∴sin θ=-3cos θ, ∴tan θ=sin θcos θ=-3.答案:-35.如果sin(π+A )=12,那么cos ⎝ ⎛⎭⎪⎫3π2-A 的值是________.解析:因为sin(π+A )=12,所以-sin A =12.所以cos ⎝ ⎛⎭⎪⎫3π2-A =-sin A =12. 答案:126.若sin θ+cos θ=23,则tan θ+1tan θ=________.解析:由sin θ+cos θ=23,得1+2sin θcos θ=49,即sin θcos θ=-518,则tan θ+1tan θ=sin θcos θ+cos θsin θ=1sin θcos θ=-185.答案:-185二保高考,全练题型做到高考达标1.(2019·启东中学高三检测)已知α∈⎝ ⎛⎭⎪⎫π2,3π2,tan(α-π)=-34,则sin α+cos α的值是________.解析:已知tan(α-π)=tan α=-34,又α∈⎝ ⎛⎭⎪⎫π2,3π2,所以sin α=35,cos α=-45,所以sin α+cos α=-15.答案:-152.已知sin ⎝ ⎛⎭⎪⎫α-π4=13,则cos ⎝ ⎛⎭⎪⎫π4+α=________.解析:因为cos ⎝⎛⎭⎪⎫π4+α=sin ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π4+α=sin ⎝ ⎛⎭⎪⎫π4-α=-sin ⎝ ⎛⎭⎪⎫α-π4=-13. 答案:-133.(2018·如东中学调研)若f (x )=sin ⎝ ⎛⎭⎪⎫π2x +α+1,且f (2 018)=2,则f (2 019)=________.解析:因为f (2 018)=sin ⎝ ⎛⎭⎪⎫π2×2 018+α+1=sin(1 009π+α)+1=-sin α+1=2,所以 sin α=-1,cos α=0.所以f (2 019)=sin ⎝ ⎛⎭⎪⎫π2×2 019+α+1=sin ⎝ ⎛⎭⎪⎫1 009π+π2+α+1=-cos α+1=1.答案:14.(2019·苏州调研)当θ为第二象限角,且sin ⎝ ⎛⎭⎪⎫θ2+π2=13时,1-sin θcos θ2-sinθ2=________.解析:因为sin ⎝⎛⎭⎪⎫θ2+π2=13,所以cos θ2=13,所以θ2在第一象限,且cos θ2<sin θ2,所以1-sin θcos θ2-sin θ2=-⎝ ⎛⎭⎪⎫cos θ2-sin θ2cos θ2-sinθ2=-1.答案:-15.计算:cos 350°-2sin 160°-=________.解析:原式=----+=cos 10°----sin 10=cos 10°-2⎝ ⎛⎭⎪⎫12cos 10°-32sin 10°sin 10°= 3. 答案: 36.已知sin(3π-α)=-2sin ⎝ ⎛⎭⎪⎫π2+α,则sin αcos α=______. 解析:因为sin(3π-α)=-2sin ⎝ ⎛⎭⎪⎫π2+α, 所以sin α=-2cos α, 所以tan α=-2,所以sin αcos α=sin αcos αsin 2α+cos 2α =tan αtan 2α+1=-2-2+1=-25. 答案:-257.已知α为第二象限角,则cos α1+tan 2α+sin α1+1tan 2α=________. 解析:原式=cos αsin 2α+cos 2αcos 2α+sin α sin 2α+cos 2αsin 2α=cos α·1|cos α|+sin α·1|sin α|,因为α是第二象限角,所以sin α>0,cos α<0,所以原式=cos α-cos α+sin αsin α=-1+1=0.答案:08.(2019·淮安调研)若tan α+1tan α=52,α∈⎝ ⎛⎭⎪⎫π4,π2,则π-2α-sin 2⎝ ⎛⎭⎪⎫π2+α-2α+1+sin 2α的值为________.解析:∵tan α+1tan α=52,α∈⎝ ⎛⎭⎪⎫π4,π2, ∴tan α=2或tan α=12(舍去),∴π-2α-sin 2⎝⎛⎭⎪⎫π2+α-2α+1+sin 2α=sin 2α-cos 2αcos 2α+1+sin 2α=cos αα-cos α2cos 2α+sin 2α=2tan α-12+tan 2α=12. 答案:129.(2019·如东模拟)(1)化简:sin2α+πα+π-α-2πα+π3⎝ ⎛⎭⎪⎫π2+α-α-2π;(2)已知cos ⎝ ⎛⎭⎪⎫π6-θ=a ,求cos ⎝ ⎛⎭⎪⎫5π6+θ+sin ⎝ ⎛⎭⎪⎫2π3-θ的值.解:(1)原式=sin 2α-cos ααtan α·cos 3α-sin α=1. (2)∵cos ⎝ ⎛⎭⎪⎫π6-θ=a ,∴cos ⎝ ⎛⎭⎪⎫5π6+θ+sin ⎝⎛⎭⎪⎫2π3-θ=-cos ⎝ ⎛⎭⎪⎫π6-θ+sin ⎝ ⎛⎭⎪⎫π3+θ=-a +cos ⎝ ⎛⎭⎪⎫π6-θ =-a +a =0.10.已知-π2<α<0,且函数f (α)=cos ⎝ ⎛⎭⎪⎫3π2+α-sin α·1+cos α1-cos α-1.(1)化简f (α);(2)若f (α)=15,求sin αcos α和sin α-cos α的值.解:(1)f (α)=sin α-sin α·+cos α21-cos 2α-1=sin α+sin α·1+cos αsin α-1=sin α+cos α.(2)法一:由f (α)=sin α+cos α=15,平方可得sin 2α+2sin αcos α+cos 2α=125, 即2sin αcos α=-2425.所以sin αcos α=-1225.因为()sin α-cos α2=1-2sin αcos α=4925, 又-π2<α<0,所以sin α<0,cos α>0,所以sin α-cos α<0,所以sin α-cos α=-75.法二:联立方程⎩⎪⎨⎪⎧sin α+cos α=15,sin 2α+cos 2α=1,解得⎩⎪⎨⎪⎧sin α=-35,cos α=45或⎩⎪⎨⎪⎧sin α=45,cos α=-35.因为-π2<α<0,所以⎩⎪⎨⎪⎧sin α=-35,cos α=45.所以sin αcos α=-1225,sin α-cos α=-75.三上台阶,自主选做志在冲刺名校 1.(2018·淮安高三期中)已知sin α=cos 2π5,0<α<π,则α的取值集合为________.解析:由sin α=cos ⎝ ⎛⎭⎪⎫π2-α,得cos ⎝ ⎛⎭⎪⎫π2-α=cos 2π5,因为0<α<π,所以-π2<π2-α<π2,所以π2-α=±2π5,所以α=π10或9π10,所以α的取值集合为⎩⎨⎧⎭⎬⎫π10,9π10.答案:⎩⎨⎧⎭⎬⎫π10,9π102.(2019·通州模拟)如图是由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若直角三角形中较小的内角为θ,大正方形的面积是1,小正方形的面积是125,则sin 2θ-cos 2θ的值是________.解析:由图可知,每个直角三角形的长直角边为cos θ,短直角边为sin θ,小正方形的边长为cos θ-sin θ,∵小正方形的面积是125,∴(cos θ-sin θ)2=125,又θ为直角三角形中较小的锐角, ∴cos θ>sin θ,∴cos θ-sin θ=15.又(cos θ-sin θ)2=1-2sin θcos θ=125,∴2sin θcos θ=2425.∴(cos θ+sin θ)2=1+2sin θcos θ=4925,∴cos θ+sin θ=75.∴sin 2θ-cos 2θ=(sin θ-cos θ)(cos θ+sin θ) =-15×75=-725.答案:-7253.已知f (x )=cos2n π+x2n π-xcos2n +π-x ](n ∈Z).(1)化简f (x )的表达式;(2)求f ⎝ ⎛⎭⎪⎫π2 018+f ⎝ ⎛⎭⎪⎫504π1 009的值.解:(1)当n 为偶数,即n =2k (k ∈Z)时, f (x )=cos 2k π+x2k π-xcos2k +π-x ]=cos 2x ·sin 2-xcos 2π-x =cos 2x -sin x 2-cos x 2=sin 2x ;当n 为奇数,即n =2k +1(k ∈Z)时, f (x )=cos 2k +π+x ]·sin 2k +π-x ]cos2k ++1]π-x }=cos 2[2k π+π+x 2[2k π+π-x cos 2k +π+π-x=cos2π+x2π-xcos 2π-x=-cos x 2sin 2x -cos x 2=sin 2x , 综上得f (x )=sin 2x .(2)由(1)得f ⎝ ⎛⎭⎪⎫π2 018+f ⎝ ⎛⎭⎪⎫504π1 009=sin 2π2 018+sin 21 008π2 018 =sin 2π2 018+sin 2⎝ ⎛⎭⎪⎫π2-π2 018 =sin 2π2 018+cos 2π2 018=1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.2 同角三角函数基本关系式及诱导公式
一、选择题
1. cos ⎝
⎛⎭⎪⎫-20π3=( )
A.12
B.32 C .-12 D .-32
解析 cos ⎝ ⎛⎭⎪⎫-20π3=cos ⎝ ⎛⎭⎪⎫6π+2π3=cos 2π3=cos ⎝ ⎛⎭⎪⎫π-π3=-cos π3=-12,故选C.
答案 C
2. 若tan α=3,则2
sin 2cos a
α
的值等于( ) A .2 B .3
C .4
D .6
解析 因为2sin 2cos a α=22sin cos cos a
αα
=2tan 6α=,所以选D.
答案 D
3.若cos(2π-α)=53且α∈⎝ ⎛⎭
⎪⎫-π2,0,则sin(π-α)=( ). A .-
53 B .-23 C .-13 D .±23
解析 cos(2π-α)=cos α=
53,又α∈⎝ ⎛⎭⎪⎫-π2,0,
∴sin α=-1-cos 2
α=-1-⎝
⎛⎭
⎪⎫532
=-23. ∴sin(π-α)=sin α=-2
3.
答案 B
4.若角α的终边落在直线x +y =0上,则sin α
1-sin 2
α+1-cos 2
α
cos α的值等于( ). A .-2 B .2 C .-2或2 D .0
解析 原式=sin α|cos α|+|sin α|
cos α,由题意知角α的终边在第二、四象限,sin α与cos α
的符号相反,所以原式=0. 答案 D
5.已知sin 2α=-2425,α∈⎝ ⎛⎭⎪⎫-π4,0,则sin α+cos α=( )
A .-15 B.1
5
C .-75 D.75
解析:(sin α+cos α)2
=1+2sin αcos α=1+sin 2α=125
,
又α∈⎝ ⎛⎭
⎪⎫-π4,0,sin α+cos α>0, 所以sin α+cos α=1
5.
答案:B
6.已知f (cos x )=cos 3x ,则f (sin 30°)的值为( ). A .0 B .1 C .-1 D.32
解析 ∵f (cos x )=cos 3x ,
∴f (sin 30°)=f (cos 60°)=cos 180°=-1. 答案 C
7.若sin θ,cos θ是方程4x 2
+2mx +m =0的两根,则m 的值为
( ).
A .1+ 5
B .1- 5
C .1± 5
D .-1- 5 解析 由题意知:sin θ+cos θ=-m 2,sin θcos θ=m
4,
又(sin θ+cos θ)2
=1+2sin θcos θ, ∴m 24=1+m
2
,
解得:m =1±5,又Δ=4m 2
-16m ≥0, ∴m ≤0或m ≥4,∴m =1- 5. 答案 B 二、填空题
8.若sin(π+α)=-12,α∈⎝ ⎛⎭⎪⎫π2,π,则cos α=________.
解析 ∵sin(π+α)=-sin α,∴sin α=12,又α∈⎝ ⎛⎭⎪⎫π2,π,
∴cos α=-1-sin 2
α=-32
. 答案 -
3
2
9.已知cos α=-5
13
,且α是第二象限的角,则tan(2π-α)=________.
解析 由α是第二象限的角,得sin α=1-cos 2
α=1213,tan α=sin αcos α=-125
,则tan(2π
-α)=-tan α=12
5
.
答案 125
10.已知α为第二象限角,则cos α1+tan 2
α+sin α1+1
tan 2α
=________. 解析:原式=cos α1+sin 2
α
cos 2α
+sin α1+cos 2
αsin 2α
=cos α1
cos 2
α+sin α 1sin 2
α=cos α1-cos α+sin α1
sin α
=0. 答案:0
11.已知sin αcos α=18,且π4<α<π
2,则cos α-sin α的值是________.
解析 (sin α-cos α)2
=1-2sin αcos α=34
,
又∵π4<α<π2,sin α>cos α.∴cos α-sin α=-32.
答案 -
3
2
12.已知sin α=12+cos α,且α∈⎝ ⎛⎭⎪⎫0,π2,则cos 2αsin ⎝ ⎛⎭⎪⎫α-π4的值为________.
解析 依题意得sin α-cos α=1
2
,又(sin α+cos α)2+(sin α-cos α)2=2,即(sin
α+cos α)2+⎝ ⎛⎭
⎪⎫122=2,故(sin α+cos α)2=74
;又α∈⎝
⎛⎭
⎪⎫
0,π2
,因此有sin α+cos α
=72,所以cos 2αsin ⎝ ⎛⎭⎪⎫α-π4=cos 2α-sin 2
α22sin α-cos α=-2(sin α+cos α)=-142. 答案 -14
2
三、解答题
13.已知sin α=255,求tan(α+π)+sin ⎝ ⎛⎭
⎪
⎫5π2+αcos ⎝
⎛⎭
⎪⎫5π2-α的值.
解析 ∵sin α=25
5>0,∴α为第一或第二象限角.
当α是第一象限角时,cos α=1-sin 2
α=
55
, tan(α+π)+sin ⎝ ⎛⎭
⎪
⎫5π2+αcos ⎝ ⎛⎭
⎪⎫5π2-α=tan α+cos αsin α
=sin αcos α+cos αsin α=1sin αcos α=52
. 当α是第二象限角时,cos α=-1-sin 2
α=-55
, 原式=1sin αcos α=-5
2.
14.已知1+tan π+α
1+tan 2π-α=3+22,
求cos 2
(π-α)+sin ⎝
⎛⎭⎪⎫3π2+α·cos ⎝ ⎛⎭
⎪
⎫π2+α+2sin 2(α-π)的值.
解析:由已知得1+tan α
1-tan α=3+22,
∴tan α=2+224+22=1+22+2=2
2.
∴cos 2
(π-α)+sin ⎝
⎛⎭⎪⎫3π2+αcos ⎝ ⎛⎭
⎪
⎫π2+α+2sin 2(α-π)
=cos 2α+(-cos α)(-sin α)+2sin 2
α =cos 2
α+sin αcos α+2sin 2
α =cos 2
α+sin αcos α+2sin 2
α
sin 2α+cos 2
α =1+tan α+2tan 2
α1+tan 2
α =1+22+1
1+12
=4+23.
15.化简:sin k π-αcos[k -1π-α]
sin[k +1π+α]cos k π+α(k ∈Z).
解析 当k =2n (n ∈Z)时,
原式=sin 2n π-αcos[2n -1π-α]sin[2n +1π+α]cos 2n π+α
=sin -α·cos -π-αsin π+α·cos α=-sin α-cos α-sin α·cos α=-1;
当k =2n +1(n ∈Z)时,
原式=sin[2n +1π-α]·cos[2n +1-1π-α]sin[2n +1+1π+α]·cos[2n +1π+α]
=sin π-α·cos αsin α·cos π+α=sin α·cos αsin α-cos α=-1. 综上,原式=-1.
16.已知关于x 的方程2x 2
-(3+1)x +m =0的两根sin θ和cos θ,θ∈(0,2π),求: (1)sin 2
θsin θ-cos θ+cos θ1-tan θ的值; (2)m 的值;
(3)方程的两根及此时θ的值.
解析 (1)原式=sin 2
θsin θ-cos θ+cos θ
1-
sin θ
cos θ
=sin 2
θsin θ-cos θ+cos 2θcos θ-sin θ =sin 2
θ-cos 2
θsin θ-cos θ=sin θ+cos θ. 由条件知sin θ+cos θ=
3+1
2
, 故sin 2
θsin θ-cos θ+cos θ1-tan θ=3+1
2
. (2)由sin 2
θ+2sin θcos θ+cos 2
θ=1+2sin θcos θ =(sin θ+cos θ)2
,得1+m =⎝
⎛⎭
⎪⎫3+122
,即m =32.
(3)由
⎩⎪⎨⎪⎧
sin θ+cos θ=3+1
2,sin θ·cos θ=34
得
⎩⎪⎨⎪⎧
sin θ=3
2,cos θ=12
或
⎩⎪⎨⎪
⎧
sin θ=12
,
cos θ=32
.
π6或θ=
π
3
.
又θ∈(0,2π),故θ=。
