初三数学综合复习题(一)
初三数学综合测试卷及答案

一、选择题(每题3分,共30分)1. 下列各数中,有理数是()A. √16B. √-9C. πD. 0.1010010001……2. 已知等腰三角形底边长为8cm,腰长为10cm,则其面积为()A. 32cm²B. 40cm²C. 48cm²D. 80cm²3. 下列函数中,一次函数是()A. y = 2x² - 3x + 1B. y = √x + 1C. y = 2x + 3D. y = 3/x4. 已知一元二次方程x² - 5x + 6 = 0,则其解为()A. x₁ = 2, x₂ = 3B. x₁ = 3, x₂ = 2C. x₁ = 6, x₂ = 1D. x₁ = 1, x₂ = 65. 在平面直角坐标系中,点A(2,3)关于原点的对称点是()A.(-2,-3)B.(2,-3)C.(-2,3)D.(3,-2)6. 下列各组数中,成等差数列的是()A. 1,4,7,10B. 2,5,8,11C. 3,6,9,12D. 4,7,10,137. 若直角三角形的两条直角边长分别为3cm和4cm,则斜边长为()A. 5cmB. 6cmC. 7cmD. 8cm8. 下列命题中,正确的是()A. 若a > b,则a² > b²B. 若a > b,则ac > bcC. 若a > b,则a² > b²D. 若a > b,则ac > bc9. 已知正方形的边长为a,则其对角线长为()A. aB. √2aC. 2aD. a√210. 在等腰三角形ABC中,若底边BC=8cm,腰AB=AC=10cm,则三角形ABC的周长为()A. 24cmB. 26cmC. 28cmD. 30cm二、填空题(每题4分,共40分)11. 分数 3/4 与 -1/2 的差是 ________。
初三数学总复习《数与式》单元测试 (一),含答案

单 元 测 试 (一) [测试范围:第一单元(数与式) 时间:45分钟 分值:100分] 一、选择题(每题3分,共36分) 1.49的平方根为( )A .7B .-7C .±7D .±7 2.计算:(-1)2017-(π-3.14)0=( ) A .-2 B .2 C .1 D .03.在实数:3.14159,364,1.010010001,4.2·1·,π,227中,无理数有( )A .1个B .2个C .3个D .4个4.4月份全省旅游住宿接待游客约27700000人,将27700000用科学记数法表示为( ) A .0.277×107 B .0.277×108 C .2.77×107 D .2.77×108 5.下列等式一定成立的是( )A .a 2·a 5=a 10B .a +b =a + bC .(-a 3)6=a 18D .a 2=a 6.下列运算正确的是( )A .|-3|=3B .-⎝⎛⎭⎫-12=-12 C .(a 2)3=a 5 D .2a ·3a =6a 7.定义[a ]表示不大于a 的最大整数,如[3.8]=3,则⎣⎢⎡⎦⎥⎤19+32=( )A .2B .3C .4D .5 8.下列计算正确的是( )A .(-p 2q )3=-p 5q 3B .(12a 2b 3c )÷(6ab 2)=2abC .3m 2-(3m -1)=3m 2-3m -1D .(x 2-4x )÷x =x -49.化简⎝⎛⎭⎫1+4a -2÷aa -2的结果是( ) A .a +2a B .a a +2 C .a -2a D .aa -210.实数a ,b 在数轴上对应点的位置如图D1-1所示,则化简|a |+(a -b )2的结果是( )A .-2a +bB .2a -bC .-bD .B 图D1-1 11.[2016·重庆B 卷] 观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星, 图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形⑧中五角星的颗数是( )A .43B .45C .51D .12.将一组数3,6,3,2 3,6,3,2 3,15;3 2,21,2 6,3 3,30; …若2 3的位置记为(1,4),2 6的位置记为(2,3),则这组数中最大的有理数的位置记为( ) A .(5,2) B .(5,3) C .(6,2) D .(6,5) 二、填空题(每题4分,共28分)13.代数式3x 3-6x 2y +3xy 2分解因式为____________. 14.当x =________时,分式x 2-4x +2的值为零. 15.若等式⎝⎛⎭⎫x 3-20=1成立,则x 的取值范围是___________.16.计算:(348-227)÷3=________. 17.若m 为正实数,m 2-3m -1=0,则m 2-1m 2=________. 18.当a =2+1,b =2-1时,代数式a 2-2ab +b 2a 2-b 2的值是________.19.若||6-3m +(n -5)2=3m -6-(m -3)n 2,则m -n =________. 三、解答题(共36分)20.(7分)[2016·内江] 计算:|-3|+3·tan30°-38-(2016-π)0+(12)-1.21.(7分)[2016·宁夏] 化简求值:(a a +2+1a 2-4)÷a -1a +2+1a -2,其中a =2+ 2.22.(10分)观察与探究:某礼堂共有25排座位,第一排有20个座位,后面每一排比前一排多1个座位,写出第25排的座位数. 在以上其他条件不变的情况下,请探究下列问题:(1)当后面每一排都比前一排多2个座位时,写出第n 排的座位数;(2)当后面每一排都比前一排多3个座位时,4个座位时,分别写出第n 排的座位数;(3)若共有P 排座位,第一排有a 个座位,后面每一排都比前一排多b 个座位,试写出第n 排的座位数.23.(12分)阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方, 如3+2 2=(1+2)2.善于思考的小明进行了以下探索:设a +b 2=(m +n 2)2(其中a ,b ,m ,n 均为整数),则有a +b 2=m 2+2n 2+2mn 2, ∴a =m 2+2n 2,b =2mn .这样小明就找到了一种把类似a +b 2的式子化为平方式的方法. 请你仿照小明的方法探索并解决下列问题:(1)当a ,b ,m ,n 均为正整数时,若a +b 3=(m +n 3)2,用含m ,n 的式子分别表示a ,b , 得a =________,b =________;(2)利用探索结论,找一组正整数a ,b ,m ,n 填空:______+______×3=(______+______×3)2; (3)若a +4 3=(m +n 3)2,且a ,m ,n 均为正整数,求a 的值.参考答案1.C 2.A3.A [解析] 364=4,根据无理数的定义可知本题中只有π是无理数. 4.C 5.C 6.A 7.B 8.D 9.A10.A [解析] 由数轴可知a <0,b >0,a <b ,∴a -b <0,|a |=-a ,(a -b )2=b -a ,∴|a |+(a -b )2=-a +b -a =-2a +b .故选A.11.C [解析] 第①个图形中共有1+1=2(颗)星;第②个图形中共有1+2+3=6(颗)星,第③个图形中共有1+2+3+5=11(颗)星,…,按此规律可知,第⑧个图形中五角星的颗数为1+2+3+…+8+15=51(颗).故选C.12.C13.3x (x -y )2 [解析] 先提取公因式,再用完全平方公式.14.2 [解析] 分式的值为零的条件是分子为零,且分母不为零.15.x ≥0且x ≠12 [解析] 依题意,得⎩⎨⎧x3≥0,x3-2≠0,所以x ≥0且x ≠12.16.6 [解析] 原式=(12 3-6 3)÷3=6 3÷3=6.17.3 13 [解析] 由m 2-3m -1=0,得m -1m=3,所以⎝⎛⎭⎫m +1m 2=⎝⎛⎭⎫m -1m 2+4=32+4=13,所以m +1m=13,则m 2-1m 2=⎝⎛⎭⎫m +1m ⎝⎛⎭⎫m -1m =3 13. 18.22 [解析] a 2-2ab +b 2a 2-b 2=(a -b )2(a +b )(a -b )=a -b a +b,当a =2+1,b =2-1时,原式=2+1-(2-1)2+1+2-1=22 2=22,故答案为22.19.-2 [解析] 依题意有(m -3)n 2≥0,所以m -3≥0, 所以3m -6+(n -5)2=3m -6-(m -3)n 2, 所以(n -5)2+(m -3)n 2=0,所以⎩⎪⎨⎪⎧n -5=0,(m -3)n 2=0,所以⎩⎪⎨⎪⎧m =3,n =5, 所以m -n =-2.20.解:原式=3+3×33-2-1+2=3+1-2-1+2=3.21.解:(a a +2+1a 2-4)÷a -1a +2+1a -2=[a (a -2)(a +2)(a -2)+1(a +2)(a -2)]·a +2a -1+1a -2 =(a -1)2(a +2)(a -2)·a +2a -1+1a -2 =a -1+1a -2=a a -2. 当a =2+2时,原式=2+1.22.解:第一排的座位数:20+0,第二排的座位数:20+1, 第三排的座位数:20+2, …第n 排的座位数:20+(n -1),∴第25排有20+(25-1)=44(个)座位.(1)当后面每一排都比前一排多2个座位时,第n 排的座位数是20+2(n -1)=2n +18. (2)当后面每一排都比前一排多3个座位时,第n 排的座位数是20+3(n -1)=3n +17. 当后面每一排都比前一排多4个座位时,第n 排的座位数是20+4(n -1)=4n +16. (3)每一排都比前一排多出b 个座位,∴第n 排多出b (n -1)个座位, ∴第n 排的座位数是a +b (n -1). 23.解:(1)∵a +b 3=(m +n 3)2, ∴a +b 3=m 2+3n 2+2mn 3, ∴a =m 2+3n 2,b =2mn . 故答案为m 2+3n 2,2mn .(2)答案不唯一:如设m =1,n =1, 则a =m 2+3n 2=4,b =2mn =2. 故答案为4,2,1,1.(3)由题意得a =m 2+3n 2,b =2mn , ∴4=2mn ,且m ,n 为正整数, ∴m =2,n =1或m =1,n =2,∴a =22+3×12=7或a =12+3×22=13.。
专题01 一元二次方程(解析版)-2020-2021学年九年级数学上册期末综合复习专题提优训练

2020-2021学年九年级数学上册期末综合复习专题提优训练(人教版)专题01 一元二次方程【典型例题】1.(2020·青浦区实验中学期中)下列方程中,关于x 的一元二次方程是( )A .3(x +1)2=2(x +1)B .21x +1x-2=0 C .ax 2+bx +c =0 D .x 2+2x =x 2-1 【答案】A2.(2020·山东泗水初三期中)若()11620m m x mx +++-=是关于x 的一元二次方程,则m =________.【答案】1【专题训练】一、选择题1.(2020·湖南湘潭初三期末)已知关于x 的一元二次方程2240x ax -+=的一个根是2,则a 的值为( )A .-1B .1C .-2D .2 【答案】D2.(2020·山东东平期末)下列方程中一定是一元二次方程的是( )A .22731x y -=+B .25620x y --= C .22x x x x -=+ D .()2320ax b x c +-++=【答案】C3.(2020·安徽安庆期末)若x =2是关于x 的一元二次方程x 2-mx +8=0的一个解.则m 的值是( )A .6B .5C .2D .-6【答案】A4.(2019·四川雁江初三期末)如果关于x 的方程27(3)30m m x x ---+=是一元二次方程,那么m 的值为:( ) A .3± B .3 C .-3 D .都不是【答案】C5.(2020·安徽蚌埠期末)一元二次方程4x 2﹣1=5x 的二次项系数、一次项系数、常数项分别为( ) A .4,﹣1,5 B .4,﹣5,﹣1 C .4,5,﹣1 D .4,﹣1,﹣5【答案】B6.(2020·四川米易初三期末)已知a 是方程22430x x --=的一个根,则代数式224a a -的值等于( )A .3B .2C .0D .1 【答案】A7.(2020·安徽铜陵初三期末)已知关于 x 的方程20x ax b ++=有一个根是(0)b b ≠,则a b +的值是( ) A .-1 B .0 C .12 D .1 【答案】A8.(2020·全国初三课时练习)已知m 是方程23220x x --=的值( )A .2BC D【答案】C9.(2019·贵州印江初三期末)将一元二次方程22(1)1(1)2x x x +-=+-写成一般形式_____.【答案】2330x x ++=10.(2020·湖南雨花期末)已知方程ax 2+bx +c =0的一个根是﹣1,则a ﹣b +c =_____.【答案】011.(2020·银川市第十五中学初三一模)关于x 的一元二次方程(m -1)x 2+6x +m 2-m =0的一个根x =0,则m 的值是_____.【答案】012.(2020·贵州印江初三期末)若关于x 的方程||(m 2)m 20m x x --+=为一元二次方程,则m =__________.【答案】-213.(2020·全国初三课时练习)下列方程中,①7x 2+6=3x ;②212x =7;③x 2﹣x =0;④2x 2﹣5y =0;⑤﹣x 2=0中是一元二次方程的有_____. 【答案】①③⑤.14.(2020·全国初三课时练习)把一元二次方程(x ﹣2)2﹣x =7x +6化为一般形式是_____,二次项系数是_____,一次项是_____,常数项是_____.【答案】x 2﹣12x ﹣2=0 1 ﹣12x ﹣215.(2020·河北初三二模)若m 是方程2x 2﹣3x ﹣1=0的一个根,则6m 2﹣9m +2020的值为_____.【答案】202316.(2020·南宁市新民中学初三期中)若关于x 的一元二次方程22(1)410a x x a --+-=的一根是0,则a =___________. 【答案】-117.(2019·全国初二单元测试)把关于x 的方程()()()23x x x -=化成一元二次方程的一般形式,并写出方程中各项与各项的系数. 【答案】解:原方程整理得226918x x x -+=-∴22690x x∴各项与各项的系数分别为:二次项22x ,二次项系数2;一次项-6x ,一次项系数-6;常数项-9.18.(2020·安徽天长龙集九年制学校期中)关于x 的方程27(3)5m m x x ---=是一元二次方程,求m 的值.【答案】解:关于x 的方程27(3)5m m x x ---=是一元二次方程,依题意有,27230m m ⎧-=⎨-≠⎩∴m =-3∴当m =-3时方程27(3)5m m x x ---=是一元二次方程.19.(2018·陕西洛南)如果关于x 的方程(m ﹣3)x |m ﹣1|﹣x +3=0是一元二次方程,求m 的值.【答案】由题意,得|m ﹣1|=2且m ﹣3≠0.解得m =﹣3.即m 的值是﹣3.20.(2020·全国初三课时练习)已知m 是方程x 2-x -2=0的一个实数根,求代数式()221m m m m ⎛⎫--+ ⎪⎝⎭的值. 【答案】解:∵m 是方程x 2-x -2=0的根,∴m 2-m -2=0,即m 2-m =2,m 2-2=m .∴()()222221121224m m m m m m m m m m ⎛⎫-⎛⎫⎛⎫--+=-+=+=⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.21.(2020·全国初三课时练习)若m 是一元二次方程||120a x x ---=的一个实数根. (1)求a 的值;(2)不解方程,求代数式()221m m m m ⎛⎫-⋅-+ ⎪⎝⎭的值. 【答案】(1)由于||120a x x ---=是关于x 的一元二次方程, 所以||12a -=,解得3a =±;(2)由(1)知,该方程为220x x --=, 把x =m 代入,得220m m --=,所以22m m -=,①由220m m --=,得210m m --=, 所以21m m-=,② 把①和②代入()221m m m m ⎛⎫-⋅-+ ⎪⎝⎭, 得()2212(11)4m m m m ⎛⎫-⋅-+=⨯+= ⎪⎝⎭, 即()2214m m m m ⎛⎫-⋅-+= ⎪⎝⎭.。
初三数学综合试题一10732

1
24、问渠那得清如许,为有源头活水来——朱熹
24、问渠那得清如许,为有源头活水来——朱熹 初三数学综合试题一 第一部分(100分) 一、 填空题(24分,每空2分) 1、当k___时,关于x的方程(k+1)x2+2x+3=0是一元二次方程 2、方程x(x+2)=3(x+2) 的根是______ 3、函数y=中自变量x的取值范围是_____ 4、点P的坐标为(3,-4),则点P关于原点的对称点P1的坐标是_____ 5、抛物线y=-x2-5的顶点坐标是________ 6、在Rt△ABC中,∠C=900,, tanA=,则cosA=_______ C B 7、圆内接四边形ABCD中,∠A:∠B:∠C=2:3:4,则∠D=____度 8、AB为⊙O的直径,弦CD⊥AB于M,AM=4,BM=9,则弦CD=_______ 9、若两圆共有三条公切线,则两圆的位置关系是______ A P 10、如图,PA切⊙O于A,∠PAB=500,∠ABC=700,则∠BAC=_______度 (图10) 11、已知外切两圆半径分别为6和2,则两圆的外公切线长等于________ 12、已知⊙O的半径为6cm,⊙O的一条弦AB的长为6cm,则弦AB所对的圆周角的度 数是____ 二、 选择题(24分) 13、一元二次方程x2+x-3=0的根的情况是 ( ) B、有两个相等的实数根 A、有两个不相等的实数根 C、没有实数根 D、不能确定 14、如果点P(a,b)在第四象限,则点P1(-b,-a)所在的象限是 ( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限 15、Rt△ABC中,∠C=900,a,b分别为∠A,∠B的对边,若sinA:sinB=2:3,则a:b= ( ) A、2:3 B、3:2 C、4:9 D 、9:4 16、直线y=-4x+3不经过的象限是 ( ) A、第一象限 B第二象限 C、第三象限 D、第四象限 17、如图,PA,PB切⊙O于A、B,C是优弧AB上的点,∠C=640,则∠P等于 ( ) A A、 260 B、620 P C
初三下学期期末数学综合复习资料(一)-初中三年级数学试题练习、期中期末试卷、测验题、复习资料-初中数

初三下学期期末数学综合复习资料(一)-初中三年级数学试题练习、期中期末试卷、测验题、复习资料-初中数学试卷-试卷下载---------------------------------------初二下学期期末数学综合复习资料(一)_____班姓名__________学号___________成绩_________一、选择题(每题2分,共36分)1、如果是二次根式,那么应满足的条件是()A、≠2的实数B、<2的实数C、>2的实数D、>0且≠2的实数2、一个多边形的内角和与外角和相等,则这个多边形是()A、三角形B、四边形C、五边形D、六边形3、在、、中、、中,最简二次根式的个数有()A、4B、3C、2D、14、即是轴对称图形,又是中心对称图形的是()A、菱形B、等腰梯形C、平行四边形D、等腰三角形5、下面结论正确的是()A、无限小数是无理数B、无理数是开方开不尽的数C、带根号的数是无理数D、无限不循环小数是无理数6、一个多边形的内角和与外角的和为540°,则它是()边形。
A、5B、4C、3D、不确定7、计算的值为()A、-2B、2C、±2D、8、矩形各内角的平分线能围成一个()A、矩形B、菱形C、等腰梯形D、正方形9、二次根式中的取值范围是()A、>-1B、<-1C、≠-1D、一切实数10、平行四边形、矩形、菱形、正方形共有的性质是()A、对角线相等B、对角线互相平分C、对角线互相垂直D、对角形互相垂直平分11、计算的值是()A、B、-0.14C、D、12、矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=5cm,则矩形的对角线长是()A、5cmB、10cmC、D、2.5cm13、的算术平方根是()A、B、C、D、±14、直角梯形的一个内角为120°,较长的腰为6cm,一底为5cm,则这个梯形的面积为()A、B、C、D、或15、将中的根号外的因式移入根号内后为()A、B、C、D、16、下面四组二次根式中,同类二次根式是()A、B、C、D、17、不能判定四边形ABCD为平行四边形的题设是()A、AB=CD AB ∠CDB、∠A=∠C∠B=∠DC、AB=AD BC=CDD、AB=CD AD=BC18、若等于()A、B、C、2D、二、填空题(每题3分,共15分)1、一个菱形的两条对角线分别为12cm、16cm,这个菱形的边长为______;面积S=_________。
初三数学考试综合复习题 2015
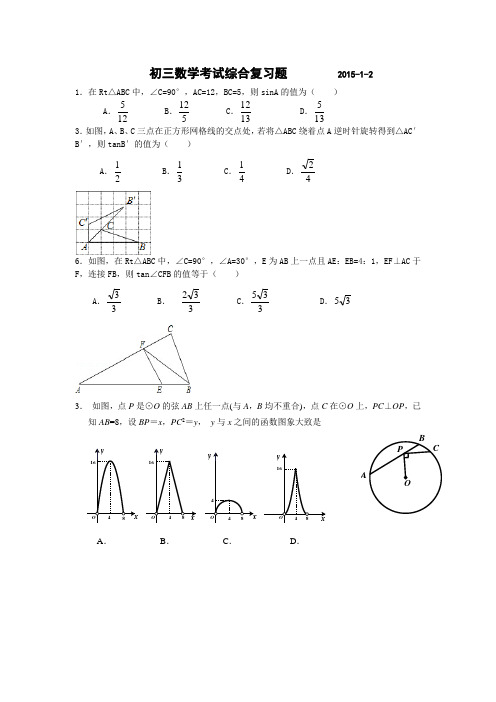
初三数学考试综合复习题 2015-1-2 1.在Rt △ABC 中,∠C=90°,AC=12,BC=5,则sinA 的值为( )A .125 B .512 C .1312 D .135 3.如图,A 、B 、C 三点在正方形网格线的交点处,若将△ABC 绕着点A 逆时针旋转得到△AC ′B ′,则tanB ′的值为( )A .21 B .31 C .41 D .426.如图,在Rt △ABC 中,∠C=90°,∠A=30°,E 为AB 上一点且AE :EB=4:1,EF ⊥AC 于F ,连接FB ,则tan ∠CFB 的值等于( ) A .33B . 332C .335D .353. 如图,点P 是⊙O 的弦AB 上任一点(与A ,B 均不重合),点C 在⊙O 上,PC ⊥OP ,已知AB =8,设BP =x ,PC 2=y , y 与x 之间的函数图象大致是A .B .C .D .A11.如图,有一个球体正好与一个足够大的平面相切。
现在固定球体不动,让平面匀速上升,则下面能反映球体被平面所截得的圆(阴影部分)的面积S与移动时间t之间关系的大致图象是( )。
设平面上升的速度为v,球体的半径为R,阴影部分的半径为r,当平面在半个球体的下方时,由图可得OB=R-vt,根据勾股定理可得OA²=OB²+r²,即R²=(R-vt)²+r²,解得r²=2vtR-v²t²;当平面运动到半个球体的上方时,由图可得OB=vt-R,根据勾股定理可得OA²=OB²+r²,即R²=(vt-R)²+r²,解得r²=v²t²-2vtR。
故S-t的图像大致为(其中v,R是常量)8.如图,在△ABC中,AB=AC,tan∠B=2,BC边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°. 设BE=x,MN=y,则能表示y与x的函数关系的大致图象是ABC D二、填空题(共4道小题,每小题4分,共16分)12.如图,将△ABC 放在每个小正方形的边长为1的网格中,点A 、B 、C 均落在格点上,用一个圆面去覆盖△ABC ,能够完全覆盖这个三角形的最小圆面的半径是 _________.15、已知tan α=125,α是锐角,则sin α= 。
初三数学专题复习试题九年级最新中考专题训练试卷含答案解析(20套)

1.32的倒数是( ). A .32 B .23 C .32- D .23-2.据报道,2010年苏州市政府有关部门将在市区完成130万平方米老住宅小区综合整治工作.130万(即1 300 000)这个数用科学记数法可表示为( ).A .1.3×104B .1.3×105C .1.3×106D .1.3×1073.记n S =n a a a +++ 21,令12n n S S S T n+++=,称n T 为1a ,2a ,……,n a 这列数的“理想数”。
已知1a ,2a ,……,500a 的“理想数”为2004,那么8,1a ,2a ,……,500a 的“理想数”为 ( ). A .2004 B .2006 C .2008 D .20104.某汽车维修公司的维修点环形分布如图。
公司在年初分配给A 、B 、C 、D 四个维修点某种配件各50件。
在使用前发现需将A 、B 、C 、D 四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行。
那么要完成上述调整,最少的调动件次(n 件配件从一个维修点调整到相邻维修点的调动件次为n )为 ( ).A .15B .16C .17D .185.在2,1,0,1-这四个数中,既不是正数也不是负数的是…………………………( )A )1- B )0 C )1 D )26. 2010年一季度,全国城镇新增就业人数为289万人,用科学记数法表示289万正确的是( )A )2.89×107.B )2.89×106 .C )2.89×105.D )2.89×104.7.下面两个多位数1248624……、6248624……,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位。
对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的。
初三中考数学函数综合题含答案

初三中考数学函数综合题含答案一、单选题1.已知点A (1,y 1),B (2,y 2)在抛物线y =(x +1)2+2上,则下列结论正确的是( ). A .122y y >> B .212y y >> C .122y y >>D .212y y >>2.抛物线y =14(x ﹣6)2+3的顶点坐标是( )A .(6,﹣3)B .(6,3)C .(﹣6,3)D .(﹣6,﹣3) 3.抛物线y =2(x -1)2-3的顶点坐标是( ) A .()1,3-- B .()1,3- C .()1,3- D .()1,3 4.一次函数y =-2x +5的图像不经过的象限是( )A .一B .二C .三D .四 5.将函数y =2x 的图象向上平移4个单位后,下列各点在平移后的图象上的是( ) A .()1,5 B .()0,4 C .()1,3- D .()2,3- 6.在直角坐标系的x 轴的负半轴上,则点P 坐标为( )A .()4,0-B .()0,4C .()0,3-D .()1,0 7.直线7y x =--一定不经过( )A .第一象限B .第二象限C .第三象限D .第四象限8.下列各点中,在反比例函数2y x=-图象上的是-( )A .(21),B .233⎛⎫⎪⎝⎭, C .(21)--, D .(12)-,9.已知点()11,A x y ,()22,B x y 在直线()0y kx b k =+≠上,当12x x <时,12y y >,且0kb <,则直线()0y kx b k =+≠在平面直角坐标系中的图象大致是( )A .B .C .D .10.下列一次函数中,y 随x 的增大而减小的是( ) A .y =x ﹣3 B .y =1﹣x C .y =2x D .y =3x +2 11.下列二次函数中,对称轴是直线1x =的是( )A .21y x =+B .()221y x =+C .()21y x =-+D .()231y x =--12.反比例函数y =2x的图象位于( )A .第一、三象限B .第二、三象限C .第一、二象限D .第二、四象限13.如图,△ABC 中,点B ,C 是x 轴上的点,且A (3,2),以原点O 为位似中心,作△ABC 的位似图形△A ′B ′C ′,且△ABC 与A ′B ′C ′的相似比是1:2,则点A ′的坐标是( )A .(﹣6,﹣4)B .(﹣1.5,﹣1)C .(1.5,1)或(﹣1.5,﹣1)D .(6,4)或(﹣6,﹣4)14.已知点P (a ,a ﹣1)在平面直角坐标系的第四象限,则a 的取值范围在数轴上可表示为( ) A .B .C .D .15.要得到抛物线()2321y x =-++可以将抛物线232y x =-+( ) A .先向右平移2个单位,再向上平移1个单位 B .先向右平移2个单位,再向下平移1个单位C .先向左平移2个单位,再向上平移1个单位D .先向左平移2个单位,再向下平移1个单位二、填空题16.已知点(),P m n 在一次函数1y x =+的图象上,则n m -=______.17.已知某函数图像过点(-1,1),写出一个符合条件的函数表达式:______.18.将一次函数123=+y x 向上平移5个单位长度后得到直线AB ,则平移后直线AB 对应的函数表达式为______.19.将抛物线22(3)y x m =-+向右平移3个单位,再向上平移1个单位后恰好经过点(2,3),则m 值是 __.20.若抛物线y =x 2+bx +经过点A (0,5),B (4,5),则其对称轴是直线______三、解答题21.已知抛物线y =-(x -m )2+1与x 轴的交点为A ,B (B 在A 的右边),与y 轴的交点为C .(1)写出m =1时与抛物线有关的三个正确结论.(2)当点B 在原点的右边,点C 在原点的下方时,是否存在△BOC 为等腰三角形的情形?若存在,求出m 的值;若不存在,请说明理由. (3)请你提出两个对任意的m 值都能成立的正确命题.22.在平面直角坐标系xOy 中,点()11,A x y ,()22,B x y 在抛物线()2210y ax ax a =-+>上,其中12x x < (1)求抛物线的对称轴;(2)若122x x a +=-,比较1y 与2y 的大小关系,并说明理由.23.如图,在平面直角坐标系中,二次函数243y ax x =+-图象的顶点是A ,与x 轴交于B ,C 两点,与y 轴交于点D .点B 的坐标是()1,0.(1)求A ,C 两点的坐标,并根据图象直接写出当0y >时x 的取值范围;(2)将图象向上平移m 个单位后,二次函数图象与x 轴交于E ,F 两点,若6EF =,求m 的值.24.一抛物线以()1,9-为顶点,且经过x 轴上一点()4,0-,求该抛物线解析式及抛物线与y 轴交点坐标.25.已知抛物线y =(x ﹣1)2+k 与y 轴相交于点A (0,﹣3),点P 为抛物线上的一点. (1)求此抛物线的解析式;(2)若点P 的横坐标为2,则点P 到x 轴的距离为 .【参考答案】一、单选题 1.D 2.B 3.C 4.C 5.B 6.A 7.A 8.D 9.C 10.B 11.D 12.A 13.D 14.C 15.D 二、填空题 16.117.y =-x (答案不唯一) 18.y =13x +719.-3020.2x = 三、解答题21.(1)抛物线的对称轴为直线x =1,抛物线与x 轴的两个交点为(0,0),(2,0),抛物线开口向下 (2)存在,2(3)无论m 为何值,函数的始终有最大值1;无论m 为何值,函数始终与x 轴有两个不同的交点 【解析】 【分析】(1)当m =1时,y =-(x -1)2+1,根据()2y a x h k =-+的性质写出三个结论即可; (2)求得C (0,1-m 2),根据点B 在原点的右边,点C 在原点的下方,可得m >1,根据等腰三角形的性质可得1+m =m 2-1,解方程求解即可;(3)根据()2y a x h k =-+的性质,可知无论m 为何值,函数的始终有最大值1;无论m为何值,函数始终与x 轴有两个不同的交点. (1)解:当m =1时,y =-(x -1)2+1, ∴抛物线的对称轴为直线x =1, 令0y =,-(x -1)2+1=0, 解得120,2x x ==,抛物线与x 轴的两个交点为(0,0),(2,0), 抛物线开口向下; (2)存在,理由如下: 令x =0,则y =1-m 2, ∴C (0,1-m 2),令y =0,则x =1+m 或x =m -1, ∴B (1+m ,0),∵点B 在原点的右边,点C 在原点的下方, ∴1+m >0,1-m 2<0, ∴m >1,∵△BOC 为等腰三角形, ∴1+m =m 2-1,解得m =2或m =-1(舍), ∴m =2; (3)无论m 为何值,函数始终有最大值1;无论m 为何值,函数始终与x 轴有两个不同的交点. 【点睛】本题考查了()2y a x h k =-+的性质,等腰三角形的性质,解一元二次方程,二次函数与坐标轴交点问题,掌握()2y a x h k =-+的性质是解题的关键. 22.(1)直线1x = (2)12y y >,见解析 【解析】 【分析】(1)将解析式整理成顶点式,直接写出对称轴;(2)方法一:利用作差法,将12y y -表示出来,再进行判断正负,据此判断大小即可;方法二:判断12,y y 距离对称轴的大小,根据函数增减性判断. (1)解:∵()222111y ax ax a x a =-+=--+, ∴抛物线的对称轴为直线1x = (2)方法一:()()221211222121y y ax ax ax ax -=-+--+,()()22122122ax ax ax ax =-+-,()()12122a x x x x =-+-, ()212a x x =--,∵0a >,12x x <, ∴120y y ->, 即12y y >,方法二:∵0a >,122x x a +=-, ∴122x x +<, ∴1212x x +<, 又∵抛物线对称轴是直线1x =,开口向上,且12x x <, ∴1211x x ->-, ∴12y y >. 【点睛】本题主要考查二次函数中系数的运用,以及比较函数值的大小,熟练掌握二次函数的基础运算是解题的关键.23.(1)(2,1)A ,(3,0)C ,当0y >时,13x <<. (2)8m = 【解析】 【分析】(1)利用待定系数法求出a ,再求出点C 的坐标即可解决问题.(2)由题意得抛物线的解析式为243y x x m =-+-+,设二次函数图象与x 轴交于1(E x ,0),2(F x ,0)两点,则124x x +=,123x x m =-,由12|6|x x -=可得出答案.(1)解:把(1,0)B 代入243y ax x =+-,得043a =+-,解得1a =-,2243(2)1y x x x ∴=-+-=--+,)1(2,A ∴,对称轴为直线2x =,B ,C 关于2x =对称,(3,0)C ∴,∴当0y >时,13x <<.(2)解:抛物线向上平移m 个单位,可得抛物线的解析式为243y x x m =-+-+,设二次函数图象与x 轴交于1(E x ,0),2(F x ,0)两点,则124x x +=,123x x m =-,12||6x x ∴-=,212()36x x ∴-=,21212()436x x x x ∴+-=,164(3)36m ∴-⨯-=,8m ∴=.【点睛】本题考查了抛物线与x 轴的交点,二次函数的性质和二次函数图象上点的坐标特征,解决问题的关键是能够把二次函数的一般形式化为顶点式. 24.y =﹣x 2-2x +8;抛物线与y 轴交点为()0,8 【解析】 【分析】知道顶点和抛物线上一点,可以用抛物线的顶点式求答; 【详解】解:设抛物线解析式为()2y a x h k =-+,依题意1h =-,9k =,将()4,0-代入()219y a x =++中,得099a =+,解得1a =-,∴抛物线解析式为()219y x =-++,即y =﹣x 2-2x +8; 令0x =,则8y =,∴抛物线与y 轴交点为()0,8. 【点睛】本题考查待定系数法求二次函数的解析式;在知道顶点坐标的时候,利用顶点式求二次函数解析式十分方便. 25.(1)223y x x =-- (2)3 【解析】 【分析】(1)把点A (0,﹣3),代入抛物线解析式,即可求解;(2)根据抛物线()214y x =--的对称轴为直线1x =,可得点P 和点A (0,﹣3)关于直线1x =对称,从而得到点的纵坐标为-3,即可求解.(1)解:∵抛物线y =(x ﹣1)2+k 与y 轴相交于点A (0,﹣3), ∴()2301k -=-+, 解得:4k =-,∴此抛物线的解析式为()221423y x x x =--=--; (2)解:∵抛物线()214y x =--的对称轴为直线1x =, ∴点P 和点A (0,﹣3)关于直线1x =对称, ∴点的纵坐标为-3, ∴点P 到x 轴的距离为3. 【点睛】本题主要考查了求二次函数的解析式,利用抛物线的对称性求函数值,熟练掌握利用待定系数法求函数解析式的步骤是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级上学期数学期末综合复习测试题(一)
(满分120分, 时限120分钟)
班级 姓名 得分
一.选择题(每小题3分,共30分)
1.下列二次根式中,最简二次根式是( )A.2 B.
8 C. 12 D. 18
2.一元二次方程x(x-1)=0的解是( )A.x=0 B.x=1 C.x=0或x=1 D.x=0或x=-1 3下列图形中,既是轴对称图形又是中心对称图形的是( )
4.如图所示,AB 为⊙O 的直径,点C 在⊙O 上,若∠A=15°,则∠BOC 的度数是( ) A.15° B.30° C.45° D.75°
5.下列事件中,必然发生的是( )
A.某射击运动射击一次,命中靶心
B.通常情况下,水加热到100℃时沸腾
C.掷一次骰子,向上的一面是6点
D.抛一枚硬币,落地后正面朝上
6.如图所示,△ABC 中,DE//BC ,AD=5,BD=10,DE=6,则BC 的值为( ) A.6 B.12 C.18 D.24
7.如图所示,两个同心圆的半径分别为3cm 和5cm,弦AB 与小圆相切于点C , 则AB 的长为( )A.8cm B.6cm C.5cm D.4cm
8.如图,在平行四边形ABCD 中,E 为CD 上一点,连接AE,BD 且AE,BD 交于 点F ,S △DEF:S △ABF=4:25,则DE:EC=( ) A.2:5 B.4:25 C.2:3 D .无法确定法
9. 如图,已知AB ∥CD ∥EF ,那么下列结论正确的是( )A .AD DF =BC CE B .BC CE =DF AD C .CD EF =BC BE D .CD EF =AD AF
10.如图所示,当b<0时,函数y ax b =+与2y ax bx c =++在同一坐标系内的图象可能是
( )
二.填空题(每小题3分,共18分)
11.下列四个函数中,y 的值随着x 值的增大而减小的是. _________.( 填序号 ) (1)x y 2=;(2)()01>=x x
y ;(3)1+=x y ;(4)()02
>=x x y 12. 如图,⊙A 、⊙B 、⊙C 、⊙D 相互外离,它们的半径都是1,顺次联结四个圆心得到四边形ABCD ,则圆形中四个扇形(阴影部分)的面积之和是 (结果中保留π)
13.如图所示,某公司里有一块圆形地面被黑白石子铺成了面积相等的八部分,阴影部分是
黑石子,小华随意向其内部抛一个小球,则小球落点在黑石子区域内的概率是_________
14.某小区2011年底绿化面积为2000平方米,计划2013年底绿化面积要达到2880平方米,
如果每年绿化面积的增长率相同,那么这个增长率是________________________________
15. 如图,⊙O 的直径为10,弦8=AB ,P 是AB 上一动点,则OP 的取值范围________
16.如图,半径为5的⊙P 与轴交于点M (0,-4),N (0,-10),函数(0)k
y x x
=<的图像过点P ,则k = .
第12题图 第15题
三.解答题(1 0小题,共72分) 17.(本题共6分) (1)计算:65027÷⨯22 (2)解方程:(x+3)2 =2(x+3)
第9题图
第8题图 第16题图 x A y O x B y O x C y O x D y
O
18.(本题8分)已知△ABC 在平面直角坐标系中的位置如图所示。
⑴分别写出图中点A 和点C 的坐标;
⑵画出△ABC 绕点A 按逆时针方向旋转90°后的△AB ′C ′;
⑶在⑵的条件下,求点C 旋转到点C ′所经过的路线长(结果保留π)
第18题图
19.(本题8分)如图所示,AB 是⊙O 的直径,AD 是弦,DBC A ∠=∠,OC BD
⊥于点E .
(1)求证:BC 是⊙O 的切线;
(2)若1210BD EC ==,,求AD 的长.
20.(本题8分)如图所示,AB 是⊙O 直径,∠B=30°,弦BC=6,∠ACB 的平分线交⊙O 于D ,连AD 。
⑴求直径AB 的长;⑵求阴影部分的面积(结果保留π)。
第16题
第19题图 第20题图
21.(本题6分)在一个不透明的纸箱里装有2个红球、1个白球,它们除颜色外完全相同,
小明和小亮做摸球游戏,游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出一个
球,记录颜色后放回,将小球摇匀,再由小亮随机摸出一个球,若两人摸到的球颜色相同,
则小明赢,否则小亮赢。
这个游戏规则对双方公平吗?请你用树状图或列表法说明理由。
22.(本题8分)已知关于x 的一元二次方程()222110x m x m +++-=. (1)若方程有实数根,求实数m 的取值范围;
(2)若方程两实数根分别为1
x ,2
x ,且满足()2
1
2
12
16x x x x -=-,求实数m 的值.
23.(本题8分)已知双曲线 y =k
x (K<0)经过直角三角形OAB 的斜边D ,且与直角边相交
于点C ,若点A 的坐标为(-4, 2),试求△AOC 的面积。
24.(本题10分)如图,△ABC 中,∠C =90°,AC =4,BC =3,半径为1的圆的圆心P 以1个单位/s 的速度由点A 沿AC 方向在线段AC 上移动,设移动时间为t (单位:s ). (1)如图1,试探究:
①当t 为________时,⊙p 与线段BC 相离; ⑵当t 为 时,⊙P 与线段BC 相切; ③当t 为 时,⊙P 与线段BC 相交.
(2)如图2,过P 作PD ⊥AC 交AB 于点D ,如果⊙P 和线段BC 交于点E ,试探究:当t 为何值时,四边形PDBE 为平行四边形?请说明理由。
第23题图 第24题图
25.(本题12分)如图,已知抛物线与x 轴相交于A (-1,0)、 E (3,0)两点,与y 轴相交于点B (0,3). (1)求抛物线的解析式;(3分) (2)设抛物线顶点为D ,求四边形AEDB 的面积;(4分) (3)△AOB 与△DBE 是否相似?如果相似,请给以证明;如果不相似,请说明理由。
(5分)
第25题图
X。
