2.3.2双曲线的简单几何性质(1)
2.3.2 双曲线的简单几何性质

思路分析将双曲线方程化为标准方程,先求出参数a,b,c的值,再写
出各个结果.
解双曲线的方程化为标准形式是������2
9
−
���4���2=1,
∴a2=9,b2=4,
∴a=3,b=2,c= 13.
又双曲线的焦点在 x 轴上,
∴顶点坐标为(-3,0),(3,0),
焦点坐标为(- 13,0),( 13,0),
������2+������2 ������2
=
1+
������ ������
2,所以������������ =
������2-1,所以离心率
的大小决定了渐近线斜率的大小,从而决定了双曲线开口的大小,离
心率越大,开口越开阔,离心率越小,开口越扁狭.
4.等轴双曲线是指实轴长与虚轴长相等的双曲线,其渐近线方程
������2
������
−
������2
������
=1(λ≠0),由题意得
49
a=3.
当 λ>0 时,4������=9,λ=36,双曲线方程为���9���2 − ���4���2=1;
当 λ<0 时,-9������=9,λ=-81,双曲线方程为���9���2 − 48���1���2=1.
为 y=±x,离心率等于 2.
课前篇自主预习
【做一做1】 若点M(x0,y0)是双曲线
������2 4
−
������2 25
=1上支上的任意一点,
则x0的取值范围是
,y0的取值范围是
.
解析因为a2=4,b2=25,所以a=2,b=5,所以x0∈R,y0≥2.
ቤተ መጻሕፍቲ ባይዱ
教学设计2:3.2.2 第1课时 双曲线的简单几何性质

21yb的哪些代数特性获得的?椭圆的顶点、长轴、短轴、中心是如何定义的?类比椭圆几何性质的研究,从双曲线方程21yb,你可以独立发现哪些几何性质?有没有双曲线所特有的性质?问题1如何研究双曲线的几何性质?师生活动:类比椭圆几何性质的研究方法,对双曲线21,(0,0)ya bb的角度分析)类比椭圆的范围、对称性、顶点的研究,通过方程2221x yb研究双曲线的范21yb,可以直观发现双曲线上的(,纵坐标的范围是y R.“数”的角度:根据方程22221x y ab ①, 得到222211x y a b,∴x ≤-a ,或x ≥a ;y R .由(x ,y )的范围,可以发现双曲线不是封闭的曲线.双曲线位于直线x a 及其左侧,以及直线x a 及其右侧的区域,并且两支都向外无限延伸. (2)对称性“形”的角度:双曲线既关于坐标轴对称,又关于原点对称.“数”的角度:用−x 代x ,−y 代y ,−x ,−y 分别代x ,y ,方程的形式不变,所以双曲线关于坐标轴、原点对称.双曲线的对称中心叫做双曲线的中心. (3)顶点“形”的角度:从图形直观上可以发现双曲线与x 轴有两个交点A 1(-a ,0)和A 2(a ,0),与y 轴没有公共点.这与椭圆不同. “数”的角度:令y =0,得到x =a 或x =−a ,所以A 1(-a ,0)和A 2(a ,0), 令x =0,y 2=−b 2,没有实数解。
追问2:能否类比椭圆把B 1(0,-b ),B 2(0,b )两点画在y 轴上?线段B 1B 2有何几何意义?师生活动:引导学生画图,学习线段B 1B 2称为双曲线的虚轴,△22A OB 是直角三角形,且2OA a ,22A B c ,2OB b ,线段A 1A 2叫做双曲线的实轴,它的长等于2a ,a 叫做双曲线的实半轴长;线段B 1B 2叫做双曲线的虚轴,它的长等于2b ,b 叫做双曲线的虚半轴长.并且在紧接着的渐近线的研究中就要用到它.追问3:在双曲线29x -24y =1位于第一象限的曲线上画一点M ,测量点M 的横坐标x M 以及它到直线3x -2y=1的距离d ,向右拖动点M ,观察x M 与d 的大小关系,你发现了什么? 师生活动:通过GGB 软件作图,在向右拖动点M 时,点M 的横坐标M x 越来越大,d 越来越小,但是d 始终不等于0.经过两点A 1,A 2作y 轴的平行线x =±3,经过两点B 1,B 2作x 轴的平行线y =±2,四条直线围成一个矩形,矩形的两条对角线所在直线的方程是032xy .可以发现,双曲线22194x y 的两支向外延伸时,与两条直线032x y 逐渐接近,但永远不相交.一般地,双曲线22221x y ab (0a ,0b )的两支向外延伸时,与两条直线0x ya b逐渐接近,我们把这两条直线叫做双曲线的渐近线.实际上,双曲线与它的渐近线无限接近,但永远不相交。
高中数学选修2-1第二章第8课时同步练习§2.3.2双曲线的简单几何性质(1)

§2.3.2双曲线的简单几何性质(1)1、双曲线22154x y -=的( )A 、实轴长为 4B 、23实轴长为8C 、实轴长为10,虚轴长为4D 、实轴长为820,2),则双曲线的标准方程为( )A 、22144x y -=B 、22144y x -=C 、22148y x -=D 、22184x y -= 3、椭圆222134x y n +=和双曲线222116x y n -=有共同的焦点,则实数n 的值是( ) A 、5± B 、3± C 、25 D 、94、P 是双曲线22219x y a -=上一点,双曲线的一条渐近线方程为320x y -=, 1F 、2F 分别为双曲线左、右焦点,若1||3PF =,则2||PF =( )A 、1或5B 、6C 、7D 、95、双曲线的渐近线方程为34y x =±,则双曲线的离心率为( )A 、53BCD 、53或546 )A 、045B 、030C 、060D 、090 7、双曲线与椭圆2211664x y +=有相同的焦点,它的一条渐近线为y x =,则双曲线的方程为 ;8、双曲线22194x y -=的渐近线方程为 。
9、已知1(F ,2F ,动点P 满足21||||2PF PF -=,当点P 的纵坐标是12时,点P 到原点的距离是 ;10、已知平面内有一条长度为4的定线段AB ,动点P 满足||||3PA PB -=,O 为AB 的中点,则||OP 的最小值为 ; 11、过双曲线22221(0,0)x y a b a b-=>>的左焦点且垂直于x 轴的直线与以曲线相交于M 、N 两点,以MN 为直径的圆恰好过双曲线的右顶点,则双线的离心率等于 ;12、已知双曲线的中心在原点,焦点1F 、2F 在坐标轴上,e =(4,P 。
(1)求此双曲线的方程;(2)若(3,)M m 在双曲线上,求证12MF MF ⊥(3)求12F MF ∆的面积。
2021_2022高中数学第二章圆锥曲线与方程3双曲线2双曲线的简单几何性质1课件新人教A版选修2

渐近线方程为
y=±
2 2 x.
典例剖析
一.已知双曲线的方程,研究其几何性质
• 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长 、离心率和渐近线方程,并作出草图.
• [分析] 将双曲线方程化成标准方程,求出a、b、c的值,然后依 据各几何量的定义作答.
[解析] 将 9y2-4x2=-36 变形为x92-y42=1, 即3x22-2y22=1,∴a=3,b=2,c= 13, 因此顶点为 A1(-3,0),A2(3,0), 焦点坐标为 F1(- 13,0),F2( 13,0), 实轴长是 2a=6,虚轴长是 2b=4,
∴双曲线的标准方程为y22-x42=1.
三.双曲线的离心率
已知 F1、F2 是双曲线ax22-by22=1(a>0,b>0)的两个焦点,PQ 是经过 F1 且垂直于 x 轴的双曲线的弦.如果∠PF2Q=90°,求 双曲线的离心率.
• [解析] 设F1(c,0),由|PF2|=|QF2|, ∠PF2Q=90°,
)
B.x42-y52=1 D.x22- y25=1
• [答案] B
[解析] e=32,c=3,∴a=2,∴b2=c2-a2=5, 即双曲线的标准方程为x42-y52=1.
4.已知双曲线ax22-y52=1 的右焦点为(3,0),则该双曲线的
离心率等于( )
A.3 1414
B.3 4 2
C.32
D.43
第二章 圆锥曲线与方程
2.3 双曲线
2.3.2 双曲线的简单几何性质
学习目标
• 1.类比椭圆的性质,能根据双曲线的标准方程,讨论它的几何性质 .
• 2.能运用双曲线的性质解决一些简单的问题.
2.3.2双曲线的简单几何性质

2.3.2双曲线的简单几何性质【知识目标】 1.完成下表2.直线与双曲线的位置关系断定(与椭圆的区别):3.直线与椭圆相交的弦长公式。
【能力目标】题型一:双曲线的几何性质研究运用例1.求14416922=-x y 双曲线的半实轴和半虚轴长、焦点坐标、离心率,渐近线方程、准线方程。
例2根据下列条件求出双曲线的标准方程 (1)已知双曲线的渐近线的方程x y 21±=,焦距为10;(2)已知双曲线的渐近线的方程x y 32±=,且过点,1,29⎪⎭⎫⎝⎛-M ;(3)与椭圆14922=+yx有公共焦点,且离心率25=e 。
例3.(课本)双曲线型冷却塔外形是双曲线的一部分绕虚轴旋转成的曲面,他的最小半径为12m,上口半径为13m.下口半径25m,高为55m ,建立适当坐标系,求出此双曲线的的方程。
2010福建理7.若点O 和点F (-2,0)分别为双曲线)0(1222>=-a ya x的中心和左焦点,点P 为双曲线右支上的任意一点,则FP OP ⋅的取值范围为( )A .),323[+∞-B .),323[∞++C .),47[+∞-D .),47[+∞题型二:第二定义及其双曲线的离心率求解(jianjingxian ) 例1.双曲线1366422=-yx上的一点到它的右焦点距离为8,那么它到左准线的距离为( ) A.10 B.7732 C.212 D.532例2.求适合下列条件的双曲线离心率 (1)双曲线的渐近线的方程x y 21±=;(2)过焦点求垂直于实轴的弦与另一焦点的连线所成角为直角。
(3)双曲线)0(12222b a by ax <<=-的半焦距为c ,直线l 过两点),0(),0,(b a ,且原点到直线的距离为.43c2011全国新理(7)设直线L 过双曲线C 的一个焦点,且与C 的一条对称轴垂直,L 与C 交于A ,B 两点,A B 为C 的实轴长的2倍,则C 的离心率为 (A)(B)(C )2 (D )3例3(综合)双曲线的中心为原点O ,焦点在x 轴上,两条渐近线分别为12l l ,,经过右焦点F 垂直于1l 的直线分别交12l l ,于A B ,两点.已知O A AB O B 、、成等差数列,且BF与FA同向.(Ⅰ)求双曲线的离心率;(Ⅱ)设A B 被双曲线所截得的线段的长为4,求双曲线的方程.练习:双曲线)1,0(12222a b by ax <<=-的焦距为2c,直线l 过点(a,0),(0,b ),且点(1,0)到直线l 的距离与点(-1,0)到直线l 的距离之和c s 54≥,求双曲线的离心率e 。
第二章 2.3.2 双曲线的简单几何性质
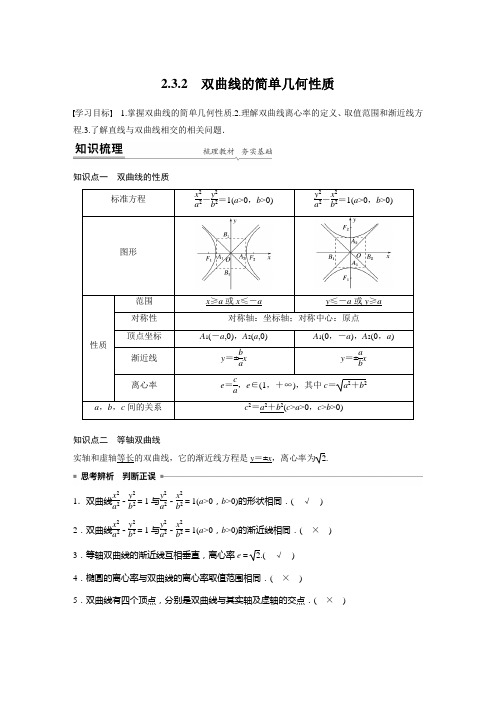
2.3.2双曲线的简单几何性质学习目标 1.掌握双曲线的简单几何性质.2.理解双曲线离心率的定义、取值范围和渐近线方程.3.了解直线与双曲线相交的相关问题.知识点一双曲线的性质标准方程x2a2-y2b2=1(a>0,b>0)y2a2-x2b2=1(a>0,b>0)图形性质范围x≥a或x≤-a y≤-a或y≥a对称性对称轴:坐标轴;对称中心:原点顶点坐标A1(-a,0),A2(a,0)A1(0,-a),A2(0,a)渐近线y=±ba x y=±ab x离心率e=ca,e∈(1,+∞),其中c=a2+b2a,b,c间的关系c2=a2+b2(c>a>0,c>b>0)知识点二等轴双曲线实轴和虚轴等长的双曲线,它的渐近线方程是y=±x,离心率为 2.1.双曲线x2a2-y2b2=1与y2a2-x2b2=1(a>0,b>0)的形状相同.(√)2.双曲线x2a2-y2b2=1与y2a2-x2b2=1(a>0,b>0)的渐近线相同.(×)3.等轴双曲线的渐近线互相垂直,离心率e= 2.(√)4.椭圆的离心率与双曲线的离心率取值范围相同.(×)5.双曲线有四个顶点,分别是双曲线与其实轴及虚轴的交点.(×)一、由双曲线方程研究其几何性质例1 求双曲线9y 2-4x 2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率、渐近线方程. 解 将9y 2-4x 2=-36化为标准方程为x 29-y 24=1,即x 232-y 222=1, 所以a =3,b =2,c =13.因此顶点坐标为A 1(-3,0),A 2(3,0), 焦点坐标为F 1(-13,0),F 2(13,0), 实轴长2a =6,虚轴长2b =4, 离心率e =c a =133,渐近线方程为y =±b a x =±23x .延伸探究求双曲线nx 2-my 2=mn (m >0,n >0)的实半轴长、虚半轴长、焦点坐标、离心率、顶点坐标和渐近线方程. 解 把方程nx 2-my 2=mn (m >0,n >0)化为标准方程为x 2m -y 2n=1(m >0,n >0), 由此可知,实半轴长a =m , 虚半轴长b =n ,c =m +n ,焦点坐标为(m +n ,0),(-m +n ,0),离心率e =ca=m +nm=1+n m, 顶点坐标为(-m ,0),(m ,0), 所以渐近线方程为y =±n mx ,即y =±mn m x .反思感悟 由双曲线的方程研究几何性质的解题步骤 (1)把双曲线方程化为标准形式是解决此类题的关键.(2)由标准方程确定焦点位置,确定a,b的值.(3)由c2=a2+b2求出c的值,从而写出双曲线的几何性质.跟踪训练1 求双曲线9y 2-16x 2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.解 把方程9y 2-16x 2=144化为标准方程为 y 242-x 232=1. 由此可知,实半轴长a =4,虚半轴长b =3; c =a 2+b 2=42+32=5,焦点坐标是(0,-5),(0,5);离心率e =c a =54;渐近线方程为y =±43x .二、由双曲线的几何性质求标准方程 例2 根据以下条件,求双曲线的标准方程. (1)过点P (3,-5),离心率为2;(2)与椭圆x 29+y 24=1有公共焦点,且离心率e =52;(3)与双曲线x 29-y 216=1有共同渐近线,且过点(-3,23).解 (1)若双曲线的焦点在x 轴上, 设其方程为x 2a 2-y 2b 2=1(a >0,b >0),∵e =2,∴c 2a2=2,即a 2=b 2.①又双曲线过P (3,-5),∴9a 2-5b 2=1,②由①②得a 2=b 2=4,故双曲线方程为x 24-y 24=1. 若双曲线的焦点在y 轴上, 设其方程为y 2a 2-x 2b 2=1(a >0,b >0),同理有a 2=b 2,③ 5a 2-9b 2=1,④ 由③④得a 2=b 2=-4(舍去). 综上,双曲线的标准方程为x 24-y 24=1.(2)由椭圆方程x 29+y 24=1,知半焦距为9-4=5,∴焦点是F 1(-5,0),F 2(5,0). 因此双曲线的焦点为(-5,0),(5,0). 设双曲线方程为x 2a 2-y 2b 2=1(a >0,b >0),由已知条件,有⎩⎪⎨⎪⎧c a =52,a 2+b 2=c 2,c =5,解得⎩⎪⎨⎪⎧a =2,b =1.∴所求双曲线的标准方程为x 24-y 2=1.(3)设所求双曲线方程为x 29-y 216=λ(λ≠0),将点(-3,23)代入得λ=14,∴双曲线方程为x 29-y 216=14,即双曲线的标准方程为x 294-y 24=1.反思感悟 (1)根据双曲线的某些几何性质求双曲线方程,一般用待定系数法转化为解方程(组),但要注意焦点的位置,从而正确选择方程的形式. (2)巧设双曲线方程的六种方法与技巧①焦点在x 轴上的双曲线的标准方程可设为x 2a 2-y 2b 2=1(a >0,b >0).②焦点在y 轴上的双曲线的标准方程可设为y 2a 2-x 2b2=1(a >0,b >0).③与双曲线x 2a 2-y 2b 2=1共焦点的双曲线方程可设为x 2a 2-λ-y 2b 2+λ=1(λ≠0,-b 2<λ<a 2).④与双曲线x 2a 2-y 2b 2=1具有相同渐近线的双曲线方程可设为x 2a 2-y 2b 2=λ(λ≠0).⑤渐近线为y =kx 的双曲线方程可设为k 2x 2-y 2=λ(λ≠0). ⑥渐近线为ax ±by =0的双曲线方程可设为a 2x 2-b 2y 2=λ(λ≠0). 跟踪训练2 求适合下列条件的双曲线的标准方程:(1)焦点在x 轴上,虚轴长为8,离心率为53;(2)渐近线方程为y =±12x 且过点A (2,-3).解 (1)设所求双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0),由题意知2b =8,e =c a =53,从而b =4,c =53a ,代入c 2=a 2+b 2,得a 2=9, 故双曲线的标准方程为x 29-y 216=1.(2)方法一 ∵双曲线的渐近线方程为y =±12x ,若焦点在x 轴上,设所求双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0),则b a =12.①∵A (2,-3)在双曲线上,∴4a 2-9b 2=1.②由①②联立,无解.若焦点在y 轴上,设所求双曲线的标准方程为y 2a 2-x 2b 2=1(a >0,b >0),则a b =12.③∵A (2,-3)在双曲线上,∴9a 2-4b 2=1.④由③④联立,解得a 2=8,b 2=32. ∴所求双曲线的标准方程为y 28-x 232=1.方法二 由双曲线的渐近线方程为y =±12x ,可设双曲线方程为x 222-y 2=λ(λ≠0),∵A (2,-3)在双曲线上, ∴2222-(-3)2=λ,∴λ=-8 ∴所求双曲线的标准方程为y 28-x 232=1.三、双曲线的离心率例3 设F 1,F 2分别为双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点,双曲线上存在一点P 使得|PF 1|+|PF 2|=3b ,|PF 1|·|PF 2|=94ab ,则该双曲线的离心率为________.答案 53解析 不妨设P 为双曲线右支上一点, |PF 1|=r 1,|PF 2|=r 2.根据双曲线的定义,得r 1-r 2=2a , 又r 1+r 2=3b ,故r 1=3b +2a 2,r 2=3b -2a 2.又r 1·r 2=94ab ,所以3b +2a 2·3b -2a 2=94ab ,解得b a =43(负值舍去),故e =c a =a 2+b 2a 2=⎝⎛⎭⎫b a 2+1 =⎝⎛⎭⎫432+1=53. 反思感悟 求双曲线离心率的两种方法(1)直接法:若已知a ,c 可直接利用e =ca求解,若已知a ,b ,可利用e =1+⎝⎛⎭⎫b a 2求解.(2)方程法:若无法求出a ,b ,c 的具体值,但根据条件可确定a ,b ,c 之间的关系,可通过b 2=c 2-a 2,将关系式转化为关于a ,c 的齐次方程,借助于e =ca ,转化为关于e 的n 次方程求解.跟踪训练3 (1)已知F 1,F 2是双曲线x 2a 2-y 2b 2=1(a >0,b >0)的两焦点,以线段F 1F 2为边作正三角形MF 1F 2,若边MF 1的中点P 在双曲线上,则双曲线的离心率是( ) A .4+2 3 B .23-1 C.3+12D.3+1答案 D解析 因为MF 1的中点P 在双曲线上,所以|PF 2|-|PF 1|=2a ,因为△MF 1F 2为正三角形,边长都是2c ,所以3c -c =2a, 所以e =c a =23-1=3+1.(2)如果双曲线x 2a 2-y 2b 2=1右支上总存在到双曲线的中心与右焦点距离相等的两个相异点,则双曲线离心率的取值范围是________. 答案 (2,+∞)解析 如图,因为AO =AF ,F (c ,0),所以x A =c2,因为A 在右支上且不在顶点处,所以c 2>a ,所以e =c a>2.1.双曲线mx 2+y 2=1的虚轴长是实轴长的2倍,则m 的值为( ) A .4 B .-4 C .-14D.14答案 C解析 由双曲线方程mx 2+y 2=1,知m <0, 则双曲线方程可化为y 2-x 2-1m=1, 则a 2=1,a =1,又虚轴长是实轴长的2倍, ∴b =2,∴-1m =b 2=4,∴m =-14,故选C.2.中心在原点,焦点在x 轴上,且一个焦点在直线3x -4y +12=0上的等轴双曲线的方程是( )A .x 2-y 2=8B .x 2-y 2=4C .y 2-x 2=8D .y 2-x 2=4答案 A解析 令y =0,得x =-4, ∴等轴双曲线的一个焦点为(-4,0), ∴c =4,a 2=b 2=12c 2=12×16=8,故选A.3.双曲线x 2-y 2m=1的离心率大于2的充要条件是( ) A .m >12B .m ≥1C .m >1D .m >2 答案 C解析 由题意得,a 2=1,b 2=m >0,∴c 2=m +1 ∴e =c a=m +1>2,∴m >1.4.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为233,则其渐近线方程为________________.答案 y =±33x解析 由题意知,e =c a =233,得c 2a 2=43.又c 2=b 2+a 2,所以b 2+a 2a 2=43. 故b 2a 2=13. 所以b a =33,所以该双曲线的渐近线方程为y =±33x .5.若直线y =kx 与双曲线4x 2-y 2=16相交,则实数k 的取值范围为________. 答案 (-2,2)解析 易知k ≠±2,将y =kx 代入4x 2-y 2=16得关于x 的一元二次方程(4-k 2)x 2-16=0,由Δ>0可得-2<k <2.1.知识清单: (1)双曲线的几何性质. (2)双曲线的离心率的求法.2.方法归纳:定义法、函数与方程、数形结合. 3.常见误区:忽略双曲线中x ,y 的范围.1.已知双曲线x 2a 2-y 25=1(a >0)的右焦点为(3,0),则双曲线的离心率等于( )A.31414B.324C.32D.43答案 C解析 由题意知a 2+5=9,解得a =2,e =c a =32.2.双曲线x 2-y 2=1的顶点到其渐近线的距离等于( ) A.12 B.22 C .1 D. 2 答案 B解析 双曲线x 2-y 2=1的渐近线方程为x ±y =0,顶点坐标为(1,0),(-1,0),故顶点到渐近线的距离为22. 3.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为52,则双曲线C 的渐近线方程为( )A .y =±14xB .y =±13xC .y =±12xD .y =±x答案 C解析 已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为52,故有a 2+b 2a 2=54,所以b 2a 2=14,解得b a =12. 故双曲线C 的渐近线方程为y =±12x ,故选C. 4.已知双曲线方程为x 2-y 24=1,过点P (1,0)的直线l 与双曲线只有一个公共点,则l 共有( ) A .4条 B .3条 C .2条 D .1条答案 B解析 因为双曲线方程为x 2-y 24=1,则P (1,0)是双曲线的右顶点,所以过P (1,0)并且和x 轴垂直的直线是双曲线的一条切线,与双曲线只有一个公共点,另外两条就是过P (1,0)分别和两条渐近线平行的直线,所以符合要求的有3条.5.已知双曲线C :x 2a 2-y 2b 2=1的焦距为10,点P (2,1)在C 的渐近线上,则双曲线C 的方程为( )A.x 220-y 25=1 B.x 25-y 220=1 C.x 280-y 220=1 D.x 220-y 280=1 答案 A解析 双曲线C 的渐近线方程为y =±b a x ,点P (2,1)在渐近线上,∴4a 2-1b 2=0,即a 2=4b 2, 又a 2+b 2=c 2=25,解得b 2=5,a 2=20,故选A.6.过双曲线x 2-y 23=1的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A ,B 两点,则|AB |等于________.答案 4 3解析 由题意知,双曲线x 2-y 23=1的渐近线方程为y =±3x ,将x =c =2代入得y =±23,所以|AB |=4 3.7.已知双曲线方程为8kx 2-ky 2=8(k ≠0),则其渐近线方程为________________. 答案 y =±22x解析 由已知令8kx 2-ky 2=0,得渐近线方程为y =±22x .8.过双曲线x 2-y 23=1的左焦点F 1作倾斜角为π6的弦AB ,则|AB |=________.答案 3解析 易得双曲线的左焦点F 1(-2,0),∴直线AB 的方程为y =33(x +2), 与双曲线方程联立,得8x 2-4x -13=0.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=12,x 1x 2=-138, ∴|AB |=1+k 2·(x 1+x 2)2-4x 1x 2 =1+13×⎝⎛⎭⎫122-4×⎝⎛⎭⎫-138=3. 9.求适合下列条件的双曲线的标准方程.(1)两顶点间的距离是6,两焦点所连线段被两顶点和中心四等分;(2)渐近线方程为2x ±3y =0,且两顶点间的距离是6.解 (1)由两顶点间的距离是6,得2a =6,即a =3.由两焦点所连线段被两顶点和中心四等分可得2c =4a =12,即c =6,于是有b 2=c 2-a 2=62-32=27.由于焦点所在的坐标轴不确定,故所求双曲线的标准方程为x 29-y 227=1或y 29-x 227=1. (2)设双曲线方程为4x 2-9y 2=λ(λ≠0),即x 2λ4-y 2λ9=1(λ≠0),由题意得a =3. 当λ>0时,λ4=9,λ=36, 双曲线方程为x 29-y 24=1; 当λ<0时,-λ9=9,λ=-81, 双曲线方程为y 29-x 2814=1. 故所求双曲线的标准方程为x29-y24=1或y29-x2814=1.10.过双曲线C:x2a2-y2b2=1(a>0,b>0)的右焦点作一条与其渐近线平行的直线,交C于点P.若点P的横坐标为2a,求双曲线C的离心率.解如图所示,不妨设与渐近线平行的直线l的斜率为ba,又直线l过右焦点F(c,0),则直线l的方程为y=ba(x-c).因为点P的横坐标为2a,代入双曲线方程得4a2a2-y2b2=1,化简得y=-3b或y=3b(点P在x轴下方,故舍去),故点P的坐标为(2a,-3b),代入直线方程得-3b=ba(2a-c),化简可得离心率e=ca=2+ 3.11.如图,双曲线C:x29-y210=1的左焦点为F1,双曲线上的点P1与P2关于y轴对称,则|P2F1|-|P1F1|的值是()A.3 B.4 C.6 D.8答案 C解析 设F 2为右焦点,连接P 2F 2(图略),由双曲线的对称性,知|P 1F 1|=|P 2F 2|,所以|P 2F 1|-|P 1F 1|=|P 2F 1|-|P 2F 2|=2×3=6.12.如图,中心均为原点O 的双曲线与椭圆有公共焦点,M ,N 是双曲线的两顶点,若M ,O ,N 将椭圆的长轴四等分,则双曲线与椭圆的离心率的比值是()A .3B .2 C. 3 D. 2答案 B解析 设椭圆与双曲线的标准方程分别为x 2a 2+y 2b 2=1(a >b >0), x 2m 2-y 2n 2=1(m >0,n >0), 因为它们共焦点,所以设它们的半焦距均为c ,所以椭圆与双曲线的离心率分别为e 1=c a ,e 2=c m, 由点M ,O ,N 将椭圆长轴四等分可知m =a -m ,即2m =a ,所以e 2e 1=c m c a=a m=2. 13.已知F 为双曲线C :x 29-y 216=1的左焦点,P ,Q 为C 上的点.若PQ 的长等于虚轴长的2倍,点A (5,0)在线段PQ 上,则△PQF 的周长为________.答案 44解析 由双曲线C 的方程,知a =3,b =4,c =5,∴点A (5,0)是双曲线C 的右焦点,且|PQ |=|QA |+|P A |=4b =16,点P ,Q 在双曲线的右支上,由双曲线的定义,得|PF |-|P A |=6,|QF |-|QA |=6.∴|PF |+|QF |=12+|P A |+|QA |=28,∴△PQF 的周长为|PF |+|QF |+|PQ |=28+16=44.14.设双曲线x 2-y 22=1上有两点A ,B ,AB 中点M (1,2),则直线AB 的方程为________________. 答案 y =x +1解析 方法一 (用根与系数的关系解决)显然直线AB 的斜率存在.设直线AB 的方程为y -2=k (x -1),即y =kx +2-k ,由⎩⎪⎨⎪⎧y =kx +2-k ,x 2-y 22=1,得(2-k 2)x 2-2k (2-k )x -k 2+4k -6=0,当Δ>0时,设A (x 1,y 1),B (x 2,y 2),则1=x 1+x 22=k (2-k )2-k 2, 所以k =1,满足Δ>0,所以直线AB 的方程为y =x +1.方法二 (用点差法解决)设A (x 1,y 1),B (x 2,y 2), 则⎩⎨⎧ x 21-y 212=1,x 22-y 222=1,两式相减得(x 1-x 2)(x 1+x 2)=12(y 1-y 2)(y 1+y 2). 因为x 1≠x 2,所以y 1-y 2x 1-x 2=2(x 1+x 2)y 1+y 2, 所以k AB =2×1×22×2=1, 所以直线AB 的方程为y =x +1,代入x 2-y 22=1满足Δ>0. 所以直线AB 的方程为y =x +1.15.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,点P 在双曲线的右支上,且|PF 1|=4|PF 2|,则此双曲线的离心率e 的最大值为( ) A.43 B.53 C .2 D.73答案 B解析 ∵P 在双曲线的右支上,∴由双曲线的定义可得|PF 1|-|PF 2|=2a , ∵|PF 1|=4|PF 2|,∴4|PF 2|-|PF 2|=2a ,即|PF 2|=23a , 根据点P 在双曲线的右支上,可得|PF 2|=23a ≥c -a , ∴53a ≥c ,又∵e >1,∴1<e ≤53, ∴此双曲线的离心率e 的最大值为53. 16.已知双曲线C 1:x 2-y 24=1. (1)求与双曲线C 1有相同的焦点,且过点P (4,3)的双曲线C 2的标准方程;(2)直线l :y =x +m 分别交双曲线C 1的两条渐近线于A ,B 两点,当OA →·OB →=3时,求实数m的值.解 (1)双曲线C 1的焦点坐标为(5,0),(-5,0),设双曲线C 2的标准方程为x 2a 2-y 2b 2=1(a >0,b >0), 则⎩⎪⎨⎪⎧ a 2+b 2=5,16a 2-3b 2=1,解得⎩⎪⎨⎪⎧a 2=4,b 2=1, 所以双曲线C 2的标准方程为x 24-y 2=1. (2)双曲线C 1的渐近线方程为y =2x ,y =-2x ,设A (x 1,2x 1),B (x 2,-2x 2),由⎩⎪⎨⎪⎧ x 2-y 24=0,y =x +m ,消去y 化简得3x 2-2mx -m 2=0, 由Δ=(-2m )2-4×3×(-m 2)=16m 2>0,得m ≠0.因为x 1x 2=-m 23, OA →·OB →=x 1x 2+2x 1(-2x 2)=-3x 1x 2=m 2, 所以m 2=3,即m =±3.。
2014-2015学年高中数学(人教版选修2-1)配套课件第二章 2.3.2 双曲线的简单几何性质(一)

栏 目 链 接
x2 y2 - =1(a>0,b>0). a2 b2 c 5 由题设知:2b=12, = ,且 c2=a2+b2, a 4 ∴b=6,c=10,a=8, x2 y2
∴所求的双曲线标准方程为 - =1. 64 36
(2)设与双曲线 -y2=1 有公共渐进线的双曲线方程为 2 2 -y2=λ (λ ≠0). 将点 M(2,-2)代入 -y2=λ (λ ≠0)得:λ =-2. 2 y2 x2 ∴所求的双曲线标准方程为 - =1. 2 4
n mn 渐近线方程为 y=± x=± x. m m
点评:已知双曲线的方程求其几何性质时,若方程不是标准形式的 先化成标准方程,弄清方程中的 a,b 对应的值,再利用 c2=a2+b2 得到
栏 目 链 接
c,然后确定双曲线的焦点位置,从而写出双曲线的几何性质.
变 式 迁 移
x 2 y2 1.(2013·北京卷)若双曲线 2- 2=1 的离心率为 a b
解析:把方程 nx2-my2=mn 化为标准方程
栏 目 链 接
x2 y2 - =1 , m n
由此可知,实半轴长 a= m, 虚半轴长 b= n,c= m+n, 焦点坐标是(- m+n,0),( m+n,0),
c m+n m2+mn 离心率 e= = = . a m m
顶点坐标为(- m,0),( m,0).
x2
y2
)
3 A.y=± x 4 9 C.y=± x 4
栏 目 链 接
解析:由双曲线方程可得焦点在 x 轴上,a=4,b=3. b 3 ∴渐近线方程为 y=± x=± x. a 4 答案:A
自 测 自 评
1.双曲线 - =1 的( A ) 5 4 A.实轴长为 2 5,虚轴长为 4,渐近线方程为 2 5 3 5 y=± x,离心率 e= 5 5 B.实轴长为 2 5,虚轴长为 4,渐近线方程为
2.3.2双曲线的简单几何性质(第1课时)学案

2.3.2双曲线的简单几何性质(第1课时)【学习目标】1、通过对双曲线标准方程的讨论,掌握双曲线的范围,对称性,顶点,渐近线和离心率等几何性质与双曲线的中心,实轴,虚轴,渐进线,等轴双曲线的概念,加深对a 、b 、c 、e 的关系及其几何意义的理解。
2、能利用双曲线的简单几何性质及标准方程解决相关的基本问题。
【学习重点】双曲线的简单几何性质及其应用。
【学习难点】渐近线方程的导出。
一、课前预习要求及内容回顾:1、双曲线的定义:2、双曲线的标准方程:3、回想我们是怎样利用椭圆的标准方程探究椭圆性质的?二、预习整理(一)试一试类比探究椭圆的简单几何性质的方法,根据双曲线的标准方程)0,0(,12222>>=-b a b y a x ,研究它的几何性质。
①范围 :由双曲线的标准方程可得:=22by 从而得x 的范围: ;即双曲线在不等式 和所表示的区域内。
22ax = 从而得y 的范围为 。
②对称性:以x -代x ,方程不变,这说明所以双曲线关于 对称。
同理,以y -代y ,方程不变得双曲线关于 对称,以x -代x ,且以y -代y ,方程也不变,得双曲线关于 对称。
③顶点:即双曲线与对称轴的交点。
在方程12222=-by a x 里,令y=0,得x= 得到双曲线的顶点坐标为1A ( )2A ( ) ;我们把1B ( )2B ( )也画在y 轴上(如图)。
线段 分别叫做双曲线的实轴和虚轴,它们的长分别为 。
④离心率:双曲线的离心率e= ,范围为 。
(二)想一想1、根据上述四个性质,画出椭圆 191622=+y x 与双曲线191622=-y x 的图象。
2、渐近线:双曲线22221x ya b-=的渐近线方程为,双曲线各支向外延伸时,与它的渐近线,。
叫做等轴双曲线,它的渐近线为,离心率为。
思考:离心率可以刻画椭圆的扁平程度,双曲线的离心率刻画双曲线的什么几何特征?三、合作探究四、小组展示例题1、求下列双曲线的实轴和虚轴的长、顶点和焦点的坐标、离心率,渐近线方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、顶点 、
(1)双曲线与对称轴的交点,叫做双曲线的顶点 )双曲线与对称轴的交点,叫做双曲线的顶点
顶点是 A1 ( − a ,0 )、 A2 ( a ,0 )
(2)线段 1A2叫做双曲线的实轴, 线段A 线段 线段B 叫做双曲线的虚轴。 线段B1B2叫做双曲线的虚轴。
实轴的长为2a,虚轴的长为2b; 实轴的长为 ,虚轴的长为 a称为半实轴的长,b称为半虚轴的长;; 称为半实轴的长, 称为半虚轴的长; 称为半实轴的长 称为半虚轴的长
能力提升: 能力提升:
例1.已知焦点在x轴上的双曲线的渐近线方程为 3 x ± y = 0,且焦点到渐近线的距离为3, 求双曲线的标准方程。
x y 例2.已知双曲线 2 − 2 = 1(0 < a < b)的半焦距为c, a b 直线l过(a,0 ), (0, b )两点,且原点到直线的距离为 3 c, 求双曲线的离心率? 4
一、复习回顾: 复习回顾:
平面内与两个定点F 的距离的差的绝对值等于常数(小于 小于|F 平面内与两个定点 1、F2的距离的差的绝对值等于常数 小于 1 F2|)的点的轨迹叫做双曲线 这两个定点叫做双曲线的焦点,两焦 的点的轨迹叫做双曲线 这两个定点叫做双曲线的焦点 的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点, 双曲线的焦距。 点的距离叫做双曲线的焦距 点的距离叫做双曲线的焦距。 即 || MF1 | − | MF2 ||= 2a, ( 2a < 2c )
1.双曲线的定义: 双曲线的定义: 双曲线的定义
2.双曲线的标准方程: 双曲线的标准方程: 双曲线的标准方程
c2 = a 2 + b2
x y − 2 = 1(a > 0, b > 0). 2 a b
2 2
y2 x2 − 2 = 1(a > 0, b > 0). 2 a b
3.前面我们学习了椭圆的哪些几何性质? .前面我们学习了椭圆的哪些几何性质?
x
5、离心率 、 c 双曲线的焦距与实轴长 的比 e = ,叫做 (1)定义: )定义: a 双曲线的 离心率。
(2)e的范围 ) 的范围: (3)e的含义: ) 的含义:
c2 − a2 c 2 = ( ) −1 = e2 −1 a a b b ∴当 e ∈ (1,+∞ )时, ∈ (0,+∞ ), 且 e增大 , 也增大 a a ⇒ e增大时,渐近线与实轴 的夹角增大 b = a
你能类比探究出双曲线的几何性质吗? 你能类比探究出双曲线的几何性质吗?
x2 y 2 方程 + 2 = 1(a > b > 0) 2 性质 a b x2 y 2 − 2 = 1(a > 0, b > 0) 2 a b
图形
范围 对称性
− a ≤ x ≤ a,−b ≤ y ≤ b
关于x, y轴及原点对称 A1 (−a,0), A2 (a,0)
y
M
Y
p F2 X
F1
0
F2
X
F1
0
范围
|x|≤a,|y|≤b ≤
对称性
对称轴: 轴 对称轴:x轴,y轴 轴 对称中心: 对称中心:原点
|x| ≥ a,y∈R , ∈
对称轴: 轴 对称轴:x轴,y轴 轴 对称中心: 对称中0,b) (0,-b) 长轴: 短轴: 长轴:2a 短轴:2b
例3.已知双曲线的渐近线方程为2 x ± 3 y = 0. (1)若双曲线过点P ( 6 ,2), 求双曲线的标准方程。
(2)若双曲线的焦距是2 13 , 求双曲线的标准方程。
(3)求双曲线的离心率? )求双曲线的离心率?
x2 y2 例4.求与双曲线 − = 1有相同的渐进线,且经过 25 16 点P(−5,2)的双曲线标准方程。
(-x,y)
(x,y)
-a (-x,-y)
o
a (x,-y)
x
2、对称性 、
关于x轴 轴和原点都是对称。 关于 轴、y轴和原点都是对称 轴和原点都是对称 x轴、y轴是双曲线的对称轴,原点是对称中心, 轴是双曲线的对称轴, 轴 轴是双曲线的对称轴 原点是对称中心, 又叫做双曲线的中心 中心。 又叫做双曲线的中心。
Q c>a>0 ∴
e >1
e是表示双曲线开口大小的一个量,e越大开口越大
6.类比 类比 方程 图形 顶点 对称 范围 焦点 离心率 渐近线
x2 y2 − 2 = 1( a , b > 0 ) 2 a b
y o x
x2 y2 − 2 + 2 = 1( a , b > 0 ) b a
y o x
(±a , 0 ) ±
( 0, ±a )
x 轴、y 轴、原点 ( 原点是双曲线的中心 ) |x|≥a (±c , 0 ) ±
e= c ( e > 1) a
|y|≥a ( 0, ±c )
y = ±
b x a
y = ±
a x b
典例讲解: 典例讲解:
求双曲线9x 的实半轴长和虚半轴长、 例1. 求双曲线 -16y =144的实半轴长和虚半轴长、 的实半轴长和虚半轴长 焦点坐标、离心率、渐近线方程。 焦点坐标、离心率、渐近线方程。
B1 (0,−b), B2 (0, b) A1 A2叫长轴, B1 B2叫短轴
c e = , (0 < e < 1) a
顶点坐标 离心率
课堂新授
一、研究双曲线 1、范围 、 2
x2 y 2 − 2 = 1(a > 0, b > 0) 2 a b
的简单几何性质
y
x Q 2 ≥ 1,即x 2 ≥ a 2 a ∴ x ≥ a, x ≤ −a
(-a,0) (a,0) 实轴: 实轴:2a 虚轴:2b 虚轴:
离心率
e=
c < a ( 0<e <1 )
e=
c (e>1) a
b a x
渐近线
无
a2 x = ± c
y= ±
准线
a2 x = ± c
5 例2 已知双曲线顶点间的距 离是16,离心率 e = , 4 焦点在 x轴上,中心在原点,写 出双曲线的方 程,并且求出它的渐近 线和焦点坐标 .
练一练.求一渐近线为 练一练 求一渐近线为3x+4y=0,一个焦点为 一个焦点为(4,0)的双曲线 的双曲线 求一渐近线为 一个焦点为 的标准方程. 的标准方程
2 2
小
结
椭 圆
双曲线
方程
a b c关系
图象
2 x2 + y = 1 a> b >0) 2 ( > ) 2 a b
x 2 − y 2 = ( a> 0 b>0) > 1 > a 2 b2
c 2= a 2 + b 2 (a> 0 b>0) > >
c 2= a 2 − b 2 (a> b>0) > >
x2 y 2 − 2 =1 2 a b y2 x2 − 2 =1 2 a b x2 y 2 − 2 =0 2 a b
y2 x2 − 2 =0 2 a b
b y = ± x a
3.双曲线的画法: 双曲线的画法: 双曲线的画法
a y=± x b
y
B2 A1 O B1 A2
①定顶点 ③画渐近线 ②画矩形 ④画双曲线
y
(3)实轴与虚轴等长的双曲线叫等轴双曲线。 (3)实轴与虚轴等长的双曲线叫等轴双曲线。 B2 实轴与虚轴等长的双曲线叫等轴双曲线 b
x − y = m (m ≠ 0)
2 2
A1 -a
-b
o
a
A2
x
B1
4、渐近线 、
(1)
x2 y2 双曲线 2 − 2 = 1( a > 0, b > 0 ) a b b 的渐近线为 y = ± x a
x2 y2 解:设双曲线方程为: − = λ , (λ ≠ 0) 25 16
将P(−5,2)代入双曲线方程得:
3 25 4 − =λ ⇒λ = 4 25 16
4x2 y2 ∴ 双曲线方程为: − =1 75 12
小结:与双曲线 小结:与双曲线x2/a2-y2/b2=1有共同渐近线 有共同渐近线 的双曲线方程可设为 可设为: 的双曲线方程可设为:x2/a2-y2/b2=λ。 。
x2 y2 解:把方程化为标准式 2 − 2 = 1 把方程化为标准式 4 3
虚半轴长b=3, c =5 ∴实半轴长 a= 4, 虚半轴长 ± 焦点坐标为 (±5,0)
O
2 2
y
3 y= x 4
x
3 y=− x 4
3 渐近线方程为 y = ± x 4
2 2
5 离心率为 e = 4
练一练. 求双曲线16x -25y =-400的实半轴长和虚半轴 练一练 求双曲线 的实半轴长和虚半轴 焦点坐标、离心率、渐近线方程。 长、焦点坐标、离心率、渐近线方程。
2 2
y Q b
N(x,y’) M(x,y)
等轴双曲线 x − y = m (2) ( m ≠ 0 )的渐近线为
B2
A1
o
A2
a x
y = ±x
(3) 利用渐近线可以较准确的 画出双曲线的草图
B1
b y =− x a
b y= x a
双曲线的渐近线 2 2 x y b 渐近线. 规定: ▲规定:直线 y = ± a x 叫做双曲线 2 − 2 =1 的渐近线.。 a b 2 2 y x 思考: 的渐近线方程是什么? ▲思考: 双曲线 2 − 2 = 1的渐近线方程是什么? a ① y=± x a b b 两种双曲线的渐近线方程,怎样统一记忆? ②两种双曲线的渐近线方程,怎样统一记忆?
