五年级第四讲 图形问题
期末复习专题四图形与几何—平面图形篇-五年级数学(解析版)沪教版

2022-2023学年五年级数学下册典型例题系列之期末复习专题四:图形与几何—平面图形篇(解析版)【篇目一】长方形和正方形的周长与面积。
【知识总览】长方形的周长=(长+宽)×2 公式:C长=2(a+b)正方形的周长=边长×4 公式:C正=4a正方形的面积=边长×边长公式:S=a×a长方形的面积=长×宽公式:S=a×b【典型例题1】长方形的周长和面积。
一个长方形的运动场,长150米,宽100米,这个运动场的周长是多少米?解析:(150+100)×2=250×2=500(米)答:这个运动场的周长是500米。
【对应练习1】长方形的长是12米,宽是长的,长方形的面积是( )。
解析:108平方米【对应练习2】用一根长50厘米的铁丝,围一个长为12厘米、宽为10厘米的长方形,还剩下铁丝多少厘米?解析:(12+10)×2=44(厘米)50-44=6(厘米)答:还剩下铁丝6厘米。
【典型例题2】正方形的周长和面积。
一个正方形边长是20分米,它的周长是( )分米,面积是( )平方分米.解析:正方形的周长为:20×4=80(分米)正方形的面积为:20×20=400(平方分米)答:正方形的周长是80分米,面积是400平方分米。
【对应练习1】用一根长28厘米的铁丝围成一个正方形,正方形的边长是(),面积是()。
解析:28÷4=7(厘米)7×7=49(平方厘米)答:这个正方形的边长是7厘米,面积是49平方厘米。
【对应练习2】一个正方形的周长是12厘米,边长是( )厘米,面积是( )平方厘米。
解析:3;9【对应练习3】用一根长12厘米的铁丝围成一个正方形,这个正方形的周长是()厘米,面积是()平方厘米。
解析:12;9【典型例题3】长方形和正方形等长问题。
一根绳子,刚好可以做一个边长为8cm的正方形,如果用这根绳子做一个长是10cm的长方形,这个长方形的面积是( )cm2。
最新人教版五年级数学下册《第9单元单元第4课时 图形与几何(2)》精品PPT优质课件

三、巩固深化
1.下列运动属于什么现象,填一填。 ①电梯的上、下,属于( 平移 )现象。 ②车轮的转动,属于( 旋转 )现象。 ③观光缆车的移动,属于( 平移 )现象。 ④直升机螺旋桨的转动,属于( 旋转 )现象。
点D′、点C′,即可得 到旋转后的图形。
D′
C′
B′
问题 一个长方体的底面周长是28cm,高是4cm。这 个长方体的棱长总长是多少?
长方长体方有体多的少对条应棱的呢棱? 有底什面么周关长系等呢于?什么?
长方体有12条棱,相 底面周长= 对的棱的长度相等。 (长+宽)×2。
相交于同一顶点的三条棱的长 度分别是长方体的长、宽、高。
7.5×4×4+42×2=152(cm2) 4×4×7.5=120(cm3)
1.52×6=13.5(cm2) 1.53=3.375(cm3)
四、课堂小结
1. 观察物体 2. 旋转的特征和性质 3. 长方体、正方体的特征和性质
课堂作业
1.从书本练习中选择题目, 完成与本课时相关练习;
2.完成练习册本课时内容。
第4课时 图形与几何(2)
R·五年级下册
学习目标
1. 进一步提高学生观察立体图形的能力。把握立 体图形的特点。
2.进一步掌握旋转图形的特点,培养学生动手能 力。
3. 提高学生运用长方体正方体表面积和体积知识 解决实际问题的能力。
一、复习导入
思考
这是小明从正面看到的图形,如果用 6个同样的小正方体可以怎样摆呢?
今自天己我想们一继想续,复画习一图画。 形与几何的内容。
二、知识梳理
五年级数学图形的变换知识点讲解

五年级数学图形的变换知识点讲解
关于五年级数学图形的变换知识点讲解
1、轴对称图形:把一个图形沿着某一条直线对折,两边能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
2、成轴对称图形的`特征和性质:
①对称点到对称轴的距离相等;
②对称点的连线与对称轴垂直;
③对称轴两边的图形大小形状完全相同。
3、物体旋转时应抓住三,不改变物体的形状、大小。
北师大版五年级上册数学 第4课时 图形与几何 知识点梳理重点题型练习课件

解析:种花的面积=梯形空地的面积-两条平行四 边形小路的面积;用种花的面积乘每平方米花的费 用即可求出在这块梯形空地上种满花的费用。
解析:根据长方形的特征可知,长方形AEDF的面 积等于三角形AED面积的2倍,又因为三角形AED 的面积等于平行四边形ABCD面积的一半,所以长 方形AEDF的面积等于平行四边形ABCD的面积。
2.选择。 (1)下面的图形中,对称轴条数最多的是( A )。
解析:选项A有无数条对称轴;选项B有5条对 称轴;选项C有6条对称轴,故选A。
解析:借助方格图数格子估算,大于等于半格的 算1格,不满半格的舍去,大约有31格,所以这片 叶子的面积约是31 cm2。
(3)如图,一个平行四边形被分成3个三角形A、B和 C。已知三角形C的面积是12平方厘米,且三角形 B的面积是三角形C面积的一半,那么这个平行四 边形的面积是( 36 )平方厘米。
(2)从一张面积是48 cm2、上底是5 cm、下底是11 cm 的直角梯形纸中剪下一个最大的直角三角形,这 个直角三角形的面积是( C )cm2。 A.15 B.22 C.33
解析:根据题意易求得梯形的高为48×2÷(5+ 11)=6(cm),所以剪下的最大直角三角形的底是 11 cm,高是6 cm。
解析:三角形C的面积是12平方厘米,三角形B的 面积是它的一半,则三角形B的面积是12÷2=6(平 方厘米)。由图可知,三角形B和三角形C的面积之 和是平行四边形面积的一半,所以平行四边形的面 积是(12+6)×2=36(平方厘米)。
(4)平行四边形ABCD的底是10 cm,高是4.9 cm (如图),长方形AEDF的面积是( 49 )cm2。
3.(1)求组合图形的面积。(单位: cm) 45×30-(8+12)×10÷2= 1250(cm2)
第四讲组合体视图线面分析法

运用线、面的空间性质和投影规律,分析形体 的表面或表面间的交线与视图中图线和线框的对应 关系,进行画图、看图的方法,称为线面分析法。
这种方法主要用来分析视图中的局部复杂投影。
对于用切割方式形成的组合体,常常利用“视图 上的一个封闭线框一般情况下代表一个面的投影”的 投影特性,对体的主要表面的投影进行分析、检查, 可以快速、正确地读、画出图形。
二.看图时要注意的几个问题
① 要弄清视图中“图线”的含义 通常,视图中的图线表示:
1. 具有积聚性的表面(平面或柱面)的投影; 2. 两个邻接表面(平面或曲面)交线的投影; 3. 曲面的转向线的投影。
② 要弄清视图中“线框”的含义 通常,视图中的线框表示:
1. 形体表面(平面或曲面)的投影(封闭线框); 2. 孔洞的投影(封闭线框); 3. 相切表面的投影(表示为封闭线框或含有不封闭线 框)。
1'4'5'8'
6'7'
2'3' 4
3 65
27 8 1
4"
5"
8"
1" 步骤二
6"
7"
3"
2"
步步骤骤三三
完成
例5.由主、俯视图,画左视图 分 析
小结:
⑴ 形体分析法和面形分析法两者的读图步骤虽然相 似,但形体分析法是从体的角度出发,划分视图所 得的三个投影是一个形体的投影;而线面分析法是 从面的角度出发,“分线框对投影”所得的三个投 影是一个面的投影。
⑵ 形体分析法较适合于以叠加方式形成的组合体, 面形分析法较适合于以挖切方式形成的组合体。
由于组合体的组合方式往往既有叠加又有挖切, 所以看图时一般不是独立地采用某种方法,而是两 者综合使用,互相配合,互相补充。
北师大版五年级数学下册总复习 第4课时 图形与几何(1)课件ppt

正方体的展开图有以下几种情况:
第一类,中间四连方,两侧各一个,共六种。(141)
第二类,中间三连方,两侧各一、二个,共三种。(231)
第三类,中间二连方,两侧各二个,只有一种。(222) 第四类,两排各有3个,只有一种。(33)
观察展开图,你发现了什么?
正方体展开图的每个面都是正方形, 正方形的边长就是正方体的棱长。
无盖的长方体的表面积=长×宽+长×高× 2+宽×高× 2
无盖的正方体的表面积=棱长×棱长× 5
随堂练习
课堂小结
通过这节课的学习活动,你有什么收获?
课后作业
1.从课后习题中选取; 2.完成练习册本课时的习题。
生命是一种语言,它为我们转达了某 种真理;如果以另一种方式学习它, 我们将不能生存。 —— 叔本华
长方体的展开图。
长方体6个面的总面积,叫做它的表面积。 长方体的表面积=上+下+前+后+左+右
长高宽
长方体的表面积 =上+下+前+后+左+右 =长×宽+长×宽+长×高+长×高+宽×高+宽×高 =(长×宽)×2+(长×高)×2+ (宽×高)×2 =(长×宽 + 长×高 + 宽×高)×2
正方体的表面积=棱长×棱长× 6
总复习
第4课时 图形与几何(1)
北师大版 五年级下册
知识回顾
1.关于长方体和正方体,你都学会了哪 些知识?
长方体 长=宽=高
正方体
正方体是特殊的长方。
正方体可以看成是长、宽、高都相等的长方体。 我们可以用下图来表示长方体和正方体的关系。
长方体 正方体
2.下面哪个平面展开图折叠后所围成的图 形是正方体?说一说你是如何判断的。
新北师大版五年级数学上册:第4讲轴对称与平移2--学生版

教学辅导教案1、下面的图形中,()不是轴对称图形。
A. B. C. D.2、画出下面各轴对称图形所有的对称轴。
3、以虚线为对称轴,在方格纸上画出轴对称图形的另一半。
第1页共12页4、看镜子,写出数字或时间。
(1)看镜子,写数字:(2)看镜子,写时间:5、甲乙两个粮库原来存粮一样多,乙粮库运走12吨后,甲粮库的粮食是乙粮库的2倍。
甲乙粮库原来各有多少吨?一、填空:1、在属于平移的图形旁边的括号里画上“√”.2、平移不改变图形的()和(),只改变图形的()。
3、平移前后图形的面积()。
(选填“变大”“变小”或“不变”)二、判断:1.风车运动是平移。
()2.一个三角形经过平移后得到。
()3.火箭升空是平移现象。
()知识梳理:1.平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
2.平移的基本性质:(1)平移不改变图形的形状和大小,只改变图形的位置。
(2)经过平移,对应线段,对应角分别相等;对应点所连的线段平行且相等。
3.平移图形的画法:(1)确定平移的方向与距离。
(2)将关键点按所需方向平移所需距离。
(3)按原来图形的连接方式依次连接各对应点并标上相应字母。
设计图案的基本方法:平移、对称、旋转。
1.运用旋转设计图案的方法:(1)选好基本图案;(2)根据所选的基本图案确定旋转点;(3)确定旋转度数;(4)依次沿每次旋转后的基本图形的边缘画图。
2.运用对称设计图案的方法:(1)先选好基本图案;(2)依据基本图案的特点定好对称轴;典例分析:【知识点一:平移的概念和规则图形的平移进行辨析】【例1】(1)下列日常生活中,不属于平移现象的是()A、飞机在跑道上加速滑行B、大楼电梯上上下下迎送来客C、时钟上的秒针不断地转动D、滑雪运动员在白茫茫平坦的雪地上滑行(2)下列现象属于平移的是()A、钟摆的摆动B、打气筒打气时,活塞的运动C、拉开门开门或者关门D、司机手中转动的方向盘【例2】(1)下列图形中,是由原图平移得到的图形的是()(2)下列图案通过平移得到的是()(3)下列图形中,经过平移可以完全重合的是()(4)下列三幅图,那个是通过平移得到的()(5)下列三幅图,哪个是通过平移得到的(【例3】(1)将图形平移,只要知道()就能确定平移后的位置A、平移的方向B、平移的距离C、平移的角度D、平移的方向和距离(2)经过平移后,图形与原图形()A、重合B、不重合C、不一定重合(3)关于图形平移,下列说法错误的是()A、图形上每一点移动的方向相同B、图形上每一点移动的距离相等C、图形上对应两点的连线长度不变D、图形上可能存在不动点【知识点二:图形在方格中的上、下、左右平移及平移格数的数法和路线】【例4】(1)图中的松树()(2)图形①向右平移()格得到图形②(3)图形A向右平移()格得到图形B(4)将下图方格纸图中上面的图形平移后与下面的图形拼成一个长方形,那么正确的平移方法是()A. 先向下移动1格,再向左移动1格B. 先向下移动1格,再向左移动2格C. 先向下移动2格,再向左移动1格D. 先向下移动2格,再向左移动2格(5)虚线图形向右平移()格得到实线图形【例5】(1)填空(2)如下图所示,图形(1)向______平移了_______格;图形(2)向______平移了_______格图形(3)向______平移了_______格(3)仔细观察,回答下列问题:小船先向______平移了_______格,再向______平移了_______格,最后向______平移了_______格。
学而思-第四讲-长方体和正方体
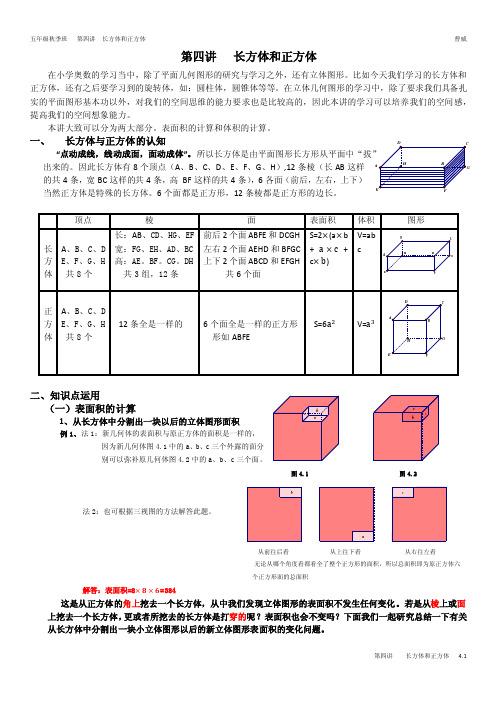
小的长方体 60块 ,那么这 60块长方体表面积的总和是 多少平方米?答案: 96平方米
(2)三个小正方体拼成如图右所示,表面积比原来少了 100平方厘米,求这个图形的体积?
答案:375立 方厘米
3、堆积体的 表面积问题 对于 由若干个小正方体堆积而成的不规则 立体图形的表面积,只要掌握“三视 图”的这个法宝即可 。
比原来正方体的总面积多两个 AEFB 的面积。
解答:表面积=8
+(2 ) =396
(2)如图 4.4 从棱长为 8 的正方体的面上挖去一个 2
的长方体形成一个新的几何体, 求该几何体的表面积?
分析:由图 4.4 可知,挖去后新几何体中的 BFHC 面可弥补原正方体的 AEGD 面。此时已经构成了原正方体的 6 个
2 个 AEFB 面,上下面则没有发生变化,( EHGF 面可弥补 ABCD 面)。因此,新几何体的表面积总体来说比
原来正方体的总面积少了 2 个 AEHD 面而多了 2 个 AEFB 面。
解答:表面积=8
-(2 ) +(2 ) =400
(5)如图 4.7 从棱长为 8 的正方体的面上挖去一个 2
的长方体形成一个新的 几何体,求该几何体的表面积?
分析:由图 4.7 可知,新几何体的前后两个面比原来的正方体前后面也是共少了 2 个 AEHD 面,而左右面共多了
2 个 AEFB 面,上下面也多了 2 个 EHGF 面。因此,新几何体的表面积总体来说比原来正方体的总面积少了
2 个 AEHD 面而多了 4 个内壁面积(2 个 AEFB+2 个 EHGF)。
体有几个。答案:8块 (此题为1层的长方体)
第四讲 长方体和正方体 4.4
五年级秋季班 第四讲 长方体和正方体
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四讲图形问题
【本讲知识点】
1、图形的计数
2、图形的计量
3、图形的变换
4、立体图形
【例题】
1、下图有10个点,连结相邻3个点所构成的三角形面积均为1,以其中任意3个点为顶点且面积为2的三角形有几个?
2、在一个正方形内有n个点,加上正方形的4个顶点共(n+4)个点,现将正方形分割成以这(n+4)个点为顶点的三角形,最多能分成多少个?
3、用同样大小的长方形小纸片摆成下图所示图形,已知每张小纸片的宽是12cm,求阴影部分面积。
4、在下图的平行四边形ABCD中,E,F分别是所在边的中点。
问:与△BFC面积相等的三角形有哪些?
5、如下图所示,将四边形ABCD的各边都延长一倍,得到的新四边形A’B’C’D’的面积是原四边形ABCD的几倍?
6、如下图所示的长方形ABCD 中,
2
1
==FD CF ED AE ,求△ABE 与△DEF 的面积之比。
7、将下图分成大小、形状都相同的四块,并且每块带黑子和白子各一个。
8、将一个4×4的正方形分割成三块,其中只有一块是正方形,并且它们拼成一个8×2的长方形。
9、在棱长为3cm 的正方体木块的每个面的中心上打一个直穿木块的洞,洞口是边长为1cm 的正方形(见下图)。
求挖洞后木块的体积及表面积。
10、一个正方体木块,棱长是15。
从它的八个顶点处各截去棱长分别是1,2,3,4,5,6,7,8的小正方体。
这个木块剩下部分的表面积最少是多少?
【习 题】
1、有一堆砖堆放如下图。
第一层有3块,第二层有8块。
第三层有15块……第99层有多少块?
2、用6条直线最多能将一个圆分成几部分?用100条直线呢?
3、在下图的平行四边形ABCD 中,E 、F 分别是AB 、BC 的中点,求三角形BEF 与平行四边形ABCD 的面积比。
4、在下图中,长方形的宽为长的3
2
,2AC=CD ,DE=EF ,△ABC 的面积是14cm ²,求阴影部分的面积。
5、两个边长为2cm 的正方形,其中一个的顶点在另一个的中心上(如下图),求这两个正方形不重合部分的面积和。
6、将下图所示的图形剪拼成一个中间有一个方孔的正方形。
7、有一个棱长为5cm 的正方体木块,从它的每个面看都有一个穿透的完全相同的孔(下图),求这个立体图形的内、外表面的总面积。
8、用6块下图所示(单位:cm )的长方体木块拼成一个大长方体,有许多种拼法。
其中表面积最小的是多少?。
