太原理工大学2011级《线性代数》练习册(一)

合集下载

(完整word版)线性代数习题集(带答案)

第一部分专项同步练习第一章行列式一、单项选择题1．下列排列是5阶偶排列的是 ( ）.（A) 24315 （B) 14325 （C ） 41523 (D)24351 2．如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是（）. (A ）k (B ）k n - （C)k n -2! （D)k n n --2)1(3. n 阶行列式的展开式中含1211a a 的项共有( ）项。

(A) 0 （B ）2-n （C ） )!2(-n (D) )!1(-n4．=0001001001001000( ）。

(A ） 0 (B)1- (C) 1 （D) 25. =0001100000100100( ）.(A) 0 (B)1- (C ） 1 (D) 26．在函数100323211112)(x x x x x f ----=中3x 项的系数是( ）.(A) 0 （B ）1- (C) 1 （D) 27。

若21333231232221131211==a a a a a a a a a D ，则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ）. (A ） 4 (B) 4- (C) 2 （D ） 2-8．若a a a a a =22211211，则=21112212ka a ka a ( ）。

（A)ka (B)ka - (C ）a k 2 (D)a k 2-9．已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-，则=x （ )。

（A) 0 (B)3- (C) 3 (D) 210. 若5734111113263478----=D ,则D 中第一行元的代数余子式的和为( ). (A ）1- (B ）2- (C ）3- （D ）011. 若2235001011110403--=D ，则D 中第四行元的余子式的和为( ）。

线性代数习题及解答完整版

线性代数习题及解答完整版线性代数习题及解答HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】线性代数习题一说明：本卷中，A -1表示方阵A 的逆矩阵，r (A )表示矩阵A 的秩，||α||表示向量α的长度，αT表示向量α的转置，E 表示单位矩阵，|A |表示方阵A 的行列式. 一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1．设行列式111213212223313233a a a a a a a a a =2，则111213313233213122322333333a a a a a a a a a a a a ------=（） A ．-6 B ．-3 C ．3D ．62．设矩阵A ，X 为同阶方阵，且A 可逆，若A （X -E ）=E ，则矩阵X =（） A ．E +A -1B ．E -AC ．E +AD ．E -A -13．设矩阵A ，B 均为可逆方阵，则以下结论正确的是（）A ．??A B 可逆，且其逆为-1-1A B B ．??A B 不可逆 C ．??A B 可逆，且其逆为-1-1?? ???B AD ．??A B 可逆，且其逆为-1-1??A B 4．设α1，α2，…，αk 是n 维列向量，则α1，α2，…，αk 线性无关的充分必要条件是（）A ．向量组α1，α2，…，αk 中任意两个向量线性无关B ．存在一组不全为0的数l 1，l 2，…，l k ，使得l 1α1+l 2α2+…+l k αk ≠0C ．向量组α1，α2，…，αk 中存在一个向量不能由其余向量线性表示D ．向量组α1，α2，…，αk 中任意一个向量都不能由其余向量线性表示5．已知向量2(1,2,2,1),32(1,4,3,0),T T+=---+=--αβαβ则+αβ=（） A ．（0，-2，-1，1）TB ．（-2，0，-1，1）TC ．（1，-1，-2，0）TD ．（2，-6，-5，-1）T6．实数向量空间V ={(x , y , z )|3x +2y +5z =0}的维数是（）A ．1B ．2C ．3D ．47．设α是非齐次线性方程组Ax =b 的解，β是其导出组Ax =0的解，则以下结论正确的是（）A ．α+β是Ax =0的解B ．α+β是Ax =b 的解C ．β-α是Ax =b 的解D ．α-β是Ax =0的解8．设三阶方阵A 的特征值分别为11,,324，则A -1的特征值为（） A ．12,4,3 B ．111,,243C ．11,,324D ．2,4,39．设矩阵A =121-，则与矩阵A 相似的矩阵是（）A ．11123--B ．01102C ．211- D ．121-10．以下关于正定矩阵叙述正确的是（） A ．正定矩阵的乘积一定是正定矩阵 B ．正定矩阵的行列式一定小于零 C ．正定矩阵的行列式一定大于零D ．正定矩阵的差一定是正定矩阵二、填空题（本大题共10小题，每空2分，共20分）请在每小题的空格中填上正确答案，错填、不填均无分。

线性代数习题集(带答案)

第一部分专项同步练习第一章行列式一、单项选择题1．下列排列是 5 阶偶排列的是( ).(A) 24315 (B) 14325 (C) 41523 (D)243512．如果n 阶排列j1 j2 j n 的逆序数是k , 则排列j n j2 j1的逆序数是( ).n!(A) k (B) n k (C) k2n(n 1) (D) k23. n 阶行列式的展开式中含a11a12 的项共有( )项.(A) 0 (B) n 2 (C) (n 2)! (D) (n 1)!0 0 0 14．11( ).1 0 0 0(A) 0 (B) 1 (C) 1 (D) 20 0 1 05.011( ).1 0 0 0(A) 0 (B) 1 (C) 1 (D) 22x x 1 16．在函数1 x 1 2f (x) 中3 2 x 33x 项的系数是( ).0 0 0 1(A) 0 (B) 1 (C) 1 (D) 217. 若a a a11 12 131D a a a ，则21 22 232a a a31 32 332aa13a33a11a312a122a3211D 2a a a 2a ( ).1 21 23 21 222a31(A) 4 (B) 4 (C) 2 (D) 2a a11 ，则128．若 aa a21 22 a12a11ka22ka21( ).2 (D) k2a (A)ka (B) ka (C) k a9．已知 4 阶行列式中第 1 行元依次是4, 0, 1, 3, 第 3 行元的余子式依次为2, 5,1, x, 则x ( ).(A) 0 (B) 3 (C) 3 (D) 28 7 4 310. 若6 2 3 1D ，则D 中第一行元的代数余子式的和为( ).1 1 1 14 3 7 5(A) 1 (B) 2 (C) 3 (D) 03 04 011. 若1 1 1 1D ，则D 中第四行元的余子式的和为( ).0 1 0 05 3 2 2(A) 1 (B) 2 (C) 3 (D) 0x 1 x2kx312. k 等于下列选项中哪个值时，齐次线性方程组x1 kx2x30 有非零解.kx1 x2x3( )(A) 1 (B) 2 (C) 3 (D) 0二、填空题21.2n阶排列24 (2n)13 (2n 1) 的逆序数是.2．在六阶行列式中项a32a54a41a65a13a26 所带的符号是.3．四阶行列式中包含a22a43 且带正号的项是.2 n4．若一个n 阶行列式中至少有n 1个元素等于0 , 则这个行列式的值等于.1 1 1 05.行列式11111.0 0 1 00 1 0 00 0 2 06．行列式.0 0 0 n 1n 0 0 0a 11 a1(n1)a1n7．行列式a21a2(n1) 0 .an10 0a11a12a13a11a133a123a128．如果D a a a M21 22 23 ，则D a a 3a 3a .1 21 23 22 22a 31 a32a33a31a333a323a329．已知某5 阶行列式的值为5，将其第一行与第 5 行交换并转置，再用 2 乘所有元素，则所得的新行列式的值为.31 1 1 x 110．行列式11 x11x 1111. x 1 1 1 11 1 11 1 111．n 阶行列式.1 1 112．已知三阶行列式中第二列元素依次为1,2,3, 其对应的余子式依次为3,2,1，则该行列式的值为.1 2 3 413．设行列式5 6 7 8D ，A4 j ( j 1,2, 3, 4) 为 D 中第四行元的代数余子式，4 3 2 18 7 6 5则4A41 3A42 2A43 A44 .a b c a14．已知c b a bD ， D 中第四列元的代数余子式的和为.b ac ca cb d1 2 3 43 34 4D ，A4 j 为a4 j ( j 1,2, 3, 4) 的代数余子式，则15．设行列式 61 5 6 71 12 2A41 A ，A43 A44 .4241 3 5 2n 11 2 0 016．已知行列式D 1 0 3 0 ，D 中第一行元的代数余子式的和为1 0 0 n.kx1 2x2x317．齐次线性方程组2x1 kx20 仅有零解的充要条件是.x 1x2x3x12x2x318．若齐次线性方程组2x2 5x30有非零解，则k = .3x1 2x2kx3三、计算题b a 2a 3a c dab2b3bcd ac2c3cbd ad2d3dbc;2．xyxyxyxyxyxy1.；x a1 a2an210 1 x 1 a1 x a2an211 0 1 x 3．解方程0x 1 1 0 ；4．a1a2x an21；1 x 1 0 a1 a2a x31a 1 a2a3an115a1 1 11 a 11 15. 1 1 a 12( a j 1,j 0,1, , n)；1 1 1 an1 1 1 13 1 b 1 16. 1 1 2 b 11 1 1 (n 1) b1 1 1 1 x a1a2anb 1 a1a1a1a1x a2an7. b1 b2a2a2；8．a1a2x an;b 1 b2b3ana1a2a3x2 1 0 0 01 2 x1 x x1 2x x1 n1 2 1 0 09. x2x11 22xx x2 n ; 10.0 1 2 0 0xnx1xnx21 2 xn0 0 0 2 10 0 0 1 21 a a 0 0 01 1 a a 0 011．D 0 1 1 a a 0 .0 0 1 1 a a0 0 0 1 1 a6四、证明题21 1a a 12a a21 1b b 12b b 1．设abcd 1，证明：021 1c c 12c c21 1d d 12d d .a 1b x1a x1b1c1a1b1c12． a2 bx2ax2b2c2(1 2 x ) a2b2c2.a 3b x3a x3b3c3a3b3c31 1 1 1a b c d3． 2 (b a)( c a)( d a)(c b)( d b)(d c)( a b c d)2 2 2a b c d .4 a4b4c d41 1 1a 1 a2an4．2a12a22nanai(a aj i) .i 1 1 i j nna12n2a2 nan2na1na2nna1 1 15．设a, b, c两两不等，证明 a b c 0的充要条件是 a b c 0.3 b3 c3 a7参考答案一．单项选择题A D A C C D ABCD B B二．填空题1. n ;2.“”;3. a14 a22 a31a43 ;4. 0 ;5. 0 ;6. ( 1) !n 1 n ;n( n1)7.( 1) 2 a1n a2(n1) a n1 ; 8. 3M ; 9. 160; 10. 4 x ; 11.( n 1n) ; 12. 2 ;n113. 0 ; 14.0 ;15. 12, 9; 16.n! (1 ) ; 17. k 2,3 ;18. k7k k1三．计算题3 y3 1．(a b c d)(b a)(c a)( d a)(c b)( d b)( d c) ； 2. 2(x ) ；n 13. x 2,0,1;4. (xk 1 a k )n n15. (a 1) (1 ) ;6. (2 b)(1 b) ((n 2) b) ;k a1k 0 k 0 k7.nn b a( 1) ( ) ; 8.k kn n( x a k ) (x a ) ;k k 1 k 1 k 1 n9. 1x ; 10. n 1;kk 12 a411. (1 a)(1 a ) .四. 证明题(略)8第二章矩阵一、单项选择题1. A 、B为n 阶方阵，则下列各式中成立的是( ) 。

2011考研数学1线性代数教材上要学习的任务和课后题

《考研数学学习进程监控习题汇编》线性代数部分
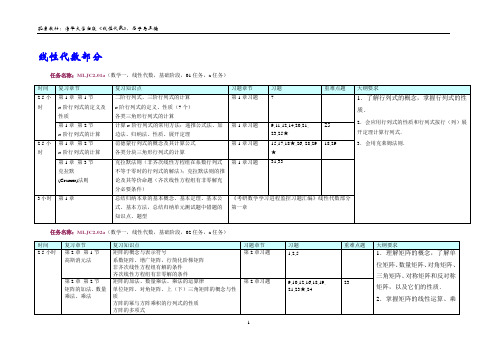
第二章
2.5小时
第3章第1节
n维向量及其线性相关性
n维向量的概念，n维实向量空间Rn的定义
向量的加法、数乘运算及其运算规则
向量的线性组合和线性表示的定义
向量组的线性相关、线性无关的定义
向量组线性相关性判定的几个定理
第3章习题
1,3,5,8,9,10,11★
26,27,28,29
25
3小时
第6章
总结归纳本章的基本概念、基本定理、基本公式、基本方法，总结归纳单元测试题中错题的知识点、题型
《考研数学学习进程监控习题汇编》线性代数部分
第五章
4
3(2)(3)
1．了解维向量空间、子空间、基底、维数、坐标等概念．
2．了解基变换和坐标变换公式，会求过渡矩阵．
3．了解内积的概念，掌握线性无关向量组正交规范化的施密特（Schmidt）方法．
4．了解规范正交基、正交矩阵的概念以及它们的性质．
第4章第2节
Rn中向量的内积、标准正交基和正交矩阵
内积的定义和运算性质
2．理解齐次线性方程组的基础解系、通解及解空间的概念，掌握齐次线性方程组的基础解系和通解的求法.
3．理解非齐次线性方程组解的结构及通解的概念．
4．掌握用初等行变换求解线性方程组的方法．
第3章第5节
非齐次线性方程组有解的条件及解的结构
非齐次线性方程组有解的几个等价命题（定理3.15）和推论
非齐次线性方程组的解的性质
2．掌握用正交变换化二次型为标准形的方法，会用配方法化二次型为标准形．
3．理解正定二次型、正定矩阵的概念，并掌握其判别法．
第6章第2节
化二次型为标准形

线性代数练习册附答案

姓名班级学号第1章矩阵习题1.写出下列从变量 x, y 到变量 x1, y1的线性变换的系数矩阵：x1x x1x cos y sin(1)；(2)x sin ycos y10y12.( 通路矩阵 ) a 省两个城市1 2和b省三个城市b1 2 3的交通联结情况如图所示，每条线a ,a,b ,b上的数字表示联结这两城市的不同通路总数.试用矩阵形式表示图中城市间的通路情况.4。

b1a1。

3 1。

b2a2。

22。

b3 1111233.设Α11 1 ，B124，求 3AB- 2A和A T B.1110514.计算22 11(1) 3 1 00 1 2a11a12b1x(2) (x, y, 1) a12a22b2yb1 b 2c1x1 2 y1y3y13z1z25.已知两个线性变换x22y13y 2 2 y3,y22z1z3, 写出它们的矩阵表x34y1y2 5 y3y3z23z3示式 ,并求从 z1 , z2 , z3到 x1 , x2 , x3的线性变换.姓名班级学号6.设0 m1 m- 1+,+ am，A是n阶方阵，定义f (A)= a0m1m- 1mE.f (x)= a x + a x A + a A+,+ a当 f (x)=x2- 5x+3，A21时，求 f (A).3 37.举出反例说明下列命题是错误的.2(1) 若A=O，则A=O.(2) 若A2= A，则A= O或A= E..7.设方阵 A 满足 A2- 3A- 2E =O，证明 A 及 A- 2E 都可逆，并用 A 分别表示出它们的逆矩阵．8.用初等行变换把下列矩阵化成行最简形矩阵：1 2 31(1)A2 4 621 231姓名班级学号3 14 2 2 10 1 1.(2) B2 134 1 1 433 09. 对下列初等变换，写出相应的初等方阵以及B 和 A 之间的关系式 .1 0 1 210 1 21 0 0 2A 23 1 2 ~0 3 3 2 ~0 332 =B .112r2 r112cc11 3 112113110.设P1APΛ，其中P1 4，Λ10，求A9. 11024 0011. 设A0 30，矩阵B满足AB=A+2B，求B.0 02姓名班级学号10212. 设A212, 利用初等行变换求A-1 .533复习题一1. 设A ,B , C 均为 n 阶矩阵，且 ABC =E , 则必有（） .( A) ACB =E ； (B) CBA = E ； ( C) BAC =E ； (D ) BCA =E .a 11 a 12 a 13a 21 a 22 a 23 2. 设 Aa 21a 22a23, Ba11a12a13,a31a32a33a 31 a 11 a 32a 12a 33 a 130 1 0 1 0 0P 11 0 0 , P2 0 1 0 ，则必有 () .0 0 11 0 1(A) AP 1 2=B ；（） 2 1 ； 1 2A =B ；2 1A =B .P B AP P =B ( C)PP( D)PP 3. 设A 为4 阶可逆矩阵，将 A 的第１列与第４列交换得B ，再把 B 的第 2 列与第 3 列交换得 C ，设0 0 11 0 0 0P 10 10 0，P 20 01 0 ，则 C -1=（） .0 0 1 0 0 1 0 0 1 0 0 00 0 0 1- 11 2 ； (B) P 1 -1 2 ；(C) P 2 1 - 1；(D) P 2-11.(A)A PPA P P AA P4. 设 n 阶矩阵 A 满足 A 2- 3A +2E =O ，则下列结论中一定正确的是（）.(A) A - E 不可逆； (B) A - 2E 不可逆； (C) A - 3E 可逆；(D) A -E 和 A -2E 都可逆 .Tn5. 设 A =(1,2,3) ， B =(1,1/2,1/3) ，令 C =A B ，求 C .姓名班级学号6.证明：如果 A k=O，则(E- A)-1=E+A+A2+, +A k-1，k为正整数.10031 7.设A, B为三阶矩阵 , A00-14,且A BA=6A+BA，求B.10071O A8. 设 n 阶矩阵A及 s 阶矩阵B都可逆，求.B O0a100000a2009. 设X（ a1 a2a n 0 ），求X-1.0000a n 1a n0000姓名班级学号第 2章行列式习题1.利用三阶行列式解下列三元线性方程组x12x2x322x1x23x31x1x2x303 1 x2.当 x 取何值时， 4 x 00 .1 0 x3.求下列排列的逆序数：(1) 315624 ；(2)13 ⋯(2n-1)24 ⋯(2n).a b c4.证明： a a b a b c a3.a 2ab 3a 2b c5. 已知四阶行列式|A|中第 2 列元素依次为1,2,-1,3，它们的余子式的值依次为3,-4,-2,0 , 求 |A|.姓名班级学号6.计算下列行列式 :11111 111(1)1 1 111111x y x y(2)y x y xx y x y0 1 111 0 11(3)1 1 011 1 101 x1x2(4) 1 x12x221 x13x231 a1111 1 a21a0 ．（5）D n，其中a a1 2n11 1 a n姓名班级学号7．设 n 阶矩阵A的伴随矩阵为A* ，证明：|A*| =|A|n-1， ( n ≥2) ．8.设 A, B 都是三阶矩阵，A*为 A 的伴随矩阵，且|A|=2， |B|=1，计算|-2A* B-1 |．2 119. 设A 2 10，利用公式求A-1.111姓名班级学号复习题二1．设A, B都是 n 阶可逆矩阵，其伴随矩阵分别为A*、B*，证明：( AB)* = B* A*．3 4 004 3 00，求 A-1．2.设 A0 0 200 0 223. 已知A1, A2, B1, B2都是 3 1 矩阵，设A=( A1, A2, B1,)，B=( A1, A2, B2 )，|A|=2，|B|=3，求 |A+2B|．E B4．设A, B都是 n 阶方阵，试证： E AB ．A E姓名班级学号第 3 章向量空间T2习题1T3T，计算 3α1- 2α23．1. 设α=(1,-1,1), α=(0,1,2), α=(2,1,3)+α2. 设α1=(2,5,1,3) T, α2=(10,1,5,10) T, α3=(4,1,-1,1) T, 且 3(α1- x)+2( α2+x)=5( α3+x) , 求向量x.3.判别下列向量组的线性相关性:T T T(1) α1=(-1,3,1) , α2=(2,-6,-2) , α3=(5,4,1)；Tβ2=(-1,4,0)T, βT .(2) β1=(2,3,0) ,3=(0,0,2)4. 设β1=α1, β2=α1+α2, β3=α1+α2+a3，且向量组α线性无关，证明向量组β, β2, β3线1,α2,α31性无关．5.设有两个向量组α1,α2,α3 和β1=α1-α2+α3,β2=α1+α2-α3,β3= -α1+α2+α3，证明这两个向量组等价 .6. 求向量组αT T T, αT 的一个极大无关组，并将其1=(1,2,-1), α2=(0,1,3), α3=(-2,-4,2)4=(0,3,9)余向量用此极大无关组线性表示.姓名班级学号7. 设 α1, α2,, , αn是一组 n 维向量，已知n 维单位坐标向量 ε能由它们线性表示，1, ε2,, , εn证明： α, αn 线性无关．1 , α2,,，其中 α线性无关， α+b α2,α5=c α2+d α3(a, b, c, d8. 设有向量组 α1, α2, α3, α4, α51, α2, α34=a α1均为不为零的实数 ) ，求向量组 αα3, α4, α5 的秩．1,9. 设矩阵 A = (1,2, ⋯ ,n), B =(n,n-1,⋯ ,1)，求秩 R(A T B ).212 1 1 1 21 12 1 4A 的一个最高阶非零子式 .10. 设矩阵 A6 2 2 ，求 A 的秩，并写出 4 4 3697 91 2 0 3 2 0 4 211. 已知矩阵 At 5 t 4 1 1 02 1，若 A 的秩 R(A )=2 ，求参数 t 的值 .22姓名班级学号23540 2 6412.设A，求A的列向量组的秩，并写出它的一个极大无关组.1 1533 1 95213. 设A为 n 阶矩阵，E为 n 阶单位矩阵，证明：如果A =A,则R( A)+ R(A- E )=n．2314.已知向量空间R3的两组基为100- 110α11 , α21, α31和β1 1 , β21, β31，001011求由基α, α3到基β的过渡矩阵 .1,α21,β2,β3 24姓名班级学号复习题三k 1 111 k 111.设矩阵A1 1 k11 1 1 k，已知 A 的秩为3，求k的值.2．设向量组A: α1, , , αs与B: β1,,, βr，若A组线性无关且 B 组能由 A 组线性表示为( β1,βr)＝(α1, , ,αs)K，其中K为s r矩阵 , 试证：B组线性无关的充分必要条件是矩阵K,,的秩 R(K)＝ r .253．设有三个n维向量组A：α1,α2 α3；B：α1α2,α3α4；C：α1α2,α3α5．若 A 组和 C 组,,,,,都线性无关，而 B 组线性相关，证明向量组α1,α2,α3,α4-α5 线性无关．T T T T T T 4．设向量组A: α1=(1,1,0) , α2=(1,0,1) , α3=(0,1,1)和B:β1=(-1,1,0) ,β2=(1,1,1) ,β3=(0,1,-1)3(1) 证明：A组和B组都是三维向量空间R 的基；(2)求由 A 组基到 B 组基的过渡矩阵；(3)已知向量α在 B 组基下的坐标为(1,2,-1)T,求α在 A 组基下的坐标．26姓名班级学号第4 章线性方程组习题x1x251. 写出方程组2x1x2x32x4 1的矩阵表示形式及向量表示形式.5x13x22x32x432.用克朗姆法则解下列线性方程组bx ay2ab2cy 3bz bc ,其中 abc0cx az027x1x2x303.问,取何值时，齐次线性方程组x1x2x30 有非零解？x1 2 x2x30x1x2k x344.设有线性方程组 - x1kx2x3k 2，讨论当k为何值时，(1) 有唯一解？ (2)有无穷x1x22x34多解？(3) 无解？28姓名班级学号x18x210 x32x405. 求齐次线性方程组2x14x25x3x40的一个基础解系.3x18x2 6 x32x406. 设四元非齐次线性方程组的系数矩阵的秩为3，已知η是它的三个解向量，且1,η2,η3η1=(2,3,4,5) T, η2+η3=(1,2,3,4) T，求此方程组的的通解．297 . 求下列非齐次线性方程组的通解：x 1 x 252x 1 x 2 x 3 2x 415x 1 3x 2 2 x 3 2x 431 2 1 112 ,2131及向量3，8.设有向量组 A ： αα， α311问向量 β能否由向量组A 线性表示？30姓名班级学号9.设η* 是非齐次线性方程组AX=b的一个解，ξ1, ξ2,, , ξn-r是它的导出组的一个基础解系，证明：（ 1）η*, ξ线性无关；1,ξ2,, ,ξn-r n-r 线性无关．（ 2）η*, η*+ ξ12, η*+ ξ,,, η*+ ξ复习题四1 2 121. 设A0 1 a a ，且方程组AX =θ的解空间的维数为2，则 a=.1 a 012．设齐次线性方程组a1 x1+a2x2+⋯ +a n x n=0,且 a1,a2,⋯,a n不全为零，则它的基础解系所含向量个数为.3. 设有向量组π：α1=( a,2,10)T2T3T及向量β=(1,b,-1) T，问 a, b 为何值时 , , α=(-2,1,5), α=(-1,1,4)（1）向量β不能由向量组π线性表示；（2）向量β能由向量组π线性表示，且表示式唯一；（3）向量β能由向量组π线性表示，且表示式不唯一，并求一般表示式．姓名班级学号4．设四元齐次线性方程组x1x20x1x2x30（Ⅰ）（Ⅱ）x2x40x2x3x40求:(1) 方程组 (Ⅰ ) 与(Ⅱ )的基础解系； (2)方程组 (Ⅰ )与( Ⅱ)的公共解．5．设矩阵A=(α,α,α,α)，其中α,α,α线性无关，α=2α-α，向量β=α+α+α+α，12342341231234求非齐次线性方程组Ax= β的通解．a1b1c16. 设a2,b2,c2,证明三直线a3b3c3l1 : a1x b1y c10l 2 : a2 x b2 y c20a i2b i20, i1,2,3l 3 : a3 x b3 y c30相交于一点的充分必要条件是向量组,线性无关，且向量组,, 线性相关．姓名班级学号第5 章矩阵的特征值和特征向量习题1. 已知向量α1=(1,-1,1)T，试求两个向量α23，使α1 2 3为R3的一组正交基．, α, α, α2. 设A, B都是 n 阶正交矩阵，证明AB 也是正交矩阵．3.设A是n阶正交矩阵，且|A|=-1 ，证明： -1 是A的一个特征值．2124.求矩阵533的特征值和特征向量.1 02姓名班级学号5. 已知三阶矩阵 A 的特征值为1,2,3 ，计算行列式|A3-5 A2+7E|．1245006.设矩阵A2x2与Λ0y0相似，求 x, y ；并求一个正交矩阵P，421004使 P-1AP=Λ．7.将下列对称矩阵相似对角化：220（1）212020400（2）031．013姓名班级学号A8. 设λ是可逆矩阵 A 的特征值，证明：(1)是A*的特征值．(2)当1,-2,3是3阶矩阵A 的特征值时，求A*的特征值．9. 设三阶实对称矩阵 A 的特征值为λ=6,λ=λ=3，属于特征值λ=6的特征向量为1231p1=(1,1,1)T，求矩阵A．姓名班级学号复习题五1.设 n 阶矩阵A的元素全为1，则A的 n 个特征值是．2.已知 3阶矩阵 A, A- E , E+2A 都不可逆，则行列式|A+E|=．1a10003.设 A a1 b ，B010 ，已知A与B相似，则a, b满足．1b10024.设 A 为2阶矩阵,α1,α2为线性无关的2维列向量， Aα1=0, Aα2=2α1+,α2，则 A 的非零特征值为.2 015. 已知矩阵A 3 1 x 可相似对角化，求x ．4 056. 设矩阵A满足A2- 3A+2E=O，证明A的特征值只能是1或 2．412 1 27. 已知 p 1 =(1,1,-1) T 是对应矩阵 A5a 3 的特征值的一个特征向量．1 b2(1) 求参数 a, b 及特征值； (2) 问 A 能否相似对角化？说明理由．8. 设3 2 ，求 φ 10- 5A 9．A3 ( A )=A242姓名班级学号第6章二次型习题1.写出下列二次型的矩阵表示形式：f x12x22x32x422x1 x24x1 x32x1 x46x2 x34x2 x411122.写出对称矩阵A 1 0 2 所对应的二次型．12233.已知二次型 f (x1, x2 , x3 ) x12x22ax324x1 x26x2 x3的秩为２，求a 的值．434.求一个正交变换将 f ( x1 , x2 , x3 ) 2x123x223x324x2 x3化成标准形．44姓名班级学号5.用配方法将二次型f x123x225x322x1 x2 4x1 x3化成标准形，并写出所用的可逆线性变换．6.设二次型 f2x123x223x322ax2 x3 (a 0) ，若通过正交变换x Py 化成标准形f y12 2 y22 5 y32，求a的值．457.判别下列二次型的正定性：（ 1）f2x126x224x322x1x2 2x1 x3（ 2）f x123x229x3219x422x1 x2 4x1 x3 6x2 x4 12x3 x48.设f x12x225x322ax1 x22x1 x34x2 x3为正定二次型，求 a 的取值范围．46姓名班级学号复习题六1. 设A为mT时，矩阵 B 为正定矩阵．n 矩阵，B=λE+A A，试证：λ>001001000,写出以A, A-1为矩阵的二次型，并将所得两个二次型化成标准形．2.设A0210012473. 已知二次曲面方程x12x22ax322bx1 x2 2x1 x3 5 ，通过正交变换X=PY 化为椭圆柱面方程y122y225，求 a， b 的值．101， B （k E 24.设矩阵A020A），其中k为实数，求对角矩阵Λ，使B101与Λ相似，并讨论k 为何值时，B为正定矩阵．48姓名班级学号测试题一一、计算题：2111. 计算行列式D n 131. 11n111002．设A0， B03 5 ，计算A3B T．20123．设A、B都是四阶正交矩阵，且B0， A * 为 A 的伴随矩阵,计算行列式2BAA * ．14．设三阶矩阵A与B相似，且A2，计算行列式 B 22E．31025．设A0a2，且 A 的秩为2，求常数 a, b 的值．11b142二、解答题：6．设i(1,t i ,t i2 ,t i3 ) T i 1,2,3, 4 ，其中 t1 ,t 2 , t3 , t4是各不相同的数，问4维非零向量能否由 1 , 2 , 3 , 4 线性表示？说明理由．x12x2x3x407．求齐次线性方程组3x16x2x33x40的一个基础解系．5x110 x2x35x40x1x2kx318．问k取何值时，线性方程组x1kx2x3kkx1x2x3k 2(1)有唯一解； (2) 有无穷多解； (3) 无解．9．已知四阶方阵A＝（1,2,3,4），其中1,2,3线性无关，42 3 3，求方49。

线性代数练习册第一章部分答案(本)

AAT AA A2 E
1 .AAT E; 3 . A2 E 2. AT A
AAT E A1 AT ; A2 E A1 A AT A1 A
或或
AAT E AAAT AE AT A
AAT E, A2 E A( AT A) 0, A可逆 A1 A( AT A) A1 0 AT A
2 −3 1 r2 − 2 r1 0 0 1 3 0 2r2 0 −1 −3 r − 2r 0 4 1
2 0 0
−3 1 10
2 −3 1 r1 + 3r2 0 1 0 1 3 0 r1 0 0 0 0 2 −4 −4 −2 −2 3 5 3 4 3 1 0 −1 −4 3 −4 1 −2 0 −2 −1
而 B11 所以，
(1)11 0 1 0 1 0 ， 11 211 0 2 0 2 0
11
1 4 1 0 1 1 4 A11 PB11 P 1 11 1 1 0 2 3 1 1 4 213 1 1 213 1 4 1 1 213 3 1 211 1 1 3 1 211 4 211 2731 2732 683 684
1 0 0
0 5 1 3 0 0
1 （2）B = 3 2 3 解：
−1 −3 −2 −3
3 5 3 4 −1 −3 −2 −3
1 B= 3 2 3 r2 − 3r1 r3 − 2r1 r4 − 3r1
1 0 0 0
3 −1 3 − 4 −8 0 −4 8 0 −3 6 −6 0 −5 10 −10 3 1 0 0 0 1 0 0 −4 −2 0 0 2 −2 0 0 3 2 0 0 −3 2 0 0

线性代数习题册参考解答.docx

第一章行列式1、求下列排列的逆序数，并确定它们的奇偶性。

(1) 1347265； (2) 〃(〃 —1)・・・321。

【解(1) r(1347265)=0 + 0 + 0 + 0 + 3 + l + 2 = 6,偶排列；(2) "〃(〃_1)...321] = 0 + ] + 2 + ... + (〃_1) = 〃(；1)。

当〃=4奴4女+ 1时，〃(〃；1)=2机4*—1),2机4* + 1)为偶数，即为偶排列；当〃 = 412,413时，丝* = (2*+1)(4*+ 1),(2*+1)(4*+ 3)为奇数,即为奇排列。

■2、用行列式定义计算2x x 1 21x1-1 f (X )=-- [3 2x1111%中『和r 的系数，并说明理由。

【解】由行列式定义可知：含b 有的项只能是主对角线元素乘积，故的系数为2；含有尸的项只能是(1, 2), (2, 1), (3, 3), (4, 4)的元素乘积项，而7(2134) = 0 + 1 + 0 + 0 = 1,故/的系数为一1. ■2-512 --37-14 3、求 =o45 -9 2 7 4-612【解】三角化法：2-5121-522 1-522 尸2+八1-12 0 6C[0 2-160 113D 4 =- _八3-211 1 0 3 0 113 0 2-16 r 4+r 211 0 60 1160 1161 -52 2 r3~2r 2 0 11 3r4~r 2 00 -3 00 0 31111 rk~r l0 10 0=120= 120o )l=2,3,40 0 100 0 0 1【解】箭形行列式（爪形行列式）：利用对角线上元素将第一行（或列）中元素1化为零。

1 x 2q+C2 +•••+&n D"=(，-就1 x 2-mi=l1x21 0 0C k -X L C I 凡 q (»i) k=2,3,---,n1 —m ••- 01 0…-m【解】观察特点: 行和相等。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一. 判断题（正确打√，错误打×）1. n 阶行列式ij a 的展开式中含有11a 的项数为1-n .( × ) 正确答案：)!(1-n解答：方法1因为含有11a 的项的一般形式是n nj j a a a 2211，其中n j j j 32是1-n 级全排列的全体，所以共有)!(1-n 项. 方法2 由行列式展开定理=212222111211nnn n nn a a a a a a a a a n n A a A a A a 111111+++2211 ，而n n A a A a 1111++22 中不再含有11a ，而11A 共有)!(1-n 项，所以含有11a 的项数是)!(1-n .注意：含有任何元素ij a 的项数都是)!(1-n .2. 若n 阶行列式ij a 中每行元素之和均为零，则ij a 等于零.( √ )解答：将nnn n nna a a a a a a a a 212222111211中的n 、、、 32列都加到第一列，则行列式中有一列元素全为零，所以ij a 等于零.3.3322441144332211000000a b b a a b b a a b a b b a b a =.( √ )解答：方法1按第一列展开332244114411414133224133224144332211=-=-=000000a b b a a b b a a b b a b b a a a b b a b b a b b a a a a b a b b a b a )(.方法2 交换2，4列，再交换2，4行2233441144332211443322110000000=0000000-=0000000a b b a a b b a a b b a a b b a a b a b b a b a =33224411a b b a a b b a . 方法3 Laplace 展开定理：设在n 阶行列式D 中任意取定了)(1-≤≤1n k k 个行，由这k 行元素所组成的一切k 阶子式与它们的代数余子式的乘积之和等于行列式D . 所以按2，3行展开3+2+3+2443322111-=000000)(a b a b b a b a 33224411a b b a a b b a =33224411a b b a a b b a . 4. 若n 阶行列式ij a 满足ij ij A a =,n j i ，， ,,21=,则0≥ij a .(√) 解答：由行列式展开定理nnn n nna a a a a a a a a 212222111211n n A a A a A a 111111+++=22110≥+++=2n a a a 1212211 .5. 若n 阶行列式ij a 的展开式中每一项都不为零,则0≠ij a .( × )解答：反例如0=4221.二. 单项选择题1. 方程0881441221111132=--x x x的根为（B ）. （A ）3,2,1；（B ）2,2,1-；（C ）2,1,0；（D ）2,1,1-. 解答：（范德蒙行列式）0=2-2+1-2+21-21-2-=88-144122-1111132))()()()()((x x x x x x ，所以根为2,2,1-.2. 已知a a a a a a a a a a =332312322211312113,那么=+2+2+232313312221232112111311a a a a a a a a a a a a 3（D ）. （A ）a ；（B ）a -； (C)a 2；（D ）a 2-. 解答： =+2+2+232313312221232112111311a a a a a a a a a a a a 3a a a a a a a a a a -223=32331222321121311。

3. 已知齐次线性方程组⎪⎩⎪⎨⎧=+-=-+=++0030z y z y x z y x λλλ仅有零解，则（A ）.（A ）0≠λ且1≠λ；（B ）0=λ或1=λ；（C ）0≠λ且1-≠λ；（D ）0=λ或1-=λ解答：因为⎪⎩⎪⎨⎧=+-=-+=++0030z y z y x z y x λλλ仅有零解，所以02-21-02-2111-01-311≠==）（λλλλλλλ，所以0≠λ且1≠λ.4.下列行列式中不一定等于n λλλ 21的是（B ）.（A ）nnna a a λλλ 000221121；（B ）nn n nna a a222100λλλ；（C ）nn n a a a λλλ 21221100；（D ）0-0000-0000-01-21nn λλλλ. 解答：注意nn n nna a a2221λλλ=21-1-)()(n n n λλλ 21；而0-0000-0000-01-21nn λλλλ =n n n λλλ 211-1-1-1-)()(=n λλλ 21. 5.n 阶行列式ij a D =展开式中项12,12,31,21n n n n n a a a a a --- 的符号为(D ).（A ）- ；（B ）+；（C ）2)1()1(+-n n ；（D ）2)1()1(--n n .三. 填空题1. 已知方程组⎪⎩⎪⎨⎧=+-=-+=++c z y x b z y x az y x 有唯一解,且1=x ,那么=--111111c b a 4 .解答：系数行列式4-=11-21-1=11-11-11=110111D ，而4-===11DD D x 1,所以4-=1D , 所以4=-=11-1-111-=1-111-11=1-1111-11D cba cb ac ba. 2. 已知4阶行列式中第3行的元素依次为4201-,,,，第4行的余子式依次为2510,,,a ，则=a 9.解答：行列式第4行的代数余子式依次为2=2⋅1--=⋅1-5=5⋅1-10-=10⋅1-4+43+42+41+4)(,)()(,)(a a故 0=2⨯4+-⨯2+5⨯0+10-⨯1-)()()(a ，解得 9=a .3. 若V 为n 阶范德蒙行列式,ij A 是代数余子式，则=∑=nj i ijA1,V .解答：V V AA A A Anj i ijn nj i ij=+=++++=∑∑===01,2112111, .4. =567890120114001030020001000 120 . 解答：方法1 1205678901201140010302010005541322314==a a a a a . 方法2 12024501141030200-51201140103002001000556789012011400103002001000=⨯===.5. 设xx x x xD 111123111212-=，则D 的展开式中3x 的系数为 -1 .解答：D 的展开式中有一项是344332112x a a a a -=-.或者按第一行展开：11123112111231111131111112112111123111212x x x x x x x x x x x xx x x x D ---+---=-=，由此可以看出3x 的系数为-1.四.计算题1. 已知4521011130112101--=D ，计算44434241A A A A +++.解答：方法144434241A A A A +++1111011130112101-=11111002011110112011011001131112001-=--=-=-=. 方法2=++434241A A A 00111011130112101=-，所以14444434241-==+++A A A A A .方法31172544434241-=-+--=+++A A A A .2. 计算行列式2-2-415-021-051-4611-2=D解答：2-2-415-021-051-4611-2=D 14125-2+c c c c 7-2-610001-20-5744-1327-2-620-574-131-⋅1-=1+3)()(7-2-6008-4-13-=120=7-2-4-11-8--=1+2))((.3. 计算行列式3833262290432231----解答：12811-1201565-022312383313119043223123833262290432231-=----=----5075462515-01281-215651121281-2-=-=--=.4. 计算行列式1111111111111111--+---+---x x x x解答：（行和相等）11111111111111111111111111111111-----+---=--+---+---x x x x x x x x .0000011110000011114x xx x x x x xxx x x x x x =------=-----=5. 计算行列式cc b b a a ------1100110011001解答：方法一110001000100011100100100011111001000111110011001==--=----=------c b a ccb a cc b ba cc b b a a 方法二cc b b a a ------11001100110011=1-0-11-0-11--=-11-00-11-00-11-10b b a cc bba 各行往第一行加5075462515-01281-215651121281-2-=-=--=.6. 计算行列式ba a a a a a ba a a a ab a n nn +++ 321321321解答：（行和相等）ba a a a a ba a a a ab b a a a a a a b a a a a a b a n nn n i i n n n +++=+++∑= 3232321321321321111)（.)0000001)11321-==∑∑+=+=n n i i nn i i b a b bb a a a a b （（7. 计算行列式n222232222222221. 解答：当2=n 时：22221-=；当2>n 时：各行分别减第二行得)!.2(22-000010022220001-222232222222221--==n n n 五．证明题1.设343123211211)(------=x x x x x x x f ，证明：存在(0,1) ξ∈，使得()0f ξ'=.证明：)(x f 是多项式，在[0,1]上连续，（0,1）内可导，且0=1=0)()(f f ，由罗尔定理即得结论.2.证明当1=λ时，行列式074717171616361615151525141414141=----λλλλ.证明：当1=λ时0.3-11013-10113-0111084013-11113-11113-11113-840174717171616361615151525141414141===----λλλλ（注：可编辑下载，若有不当之处，请指正，谢谢!）。