定位误差的计算方法.
定位误差的分析与计算_new

为保证加工要求,上述三项误差合成后应小于或等于
工件公差δ。
3
即:
△定+ △安-调+ △过 ≤ δ
在对定位方案进行分析时,可以假设上述三项误差各占工 件公差的1/3。
则有:
△定≤ δ/3
此就是夹具定位误差验算公式。
4
1. 造成定位误差的原因
造成定位误差的原因有两个。
⑴定位基准与设计基准不重合,产生基准不重合误 差△不。 ⑵定位基准与限位基准不重合,产生基准位移误差 △基(也叫定位副制造不准确误差)。
17
合成时,若设计基准不在定位基面上(设计基准 与定位基面为两个独立的表面),即基准不重合误 差与基准位移误差无相关公共变量。
△定=△基+△不 合成时,若设计基准在定位基面上,即基准不重 合误差与基准位移误差有相关的公共变量。
△定=△基±△不
18
+ - 确定方法:
定位基面与限位基面接触,定位基面直径由小变 大(或由大变小),分析定位基准变动方向。
本例中∆定1 > ∆定2 > ∆定3 。
26
3.常见定位方式定位误差的计算
⑴工件以平面定位
平面为精基面
基准位移误差 △基=0
定位误差
△定=△不
注:若为毛坯面,则仍有△基
27
⑵工件以内孔定位
28
①工件孔与定位心轴(或销)采用间隙配合的定位误 差计算 △定 = △不 + △基
工件以内孔在圆柱心轴、圆柱销上定位。由于孔与轴有配 合间隙,有基准位移误差,分两种情况讨论:
a.心轴(或定位销)垂直放置,按最大孔和最销轴求得孔 中心线位置的变动量为:
△基 = δD + δd + △min = △max =孔Dmax-轴dmin (最大间隙) b.心轴(或定位销)水平放置,孔中心线的最大变动量
一种简单的定位误差计算方法

一种简单的定位误差计算方法定位误差是物理系统和测量系统中非常重要的性能参数之一,它直接反映了定位精度和准确度,是衡量定位系统能力和性能的一个重要指标。
定位误差是指被测定位系统在被测点到它理论上应该对准的目标点上产生的位置偏移值,用来衡量系统定位准确度的指标。
本文主要介绍一种简单的定位误差计算方法。
在定位系统的测试中,测量系统的位置定位误差是一项重要的指标,但通常来说,一个点上的测量可能会出现多种错误,这些错误需要仔细计算才能得出最终的定位误差。
定位误差计算其实非常简单,当测量系统在一个点上进行测量时,有两个重要的量可以利用:测试点的绝对坐标和实际测量值(即系统实际定位到的位置坐标)。
有了这两个量,就可以很容易地计算出定位误差,方法是将两组坐标相减,差值就是定位误差。
定位误差计算方法的具体步骤如下:(1)测量系统在一个点上测量,标定实际位置的绝对坐标;(2)记录实际测量值,即系统实际定位到的位置坐标;(3)计算实际测量值和标定坐标的差值,结果就是定位误差;(4)若要精确衡量定位误差,可以按坐标轴,分别求出X轴和Y轴上的定位误差值;(5)根据测试结果,得出定位系统的性能参数,进而指导性能的改进和维护。
以上就是一种简单的定位误差计算方法,简单易行,同时可以准确测量定位系统的性能指标,有助于定位系统的运行和维护。
定位误差计算方法的应用非常广泛,它可以用于检测自动定位系统的性能,也可以用于映射定位和测试系统,还可以用于指导定位系统优化和改进。
因此,定位误差计算方法是极其有用的,它不仅可以测量定位系统的性能,还能帮助定位系统持续保持高性能。
另外,应用定位误差计算方法时,还需注意系统的温度变化、外部干扰等因素,可能会影响测量结果,甚至造成测量误差。
因此,在实际应用时,要根据不同的环境和条件来进行改进和调整,以提高测量精度。
总之,定位误差计算方法是一种简单而有用的测试方法,可以清楚地了解定位系统的性能参数,为定位系统的优化和改进提供有力的支持。
常见定位方式定位误差的计算
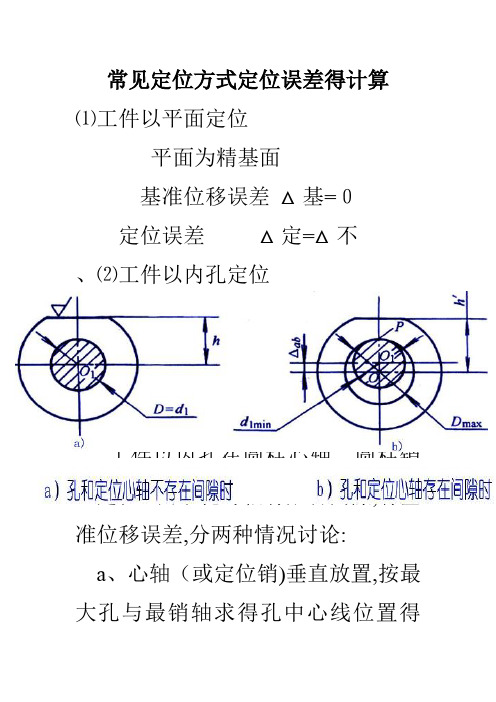
常见定位方式定位误差得计算⑴工件以平面定位平面为精基面基准位移误差△基=0定位误差△定=△不、⑵工件以内孔定位①工件孔与定位心轴(或销)采用间隙配合得定位误差计算△定= △不+ △基工件以内孔在圆柱心轴、圆柱销上定位。
由于孔与轴有配合间隙,有基准位移误差,分两种情况讨论:a、心轴(或定位销)垂直放置,按最大孔与最销轴求得孔中心线位置得变动量为:△基= δD+ δd+△min = △max =孔Dmax-轴dmin (最大间隙)b、心轴(或定位销)水平放置,孔中心线得最大变动量(在铅垂方向上)即为△定△基=OO'=1/2(δD+δd+△mi n)=△max/2或△基=(Dmax/2)-(dmin /2)=△max/2= (孔直径公差+轴直径公差) / 2②工件孔与定位心轴(销)过盈配合时(垂直或水平放置)时得定位误差此时,由于工件孔与心轴(销)为过盈配合,所以△基=0。
对H1尺寸:工序基准与定位基准重合,均为中心O,所以△不=0对H2尺寸:△不=δd/2⑶工件以外圆表面定位A、工件以外圆表面在V型块上定位由于V型块在水平方向有对中作用。
基准位移误差△基=0B.工件以外圆表面在定位套上定位定位误差得计算与工件以内孔在圆柱心轴、圆柱销上定位误差得计算相同。
⑷工件与"一面两孔"定位时得定位误差①“1”孔中心线在X,Y方向得最大位移为:△定(1x)=△定(1y)=δD1+δd 1+△1min=△1max(孔与销得最大间隙)②“2”孔中心线在X,Y方向得最大位移分别为:△定(2x)=△定(1x)+2δLd(两孔中心距公差)△定(2y)=δD2+δd2+△2min=△2max③两孔中心连线对两销中心连线得最大转角误差:△定(α)=2α=2tan-1[(△1max+△2max)/2L](其中L为两孔中心距)以上定位误差都属于基准位置误差,因为△不=0。
需要指出得就是定位误差一般总就是针对批量生产,并采用调整法加工得情况而言。
2.5定位误差的分析与计算(二) 改

D2 min X 2 min 则 b 2a
式中
X 2 min—菱形销与孔之间的最小配合间隙,mm;
a—满足工件顺利装卸的补偿量,mm。
a TLD TLd 2
LOGO
2.5 定位误差的分析与计算(二)
菱形销圆柱部分的宽度b可查手册确定, 则由上式得
Y O 1O 2 δ d 2 sin( / 2)
LOGO
2.5 定位误差的分析与计算(二)
M1
d max /2
d min /2
工序尺寸A3的定位误差
δ d 2
M2 O
工件定位 外圆直径 由大变小
δ d
ΔY O 1O 2
δ d 2 sin( α/ 2)
ΔB与ΔY同向
δ 1 Δ D=Δ Y+Δ B= d [ +1] 2 sin(α/ 2)
LOGO
A3
M2
2.5 定位误差的分析与计算(二)
M1
d max /2
d m in /2
O
δ d 2
d max /2
d mi n /2
C1 C2
ΔY O 1O 2
δ d 2 sin( α/ 2)
工件定位 外圆直径 由大变小
δ d
δ 1 Δ D=Δ Y-Δ B= d [ -1] 2 sin(α/ 2)
复习
1.定位误差的概念
(1)基准不重合误差 △ B (2)基准位移误差 △Y
2.工件以平面定位误差计算
精基准平面定位时,一般认定△Y=0, △D=△B
3.以圆孔定位时的定位误差计算
LOGO
Page 2
2.5 定位误差的分析与计算(二)
定位误差计算

• 4)计算出的定位误差数值是指加工一批工件时某加工精度参 数可能产生的最大误差范围(加工精度参数最大值与最小值 之间的变动量)。它是个界限范围,而不是某一个工件定位 误差的具体值。 • 5)一批工件的工序基准(设计基准)相对定位基准、定位基 准相对对刀基准产生最大位置变动量是产生定位误差的原因, 而不一定就是定位误差的数值。
关键:找出同一批工件的工序基准在工序尺寸方向上可能的最大位移变动量
方法1—合成法:
先分别求出基准位移误差和基准不重 合误差,再求出其在加工尺寸方向上的矢 量合,即Δdw =Δjb +Δjw
•当 Δjb 和Δjw 由两个互不相关的变量引起时,用“+”;
•当Δjb 和Δjw 是同一变量引起时,要判断两者对Δdw 的影
响是否同向,方向相同时“+”,方向相反时“-”。
分析计算定位误差时应注意的问题:
• 1)定位误差是指工件某工序中某加工精度参数的定位误差。 它是该加工精度参数(尺寸、位置)的加工误差的一部分。 • 2)某工序的定位方案对本工序的多个不同加工精度参数产生 不同的定位误差,应分别逐一计算。 • 3)分析计算定位误差的前提是用夹具装夹加工一批工件,用 调整法保证加工要求。
定位误差计算实例
1. L1
Δdw= Δjw
2. L2
L2 的定位误差为两者的合成。两者都是由外圆直径的变化同时引 起的,所以要判断两者的方向特点。
要判断两者的方向特点。
当外圆直径从大到小时,工序基准M相对定位基准O是向O 方向即向下偏移的。 当放入V形块中后,当外圆直径由大变小时,定位基准相对 与理论也是向下偏移的。 综合起来两者合成方向相同。
dw T (d ) T (d ) jw jb 2 sin 2 2
定位误差
解: 定位基准与工序基准重合 ΔB=0 定位基准O的变动方向与 加工尺寸39±0.04方向间的夹 角为30°
定位误差计算实例6
例6:如下图所示,求加工尺 寸A的定位误差。 解:(1)定位基准为底面, 工序基准为圆孔中心线O ,定 位基准与工序基准不重合。 ΔΒ=0.2mm 工序基准O的变动方向与加工 尺寸的方向间夹角为45º ,则: ΔΒ=0.2×cos45º =0.1414mm (2)平面定位ΔY=0 (3)ΔD=ΔΒ=0.1414mm
16
(2)工件以圆孔定位 2)水平放置时(单边接触)
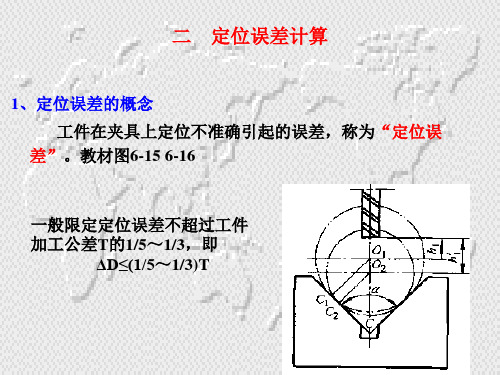
定 位 误 差 的 概 念 与 计 算
17
(2)工件以圆孔在圆柱销(心轴)上定位
定 位 误 差 的 概 念 与 计 算
D d D d m ax m i n m i n m ax O O OO OO Y 1 2 1 2 2 2
定位误差计算实例7
解: (1)对称度的工序 基准是Φ12H8的轴线,定 位基准是工件 Φ80±0.05mm的轴线, 两者不重合, ΔΒ=0.02mm
3)工件以外圆在V形块上定位
定 位 Td 误 Y 差 2 sin 2 的 概 如在加工尺寸方向上与垂直方向有一夹角β,则 念 在加工尺寸方向上的基准位移误差为 与 计 Td Y cos 算
2sin 2
V形块的对中性好,所以沿其水平方向的位移量为零。 如工件的加工尺寸方向与垂直方向相同,则在加 工尺寸方向上的基准位移误差为:
解:(1)A1的定位误差 1)工序基准是圆柱轴线,定位基准也是圆柱轴线, 两者重合,ΔB1 =0。 2)以圆柱面在的V形块上定位时, Td Y1 2 sin 2
定位误差计算实例4
机械制造工艺学03(定位误差)

(3)定位误差由基准位置误差和基准不重合误差两部
分组成,但并非在任何情况下这两部分都存在。定 位基准无位置变动,基准位置误差为零;定位基准 与工序基准重合,基准不重合误差为零。 (4)定位误差的计算可按定位误差的定义,根据所 画出的一批工件定位可能产生定位误差的良种极端 位置,再通过集合关系直接求得。也可按定位误差 的组成,由公式: δ定位=δ位置± δ不重 计算得到,根据一批工件的定位由一种可能的极端 位置变为另一种极端位置时δ位置和δ不重的方向的异同, 以确定公式中的加减号。
2、消除或减小基准不重合误差的措施 (1)尽可能以工序基准作为定位基准
(2)根据加工精度高低,选择第一、第二定位基准
四、工件定位方案设计及定位误差计算举例
1、 2、槽两侧面C、D对 B面的垂直度公差 0.05mm 3、槽的对称中心面 与两孔中心连线之 间的夹角为
(一)定位方案设计
1、按加工精度要求, 至少应限制五个不 定度,从加工稳定 性来说,可限制六 个不定度。 2、为保证垂直度,应 以B面作为定位基准, 但因B面较小,为稳 定考虑,选择A作为 基准。 3、为保证角度精度, 应以两孔轴线作为 定位基准。
2、圆孔表面定位时的定位误差 (1)工件上圆孔与刚性心轴或定位销过盈配合 基准位置误差: δ位置(O)=0
基准不重合误差:
(四)提高工件在夹具中定位精度的措施 即如何减少或消除基准位置误差和基准不重合误差。 1、减少或消除基准位置误差的措施 (1)选用基准位置误差小的定位元件 A、以毛坯平面作为定位基准时,可以多点自位支承取代 球头支承钉。 B B、以内孔和端面定位时,可应用浮动球面支承,以减小 轴向定位误差。
2、定位误差的组成及计算 定位误差主要由基准位置误差δ位置(O)和基准不重合误差δ不重(A) 组成。
定位误差的计算
差 范围±ΔH内波动),因而也就产生了定位误差(εA )。
定位误差大小计算
(1) 画出被加工零件定位时的两个极限尺寸的位置 (2) 从图形中的几何关系,找出零件图上被加工尺寸方向上
• ① ∆jb≠0, ∆jw=0 时, ∆dw=∆jb; • ② ∆jb=0, ∆jw≠0时, ∆dw=∆jw; • ③ ∆jb≠0,∆jw≠0时: 如果工序基准不在定位基准面上(工序基准与定位基面
是两个独立的表面),即∆jb 与∆jw无关联时, ∆dw=∆jb+∆jw; 如果工序基准在定位基准面上,即∆jb 与∆jw有关联时, ∆dw=∆jb±∆jw。
总结
二、定位误差的计算
1、定位误差计算的方法
工件定位误差的实质是工件上被加工表面的工序基准相对 于定位元件工作表面在加工尺寸方向上的最大变动量,因此, 计算定位误差时, 首先要找出工序尺寸的工序基准; 然后求其在工序尺寸方向上的最大变动量。
极限法
定位误差计算的方法
合成法
微分法
1)极限法
2
2
O E
A
(a)
用微小增量代替微分,并将尺寸误差视为微小增量, 且考虑到尺寸误差可正可负,各项误差应取绝对值,故定 位误差为:
dh
1
d cosa
Td
2 Ta
2sina
4sin2(a )
2
2
若使用同一夹具进行加工,则Ta=0
所以
H1
Td a
2 si n
2
同理:
CA
OA OC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定位误差的计算方法:
(1)合成法
为基准不重合误差和基准位移误差之和; (2)极限位置法
工序基准相对于刀具(机床)的两个极限位置间的距离就是定位误差; (3)微分法
先用几何方法找出工序基准到定位元件上某一固定点的距离,然后对其全微分,用微小增量代替微分,将尺寸误差视为微小增量代入,就可以得到某一加工尺寸的定位误差。
注:基准不重合误差和基准位移误差它们在工序尺寸方向上的投影之和即为定位误差。
例如:用V 型块定位铣键槽,键槽尺寸标注是轴的中心到键槽底面的尺寸H 。
T D 为工件定位外圆的公差;α为V 型块夹角。
1. 工序基准为圆柱体的中心线。
表示一批工件依次放到V 型块上定位时所处的两个极端位置情形,当工件外圆直径尺寸为极大和极小时,其工件外圆中心线分别出于点
O '和点O ''。
因此工序基准的最大位置变动量O O ''',便是对加工尺寸H 1所产生的定位误差: 故得:O
E O E H H O O 11DH
1
''-'='-''='''=ε O A E Rt 1''∆中: max 1
D 2
1A O ='' 2
sin A O O E 1α''=
'
O A E Rt 1''''∆中:min 1
D 2
1
A O ='''' 2
sin A O O E 1α''''=
''
2
sin 2T 2sin 2T 2sin A O A O O E O E D D
11DH
1
α=α=α''''-''=''-'=ε
2. 工序基准为圆柱体的下母线:
工件加工表面以下母线C 为其工序基准时,工序基准的极限位置变动量C C '''就是加工尺寸H2所产生的定位误差。
C
S C S C O O O H H 22DH 2
'-''=''-'''='-''=ε C O C O O O )
C O O S ()C O O S ('
'-''''+'''=''+'-'''+'=
而 2
sin
2T O O D α=
'''
min D 2
1C O =''''
max D 2
1
C O =''
所以:C O C O O O 2
DH ''-''''+'''=ε
)
12
sin
1(2T 2T 2sin 2T 2D D 2
sin
2T )D (21
)D (212sin 2T D D D max min D max min D
DH 2
-α=-α=-+
α=-+α=ε
3. 工序基准为上母线
如果键槽的位置尺寸采用上母线标注时,上母线K的极限位置变动量为K
K''
',就是对加工尺寸H3所产生的定位误差。
)1
2
sin
1
(
2
T
2
sin
2
T
2
T
2
sin
2
T
2
D
D
2
sin
2
T
)
D
(
2
1
)
D
(
2
1
O
O
K
O
K
O
)
O
O
K
O
(
K
O
K
O
K
O
H
H
K
K
D
D
D
D
min
max
D
min
max
3
3
DH
3
+
α
=
α
+
=
α
+
-
=
α
+
-
=
''
'
+''
''
-'
'
=
''
'
-''
''
-'
'
=
''
''
-'
'
=''
-
'
=''
'
=
ε
在V 型块中定位时的定位误差:
另外一种解法:
V 型块是一种对中定位元件,当V 型块和工件外圆制作的非常精确时,这时外圆中心应在V 型块理论中心位置上,即两中心重合而无基准位移误差。
但是实际上对于一批工件而言外圆直径是有偏差的,当外圆直径从Dmax 到Dmin 时,虽然工件外圆中心始终在V 型块的对称中心平面内而不发生左右移动,即V 型块在垂直于对称平面的方向无基准位移误差Δjw =0,但是工件外圆中心在V 型块的对称平面内发生上下偏移,即造成基准位移误差。
2
sin
2T 2sin 2T 2sin A O A O O E O E D
D
11jw α=α=α''''-''=''-'=∆
式中 T D ——工件定位外圆的公差;
即为基准位移误差大小。
当工序尺寸的标注方法不同时还可能产生基准不重合误差,铣键槽分别以中心线,上母线和下母线为工序基准,其基准不重合误差分别为:
0)H (1bc =∆
2T )H (D
2bc =∆
2
T )H (D
3bc =∆
而定位误差为基准不重合误差和基准位移误差在加工尺寸方向上的代数和。
)H ()H (i jw i bc dw ∆±∆=∆
2
sin
2T )H ()H ()H (D 1jw 1bc 1dw α=
∆±∆=∆
)12
sin
1(2T 2sin 2T 2
T )H ()H ()H (D D
D
2jw 2bc 2dw +α=α+
=∆+∆=∆)
12
sin
1
(2T 2T 2sin 2T )H ()H ()H (D D D
3bc 3jw 3dw -α=-α=∆±∆=∆补充作业:
如图所示工件以外圆柱面在V 型块上
定位,对内孔进行插键槽工序,
已知:外径d 为mm 500
03.0-φ; 内径D 为mm 3005.00
+φ
内外圆同轴度为0.02mm ,试计算用调整法加工这批工件时,工序尺寸H 的定位误差是多少?
解:
基准不重合误差:mm 025.02
05
.0c ==ε 基准位移误差: mm 021.02
90sin
203
.02sin 2T D
w ==α=ε
同轴度误差:mm 02.0=∆同轴度
则,定位误差为:
mm 066.002.0021.0025.0W C D =++ε+ε+ε=ε=同轴度。
