管道运输与订购优化模型(CAI)12
管道订购与运输问题-2000年全国数学建模竞赛B题优秀论文
管道订购与运输问题1 问题重述2 基本假设(1)只考虑订购费用和运输费用,不考虑装卸等其它费用. (2)钢管单价与订购量、订购次数、订购日期无关.(3)订购汁划是指对每个厂商的定货数量;运输方案是指具有如下属性的一批记录:管道区间,供应厂商,具体运输路线.(4)将每一单位的管道所在地看成一个需求点,向一单位管道的所在地运输钢管即为向一个点运输钢管.3 符号说明M :钢厂总数. n :单位管道总数.:i S 第i 个钢厂 :i S 第i 个钢厂的产量上限。
:i p 第i 个钢厂单位钢管的销售价 i A 管道线上第i 个站点。
i d 管道线上第i 个单位管道的位置。
F :总费用。
:ij C 从钢厂(1,2,,)i S i m =到点(1,2,,)j d j n =的最低单位费用。
4 问题的简化求 S AP 矩阵的基本思路是图的最短路算法 . 由于铁路的运输费用与线路的长度不是线性关系 ,必须对铁路网做一些预处理才能套用图的标准最短路算法 . 下面叙述求 S AP 矩阵的过程:1.利用图的标准最短路算法 ,从铁路网络得出图中任两个点之间的最短路径表 T (如果两个点之间不连通 ,认为它们之间的最短路长度为+ ∞ ) .2.利用题中的铁路运价表将 T 中的每个元素 (即最短距离 )转化为运输费用 ,将运输费用表记为 C.3.将公路的长度换算为运输费用 ,由公路路程图 (包括要沿线铺设管道的公路 )得出公路费用图 G,若 i, j 不连通 ,则令 Gij = + ∞ .4.对于任一组 ( i , j)∈ { 1,… n }× { 1,… m } 如果 Cij <+ ∞ ,且小于 Gij ,那么就在公路费用图中加一条边. 即令 Gij = min{Cij , Gij } .5.利用图的标准最短路算法 ,求公路费用图中任一个 S 点到任一个 A 点的最小费用路径 ,得出 S AP 矩阵. 如表 1所示:SAP 矩阵A123 4 5 6 7 8 9 10 11 12 13 14 15 S1 170716031402986 380 205 31 212 642 920 960 1060 1212 1280 14202 215720531902 1716 1110 955 860 712 1142 1420 1460 1560 1712 1780 19203 230722032002 1816 1210 1055 960 862 482 820 860 960 1112 1180 13204 260725032352 2166 1560 1405 1310 1162 842 620 510 610 762 830 9705 255724532252 2066 1460 1305 1210 1112 792 570 330 510 712 730 8706 265725532352 2166 1560 1405 1310 1212 842 620 510 450 262 110 2807 275726532452 2266 1660 1505 1410 1312 992 760 660 560 382 260 205问题分析运输费用等价转换法则:按单位运费相等原则将任意两点间的最短铁路线转换为公路 线.对于铁路线上的任意两点,i j V V ,用F1oyd 算法找出两点间最短铁路路线的长度ij L 查铁路运价表求得ij L ,对应的铁路单位运费ij f ;又设与该段铁路等费用的公路长度为ij l ,则:0.1ij ij f l =⨯由此,我们就在,i j V V 之间用一条等价的公路线来代替,i j V V 间的最短铁路线.如果,i j V V 之间原来就有公路,就选择新旧公路中较短的一条.这样,我们就把铁路运输网络转换成了公路运输网络.销价等价转换法则:按单位费用相等将任意钢厂的单位销价转换为公路单位运价.对于钢厂S i 的销售单价P i ,我们可以虚设一条公路线,连接钢厂S i 及另一虚拟钢厂'i s ,其长度为i l ,并且满足0.1i i l p =⨯;从而将钢厂的销售单价转换成公路运输单价,而新钢厂'i s 的销售价为0.将铁路和销价转换为公路的过程可以由计算机编程实现. 通过上述的分析,我们可以将原问题化为一个相对简单的产量未定的运输问题,利用115A A 到之间的管道距离和钢厂和站点之间的公路距离建立一个产量未定的运输问题的模型.但是由于1215,A A A ,并不能代表所有的实际需求点(实际需求点是n 个单位管道),因此,我们可以用F1oyd 算法进一步算出7个钢厂到所有实际的n 个需求点(对于问题一,n =5171;对于问题三,n =5903)的最短路径,并由此得出一个具有7个供应点、n 个需求点的产址未定的运输模型.6 模型的建立产量未定的运输模型根据假设4,我们可以将每一单位的管道看成一个需求点,向一单位管道的所在地运输钢管即为向一个点运输钢管.对每个点,我们可以根据该点的位置和最短等价公路距离,求出各钢厂与该点之间最小单位运输费用ij C (销价已经归人运输费用之中了).设总共有m 个供应点(钢厂),n 个需求点,我们就可以得到一个产量未定的运输模型:有m 个供应点、n 个需求点,每个供应点的供应量{0}{500,}i i u s ∈;每个需求点需要1单位,运输单价矩阵为C ,求使得总运输费用最小的运输方案.其数学规划模型: 11minmnij ij i j F C x ===∑∑11{0}{500,}1,2,,..11,2,01nij i j mij i ij x S i ms tx j n x ==⎧∈=⎪⎪⎪==⎨⎪⎪=⎪⎪⎩∑∑或其中: 1112112n m m mn C C C C CC C ⎛⎫⎪=⎪ ⎪⎝⎭为单位费用矩阵 1112112n m m mn x x x X x x x⎛⎫⎪=⎪ ⎪⎝⎭为决策矩阵,也为0-1矩阵 代码如下7 模型的求解对于本题,上述0-1规划规模宏大,现有的一些算法不能胜任,我们必须具体问题具体分析,结合本题实际情况,寻找行之有效的算法.(1)初始方案的改进的最小元素法和改进的伏格尔法 *改进的最小元素法改进的最小元素法又称为贪婪法或瞎子爬山法,它的宗旨是每一步都取当前的最优值算法步骤为,对费用矩阵C 作n 次下列循环:①C 中找一个最小值ij C ; ②令1;ij x =③C 的第j 的所有数据改为+∞;④如果1nij i j x s ==∑,第i 个供应点的供应量已达上限,将C 的第i 行数据全改为+∞。
物流配送优化模型及算法综述

物流配送优化模型及算法综述随着互联网和电商的发展,物流配送的重要性越来越受到关注。
物流配送的效率直接关系到企业运营的成本和客户满意度,因此,如何优化物流配送成为了重要的问题。
目前,随着信息技术和数学模型的发展,物流配送优化模型及算法也日渐成熟。
本文将对物流配送优化模型及算法进行综述。
一、物流配送优化模型物流配送优化模型主要分为单一时间窗口模型和多时间窗口模型两类。
1. 单一时间窗口模型单一时间窗口模型是指整个配送过程中,每个客户的配送时间窗口都是相同的。
该模型通常采用的是车辆路径问题(Vehicle Routing Problem, VRP)模型。
VRP模型一般会考虑以下多个因素:客户需求量、车辆容量、时间窗口、路线长度、人力成本等。
其中,车辆路径规划是最重要的一环。
在车辆路径规划时,需要考虑配送顺序和路线,使得每个配送点的需求得到满足,同时尽量缩短路径长度和时间成本。
近年来,多种求解VRP问题的算法被提出。
例如,Tabu搜索、模拟退火、粒子群优化等。
这些算法主要基于启发式算法,能够有效地解决VRP问题。
2. 多时间窗口模型多时间窗口模型是指每个客户的配送时间窗口不同,该模型通常采用的是遗传算法(Genetic Algorithm, GA)模型。
GA模型的迭代过程包括评估当前解的质量、选择优良的解、通过交叉和变异生成新的解。
这样的迭代过程以欧几里得距离作为距离函数,可实现基于时间窗口的最优解搜索,进而有效提升物流配送效率。
二、物流配送优化算法1. Ant Colony Optimization蚁群算法(Ant Colony Optimization, ACO)是基于蚂蚁寻路行为的一种启发式算法。
该算法主要通过模拟蚂蚁在寻找食物时释放的信息素来构造解空间。
在物流配送中,该算法可用于规划车辆路径,寻找最佳路线。
2. Particle Swarm Optimization粒子群优化算法(Particle Swarm Optimization, PSO)也是一种启发式算法。
管道输运模型优化研究与实践

管道输运模型优化研究与实践第一章管道输运模型的基本概念和应用管道输运是一种重要的物流方式,在石油、天然气、化工等领域有广泛的应用。
管道输运模型优化可以提高输运效率、降低成本、减少资源浪费,因此受到了广泛的研究与实践。
1.1 管道输运模型的基本原理管道输运模型是通过建立数学模型来描述管道输送流体的运动、物质平衡、能量平衡、动量平衡等基本原理。
在建立模型时,需要考虑管道的几何结构、流体的性质、运输条件等因素。
1.2 管道输运模型的应用领域管道输运模型广泛应用于石油、天然气、化工等领域。
在石油行业,通过优化管道输送方案,可以提高油品的供应效率;在天然气行业,可以通过优化管道网络设计,提高天然气的输送能力;在化工行业,可以通过优化管道运输过程,降低能源消耗和环境污染。
第二章管道输运模型的优化方法和算法管道输运模型的优化是一个复杂的问题,需要综合考虑多个因素和约束条件。
本章将介绍常用的管道输运模型优化方法和算法。
2.1 数学规划方法数学规划方法是目前广泛应用于管道输运模型优化的一种方法。
它通过建立数学模型和运用优化算法,寻找最优的输送方案。
常用的数学规划方法包括线性规划、整数规划、多目标规划等。
2.2 启发式算法启发式算法是一种通过模拟人类的启发式搜索策略来求解问题的方法。
在管道输运模型优化中,可以采用启发式算法来搜索最优的方案。
常用的启发式算法包括遗传算法、蚁群算法、模拟退火算法等。
第三章管道输运模型优化的实践案例本章将结合实际案例,介绍管道输运模型优化在实践中的应用。
3.1 石油管道输送模型优化案例以某石油公司的管道输送为例,介绍如何通过优化输送方案,提高输送效率,降低成本和减少资源浪费。
3.2 天然气管道网络设计优化案例以某天然气公司的管道网络设计为例,介绍如何通过优化网络结构和输送方案,提高天然气的输送能力,并满足用户需求。
3.3 化工管道运输过程优化案例以某化工企业的管道运输过程为例,介绍如何通过优化运输路径、控制运输条件,降低能源消耗和环境污染。
管道订购与运输

《数学模型》课程结业论文管道订购与运输任 务 书[要求]1、将所给的问题翻译成汉语;2、给论文起个题目(名字或标题)3、根据任务来完成数学模型论文;4、论文书写格式要求按给定要求书写;5、态度要认真,要独立思考,独立完成任务;6、论文上交时间:6月1日前(要求交纸质论文和电子文档)。
7、严禁抄袭行为,若发现抄袭,则成绩记为“不及格”。
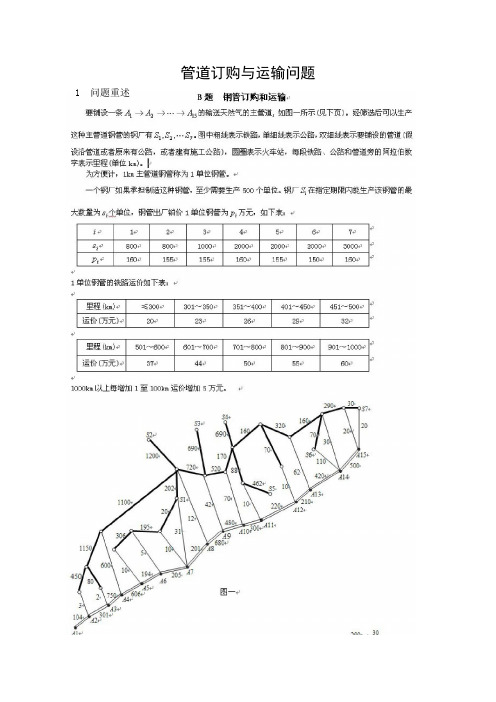
[任务]要铺设一条1521A A A →→→ 的输送天然气的主管道, 如图一所示(见下页)。
经筛选后可以生产这种主管道钢管的钢厂有721,,S S S 。
图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km)。
为方便计,1km 主管道钢管称为1单位钢管。
一个钢厂如果承担制造这种钢管,至少需要生产500个单位。
钢厂iS 在指定期限内能生产该钢管的最大数量为i s 个单位,钢管出厂销价1单位钢管为p 万元,如下表:1单位钢管的铁路运价如下表:1000km 以上每增加1至100km 运价增加5万元。
公路运输费用为1单位钢管每公里0.1万元(不足整公里部分按整公里计算)。
钢管可由铁路、公路运往铺设地点(不只是运到点1521,,,A A A ,而是管道全线)。
(1)请制定一个主管道钢管的订购和运输计划,使总费用最小(给出总费用)。
(2)请就(1)的模型分析:哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大,并给出相应的数字结果。
(3)如果要铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构成网络,请就这种更一般的情形给出一种解决办法,并对图二按(1)的要求给出模型和结果。
77成绩评定单评语:成绩任课教师签字年月日摘 要本文建立的是一个有关钢管运输和订购费用的数学模型。
钢管的运输和订购的总费用可由以下三个因素决定:一,从各个钢厂到各铺设节点的运输路径;二,所订购钢管的总成本;三,沿管道上运输钢管的费用。
供应链管理中物流运输策略的优化模型

供应链管理中物流运输策略的优化模型在供应链管理中,物流运输策略的优化模型扮演着至关重要的角色。
物流运输策略的合理选择和优化对于供应链的效率、成本和顾客满意度都有着深远的影响。
因此,建立一个可行的、科学的物流运输策略的优化模型是供应链管理中的重要课题之一。
物流运输策略的优化模型旨在寻找最佳的物流运输方案,以最小化运输成本、最大化运输效率、减少运输时间和提高服务质量。
下面将介绍一些常见的物流运输策略的优化模型。
1. 路线优化模型:路线优化模型是用于优化运输路径的一个重要模型。
它考虑了各种因素如运输距离、交通条件、货物特性、供应链中的环境因素等。
通过选择最佳的运输路径,可以减少时间、成本和能源消耗。
在路线优化模型中,需要考虑以下几个环节:起点和终点的选择、中途停留点的选择、运输方式的选择等。
通过数学建模、运筹学和优化算法,可以找到最佳路径,以降低物流成本并提高效率。
2. 调度优化模型:调度优化模型是为了最大程度地利用运输资源,提高运输效率。
调度优化模型可以帮助确定最佳的车辆安排、装货顺序、交货时间等,以最大限度地减少等待时间和非运输时间。
这可以帮助减少运输成本,提高运输效率和顾客满意度。
通过调度优化模型,可以实现以下目标:提高车辆利用率、减少货物滞留时间、缩短运输周期、提高送货准时率等。
这些目标的达成将带来更高的效益和更好的客户服务。
3. 仓储和配送模型:在供应链管理中,仓储和配送环节也是关键环节之一。
通过仓储和配送模型,可以确定最佳的仓储位置、库存水平、配送策略等,以最大程度地减少仓储成本和配送成本。
仓储和配送模型需要考虑以下因素:仓储设备的选择、仓储设施的布局、库存管理策略、配送路线的选择等。
通过综合考虑这些因素,并运用数学建模和优化算法,可以找到最佳的仓储和配送方案,以提高运输效率并降低成本。
4. 物流信息管理模型:物流信息管理模型是指利用信息技术和系统来管理和优化物流运输过程。
它包括信息采集、信息传输、信息分析等各个环节,通过准确获取和处理内外部的物流信息,可以提高物流运输的可见性、响应速度和决策效果。
钢管的订购及运输优化方案

钢管的订购及运输优化方案摘要:从本题中可以看出我们要解决的问题是钢管怎样订购,怎样运输,才能使得总费用最少。
所以,我们从两个方面着手考虑这个问题,首先我们考虑怎样从钢厂订购货物,接下来我们考虑在订购好货物后我们怎样把货物运输到目的地。
对于这两个问题,从题目可知,订购和运输联系密切,所以,我们必须同时考虑考虑钢管的订购与运输。
再由题中给的钢厂与天然气管道路线分布图可以看出,该问题等同于把起点的信息通过最优路(即就是花费最少的路径)径送到目的地,在送往的途中可以有信息的流失,流失的信息即就是用于铺设道路的货物,但不管流失多少信息,到达目的地时,总还有剩余的信息。
所以,我们就把钢管的运输看成了最小费用最大流问题。
所以,我们通过对线路的标号,我们利用floyd算出最大流问题算出每一个钢厂到每个点的单位最优路径,然后,再算出在运送途中钢管用于铺设管道所花费的费用,我们把这两种费用相加,就得到了总的费用。
我们通过计算,得出应从哪些钢厂订购多少货物,以怎样的路径进行运送才能使总费用最小。
经过计算我们得出最优解:其最小费用为万元。
在第二问中,我们通过对问题一的精度分析可得:钢厂6S的钢管销价的变化对购运计划和总费用的影响最大;钢管厂1S的钢管产量的上限的变化对总费用的影响最大,钢管厂3S的产量上限的变化对购运计划的影响最大。
对于第三问,我们同样运用问题一的解决办法,先求出每一个钢厂到每段道路的最短路径,然后再求出每一钢厂运送的数量,还有运送途中铺路石所花费的单位费用,最后得出最优解:其最小费用为万元。
问题重述:(略)问题分析:本题看似复杂,但经过分析我们可以看出该问题是求在一个有权图中寻求最优路径的问题,然后再求各个钢厂的运送花费问题,对于运送费用问题,由于我们不知道在哪一个钢厂订货,也不知道定多少,也不知道走哪一条路最合适,所以我们我们利用线性规划中的方法,先利用0—1规划模型,当取0时,我们就认为不在该厂订货,或者说我们不选择某一条路径,这样我们就轻易的将这个复杂的问题分解为线性规划问题。
钢管定购与运输问题的数学模型与求解的新方法

钢管定购与运输问题的数学模型与求解的新方法一、本文概述钢管作为一种重要的建筑材料,在各类工程项目中具有广泛的应用。
钢管的定购与运输问题涉及到供应链管理、物流优化等多个领域,是工业界和学术界共同关注的重要问题。
随着市场需求的不断变化和物流技术的快速发展,传统的钢管定购与运输方法已经难以满足现代工业的需求。
因此,本文旨在探讨钢管定购与运输问题的数学模型与求解的新方法,以提高钢管供应链的效率和经济性。
本文将首先分析钢管定购与运输问题的特点和难点,包括需求量的不确定性、运输成本的波动性、供应链中的信息不对称等。
在此基础上,建立适用于钢管定购与运输的数学模型,包括需求量预测模型、运输优化模型等。
这些模型将综合考虑市场需求、库存成本、运输费用等多个因素,为钢管的定购与运输提供决策支持。
接下来,本文将介绍求解钢管定购与运输问题数学模型的新方法。
这些方法将结合现代优化算法和计算机技术,对模型进行高效求解。
同时,本文还将探讨如何将这些方法应用于实际钢管供应链管理中,以提高供应链的整体效益。
本文将通过案例分析和仿真实验来验证所提出数学模型和求解方法的有效性和实用性。
这些案例和实验将基于实际钢管供应链数据,对模型和方法进行测试和评估。
通过对比分析不同方案的效果,本文将为钢管定购与运输问题的求解提供新的思路和方法。
本文旨在深入研究钢管定购与运输问题的数学模型与求解的新方法,以提高钢管供应链的效率和经济性。
通过建立适用的数学模型和采用先进的求解方法,本文将为钢管定购与运输问题的优化提供理论支持和实践指导。
二、钢管定购与运输问题的数学模型钢管定购与运输问题是一个涉及供应链管理和物流优化的复杂问题。
为了有效地解决这一问题,首先需要建立一个合适的数学模型。
这个模型需要能够准确地描述钢管的定购、库存、运输以及相关的成本和约束条件。
定购决策:根据预测需求、库存量和供应商条件,决定何时从哪些供应商定购钢管。
运输优化:选择最经济、最高效的运输方式,确保钢管按时送达目的地。
数学建模 钢管订购和运输

钢管的订购和运输优化模型摘要本文建立的多元非线性优化模型。
问题一在保证天然气管道铺设可以顺利实施的情况下,给出了钢管的订购与运输总费用最小的方案。
在求钢管由钢厂运输到站点的费用和铺设钢管时产生的运输费,根据图一,我们通过深度优先遍历的方法对整个图一进行路径搜索,然后根据每条搜索到的路径上的铁路和公路上的不同权重,找到了各个钢厂到各个天然气管道上的站点的最佳路径。
对于整个优化过程我们给出了相关的算法,并用matlab 软件编程,经过一系列计算之后,得出了最优的订购与运输方案。
对于问题 1,我们求得的最优解为对于问题2我们经过计算比较得出:6S 钢管销价的变化对购运计划和总费用影响最大。
1S 的生产上限的变化购运计划和总费用影响最大。
对于问题 3,当天然气管道呈现的是一个树状图的时候,我们得到的最优关键字:非线性优化 深度优先遍历 最佳路径一、问题重述要铺设一条1521A A A →→→ 的输送天然气的主管道, 如图一所示(见下页)。
经筛选后可以生产这种主管道钢管的钢厂有721,,S S S 。
图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km)。
为方便计,1km 主管道钢管称为1单位钢管。
一个钢厂如果承担制造这种钢管,至少需要生产500个单位。
钢厂i S 在指定期限内能生产该钢管的最大数量为i s 个单位,钢管出厂销价1单位钢管为i p i 1 2 3 4 5 6 7 i s80080010002000 2000 2000 3000 i p160 155 155160 155150160 1里程(km) ≤300 301~350351~400 401~450 451~500 运价(万元) 2023262932里程(km) 501~600601~700 701~800 801~900 901~1000 运价(万元)37445055601000km 以上每增加1至100km 运价增加5万元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 钢管订购和运输优化模型 要铺设一条1521AAA的输送天然气的主管道, 如图1所示(见反面).经筛选后可以生产这种主管道钢管的钢厂有127,,,SSS.图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示里程(单位:km). 为方便计,1km主管道钢管称为1单位钢管. 一个钢厂如果承担制造这种钢管,至少需要生产500个单位.钢厂iS在指定期限内能生产该钢管的最大数量为is个单位,钢管出厂销价1单位钢管为ip万元,如下表: i 1 2 3 4 5 6 7
is 800 800 1000 2000 2000 2000 3000
ip 160 155 155 160 155 150 160
1单位钢管的铁路运价如下表: 里程(km) ≤300 301~350 351~400 401~450 451~500 运价(万元) 20 23 26 29 32
里程(km) 501~600 601~700 701~800 801~900 901~1000 2
运价(万元) 37 44 50 55 60
1000km以上每增加1至100km运价增加5万元. 公路运输费用为1单位钢管每千米0.1万元(不足整千米部分按整千米计算). 钢管可由铁路、公路运往铺设地点(不只是运到点
1521,,,AAA,而是管道全线).
问题: (1)请制定一个主管道钢管的订购和运输计划,使总费用最小(给出总费用).
思考题: (2)请就(1)的模型分析:哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大,并给出相应的数字结果. (3)如果要铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构成网络,请就这种更一般的情形给出一种解决办法,并对图2按(1)的要求给出模型和结果. 3
A1 3 2 5 80 10
10
31 20 12
42 70 10
88 10
70 62
70 30
20 20 30 450 104 301 750 606 194 205 201 680 480 300 220 210 420 500 600 306195 202 720 690 520 170 690 462 160
320 160
110
290
1150 1100 1200
A2 A3 A4
A5 A6 A7
A8
A9
A10
A11
A12
A13 A14 A15 S1 S2 S3 S4 S5 S6 S7
图1 4 一、 基本假设 1. 沿铺设的主管道以有公路或者有施工公路. 2. 在主管道上,每千米卸1单位的钢管. 3. 公路运输费用为1单位钢管每千米0.1万元(不足整千米部分按整千米计算) 4. 在计算总费用时,只考虑运输费和购买钢管的费用,而不考虑其他费用.
A1 3 2 5 80 10
10
31 20 12
42 70 10
88 10
70 62
70 30 20 20 30 450 104 301 750 606 194 205 201 680 480 300 220 210 420 500 600 306195 202 720 690 520 170 690 462 160
320
160
110
290
1150 1100 1200 A19 130
190
260
100
A2 A3 A4 A5 A6 A7 A8
A9 A10 A11 A12 A13 A14 A15 S1
S2 S3 S4
S5 S6
S7
A16 A17
A18 A20
(A21)
图2 5 5. 在计算钢厂的产量对购运计划影响时,只考虑钢厂的产量足够满足需要的情况,即钢厂的产量不受限制. 6. 假设钢管在铁路运输路程超过1000km时,铁路每增加1至100km,1单位钢管的运价增加5万元.
二、符号说明: iS:第i个钢厂; 7,,2,1i
is:第i个钢厂的最大产量; 7,,2,1i
jA:输送管道(主管道)上的第j个点; 15,,2,1j
ip:第i个钢厂1单位钢管的销价; 7,,2,1i
ijx:钢厂iS向点jA运输的钢管量; 7,,2,1i 15,,2,1j
jt:在点jA与点1jA之间的公路上,运输点jA向点1jA方向铺设的钢管量; 14,,3,2,1j(01t)
ija:1单位钢管从钢厂iS运到结点jA的最少总费用,即公路运费﹑铁路运费和 钢管销价之和; 7,,2,1i 15,,2,1j
jb:与点jA相连的公路和铁路的相交点; 15,,3,2j
1.jjA:相邻点jA与1jA之间的距离; 14,,2,1j 6
三、模型的建立与求解 问题一:讨论如何调整主管道钢管的订购和运输方案使总费用最小 由题意可知,钢管从钢厂iS到运输结点jA的费用ija包括钢管的销价﹑钢管的铁路运输费用和钢管的公路运输费用.在费用ija最小时,对钢管的订购和运输进行分配,可得出本问题的最佳方案.
1. 求钢管从钢厂iS运到运输点jA的最小费用 1)将图1转换为一系列以单位钢管的运输费用为权的赋权图.
由于钢管从钢厂iS运到运输点jA要通过铁路和公路运输,而铁路运输费用是分段函数,与全程运输总距离有关.又由于钢厂iS直接与铁路相连,所以可先求出钢厂iS到铁路与公路相交点jb的最短路径.如图3 7
图3 铁路网络图 依据钢管的铁路运价表,算出钢厂iS到铁路与公路相交点jb的最小铁路运输费用,并把费用作为边权赋给从钢厂iS到jb的边.再将与jb相连的公路、运输点iA及其与之相连的要铺设管道的线路(也是公路)添加到图上,根据单位钢管在公路上的运价规定,得出每一段公路的运费,并把此费用作为边权赋给相应的边.以1S为例得图4. 8
图4 钢管从钢厂1S运到各运输点jA的铁路运输与公路运输费用权值图
2)计算单位钢管从1S到jA的最少运输费用 根据图4,借助图论软件包中求最短路的方法求出单位钢管从1S到jA的最少运输费用依次为:170.7,160.3,140.2,98.6,38,20.5,3.1,21.2,64.2,92,96,106,121.2,128,142(单位:万元).加上单位钢管的销售价ip,得出从钢厂1S购买单位钢管运输到点jA的最小费用ja1依次为:330.3,320.3,300.2,258.6,198,180.5,163.1,181.2,224.2,252,256,266,281.2,288,302(单位:万元). 同理,可用同样的方法求出钢厂2S﹑3S﹑4S﹑5S﹑6S﹑7S
到点jA的最小费用,从而得出钢厂到点的最小总费用(单位:万元)为: 表1 iS到点jA最小费用 9
A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14 A15 S1 320.3 300.2 258.6 198 180.5 163 181.2 224.2 252 256 266 281.2 288 302
2S 360.3 345.2 326.6 266 250.5 241 226.2 269.2 297 301 311 326.2 333 347
3S 375.3 355.2 336.6 276 260.5 251 241.2 203.2 237 241 251 266.2 273 287
4S 410.3 395.2 376.6 316 300.5 291 276.2 244.2 222 211 221 236.2 243 257
5S 400.3 380.2 361.6 301 285.5 276 266.2 234.2 212 188 206 226.2 228 242
6S 405.3 385.2 366.6 306 290.5 281 271.2 234.2 212 201 195 176.2 161 178
7S 425.3 405.2 386.6 326 310.5 301 291.2 259.2 237 226 216 198.2 186 162
2. 建立模型 运输总费用可分为两部分: 运输总费用=钢厂到各点的运输费用+铺设费用. 运输费用:若运输点jA向钢厂iS订购ijx单位钢管,则钢管从钢厂iS运到运输点jA所需的费用为ijijxa.由于钢管运到1A必须经过2A,所以可不考虑1A,那么所有钢管从各钢厂运到各运输点上的总费用为:15271jiijijax.
