中考综合题
中考数学总复习《圆的综合题》练习题(附答案)
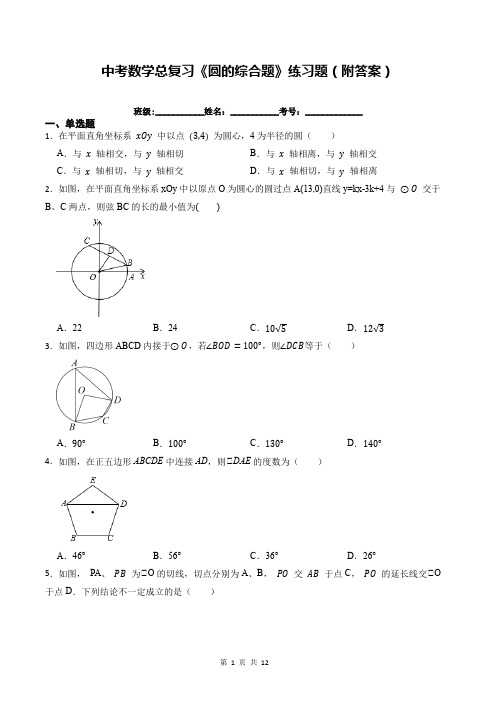
中考数学总复习《圆的综合题》练习题(附答案)班级:___________姓名:___________考号:_____________一、单选题1.在平面直角坐标系xOy中以点(3,4)为圆心,4为半径的圆()A.与x轴相交,与y轴相切B.与x轴相离,与y轴相交C.与x轴相切,与y轴相交D.与x轴相切,与y轴相离2.如图,在平面直角坐标系xOy中以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与⊙O交于B、C两点,则弦BC的长的最小值为()A.22B.24C.10√5D.12√33.如图,四边形ABCD内接于⊙O,若∠BOD=100°,则∠DCB等于()A.90°B.100°C.130°D.140°4.如图,在正五边形ABCDE中连接AD,则∠DAE的度数为()A.46°B.56°C.36°D.26°5.如图,PA、PB为∠O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交∠O 于点D.下列结论不一定成立的是()A.△BPA为等腰三角形B.AB与PD相互垂直平分C.点A,B都在以PO为直径的圆上D.PC为△BPA的边AB上的中线6.如图,四边形ABCD内接于半径为6的∠O中连接AC,若AB=CD,∠ACB=45°,∠ACD=12∠BAC,则BC的长度为()A.6 √3B.6 √2C.9 √3D.9 √27.如图,点A,B,D,C是∠O上的四个点,连结AB,CD并延长,相交于点E,若∠BOD=20°,∠AOC=90°,则∠E的度数为()A.30°B.35°C.45°D.55°8.∠ABC中∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB,BC分别交于点E,D,则AE的长为()A.95B.125C.185D.3659.如图,AB为∠O的直径,点C在∠O上,若∠B=60°,则∠A等于()A.80°B.50°C.40°D.30°10.两个圆的半径分别是2cm和7cm,圆心距是5cm,则这两个圆的位置关系是() A.外离B.内切C.相交D.外切11.已知正三角形的边长为12,则这个正三角形外接圆的半径是()A.B.C.D.12.一个扇形的弧长为4π,半径长为4,则该扇形的面积为()A.4πB.6πC.8πD.12π二、填空题13.在Rt∠ABC中∠C=90°,AB=5,BC=4,求内切圆半径14.如图,∠C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧OB上一点,∠BMO=120°,则∠C的半径为.15.一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的侧面积为.16.一个半径为5cm的球形容器内装有水,若水面所在圆的直径为8cm,则容器内水的高度为cm.17.如图,在直角坐标系中以点P为圆心的圆弧与x轴交于A,B两点,已知P(4,2)和A(2,0),则点B的坐标是.18.下面是“作一个30°角”的尺规作图过程.已知:平面内一点A.求作:∠A,使得∠A=30°.作法:如图①作射线AB;②在射线AB取一点O,以O为圆心,OA为半径作圆,与射线AB相交于点C;③以C为圆心,OC C为半径作弧,与⊙O交于点D,作射线AD.则∠DAB即为所求的角.请回答:该尺规作图的依据是.三、综合题19.如图,在△ABC中AC=BC=BD,点O在AC边上,OC为⊙O的半径,AB是⊙O 的切线,切点为点D,OC=2,OA=2√2.(1)求证:BC是⊙O的切线;(2)求阴影部分的面积.20.如图,△ABC内接于⊙O,CD是直径,∠CBG=∠BAC,CD与AB相交于点E,过点E作EF⊥BC,垂足为F,过点O作OH⊥AC,垂足为H,连接BD、OA.(1)求证:直线BG与⊙O相切;(2)若BEOD=54,求EFAC的值.21.如图,四边形ABCD 内接于∠O,BD是∠O的直径,过点A作∠O的切线AE交CD的延长线于点E,DA平分∠BDE.(1)求证:AE∠CD;(2)已知AE=4cm,CD=6cm,求∠O的半径.22.如图,∠O是∠ABC的外接圆,BC为∠O的直径,点E为∠ABC的内心,连接AE并延长交∠O 于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.(1)求证:DB=DE;(2)求证:直线CF为∠O的切线.23.公元前5世纪,古希腊哲学家阿那克萨哥拉因“亵渎神灵罪”而被投人监狱,在狱中他对方铁窗和圆月亮产生了兴趣.他不断变换观察的位置,一会儿看见圆比正方形大,一会儿看见正方形比圆大,于是伟大的古希腊尺规作图几何三大问题之--的化圆为方问题诞生了:作一个正方形,使它的面积等于已知圆的面积(1)设有一个半径为√3的圆,则这个圆的周长为,面积为,作化圆为方得到的正方形的边长为(计算结果保留π)(2)由于对尺规作图的限制(只能有限次地使用没有刻度的直尺和圆规进行作图),包括化圆为方在内的几何三大问题都已被证明是不可能的.但若不受标尺的限制,化圆为方并非难事。
山东省青岛市初中物理中考专项训练09:综合计算题

山东省青岛市初中物理中考专项训练09:综合计算题姓名:________ 班级:________ 成绩:________一、综合题 (共21题;共341分)1. (10分)在弹簧测力计下悬挂一个小球,示数为4.2N.当把小球的一半体积浸没在水中时,弹簧测力计的示数为1.7N.已知水=1.0×103kg/m3 , g取10N/kg.问:(1)小球所受的浮力为多大?(2)小球的总体积为多大?(3)把小球从弹簧测力计取下,浸没在水中后放手,请通过计算判断小球为什么不能悬浮在水中.2. (15分)(2012·海南) 我国自行设计的“蛟龙号”载人潜水器挑战7000米深度.(1)“蛟龙号”具有先进的水声通信功能,声音从7000m 深处的“蛟龙号”垂直传到海面需要多长时间?(声音在海水中的传播速度是1500m/s,计算结果保留一位小数)(2)“蛟龙号”在7000m 深处受到的压强是7×107Pa,求面积为0.03m2 的观察窗受到的压力.(3)“蛟龙号”在某深度悬浮作业,任务完成后,抛弃自身携带的压载铁便能上浮.请分析“蛟龙号”上浮的原因.3. (15分)底面积为S0的圆柱形薄壁容器内装有密度为ρ0的液体,横截面积为S1的圆柱形木块由一段非弹性细线与容器底部相连,且部分浸入液中,此时细线刚好伸直,如图所示.已知细线所能承受的最大拉力为T,现往容器中再缓慢注入密度为ρ0的液体,直到细线刚好被拉断为止.请解答下列问题;(1)画出细线刚好伸直时,木块在竖直方向上的受力示意图;(2)导出细线未拉断前,细线对木块拉力F与注入的液体质量m之间的关系式;(3)求出细线刚好被拉断时与细线断后容器中液面恢复稳定时,容器底部所受液体压强的变化量.4. (15分) (2016八下·武侯期末) 小明学习了浮力知识后,想利用一弹簧测力计个和一铁块制作一个测定液体密度的仪器,如图甲所示.G取10N/kg,铁的密度ρ铁=7.9×103kg/m3 .(1)首先,他测得此铁块重为G=7.9N,铁块的体积V=1×10﹣4m3;然后,将铁块浸没在待测液体中,设此时弹簧测力计的示数为F,则待测液体的密度表达式为ρ=________(相关物理量用题目中的字母符号表示).小明依据此规律,在测力计右侧标注出了液体的密度值,做成了一支密度计.(2)当利用该密度计测某液体密度时,指针在6.9N的位置,则该液体的密度为________ kg/m3.(3)图乙中能正确反映液体的密度ρ与测力计示数F之间关系的是________.5. (15分) (2018八下·安庆期末) 如图所示,质量不计的光滑木板AB长1.2m,可绕固定点O转动,离O点0.2m的B端挂一重50N的物体,板的A端用一根与水平地面成30∘夹角的细绳拉住,木板始终在水平位置平衡。
中考数学总复习《三角形的综合题》练习题及答案

中考数学总复习《三角形的综合题》练习题及答案班级:___________姓名:___________考号:_____________一、单选题1.如图,在平面直角坐标系中直线y=−x与双曲线y=kx交于A、B两点,P是以点C(2,2)为圆心,半径长1的圆上一动点,连结AP,Q为AP的中点.若线段OQ长度的最大值为2,则k的值为()A.−12B.−32C.−2D.−142.如图,已知AB∥CD,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=()A.10°B.20°C.30°D.40°3.如图,在Rt△ABC中AD是∠BAC的平分线,DE⊥AB垂足为E.若BC=8cm,BD=5cm则DE的长为()A.2√3cm B.3cm C.4cm D.5cm4.如图,矩形纸片ABCD中AD=8cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=10cm,则AB的长为()A.12cm B.14cm C.16cm D.18cm5.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为()A.20°B.25°C.30°D.15°6.如图,锐角∠ABC的两条高BD,CE相交于点O,且CE=BD,若∠CBD=20°,则∠A的度数为()A.20°B.40°C.60°D.70°7.下列长度的三条线段与长度为5的线段能组成四边形的是()A.1,1,1B.1,1,8C.1,2,2D.2,2,28.如图,在∠ABC中AB=AC,BE=CD,BD=CF,若∠A=40°,则∠EDF等于()A.40°B.50°C.60°D.70°9.若点O是等腰∠ABC的外心,且∠BOC=60°,底边BC=2,则∠ABC的面积为() A.2+√3B.2√3C.2+√3或2-√3D.4+2√3或2-√3310.如图,等边ΔABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为()A.15°B.22.5°C.30°D.45°11.如图,在△ABC中∠A=30°,∠ABC=100°,观察尺规作图的痕迹,则∠BFC的度数为()A.130°B.120°C.110°D.100°12.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=5厘米,EF=6厘米,圆形容器的壁厚是()A.5厘米B.6厘米C.2厘米D.12厘米二、填空题13.如图,要测量河两岸相对的两点A、B的距离,在AB的垂线段BF上取两点C、D,使BC=CD,过D作BF的垂线DE,与AC的延长线交于点E,若测得DE的长为20米,则河宽AB长为米.14.如图1,点P从△ABC的项点A出发,以每秒2个单位长度的速度沿A→B→C→A的方向匀速运动到点A.图2是点P运动时线段AP的长度y随时间t(s)变化的关系图象,其中点M为曲线部分的最低点,则△ABC的面积是.15.如图,在正方形ABCD中AC为对角线,E为AC上一点,连接EB,ED,BE的延长线交AD于点F,∠BED=120∘,则∠EFD的度数为.16.如图,△ABC中∠A=40°,D、E是AC边上的点,把△ABD沿BD对折得到△A′BD,再把△BCE沿BE对折得到△BC′E,若C′恰好落在BD上,且此时∠C′EB=80°,则∠ABC=.17.如图,测量三角形中线段AB的长度为cm.判断大小关系:AB+AC BC(填“ >”,“ =”或“ <”).18.如图,已知AB是∠O的弦,AB=8,C是∠O上的一个动点,且∠ACB=45°.若M,N分别是AB,BC的中点,则线段MN长度的最大值是三、综合题19.已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a,b,c分别为∠ABC三边的长.(1)如果x=﹣1是方程的根,试判断∠ABC的形状,并说明理由;(2)如果∠ABC是等边三角形,试求这个一元二次方程的根.20.如图,在Rt∠OAB中∠OAB=90°,OA=AB=6,将∠OAB绕点O沿逆时针方向旋转90°得到∠OA1B1.(1)线段OA1的长是,∠AOB1的度数是;(2)连接AA1,求证:四边形OAA1B1是平行四边形.21.已知一次函数y=2x−2的图像为l1,函数y=12x−1的图像为l2.按要求完成下列问题:(1)求直线l1与y轴交点A的坐标;求直线l2与y轴的交点B的坐标;(2)求一次函数y=2x−2的图象l1与y=12x−1的图象l2的交点P的坐标;(3)求由三点P、A、B围成的三角形的面积.22.在图中利用网格点和三角板画图或计算:(1)在给定方格纸中画出平移后的△A′B′C′;(2)图中AC与A′C′的关系怎样?(3)记网格的边长为1,则△A′B′C′的面积为多少?23.如图,在∠ABC中点D在AB上,且CD=CB,E为BD的中点,F为AC的中点,连接EF交CD 于点M,连接AM.(1)求证:EF= 12AC;(2)若EF∠AC,求证:AM+DM=CB.24.如图①,Rt△ABC中∠C=90°,AC=6cm.动点P以acm/s的速度由B出发沿线段BA 向A运动,动点Q以1cm/s的速度由A出发沿射线AC运动.当点Q运动2s时,点P开始运动;P点到达终点时,P、Q一起停止.设点P运动的时间为ts,△APQ的面积为ycm2,y与t的函数关系图像如图②所示.(1)点P运动的速度a=cm/s,AB=cm;(2)当t为何值时,△APQ的面积为12cm2;(3)是否存在t,使得直线PQ将Rt△ABC的周长与面积同时平分?若存在,求出t的值;若不存在,请说明理由.参考答案1.【答案】A2.【答案】C3.【答案】B4.【答案】C5.【答案】A6.【答案】B7.【答案】D8.【答案】D9.【答案】C10.【答案】C11.【答案】C12.【答案】D13.【答案】2014.【答案】1215.【答案】105º16.【答案】60°17.【答案】2.0;>18.【答案】4√219.【答案】(1)解:ΔABC是等腰三角形;理由:把x=−1代入方程得a+c−2b+a−c=0,则a=b,所以ΔABC为等腰三角形(2)解:∵ΔABC为等边三角形∴a=b=c∴方程化为x2+x=0解得x1=0,x2=−1.20.【答案】(1)6;135°(2)证明:∵∠OAB绕点O沿逆时针方向旋转90°得到∠OA1B1∴∠AOA1=90°,∠OA1B1=90°,OA1=A1 B1=OA=6∴∠AO A1=∠O A1B1∴OA∠A1B1∵A1B1=OA∴四边形OAA1B1是平行四边形.21.【答案】(1)解:当x =0时,y= -2,即直线l 1与y 轴交点A 的坐标为(0,−2)当x =0时,y= -1,即直线l 2与y 轴交点B 的坐标为(0,−1);(2)解:∵一次函数y =2x −2的图象l 1与y =12x −1的图象l 2相交∴2x −2=12x −1∴x =23∴y =2×23−2=−23∴交点P 的坐标为(23,−23);(3)解:三点P 、A 、B 围成的三角形,如下图,作PD ⊥AB 交y 轴于点DAB =|−1−(−2)|=1△ABP 的高DP 为:23∴S △ABP =12AB ×DP =12×1×23=13即由三点P 、A 、B 围成的三角形的面积:13.22.【答案】(1)解:如图,∠A′B′C′为所作;(2)解:线段AC 与A′C′的位置关系是平行,数量关系是相等 (3)解:∠A′B′C′的面积=12×4×4=8.23.【答案】(1)证明:连接CE∵CD=CB,点E为BD的中点∴CE⊥BD∵点F为AC的中点∴EF=12AC;(2)解:∵点F是AC中点∴AF=FC,又EF⊥AC∴∠AFM=∠CFM,且AF=FC∴ΔAFM≅ΔCFM(SAS)∴AM=CM∵BC=CD=DM+CM=DM+AM.24.【答案】(1)1;10(2)解:当运动时间为t时,AQ=t+2,BP=t,AP=10−t 如图,作PH⊥AC,则△APH∽△ABC∴PH=APAB·BC=4(10−t)5∴S△APQ=12AQ·PH=12(t+2)4(10−t)5=2(t+2)(10−t)5∴△APQ的面积为12cm2时,解方程12=2(t+2)(10−t)5,得t1=4+√6∴当t=4+√6或4−√6时,△APQ的面积为12cm2;(3)解:∵S△ABC=24cm2,C△ABC=6+8+10=24cm∴12S△ABC=12cm2①当0<t≤4时由(2)可知,当t=4−√6时,△APQ的面积为12cm2此时,AQ=4−√6+2=6−√6∴AP+AQ=6+√6+6−√6=12,即AP+AQ=12C△ABC∴t=4−√6时,直线PQ将Rt△ABC的周长与面积同时平分;②当4<t≤10时设PQ与BC交于点N,作PM⊥BC则有:△PBM∽△ABC∴PM AC=BPBA=BMBC,∴PM=3t5,BM=4t5,MC=8−4t5∵PM QC=MNCN,∴MN=3t2−30t25−10t当BN+BP=12时,解方程4t5+3t2−30t25−10t+t=12,得t=5或t=4(舍去)此时,PM=3,BM=4,BP=5∴BN=4+3=7∴当4<t≤10时,不存在t使得直线PQ将Rt△ABC的周长与面积同时平分;∴综上,当t=4−√6时,直线PQ将Rt△ABC的周长与面积同时平分;当4<t≤10时,不存在t使得直线PQ将Rt△ABC的周长与面积同时平分.第11页共11页。
人教版初中毕业九年级中考物理 作业 第二篇 中考重难题型突破 题型四 综合题

7.(2021·随州)图甲是《天工开物》中记载古人利用杠杆从水井提水的 情景.现简化成图乙模型,轻质杠杆 AB,支点为 O,AO∶OB=3∶2,在 B 端用轻绳系着石块 P,石块质量 m=15 kg;在 A 端用轻绳系着一只木桶 Q, 木桶以及桶内的水总质量 M=40 kg;水井边站着提水人阿宝(g 取 10 N/kg).求:
题型四 综合题
一、力学综合题 类型 1:有关速度、压强、功和功率的综合题 1.(2022·重庆)“共建卫生城市,构建美好家园”,如图所示是“雾炮 车”喷洒水雾以减少扬尘的情景.某次喷洒完后,该车在 4×103 N 的牵 引力作用下,匀速通过 200 m 的平直道路用时 20 s.求:(g 取 10 N/kg) (1)此过程中该车的速度; (2)此过程中该车牵引力的功率.
=1.0×103 kg/m3×1×10-4 m3×10 N/kg=1 N, 细线 T2 对合金球 B 的拉力: FB=G-F 浮B=3 N-1 N=2 N;
(3)物体 A 的重力: GA=F 浮 A-FB=9 N-2 N=7 N, 当细绳即将断裂时,由力的平衡条件可得,A 物体此时的浮力: F 浮′+F 拉最大=GA+FB,设此时木块排开水的体积为 V 排′,则: ρ水 V 排′g+F 拉最大=GA+FB,即 1.0×103 kg/m3×V 排′×10 N/kg+5 N=7 N+2 N,解得: V 排′=4×10-4 m3;
2.(2022·六盘水)如图所示的电路中,小灯泡 L 标有“6 V 3.6 W”字 样.闭合开关 S,小灯泡正常发光,电流表示数为 0.3 A.设灯丝电阻不 变.求: (1)小灯泡的额定电流; (2)定值电阻 R 的阻值; (3)电路消耗的总功率.
(3)改变橡皮泥“船”的形状,使其空心部分的体积适当增大,增大可利 用的浮力,从而提高橡皮泥“船”的装载能力.
湖北省武汉市新洲区2024年九年级中考英语综合训练题 (一)(含答案及听力原文,无音频)

新洲区2024年英语综合训练题(一)亲爱的同学,在你答题前,请认真阅读下面的注意事项:1. 本试卷由第1卷(选择题) 和第II卷(非选择题) 两部分组成。
全卷共10页,七大题,满分120分。
考试用时120分钟。
2. 答题前,请将你的姓名、准考证号填写在”答题卡”相应位置,并在”答题卡”背面左上角填写姓名和座位号。
3. 答第Ⅰ 卷(选择题) 时,选出每小题答案后,用2B 铅笔把”答题卡”上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案。
答在”试卷”上无效。
4. 答第Ⅰ卷(非选择题) 时,答案用0. 5 毫米黑色笔迹签字笔书写在”答题卡”上。
答在”试卷”上无效。
5. 认真阅读答题卡上的注意事项。
预祝你取得优异成绩!第Ⅰ卷(选择题共80分)第一部分听力部分一、听力测试(共三节)第一节(共4小题,每小题1分,满分4分)听下面4个问题。
每个问题后有三个答语,从题中所给的A、B、C三个选项中选出最佳选项。
听完每个问题后,你都有 5 秒钟的时间来作答和阅读下一小题。
每个问题仅读一遍。
1. A. China. B. On Friday. C. I’m a student.2. A. Fifteen. B. He likes soccer. C. Grade Nine.3. A. Half an hour. B. At hotel. C. Salad.4. Α. Ζ24. B. 30 minutes ago. C. Let’s go.第二节(共8小题,每小题1分,满分8分)听下面8段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来作答有关小题和阅读下一小题。
每段对话仅读一遍。
5. How is the Lake Park according to the woman?A. BlueB. Big.C. Great.6. What does the man suggest bringing?A. An apple.B. A sandwich.C. Some cookies.7. How does the woman feel?A. Excited.B. Tired.C. Worried.8. What time does Dave’s meeting start?A. At 8: 30.B. At 9: 00.C. At 10: 009. What are the speakers talking about?A. Gifts for Jason.B. A baseball game.C. The woman’s birthday.10. What would the woman probably say to the man next?A. You are so direct!B. Seem to have a point!C. What a music fan!11. Where does this conversation most probably take place?A. B. C.12. What will the speakers most probably do then?A. Look for more information.B. Ask for more time to improve their plan.C. Finish their plan with the information available.第三节(共13小题,每小题1分,满分13分)听下面4 段对话或独白。
九年级中考数学综合训练题(4)

九年级中考数学综合训练题(4)一.选择题(共12小题,满分36分,每小题3分)1.(3分)=()A.B.C.D.2.(3分)如图所示的几何体的主视图是()A.B.C.D.3.(3分)如图,P A、PB是⊙O的切线,切点分别为A、B,点C在⊙O上,如果∠P=50°,那么∠ACB等于()A.40°B.50°C.65°D.130°4.(3分)为了比较某校同学汉字听写谁更优秀,语文老师随机抽取了10次听写情况,发现甲乙两人平均成绩一样,甲、乙的方差分别为2.7和3.2,则下列说法正确的是()A.甲的发挥更稳定B.乙的发挥更稳定C.甲、乙同学一样稳定D.无法确定甲、乙谁更稳定5.(3分)如图所示,三角形ABC中,∠BAC=90°,过点A画AD⊥BC,则下列说法不正确的是()A.线段AD是点A与直线BC上各点连接的所有线段中最短的B.线段AB是点B到直线AD的垂线段C.点A到直线BC的距离是线段AD的长D.点C到直线AB的距离是线段AC的长6.(3分)某校数学课外活动探究小组,在老师的引导下进一步研究了完全平方公式.结合实数的性质发现以下规律:对于任意正数a、b,都有a+b≥2成立.某同学在做一个面积为3 600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来作对角线用的竹条至少需要准备xcm.则x的值是()A.120B.60C.120D.607.(3分)如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在边DC中点E处,若BC=2,则线段AB的长为()A.2B.C.2D.8.(3分)在函数中,自变量x的取值范围是()A.x<B.x≠﹣C.x≠D.x>9.(3分)如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,AB=2AD=4,则CF长度是()A.B.C.D.110.(3分)如图,反比例函数(k>0)与一次函数的图象相交于两点A(x1,y1),B(x2,y2),线段AB交y轴与C,当|x1﹣x2|=2且AC=2BC时,k、b的值分别为()A.k=,b=2B.k=,b=1C.k=,b=D.k=,b=11.(3分)如图,直线y=kx+b(k<0)交y轴于点A,交x轴于点B,且(AB+OA)(AB ﹣OA)=,则不等式kx+b>0的解集为()A.x>B.x>3C.x<D.x<312.(3分),,,=﹣…从计算结果中找出规律,并用这一规律计算:(+++…+)(+1)结果为()A.2005B.2006C.2007D.2008二.填空题(共6小题,满分18分,每小题3分)13.(3分)如图,海平面上灯塔O方圆100千米范围内有暗礁.一艘轮船自西向东方向航行,在点A处测量得灯塔O在北偏东60°方向,继续航行100千米后,在点B处测量得灯塔O在北偏东37°方向.请你作出判断,为了避免触礁,这艘轮船是否要改变航向?.(填“是”或“否”,参考数据:sin37°≈0.6018,cos37°≈0.7986,tan37°≈0.7536,cot37°≈1.327,≈1.732).14.(3分)不等式组的整数解的积为.15.(3分)+(b+2)2+|c﹣2022|=0,则(a+b)c的值为.16.(3分)定义新运算“*”.规则:a*b=a(a≥b)或者a*b=b(a<b)如1*2=2,(﹣3)*2=2.若x2+x﹣1=0的根为x1、x2,则x1*x2的值为:.17.(3分)如图,已知矩形DEFG内接于Rt△ABC,D在AB上,E、F在BC上,G在AC 上,∠BAC=90°,AB=6cm,AC=8cm,,则矩形的边长DG=.18.(3分)已知在平面直角坐标系中,点O为坐标原点,过O的直线OM经过点A(6,6),过A作正方形ABCD,在直线OA上有一点E,过E作正方形EFGH,已知直线OC经过点G,且正方形ABCD的边长为2,正方形EFGH的边长为3,则点F的坐标为.三.解答题(共7小题,满分66分)19.(6分)化简求值:(﹣)÷,其中a=+1,b=﹣1.20.(8分)阅读下面材料,再回答问题:有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”.解决下列问题:(1)菱形的“二分线”可以是.(2)三角形的“二分线”可以是.(3)在图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”,并说明你的画法.21.(10分)掷①②两枚正六面体骰子,它们的点数和可能有哪些值?请在下表中列出来,并用表中的信息求:(1)“点数和为7点”的概率P1;(2)“两颗骰子点数相同”的概率P2;(3)“两颗骰子点数都是相同偶数”的概率P3.22.(10分)已知关于x的方程(a+c)x2+bx﹣(a+2c)=0的两根之和为1,两根的倒数和为﹣2.(1)求这个方程的两根之积;(2)求a:b:c.23.(10分)采购员用一张1万元支票去购物.购单价为590元的A种物品若干件,又购单价为670元的B种物品若干件,其中B种件数多于A种件数,找回了几张100元和几张10元的(10元的不超过9张).如把购A种物品和B种物品的件数互换,找回的100元和10元的钞票张数也恰好相反,则原来购B种物品多少件?24.(10分)如图,已知AC、AB是⊙O的弦,AB>AC.(1)在图(a)中,能否在AB上确定一点E,使得AC2=AE•AB,为什么?(2)在图(b)中,在条件(1)的结论下延长EC到P,连接PB,如果PB=PE,试判断PB和⊙O的位置关系,并说明理由.25.(12分)如图,一次函数y=﹣x+3的图象交x轴于点A,交y轴于点Q,抛物线y=ax2+bx+c (a≠0)的顶点为C,其图象过A、Q两点,并与x轴交于另一个点B(B点在A点左侧),△ABC三内角∠OAC、∠ABC、∠ACB的对边为a1,b1,c1.若关于x的方程a1(1﹣x2)+2b1x+c1(1+x2)=0有两个相等实数根,且a1=b1;(1)试判定△ABC的形状;(2)当时求此抛物线的解析式;(3)在(2)的条件下,抛物线上是否存在点P,使S△ABP=S四边形ACBQ?若存在,求出P点坐标;若不存在,请说明理由.。
2022年山西太原中考文科综合试题及答案

2022年山西太原中考文科综合试题及答案文科综合(历史)第I卷选择题(共30分)一、选择题(在每小题的四个选项中,只有一项最符合题意,请选出并在答题卡上将该选项涂黑。
本大题有15个小题,每小题2分,共30分)1.考古发现是了解史前社会历史的重要依据。
下面的出土文物从器物造型和图案设计上可以印证我国原始居民()A.会农业种植B.具有朴素审美观念C.会制作陶器D.开始饲养家禽家畜2.观察右面的《北魏帝王出御图》,图中人物的衣着均是峨冠博带、长袍宽袖,与北魏传统的小袖短袄截然不同。
这一现象反映出()A.北方经济的发展B.民族文化的交融C.社会矛盾的缓和D.民族政权的分立3.“川中水车如纺车,以细竹为之,车骨之末,缚以竹筒,旋转时低则舀水,高则泻水”。
材料描述的这种以水力作动力的灌溉工具是()A.耧车B.翻车C.筒车D.秧马4.同学们运用史论结合、论从史出的方法,对中国古代“专制主义中央集权制度”形成了如下评价。
据此补全省略号处的论点()A.强化君权,禁锢思想B.各民族经济文化的交流C.监督地方,巩固统治D.统一多民族国家的巩固5.京剧脸谱各具特色,悲剧人物西楚霸王项羽,眼角下斜,嘴角下撇,虽不失庄重,却也预示着兵败垓下,自刎乌江的命运;关羽“面如重枣”,自然画红脸;包拯“铁面无私”,则黑脸非他莫属。
由此可知,京剧脸谱()A.真实再现历史场景B.渗透人们的价值取向C.客观评价历史人物D.刻画善变的人物性格6.“现在有五口通商,外人可以横行天下,防不胜防。
直到清朝末年,文人忧国者莫不以五口通商为后来的祸根。
”与材料所述“五口通商”相关的条约是()A.《南京条约》B.《北京条约》C.《马关条约》D.《辛丑条约》7.1919年12月,蔡元培表示北京大学开始招收女学生,随后,录取了邓春兰、王兰在内的九名女学生,其他学校也纷纷效仿。
两年后,已经有七个院校解除了大学女禁。
这说明()A.新文化运动推动观念革新B.男尊女卑现象得以根除C.杰出人物能决定社会发展D.男女平等已经完全实现8.《翻身一中国一个村庄的革命纪实》中写道:通过解放战争时期的土地改革,农民获得了土地等生产资料,破除了迷信,实现了民主和平等。
中考语文综合模拟试题(附答案解析)

语文中考综合模拟检测试题学校________ 班级________ 姓名________ 成绩________(满分120分,考试时间120分钟)一、积累运用(22分)1.下列选项字音、字形完全正确的一项是( )读书对人有潜.( )移默化的影响。
读一本好书,就等于和一个高尚的人对话。
大师们的一句句箴.( )言都在敲击我们的灵魂。
我听到杜小康了战胜孤独之后的感( );我看到孙少平经长途( )涉之后获得了不平凡的人生;我看到桑提亚哥大战马林鱼和鲨鱼的锲而不舍。
他们都在我心里种下了勇敢、无畏的种子。
A.qián zhēn概拔B.qián zhēn慨跋C.qiǎn jiān概跋D.qiǎn zhēn慨拔2.在下面语段中,(甲)(乙)两处分别填入标点符号,最恰当的一项是( )因为崇尚英雄,争做英雄,所以才会英雄辈出,国家强盛。
学习英雄模范,就是学习他们身上的鲜明品格。
忠诚,就是矢志不渝,坚守初心(甲)执着,就是埋头苦干,坚守事业;朴实,就是认真工作,不计个人得失。
伟大出自平凡,平凡造就伟大。
只要有坚定的理想信念(乙)不懈的奋斗精神,就一定能在平凡中造就伟大。
A.(甲)句号 (乙)逗号B.(甲)分号 (乙)顿号C.(甲)分号 (乙)逗号D.(甲)句号 (乙)顿号3.下列各句中加点词语使用不恰当的一项是A.在众目睽睽....之下,这个本来从容自若的姑娘也不禁有点窘迫了。
B.小猴子总是担心月亮会掉下来,天天失眠,真是杞人忧天....。
C.大家认为他提出的这条建议很有价值,都随声附和....表示赞成。
D.谢老师的讲学, 语言幽默、精彩、机智,常常引得学生哄堂大笑....。
4.下列句子没有语病的一项是( )A.这次抗疫中,社会各界给学校捐赠了口罩、体温计、保健手册等医疗用品。
B.去年六月,首府南宁地铁3号线开通试运营,很大程度上缓解了市内交通拥堵。
C.南宁积极推动旅游休闲业的发展,打造多条景区体闲路线,逐步改善广西国际影响力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(第 24 题)
(备用图)
第 4 页 共 4 页
Dongguan
东莞市敏学教育发展有限公司 Minxue Education Development Co.Ltd
模拟试题二
25.Rt△ ABC在直角坐标系内的位置如图1所示, 反比例函数 y
k (k 0) 在第一象限内的图像与BC x
边交于点D(4,m) ,与AB边交于点E(2,n) ,△ BDE的面积为2. (1)求 m 与 n 的数量关系; (2)当 tan∠ A=
1 时,求反比例函数的解析式和直线 AB 的表达式; 2
(3)设直线 AB 与 y 轴交于点 F,点 P 在射线 FD 上,在(2)的条件下,如果△ AEO 与△ EFP 相 似,求点 P 的坐标.
备用图
第 5 页 共 5 页
Dongguan
东莞市敏学教育发展有限公司 Minxue Education Development Co.Ltd
个性化教学辅导方案
课时统计:第(10)课时 共( )课时 教学 内容 教学 目标 重点 难点 教 学 过 程 M O· 授课时间:2015 年 2 月 11 日
综合题 中考9分题表达训练 数学语言的组织
模拟试题一
23.如图所示,△ABC 的外接圆圆心 O 在 AB 上,点 D 是 BC 延长线上一点,DM⊥AB 于 M,交 AC 于 N,且 AC=CD.CP 是△CDN 的边 ND 上的中线. (1)求证:△ABC≌△DNC; (2)试判断 CP 与⊙O 的位置关系,并证明你的结论. A N P
B
C
(第 22 题)
D
A M O· N P
B
C
(备用图)
D
第 2 页 共 2 页
Dongguan
东莞市敏学教育发展有限公司 Minxue Education Development Co.Ltd
24.如图,已知一次函数 y kx b 的图象经过 A(2, 1) , B(1, 3) 两点,并且交 x 轴于点 C,交 y 轴于点 D. (1)求该一次函数的解析式; (2)求 tan OCD 的值; (3)求证: AOB 135 . y B
备用图
第 6 页 共 6 页
Dongguan
东莞市敏学教育发展有限公司 Minxue Education Development Co.Ltd
23.如图,AE 是△ABC 中 BC 边上的高线也是中线,点 D 在线段 AE 上(不与两端点重合). (1) 证明:△ADB≌△ADC; (2) 当△AEB∽△BED 时,若 sin∠BAE =
教研组长核查
教学主任核查
第 7 页 共 7 页
1 ,BC= 4,求线段 DE 的长度. 3
C D
A
E
B
Байду номын сангаас
C D
A
E
B
备用图
本节课知识传授完成情况:完全能接受□ 学生的接受程度: 很积极□ 比较积极□ %
部分能接受□ 一般□
不能接受□
不积极□ 良□ 中□
学生上次的作业完成情况:数量 课 后 小 结 下节课的教学内容: 备 核 查 时 间 注
完成质量:优□
24.如图,要设计一个等腰梯形的花坛,花坛上底长 120 米,下底长 180 米,上下底相距 80 米,在 两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬 道的宽为 x 米. (1)用含 x 的式子表示横向甬道的面积; (2)当三条甬道的总面积是梯形面积的八分之一时,求甬道的宽; (3)根据设计的要求,甬道的宽不能超过 6 米.如果修建甬道的总费用(万元)与甬道的宽度成正 比例关系,比例系数是 5.7,花坛其余部分的绿化费用为每平方米 0.02 万元,那么当甬道的 宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
D 1 C O A
(第 23 题)
1
x
y
B
D 1 C O A
(第 23 题)
1
x
第 3 页 共 3 页
Dongguan
东莞市敏学教育发展有限公司 Minxue Education Development Co.Ltd
25.平面直角坐标系中,□ABOC 如图放置,点 A、C 的坐标分别为(0,3) 、 (-1,0) ,将此平行 四边形绕点 O 顺时针旋转 90°,得到□ ABOC . (1)若抛物线过点 C , A , A ,求此抛物线的解析式; (2)求□ABOC 和□ ABOC 重叠部分 △OC D 的周长; (3)点 M 是第一象限内抛物线上的一动点,问:点 M 在何处时△ AMA 的面积最大?最大面积是多少? 并求出此时点 M 的坐标.
Dongguan
东莞市敏学教育发展有限公司 Minxue Education Development Co.Ltd
教学科目 授课老师 学 生
九年级数学 王老师
档案序号
第 1 页 共 1 页
Dongguan
东莞市敏学教育发展有限公司 Minxue Education Development Co.Ltd
