半角模型(八年级人教版)
第12章旋转全等模型之夹半角模型讲义人教版八年级数学上册

“夹半角”模型模块一:夹半角模型知识导航夹半角,顾名思义,是一个大角夹着一个大小只有其一半的角,如图所示。
这类题目有其固定的做法,当a取不同的值的时候,也会有类似的结论,下面我们就来看一看这一类问题。
夹半角的常见分类:(1)90度夹45度(2)120度夹60度(3)2a夹a题型一:90°夹45°例1 、如图,在四边形ABCD中,∠BAD=∠B=∠C=∠D=90°,AB=BC=CD=AD,E在BC上,F在CD 上,且∠EAF=45°,求证:(1)BE+DF=EF;(2练习:1、在例1的条件下,若E在CB延长线上,F在DC(1)DF-BE=EF;(2)∠AEB+∠AEF=180°.2、如图,在四边形ABCD中,已知∠BAC=∠、CN、MN之间的数量关系并证明。
题型二:120°夹60°例2、已知如图所示,△ABC为等边三角形,∠且∠MDN=60°.(1)求证:BM+CN=MN;(2)若将上题条件中的“△ABC的一个内角∠A=60°明:若不成立,请说明理由。
练习:1、如图,四边形ABCD中,∠A=∠BCD=90°,∠且∠EBF=60°,求证:AE=EF+CF.2、如图所示,四边形ABCD中,∠A=∠BCD=90°DC延长线上,且AE=EF+CF,求证:∠EBF=60°.题型三:2a夹a例3、如图,在四边形ABCD中,M、N分别为AB、,∠∠BDC,求证:BM+CN=MN.例4 在等边△ABC的两边AB、AC,BD=DC,当M、N分别在直线AB、AC(1)当点M、N在边AB、AC上,试求出BM、NC、ABC的周长L 的关系;(2)当M 、N 分别在边AB 、CA 的延长线上试,若AN=2,则Q=__________(用含有L 的式子表示)。
练习:如图,在平面直角坐标系中,△AOB 为 等腰直角三角形,A (4,4). (1)求B 点坐标;(2)过点A 作y 轴的垂线交y 轴于E ,F 为x 轴负半轴上的一点,G 为EF 的延长线上,以EG 为直角边作等腰直角Rt △EGH ,过A 作x 轴垂线交EH 于点M ,连FM ,等式1AM FM-=是否成立?若成立,请证明;若不成立,说明理由。
八年级数学多边形之手拉手模型和半角模型 专题讲义

八年级数学多边形之手拉手模型和半角模
型专题讲义
一、手拉手模型
1. 理解手拉手模型
手拉手模型是多边形的一种折纸模型,常用于辅助理解和记忆多边形的性质。
通过将多边形沿一条边折叠后,将该边两端的顶点对齐,可以得到手拉手模型。
2. 制作手拉手模型
制作手拉手模型的具体步骤如下:
1. 将多边形沿一条边折叠。
2. 将该边两端的顶点对齐。
3. 将折线处剪开。
3. 应用手拉手模型
手拉手模型可用于辅助证明多边形的性质。
例如,证明凸多边
形的内角和公式,可以用手拉手模型将多边形分割成若干个三角形,再计算各个三角形的内角和。
二、半角模型
1. 理解半角模型
半角模型是多边形的一种立体模型,常用于辅助理解和记忆多
边形的性质。
通过将多边形沿一条边折叠后,将两条邻边上的点对齐,可以得到半角模型。
2. 制作半角模型
制作半角模型的具体步骤如下:
1. 将多边形沿一条边折叠。
2. 将两条邻边上的点对齐。
3. 将折线处剪开。
3. 应用半角模型
半角模型可用于辅助证明多边形的性质,特别是相邻内角互补
的性质。
例如,证明正多边形的内角和公式,可以用半角模型将正
多边形分割成若干个等腰三角形,再计算各个等腰三角形的内角和。
+2025年中考数学一轮专题复习(河南)+微专题6 半角模型+++课件

∠=∠, ∴Rt△AEB≌Rt△AND(SAS),
=,
∴AE=AN,∠EAB=∠NAD,∴∠EAM=∠NAM=45°.
=,
在△AEM和△ANM中, ∠=∠, ∴△AEM≌△ANM(SAS),
=,
∴S△AEM=S△ANM,EM=MN,
∵AB,AH是△AEM和△ANM对应边上的高,∴AB=AH.
∴DG=
CD= ×2=
,CG= CD=1,
∴FG=CF-CG=9-x.
∵∠DGF=90°,∴FG2+DG2=DF2,
∴(9-x)2+( )2=x2,
∴x= ,∴DE= .
图2
微专题6 半角模型
•人教版
3.已知,在正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的
图1
图2
•人教版
解:(1)∵四边形ABCD是正方形,∴AB=AD,∠B=∠D=90°.
=,
在△ABM与△ADN中, ∠=∠, ∴△ABM≌△ADN,
=,
∴∠BAM=∠DAN,AM=AN.
∵AH⊥MN,∴∠MAH= ∠MAN=22.5°.
∵∠BAM+∠DAN=45°,∴∠BAM=∠DAN=22.5°.
发现,如图2,在AB的延长线上截取BG=DF,连接CG.通过两次证明,证明三角形
全等,可以解决问题.
图1
请你直接写出(1)中的结论.
图2
图3
•人教版
解:结论:BE+DF=EF,理由如下:
∵∠ABC=∠ADC=90°,∴∠GBC=∠FDC=90°.
∵BG=DF,BC=DC,
∴△GBC≌△FDC(SAS),
人教版八年级上册数学 第12章 全等三角形 等线夹半角模型 专项训练

等线夹半角模型基本图形:指的是一个大角夹着一个大小只有它的一半的角.常见类型:①90°夹45°;②120°夹60°;③2α°夹α°.板块一90°角夹45°角典例精讲例1.如图,B(4,4),.BC⊥y轴于点C,BA⊥x轴于点A,E为BC上一动点(不与B,C重合),F为AB上一动点,且满足.∠OEF=∠AOE,,在运动过程中,△BEF的周长变吗?若不变求其值;若变化求其变化范围.例2.正方形ABCD中,E,F分别是BC,CD上的点,∠EAF=45°.(1)求证:EF=BE+DF;(2)求证:EA平分∠BEF,FA平分∠DFE.实战演练1.如图,四边形ABCD中,AB=AD,∠BAD=∠C=90°,,E,F分别为BC,CD上的点,∠EAF=45°..探究E F,BE,DF之间的数量关系并证明.D2.如图,在平面直角坐标系中,已知点A(0,2),B(2,0),点C在.∠ABO的平分线上,∠ACO=67.5°,求∠AOC的度数.3.在例1的条件下,若点E在BC的延长线上,点F在CD的延长线上,其余条件不变.(1)探究EF和BE,DF三条线段之间的数量关系并证明;(2)探究∠AFD与∠AFE之间的数量关系并证明.板块二120°角夹60°角典例精讲例1.如图,四边形ABCD中,BC=CD,∠BCD=120°,,E,F分别为AB,AD上的点,∠ECF=∠A=60°.(1)求证:.EF=BE+DF;(2)求证:点C在.∠BAD的平分线上.实战演练(1)如图1,将例题中点E移至BA延长线上,点F移至AD延长线上,其余条件不变,写出EF和BE,DF 之间的数量关系并证明;(2)如图2,将例题中点E移至AB延长线上,点F移至DA延长线上,其余条件不变,写出EF和BE,DF 之间的数量关系并证明.板块三2α°角夹α°角典例精讲基本模型:如图1,四边形ABCD中,点E为AB上一点,点F为AD上一点,具备以下三个条件:①CB=CD;②∠BCD=2∠ECF;③∠B+∠D=180°(或∠A+∠BCD=180°).基本结论:①EF=BE+DF;②EC平分∠BEF,FC平分∠DFE.当点E,F分别移到AB,AD延长线或反向延长线上时,E F=BE-DF或EF=DF-BE.方法技巧:①延长AD至点G(若点E,F在延长线上一般在长线段上截取),使DG=BE,连接CG;②证明△BCE≌△DCG(SA S),全等条件:∠B+∠ADC=180°得∠CDG=∠B,CB=CD,DG=BE;∴CG=CE,∠3=∠1;③证明△ECF≌△GCF(SAS).由∠3=∠1得∠ECG=∠BCD=2∠ECF,得∠ECF=∠GCF.又CE=CG,CF公共,∴△ECF≌△GCF(SAS),得EF=FG=DG+DF=B E+DF.由△ECF≌△GCF得∠CFE=∠CFD,得FC平分∠DFE;∠BEC=∠G=∠CEF得EC平分∠BEF.本质特征:①等腰三角形腰的旋转;②通过旋转对剩余半角进行拼凑;③产生一组旋转全等和一组轴对称全等;④旋转全等的旋转角度为2α;⑤对角互补使夹半角模型产生一组“截长补短”的相应结论.实战演练如图,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°.(1)求证:DA平分∠CDE;(2)求证:∠BAE=2∠CAD.。
八年级数学全等三角形“半角”模型

八年级数学全等三角形“半角”模型一、什么叫半角模型定义:我们习惯把过等腰三角形顶角的顶点引两条射线,使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。
1、常见的图形正方形,正三角形,等腰直角三角形等。
2、解题思路① 将半角两边的三角形通过旋转到一边合并形成新的三角形;② 证明与半角形成的三角形全等;③ 通过全等的性质得出线段之间的数量关系,从而解决问题。
二、基本模型1、正方形内含半角例题1、如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°,求证:EF=BE+DF。
例题1图证明:将△ADF 绕点 A 顺时针旋转90° ,使点 D 与点 B ,点 F 与点 G 重合(△ADF ≌ △ABG),如下图所示:例题1旋转图在△AGE 和△AFE 中∵ AG = AF , ∠GAE = ∠EAF = 45° , AE = AE∴ △AGE ≌ △AFE ∴ GE = EF∵ GE = GB + BE = DF + BE∴ EF= BE + DF2、等边三角形内含半角例题2、如图,已知△ABC 是等边三角形,点 D 是△ABC 外一点,DB = DC 且∠BDC = 120° ,∠EDF = 60° ,DE ,DF 分别交 AB ,AC 于点 E , F 。
求证: EF = BE + CF例题2图证明:将△BDE 绕点 D 旋转至△CDG ,使△BDE ≌ △CDG(注:题目中已知条件 DB = DC 且∠BDC = 120°,易证∠EBD = ∠GCD = 90°,F、C、G 三点共线)例题2旋转图在△EDF 和△GDF 中∵ ED = GD , ∠EDF = ∠GDF = 60° , DF = DF∴ △EDF ≌ △GDF ∴ EF = GF∵ GF = GC + CF = BE + CF∴ EF = BE + CF3、等腰直角三角形内含半角例题3、如图,已知△ABC 是等腰直角三角形,点 D ,E 在 BC 上,且满足∠DAE = 45° 。
半角模型(初中数学最全半角模型专题)

变式练习
变式4.在平面直角坐标系中,已知A(x,y),点A作AB⊥y
轴,垂足为B.若在x轴正半轴上取一点M,连接BM并延长至
N,以BN为直角边作等腰Rt△BNE,∠BNE=90°,过点A作
AF∥y轴交BE于点F,连接MF,设OM=a,MF=b,AF=c,试
1 1
证明: + =
.
例2.如图所示,过正方形ABCD的顶点A在正方形ABCD的内
几何模型一:半角模型
类型一、正方形中夹半角模型(45°)
例1.如图,已知正方形ABCD中,E、F分别是BC、CD上
的点,且∠EAF=45°
求证:EF=BE+DF;
变式练习
变式1.如图,已知正方形ABCD的边长为6,E,F分别是AB、
BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋
转90°,得到△DCM.
∠BAD.证明:EF=BE﹣FD
变式练习
变式3.已知,如图,在四边形ABCD中,∠B+∠D=180°,
AB=AD,E,F分别是线段BC,CD上的点,且BE+FD=EF.求
证:2∠EAF=∠BAD.
变式练习
变式4.已知△ABC中,AB=AC,∠BAC=120°.点M在BC上,
点N在BC的上方,且∠MBN=∠MAN=60°,
求证:MC=BN+MN;
则MN的长为
.
变式练习
变式2.如图,在△ABC中,AB=AC,点E,F是边BC所在直线
上与点B,C不重合的两点.∠BAC=90°,∠EAF=135°,
证明:EF2=EC2+BF2
类型三、其他半角模型
例4.在等边△ABC的两边AB,AC上分别有两点M,N,点D为
八年级数学——半角模型

例:如图E、F分别在正方形ABCD的边BC、CD上,且∠EAF=45°。
求证:EF=BE+DF;解析:延长CB到G,使GB=DF,连接AG,证△ABG≌△ADF,得∠3=∠2,AG=AF,进而求证△AGE≌△AFE,可得GB+BE=EF,所以DF+BE=EF特征描述:过等腰△ABC(AB=AC)顶角顶点(设顶角为A),引两条射线且它们的夹角为A/2;这两条射线与过底角顶点的相关直线交于两点M、N,则BM,MN,NC之间必存在固定关系。
这种关系仅与两条相关直线及顶角A相关.题型识别:“等线段、共顶点、半角度”解决方法:①以公共顶点为中心,旋转三角形,使得相等的两线段重合;②找出两组全等三角形,得到对应的边角相等关系。
如图,在正方形ABCD的边BC,CD上分别有点E,F,∠EAF=45°,AH⊥EF.求证:AH=AB;分析:将△ADF 绕点A 顺时针旋转90°得到△ABG ,根据旋转的性质可得DF =BG ,AF =AG ,∠DAF =∠BAG ,然后求出∠EAF =∠EAG =45°,再利用“边角边”证明△AEF 和△AEG 全等,根据全等三角形对应边上的高相等可得AH =AB .证明:将△ADF 绕点A 顺时针旋转90°得到△ABG ,由旋转的性质得,DF =BG ,AF =AG ,∠DAF =∠BAG .∵∠F AG =∠BAG +∠BAF =∠DAF +∠BAF =∠BAD =90°,∠EAF =45°,∴∠EAF =∠EAG =45°.在△AEF 和△AEG 中,AF AG EAF EAG AE AE =⎧⎪∠=⎨⎪=⎩∴△AEF ≌△AEG (SAS ),∵AH 、AB 分别是△AEF 和△AEG 对应边上的高,∴AH =AB .(1)如图1,在正方形ABCD 中,E 、F 分别是BC 、CD 上的点,且∠EAF =45°,试判断BE 、DF 与EF 三条线段之间的数量关系,直接写出判断结果:___________.(2)如图2:在四边形ABCD 中,AB =AD ,∠BAD =120°,∠B =∠ADC =90°.点E 、F 分别是BC 、CD 上的点,且∠EAF =60°,探究图中线段BE 、EF 、FD 之间的数量关系.小王同学探究此问题的方法是,延长FD 到点C ,使DG =BE ,连结AG ,先证明△ABE ≌△ADG ,再证明△AEF ≌△AGF ,可得出结论,他的结论应是___________.请你帮小王同学写出完整的证明过程.(1)如图1,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,试判断BE、DF与EF三条线段之间的数量关系,直接写出判断结果:___________;(2)如图2,若把(1)问中的条件变为“在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且12EAF BAD∠=∠”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;(3)在(2)问中,若将△AEF绕点A逆时针旋转,当点分别E、F运动到BC、CD延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明.已知:如图,Rt△ABC中,∠ACB=90°,AC=BC,将直角三角板中45°角的顶点放在点C处,并将三角板绕点C旋转,三角板的两边分别交AB边于D、E两点(点D在点E的左侧,并且菁优网点D不与点A重合,点E不与点B重合),设AD=m,DE=x,BE=n.(1)判断以m、x、n为三边长组成的三角形的形状,并说明理由;(2)当三角板旋转时,找出AD、DE、BE三条线段中始终最长的线段,并说明理由.倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径.下面是一案例,请同学们认真阅读、研究,完成“类比猜想”的问题.(1)如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.完成解题过程.解:把△ABE绕点A逆时针旋转90°至△ADE′,点F、D、E′在一条直线上.(2)类比猜想请,同学们研究:如图(2),在菱形ABCD 中,点E 、F 分别在BC 、CD 上,当∠BAD =120°,∠EAF =60°时,还有EF =BE +DF 吗?请说明理由.如图,在等腰直角△ABC 的斜边AB 上任取两点M 、N ,使∠MCN =45°,记AM =m ,MN =n ,BN =k .试猜想:以m 、n 、k 为边长的三角形的形状是(在下列括号中选择)__________.(锐角三角形;钝角三角形;直角三角形;等腰三角形;等腰直角三角形;等边三角形)已知:如图1在Rt △ABC 中,∠BAC =90°,AB =AC ,点D 、E 分别为线段BC 上两动点,若∠DAE =45度.探究线段BD 、DE 、EC 三条线段之间的数量关系.小明的思路是:把△AEC 绕点A 顺时针旋转90°,得到△ABE ′,连接E ′D ,使问题得到解决.请你参考小明的思路探究并解决下列问题:(1)猜想BD 、DE 、EC 三条线段之间存在的数量关系式,并对你的猜想给予证明;(2)当动点E 在线段BC 上,动点D 运动在线段CB 延长线上时,如图2,其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明.问题1:如图1,在等腰梯形ABCD 中,AD ∥BC ,AB =BC =CD ,点M ,N 分别在AD ,CD 上,若12MBN ABC ∠=∠,试探究线段MN ,AM ,CN 有怎样的数量关系?请直接写出你的猜想,不用证明;问题2:如图2,在四边形ABCD 中,AB =BC ,∠ABC +∠ADC =180°,点M ,N 分别在DA ,CD 的延长线上,若12MBN ABC ∠=∠仍然成立,请你进一步探究线段MN ,AM ,CN 又有怎样的数量关系?写出你的猜想,并给予证明.。
初中数学几何模型:半角模型
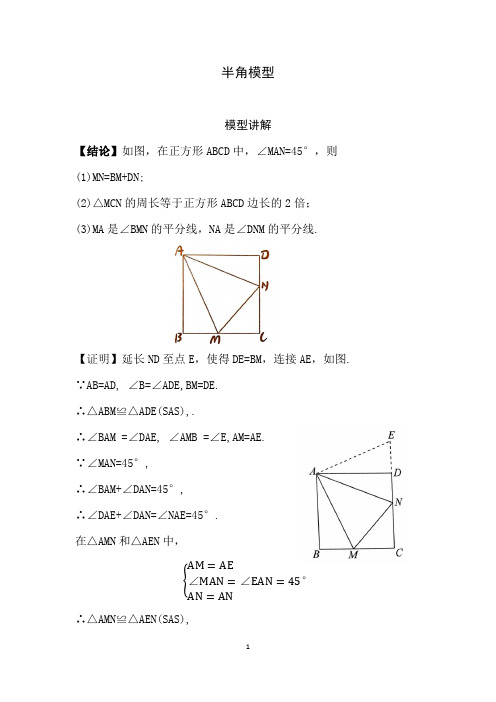
半角模型模型讲解【结论】如图,在正方形ABCD 中,∠MAN=45°,则(1)MN=BM+DN;(2)△MCN 的周长等于正方形ABCD 边长的2倍;(3)MA 是∠BMN 的平分线,NA 是∠DNM 的平分线.【证明】延长ND 至点E ,使得DE=BM ,连接AE ,如图. ∵AB=AD, ∠B=∠ADE,BM=DE.∴△ABM ≌△ADE(SAS),.∴∠BAM =∠DAE, ∠AMB =∠E,AM=AE.∵∠MAN=45°,∴∠BAM+∠DAN=45°,∴∠DAE+∠DAN=∠NAE=45°.在△AMN 和△AEN 中,{AM =AE∠MAN =∠EAN =45°AN =AN∴△AMN ≌△AEN(SAS),∴MN=EN=DE+DN=BM+DN.∠AMB=∠AMN=∠E,∠ANM=∠AND,即MA是∠BMN的平分线,NA是∠DNM的平分线.CM+CN+MN=CM+BM+ND+CN=BC+CD=2BC,即△MCN的周长等于正方形ABCD边长的2倍.拓展【结论1】(等腰三角形中的半角模型)如图,△ABC是边长为a的等边三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则(1)MN=BM+CN;(2)△MAN的周长等于△ABC边长的2倍;(3)MD是∠BMN的平分线,ND是∠CNM的平分线.【证明】:∵△BDC是等腰三角形,且∠BDC=120°,∴∠BCD=∠DBC=30°.∵△ABC是边长为a的等边三角形,∴∠ABC=∠BAC=∠BCA=60°,∴∠DBA=∠DCA=90°.延长AB至点F,使BF=CN,连接DF,如图. 在△BDF和△CDN中,{DB=DC ∠DBF=DCN BF=CN∴△BDF≌△CDN(SAS),∴∠BDF=∠CDN,∠F=∠CND,DF=DN. ∵∠MDN=60°,∴∠BDM+∠CDN=60°,∴∠BDM+∠BDF=60°,即∠FDM=60°=∠MDN.在△DMN和△DMF中,{DN=DF∠MDN=∠MDF DM=DM∴△DMN≌△DMF(SAS),∴MN=MF=BM+CN,∠F=∠MND=∠CND,∠FMD=∠DMN,∴△AMN的周长是AM+AN+MN=AM+MB+CN+AN=AB+AC=2a.【结论2】(对角互补且一组邻边相等的半角模型)如图所示,在四边形ABCD中,∠B+∠D=180°,∠BAD=2∠EAF,AB=AD,则(1)EF=BE+FD;(2)EA是∠BEF的平分线,FA是∠DFE的平分线.典型例题典例1如图,已知正方形ABCD中,∠MAN=45°,则线段MN,BM与DN之间的关系是( ).A.MN=BM+DNB.BM=MN+DNC.DN=MN+BMD.无法确定典例2如图,△ABC是边长为a的等边三角形,△BDC是等腰三角形,且∠BDC=120°,以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长是( ).A.aB.2aC.3aD.不能确定典例3(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,求证:EF=BE+FD.(2)在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF= ∠BAD,(1)中的结论是否仍然成立?(不需要说明理由)(3)如图2,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E,F分别是边BC,CD延长线上的点,且∠EAF= ∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.初露锋芒1.如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为________.2.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°.若BE=4,CD=3,则AB的长为_________.3. 如图,正方形ABCD中,∠EAF=45°,连接对角线BD交AE于点M,交AF于点N.若DN=1,BM=2,那么MN=________.感受中考1.(2020山东济南中考模拟)如图,在正方形ABCD中,E,F分别是BC,CD上的点,且∠EAF=45°,AE,AF分别交BD于点M,N,连接EN,EF.有以下结论:=2 - √2;③BE+DF=EF;④存在点E,F,①AN=EN;②当AE=AF时,BEEC使得NF>DF.其中正确的个数是( ).A.1B.2C.3D.4参考答案典型例题典例1【答案】A【解析】:∵正方形ABCD中,∠MAN=45°,∴根据半角模型结论可知MN=BM+DN.故选A.典例2【答案】B【解析】:∵△BDC是等腰三角形,观察图形,能发现图形为等腰三角形的半角模型,根据半角模型结论可知,△AMN的周长为△ABC边长的2倍,即为2a.故选B.典例3【解析】(1)如图,延长EB到点G,使BG=DF,连接AG.∵∠ABG=∠ABC=∠D=90°,AB=AD,∴△ABG≌△ADF(SAS), ∴AG=AF. ∠1=∠2.∴∠1+∠3=∠2+∠3=∠EAF= 1∠BAD,2∴∠GAE=∠EAF.又 AE=AE. ∴△AEG≌△AEF(SAS),∴EG=EF.∵EG=BE+BG, ∴EF=BE+FD.(2)(1)中的结论EF=BE+FD仍然成立.(3)结论EF=BE+FD不再成立,应当是EF=BE-FD.证明:如图,在BE上截取BG,使BG=DF,连接AG.∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,∴∠B=∠ADF.又∵AB=AD, ∴△ABG≌△ADF(SAS),∴∠BAG=∠DAF,AG=AF.∠BAD.∴∠BAG +∠EAD=∠DAF+∠EAD=∠EAF= 12∴∠GAE=∠EAF.又∵AE=AE, ∴△AEG≌△AEF(SAS),∴EG=EF.∵EG=BE-BG. ∴EF=BE-FD.初露锋芒1.【答案】6.【解析】∵△BDC 是等腰三角形,且∠BDC=120°,∠MDN=60°,△ABC 是边长为3的等边三角形,∴根据等腰三角形的半角模型结论可知,△AMN 的周长是△ABC 边长的2倍,即为6.2. 【答案】6√2.【解析】如图,过点B 作BC 的垂线,垂足为B ,并截取BF=CD ,连接FE ,AF.∵∠FBE=90°,FB=3,BE=4,∴在Rt △FBE 中,FE 2=FB 2+BE 2=32+42=52,∴FE=5.∵Rt △ABC 中,AB=AC,∴∠ABC=∠ACB=45°,∴∠FBA=∠FBC-∠ABC=90°- 45°= 45°.在△AFB 与△ADC 中,{BF =CD∠ABF =∠ACD =45AB =AC∴△AFB ≌△ADC(SAS),∴∠2=∠3,AF=AD.又∵∠1+∠EAD+∠2=90°,∠DAE=45°,∴∠1+∠2=45°,∴∠FAE=∠1+∠3=45°,∴∠FAE=∠DAE.在△AFE 与△ADE 中,{AF =AD∠FAE =∠DAE AE =AE,∴△AFE ≌△ADE(SAS),∴FE=DE=5,∴BC=BE+ED+DC=4+5+3=12.又∵在Rt △ABC 中,AB=BC ·cos ∠ABC ,∴AB=12×cos 45°=12×√22 = 6√2.3. 【答案】√5.【解析】如图,延长CB 到点G ,使BG=DF ,连接AG ,在AG 上截取AH=AN ,连接MH,BH.∵四边形ABCD 为正方形,∴AB=BC=CD=AD,∠4=∠5=45°,∠BAD=∠ADF=∠ABE=∠ABG=90°.在△ABG 和△ADF 中,{AB =AD∠ABG =∠ADF =90BG =DF,∴△ABG ≌△ADF(SAS),∴∠1=∠2,∠7=∠G,AG=AF ,∴∠GAE=∠2+∠3=∠1+∠3=∠BAD-∠EAF=90°-45°=45°=∠EAF. 在△AMN 和△AMH 中,{AN =AH∠MAN =∠MAH =45°AM =AM∴△AMN ≌△AMH(SAS),∴MN=MH.∵AF=AG,AN=AH ,∴FN=AF-AN=AG-AH=GH.在△DFN 和△BGH 中,{DF =BG∠7=∠G FN =GH∴△DFN ≌△BGH(SAS),∴∠6=∠4=45°,DN=BH.∴∠MBH=90°-45°+45°=90°,∴BM+DN=BM+BH=MH=MN.又∵DN=1,BM=2,∴22+12=MN 2,∴MN=√5.感受中考1.【答案】 B【解析】①如图,∵四边形ABCD是正方形,∴∠EBM = ∠ADM =∠FDN =∠ABD=45°.∵∠MAN=∠EBM=45°,∠AMN=∠BME,∴△AMN∽BME,∴AMBM = MNEM.又∵∠AMB=∠EMN,∴△AMB∽△NME,∴∠AEN=∠ABD=45°.∴∠NAE=∠AEN=45°,∴△AEN是等腰直角三角形,∴AN=EN,故①正确.②∵∠ABE=∠ADF=90°,在Rt △ABE 和Rt △ADF 中,{AB =AD AE =AF∴Rt △ABE ≌Rt △ADF(HL),∴BE=DF.又∵BC=CD ,∴CE=CF.假设正方形ABCD 的边长为1,设CE=x则BE=1-x.如图,连接AC ,交EF 于点O.∵AE=AF,CE=CF ,∴AC 是EF 的垂直平分线,∴AC ⊥EF,OE=OF.在Rt △CEF 中,OC= 12 EF= √22x. 在△EAF 中,∠EAO=∠FAO=22.5°=∠BAE=22.5°, ∴OE=BE.又∵AE=AE ,∴Rt △ABE ≌RtAOE(HL),∴AO=AB=1.∴AC=√2=AO+OC, ∴1+√22x=√2,解得x=2 -√2.∴BEEC = √2)2−√2= (√2−1)(2+√2)2=√22,故②不正确.③∵正方形ABCD中,∠EAF=45°,∴根据半角模型结论可知EF=BE+DF,故③正确.④∵∠FND=∠ADN+∠NAD>45°.而∠FDN=45°,∴DF>FN.故不存在点E,F,使得NF>DF,故④不正确. 因此,正确结论的个数是2.故选B.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
半角模型(八上人教版)
知识导航
夹半角模型是初二全等几何另一个非常重要的模型,其证明过程值巧妙,图形变化之丰富,还能与很多知识点(如角平分线定理,勾股定理)相结合,是很多区、校大型考试压轴题中的常客。
其辅助线的思路有两种:一是截长补短,二是旋转。
学会截长补短可以解决基本问题,而理解旋转才能真正理解这种模型.
已知如图:
1. 1
2=
AOB 2
∠∠ 2. OA OB =。
连接FB ,将△FOB 绕点O 旋转至△FOA 的位置, 连接F ′E 、FE ,可得△OEF ′≌△OEF 。
模型分析
(1)半角模型的命名:存在两个角度是一半关系,并且这两个角共顶点; (2)通过先旋转全等再轴对称全等,一般结论是证明线段和差关系; 夹半角模型分类: (1)90度夹45度;(2)120度夹60度;(3)2α夹α.
题型一 90度夹45度
例1.如图,在四边形ABCD 中,∠BAD =∠B =∠C =∠D =90°,AB =BC =CD =AD ,E 在BC 上,F 在
CD 上,且∠EAF =45°,求证:(1)BE +DF =EF (
2)∠AEB =∠AEF .
例2. 如图,在正方形ABCD中,E、F分别是BC、CD边上的点,45
∠=︒.
EAF
(1)如图(1),试判断EF,BE,DF间的数量关系,并说明理由;
(2)如图(2),若AH EF
⊥于点H,试判断线段AH与AB的数量关系,并说明理由.
例3. 如图,正方形ABCD中,1
AB=,以线段BC、CD上两点P、Q和方形的点A为顶点作正方形的内接等边APQ
∆的边长.
∆,求APQ
例4.(1)如图①,在正方形ABCD中,E、F分别是BC、CD上的点且
45EAF ∠=︒.猜测线段EF 、BE 、FD 三者存在哪种数量关系?直接写出结论.(不用证
明)结论: .
(2)如图②,在四边形ABCD 中,AB AD =,90B D ∠=∠=︒,E 、F 分别是BC 、CD 上的点,且EAF ∠是BAD ∠的一半.(1)中猜测的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;
例5. 如图, 在四边形ABCD 中,AB AD =,90B D ∠=∠=︒,E 、F 分别是边
BC 、CD 上的点, 且1
2
EAF BAD ∠=∠. 求证:EF BE FD =+.
例6.(1)如图1,在正方形ABCD 中,E 、F 分别是边BC 、CD 上的点,且
45EAF ∠=︒,把ADF ∆绕着点A 顺时针旋转90︒得到ABG ∆,请直接写出图中所有的全等
三角形;
(2)在四边形ABCD中,AB AD
=,90
∠=∠=︒.
B D
①如图2,若E、F分别是边BC、CD上的点,且2EAF BAD
∠=∠,求证:
EF BE DF
=+;
②若E、F分别是边BC、CD延长线上的点,且2EAF BAD
∠=∠,①中的结论是否仍然成立?请说明理由.
例7. 已知在正方形ABCD中,45
∠绕点A顺时针旋转.
∠=︒,EAF
EAF
(1)当点E,F分别在边CB,DC上时(如图①),线段BE,DF和EF之间有怎样的数量关系?写出猜想,并加以证明.
(2)当EAF
∠绕点A旋转到如图②的位置时,线段BE,DF和EF之间又有怎样的数量关系?直接写出你的猜想.
例8. 已知如图1,四边形ABCD 是正方形,45EAF ∠=︒.
(1)如图1,若点E 、F 分别在边BC 、CD 上,延长线段CB 至G ,使得BG DF =,若
3BE =,2BG =,求EF 的长;(2)如图2,若点E 、F 分别在边CB 、DC 延长线上时,
求证:EF DF BE =−.
(3)如图3,如果四边形ABCD 不是正方形,但满足AB AD =,90BAD BCD ∠=∠=︒,
45EAF ∠=︒,且7,6DF EF ==,请你直接写出BE 的长.
例9. 如图,四边形ABCD是正方形,点E是边BC上的一点,90
∠=︒,且EF交正
AEF
方形外角的平分线CF于点F.
(1)如图1,当点E是BC的中点时,猜测AE与EF的关系,并说明理由.
(2)如图2,当点E是边BC上任意一点时,(1)中所猜测的AE与EF的关系还成立吗?请说明理由.
题型二120度夹60度
例1. 已知如图,△ABC为等边三角形,∠BDC=120°,DB=DC,M、N分别是AB、AC上的动点,且∠MDN=60°,求证:MB+CN=MN.
例2. 如图,D是等边三角形ABC外一点,且满足DB DC
∠=︒,M,N分
BDC
=,120
别是AB,AC上的点,且60
∠绕点D旋转时,MN,BM,CN的
∠=︒,当MDN
MDN
关系是否发生变化?请简述理由.
例3. 如图,等边ABC
MDN
∠=︒,其
∠=︒,现有60
∆的边长为2,且DB DC
BDC
=,120
两边分别与AB,AC交于点M,N,连接MN,将MDN
∠绕着D点旋转,使得M,N 始终在边AB和边AC上.试判断在这一过程中,AMN
∆的周长是否发生变化,若没有变化,请求出其周长;若发生变化,请说明理由.
例4. 如图①,ABC
∠=︒的等腰三角形,以D为
BDC
∆是顶角120
∆是等边三角形,BDC
顶点作60︒的角,它的两边分别与AB,AC交于点M和N,连结MN.
(1)探究:BM,MN,NC之间的关系,并加以证明;
(2)若点M,N分别在射线AB,CA上,其他条件不变,再探究线段BM,MN,NC 之间的关系,在图②中画出相应的图形,并就结论说明理由.
例5. 在等边三角形ABC的两边AB、AC所在直线上分别有两点M、N,D为三角形
∠=︒,BD DC
BDC
=,探究:当M、N分别在直线MDN
ABC外一点,且60
∠=︒,120
AB、AC上移动时,BM、NC、MN之间的数量关系.
(1)如图1,当点M、N在边AB、AC上,且DM DN
=时,BM、NC、MN之间的数量关系;
(2)如图2,点M、N在边AB、AC上,且当DM DN
≠时,猜想(1)问的结论还成立吗?写出你的猜想并加以证明.
例6. 如图,四边形ABCD中,∠A=∠BCD=90°,∠ADC=60°,AB=BC,E、F分别在AD、DC
延长线上,且∠EBF=60°,求证:AE=EF+CF.
例7. 在等边△ABC的两边AB、AC所在直线上分别有两点M、N.D为△ABC外一点,且
∠MDN=60°,∠BDC=120°,BD=DC.探究:当M、N分别在直线AB、AC上移动时,BM、NC、MN之间的数量关系以及△AMN的周长Q与等边△ABC的周长L的关系.
(1)当点M、N在边AB、AC上,且DM=DN时,BM、NC、MN之间的数量关系是
(2)当点M、N在边AB、AC上,且当DM≠DN时,猜想(1)问的两个接刘海成立吗?写出你的猜想并加以证明;
(3)当M、N分别在边AB、CA的延长线上时,若AN=2,则Q=__________(用含有L的式子表示)
题型三2α夹α
例1.(1)如图(1),点E 、F 分别在正方形ABCD 的边BC 、CD 上,45EAF ∠=︒,连接EF ,则EF BE DF =+,说明理由.
(2)在四边形ABCD 中,点E 、F 分别在BC 、CD 上,当AB AD =,180B D ∠+∠=,1
2
EAF BAD ∠=∠时,EF BE DF =+成立吗?请直接写出结论.
例2. 如图,在四边形ABDC 中,M 、N 分别为AB 、AC 上的点,若∠BAC +∠BDC =180°,
例3. 如图,若四边形ABCD 中,AB AD =,180B D ∠+∠=︒,E ,F 分别是BC ,CD 上
的点,且3BE =,4DF =,12
EAF BAD ∠=∠,求EF 的长度.
例4.(1)如图1,在四边形ABCD 中,AB AD =,90B D ∠=∠=︒,E 、F 分别是边BC 、CD 上的点,若EF BE FD =+. 求证:12
EAF BAD ∠=∠ (2)如图2,在四边形ABCD 中,AB AD =,180B ADC ∠+∠=︒,E 、F 分别是边BC 、CD 延长线上的点,且12
EAF BAD ∠=∠,试探究线段EF 、BE 、FD 之间的数量关系,证明你的结论.
例5. 问题背景:
(1)如图①:在四边形ABCD 中,AB AD =,120BAD ∠=︒,90B ADC ∠=∠=︒,E ,
F分别是BC,CD上的点,且60
EAF
∠=︒.探究图中线段BE,FE,FD之间的数量关系,请在右面横线上直接写出结论.
(2)如图②,若在四边形ABCD中,AB AD
=,180
B ADC
∠+∠=︒.E、F分别是
BC、CD上的点,且
1
2
EAF BAD
∠=∠,上述结论是否仍然成立?说明理由.。
